CBF/CMRO₂ Coupling Measured with Calibrated-BOLD fMRI: Sources of Bias

Abstract

The coupling between cerebral blood flow (CBF) and cerebral metabolic rate of oxygen (CMRO₂) during brain activation can be characterized by an empirical index n, the ratio of fractional CBF changes to fractional CMRO₂ changes. Measurements of n have yielded varying results, and it is not known if the observed variability is due to measurement techniques or underlying physiology. The calibrated BOLD approach using hypercapnia offers a promising tool for assessing changes in CBF/CMRO₂ coupling in health and disease, but potential systematic errors have not yet been characterized. The goal of this study was to experimentally evaluate the magnitude of bias in the estimate of n that arises from the way in which a region of interest (ROI) is chosen for averaging data, and to relate this potential bias to a more general theoretical consideration of the sources of systematic errors in the calibrated BOLD experiment. Results were compared for different approaches for defining an ROI within the visual cortex based on: 1) retinotopically-defined V1; 2) a functional CBF localizer; and 3) a functional BOLD localizer. Data in V1 yielded a significantly lower estimate of n (2.45) compared to either CBF (n = 3.45) or BOLD (n = 3.18) localizers. Different statistical thresholds produced biases in estimates of n with values ranging from 3.01 (low threshold) to 4.37 (high threshold). Possible sources of the observed biases are discussed. These results underscore the importance of a critical evaluation of the methodology, and the adoption of consistent standards for applying the calibrated BOLD approach to the evaluation of CBF/CMRO₂ coupling.

Introduction

Blood oxygenation level dependent (BOLD) functional magnetic resonance imaging (fMRI) has been used extensively to map brain activation in response to functional tasks. The physiological basis of these methods is that the fractional increase in cerebral blood flow (CBF) is much greater than the fractional increase in the cerebral metabolic rate of oxygen (CMRO₂) following an increase in neural activity. The resulting increased local oxygenation of the blood creates a slight increase in the measured T2*-weighted magnetic resonance signal. This phenomenon provides a sensitive mapping tool for identifying where activation occurs, but a quantitative interpretation of the magnitude of the BOLD signal, to address questions related to the degree of change with activation, is more problematic. The magnitude of the BOLD-response depends on the interplay between the relative changes in CBF, CMRO₂, and the cerebral blood volume (CBV). Any variability of the coupling of these physiological quantities across brain regions, during development and aging, or in disease could lead to significant variability of the BOLD response despite similar underlying changes in metabolism. The key relationship determining the BOLD response is the relative change in CBF compared with CMRO₂ following activation, which we can characterize by an index n defined as the fractional change in CBF divided by the fractional change in CMRO₂ (e.g., a 30% change in CBF associated with a 10% change in CMRO₂ is an n value of 3). Differences in n for the same change in CMRO₂ translate into large differences in the magnitude of the BOLD signal. For example, the BOLD signal differs by about 100% for n=2 and n=3 for the same underlying change in CMRO₂ (estimated from standard models described below). For this reason, understanding the physiological variability of n is critical for any quantitative interpretation of the BOLD signal.

Studies using positron emission tomography (PET) to measure CBF and CMRO₂ in human subjects have reported a wide range of estimates of n. Early studies (Fox and Raichle 1986; Fox et al. 1988; Kuwabara et al. 1992) found significant increases in CBF with little or no CMRO₂ increases with activation, and this phenomenon was initially termed “uncoupling”. However, more recent PET studies (Marrett and Gjedde 1997; Roland et al. 1987; Seitz and Roland 1992; Vafaee et al. 1998; Vafaee and Gjedde 2004) have found more substantial CMRO₂ changes with estimates of n in the range of 0.9-2.4.

Davis and co-workers (Davis et al. 1998) introduced an approach for calibrating the BOLD signal that makes possible an MRI methodology for measuring CMRO₂ changes from combined measurements of the BOLD response and the CBF response. The CBF response is measured with an arterial spin labeling (ASL) technique (Detre et al. 1992; Wong et al. 1998; Wong et al. 1997b) and the essential idea is to exploit the fact that the ASL signal depends just on CBF changes, while the BOLD signal depends on CBF and CMRO₂ changes. The key innovation of the Davis et al study was to compare CBF and BOLD responses to activation with the same two responses to breathing a gas mixture with an elevated concentration of CO₂. The latter hypercapnia experiment is thought to produce a large change in CBF with an insignificant change in CMRO₂ (Jones et al. 2005). By analyzing this data within the context of a mathematical model for the BOLD signal, one can estimate the change in CMRO₂ in the activation experiment and thus estimate n. This calibrated-BOLD approach provides a potentially powerful tool for quantitative assessment of the physiological changes following neural activation. In addition to resolving the ambiguities of the BOLD signal noted above, this approach could provide the basis for advancing fMRI from a mapping tool to a quantitative physiological probe for the early assessment of dysfunction in disease.

Several groups have adopted this approach and reported values of n in the range of 2-4;(Davis et al. 1998; Fujita et al. 2006; Hoge et al. 1999b; Kastrup et al. 2002; Kim et al. 1999; St Lawrence et al. 2003; Stefanovic et al. 2005; Stefanovic et al. 2004; Uludag and Buxton 2004). Other studies have used the framework of the calibrated BOLD approach to argue that CBF and CMRO₂ are coupled in a similar way in deactivations and activations (Shmuel et al. 2002; Stefanovic et al. 2005; Stefanovic et al. 2004; Uludag et al. 2004). As this approach matures, it is important to critically assess the methodology to establish whether reported differences in n are due to physiological differences, population variability, or intrinsic biases in the methods used. For example, the nature of tagging is different between pulsed quantitative and non-quantitative ASL techniques, creating the possibility of systematic errors in the CBF measurements (Wong et al. 1997).

Because of the intrinsic noise in the data, voxel-by-voxel assessments of n are often not practical, and because of the nonlinear way in which n affects the signal, the effect of noise on the resulting distribution of estimates of n would need to be interpreted with caution. Instead, a relatively straight-forward approach to reduce the effects of noise is to choose a region of interest (ROI) and average the data over the ROI before calculating n. However, this raises an important question: to what degree does the method of defining an ROI bias the resulting estimate of n? This study explores voxel selection as a potential source of variability. For fMRI studies based on combined measurements of BOLD and perfusion (Buxton et al. 1998), the ability to select voxels based on different types of contrast (perfusion change, BOLD change or a combination) is possible. For studies in the visual cortex, retinotopic mapping of early visual areas (Engel et al. 1994; Sereno et al. 1995) is available as an additional method of defining an ROI. Additionally, various statistical criteria, such as the threshold used for including voxels in the ROI, may also introduce a bias in the estimates. The intrinsic differences in SNR between BOLD and ASL data makes the definition of selection criteria for defining activated regions somewhat difficult. In this study two major categories of voxel selection criteria were compared: 1) ROIs based on differences in functional contrast (retinotopy, perfusion, BOLD) while keeping the activation-defining statistical threshold constant across the ROIs. 2) ROIs based on graded increases of the statistical threshold used to define an area of activation. The variability of the estimate of n with the ROI selection method is then discussed within a more general framework for considering the sources of systematic errors in the calibrated BOLD experiment.

Methods

Eleven healthy subjects (6 male, 5 female, age range 24-39 year) were recruited and scanned in a 3 Tesla MR imaging system according to the guidelines set by the University of California San Diego (UCSD) Institutional Review Board (IRB). All subjects underwent a preliminary scan session on a different day in which retinotopic mapping was performed. Each calibrated-BOLD imaging session lasted approximately 50 minutes and consisted of a functional localizer run to define functionally active regions in the visual cortex, three activation runs from which response data was measured, two hypercapnia runs and a high-resolution anatomical scan.

Experimental Task

The first portion of the experiment was dedicated to functional activation and consisted of four imaging runs. The first of these runs was used exclusively to construct a functional localizer (a map of activated voxels) and the remaining runs were averaged to measure BOLD and CBF responses in the defined region of interest (ROI) within the visual cortex. For all functional runs, a block design paradigm was used with subjects viewing a black and white radial checkerboard flickering at 8 cycles of dark and light per second for 4 blocks (20 s on, 60 s off, 40 s initial “off” period). During the off period, subjects viewed a gray screen with a white fixation square in the middle. To reduce differences in activated cortical regions between experiments, visual stimuli used for both retinotopic mapping and calibrated-BOLD studies spanned identical visual fields (horizontally, 25°; vertically, 20°) and consisted of identical contrast and flickering frequency.

For the second portion of the experiment, subjects breathed a hypercapnic air mixture (5% CO₂, 21% O₂, 74% N₂) through a non-rebreathing face mask (Hans Rudolph 2700 Series, St. Louis, MI) for two runs separated by 4 minutes. Each run consisted of 1 minutes of breathing air, 2 minutes of breathing CO₂, and 3 minutes of breathing air, without performing any task. Physiological measures were recorded throughout all experiments using a PC located in the MR console room. Respiratory motions were measured with a bellows around the lower portion of the thorax, pulse waveforms were measured with a fingertip pulse oximeter, and end tidal CO₂ levels were measured via a sampling port located inside a mixing chamber near a face mask worn by subjects.

Image Acquisition

Imaging data were acquired on a 3 Tesla whole body system (3-T GE Excite, Milwaukee, WI) with an eight-channel receive head coil. For the first functional localizer activation run, data were collected with a PICORE (Wong et al. 1997a) arterial spin labeling (ASL) sequence (TR 2.0 s, 180 repetitions, TI 1400 ms, 20-cm tag width, and a 1-cm tag-slice gap) with a dual-echo gradient echo (GRE) readout and spiral acquisition of k-space (TE₁ 9.4 ms, TE₂ 30ms, flip angle 90°, FOV 24 cm, matrix 64 × 64). This type of image acquisition allowed for simultaneous acquisition of perfusion and BOLD data. Four 7-mm-thick slices centered around the calcarine sulcus were acquired in a linear fashion from bottom to top. Data from this imaging run was used to construct a region of activation and was not otherwise used in determining functional response curves. For the remainder of the experiment quantitative ASL images were acquired with a PICORE QUIPSS II (Wong et al. 1998) sequence (TR 2.0 s, 180 repetitions, TI₁ 700ms, TI₂ 1400ms, tag thickness 20cm, 1-cm gap between the tagging band and the proximal edge of the imaging band) with the same in-plane GRE parameters as the PICORE localizer run. Small bipolar crusher gradients were applied to both PICORE and QUIPSS II runs to remove signal from large vessels (b=2 s/mm²) supplying blood to more distal slices. That is, the weak added gradient pulses were designed to improve the accuracy of the blood flow measurements by destroying the signal in the larger arteries delivering tagged blood to more distal slices. This effectively lengthens the transit delay, because tagged spins do not become visible in the imaged slice until they have moved farther down the vascular tree, so it is important to use a sufficiently long TI to insure delivery of the full tagged bolus (Buxton et al. 1998a). The PICORE method is more sensitive than PICORE QUIPSS II for detecting CBF activation, but is less accurate for quantifying the CBF change. For this reason the PICORE method was used as a functional localizer only, while all of the reported changes are based on the QUIPSS II data. At the end of the experiment, a high-resolution structural scan was acquired with a magnetization-prepared 3D fast spoiled grass (FSPGR) sequence (TI 450 ms, TR 7.9 ms, TE 3.1 ms, flip angle 12°, FOV 25 × 25 × 16 cm, matrix 256 × 256 × 124).

Retinotopic Mapping

In a preliminary scan session on a different day, subjects were presented with standard visual stimuli for retinotopic mapping (Engel et al. 1997; Press et al. 2001). During presentation of visual stimuli, images were acquired with an EPI sequence with the following parameters: TR = 2 s, TE = 30 ms, flip angle 90° FOV 19cm, matrix 64 × 64, 3-mm isotropic resolution, 20 interleaved slices. The entire set of stimuli (meridian, ring and wedge) yielded a single representation of V1. A high-resolution whole brain structural scan (3D FSPGR with 1-mm isotropic resolution) was acquired for each subject. The segmented cortical gray matter of occipital cortices was flattened using surface rendering methods described in (Wandell et al. 2000). Linear trends were removed from the datasets. Activation was assessed by correlating detrended data with the first harmonic of the stimulus variation frequency (Press et al. 2001). Representations of the primary visual area V1 of each subject were delineated on the computationally flattened visual cortex to define the retinotopic ROI for each subject. A combination of in-house Matlab (www.mathworks.com) code and the mrLoadRet-1.0 (http://white.stanford.edu/software/) software package was used for retinotopic mapping.

Calculation of M and CMRO₂

For CMRO₂ calculations, the model and methods described by Davis et al.,(1998) were used. In this model, the fractional BOLD signal change (ΔS/S₀) is related to the underlying changes in CBF and CMRO₂ by

$$\frac{\mathrm{\Delta }S}{S_0}=M\left[1-{\left(\frac{\mathit{CBF}}{{\mathit{CBF}}_0}\right)}^{\alpha -\beta }{\left(\frac{{\mathit{CMRO}}_2}{{\mathit{CMRO}}_{20}}\right)}^{\beta }\right]$$ [1]

The parameter M is the proportionality constant that reflects baseline deoxyhemoglobin content and defines the maximum possible BOLD signal change for that region. In the context of the model this parameter is proportional to the baseline blood volume fraction and O₂ extraction fraction. The parameter α is the exponent in an assumed power law relationship between cerebral blood flow and cerebral blood volume, and is taken to be α = 0.38 (Grubb et al. 1974; Mandeville et al. 1998). The parameter β was introduced as an empirical description of the signal changes found in Monte Carlo simulation studies of spins diffusing near magnetized cylinders, a model for the vascular system (Boxerman et al. 1995b). In our studies the value is taken to be β = 1.5 (Boxerman et al. 1995a; Davis et al. 1998). The parameters α and β are assumed to be global properties with the same values in each subject, and all calculations are based on assumed values.

The parameter M is a local parameter estimated from the hypercapnia experiment using Equation [1] with the assumption that mild hypercapnia does not alter CMRO₂. Specifically, the ratio CMRO₂/CMRO_2o is assumed to equal one, and the measured changes in CBF and BOLD with hypercapnia within a specified region of interest (ROI) are combined with Equation [1] to calculate M. The derived value of M for each ROI was then applied to the activation data to calculate the stimulus-evoked change in O₂ metabolic rate CMRO₂/CMRO_2o. In addition to this primary use of the hypercapnia experiment to calibrate the BOLD effect, this data also provides a direct measure of the local vascular responsiveness, measured as the percent change in CBF divided by the change in end-tidal CO₂ (mm Hg), which we define as the CBF Response to CO₂ (CRC).

Eq. [1] represents the central model used in the calibrated BOLD approach. At first glance, it may appear to be too simplistic, because the original simulations that led to the parameter β did not include the role of intravascular signal changes in contributing to the BOLD signal (the Monte Carlo simulations were for diffusing spins outside magnetized cylinders). In fact, however, at lower magnetic field strengths (including 3T) the intravascular and extravascular contributions to the net signal changes are expected to be comparable (Boxerman et al. 1995a). While the extravascular signal changes primarily depend on changes in the total deoxyhemoglobin, the intravascular signal changes primarily depend on changes in the deoxyhemoglobin concentration within blood. In addition, intravascular volume changes also affect the signal when the intrinsic intra- and extravascular signals are different. However, when curves of BOLD response vs. CBF are calculated with a more complete model that includes these other effects (Obata et al. 2004), Eq. [1] still provides a close approximation (Buxton et al. 2004). That is, despite the apparently oversimplified assumptions that led to Eq. [1], it nevertheless captures the basic behavior expected for a BOLD response that includes both an extravascular and an intravascular contribution to the BOLD effect. The key to this is that β>1. The practical effect of β>1 in Eq. [1] is that the BOLD signal change is not a pure linear function of local deoxyhemoglobin content (it would be if β=1) (Buxton et al. 2004).

Data Analysis

The flattened representation of the boundaries of V1 was rendered on a high-resolution anatomical volume. This volume was registered to the anatomical volume acquired in the ASL scan session using AFNI software with displacement and rotation parameters applied to the V1 representation to create a high resolution registered region of interest (ROI). This ROI was then undersampled to the resolution of the perfusion and BOLD images, including voxels that are at least 50% occupied by the high resolution V1 ROI, to define a V1 ROI on the spiral images of the activation run.

All images were coregistered using the AFNI software package (Cox 1996). The remainder of data processing was accomplished by using in-house Matlab code. The data from the first 8 seconds of each functional run was discarded to ensure steady-state conditions. Perfusion-weighted images were constructed by performing a running subtraction of consecutive control and tag images obtained from the first echo (Liu and Wong 2005). Similarly, BOLD-weighted images were constructed by performing a running average of consecutive control and tag images obtained from the second echo. Second order Fourier series expansions of phases corresponding to chest excursions and pulse waveforms were constructed and used as regressors for the removal of physiological noise from the BOLD and ASL time series using the modified RETROICOR approach for ASL (Restom et al. 2006). Voxel-wise perfusion (first echo) and BOLD (second echo) time series of the first functional localizer run were individually correlated with a function representing our block-design paradigm convolved with a gamma-variate impulse response (Friston et al. 1994) to create two 3D correlation coefficient (r) maps. Two ROIs were constructed from these maps to include voxels that exceeded a correlation coefficient of 0.5 from the perfusion data (PICORE - CBF localizer) and BOLD data (PICORE - BOLD localizer). This threshold corresponds to a Bonferroni-corrected p value of 3.18×10^-7. To evaluate effects of variations in statistical criteria applied, we created two additional ROIs from the PICORE CBF localizer, one with a relatively low threshold (r = 0.4) and one with a relatively high threshold (r = 0.6). This range of correlation coefficients previously was found to be reasonable for reproducibility studies (Rombouts et al. 1998).

Voxel-wise perfusion and BOLD data were averaged across functional activation PICORE QUIPSS II runs (runs 2,3,4) to improve signal-to-noise. In order to evaluate whether defining a region of activation from this data alone would bias our measurements, compared to the use of a separate functional localizer run, an additional ROI was drawn for flow activation from the averaged QUIPSS II data (QUIPSS II – CBF localizer) using the same statistical threshold as both the original PICORE localizers with r = 0.5. A description of ROIs created in this study is given in Table 1, along with the average number of voxels included in each ROI.

Table 1.

Methods for choosing a Region of Interest (ROI) for averaging

ROI	Description	Number of Voxels*
V1	Primary visual cortex, defined retinotopically in a separate scan session	59 ± 19
PICORE – BOLD (r = 0.5)	voxels exceeding r = 0.5 in BOLD activation from a separate PICORE run	174 ± 80
PICORE – CBF (r = 0.4)	voxels exceeding r = 0.4 in CBF activation from a separate PICORE run	174 ± 69
PICORE – CBF (r = 0.5)	voxels exceeding r = 0.5 in CBF activation from a separate PICORE run	93 ± 46
PICORE – CBF (r = 0.6)	voxels exceeding r = 0.6 in CBF activation from a separate PICORE run	53 ± 36
QUIPSS II – CBF (r = 0.5)	voxels exceeding r = 0.5 in CBF from the averaged QUIPSS II data itself	106 ± 108

^*Reported as the mean ± standard deviation across subjects

For functional activation runs, time courses of voxels were averaged over each ROI and were normalized to an average baseline signal calculated from the initial baseline period of each run and the final 10 seconds of each “off” period within each run and then averaged over 4 cycles of activation. In order to avoid periods of rapid dynamic change, the magnitude of the BOLD (%BOLD) and CBF (%CBF) plateau were computed as the average value over the final 12 seconds of the stimulus. Similarly, for the hypercapnia runs, the voxel-wise data (CBF and BOLD) were averaged over the six ROIs and normalized to the 60s baseline period preceding hypercapnia. The magnitudes of the BOLD (%BOLD_CO2) and CBF (%CBF_CO2) responses were calculated as the average of the final 60 seconds of the hypercapnic period. The CBF Response to CO₂ (CRC) was calculated as the fractional change in CBF divided by the change in end-tidal CO₂ in mmHg. The data from the CO₂ experiment was used to compute the maximal BOLD response, M, for each ROI using Equation 1.

Percent BOLD and CBF responses from the functional activation portion of the experiment were used along with the calculated value of M to compute percent CMRO₂ changes. CBF-CMRO₂ coupling was characterized as the ratio n of the fractional blood flow change (%CBF) to the fractional change in oxygen metabolism (%CMRO₂). In addition to this primary use of the hypercapnia experiment to calibrate the BOLD effect, this data also provides a direct measure of the local vascular responsiveness, measured as the percent change in CBF divided by the percent change in end-tidal CO₂ (% mm Hg), which we define with a single variable, n_CO2. Note that this index is directly related to the CRC defined above, but expressed in a dimensionless way so that n and n_CO2 are analogous dimensionless indices of the CBF/CMRO₂ and CBF/CO₂ relationships. Paired t-tests were performed, comparing values for each ROI with those for the PICORE-CBF (r=0.5) ROI, with p values significant if p<0.05 for %BOLD, %CBF, %CMRO₂, M, n and n_CO2.

Results

End-tidal CO₂ increased 9.3 ± 1.3 mmHg (mean ± SD) on average during inhalation of the CO₂ mixture, a fractional change of 22.6 ± 5.9%. A similar value has been obtained in another study (Kastrup et al. 2002) in healthy subjects using the same CO₂ concentration. Table 2 shows the average respiratory rate (RR) and heart rate (HR) before and during 5% CO₂ inhalation. These physiological markers serve as indicators of general subject comfort and the extent of any change in ventilation rate during the inhalation of CO₂, and for this subject group there were no significant changes.

Table 2.

Physiological measurements

RRarest	RRbHypercapnia	HRcrest	HRdHypercapnia	Δ mmHg
14.4 ± 3.8	13.3 ± 3.3	56.2 ± 4.7	58.9 ± 6.2	9.3 ± 1.3

^aresting respiratory rate (during normocopnia) measured in breaths/min

^brespiratory rate during periods of hypercapnia

^cresting heart rate (during normocapnia) measured in beats/min

^dheart rate during periods of hypercapnia

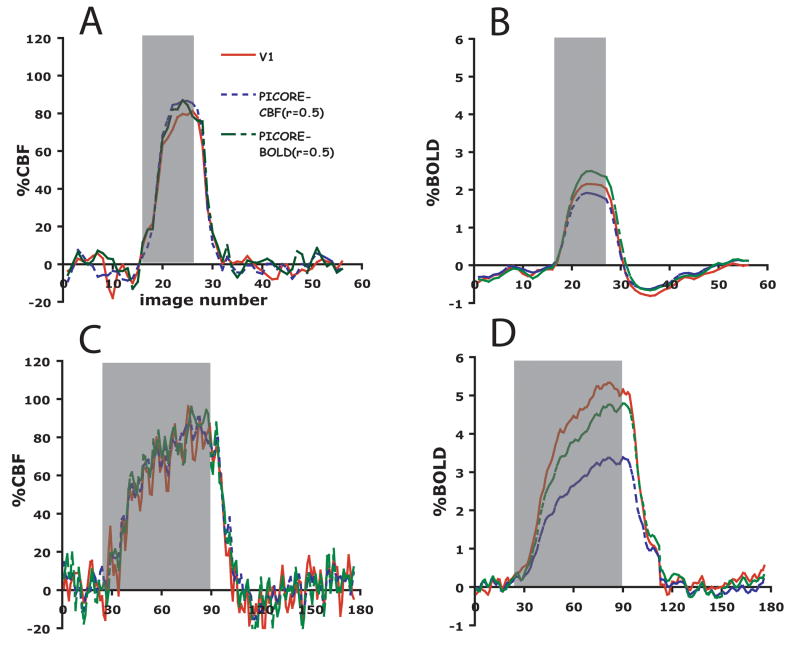
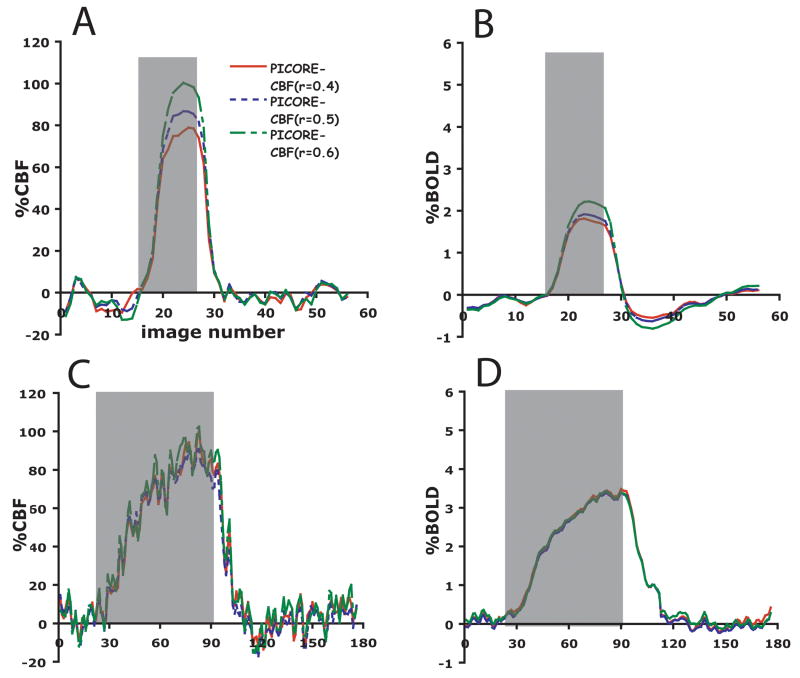
Figure 1 shows V1, BOLD and CBF ROIs for a single subject. Area V1 is overlayed onto a high resolution anatomical scan, and the CBF and BOLD ROIs are overlayed onto their respective average perfusion and average BOLD images from the PICORE run. This figure highlights differences in activation volume between the different ROIs with the PICORE BOLD ROI encompassing roughly twice as many voxels as the PICORE CBF ROI for the same level of significance (Table 1 defines the different ROI’s considered). A significant increase in CMRO₂ was seen in the visual cortex with functional activation for each ROI. Because mild hypercapnia is not expected to change CMRO₂ (Jones et al. 2005; Sicard and Duong 2005) the same CBF response will elicit a smaller BOLD response with functional activation than in response to hypercapnia. This is clearly seen in the average response curves for ROIs selected according to different types of functional contrast (Figure 2) and ROIs selected according to different levels of CBF activation (Figure 3), where roughly the same CBF response (~80%) was observed for all ROIs for both hypercapnia and functional activation and significantly larger BOLD responses were observed with hypercapnia.

Figure 1.

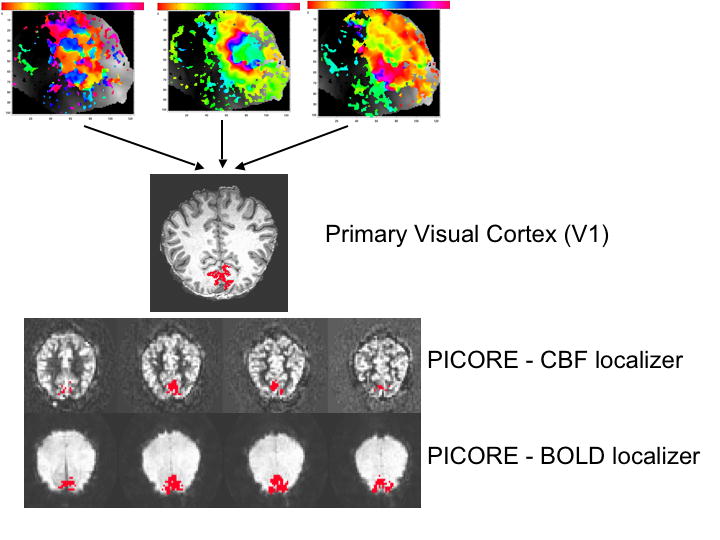
V1, BOLD and CBF ROIs for a single subject. For area V1, the subject’s retinotopic maps are shown for meridian, ring and wedge stimulus and a single slice projection of area V1 onto a high-resolution anatomical scan. The correlation coefficient threshold applied to the PICORE functional localizers was 0.5.

Figure 2.

Time courses of %BOLD and %CBF responses to functional activation (a and b) and 5% CO₂ (c and d) in three regions-of-interest encompassing area V1 (solid red line), voxels chosen by flow activation (fine-dashed blue line) and voxels chosen by BOLD activation (coarse-dashed green line) in a separate PICORE run (n=11).

Figure 3.

Time courses of %BOLD and %CBF to functional activation (a and b) and 5% CO₂ (c and d) in three regions-of-interest selected according to different thresholds of the correlation coefficient (0.4 (solid red line), 0.5 (fine-dashed blue line), and 0.6 (coarse-dashed green line)) for flow activation in the PICORE localizer (n=11).

Table 3 shows group averages (±SD) for %CBF and %BOLD responses to functional activation and hypercapnia for the 6 different ROIs. CRC is reported as percent blood flow change to CO₂ divided by the increase in end-tidal CO₂ (mmHg). Significant differences (p<0.05) from the results with the PICORE-CBF localizer (r=0.5) are reported with a single asterisk and p<0.01 is reported with a double asterisk. For the hypercapnia experiment, the CRC is similar for all ROI’s, while %BOLD responses are considerably more sensitive to the choice of ROI. Significant differences were observed for %BOLD_CO2 across the different methods for choosing ROIs, including both the type of functional contrast used (V1 vs BOLD vs CBF) and the threshold of the correlation coefficient used (r=0.4) with the PICORE-CBF localizer, although the p values with the V1 and PICORE BOLD ROI (p=0.003 and p=0.0009) were considerable lower than the PICORE CBF (r=0.4) ROI (p= 0.0431). Retinotopically-defined V1 had the largest %BOLD response to CO₂, possibly reflecting its proximity to the confluence of sinuses. For responses to functional activation, significant differences in %BOLD were observed across all ROIs with the exception of V1, while for %CBF differences were seen only across ROIs chosen according to different thresholds of CBF activation. This is not surprising given that a high statistical threshold for CBF activation is likely to preferentially include voxels with large %CBF responses.

Table 3.

Measured responses

	ACTIVATION		HYPERCAPNIA
ROI	% BOLD	% CBF	% BOLD	% CBF	CRCa
V1	2.09 ± 0.65	76.8 ± 21.0	5.25 ± 2.27**	80.5 ± 31.4	8.3 ± 2.1
PICORE - BOLD (c.c = 0.5)	2.32 ± 0.65*	74.5 ± 25.5	4.33 ± 1.17**	84.4 ± 31.8	8.5 ± 2.7
PICORE - CBF (c.c. = 0.4)	1.64 ± 0.26**	70.2 ± 19.8**	3.45 ± 1.04*	79.2 ± 26.8	8.4 ± 2.1
PICORE - CBF (c.c = 0.5)	1.84 ± 0.24	80.1 ± 26.1	3.12 ± 1.04	81.2 ± 28.1	8.7 ± 2.3
PICORE - CBF (c.c = 0.6)	2.13 ± 0.22**	89.6 ± 31.8*	3.09 ± 1.22	80.5 ± 29.8	8.8 ± 2.5
QUIPSS II - CBF (c.c = 0.5)	1.71 ± 0.24	85.1 ± 24.0	3.09 ± 0.98	85.2 ± 34.8	9.0 ± 2.7

All values reported as mean±standard deviation for 11 subjects.

^aCRC=Cerebral Response to CO₂ (the ratio of the fractional change in CBF to the change in end-tidal CO₂ in mmHg).

^*significant difference with the PICORE-CBF (r=0.5) data with p<0.05

^**significant difference with the PICORE-CBF (r=0.5) data with p<0.01

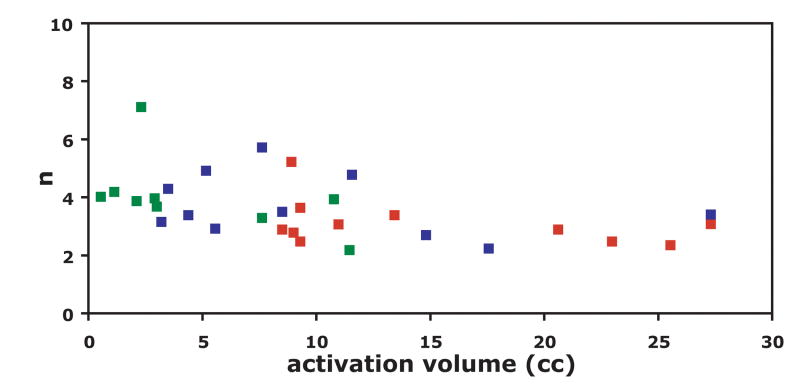
Table 4 shows the group average (mean ± SD) of computed values (M, %CMRO₂, n and n_CO2) across ROIs. Area V1 was found to have the largest %CMRO₂ measurement (30.9 ± 7.5) and the PICORE-CBF localizer (r=0.6) was found to have the lowest %CMRO₂ measurement (18.4 ± 9.9). Biases in measured M values are most obvious when comparing across ROIs generated with different types of functional contrast. Here, area V1 was found to have the largest M and the CBF localizer the smallest measured value. Variations in threshold level had a much milder effect on M. Differences in n were observed across all ROIs with the exception of the PICORE – BOLD and the QUIPSS II CBF localizer. The high threshold PICORE – CBF localizer yielded a substantially greater value for n (4.37 ± 2.14) compared to all other ROIs. In order to moderate the effect of outlier individual data points (two subjects had n>10 in the high threshold PICORE-CBF localizer) on averaged n values, 1/n was computed for each subject and the inverse of the subject-averaged 1/n value was calculated for each ROI (Stefanovic et al.,2004). In general, smaller activation volumes are associated with higher n values (Figure 4). This effect is more problematic for the high threshold localizer, which was as small as 19 voxels in one subject.

Table 4.

Calculated Responses

ROI	%CMRO2a	Mb	nc	nCO2d
V1	30.9 ± 7.5**	0.112 ± 0.042**	2.45 ± 0.42**	3.52 ± 0.99
PICORE – BOLD (c.c = 0.5)	22.3 ± 6.8	0.092 ± 0.03**	3.18 ± 0.89	3.79 ± 1.21
PICORE – CBF (c.c. = 0.4)	23.9 ± 7.8	0.072 ± 0.01	3.01 ± 0.59*	3.51 ± 0.87
PICORE – CBF (c.c = 0.5)	22.5 ± 7.9	0.067 ± 0.019	3.45 ± 0.94	3.61 ± 1.00
PICORE – CBF (c.c. = 0.6)	18.4 ± 9.9*	0.065 ± 0.024	4.37 ± 2.14*	3.57 ± 1.17
QUIPSS II – CBF (c.c = 0.5)	26.7 ± 9.0	0.064 ± 0.01	3.16 ± 0.81	3.74 ± 1.18

^aFractional change in CMRO₂ with activation computed as the average (±SD) of individual subject CMRO₂ changes

^bBOLD calibration factor estimated from the hypercapnia experiment. Reported as the average (±SD) of individual subject M calculations.

^cindex of CBF/CMRO₂ coupling, the ratio of %CBF to %CMRO₂. Reported as the inverse of the average individual subject 1/n values.

^dindex of CBF/CO₂ coupling, the ratio of %CBF to the fractional change in end-tidal

^*significant difference with the PICORE-CBF (r=0.5) data with p<0.05

^**significant difference with the PICORE-CBF (r=0.5) data with p<0.01

Figure 4.

The CBF/CMRO₂ coupling index n, defined as the ratio of the fractional change in CBF to the fractional change in CMRO₂, plotted as a function of activation volume at three levels of statistical significance (correlation coefficient threshold) used to construct ROIs based on PICORE flow activation. (red, r=0.4; blue, r=0.5; green, r=0.6). Two outlying data points for the high threshold localizer are not shown (n = 16, n = 20) in order to observe trends. It is clear that as the statistical threshold is increased, the dependence of n on activation volume becomes more significant.

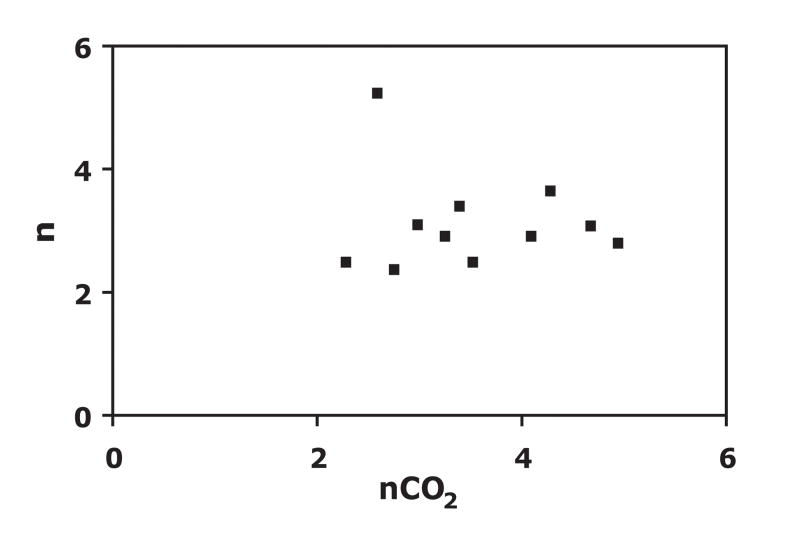
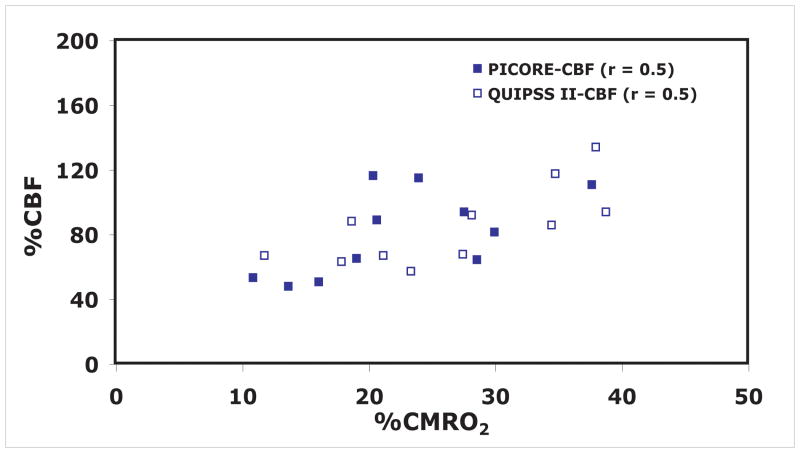
Differences in CBF-CMRO₂ coupling for different ROIs in the visual cortex are depicted for individual data points in Figure 5. In addition to observed differences in n, inter-subject variability of n is best for area V1 (SD=±0.4) and the low threshold PICORE–CBF localizer (SD=±0.6) and worst for the high threshold PICORE–CBF localizer (SD=±2.1). In order to examine whether the observed variability in n across subjects is attributable to differences in vascular responsiveness to CO₂ a plot of n vs n_CO2 was made (Figure 6). No significant trend was observed indicating that the observed variability in n is not attributable to variability in a non-neuronal component of activation-driven blood flow increases. Finally, we did not find any significant bias for any response metric associated with selecting an ROI from the averaged QUIPSS II data itself, rather than from a separate activation run (PICORE–CBF localizers) for the same level of statistical significance (r = 0.5) (Figure 7).

Figure 5.

Calculated fractional change in CMRO₂ as a function of the fractional change in CBF during functional activation, shown for different methods of choosing an ROI for averaging. A) Values calculated for ROI’s defined by retinotopy (red), flow localizer activation (blue), and BOLD localizer activation (green). B) Values calculated for three different statistical thresholds of the correlation coefficient (red, r=0.4; blue, r=0.5; green, r=0.6) applied to the flow localizer data.

Figure 6.

n as a function of percent CBF increase in response to CO₂ divided by percent increase in end-tidal CO₂ (nCO₂) for the PICORE – CBF localizer (r = 0.5) data. No trend in the data is observed suggesting that the observed variability in n is not attributable to differences in the cerebrovascular response to CO₂.

Figure 7.

Fractional changes in calculated CMRO₂ as a function of the fractional CBF change during functional activation to test for bias introduced by using the activation data itself to construct an ROI for averaging. The QUIPSS II data was analyzed with two ROI’s, one chosen from a separate localizer data set (solid squares), and one chosen from a correlation analysis of the QUIPSS II data itself (open squares), and the resulting slopes of the CBF/CMRO₂ curves (the coupling index n) are not significantly different.

Discussion

The calibrated BOLD approach provides a potentially powerful tool for investigating the coupling of blood flow and oxygen metabolism in different brain structures and in different disease states. However, because of signal to noise constraints, the calculations of CMRO₂ change are often best done using data averaged over an appropriate region of interest (ROI). This raises the important methodological question of how such an ROI should be chosen, and how severe a bias is introduced by using different methods. This study demonstrates that a great deal of variability in derived estimates of CBF-CMRO₂ coupling can be introduced by applying different criteria for voxel selection in constructing the ROI for averaging (Tables 3 and 4).

In these studies there was no “gold standard” for determining the true values of the physiological variables being measured. To assess the effects of using different methods of defining an ROI, we chose as a reference the method based on defining CBF activated voxels in a previous functional localizer with correlation coefficient greater than 0.5 (PICORE-CBF (r=0.5)). On theoretical grounds we expect that ROI selection based on CBF change will more accurately reflect brain parenchyma by avoiding voxels dominated by draining veins. For each of the other methods the measured and calculated parameters were compared with the reference data. This allowed us to explore differences due to both the choice of functional contrast and the level of significance employed in identifying an ROI. For functional contrast we compared three categories: functional anatomy defined through a retinotopy experiment, BOLD activity demonstrated in a previous functional localizer, and CBF activity demonstrated in a previous functional localizer. The effects of the level of significance were examined by applying three different thresholds to the CBF localizer data. Finally, we tested whether there was any additional bias introduced by choosing the ROI from the activation data to be analyzed, rather than the data from an initial functional localizer. The latter is a test of practical importance because for many studies looking for subtle effects it may not be feasible to design a functional localizer that can be done quickly. Because this data is discarded for the full analysis, this approach can severely cut into the available sensitivity of the experiment.

In these experiments there are four measured quantities, the CBF and BOLD responses to two challenges: a standardized neural activation experiment, and breathing 5% CO₂. From these four numbers four additional physiological quantities are calculated: a scaling parameter M that defines the maximum possible BOLD signal change for the region; the fractional change in CMRO₂ for the region in the neural activation experiment; an index n of CBF/CMRO₂ coupling during activation, defined as the fractional change in CBF divided by the fractional change in CMRO₂; and an index of CBF/CO₂ coupling n_CO2 defined as the fractional change in CBF divided by the fractional change in end-tidal CO₂. Of these calculated physiological parameters, n_CO2 was the most stable, with non-significant variations within the range of 3.5–3.8 for the different choices of ROI. The other parameters, however, showed some significant differences, indicating that the method of choosing an ROI can introduce a significant bias in quantifying these physiological changes and relationships.

When considering possible sources of bias in the estimation of these physiological parameters, it is helpful to think about the physical ideas behind the calculations. In this analysis the parameter M is calculated from the hypercapnia experiment, and this value is then used to interpret the activation CBF and BOLD changes in terms of a change in CMRO₂. Essentially, the combination of M with the observed activation CBF change defines the BOLD change that would have occurred in the activation experiment with no change in CMRO₂. The observed BOLD change with activation will be less than this theoretical maximum, and a larger discrepancy implies a larger change in CMRO₂ with activation. Because of this, for the same CBF and BOLD activation data, an overestimate of M will lead to an underestimate of n. In our data we tested whether variations in the estimate of M could account for the variations in the calculated parameters by taking the measured values of CBF and BOLD changes with activation and analyzing these with a fixed value for M equal to the average measurement across subjects (Figure 8). The correlation between CBF and CMRO₂ was improved significantly compared to calculating M for each individual subject (R² value of 0.65 vs 0.16). This suggests the possibility that the variability of n across subjects may at least partly reflect variability in the measurement of M rather than a true variability of CBF/CMRO₂ coupling. Any effect that gives an artificially high value for the BOLD change or an artificially low value for the CBF change with hypercapnia will overestimate M and lead to an underestimate of n.

Figure 8.

CBF-CMRO₂ plots determined for 1) M measured for each subject (blue boxes) and 2) a fixed value of M (0.067) equal to the average measurement for the r=0.5 CBF localizer (black diamonds). Correlation between CBF and CMRO₂ is significantly improved by using a fixed value of M, demonstrating that a large source of error in the calculation of n could be due to inaccurate estimates of M.

We can illustrate the sources of bias in the estimate of n even more directly by linearizing Eq [1], appropriate for small responses, and expressing n in terms of the four measured quantities. From this one can derive the following approximate relationship:

$$\frac{{\left(\frac{\mathrm{\Delta }S/S}{\mathrm{\Delta }F/F}\right)}_{\mathit{act}}}{{\left(\frac{\mathrm{\Delta }S/S}{\mathrm{\Delta }F/F}\right)}_{{\mathit{CO}}_2}}\approx 1-\frac{\beta }{\beta -\alpha }·\frac{1}{n}$$ [2]

While strictly accurate only for small CBF changes, this approximate form gives estimates of n within a few percent of the value derived from the full calculation when the CBF responses to neural activation and CO₂ are similar, as was the case for the data we report here. For different CBF responses, however, the errors can be larger (e.g., when the activation CBF response and the hypercapnia CBF response are large and significantly different, the error can be as large as 50%). We introduce Eq. [2] only for its heuristic value, to illustrate in an approximate way how the measured data affects the calculated value of n. For calibrated BOLD calculations, one should always use Eq. [1]. Note also that Eq.[2] illustrates why the calculation of n is only weakly sensitive to the exact assumed values for α and β, a conclusion reached in several previous numerical studies (Davis et al. 1998; Uludag et al. 2004). When β is much larger than α, the dependence on the exact values is diminished because of the way the parameters appear in a ratio. Despite the relatively weak dependence on these parameters, further studies to assess these parameters experimentally are needed.

In the form of Eq. [2], the four measured quantities enter as one combined form: the BOLD to CBF ratio in the activation experiment divided by the BOLD to CBF ratio in the hypercapnia experiment. It is clear from this form that any artifact that affects the BOLD to CBF ratio in hypercapnia will bias the estimate of n. But this also shows that a systematic error in the measurement of the CBF change, provided that it is similar in the activation and hypercapnia experiments, will not bias the estimate of n. That is, the chief problem occurs when the responses to a global CBF change due to hypercapnia are biased differently from the responses to a local CBF change.

There are two potential sources of systematic error that could produce such effects and create a biased estimate of M. The first is related to the inclusion of draining veins within the ROI that produce an artifactually large BOLD signal. The inclusion of draining veins is expected to be a small problem in ROI’s chosen from CBF activations, a more important problem for an ROI chosen from BOLD activations, and perhaps the most significant problem for area V1 determined from retinotopy. One problem in the latter case is the close proximity of area V1 and the confluence of sinuses, where the inclusion of draining veins in the ROI is difficult to prevent. Previous work has shown a disproportionate concentration of venules in the visual cortex (Marinkovic et al. 1995). This problem is compounded in the hypercapnia experiment, where every venous structure within the ROI acts as a draining vein because of the global CBF increase. This can lead to an artifactually high BOLD signal change, and a corresponding overestimate of M.

This draining vein hypothesis is based on the idea that each voxel of tissue generates a BOLD signal due to the small venous structures draining the capillary beds within that voxel, and it is this local BOLD response that should properly be combined with the CBF response of the voxel in the modeling. However, in addition to these well-localized responses there is an overlaid pattern of larger draining veins where the changes in deoxyhemoglobin do not represent activity within that voxel, and there is no associated CBF change in that voxel. The systematic error then arises if the visual stimulus and hypercapnia affect the draining veins to different degrees. That is, this argument hinges on the idea that the visual stimulus does not activate all of the voxels within our retinotopically-defined V1 and so does not affect all of the venous structures within the boundaries of V1. The presence of draining veins will artifactually raise the BOLD response in both the activation and hypercapnia experiments, but more so in the hypercapnia experiment because the CBF increase extends over all of V1, changing the oxygenation of all venous structures. This would lead to the observed progression of higher estimated M values as we move form a CBF-based ROI to a BOLD-based ROI to a V1-based ROI, following the increasing influence of venous structures. This bias is captured in Eq. [2] as an overestimation of the denominator relative to the numerator, resulting in an underestimation of n. Future studies with more rigorous measurements to identify draining veins in voxels with a large difference in the magnitude of the BOLD-response between conditions of functional activation and hypercapnia could provide a useful test of this hypothesis. In general, an important condition for calibrated-BOLD experiments is that the measured M value precisely reflects those cortical structures that exhibit activation to a functional stimulus.

The second effect that could lead to an overestimate of M is a potential error in pulsed ASL experiments that can lead to an underestimate of global CBF changes, and is best illustrated by an extreme thought experiment. In non-quantitative versions of pulsed ASL (FAIR, EPISTAR, PICORE, etc) a particular volume of blood is tagged, and after a delay this tagged blood is distributed in proportion to the CBF distribution and measured as an ASL signal difference. The problem comes in if the delay time is sufficiently long so that all of the tagged blood is delivered. Then in the hypercapnia experiment, despite the global increase in CBF, the same volume of blood is tagged and distributed, so the measured ASL signals will be the same. In this extreme case, the non-quantitative versions of pulsed ASL are insensitive to a global CBF change. Even in less extreme form this effect can lead to an underestimate of the CBF change with hypercapnia, and thus an overestimate of M.

Early studies using FAIR may have suffered from this artifact, although it would depend on details of the experiment. For example, tagging with a head coil with a more limited spatial extent would be more susceptible to this error than using a larger body coil. In addition, another potential artifact with FAIR could offset this effect. Because the slice selective inversion pulse is wider than the imaged slice thickness, there is a transit delay associated with blood crossing this gap (Buxton et al. 1998a). If the transit delays are significant, and are shortened with the global flow change due to hypercapnia, then this effect would tend to overestimate a global CBF change.

The QUIPSS II approach employed in the current study is designed to control for both of these potential artifacts with an added saturation pulse applied to the tagging region at a delay TI₁ after the initial inversion (Wong et al. 1998). This snips off the end of the tagged bolus of blood, essentially creating a tagging in time rather than in space. Then with hypercapnia a larger volume of tagged spins leaves the tagging region during TI₁, and the ASL difference signal is larger, reflecting the global increase of CBF. In addition, provided that TI₂-TI₁ is greater than the longest transit delay, the potential overestimation of a global CBF change due to shortened transit delays is controlled as well.

In the current study we report CRC values somewhat larger than prior fMRI studies. Using data reported in earlier studies of visual cortex using FAIR we calculate the CRC values to be 3.6 (Davis et al., 1998), 4.0 (Hoge et al., 1999), and 4.2 (Kim et al., 1998), all about a factor of two smaller CBF changes than we found for similar changes in end-tidal CO₂. In motor cortex, Kastrup et al., 2002 found a CRC of 5.8 with FAIR, also smaller than our values in the current experiments in visual cortex. Two recent positron emission tomography (PET) studies using 15O-labeled water found CRC values of 5.6-6.3 (Ito et al. 2002; Ito et al. 2003), intermediate between our values and the earlier values for visual cortex reported using FAIR. However, the PET ¹⁵O-labeled water technique is known to underestimate high CBF values because of incomplete extraction of the labeled water. A PET study using ¹⁵O-labeled butanol, which is thought to provide a better estimate of high flows, found an increase in CBF from 66 to 129 mL 100 g^-1 min^-1 for gray matter associated with a rise in end-tidal CO₂ from 40 to 50mmHg, giving a CRC value of about 9.5 for gray matter, in good agreement with our current results (Kemna et al. 2001). While this is not definitive and differences in CRC, in part, may reflect different measurements for describing CO₂ change with hypercapnia (end-tidal CO₂ versus arterial pCO₂), it suggests at least that the large CBF changes we measured are not unreasonable.

While the use of QUIPSS II in the current studies should minimize the potential error of underestimating global CBF changes, there are still two possible systematic errors that could be present. If TI₁ is too long, so that all of the tagged spins have already left the tagging region by the time the saturation pulse is applied, then the CBF change is underestimated. The delay from the saturation pulse to the image acquisition at TI₂ is designed to minimize the effects of transit delays from the tagging region to the image plane by allowing sufficient time for all of the bolus to be delivered. If TI₂-TI₁ is shorter than the local transit delay at rest, then the shorter transit delay with activation or with a global flow increase could allow more of the tagged bolus to be delivered, creating an overestimate of the CBF change. The latter type of error is more likely to creep into our measurements and may partly explain why our CRC and activation measurements are greater than those reported by non-MRI methods.

The goal of the current study was to try to correct for ASL technique errors using QUIPSS II and then assess remaining bias due to the method used for defining an ROI. We found that the estimate of M varied from 0.067 to 0.11, depending on the ROI selection method. In general, the M values we found are lower than most earlier reported values (0.08 Davis et al.,1998; 0.22 Hoge et al.,1999). This is perhaps surprising, because our studies were done at 3T while the others were done at 1.5T, and the higher field would be expected to increase the BOLD effect. However, the experimental details need to be taken into account when comparing M values from different studies. The derived value of M should be proportional to the echo time used in the experiment. For example, Hoge et al used TE=50 ms while we used TE=30 ms, and this difference alone should make the earlier value larger by 60%. The pulse sequence used should also be considered when comparing the BOLD-responses across studies. For example, compared to a gradient echo sequence, a spin-echo sequence may reduce the intravascular BOLD signal and the calculated M value. In our studies the largest estimate of M (0.11) was found with the ROI based on V1 mapping from the retinotopy experiment, the same approach used by Hoge et al. It is likely that both of these estimates are biased toward higher values because of the inclusion of venous structures, as noted above, and the earlier data may also be biased because of underestimated CBF changes with the FAIR technique.

From the previous arguments it is clear that an accurate value of M is critical for estimating the CBF/CMRO₂ coupling index n. In earlier studies, we (Uludag et al. 2004) and others (Shmuel et al. 2002) have assumed values of M taken from earlier studies in order to interpret combined CBF and BOLD measurements without doing a hypercapnia experiment. These studies assumed large values of M, as for example M=0.22 reported by Hoge and colleagues (Hoge et al. 1999b). However, the lower values of M near 0.07 found in the current study are quite different, and in general the hypercapnia experiment is necessary for an accurate estimate of n.

In order to avoid draining vein artifacts and explore biases associated with various levels of activation significance, two additional ROIs were constructed from the perfusion data of the PICORE run at a significance of r = 0.4 and r = 0.6. Here, the results show that CO₂ responses are mildly affected whereas estimates of responses to functional activation (BOLD and CBF) are significantly different (Table 3): the estimated mean value of n decreases as the threshold for voxel selection decreases.

Two possible explanations may explain this phenomenon. First, vascular artifacts (i.e. small feeding arteries) may be over-represented in the ROI with a high threshold due to their large flow changes (with associated high SNR). Such voxels might show a large apparent CBF change with only a small BOLD change, biasing the average toward higher values of n. A second possibility is that there could be a large variation of n across sub-populations of voxels within the ROI. For example, one can imagine that the CMRO₂ response is uniform across the ROI, but the CBF response is more variable. Then a high threshold would select those voxels with the largest CBF change and bias the calculated average to higher values of n.

The first possibility is more of an artifact in the ASL method, while the second reflects a more intrinsic physiological variability of CBF/CMRO₂ coupling. Vascular artifacts can contaminate %CBF changes if the inversion time (TI₂) is not sufficiently long to allow tagged blood to pass through feeding vessels to reach more distal capillary beds. If vascular artifacts explain this phenomenon, we would expect the BOLD responses to go down with increasing threshold levels. However, this is not observed. In addition, in these experiments we applied weak diffusion-weighting gradients specifically to minimize this type of artifact. By reducing the signal of fast flowing blood this should minimize the contribution of feeding arteries to the ASL signal. This suggests that a more likely explanation for the threshold dependence could be a true spatial variability of the local CBF response combined with a more uniform CMRO₂ response. Determination of CMRO₂ and n on a voxel-by-voxel basis would be a good approach for testing this possibility. However, this was not possible with the individual data reported here due to signal-to-noise constraints.

Figure 7 points to an important potential pitfall of calibrated BOLD fMRI if one chooses to implement a high level of significance in defining regions of activation. Since correlation coefficients are essentially a measure of the signal-to-noise ratio, the following situation may be encountered: Two subjects may elicit the same amount of neural activity in response to a task, but one subject may have a higher level of noise in the data than the other subject and therefore a lower SNR. The subject with lower SNR would therefore have a smaller area of activation that would include proportionally more voxels with high estimates of %CBF and n. This unwanted effect may be moderated by selecting a less conservative threshold to account for differences in inherent levels of noise across subjects.

A potential limitation of this study is that accurate CMRO₂ estimates rest on the assumption that mild hypercapnia does not elicit changes in neural activity. Recent work in rodents found that 5% hypercapnia produced negligible changes in CMRO₂ whereas 10% produced significant changes (Jones et al. 2005; Sicard and Duong 2005). However, a recent study (Zappe et al. 2005) reported decreases in local field potentials (LFPs) and multi-unit activity (MUA) in anesthetized macaques with 3 and 6% CO₂. If CMRO₂ correlates with reduced LFP magnitude, this would imply decreased CMRO₂ with hypercapnia, which in turn would suggest that calibrated BOLD techniques overestimate CMRO₂ and underestimate n. However, we would expect this bias to propagate equally across the ROIs examined in this study leaving measured differences between ROIs unaffected. That is, these effects, if they are confirmed by future studies, would shift all of our estimates of n, but the underlying bias due to the method for choosing an ROI would remain. Further studies in humans are necessary to examine this issue and determine whether mild hypercapnia affects CMRO₂.

Conclusions

This study demonstrates that a significant variability in CMRO₂ and CBF-CMRO₂ ratio estimates can arise from the way in which voxels are selected in fMRI experiments. Selecting ROIs based on anatomical boundaries instead of functional activation may artifactually elevate %CMRO₂ measurements through the inclusion of venous structures that lead to an artificially large BOLD response to hypercapnia. Selecting voxels based on BOLD activation may also bring in a bias based on inclusion of draining veins, but to a lesser extent than anatomical ROI selection. Selecting ROIs based on CBF activation will tend to avoid biases due to inclusion of venous structures, but may tend to introduce a different bias related to inclusion of arterial structures or selection of a sub-population of voxels with higher %CBF and n. This effect becomes more apparent when a high threshold of statistical significance is applied, which would be most likely to emphasize these types of artifacts. The use of weak diffusion-sensitizing bipolar gradients can help to reduce vascular artifacts in the ASL data. Variability of M and n across subjects can be improved by selecting voxels based on flow activation at a level of significance that defines a reasonably large ROI. The calibrated BOLD approach is a potentially powerful tool for quantitatively assessing human brain physiology in both health and disease, but it is critical to control for sources of bias in the methodology itself.