Application of a time-dependent coalescence process for inferring the history of population size changes from DNA sequence data

Abstract

Distribution of pairwise differences of nucleotides from data on a sample of DNA sequences from a given segment of the genome has been used in the past to draw inferences about the past history of population size changes. However, all earlier methods assume a given model of population size changes (such as sudden expansion), parameters of which (e.g., time and amplitude of expansion) are fitted to the observed distributions of nucleotide differences among pairwise comparisons of all DNA sequences in the sample. Our theory indicates that for any time-dependent population size, N(τ) (in which time τ is counted backward from present), a time-dependent coalescence process yields the distribution, p(τ), of the time of coalescence between two DNA sequences randomly drawn from the population. Prediction of p(τ) and N(τ) requires the use of a reverse Laplace transform known to be unstable. Nevertheless, simulated data obtained from three models of monotone population change (stepwise, exponential, and logistic) indicate that the pattern of a past population size change leaves its signature on the pattern of DNA polymorphism. Application of the theory to the published mtDNA sequences indicates that the current mtDNA sequence variation is not inconsistent with a logistic growth of the human population.

In the absence of selection and recombination, the evolution of nucleotide polymorphism in a specific DNA sequence is influenced by two genetic forces: mutation and genetic drift. Mutation introduces random changes in the sequence of nucleotides, whereas the genetic drift acts towards reducing the diversity of population by random loss of alleles.

Mathematical models of the evolution with mutation and genetic drift were studied by several researchers (1–4). In the cited references the models of mutation used were either infinite sites or stepwise, whereas the genetic drift was modeled by the Fisher–Wright process with the effective size of the population assumed constant. Under these assumptions, after time long enough, an equilibrium is attained and the statistical properties of the DNA polymorphism at the analyzed locus can be found from the model parameters.

However, it is well known that most populations undergo changes in size during the course of evolution. This information led researchers to study the polymorphism of DNA with population size changing in time. Li (5) derived formulae for distributions of pairwise differences between alleles. Tajima (6) found expected values of some important statistics for a random sample of n individuals drawn from the population. It was demonstrated by Chakraborty and Nei (7) that a bottleneck in the population’s size results in a rapid reduction of DNA diversity. Several researchers studied the effects of population growth on the distribution of nucleotide differences in pairwise comparisons of mtDNA sequences. Di Rienzo and Wilson (8) and Slatkin and Hudson (9) reported difficulties in differentiating between different types of growth and between the effect of growth and other factors like geographic structure or fixation of the fittest allele some time ago. They argued that these factors all led to star-like genealogies in populations, and therefore the distributions of pairwise differences were all close to Poisson. Rogers and Harpending (10), Rogers (11), and Rogers et al. (12) developed a method of fitting the model of sudden population expansion to the existing data. Simulations studies also were conducted to compare outcomes of simulations experiments of populations growing with time with the observed distributions of nucleotide differences among pairwise comparison of DNA sequences (9,12,13).

In the present paper, we reexamined hypotheses about different types of growth considered in the cited references. We assumed the infinite sites mutation model. We developed the results of Chakraborty and Nei (7) and Slatkin and Hudson (9) to obtain a time-dependent coalescence model describing statistical properties of pairwise differences. We studied properties of this model, focusing on the following problems: (i) Is the history of the past population size change encoded in the present distribution of allelic differences, and (ii) is it possible to find the inverse relation? We demonstrated that the inverse relation is unstable, i.e., large deviations in the history of the population size may result in only small changes of the distribution of pairwise differences. This observation is consistent with the previous findings (8, 9). We also used the time-dependent coalescence process to develop an algorithm to estimate the history of the population size change. We examined the performance of our algorithm for simulated data, and we also compared its output with the results previously published for data on human mtDNA sequences.

METHODS

A model of the time-dependent coalescence process can be derived using the fact that the generating function of pairwise differences between DNA sequences is identical with the Laplace transform of the coalescence intensity function. Let us assume that we have data on the distribution of pairwise differences for a specific DNA sequence within a population. The population is assumed to be diploid and effective size and, at present, is denoted by N₀. Also, we suppose that this population’s size has changed in time. We ask how the history of population size change is encoded in the distribution of number of differences between pairs of DNA sequences.

Assuming that population size was always large enough to allow the diffusion approximation we can use a continuous time scale, τ, representing the number of generations counted backward from the present. The population size at generation τ is N(τ). If two DNA sequences are randomly drawn from the present population, the distribution density p(τ) of the time τ to their most recent common ancestor can be represented by

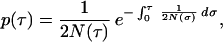1

which is called the coalescence intensity function in this work. This equation relates the coalescence intensity function p(τ) to a given history of population size change N(τ). The inverse relationship

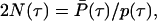2

where P̄(τ) = ∫_τ^∞ p(σ)dσ is the tail function, follows from the usual definition of the hazard rate, here equal to [2N(τ)]⁻¹ (14). The above expression enables calculating N(τ) from the coalescence intensity function.

The genetic drift described by Eq. 1 is accompanied by mutation with rate ν. The mutation events at the analyzed locus constitute a homogeneous Poisson process with intensity ν. Under the infinite sites mutation model (1), for two DNA sequences randomly drawn from the population, the number of mutations since their most recent common ancestor is equal, in expectation, to the number of segregating sites between these two sequences.

Denote the probability generating function of the number of segregating sites by α(s). Conditional on τ, the number of segregating sites in the two alleles is Poisson with parameter 2ντ. Therefore the probability generating function (pgf) of the number of segregating sites is (14)

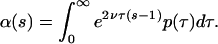3

This pgf can be rewritten in the scale of mutational time by substituting t = 2ντ

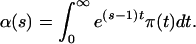4

In the above equation,

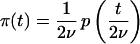5

is the coalescence intensity function in the mutational time scale.

Observe now that setting z = −(s − 1) we can interpret the probability generating function on left-hand side of Eq. 4 as the Laplace transform π̂(z) = α(1 − z) of the coalescence intensity function π(t).

Inverse Relation. The above model can be used to develop a two-step method for estimating the change of the population size from the data on the distribution of nucleotide differences between pairwise comparison of DNA sequences. First the coalescence intensity π(t) is estimated by an inverse Laplace transform and then the inverse relation (Eq. 2) is used to calculate the history of the population size change. If the mutation intensity is not known, we can rescale Eq. 2 as

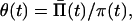6

where θ(t) = 4νN(t), Π̄(t) = P̄(t/2ν). Using Eq. 6, we can estimate the history of change of the composite growth parameter θ(t).

However, applying this method to data, we realize that the inverse relations in both steps are unstable. Small changes in the data can cause large deviations in the final estimate. This is obvious for the inverse relation for coalescence intensity (Eq. 2 or Eq. 6). The denominator is the probability density function, which may be very close to zero for substantial time intervals. Small errors in estimating this density will result in large errors for N(t) or θ(t). In other words, a population size change that occurred in the distant past is poorly estimated from extant DNA sequence polymorphism.

The problem of inverting the Laplace transform (Eq. 4) can be equivalently formulated as the problem of moments (16). Indeed, expanding e^st in Eq. 4 into the power series, and using

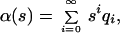7

where q_i denotes the probability that the number of segregating sites in two randomly chosen sequences is i, we get the system of relations

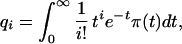8

for i = 0, 1, … , that must be satisfied by π(t).

To explain the instability in calculating π(t) either from Eq. 8 or from Eq. 4 let us quote the properties of the Laplace transform (17). Function α(s) given by the integral on the right-hand side of Eq. 4 is defined and analytic in the half-plane ℜ(s) < 1, since π(t) is integrable. For a reliable inverse transform, we need the values of α(s) in a large region in ℜ(s) < 1. However, the available data enable calculation of α(s) only in the unit disc |s| ≤ 1. This is because the pgf α(s) in the left hand side of Eq. 4 results from the series expansion (Eq. 7), which converges for |s| ≤ 1. We cannot use Eq. 7 to evaluate α(s) outside the unit disc |s| ≤ 1 because the series generally diverges. Estimating α(s) outside the unit disc as an analytical continuation of the function defined on the unit disc is an unstable process. As an example assume that α(s) is given by Eq. 4 with some π(t) and consider another time function π(t) + cos(ωt). The corresponding Laplace transform is α(s) + [(1 − s)² + ω²]⁻¹. For large enough values of ω, the maximum absolute difference between Laplace transforms α(s) and α(s) + [(1 − s)² + ω²]⁻¹ is arbitrarily small inside the unit disc, while the maximum absolute difference between π(t) and π(t) + cos(ωt) is always equal to 1.

An Algorithm for Estimating the History of Population Size. Let us assume that π(t) changes only at discrete time instants t₀, t₁, …  and that it is constant in between. We take t_k = kΔt, k = 0, 1, … . In order to describe the time function π(t) by its values π_k at t = kΔt we introduce the bar function b_k(t) = 1/Δt for kΔt ≤ t < (k + 1)Δt and b_k(t) = 0 otherwise. Using b_k(t) we can represent π(t) as

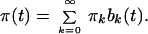9

Substituting Eq. 9 in Eq. 8 yields an infinite system of linear equations relating q_i, and π_k

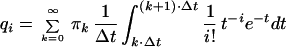10

i = 0, 1, … ; k = 0, 1, … . In numerical calculations we confine the range of k to k ≤ K_max and we assume that probabilities q_i are greater then zero only for i ≤ I_max. This allows us to consider a finite-dimensional system of equations of the form

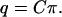11

in which q is the I_max + 1 dimensional column vector with elements q₀, q₁, … , q_Imax, π is the K_max + 1 dimensional column vector with elements π₀, π₁, … , π_Kmax, and C is the (I_max + 1) × (K_max + 1) dimensional matrix of coefficients with entries c_ik given by

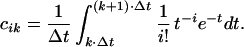12

Elements of the vector π cannot be calculated from the system of Eq. 11 because this system is always (for all choices of Δt, I_max and K_max) ill conditioned. To reduce instability, we add constraints on π:

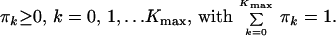13

Following the methodology of L₁ estimation (18), we can then estimate the vector π by minimizing the sum of absolute differences,

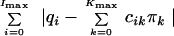14

with respect to π_k, k = 0, 1, … , K_max, subject to constraints given by Eq. 13.

However, numerical calculations prove that estimates of π_i obtained by solving the minimization problem (Eqs. 13 and 14) are still insufficient to estimate the history of population size. The reason is that, without regularity assumptions, the sequence {π_i} that minimizes Eq. 14 is subject to much random fluctuation. Aiming at further regularization of the problem, we assume that population size was always increasing. This gives additional constraints described below.

Denote the estimates of values of the survival function by

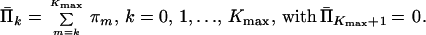15

We can substitute variables Π̄_k in the expressions for constraints (Eq. 13) and in the index function (Eq. 14) to obtain the equivalent problem: Minimize

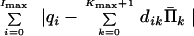16

with respect to Π̄_k, k = 0, 1, … , K_max + 1, subject to constraints

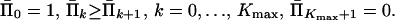17

The coefficients d_ik in the index function (Eq. 16) can be calculated as

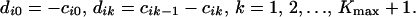We now regularize estimates of Π̄(t) by assuming that population size was always increasing, i.e., N(t) is decreasing with the backward time t. This assumption yields convexity of −ln[Π̄(t)] (19), and further due to the monotone property of Π̄(t),

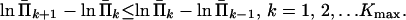18

Adding these constraints (Eq. 18) to problem (Eqs. 16 and 17) would lead to a nonlinear, nonconvex, multidimensional minimization, difficult to solve. We propose an alternative approximate approach based on the assumption that we only need to make small corrections of Π̄_k in order that the constraints (Eq. 18) be satisfied. Denote the corrected estimates by Π̂_k, and set

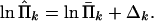19

Constraints (Eq. 18) applied to Π̂_k yield

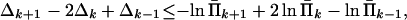20

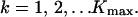We want to choose the corrected values Π̂_k, such that

21

is minimized. Let us replace q_i by their estimates Σ_k=0^K_max+1 d_ikΠ̄_k. Substituting Eq. 19 in Eq. 21 we get the following problem: Minimize

with respect to Δ_k, k = 0, 1, … , K_max + 1, subject to the constraints (Eq. 20). By our assumption, corrections Δ_k are small, i.e., 1 − e^Δ_k ≅ −Δ_k. Finally we solve the following problem: Minimize

22

with respect to Δ_k, k = 0, 1, … , K_max + 1, subject to the constraints (Eq. 20).

Estimates Π̄_k obtained in the first minimization step (Eqs. 16 and 17) appear in the problem (Eqs. 22 and 20) as parameters. Both minimizations are linear programming problems (20) and can be efficiently solved for the required dimensions I_max, K_max.

RESULTS

In this section, we give numerical examples of estimating histories of the populations sizes with the use of the proposed method. We simulate distributions of pairwise differences for three scenarios of the population growth. Then, we compare the estimated histories to the original. We also use our algorithm for pairwise differences data for mtDNA from Cann et al. (21). We compare our estimation of θ(t) to the result published by Rogers and Harpending (10).

Simulated Data. We assumed the following three scenarios of population growth: stepwise change, exponential, and logistic. Using our mathematical model, we obtained the following. Stepwise change τ_s generations ago: N_s(τ) is defined as follows: For τ > τ_s the population size was N_b (before) and for τ < τ_s it was N_n (now),

and

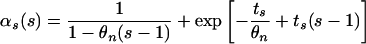23

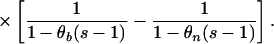In the above expressions, we used θ_n = 4N_nν, θ_b = 4N_bν, t_s = 2ντ_s.

Exponential growth: N_e(τ) = N₀e^−rτ. Here,

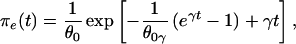and

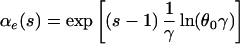24

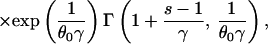where θ₀ = 4N₀ν, γ = r/2ν, and Γ(.,.) is the incomplete complementary gamma function: Γ(a, b) = Π_b^∞ t^a−1e^−tdt (22).

Logistic growth: N_l(τ) = K/(1 + Ce^bτ) results in the following expressions:

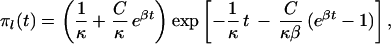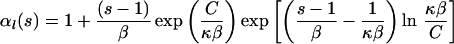25

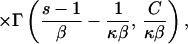where κ = 4Kν, β = b/2ν, and C = K/N_l(0) − 1.

All three distributions (Eqs. 23–25), under appropriate conditions, can resemble the Poisson distribution. They all have Poisson components.

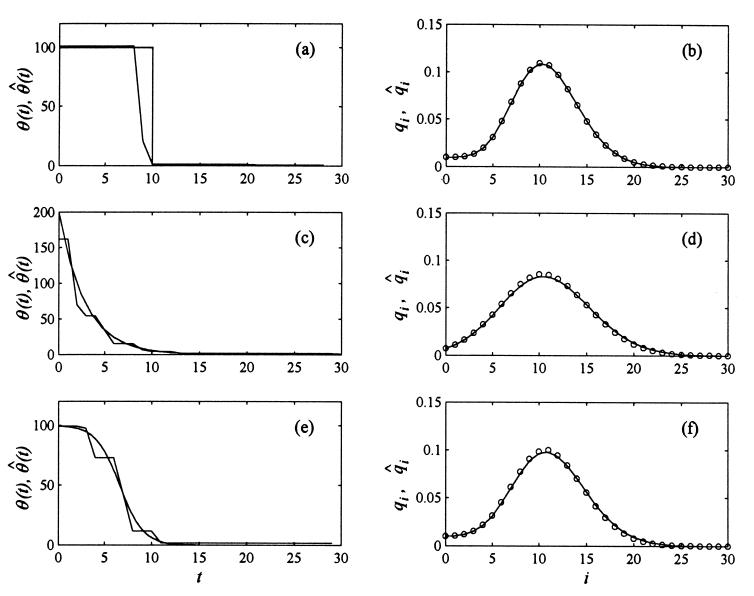
We assumed the following parameters. For stepwise change: θ_n = 100, θ_b = 1, t_s = 10. For exponential growth: θ₀ = 200, γ = 0.35. For logistic growth: κ = 100, C = 0.005, β = 0.8. We used our algorithm for probabilities q_i following from the distributions given by Eqs. 23–25, and compared estimated histories with the true functions. In our algorithm we assumed I_max = K_max = 30 and Δt = 1. The results are presented in Fig. 1. The plots on the left depict the function θ(t) (smooth line) and its estimate θ̂(t) obtained using our algorithm (irregular line). The plots on the right depict probabilities q_i (open circles) together with their estimates q̂_i = Σ_k=0^K_max+1 d_ikΠ̂_k (solid line). The plots a and b, c and d, and e and f correspond, respectively, to the stepwise, exponential and logistic growth. The agreement between q̂_i and q_i is excellent and the constraint of increasing population size is satisfied.

Figure 1.

Application of the algorithm for estimating the history of the population size for simulated data. The plots in the column on the left depict functions θ(t) (dotted line) and their estimates θ̂(t) (solid line) calculated using our method. The plots in the column on the right depict the corresponding probabilities q_i (open circles) together with their estimates q̂_i (solid line). The assumed scenarios of growth were stepwise (plots a and b), exponential (plots c, and d) and logistic (plots e and f). Parameters: For stepwise change, θ_n = 100, θ_b = 1, t_s = 10. For exponential growth: θ₀ = 200, γ = 0.35. For logistic growth: κ = 100, C = 0.005, β = 0.8.

Comparing true and estimated histories of the parameter θ(t) allows to contemplate the effects of instability. With perfect data and additional order restrictions, errors are still present, although the growth pattern is predicted reasonably well.

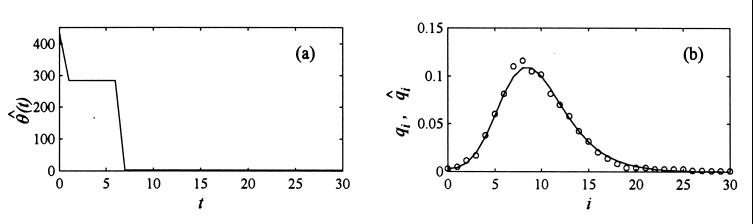
mtDNA Data. We used data on worldwide pairwise differences of mitochondrial alleles from Cann et al. (21). Application of our algorithm (I_max = K_max = 30 and Δt = 1) to this data is presented in Fig. 2. Fig. 2a depicts the estimated history of the composite parameter θ(t) = 2νN(t). Fig. 2b depicts presents probabilities q_i based on Cann et al. (21) (open circles) together with their estimates q̂_i = Σ_k=0^K_max+1 d_ikΠ̂_k (solid line).

Figure 2.

Application of our algorithm to the data on worldwide pairwise differences of mitochondrial alleles from Cann et al. (20). The plot on the left depicts the estimated history θ̂(t) of the composite parameter θ(t) = 2νN(t). The plot on the right depicts probabilities q_i based on Cann et al. (20) (open circles) together with their estimates q̂_i (solid line).

It seems interesting to compare our estimate with that obtained by Rogers and Harpending (10). They fitted a model of sudden expansion to the data from Cann et al. (21) obtaining θ_n = 410.69, θ_b = 2.44, t_s = 7.18, in our notation. Comparing these numbers to the plot in Fig. 2a, we find our estimation quite consistent with their result. Our estimate would, however, suggest a gradual increase in population size starting from t ≅ 7, rather than a stepwise change.

In order to determine the sensitivity of our estimates, we conducted a resampling study in which 200 sequences were simulated under the infinite site model with a stepwise growth of a population, corresponding to parameter values of θ_n, θ_b, and t_s as the ones obtained by Rogers and Harpending (10). In 50 replications of simulations, all of the estimates of θ(τ) were stepwise functions (with several exceptions in which the step was divided between two or three successive time points). The estimate t̂_s had a mean of 6.29 (as compared to the assumed value of 7.2) with SD of 1.73. The estimate ln θ̂_n had a mean of 7.28 (as compared to the assumed value of 6.02) with SD of 0.78. The estimate ln θ̂_b had a mean of 1.54 (as compared to the assumed value of 0.89) with SD of 1.17. Logarithmic transformation was used to account for the skewed distributions of θ̂_n and θ̂_b.

We also carried out simulations assuming exponential growth of the population. As an example, in one of them, the assumed values of parameters were θ₀ = 800 and γ = 0.7 (Eq. 24). In 50 replications of simulations, the logarithmic transformations of the estimated θ(t) were fitted by linear regression, to obtain estimates of lnθ₀ and of γ. The estimate ln θ̂₀ had a mean of 7.66 (as compared to the assumed value of 6.68) with SD of 1.47. The estimate γ̂ had a mean of 0.75 (as compared to the assumed value of 0.70) with SD of 0.20.

DISCUSSION

In the present paper, we investigated whether or not the signature of the past population change existing in the DNA sequence data is sufficiently accurate to help decipher the pattern of this change. The issue was considered by others (8–13) who provided estimates of the amplitudes and dates of changes of different world populations based on distributions of nucleotide differences in pairwise comparisons of DNA sequences. In these papers, estimation was carried out under assumptions of parametric models of growth, usually having the form of a stepwise change. Although the observed distributions of nucleotide differences in pairwise comparisons of sequences were in agreement with a stepwise growth of populations, Bertorelle and Slatkin (13) pointed out that the observed number of segregating sites is significantly lower than that expected under a population expansion model, which cannot be accounted for even if recurrent mutations occur at each nucleotide site. In addition, Marjoram and Donnelly (23) showed that a unimodal distribution of q_i (Eq. 7) also can be caused by the presence of population substructure as opposed to expansion, although the extent of substructure required has to be very severe.

Griffiths and Tavaré (24), in contrast, considered a complete likelihood function of the sample under a variety of mutation models, including the infinite site model. However, their inference regarding population growth depends on the parametric form of the population growth as well as the specific mutation model.

Our contribution involves using a general pattern of population change in conjunction with the infinite sites model of nucleotide substitution. The only regularizing assumption we use is that of the monotonic growth of the population. An approximate numerical procedure allows to solve the estimation problem, posed as a two stage optimization. Examples using simulated data demonstrate that under ideal conditions, corresponding to very large samples, the method can resolve different growth patterns. Application to the data set of Cann et al. (21) suggests a growth pattern not unlike logistic.

Although the present work explicitly uses the infinite sites model of nucleotide substitutions, we remark that the estimation procedure proposed here is more general, and should be applicable for other types of mutation models. For example, recent work (14, 23–27) indicates that the within population polymorphism at the microsatellite loci can be represented by the distribution of repeat size differences among pairwise comparisons of alleles, which can be characterized by a coalescence process.

Such a characterization is valid even when new microsatellite alleles evolve via a general forward–backward mutation model in which asymmetry is allowed (14, 26). If temporal variation in the effective population size is introduced, the coalescence process becomes time-dependent. Thus, in principle, the method proposed here should be applicable to microsatellite polymorphism for which data is abundant in the literature. Of course, the details of the numerical method to deal with the instability of prediction of N(τ) may be different for the stepwise mutation model. This requires further studies.