Abstract
Through comparison with ab initio reference data, we have evaluated the performance of various density functionals for describing π-π interactions as a function of the geometry between two stacked benzenes or benzene analogs, between two stacked DNA bases, and between two stacked Watson–Crick pairs. Our main purpose is to find a robust and computationally efficient density functional to be used specifically and only for describing π-π stacking interactions in DNA and other biological molecules in the framework of our recently developed QM/QM approach "QUILD". In line with previous studies, most standard density functionals recover, at best, only part of the favorable stacking interactions. An exception is the new KT1 functional, which correctly yields bound π-stacked structures. Surprisingly, a similarly good performance is achieved with the computationally very robust and efficient local density approximation (LDA). Furthermore, we show that classical electrostatic interactions determine the shape and depth of the π-π stacking potential energy surface.
Figure.

Additivity approximation for the π-π interaction between two stacked Watson–Crick base pairs in terms of pairwise interactions between individual bases
Electronic supplementary material
The online version of this article (doi:10.1007/s00894-007-0239-y) contains supplementary material, which is available to authorized users.
Keywords: Density functional theory, DNA stability, DNA structure, Hydrogen bonding, π-π stacking interactions
Introduction
Two major factors for the structure and stability of DNA are the hydrogen bonds between two adjacent bases from opposite strands (forming a Watson-Crick pair), and the π-π stacking interactions between two bases within each of the two DNA strands. The hydrogen bonding interactions in DNA are well understood by high-level Density Functional Theory (DFT) calculations [1–3]. They were shown to be provided by nearly equally important contributions from electrostatic attraction and donor-acceptor orbital interactions (e.g., from an N lone pair to an N-H σ* orbital), and to be sensitive to effects from the molecular environment (counter-ions, solvent) [1, 2]. A similar understanding of the π-stacking interactions is currently lacking due to several reasons: (1) π-π stacking interactions have proven to be sensitive to the methodology used (see below); (2) π-π stacking interactions have proven to be very dependent on the size of the basis set used in (ab initio) calculations, resulting in a large basis-set superposition error (BSSE); (3) high-level ab initio benchmark studies (CCSD(T) with at least triple-zeta basis sets) have only recently become available; and (4) the notorious problems of DFT to correctly describe dispersion interactions, [4–16] which constitute one of the components involved in π-stacking interactions (see below). The latter problems of DFT resulted in potential energy surfaces (PES) that, erroneously, lack any equilibrium configuration, i.e., the stacked systems were incorrectly described as being purely repulsive.
Because of the technical difficulties involved in obtaining accurate benchmarks (CCSD(T) using large basis sets), Sponer, Hobza and co-workers have studied in a ground-breaking series of papers [17–22] the stacking energies of DNA bases and DNA base analogs using a variety of ab initio methods and basis sets. Earlier studies showed that reasonable interaction energies could be obtained when employing the MP2/6-31G*(0.25) method, which was confirmed by later and more accurate studies [17–22]; in the aforementioned 6-31G*(0.25) basis set, the standard d-polarization functions (with exponent of 0.80) were replaced by more diffuse ones (exponent of 0.25) with the aim to improve description of the dispersion attraction [22]. Thus, for the anti-parallel displaced pyrimidine dimer, the MP2/6-31G*(0.25) energy is only 1.1 kcal mol−1 lower than the CCSD(T)/6-31++G*(0.25,0.15) energy, for the anti-parallel cytosine dimer it is 0.6 kcal mol−1 higher than the CCSD(T)/6-31++G**(0.25,0.15) energy, and for the twisted uracil dimer the MP2/6-31G*(0.25) is equal to the CCSD(T)/6-31++G**(0.25,0.15) energy. Although there seems to be no systematic shift in energy when comparing MP2/6-31G*(0.25) with the more elaborate CCSD(T) stacking energies, the MP2 stacking energies are always larger in magnitude than the corresponding CCSD(T) ones when using the same basis set for both methods. Interestingly, in connection with the quest for reliable ab initio benchmarks, preliminary results [23–27] indicate that the recently developed spin-component scaled MP2 (SCS-MP2) yields systematically lower stacking energies than MP2. This suggests that SCS-MP2 is in good agreement with the CCSD(T) results at only a fraction of the computational cost.
Several approaches have been proposed to remedy the “dispersion problem” of DFT, ranging from Time-Dependent DFT frameworks [28] to more ad-hoc procedures such as including (C6) van der Waals terms in the interaction energy (DFT-D) [29] or fitting (reparameterizing) the form of the density functional to some reference energies and/or distances. A more elegant solution was recently proposed by Tozer and co-workers [30], who analyzed the DFT exchange-correlation (xc) potential in comparison with the near-exact multiplicative Zhang-Morrison-Parr (ZMP) potential from coupled cluster Brueckner doubles (BD) densities. Their resulting KT1, and the related KT2, functional [30] produces xc potentials that closely resemble those from ZMP. As a result, KT1 and KT2 produce NMR chemical shifts [4, 31] that in general show smaller deviations from experimental values than those from standard density functionals. Furthermore, the ZMP potential from Brueckner (BD(T)) coupled cluster densities gives dispersion forces in good agreement with near-exact dispersion forces [32]. It is therefore to be expected that the KT1 and KT2 functionals behave properly for dispersion forces as well. However, the application of these new functionals to π-stacking interactions has so far not appeared in the literature.
Here, we report the results of a systematic investigation of π-stacking interaction energies, potential energy surfaces (PES) and stacking distances for dimers of, among others, the five DNA/RNA bases. A long list of standard as well as recent density functionals (including the KT1 and KT2 functionals) has been considered in this study, ranging from the Local Density Approximation (LDA), via the Generalized Gradient Approximation (GGA), and meta-GGA, to hybrid functionals. We have also examined BHandH, which was recently [12] shown to give reasonable agreement with ab initio data. The DFT results are compared to benchmark data that were taken from the literature, which in some cases contained energy profiles as a function of the torsion associated with the rotation of one base with respect to the other.
The present investigation is part of a larger undertaking. We aim at developing an extended QM/QM scheme, designated QUILD [33], which allows a (complex) molecular system to be decomposed into arbitrary, interpenetrating domains such that each type of interaction can be described with a different method, i.e., the density functional that performs best for that type of interaction or process, for example, electron-pair as well as hydrogen bonding (BP86: see [2, 3]), π-π stacking (LDA, KT1, KT2: this work) or reaction barriers (OLYP, OPBE: see [34, 35]). This is a pragmatic (of course not a fundamental) approach to cope with the present-day shortcomings of DFT, which features density functionals that perform satisfactorily for a number but not all types of interactions and phenomena. The present study focuses on identifying which DFT approaches serve best to describe the π-π stacking interactions in the above-mentioned QM/QM scheme.
Furthermore, we have analyzed the π-stacking interactions in more detail by decomposing the interaction energy into three physically meaningful components, namely, electrostatic energy, Pauli repulsion (i.e., the destabilizing interactions between occupied orbitals), and bonding orbital interactions [36]. Our analyses reveal, among others, that the electrostatic attraction between the stacked molecules is the most important component of the π-π stacking interaction (see also [37]) which determines the shape and depth of the PES. We have also analyzed the π-π interactions between two stacked Watson–Crick base pairs with the purpose to differentiate between inter- and intra-strand stacking interactions.
Methods
Computational details
All calculations were performed with the Amsterdam Density Functional (ADF) program. [38–49] Molecular orbitals (MOs) were expanded using a large, uncontracted set of Slater-type orbitals: TZ2P [40]. The TZ2P basis is an all-electron basis of triple-ζ quality, augmented by two sets of polarization functions (2p and 3d on H; d and f on heavy atoms). An auxiliary set of s, p, d, f, and g STOs was used to fit the molecular density and to represent the Coulomb and exchange potentials accurately in each SCF cycle.
The equilibrium structure of individual benzene analogs, DNA bases and Watson-Crick base pairs were optimized at the BP86 level of DFT, i.e., using the local density approximation (LDA; Slater exchange and VWN [42] correlation) with non-local corrections due to Becke [43] (exchange) and Perdew [44] (correlation) added self-consistently, which was previously shown to be one of the best DFT methods for the accuracy of geometries [41, 45] and hydrogen-bonding interactions [1–3]. The π-π stacking interaction energies for all density functionals were evaluated post-SCF using LDA as SCF functional. This procedure was recently shown to introduce an error of only a few tenths of a kcal mol−1 [46].
Stacking distances (vertical separation) and orientations (twist angle) were explored with the various density functionals through scans of the potential energy surface (PES) in which the BP86 geometries of the monomers (e.g., DNA bases or Watson–Crick base pairs) were kept frozen. PES scans as a function of the twist angle (see below) were done using steps of 30° in case of homo-base stacks, 60° in the case of hetero-base stacks and 36° for stacks of Watson–Crick base pairs. PES scans as a function of the vertical separation (see below) were done in steps of 0.1 Å.
The interaction energy (see below) was studied as a function of the vertical separation between the two monomers in the π-stacked dimer, and as a function of the twist angle between these monomers. The latter is defined as the right-handed rotation of the upper base around the axis that runs through the center of mass of both the upper and lower base, and perpendicular to the plane of the base (see Scheme 1).
Scheme 1.
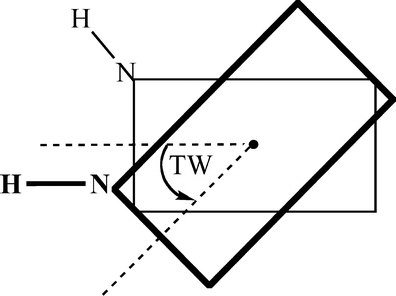
Definition of the twist angle (TW). The black dot is the center of mass
In the stacked DNA systems, the twist angle of 0° is defined as that twist angle at which the respective “glycosidic” N-H bonds (more precisely, the N-H bonds that replace the glycosidic N-C bonds to the sugar in the backbone) are oriented in parallel.
Bond-energy decomposition
The overall π-stacking energy ΔE is made up of two major components [36] (Equation 1):
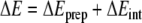 |
1 |
In this formula, the preparation energy ΔEprep is the energy needed to deform the separate molecular fragments from their equilibrium structure to the geometry that they attain in the overall molecular system. The interaction energy ΔEint is the energy released when the prepared fragments are brought together into the position they have in the overall molecule. It is analyzed for our model systems in the framework of the KS-MO model using a Morokuma-type decomposition [47] into electrostatic interaction, Pauli repulsion (or exchange repulsion), and (attractive) orbital interactions (Equation 2).
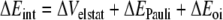 |
2 |
The term ΔVelstat corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the prepared (i.e. deformed) fragments and is usually attractive. The Pauli-repulsion, ΔEPauli, comprises the destabilizing interactions between occupied orbitals and is responsible for the steric repulsion. The orbital interaction ΔEoi in any MO model, and therefore also in Kohn-Sham theory, accounts for electron-pair bonding, charge transfer (i.e., donor-acceptor interactions between occupied orbitals on one fragment with unoccupied orbitals of the other, including the HOMO-LUMO interactions), and polarization (empty-occupied orbital mixing on one fragment due to the presence of another fragment). The orbital interaction energy can be further decomposed into the contributions from each irreducible representation ℘ of the interacting system (Equation 3) using the extended transition state (ETS) scheme developed by Ziegler and Rauk [48, 49].
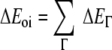 |
3 |
Results and discussion
We have analyzed π-π stacking interactions using different systems that were taken mainly from reference data present in the literature. We start with the prototypical system for studying π-π stacking, namely, the benzene dimer. The second set of reference data was taken from the supporting information of a paper by Mignon and co-workers [50], who studied hydrogen bonding and stacking in complexes of substituted benzene C6H5X with pyridine at MP2/6-31G*(0.25) with substituents X = H, F, NH2, Cl, CH3, OH, CN, COOH, CHO and NO2. All substitutions of H by another X in benzene were done at the para-position with respect to the nitrogen of pyridine (see Scheme 2). The third set of reference data was taken from a paper by Jurecka and co-workers [21], who investigated hydrogen bonding and stacking interactions in the cytosine dimer with MP2 and CCSD(T) methods, using several orientations (see Scheme 3) to investigate the potential energy surfaces. The fourth set of reference data was taken from a paper by Wu and Yang [14] (based on previous work by Hobza, Sponer and co-workers [17, 19, 22]) who studied the dependence of the stacking energy of DNA bases on the twist angle (see Scheme 4) and vertical separation using MP2/6-31G*(0.25) calculations.
Scheme 2.
Stack of substituted benzene and pyridine
Scheme 3.
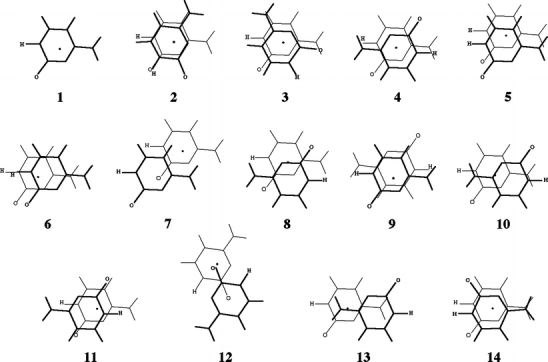
Orientations of the stacked cytosine dimer from Jurecka and co-workers ([21]). The upper base is drawn in bold, the center of mass is indicated by a black dot, and the carbonylic oxygen and the hydrogen replacing the glycosidic bond are indicated for clarity
Scheme 4.
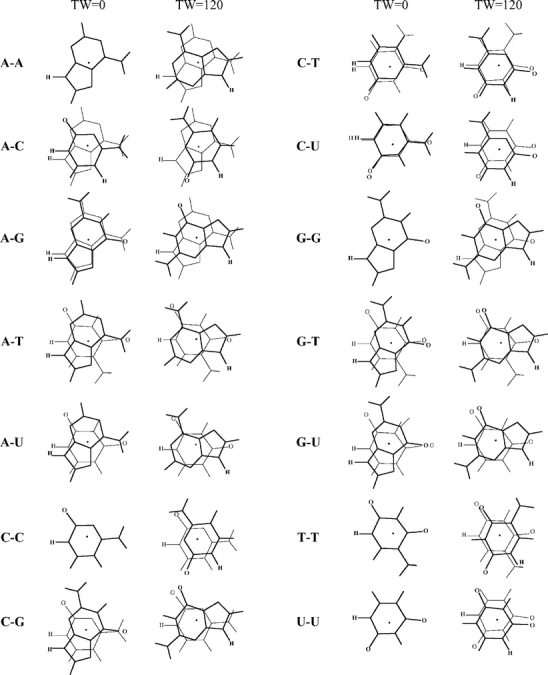
Geometries of stacked base dimers with a twist angle of 0 and 120 degrees. The upper base is drawn in bold, the center of mass is indicated by a black dot, and the hydrogens replacing the glycosidic bond are indicated for clarity. Note that for the homo dimers at zero twist angle the lower base is hidden behind the upper base
As mentioned already, the prototypical system for studying π-π stacking interactions is posed by the (parallel sandwich) benzene dimer. Because of its high symmetry (D6h), CCSD(T) energies using large basis sets (aug-cc-pVQZ) are available [51] to compare with (see Table 1). The minimum is found at 3.9 Å for this system with a stacking energy of −1.7 kcal mol−1. The standard density functionals are unable to give a proper description of this system, i.e., they either predict a purely repulsive energy surface (e.g., BP86; see Table 1), or give a shallow well (e.g., OLYP). Interestingly, the KT1 functional predicts a minimum that is very close (3.8–3.9 Å) to that of the CCSD(T) method, and has a well depth that is equally close (−1.6 kcal mol−1; see Table 1). The related KT2 and, surprisingly, the LDA functionals have a minimum at the same distance as CCSD(T) and KT1, but with a somewhat smaller well depth (−1.3 kcal mol−1). Also, the BHandH functional performs reasonably well with a similar equilibrium distance, but a reduced well depth (−0.9 kcal mol−1; see Table 1).
Table 1.
Stacking energy (in kcal mol−1) of the benzene-benzene complex as a function of the vertical separation Rvert (in Å), computed with various density functionalsa and CCSD(T)/aug-cc-pVQZ*b
| Rvert | CCSD(T)b | LDA | KT1 | KT2 | BHandH | PW91 | BLYP | BP86 | OLYP | B3LYP | X3LYP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.9 | 13.53 | 14.59 | 14.08 | 17.08 | 24.41 | 31.63 | 27.46 | 38.67 | 30.13 | 28.92 | |
| 3.0 | 8.60 | 9.29 | 9.04 | 11.27 | 17.98 | 24.20 | 20.84 | 30.93 | 22.78 | 21.65 | |
| 3.1 | 5.11 | 5.52 | 5.47 | 7.13 | 13.18 | 18.53 | 15.87 | 24.85 | 17.23 | 16.17 | |
| 3.2 | 3.71 | 2.70 | 2.90 | 2.98 | 4.23 | 9.60 | 14.22 | 12.14 | 20.05 | 13.04 | 12.06 |
| 3.3 | 1.68 | 1.06 | 1.10 | 1.29 | 2.24 | 6.93 | 10.94 | 9.34 | 16.22 | 9.89 | 8.98 |
| 3.4 | 0.30 | −0.01 | −0.09 | 0.17 | 0.92 | 4.95 | 8.45 | 7.25 | 13.14 | 7.52 | 6.68 |
| 3.5 | −0.62 | −0.68 | −0.83 | −0.54 | 0.06 | 3.48 | 6.55 | 5.68 | 10.65 | 5.73 | 4.96 |
| 3.6 | −1.19 | −1.07 | −1.27 | −0.96 | −0.45 | 2.40 | 5.10 | 4.50 | 8.63 | 4.40 | 3.69 |
| 3.7 | −1.51 | −1.27 | −1.50 | −1.17 | −0.74 | 1.59 | 3.99 | 3.62 | 6.98 | 3.39 | 2.74 |
| 3.8 | −1.66 | −1.33 | −1.58 | −1.25 | −0.86 | 1.00 | 3.15 | 2.94 | 5.62 | 2.63 | 2.04 |
| 3.9 | −1.70 | −1.31 | −1.56 | −1.25 | −0.89 | 0.57 | 2.50 | 2.43 | 4.51 | 2.06 | 1.52 |
| 4.0 | −1.67 | −1.24 | −1.48 | −1.18 | −0.85 | 0.25 | 2.00 | 2.03 | 3.60 | 1.63 | 1.14 |
| 4.1 | −1.58 | −1.13 | −1.37 | −1.09 | −0.78 | 0.02 | 1.61 | 1.72 | 2.85 | 1.30 | 0.85 |
| 4.2 | −1.46 | −1.02 | −1.24 | −0.98 | −0.68 | −0.15 | 1.31 | 1.47 | 2.24 | 1.05 | 0.64 |
| 4.3 | −0.90 | −1.11 | −0.86 | −0.58 | −0.27 | 1.07 | 1.27 | 1.75 | 0.86 | 0.49 | |
| 4.4 | −0.78 | −0.97 | −0.75 | −0.48 | −0.36 | 0.88 | 1.11 | 1.35 | 0.71 | 0.37 | |
| 4.5 | −1.08 | −0.67 | −0.85 | −0.64 | −0.39 | −0.42 | 0.73 | 0.97 | 1.03 | 0.59 | 0.28 |
| 5.0 | −0.58 | −0.28 | −0.39 | −0.26 | −0.06 | −0.45 | 0.30 | 0.52 | 0.20 | 0.26 | 0.09 |
| 5.5 | −0.27 | −0.09 | −0.15 | −0.07 | 0.08 | −0.31 | 0.13 | 0.28 | 0.00 | 0.14 | 0.04 |
| 6.0 | −0.11 | −0.01 | −0.05 | 0.00 | 0.12 | −0.16 | 0.05 | 0.15 | −0.03 | 0.08 | 0.03 |
| 6.5 | −0.04 | 0.02 | 0.00 | 0.03 | 0.12 | −0.06 | 0.02 | 0.08 | −0.03 | 0.05 | 0.03 |
| 7.0 | 0.03 | 0.02 | 0.04 | 0.11 | −0.01 | 0.00 | 0.05 | −0.01 | 0.04 | 0.03 | |
| 7.5 | 0.03 | 0.02 | 0.04 | 0.09 | 0.02 | 0.00 | 0.03 | −0.01 | 0.03 | 0.03 | |
| 8.0 | 0.03 | 0.02 | 0.09 | 0.08 | 0.01 | −0.01 | 0.02 | 0.00 | 0.02 | 0.02 |
aPost-SCF using LDA/TZ2P orbitals and densities, see Computational details
bFrom supporting information of [51]
Reference data from Mignon and co-workers
Scheme 2 shows the structure of the π-stacked complexes of pyridine with (substituted) benzene, i.e. with benzene, fluorobenzene, aminobenzene, chlorobenzene, toluene, phenol, cyanobenzene, benzoic acid, benzaldehyde and nitrobenzene. For all of these complexes the coordinates were taken from the supporting information of the original paper by Mignon and co-workers [50]. The geometry of each dimer had been fully optimized and therefore the vertical separation is different for each complex; it is found in the range of 3.2–3.4 Å.
The interaction energies for several typical density functionals are compared to the original MP2 data in Table 2. Consistent with previous reports, the mean absolute deviations (MAD) with respect to the reference MP2 data are much larger for density functionals containing the Becke88 [43] exchange functional (e.g., BP86, MAD value 7.68 kcal mol−1) than for functionals based on PW91 [52] or PBE [53] exchange (e.g., PW91, MAD value 5.33 kcal mol−1). However, these standard density functionals all show repulsive interactions, in contrast to the MP2 results that indicate bound systems (see Table 2). Much better agreement with the MP2 data is observed for the KT1, KT2 and, surprisingly, LDA functionals, with MAD values of 0.25 kcal mol−1 (see Table 2). The BHandH functional, recently [12] shown to give good agreement with MP2/CCSD(T) energies, shows a larger MAD value of 0.4 kcal mol−1 (see Table 2). Because of the uncertainty of ca. ± 0.5 kcal mol−1 in the reference MP2 data with respect to the high-level CCSD(T) data (see above), it is uncertain which of the four density functionals (LDA, KT1 , KT2 or BHandH) performs best. However, the improvement over standard density functionals is obvious and promising.
Table 2.
Stacking energy (in kcal mol−1) of substituted benzene-pyridine complexes (see Scheme 2), computed with various density functionalsa and MP2/6-31G*(0.25)b
| X= | MP2b | LDA | KT1 | KT2 | BHandH | PW91 | BLYP | BP86 | OLYP | B3LYP | X3LYP |
|---|---|---|---|---|---|---|---|---|---|---|---|
| H | −2.8 | −3.4 | −3.4 | −3.2 | −2.7 | 2.3 | 6.1 | 4.6 | 11.1 | 5.0 | 4.1 |
| F | −2.9 | −3.4 | −3.3 | −3.2 | −2.8 | 2.5 | 6.4 | 4.9 | 11.5 | 5.1 | 4.2 |
| NH2 | −3.2 | −3.6 | −3.6 | −3.3 | −3.0 | 2.2 | 6.1 | 4.7 | 11.2 | 4.9 | 3.9 |
| Cl | −3.4 | −3.4 | −3.4 | −3.2 | −2.8 | 2.6 | 6.7 | 5.1 | 11.9 | 5.4 | 4.4 |
| CH3 | −3.3 | −3.3 | −3.4 | −3.2 | −2.8 | 1.2 | 4.5 | 3.5 | 8.7 | 3.5 | 2.7 |
| OH | −2.7 | −3.2 | −3.1 | −3.0 | −2.5 | 2.8 | 6.8 | 5.2 | 11.9 | 5.5 | 4.6 |
| CN | −4.1 | −3.9 | −3.9 | −3.7 | −3.5 | 0.9 | 4.2 | 3.1 | 8.4 | 3.1 | 2.3 |
| COOH | −3.5 | −3.6 | −3.6 | −3.4 | −3.0 | 2.4 | 6.4 | 4.8 | 11.5 | 5.1 | 4.2 |
| CHO | −3.9 | −3.8 | −3.8 | −3.6 | −3.3 | 0.9 | 4.2 | 3.2 | 8.4 | 3.2 | 2.4 |
| NO2 | −3.8 | −3.8 | −3.7 | −3.6 | −3.3 | 2.0 | 5.8 | 4.3 | 10.8 | 4.6 | 3.7 |
| MADc | 0.26 | 0.25 | 0.24 | 0.39 | 5.33 | 9.07 | 7.68 | 13.90 | 7.89 | 6.99 |
aPost-SCF on LDA/TZ2P orbitals and densities, see Computational details
bFrom [50]
cMean Absolute Deviation (in kcal mol−1) of DFT energies from reference MP2 data
Reference data from Jurecka and co-workers
Scheme 3 shows the fourteen orientations of the stacked cytosine dimer that have been considered in the paper by Jurecka and co-workers [21] (with a vertical separation of 3.3 Å for the first orientation, and 3.4 Å for all others). The corresponding reference energies and our DFT interaction energies are collected in Table 3. The latter also contains the MAD values with respect to two sets of reference energies, i.e. the usual MP2/6-31G*(0.25) results (MAD1) as well as the MP2 energies obtained after complete-basis-set (CBS) extrapolation corrected for the difference between MP2 and CCSD(T) with the 6-31G*(0.25) basis set (MAD2). Similar to what was found for the benzene-pyridine systems (see above), the MAD values for standard density functionals are found between 5 and 14 kcal mol−1, resulting in many cases in erroneous repulsive stacking interactions between the cytosine fragments (see Table 3). Improved results are again obtained with LDA, KT1, KT2, and to a lesser extent BHandH, which have MAD1 values (i.e. deviations with respect to MP2/6-31G*(0.25)) of 0.9, 0.8, 0.6 and 1.5 kcal mol−1 respectively, and MAD2 values of 0.4, 0.5, 0.7 and 0.5 kcal mol−1 respectively with the CCSD(T) data (see Table 3).
Table 3.
Stacking energies (in kcal mol−1) for several orientations of the cytosine dimer (see Scheme 3), computed with various density functionals and MP2a,b
| orientation | MP2b,c | MP2ccb,d | LDA | KT1 | KT2 | BHandH | PW91 | BLYP | BP86 | OLYP | B3LYP | X3LYP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.2 | 2.5 | 2.7 | 2.3 | 2.7 | 3.9 | 8.0 | 11.7 | 10.9 | 16.5 | 10.9 | 9.9 |
| 2 | −3.1 | −3.8 | −3.7 | −3.9 | −3.5 | −3.3 | 2.6 | 6.5 | 5.4 | 12.3 | 5.2 | 4.1 |
| 3 | −7.2 | −8.9 | −8.8 | −8.7 | −8.3 | −9.0 | −2.1 | 1.7 | 0.7 | 8.0 | 0.2 | −1.0 |
| 4 | −8.3 | −9.9 | −9.4 | −9.2 | −8.9 | −10.1 | −2.9 | 0.8 | −0.1 | 6.9 | −0.9 | −2.1 |
| 5 | 0.2 | 0.3 | 0.6 | 0.1 | 0.6 | 1.5 | 6.4 | 10.3 | 9.3 | 15.7 | 9.3 | 8.3 |
| 6 | 0.5 | 0.6 | 0.8 | 0.4 | 0.8 | 1.8 | 6.8 | 10.8 | 9.7 | 16.3 | 9.8 | 8.8 |
| 7 | −0.5 | −1.0 | −0.7 | −0.9 | −0.6 | 0.2 | 2.8 | 5.5 | 5.2 | 8.7 | 5.0 | 4.2 |
| 8 | −7.3 | −9.1 | −8.4 | −8.3 | −7.9 | −8.8 | −3.0 | 0.2 | −0.2 | 5.6 | −1.2 | −2.2 |
| 9 | −7.6 | −9.1 | −8.7 | −8.5 | −8.2 | −9.4 | −2.3 | 1.5 | 0.5 | 7.3 | −0.2 | −1.4 |
| 10 | −6.6 | −8.3 | −7.9 | −7.7 | −7.5 | −8.3 | −1.8 | 1.8 | 0.9 | 7.6 | 0.3 | −0.8 |
| 11 | −7.6 | −9.4 | −8.8 | −8.5 | −8.3 | −9.5 | −2.8 | 0.6 | −0.1 | 6.2 | −1.0 | −2.1 |
| 12 | −5.5 | −7.4 | −6.7 | −6.6 | −6.2 | −7.0 | −3.6 | −1.6 | −1.4 | 1.5 | −2.4 | −3.1 |
| 13 | −7.4 | −8.8 | −8.3 | −8.1 | −7.9 | −8.6 | −3.0 | 0.4 | −0.4 | 5.2 | −1.0 | −2.0 |
| 14 | −7.0 | −9.1 | −8.8 | −8.7 | −8.4 | −9.4 | −2.1 | 1.6 | 0.7 | 8.0 | −0.1 | −1.3 |
| MAD1e | 0.94 | 0.81 | 0.60 | 1.49 | 4.87 | 8.35 | 7.58 | 13.63 | 7.06 | 6.03 | ||
| MAD2f | 0.38 | 0.47 | 0.72 | 0.52 | 6.04 | 9.52 | 8.75 | 14.80 | 8.24 | 7.21 |
aPost-SCF on LDA/TZ2P orbitals and densities, see Computational details
bFrom [21]
cMP2/6-31G*(0.25) results
dMP2 with complete-basis-set (CBS) extrapolation, i.e. MP2/CBS, corrected for Δ[CCSD(T)/6-31G*(0.25) - MP2/6-31G*(0.25)]
eMean Absolute Deviation (in kcal mol−1) of DFT energies from MP2/6-31G*(0.25) data
fMean Absolute Deviation (in kcal mol−1) of DFT energies from MP2/CBS corrected for Δ[CCSD(T)/6-31G*(0.25) - MP2/6-31G*(0.25)]
Reference data from Wu and Yang
In the paper by Wu and Yang, [14] the potential energy surface (PES) was calculated as a function of the twist angle between two stacked bases (see Scheme 1 and methodological section for the definition of the twist angle) using MP2/6-31G*(0.25), which was chosen as a reliable reference method based on the paper by Hobza and co-workers [22]. Although thymine was not included by Wu and Yang, we report here the energy profiles for all combinations of the five RNA/DNA bases, i.e., thymine, adenine, guanine, cytosine, uracil (see Scheme 4 for the geometries). The vertical separation is 3.4 Å for the C-C, G-C and G-G stacked base dimers, and 3.3 Å for all other systems. This difference in vertical separations was chosen based on earlier papers by Sponer and co-workers [19].
From the tests with the benzene dimer (Table 1), the Mignon (Table 2) and Jurecka reference data (Table 3), it is already evident that standard density functionals do not give reliable interaction energies, which is now shown to be true also for the energy profiles as function of the twist angle. Figure 1 shows the PES for two stacked bases, namely C-C and G-U, which are representative for all possible base pair combinations (the complete figure for all combinations of stacked bases can be found in the Supporting Information). Interestingly, although the standard density functionals typically underestimate the interaction energy, the shape of the PES is in all cases highly similar to that based on the more accurate MP2 data. This suggests that, at least trends and qualitative features in the rotational energy profile can be correctly reproduced with DFT which otherwise shows a (functional and basis-set dependent) constant shift with respect to the more accurate MP2 rotational profile.
Fig. 1.
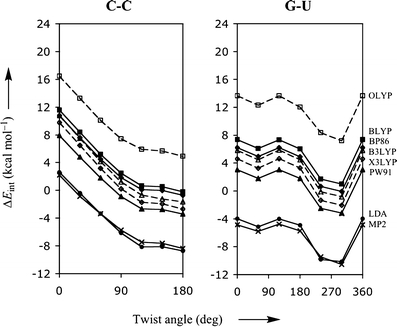
Stacking interaction (in kcal mol−1) as function of the twist angle (in degree) for π-π stacks of two bases, C-C and G-U, computed with various density functionals. The thick lineswithfilled circles, triangles, squaresand diamonds show the results obtained with LDA, PW91, BLYP, and BP86, respectively. The dashed lines with open squares, trianglesand diamonds show the results obtained with OLYP, B3LYP and X3LYP, respectively. The bold linewithcrosses represents the MP2/6-31G*(0.25) reference data
It is, however, more instructive to look at functionals that by themselves already give accurate interaction energies, such as LDA, KT1, KT2 and BHandH. Figure 2 shows the corresponding rotational-energy profiles, again for the stacked bases C-C and G-U. From Fig. 2 it is evident that the LDA, KT1, KT2, and to a lesser extent BHandH are visually (and virtually) indistinguishable from the reference MP2 data.
Fig. 2.
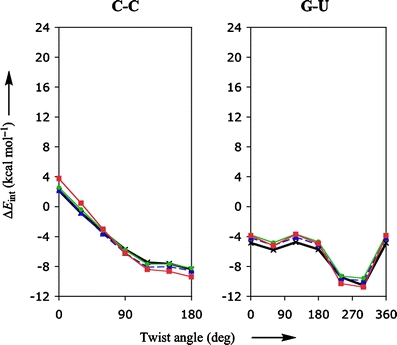
Stacking interaction (in kcal mol−1) as function of the twist angle (in degree) for π-π stacks of two bases, C-C and G-U, computed with various density functionals. The red, blue and green lines show the results obtained with BHandH, KT1 and KT2, respectively. The bold line with crosses represents the MP2/6-31G*(0.25) reference data
Figure 3 shows the interaction energy as a function of the vertical separation for both the standard (upper diagrams) and promising (lower diagrams) density functionals, together with MP2 reference curve in each of the four diagrams. Not surprisingly, the density functionals that gave larger errors for the rotational energy profile, also give larger errors for the vertical separation profiles: almost all standard density functionals show potential energy surfaces that are repulsive, or at best weakly attractive with a very shallow minimum at elongated distances. In contrast, the promising functionals (i.e., KT1, KT2, LDA and BHandH) do provide well-defined minima with equilibrium distances (3.2–3.3 Å) close to the reference MP2 data. Similar to the uncertainty in the reference energy data of some 0.5–1.0 kcal mol−1 (see above), we may expect a similar uncertainty for the vertical separation, which we very roughly estimate at 0.1–0.2 Å. The differences between the equilibrium distance of the promising density functionals and that of the reference MP2 falls well within this estimated uncertainty. Thus, KT1, KT2, LDA and BHandH perform well not only for rotational energy profiles but also for the PES as a function of the vertical separation.
Fig. 3.
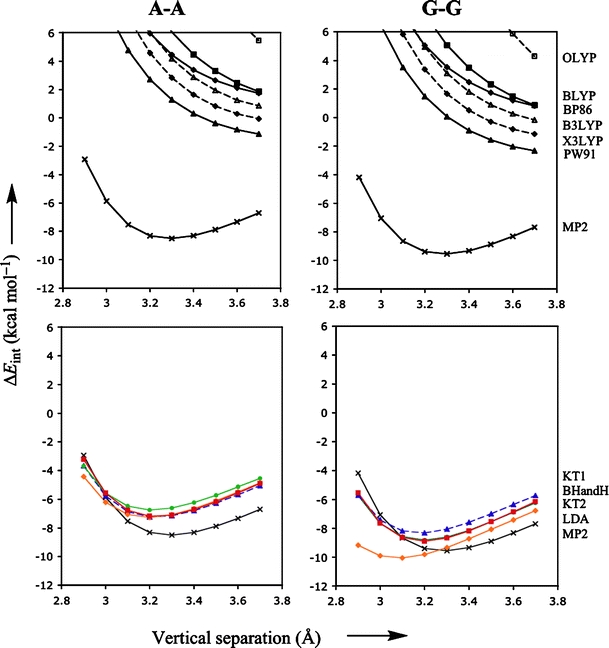
Stacking interaction (in kcal mol−1) as function of the vertical separation (in Å) for π-π stacks of two bases, A-A and G-G, computed with various density functionals. The thick lines with filled triangles, squares and diamonds in the upper diagrams show the results obtained with PW91, BLYP, and BP86, respectively. The dashed lines with open squares, triangles and diamonds in the upper diagrams show the results obtained with OLYP, B3LYP and X3LYP, respectively. The red, blue, green and orange lines in the lower diagrams that truly show well-defined minima are obtained with BHandH, KT1, KT2 and LDA respectively. The bold black line with crosses represents the MP2/6-31G*(0.25) reference data
Decomposition of interaction energy
Now that we have established the reliability of the KT1, KT2, LDA and BHandH functionals for the interaction energy of stacked DNA bases, it is interesting to study the actual interaction into greater detail. This is done through a quantitative decomposition of the interaction energy ΔEint into electrostatic attraction ΔVelstat, Pauli repulsion ΔEPauli and orbital interactions ΔEoi (see Methods). Table 4 provides the results of the energy decomposition at KT1/TZ2P for the five π-stacked homo dimers, for each one at a twist angle of 0° and 180° (which is the lowest-energy conformation) and at two different vertical separations. Note that the lowest-energy conformation is always achieved at a twist angle of 180° but that the optimal stacking distance (vertical separation) varies by 0.1 – 0.2 Å between the different π-stacked homo dimers. The energy changes by −6.8 (A-A), −11.8 (C-C), −10.2 (G–G), −11.2 (T-T) and −7.9 (U-U) kcal mol−1, respectively, when going from a twist angle of 0° to 180° (the lowest-energy conformation). This change in energy is almost completely resulting from a change in electrostatics that change by −5.4 (A-A), −13.1 (C-C), −10.3 (G-G), −6.6 (T-T) and −8.3 (U-U) kcal mol−1 respectively. The sum of Pauli repulsion and orbital interactions changes much less, by ca. 1.4 kcal mol−1 or less, except for T-T where the sum of Pauli repulsion and orbital interactions changes by 4.6 kcal mol−1 due to the influence of the peripheral methyl groups. But also the changes in each term individually, i.e., either ΔEPauli or ΔEoi, are much smaller (typically 2 to 5 times, but in some cases even more) than the changes in ΔVelstat (again, only in the case of T-T, the change in ΔEPauli is nearly as large as that in ΔVelstat). Here we note that the same energy decomposition analyses for the five π-stacked homo dimers at LDA/TZ2P instead of KT1/TZ2P yield values that differ by only 1 kcal mol−1 or less (not shown in Table 4).
Table 4.
Decomposition of interaction energiesa (in kcal mol−1) between stacked DNA bases in different geometries, computed at KT1/TZ2P
| A-A | C-C | G-G | T-T | U-U | |
|---|---|---|---|---|---|
| Twist angle 0° | |||||
| (TW, Rvert) | (0°, 3.3 Å) | (0°, 3.4 Å) | (0°, 3.4 Å) | (0°, 3.3 Å) | (0°, 3.3 Å) |
| ΔEPauli | 5.35 | 2.43 | 2.13 | 11.00 | 3.72 |
| ΔVelstat | −3.31 | 1.80 | 1.97 | −2.48 | −0.07 |
| ΔEoi | −2.30 | −1.88 | −2.49 | −5.66 | −2.11 |
| ΔEint | −0.26 | 2.35 | 1.61 | 2.86 | 1.54 |
| Lowest energy conformation | |||||
| (TW, Rvert) | (180°, 3.2 Å) | (180°, 3.1 Å) | (180°, 3.2 Å) | (180°, 3.3 Å) | (180°, 3.1 Å) |
| ΔEPauli | 5.86 | 7.01 | 4.52 | 4.28 | 6.13 |
| ΔVelstat | −8.72 | −11.32 | −8.33 | −9.04 | −8.38 |
| ΔEoi | −4.17 | −5.12 | −4.80 | −3.58 | −4.12 |
| ΔEint | −7.02 | −9.44 | −8.61 | −8.34 | −6.36 |
Additivity of interaction energies of stacked base pair dimers
With the good performance of KT1 for stacking interactions kept in mind, we went one step further, and looked also at the interactions within stacked dimersof hydrogen-bonded base pairs (see Scheme 5) [54]. The geometry was obtained by taking the geometry of one hydrogen-bonded base pair and putting another one at 3.4 Å on top of the former. The base pair dimer is stabilized by hydrogen bonding between the bases within one layer, and stacking interactions between the bases in different layers of the stack. In this case, because there are two bases per layer, there are also interactions present between bases that are, in a sense diagonally, on opposite sides and in different layers [55], the so-called cross terms. For example for the AT-AT system as shown in Scheme 5, this refers to the interaction between the thymine of the top layer with the adenine of the bottom layer.
Scheme 5.
Structure of stacked DNA base pair dimer AT-AT with twist angle of 36°. The dot represents the B-DNA helical axis of rotation.[54]
In order to investigate in more detail the importance of the various energy terms, in particular, the cross-terms, we approximate the total stacking interaction between the base pairs in the stacked base pair dimer by the sum of four pairwise interactions between two bases, i.e., we approximate the total (stacking) interaction energy ΔEint between the layers AB and CD in Scheme 6 by the sum ΔEadd of interactions A-C, B-D, A-D and B-C as shown in Equations 4a,b:
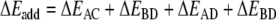 |
4a |
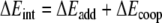 |
4b |
Scheme 6.

Additivity approximation for the π-π interaction between two stacked Watson-Crick base pairs in terms of pairwise interactions between individual bases
The remaining term ΔEcoop that, added to the approximate ΔEadd yields again the real stacking interaction ΔEint, consists of cooperativity effects between the different interactions.
In Table 5, we report the energy values resulting from the additivity scheme for the stacked AT-AT, GC-GC and AU-AU base pair dimers at three different values of the twist angle (0, 36 and 180°). Importantly, the additive approximation ΔEadd of the real stacking interaction ΔEint largely accounts for the latter. ΔEcoop has in most cases a positive sign and is small compared to either ΔEadd or ΔEint. Furthermore, the dependence of the ΔEcoop term on the twist angle is much smaller than that of the interaction energy ΔEint. For example, ΔEcoop varies from 1.0 to 1.6 kcal mol−1 whereas ΔEint varies from −1.4 to −10.7 kcal mol−1 for the stacked AT-AT base pair dimer (see Table 5). Larger cooperativity effects are found in the case of the stacked GC-GC base pair dimer, where ΔEcoop values are found between 2.0 and 4.4 kcal mol−1. Note however that the changes in ΔEcoop are again small compared to the changes in ΔEint.
Table 5.
Interaction energy (kcal mol−1) between stacked DNA base pairs in terms of the additivity scheme, computed at KT1/TZ2Pa,b
| System | TW | ΔEAC | ΔEBD | ΔEAD | ΔEBC | ΔEadd | ΔEcoop | ΔEint |
|---|---|---|---|---|---|---|---|---|
| AT-AT | 0 | −1.23 | +1.26 | −1.24 | −1.24 | −2.45 | +1.04 | −1.41 |
| AT-AT | 36 | −5.27 | −3.93 | −1.11 | −0.93 | −11.24 | +1.11 | −10.13 |
| AT-AT | 180 | −1.84 | +0.39 | −5.44 | −5.44 | −12.33 | +1.62 | −10.71 |
| AU-AU | 0 | −1.23 | +0.94 | −1.37 | −1.37 | −3.03 | +1.17 | −1.86 |
| AU-AU | 36 | −5.27 | −3.00 | −1.20 | −1.08 | −10.55 | +1.20 | −9.35 |
| AU-AU | 180 | −1.84 | +0.28 | −4.67 | −4.67 | −10.90 | +1.73 | −9.17 |
| GC-GC | 0 | +2.15 | +2.83 | −4.90 | −4.90 | −4.82 | +4.42 | −0.40 |
| GC-GC | 36 | −2.08 | −1.32 | −3.44 | −4.71 | −11.55 | +3.92 | −7.63 |
| GC-GC | 180 | −7.59 | −2.60 | −1.52 | −1.52 | −13.23 | +1.98 | −11.25 |
aSee Scheme 6: 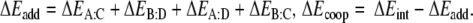
bPost-SCF on LDA/TZ2P orbitals / densities.
The cross-terms in the additivity scheme are as important as the non-cross terms, especially when rotating the base pair dimer from a twist angle of 0 degrees to finally a twist angle of 180 degrees. At the end point of 180°, the A and B base have switched, and the cross terms are no longer AD and BC, but AC and BD; this switch occurs after a twist angle of 90°. For instance for the AT-AT base pair dimer at 0°, the cross terms are stabilizing (−2.5 kcal mol−1) and dominate the ΔEadd of −2.2 kcal mol−1. At 180°, the non-cross terms dominate (−10.9 kcal mol−1) with still a substantial contribution from the cross terms (−1.4 kcal mol−1). Note also the dominance of the cross terms (−10.2 kcal mol−1) over the non-cross terms (−3.0 kcal mol−1) for the GC-GC base pair dimer at 180°. This is mainly due to favorable hydrogen-bonding interactions between the cross G-G pair.
When rotating base pair dimers from a twist angle of 0° to 36°, the cross terms in the additivity scheme reduce slightly. However, this is dominated by the increase of favorable interactions between the stacked bases. For instance for AT-AT, the cross terms drop from −2.5 to −2.0 kcal mol−1, but the non-cross terms increase from +0.0 to −9.2 kcal mol−1. The same trend is observed for the AU-AU and GC-GC base pair dimers.
Again we note that the same energy decomposition analyses for stacked DNA base pairs at LDA/TZ2P instead of KT1/TZ2P yield values that differ by only 1 kcal mol−1 or less (not shown in Table 5).
Significance of the observed trends for the structure of DNA
The stabilizing interactions for the structure of DNA mainly originate from hydrogen-bonding interactions between bases in one plane and the π-π stacking interactions between stacked bases. However, we have shown here that in addition to these terms there is also an important contribution of the cross terms that arise between bases that are neither hydrogen-bonded within one layer, nor stacked above each other. All these interaction energies can now be understood and quantified with density functional theory using appropriate functionals. For the hydrogen-bonding interactions, the BP86 and PW91 functionals seem to perform best, [3] while for π-stacking interactions KT1, KT2 and (surprisingly) LDA work well.
The experimentally observed value for the twist angle (36°) is retrieved in our study on base pair dimers as the orientation with optimal stacking interactions. We have shown that this is predominantly determined by the classical electrostatic component of the stacking energy. The rotation to a twist angle of 36° destroys part of the favorable cross terms (see above), which is however completely overcome by the increase in favorable stacking interactions between the stacked bases. The twist angle and vertical separation that are experimentally observed are of course influenced by both the sugar-phosphate backbone and the presence of solvent and/or counter ions. These factors will be tackled in forthcoming work.
Conclusions
We have analyzed π-π stacking interactions between two benzenes or benzene analogs, between two DNA bases, and between two Watson-Crick base pairs using Density Functional Theory (DFT) in combination with large basis sets. The interaction energies for a large number of density functionals have been compared with ab initio reference data. In line with previous studies, most standard density functionals recover, at best, only part of the favorable stacking interactions.
An exception is the new KT1 functional, which has been constructed to closely resemble the near-exact Zhao–Morrison–Parr (ZMP) exchange-correlation potential. Thus, not unexpectedly, KT1 gives a good description for π-π stacking energies and potential energy surfaces (PES) resulting in bound systems. Surprisingly, however, a similarly good performance is achieved with the Local Density Approximation (LDA). In view of the accurate prediction of PESes and the low computational cost, we recommend the use of either KT1 or LDA for treating the π-π stacking interactions in larger systems, using a QM/QM approach (e.g., our QUILD approach which is under development [33]) that allows this type of interaction to be separated from other types of interaction, such as hydrogen bonding but also regular covalent bonds.
To gain insight into the origin of π-π stacking interactions, we have decomposed the interaction energies into the classical electrostatic attraction, Pauli repulsion and orbital interactions. Interestingly, the electrostatic interactions appear to be the most important factor that determines the shape and depth of the PES. In the case of two stacked Watson-Crick base pairs, this classical electrostatic attraction causes a minimum to occur along the energy profile at a twist angle of 36°. Furthermore, the stabilizing contributions to the stacking interaction between two Watson-Crick base pairs is shown to originate from the inter-strand stacking terms, that is, from the interaction between two bases that are in different Watson-Crick pairs and also not directly stacked on top of each other.
The above-mentioned insight that electrostatic attraction plays an essential role in π-π stacking interactions nicely consolidates and extends the recent finding by Krapp, Bickelhaupt and Frenking [56] that classical electrostatic attraction is essential for understanding trends in bond strength of diatomic molecules. It is interesting to note that qualitative models of both “regular” chemical bonds and those of π-π stacking interactions often completely ignore classical electrostatic attraction. These qualitative models attempt to rationalize trends in bonding entirely in terms of orbital interactions (in the case of regular bonds) and dispersion interactions (in the case of π-π stacking).
Electronic supplementary material
Below is the link to the electronic supplementary material.
Energy profiles for various π-π stacked systems as a function of the twist angle and the vertical separation computed with MP2 and various density functionals (PDF 1.90 mb)
Acknowledgments
We thank the National Research School Combination - Catalysis (NRSC-C) for a postdoctoral fellowship for C.F.G., and the Netherlands organization for Scientific Research (NWO-CW and NWO-NCF) for financial support. We thank Professor W. Yang for providing us with unpublished structural data.
Footnotes
Electronic supplementary material
The online version of this article (doi:10.1007/s00894-007-0239-y) contains supplementary material, which is available to authorized users.
References
- 1.Fonseca Guerra C, Bickelhaupt FM, Snijders JG, Baerends EJ (1999) Chem Eur J 5:3581–3594 [DOI]
- 2.Fonseca Guerra C, Bickelhaupt FM, Snijders JG, Baerends EJ (2000) J Am Chem Soc 122:4117–4128 [DOI]
- 3.van der Wijst T, Fonseca Guerra C, Swart M, Bickelhaupt FM (2006) Chem Phys Lett 426:415–421 [DOI]
- 4.Allen MJ, Keal TW, Tozer DJ (2003) Chem Phys Lett 380:70–77 [DOI]
- 5.Johnson ER, DiLabio GA (2006) Chem Phys Lett 419:333–339 [DOI]
- 6.Johnson ER, Wolkow RA, DiLabio GA (2004) Chem Phys Lett 394:334–338 [DOI]
- 7.Kristyan S, Pulay P (1994) Chem Phys Lett 229:175–180 [DOI]
- 8.Lotrich VF, Bartlett RJ, Grabowski I (2005) Chem Phys Lett 405:43–48 [DOI]
- 9.Meijer EJ, Sprik M (1996) J Chem Phys 105:8684–8689 [DOI]
- 10.Schweizer WB, Dunitz JD (2006) J Chem Theor Comp 2:288–291 [DOI] [PubMed]
- 11.van Mourik T, Gdanitz RJ (2002) J Chem Phys 116:9620–9623 [DOI]
- 12.Waller MP, Robertazzi A, Platts JA, Hibbs DE, Williams PA (2006) J Comput Chem 27:491–504 [DOI] [PubMed]
- 13.Wesolowski TA, Parisel O, Ellinger Y, Weber J (1997) J Phys Chem A 101:7818–7825 [DOI]
- 14.Wu Q, Yang W (2002) J Chem Phys 116:515–524 [DOI]
- 15.Zhang YK, Pan W, Yang W (1997) J Chem Phys 107:7921–7925 [DOI]
- 16.Zhao Y, Truhlar DG (2005) Phys Chem Chem Phys 7:2701–2705 [DOI] [PubMed]
- 17.Sponer J, Hobza P (1994) J Phys Chem 98:3161–3164 [DOI]
- 18.Sponer J, Jurecka P, Marchan I, Luque FJ, Orozco M, Hobza P (2006) Chem-Eur J 12:2854–2865 [DOI] [PubMed]
- 19.Sponer J, Leszczynski J, Hobza P (1996) J Phys Chem 100:5590–5596 [DOI]
- 20.Hobza P, Sponer J (2002) J Am Chem Soc 124:11802–11808 [DOI] [PubMed]
- 21.Jurecka P, Sponer J, Hobza P (2004) J Phys Chem B 108:5466–5471 [DOI]
- 22.Hobza P, Sponer J, Polasek M (1995) J Am Chem Soc 117:792–798 [DOI]
- 23.Gerenkamp M, Grimme S (2004) Chem Phys Lett 392:229–235 [DOI]
- 24.Grimme S (2004) Chem-Eur J 10:3423–3429 [DOI] [PubMed]
- 25.Piacenza M, Grimme S (2005) ChemPhysChem 6:1554–1558 [DOI] [PubMed]
- 26.Piacenza M, Grimme S (2005) J Am Chem Soc 127:14841–14848 [DOI] [PubMed]
- 27.Grimme S, Diedrich C, Korth M (2006) Angew Chem Int Ed 45:625–629 [DOI] [PubMed]
- 28.Hesselmann A, Jansen G (2003) Chem Phys Lett 367:778–784 [DOI]
- 29.Grimme S (2004) J Comput Chem 25:1463–1473 [DOI] [PubMed]
- 30.Keal TW, Tozer DJ (2004) J Chem Phys 121:5654–5660 [DOI] [PubMed]
- 31.Keal TW, Tozer DJ (2003) J Chem Phys 119:3015–3024 [DOI]
- 32.Allen MJ, Tozer DJ (2002) J Chem Phys 117:11113–11120 [DOI]
- 33.Swart M, Bickelhaupt FM (2007) J Comput Chem 28, in press, DOI 10.1002/jcc.20834
- 34.Swart M, Solà M, Bickelhaupt FM (2007) J Comput Chem 28:1551–1560 [DOI] [PubMed]
- 35.Bento AP, Solà M, Bickelhaupt FM (2005) J Comput Chem 26:1497–1504 [DOI] [PubMed]
- 36.Bickelhaupt FM, Baerends EJ (2000) Reviews in Computational Chemistry, Vol 15. Wiley-VCH, New York
- 37.Hill G, Forde G, Hill N, Lester WA, Sokalski WA, Leszczynski J (2003) Chem Phys Lett 381:729–732 [DOI]
- 38.Baerends EJ, Autschbach J, Bérces A, Bo C, de Boeij PL, Boerrigter PM, Cavallo L, Chong DP, Deng L, Dickson RM, Ellis DE, Fan L, Fischer TH, Fonseca Guerra C, van Gisbergen SJA, Groeneveld JA, Gritsenko OV, Grüning M, Harris FE, van den Hoek P, Jacobsen H, van Kessel G, Kootstra F, van Lenthe E, McCormack DA, Michalak A, Osinga VP, Patchkovskii S, Philipsen PHT, Post D, Pye CC, Ravenek W, Ros P, Schipper PRT, Schreckenbach G, Snijders JG, Solà M, Swart M, Swerhone D, te Velde G, Vernooijs P, Versluis L, Visser O, Wang F, van Wezenbeek E, Wiesenekker G, Wolff SK, Woo TK, Yakovlev AL, Ziegler T (2005) ADF 2005.01. SCM, Amsterdam
- 39.te Velde G, Bickelhaupt FM, Baerends EJ, Fonseca Guerra C, van Gisbergen SJA, Snijders JG, Ziegler T (2001) J Comput Chem 22:931–967 [DOI]
- 40.van Lenthe E, Baerends EJ (2003) J Comput Chem 24:1142–1156 [DOI] [PubMed]
- 41.Swart M, Snijders JG (2003) Theor Chem Acc 110:34–41 Erratum: 111:156
- 42.Vosko SH, Wilk L, Nusair M (1980) Can J Phys 58:1200–1211
- 43.Becke AD (1988) Phys Rev A 38:3098 [DOI] [PubMed]
- 44.Perdew JP (1986) Phys Rev B 33:8822–8824 Erratum: 34:7406
- 45.Swart M, Ehlers AW, Lammertsma K (2004) Molec Phys 102:2467–2474 [DOI]
- 46.de Jong GT, Bickelhaupt FM (2006) J Chem Theor Comp 2:322–335 [DOI] [PubMed]
- 47.Morokuma K (1977) Acc Chem Res 10:294–300 [DOI]
- 48.Ziegler T, Rauk A (1979) Inorg Chem 18:1558–1565 [DOI]
- 49.Ziegler T, Rauk A (1979) Inorg Chem 18:1755–1759 [DOI]
- 50.Mignon P, Loverix S, De Proft F, Geerlings P (2004) J Phys Chem A 108:6038–6044 [DOI]
- 51.Omar Sinnokrot M, Sherrill CD (2004) J Phys Chem A 108:10200–10207 [DOI]
- 52.Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, Fiolhais C (1992) Phys Rev B 46:6671; E 6648 (1993) 4978 [DOI] [PubMed]
- 53.Perdew JP, Burke K, Ernzerhof M (1996) Phys Rev Lett 77:3865–3868 [DOI] [PubMed]
- 54.Olson WK, Bansal M, Burley SK, Dickerson RE, Gerstein M, Harvey SC, Heinemann U, Lu X-J, Neidle S, Shakked Z, Sklenar H, Suzuki M, Tung C-S, Westhof E, Wolberger C, Berman HM (2001) J Mol Biol 313:229–237 [DOI] [PubMed]
- 55.Guo DW, Sijbesma RP, Zuilhof H (2004) Org Lett 6:3667–3670 [DOI] [PubMed]
- 56.Krapp A, Frenking G, Bickelhaupt FM (2006) Chem-Eur J 12:9196–9216 [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Below is the link to the electronic supplementary material.
Energy profiles for various π-π stacked systems as a function of the twist angle and the vertical separation computed with MP2 and various density functionals (PDF 1.90 mb)


