Frequency of Metamerism in Natural Scenes

Abstract

Estimates of the frequency of metameric surfaces, which appear the same to the eye under one illuminant but different under another, were obtained from 50 hyperspectral images of natural scenes. The degree of metamerism was specified with respect to a color-difference measure after allowing for full chromatic adaptation. The relative frequency of metameric pairs of surfaces, expressed as a proportion of all pairs of surfaces in a scene, was very low. Depending on the criterion degree of metamerism, it ranged from about 10⁻⁶ to 10⁻⁴ for the largest illuminant change tested, which was from a daylight of correlated color temperature 25,000 K to one of 4000 K. But, given pairs of surfaces that were indistinguishable under one of these illuminants, the conditional relative frequency of metamerism was much higher, from about 10⁻² to 10⁻¹, sufficiently large to affect visual inferences about material identity.

1. INTRODUCTION

Metamerism is the phenomenon of lights appearing the same to the eye, or, more generally, sensor system, but having different spectral radiant power distributions over the visible spectrum.^1-3 Metamers arise because the number of degrees of freedom in the sensor system, three for the cones in the normal human eye or a typical camera, is smaller than the number of degrees of freedom needed to specify different spectra.^4-6 The most important example of metamerism is associated with surfaces; that is, more formally, with different spectral reflectances that with some illuminant produce equal sensor responses, or, in colorimetric terms, equal tristimulus values.¹ In practice, this metamerism may be discounted, providing that the surfaces continue to produce the same responses when the illuminant changes, for their visual identity is then an invariant and not an accident of viewing condition. Metamerism becomes a problem, however, when the reflected lights from the surfaces do become distinguishable with an illuminant change. Visual identity is then no longer a reliable guide to material identity.

Are metamers common in the natural world? There has been some speculation that they are rare^7-9; yet despite a large literature on metamerism (reviewed in Refs. 1 and 2), particularly concerning theoretical issues,^10-12 few data are available on the actual frequency of metamers in natural scenes.⁸ This is not altogether surprising, since the spatial density of any particular spectral reflectance in a natural scene is generally unknown. Moreover, any estimate of a spatial density needs to be compatible with the spatial resolution of the eye, since this sets a natural limit on the extent to which spectral reflectances may be treated as being unmixed.

To address this question and the associated methodological issues, a numerical evaluation of the discriminability of different surfaces under different daylight illuminants was performed using spectral-reflectance data obtained from 50 natural scenes with a high-resolution hyperspectral imaging system. Although the degree of the metamerism in such scenes may be expressed in terms of a metric on the space of spectral reflectances, for example, an L_p metric quantifying the differences between two reflectance functions,¹³ a more visually relevant measure is one that quantifies the extent to which initially indistinguishable spectral reflectances become visually distinguishable when the illuminant changes.¹ Such a measure is provided by a color-difference formula, which forms the basis of the CIE special metamerism index: change in illuminant,^{1, 3} but used here in conjunction with a threshold for distinguishability, as explained later. Accordingly, the frequency of metamers in each scene was estimated by the number of pairs of surfaces for which color differences were subthreshold under one phase of daylight and suprathreshold by a certain amount—the criterion degree of metamerism—under another phase of daylight.

Such frequency estimates obviously depend on the choice of threshold color difference and the criterion degree of metamerism, as well as on other variables, including the nature of the scene, the spectra of the two illuminants, and the particular color-difference formula. Nevertheless, it is still possible to make order-of-magnitude (i.e., power-of-ten) estimates of the frequency of natural metamers, and more precise comparisons of their variation across particular kinds of scenes. Thus, the relative frequency of metameric pairs, expressed as a proportion of all pairs of surfaces in a scene, was found to be very low, from about 10⁻⁶ to 10⁻⁴ for the largest illuminant change tested, which was from a daylight of correlated color temperature 25,000 K to one of 4000 K. By contrast, expressed as a proportion of just those pairs of surfaces that were indistinguishable under one of the illuminants, the relative frequency was much higher, from about 10⁻² to 10⁻¹, sufficiently large to affect visual inferences about material identity.

2. METHODS

A. Hyperspectral images

The hyperspectral imaging system that was used to acquire scene reflectances was based on a low-noise Peltier-cooled digital camera providing a spatial resolution of 1344 × 1024 pixels (Hamamatsu, model C4742-95-12ER, Hamamatsu Photonics K. K., Japan) with a fast tunable liquid-crystal filter (VariSpec, model VS-VIS2-10-HC-35-SQ, Cambridge Research & Instrumentation, Inc., Massachusetts) mounted in front of the lens, together with an infrared blocking filter. Focal length was typically set to 75 mm and aperture to f/16 or f/22 to achieve a large depth of focus. The line-spread function of the system was close to Gaussian with SD of ≈1.3 pixels at 550 nm. The intensity response at each pixel, recorded with 12-bit precision, was linear over the entire dynamic range. The peak-transmission wavelength was varied in 10-nm steps over 400–720 nm. The bandwidth (FWHM) was 10 nm at 550 nm, decreasing to 7 nm at 400 nm and increasing to 16 nm at 720 nm. Before image acquisition, the exposure time at each wavelength was determined by an automatic routine so that maximum pixel output was within 86%–90% of the CCD saturation value.

Immediately after acquisition, the spectrum of light reflected from a small neutral (Munsell N5 or N7) reference surface in the scene was recorded with a telespectroradiometer (SpectraColorimeter, PR-650, Photo Research Inc., Chatsworth, California), the calibration of which was traceable to the National Physical Laboratory. Raw images were corrected for dark noise, spatial nonuniformities (mainly off-axis vignetting), stray light, and any wavelength-dependent variations in magnification or translation. The effective spectral reflectance at each pixel was estimated by normalizing the corrected signal against that obtained from the reference surface. An analysis of the assumptions underlying this estimation procedure for directly and indirectly illuminated surfaces is given in Appendix A. Control calculations with repeated acquisitions of scenes and with scenes cropped to remove indirectly illuminated regions are described in Subsections 3.D and 3.F, respectively.

Spectral calibration of the whole system was verified against test samples in a similar way to that described in an earlier study with a different hyperspectral camera.¹⁴ Images were acquired and processed from test scenes comprising arrays of acrylic paint samples on a white background and a barium sulfate reference illuminated by an incandescent lamp. (Natural materials, e.g., leaves and flowers, were not used for calibration verification as their spatial uniformity was less predictable.) Comparison spectral reflectances were obtained at 4-nm intervals with the telespectroradiometer under the same conditions. Figure 1 shows estimated reflectances, normalized to unity, obtained with the hyperspectral imaging system (symbols) and telespectroradiometer (solid curve) for two test samples. For both, the root-mean-square error was 0.011, which fell to 0.008–0.009 when allowance was made for a 1-nm difference in wavelength calibration, smaller than the nominal spectral accuracy of both devices. For the present estimates, the system was sufficiently accurate with a 10-nm sampling interval, and, with independent sampling at each wavelength, it was capable of following the rapid variations in spectral reflectance found with some natural pigments.^{15, 16} Other details are given elsewhere.^{14, 17}

Figure 1.

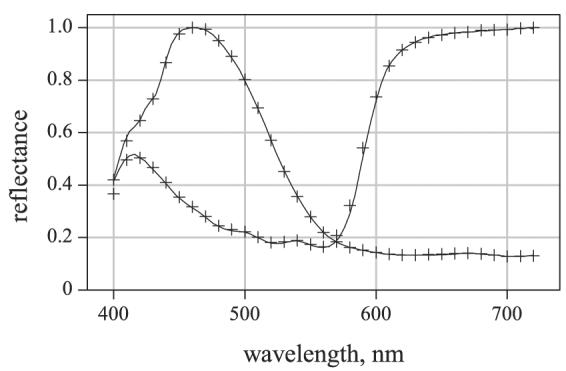
Comparison of reflectance spectra estimated by hyperspectral imaging (symbols) and by telespectroradiometry (solid curves). Data shown for two acrylic paint samples. For methods, see text and Ref. 14.

With an acceptance angle of the camera of ≈6 deg of visual angle, the spatial resolution of the system was at least as good as that of the human eye at the same viewing distance. Since it is this correspondence that is, in principle, important for the analysis⁸ rather than the absolute level of spatial resolution, each pixel was assumed to correspond to a single surface in the scene (that its spectral reflectance might be a mixture of several distinct spectral reflectances at some finer scale would be immaterial to the eye). Estimates of the frequency of indistinguishable spectra are given in Subsection 3.B, and the effects of systematically decreasing the spatial resolution of the imaging system are summarized in Subsection 3.E.

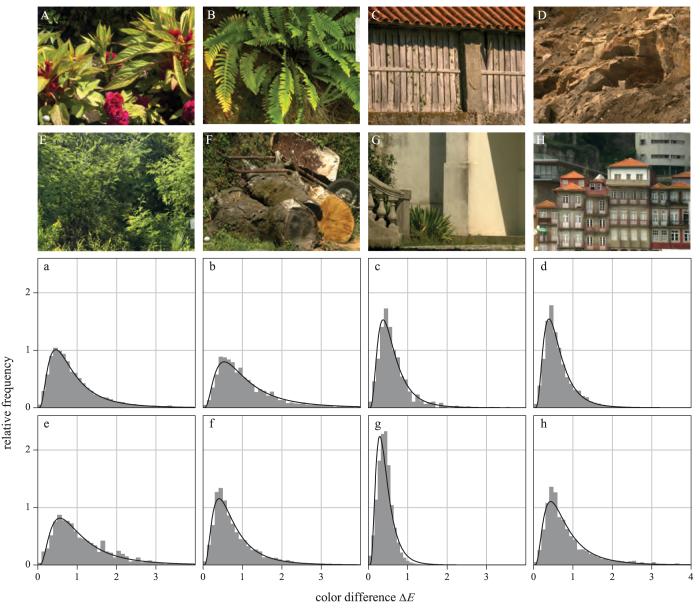
In all, 50 close-up and distant images of a large ensemble of urban and rural scenes were acquired from the Minho region of Portugal. Scenes were recorded in direct sunlight under a cloudless sky or under a sky with uniform cloud. Acquisitions containing visible light sources, including the sun and sky, were excluded, and, as far as possible, also those containing water, glass, and other materials producing specular reflections. Of the 50 scenes, 29 were classed^{18, 19} as predominantly vegetated, containing woodland, shrubland, herbaceous vegetation (e.g., grasses, ferns, flowers), and cultivated land (fields), as in Figs. 2A, 2B, 2E, and 2F; 21 were classed as predominantly nonvegetated, containing barren land (e.g., rock or stone), urban development (residential and commercial buildings), as well as farm outbuildings and painted or treated surfaces, as in Figs. 2C, 2D, 2G, and 2H.

Figure 2.

Example scenes and corresponding conditional probabilities of color differences. The eight images A–H were drawn from the 50 scenes used in this study. The small neutral spheres or rectangular plates visible in some scenes (bottom left A, F; bottom center G; right B, bottom right D) were used for calibration (or other, psychophysical experiments) and were excluded in the analysis by a mask. The relative-frequency plots a–h show the estimated conditional probabilities of the color difference ΔE between pairs of surfaces under a daylight of correlated color temperature of 4000 K given that ΔE was subthreshold under a daylight of correlated color temperature 25,000 K. Color differences were calculated with CIEDE2000,^{3, 27} the adaptation model was CMCCAT2000,²⁴ and the nominal color-difference threshold^6,29 ΔE^thr = 0.5.

B. Scene illuminant changes

In the analysis, scenes were simulated under successive, different, global daylight illuminants (see Appendix A). Changes in illuminant spectrum need to be sufficiently large to reveal metamerism, and the phases of daylight used here were taken in various combinations from those described^{1, 3} by the CIE, namely D65 and the extremes with correlated color temperatures of 4000 K and 25,000 K, characteristic of the sun and sky at different times of the day^{1, 20} (the differences in reciprocal color temperature between 4000 K and 6500 K and between 6500 K and 25,000 K are similar). These illuminants were chosen in preference to other CIE nondaylight illuminants, particularly fluorescent ones, because of the relevance of the former to vision in natural scenes. The level of illumination was assumed to be constant and such that a perfectly reflecting Lambertian surface had luminance 100 cd m⁻².

In each scene, a sample of 3000 pixels was chosen at random without replacement according to a spatially uniform distribution so as to capture the properties of the scene as a whole rather than of any particular surface in it (nonuniform sampling is considered in Subsections 2.D and 3.F). As shown later, estimates of the relative frequencies of metameric pairs differed little with larger samples of 6000 pixels. With a 1.3-pixel line-spread function, trivial correlations between pixels were excluded by avoiding adjacent pixels in the sample.

For each illuminant, the spectrum of the reflected light at each pixel in the sample was converted to tristimulus values according to the CIE 1964 standard colorimetric observer.^{1, 3} For comparison, calculations were also made with the CIE 1931 observer^{1, 3} and Judd-modified CIE observer.¹ As a preliminary to the calculation of color differences (see e.g., Refs. 21​-23), a standardized chromatic-adaptation transform CMCCAT2000²⁴ was applied to obtain the corresponding tristimulus values under a reference illuminant D65. A fixed linear transformation M defined by CMCCAT2000 was applied to convert the original tristimulus values X, Y, Z to nominal R, G, B values; these were then scaled by a diagonal (von Kries) linear transformation under the assumption of full chromatic adaptation; then the inverse transformation M⁻¹ was applied to obtain the corresponding colors X_C, Y_C, Z_C. These X_C, Y_C, Z_C values were finally converted to CIELAB L*, a*, b* values with respect to D65. Color differences between pairs of pixels for each of two selected illuminants were then derived, as described next. Similar calculations were made with a sharpened version²⁵ of the chromatic-adaptation transformation M, and with the native “wrong von Kries” scaling^{22, 26} of CIELAB alone.

C. Color differences and relative frequencies

The distinguishability of pairs of pixels was quantified with a standard color-difference formula, the CIE 2000 color-difference formula CIEDE2000,^{3, 27} which provides a reasonably uniform measure. These color differences ΔE were classified with respect to a nominal threshold value ΔE^thr. Additional calculations were made in a similar way with an alternative color-difference formula CMC⁠(1⁠:⁠c⁠) of the Colour Measurement Committee of the Society of Dyers and Colourists,^3,27 and with the default Euclidean color-difference formula of CIELAB.

With 3000 pixels in the sample, there were N = 3000×2999/2 = 4,498,500 distinct pairs (no identical spectral reflectances were recorded within the 12-bit precision of the hyperspectral camera). The number N₀ of all pairs of pixels in this sample with color differences ΔE less than ΔE^thr was determined for the first of the two selected illuminants. From this set, the number N₁ of pairs whose color differences ΔE under the second illuminant exceeded a certain multiple n = 1, …, 4 of ΔE^thr was next determined (for n > 4, frequencies were to low to estimate reliably). These multiples n defined the criterion degrees of metamerism.

The relative frequency of metameric pairs in the scene as a whole is N₁/N. Since the relative frequency of indistinguishable pairs is N₀/N, the conditional relative frequency of metameric pairs is (N₁/N)/(N₀/N) = N₁/N₀ (assuming N₀ > 0). Given a pair of indistinguishable surfaces under the first illuminant, this conditional relative frequency then estimates the probability of the pair being distinguishable under the second illuminant.

Relative frequencies were averaged separately over predominantly vegetated and nonvegetated scenes. Results are reported as logarithms to the base 10 because of the large variations in magnitude and because this transformation has a linearizing effect with the criterion degree of metamerism n.

D. Other metamerism indices and sampling regimes

The threshold-based metamerism index introduced here differs from the CIE special metamerism index: change in illuminant,³ which requires the color difference ΔE between a pair of surfaces under the first of two illuminants to be zero, a condition that makes it unsuited to a sampling application. This is because the probability of two randomly chosen natural reflectance spectra producing numerically equal tristimulus values under a particular daylight illuminant is, in principle, vanishingly small. None were found with the present data set. A more relevant requirement is that tristimulus values should merely be visually indistinguishable, that is, differ by no more than some threshold value (or, more generally, fall within some range of values defined by a psychometric function). Although the special metamerism index does allow tristimulus values not to be exactly equal, by incorporating a multiplicative adjustment (Ref. 3, Section 9.2.2.3, Note 1) or other correction,^{2, 28} the degree of approximation allowed remains arbitrary. The CMC 2002 color inconstancy index,²³ which is defined for single reflectance spectra, is also unsuited to the present application.

In using random sampling of surfaces within scenes, the present approach is neutral with respect to scene contents. It might be argued, however, that spectral reflectances should not be drawn from the same surface (such as a wall, Fig. 2G), but there are practical difficulties with this exclusive sampling approach. No matter how plain or unbroken a surface in a natural scene may appear, its spectral reflectance varies from point to point, owing to spatial variations in composition, texture, weathering, dirt, and so on (see Subsection 2.C). Introducing a physical threshold for permissible variations in “sameness” according to origin would require arbitrary categorizations and knowledge of the scene not available to the sensor system. In fact, only 3 of the 50 scenes, all classified as predominantly nonvegetated, contained smooth surfaces such as walls or pillars.

Reassuringly, uniform random sampling from such scenes still gives sensible results, even in the worst case. Thus, with a hypothetical scene of unit area consisting of one large and one small plain surface, the latter of area ε and of metameric spectral reflectance, the proportion of metameric pairs of points recorded under uniform random sampling would be 2ε(1 − ε), which is small, implying (correctly) that visual identity is a reliable guide to material identity.

3. RESULTS AND COMMENT

A. Distribution of color differences

For the purposes of illustration, consider the example scenes of Figs. 2A-2H. Beneath each image in the corresponding position (a-h) is plotted the estimated conditional relative frequency of color differences ΔE between pairs of surfaces under the second of two daylight illuminants of correlated color temperature 4000 K given that the differences ΔE were subthreshold under the first daylight illuminant of correlated color temperature 25,000 K. The adaptation model was CMCCAT2000 and the color-difference formula was CIEDE2000. The nominal threshold value ΔE^thr was set to 0.5, which is approximately equivalent²⁹ to a CIELAB threshold value ΔE_ab of 1, typical for the present task,⁶ although a value twice this size was also tested. The smooth curves are lognormal density functions, which follow the general form of the histograms, although they do not provide an exact fit. Notice the differences in the distributions with the type of scene, particularly Fig. 2e for a predominantly vegetated scene and Fig. 2g for a predominantly nonvegetated scene.

In each plot, all pairs with ΔE exceeding the nominal threshold ΔE^thr = 0.5 represent metamers. For example, for a criterion degree of metamerism of n = 2, the conditional relative frequency of metameric pairs (N₁/N₀ in Subsection 2.C) for each scene is given by the area of the tail of the distribution to the right of ΔE = 1.0 (i.e., ΔE ≥ 2ΔE^thr).

Table 1 summarizes the distributions for the 29 predominantly vegetated scenes and 21 predominantly nonvegetated scenes under three illuminant changes. Means (and SDs) of the centiles of the color differences ΔE are shown for an illuminant change from a daylight of correlated color temperature 25,000 K to 4000 K, from 4000 K to 6500 K, and from 25,000 K to 6500 K. Data for an illuminant change from 4000 K to 25,000 K were closely similar to those for 25,000 K to 4000 K and are omitted. For all three illuminant changes, mean centiles were larger with predominantly vegetated scenes than with predominantly nonvegetated scenes.

Table 1.

Centiles of color differences ΔE under the second of two illuminants for pairs of surfaces with ΔE < 0.5 under the first illuminant,^a calculated with color-difference formula CIEDE2000^{3, 27} and adaptation model CMCCAT2000²⁴

		Centilea
Illuminants	Scene	50	75	90	95	99
25,000 K–4000 K	vegetated	0.77	1.26	1.89	2.41	3.60
		(0.44)	(0.79)	(1.25)	(1.63)	(2.27)
	nonvegetated	0.57	0.86	1.27	1.60	2.42
		(0.13)	(0.27)	(0.44)	(0.58)	(0.90)
4000 K–6500 K	vegetated	0.53	0.75	1.04	1.27	1.84
		(0.16)	(0.35)	(0.55)	(0.69)	(1.17)
	nonvegetated	0.45	0.60	0.79	0.95	1.30
		(0.05)	(0.10)	(0.19)	(0.27)	(0.40)
25,000 K–6500 K	vegetated	0.54	0.78	1.12	1.41	2.10
		(0.18)	(0.36)	(0.59)	(0.80)	(1.22)
	nonvegetated	0.45	0.59	0.80	0.98	1.40
		(0.05)	(0.11)	(0.21)	(0.30)	(0.47)

^aEntries show means (SDs) of median and upper centiles evaluated over 29 predominantly vegetated scenes (e.g., trees, shrubs, grasses, flowers) and 21 predominantly nonvegetated scenes (e.g., buildings, painted or treated surfaces, rocks, stone) under successive daylight illuminants labeled by correlated color temperature. Number of pairs of surfaces sampled in each scene was 4,498,500. Data for 4000 K – 25,000 K were similar to those for 25,000 K – 4000 K and are not shown. The observer was the CIE 1964 standard observer.3

B. Relative frequencies of metamers

The estimated unconditional and conditional relative frequencies of metameric pairs (N₁/N and N₁/N₀, respectively) are shown in Table 2 for the same conditions as in Table 1, namely, adaptation model CMCCAT2000, color-difference formula CIEDE2000, and nominal discrimination threshold ΔE^thr = 0.5. Means (and SDs) of log₁₀ relative frequencies are shown for the 29 predominantly vegetated scenes and 21 predominantly nonvegetated scenes for an illuminant change from a daylight of correlated color temperature 25,000 K to 4000 K, from 4000 K to 6500 K, and from 25,000 K to 6500 K. Entries for n = 0 are for pairs of surfaces with subthreshold color differences, i.e., ΔE < ΔE^thr, under the first illuminant; those for n = 1, …, 4 are for pairs of surfaces with ΔE < ΔE^thr under the first illuminant and threshold or suprathreshold color differences under the second illuminant, i.e., ΔE ≥ ΔE^thr, ΔE ≥ 2ΔE^thr, ΔE ≥ 3ΔE^thr, ΔE ≥ 4ΔE^thr, respectively.

Table 2.

Relative frequencies and conditional relative frequencies of metameric pairs of surfaces in natural scenes, calculated with color-difference formula CIEDE2000,^{3, 27} adaptation model CMCCAT2000,²⁴ and nominal discrimination threshold ΔE^thr = 0.5^a

			Criterion degree of metamerism na
Illuminants	Scene	Estimate	0	1	2	3	4
25,000 K–4000 K	vegetated	unconditional	−3.58	−3.77	−4.16	−4.56	−4.95
			(0.42)	(0.34)	(0.36)	(0.43)	(0.50)
		conditional		−0.19	−0.59	−0.99	−1.37
				(0.14)	(0.28)	(0.45)	(0.60)
	nonvegetated	unconditional	−3.43	−3.71	−4.32	−4.80	−5.29
			(0.40)	(0.33)	(0.31)	(0.41)	(0.55)
		conditional		−0.28	−0.88	−1.37	−1.82
				(0.13)	(0.40)	(0.56)	(0.64)
4000 K–6500 K	vegetated	unconditional	−3.57	−3.91	−4.81	−5.78	−6.32
			(0.45)	(0.42)	(0.47)	(0.81)	(0.81)
		conditional		−0.34	−1.24	−2.11	−2.65
				(0.12)	(0.48)	(0.86)	(0.96)
	nonvegetated	unconditional	−3.39	−3.85	−5.02	−5.98	−6.63
			(0.41)	(0.37)	(0.52)	(0.74)	(0.60)
		conditional		−0.45	−1.63	−2.51	−3.13
				(0.16)	(0.66)	(0.83)	(0.69)
25,000 K–6500 K	vegetated	unconditional	−3.58	−3.91	−4.67	−5.36	−6.06
			(0.42)	(0.34)	(0.45)	(0.61)	(0.85)
		conditional		−0.34	−1.09	−1.80	−2.35
				(0.17)	(0.46)	(0.75)	(0.95)
	nonvegetated	unconditional	−3.43	−3.90	−5.01	−5.92	−6.48
			(0.40)	(0.32)	(0.55)	(0.74)	(0.62)
		conditional		−0.47	−1.55	−2.41	−2.97
				(0.16)	(0.59)	(0.85)	(0.77)

^aEntries show means (SDs) of log₁₀ relative frequency over 29 predominantly vegetated scenes and 21 predominantly nonvegetated scenes under successive daylight illuminants labeled by correlated color temperature. Number of pairs of surfaces sampled in each scene was 4,498,500. Entries for n = 0 are for pairs of surfaces with subthreshold color differences, i.e., ΔE < ΔE^thr, under the first illuminant and any color difference under the second illuminant; those for n = 1, …, 4 are for pairs of surfaces with ΔE < ΔE^thr under the first illuminant and suprathreshold color differences under the second illuminant, i.e., ΔE ≥ ΔE^thr, ΔE ≥ 2ΔE^thr, ΔE ≥ 3ΔE^thr, ΔE ≥ 4ΔE^thr, respectively. Conditional relative frequencies are not defined for n = 0. The observer was the CIE 1964 standard observer.3

Increasing the number of sample points from 3000 to 6000 (i.e., number of pairs from N = 3000×2999/2 = 4,498,500 to N = 6000×5999/2 = 17,997,000) and changing the observer from the CIE 1964 standard observer^{1, 3} to the CIE 1931 standard observer^{1, 3} or Judd-modified CIE observer¹ had little effect, with rms differences in log relative frequency ≤0.2^*. Reversing the direction of illuminant change, i.e., from 4000 K to 25,000 K instead of from 25,000 K to 4000 K, produced a rms difference in log relative frequency of ≈0.08.

Smaller changes in illuminant, i.e., from 4000 K to 6500 K and from 25,000 K to 6500 K, produced fewer metameric pairs. The reduction in mean log relative frequency ranged from ≈0.2 with a criterion degree of metamerism of n = 1 (i.e., ΔE ≥ ΔE^thr) to ≈1.2 with n = 4 (i.e., ΔE ≥ 4ΔE^thr).

The effect of choosing a larger nominal discrimination threshold of ΔE^thr = 1.0 is shown in Table 3 for illuminant changes only from 25,000 K to 4000 K. On average, the mean log relative frequency of metameric pairs with a criterion degree of metamerism of n = 1 increased by ≈0.7 relative to the corresponding value in Table 2 with ΔE^thr = 0.5, but with n = 4 decreased by ≈0.6 (conditional relative frequencies are discussed later). Why these opposite effects occur is not immediately obvious, although a partial rationale is provided in Appendix B.

Table 3.

Relative frequencies and conditional relative frequencies of metameric pairs of surfaces in natural scenes, calculated with color-difference formula CIEDE2000,^{3, 27} adaptation model CMCCAT2000,²⁴ and nominal discrimination threshold ΔE^thr = 1.0^a

			Criterion degree of metamerism na
Illuminants	Scene	Estimate	0	1	2	3	4
25,000 K–4000 K	vegetated	unconditional	−2.74	−3.08	−3.86	−4.58	−5.33
			(0.36)	(0.33)	(0.49)	(0.65)	(0.92)
		conditional		−0.34	−1.13	−1.84	−2.54
				(0.15)	(0.43)	(0.69)	(0.99)
	nonvegetated	unconditional	−2.63	−3.09	−4.17	−5.09	−6.05
			(0.35)	(0.28)	(0.44)	(0.69)	(0.84)
		conditional		−0.47	−1.54	−2.44	−3.29
				(0.16)	(0.56)	(0.78)	(0.92)

^aOther details as for Table 2.

The effect of replacing the color-difference formula CIEDE2000 in Tables 2 and 3 by the CMC⁠(l⁠:⁠c⁠) color-difference formula is shown in Tables 4 and 5, respectively. Rms differences between corresponding mean log relative frequencies for the two color-difference formulas were ≈0.2.

Table 4.

Relative frequencies and conditional relative frequencies of metameric pairs of surfaces in natural scenes, calculated with color-difference formula CMC⁠(1⁠:⁠c⁠),^{3, 27} adaptation model CMCCAT2000,²⁴ and nominal discrimination threshold ΔE^thr = 0.5^a

			Criterion degree of metamerism na
Illuminants	Scene	Estimate	0	1	2	3	4
25,000 K–4000 K	vegetated	unconditional	−3.84	−4.02	−4.44	−4.83	−5.16
			(0.43)	(0.32)	(0.33)	(0.41)	(0.48)
		conditional		−0.18	−0.60	−0.99	−1.32
				(0.20)	(0.43)	(0.54)	(0.65)
	nonvegetated	unconditional	−3.63	−3.89	−4.48	−4.98	−5.36
			(0.40)	(0.32)	(0.26)	(0.50)	(0.46)
		conditional		−0.26	−0.85	−1.33	−1.72
				(0.14)	(0.41)	(0.59)	(0.64)

^aOther details as for Table 2.

Table 5.

Relative frequencies and conditional relative frequencies of metameric pairs of surfaces in natural scenes, calculated with color-difference formula CMC⁠(1⁠:⁠c⁠),^{3, 27} adaptation model CMCCAT2000,²⁴ and nominal discrimination threshold ΔE^thr = 1.0^a

			Criterion degree of metamerism na
Illuminants	Scene	Estimate	0	1	2	3	4
25,000 K–4000 K	vegetated	unconditional	−2.98	−3.31	−4.14	−4.83	−5.52
			(0.37)	(0.31)	(0.47)	(0.64)	(0.93)
		conditional		−0.33	−1.16	−1.86	−2.48
				(0.19)	(0.54)	(0.78)	(1.01)
	nonvegetated	unconditional	−2.81	−3.24	−4.26	−5.16	−5.91
			(0.35)	(0.27)	(0.37)	(0.64)	(0.74)
		conditional		−0.42	−1.45	−2.31	−3.06
				(0.15)	(0.53)	(0.76)	(0.91)

^aOther details as for Table 4.

There was little effect of using a sharp²⁵ chromatic-adaptation transform. Rms differences between mean log relative frequencies in Tables 2-5 and the corresponding values obtained with a sharp transform were <0.1.

As a final exercise, simple estimates of the relative frequency of metameric pairs were obtained without a standard adaptation model (e.g., CMCCAT2000) or an approximately uniform color-difference formula (e.g., CIEDE2000). Instead, tristimulus values X, Y, Z for each pixel in the scene under the first of the two selected illuminants were converted directly to CIELAB L*, a*, b* values with respect to D65 and color differences between pairs of pixels evaluated with respect to the Euclidean metric ΔE = (ΔL*² + Δa*² + Δb*²)^1/2. The same calculation was performed for the second illuminant. The resulting frequency estimates are shown in Table 6 for an illuminant change from 25,000 K to 4000 K and a nominal discrimination threshold ΔE^thr = 1.0. Despite the limitations of CIELAB as an adaptation model and its nonuniformity as a color-difference measure,²² mean log relative frequencies were broadly similar to those with CMCCAT2000 and CIEDE2000 for predominantly vegetated scenes, although for predominantly nonvegetated scenes estimates were markedly lower. Rms differences in corresponding mean log relative frequencies were ≈0.6 with respect to CIEDE2000 with ΔE^thr = 0.5 (Table 2) and ≈0.3 with ΔE^thr = 1.0 (Table 3).

Table 6.

Relative frequencies and conditional relative frequencies of metameric pairs of surfaces in natural scenes, calculated from CIELAB³ alone, with nominal discrimination threshold ΔE^thr = 1.0^a

			Criterion degree of metamerism na
Illuminants	Scene	Estimate	0	1	2	3	4
25,000 K–4000 K	vegetated	unconditional	−3.00	−3.24	−3.98	−4.71	−5.41
			(0.47)	(0.39)	(0.41)	(0.59)	(0.84)
		conditional		−0.24	−0.97	−1.71	−2.37
				(0.17)	(0.49)	(0.80)	(1.02)
	nonvegetated	unconditional	−2.82	−3.20	−4.48	−5.60	−6.43
			(0.43)	(0.33)	(0.44)	(0.72)	(0.66)
		conditional		−0.38	−1.66	−2.73	−3.52
				(0.14)	(0.63)	(0.84)	(0.90)

^aOther details as for Table 2.

A summary of the effects of the nine different models of chromatic adaptation, color-difference formula, and threshold (including the simple CIELAB calculation with ΔE^thr = 1.0) is presented in Fig. 3 for the largest illuminant change, from 25,000 K to 4000 K. The estimated log relative frequency of metameric pairs averaged over scenes is plotted against the criterion degree of metamerism n. Data for predominantly vegetated and nonvegetated scenes are shown by solid and open symbols, respectively. For both types of scenes, there was an approximately linear downward trend (attributable to the underlying approximately lognormal distributions illustrated in Fig. 2), although there was a small difference in slope. More specifically, for predominantly vegetated scenes, the mean log relative frequency of metameric pairs varied from approximately −3.5 at n = 1 to approximately −5.2 at n = 4; for predominantly nonvegetated scenes, it varied from approximately −3.5 at n = 1 to approximately −5.7 at n = 4 (data from the simple CIELAB estimate were omitted). The difference in slopes was not statistically significant over the two types of scenes (bootstrap test based on 1000 replications, with resampling over models³⁰). The higher group of values at n = 1 in Fig. 3 was associated with the higher nominal discrimination threshold ΔE^thr = 1.0 (see Appendix B).

Figure 3.

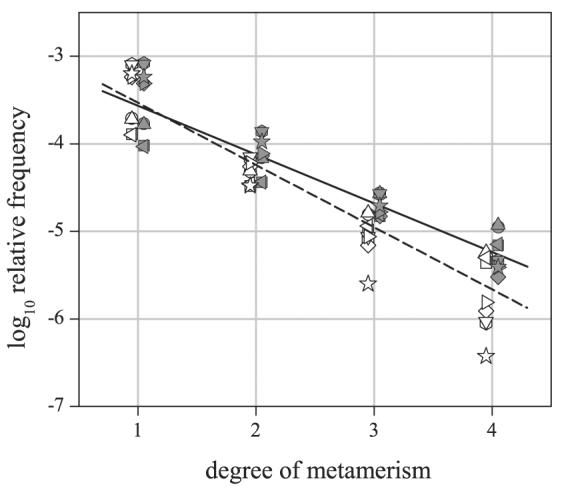
Log relative frequency of metameric pairs as a function of criterion degree of metamerism n, i.e., such that color differences ΔE were at least n times a nominal threshold ΔE^thr. The illuminant change was from a daylight of correlated color temperature 25,000 K to one of 4000 K. Data for predominantly vegetated and nonvegetated scenes are shown by solid and open symbols, respectively, offset slightly for clarity. Solid and dashed straight lines are the corresponding linear regressions, excluding data from a simple CIELAB estimate (☆). Different models of color-difference measure,^{3, 27} chromatic adaptation,²⁴ and nominal threshold^{6, 29} are indicated by different symbols (○CMCCAT2000, CIEDE2000, ΔE^thr = 0.5; CMCCAT2000, CIEDE2000, ΔE^thr = 1.0; □ CMCCAT2000, CMC⁠(1⁠:⁠c⁠), ΔE^thr = 0.5; ◇ CMCCAT2000, CMC⁠(1⁠:⁠c⁠), ΔE^thr = 1.0; △ Sharp²⁵ CMCCAT2000, CIEDE2000, ΔE^thr = 0.5; ▽ Sharp CMCCAT2000, CIEDE2000, ΔE^thr = 1.0; = ◁ Sharp CMCCAT2000, CMC⁠(1⁠:⁠c⁠), ΔE^thr = 0.5; ▷ Sharp CMCCAT2000, CMC⁠(1⁠:⁠c⁠), ΔE^thr = 1.0; ☆ CIELAB, ΔE^thr = 1.0).

There was a similar downward trend, not shown here, in the mean log conditional relative frequency of metameric pairs (unconditional and conditional relative frequencies differ by a scaling factor constant with n), but values were much higher. On average, for predominantly vegetated scenes, the mean log conditional relative frequency varied from approximately −0.3^* at n = 1 to approximately −1.9^* at n = 4, and for predominantly nonvegetated scenes, it varied from approximately −0.4^* at n = 1 to approximately −2.5^* at n = 4.

C. Differences between scenes

Although the 50 scenes used for this analysis represented a broad range of vegetated and nonvegetated environments involving most of the main land-cover classifications^{18, 19} and acquired over a range of viewing distances, there was unexpectedly little variation in the log relative frequency of metameric pairs, even between predominantly vegetated and nonvegetated scenes. From Table 2, for a criterion degree of metamerism of n = 1 (i.e., ΔE ≥ ΔE^thr), the average SD of the log relative frequency for predominantly vegetated scenes was 0.37 and for predominantly nonvegetated scenes 0.34, each less than one-tenth the magnitude of the mean. If more scenes had been included, then providing that they maintained a reasonable level of diversity, it seems unlikely that the estimates would have differed much.

Even so, the differences that were found between individual scenes appear systematic. As shown in Subsection 3.D, estimates of the log relative frequency of metameric pairs changed little on re-imaging the scene. Moreover, there are evident differences in the shapes of the histograms of the eight example scenes of Fig. 2: The maxima of the fitted lognormal distributions ranged from ΔE = 0.29 to ΔE = 0.56, each with standard error less than 0.02 (estimated with a bootstrap based on 1000 replications, with resampling over color differences³⁰).

D. Repeatability of measurements

Estimates of the frequencies of metamers of the kind obtained here depend on the reliability of the hyperspectral data. Evidence for the fidelity of the reflectance estimates has been summarized in Subsection 2.A and elsewhere,^{14, 17} but how repeatable are the estimates of log relative frequency?

Although just one hyperspectral image of each scene was used for the present analysis, each scene was actually imaged several times, at intervals typically of 5–20 min, depending on the conditions in the field. Small changes in the position of the sun can produce large changes in reflected radiance from surfaces close to producing specular reflection, as well as other changes in the distribution of shadows. Still, as an imperfect control on the repeatability of the acquisition, the relative frequencies of metameric pairs were recalculated for the eight scenes of Fig. 2 with each calculation based on one of the alternative hyperspectral images. As in Table 2, the color-difference formula was CIEDE2000, the adaptation model CMCCAT2000, the nominal discrimination threshold ΔE^thr = 0.5, and the illuminant change was the largest tested, from a daylight of correlated color temperature 25,000 K to one of 4000K. For a criterion degree of metamerism of n = 1 (i.e., ΔE ≥ ΔE^thr), the mean log relative frequency over the original eight images was −3.74 and for the alternative set −3.77. The smallest difference in log relative frequencies between original and alternative images was 0.003 and the largest 0.16; the rms difference was 0.098. For comparison, the rms difference between the pairs of the original eight images was 0.50.

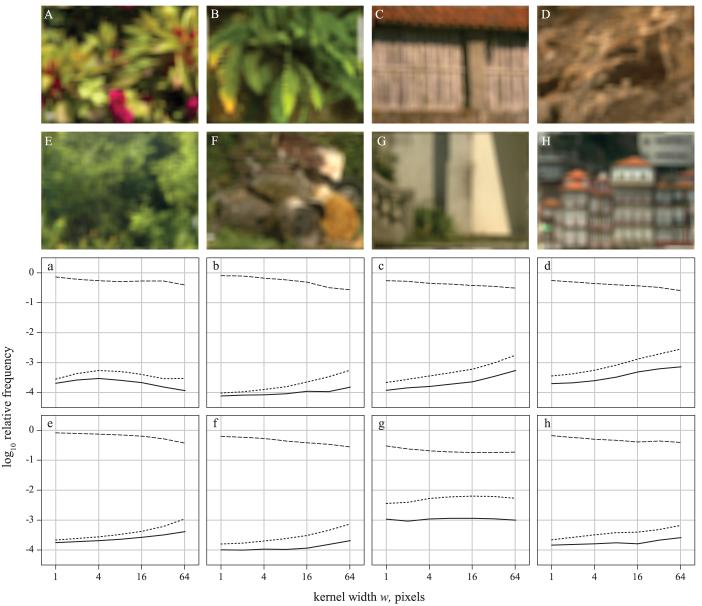
E. Mixing reflection spectra

If images had been acquired with a hyperspectral system of lower spatial resolution (or sampled by the eye at a greater viewing distance), the effective mixing of reflectance spectra would have been greater, but the influence on estimates of the frequency of metameric pairs is not easy to predict. Figures 4A-4H shows images of the eight example scenes of Fig. 2 after blurring reflectance spectra by local spatial averaging with a fixed kernel of width w = 64 pixels. Beneath each image in the corresponding position (a–h) is plotted against w on a log scale, the log of the estimated relative frequency of pairs of surfaces with subthreshold color differences, i.e., ΔE < ΔE^thr, under a daylight of 25,000 K (dotted curve) and the log of the estimated relative frequency (solid curve) and conditional relative frequency (dashed curve) of metameric pairs (N₁/N and N₁/N₀, respectively) for a criterion degree of metamerism of n = 1 (i.e., ΔE ≥ ΔE^thr), under a daylight of 4000 K. The color-difference formula was CIEDE2000, the adaptation model CMCCAT2000, and the nominal discrimination threshold ΔE^thr = 0.5. Kernel width ranged from w = 1 pixel (no averaging) to w = 64 pixels (increasing w much beyond this value introduced detectable image-boundary effects). For comparison, the line-spread function of the hyperspectral system was, as noted earlier, ≈1.3 pixels.

Figure 4.

Images of blurred reflectance spectra and variations in relative frequencies of metamers with amount of blur. The eight images A–H show for the eight example scenes of Fig. 2 the effects of local spatial averaging of reflectance functions with a fixed kernel of width w = 64 pixels. The corresponding graphs a–h show plotted against w, on a log scale, the log of the estimated relative frequency of pairs of surfaces with nominally subthreshold color differences, i.e., ΔE < ΔE^thr, under a daylight of correlated color temperature 25,000 K (dotted curve) and the log of the estimated relative frequency (solid curve) and conditional relative frequency (dashed line) of metameric pairs for a criterion degree of metamerism of n = 1, i.e., ΔE ≥ ΔE^thr, under a daylight of 4000 K (with threshold^{6, 29} ΔE^thr = 0.5).

The effect of moderate blurring on the estimated log relative frequency of metameric pairs was small, varying less than 0.2 with kernel widths w ≤ 4 pixels for all eight scenes (there was also little corresponding variation in the relative frequency of indistinguishable pairs). For five of the scenes, the variation in the estimate remained less than 0.4 over the full range of widths w ≤ 64 pixels, but for the relatively homogenous scenes C and D, estimates increased by 0.7 and 0.6 respectively.

F. Effect of shadows

Treating the spectral reflectance of a shadowed region as if it were under the same illuminant as an unshadowed region might be argued to introduce a confound that influenced the estimated frequencies of metamerism.¹⁴ The foregoing calculations assumed for simplicity that the global illuminants were uniform across corresponding pairs of surfaces in the scene, but if one of the surfaces were directly illuminated and the other were in shadow, then although the incident lights might have been related (e.g., coming mainly from the sun at one surface and from the sky at the other), their spectra would have been different. There would also have been more subtle variations in illuminant spectra arising, for example, from mutual reflections between surfaces. As a counter to these concerns, the analysis of Appendix A suggests that the device of treating indirectly illuminated surfaces as if they were illuminated directly but had different effective spectral reflectances still yields a plausible estimate of the frequency of metamerism.

Nevertheless, to test whether these estimates were consistent with those obtained from directly illuminated surfaces alone, the hyperspectral images of a subset of eight scenes, three predominantly vegetated and five predominantly nonvegetated (including those in Figs. 2A, 2C, 2D, 2E, and 2G) were individually masked to leave unshadowed regions only. The proportion of the image that was excluded from the analysis varied from 27% to 75% over the eight scenes. Estimates of the relative frequency of metameric pairs were obtained, as in Table 2, with the color-difference formula CIEDE2000, adaptation model CMCCAT2000, nominal discrimination threshold ΔE^thr = 0.5, and illuminant change from a daylight of correlated color temperature 25,000 K to one of 4000K.

There was little effect of excluding shadowed regions. The mean log relative frequency of metameric pairs was 0.1 less than the value obtained with the original unmasked images for each of the four criterion degrees of metamerism, n = 1, 2, 3, and 4.

G. Differences in color differences and generalized metamerism

Metamerism may be regarded as a special case of a more comprehensive measure of the colorimetric instability of scenes. That is, a degree of generalized metamerism may be defined that describes for any pair of surfaces the extent to which their usually non-zero difference in color appearance changes with a change in illuminant³¹ (to be distinguished from a general index of metamerism,^{28, 32} and from paramerism;³³ see also Subsection 2.D). Metamerism is therefore generalized metamerism in which the initial difference in color appearance is zero. To what extent, then, does the degree of threshold-based metamerism of the kind used here predict the degree of generalized metamerism?

Suppose that with respect to some color-difference formula the color difference between a pair of surfaces under the first of two selected illuminants is ΔE₁, based on differences in lightness, chroma, and hue of ΔL₁, ΔC₁, and ΔH₁, respectively. Suppose, analogously, that the color difference under the second illuminant is ΔE₂, based on differences in lightness, chroma, and hue of ΔL₂, ΔC₂, and ΔH₂, respectively. Let the corresponding differences in these differences be Δ²L = ΔL₂ − ΔL₁, Δ²C = ΔC₂ − ΔC₁, and Δ²H = ΔH₂ − ΔH₁. These second differences may be combined to form an overall second color difference Δ²E, which defines the degree of generalized metamerism. When ΔE₁ = 0, the second difference Δ²E coincides with the standard special index of metamerism.^1,3

Figure 5 shows the median of the distribution of Δ²E for each scene plotted against the median of the distribution of Δ²E with ΔE₁ < ΔE^thr. The latter median is closely related to the median of the distribution of ΔE₂ with ΔE₁ < ΔE^thr summarized in Table 1 (over scenes, the Pearson correlation coefficient of med{Δ²E | ΔE₁ < ΔE^thr} and med{ΔE₂ | ΔE₁ < ΔE^thr} was >0.98). As before, the color-difference formula was CIEDE2000, the adaptation model CMCCAT2000, and the illuminant change was from a daylight of correlated color temperature 25,000 K to one of 4000K. Data from the 29 predominantly vegetated scenes are shown by solid symbols and from the 21 predominantly nonvegetated scenes by open symbols. The straight line is a linear regression, which produced a correlation coefficient of 0.62. Although there are some outlying points that appear influential, the correlation was robust: The standard error of the correlation coefficient was 0.12, estimated with a bootstrap based on 1000 replications, with resampling over scenes.³⁰ While not immediately obvious from the plot, the estimated frequency of generalized metamers in scenes was very much higher than the frequency of metamers.

Figure 5.

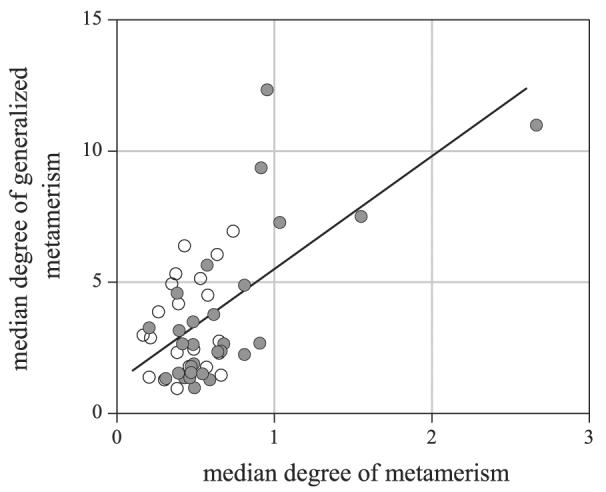
Relationship between generalized metamerism and metamerism. The median of the distribution of Δ²E for each scene under successive illuminants is plotted against the median of the distribution of Δ²E with ΔE₁ < ΔE^thr. Color differences ΔE₁ under the first illuminant and second differences Δ²E (see text) were calculated with respect to CIEDE20002^{3, 27}; the adaptation model was CMCCAT2000,²⁴ and the illuminant change was from a daylight of correlated color temperature 25,000 K to one of 4000K. The nominal color-difference threshold^{6, 29} ΔE^thr = 0.5. Data from 29 predominantly vegetated scenes are shown by solid circles and from 21 predominantly nonvegetated scenes by open circles. The straight line is a linear regression.

H. Spatial statistics

Although sampling within scenes was by pixels, it is possible that the more extended spatial properties of scenes might influence the frequency of metamers (see Subsection 2.D). A useful summary spatial statistic for natural images is the spatial power or amplitude spectrum, which is a second-order statistic. In general, the amplitude of the spectrum falls off as the reciprocal of the spatial frequency.³⁴ Both second- and higher-order statistics are important in determining spatial discrimination performance.^35-37

To test whether the amplitude spectrum might be relevant here, the discrete two-dimensional Fourier transform of the luminance distribution in each scene under a daylight of correlated color temperature 6500 K was calculated and the log of the absolute value of the amplitude plotted against log spatial frequency averaged over horizontal and vertical directions (results not shown here). On these log-log plots, the amplitude spectra were well described by linear regressions, with the correlation coefficient varying from −0.90 to −0.98 over the 50 scenes. The gradient varied from −1.6 to −1.0 (cf. Refs. 35, 36, 38, and 39), but explained little of the variation in log relative frequency of metamers: The proportion R² of variance accounted for was <2%.

4. GENERAL DISCUSSION

A. Probability of metamerism

The relative frequency of metameric pairs of surfaces in natural scenes appears to be very low. From the present analysis of 50 hyperspectral images, about 10⁻⁶ to 10⁻⁴ of all pairs of surfaces were indistinguishable under a daylight of correlated color temperature 25,000 K and distinguishable by a certain criterion degree under one of 4000 K, independent of whether the scene was classified as predominantly vegetated or nonvegetated. The estimates were robust, varying little with chromatic-adaptation model and color-difference formula. Differences between estimates from individual scenes were reliable, as were repetitions of estimates from individual scenes.

For predominantly vegetated scenes, the relative frequency of metamers was found to decline slightly less rapidly with increasing criterion degree of metamerism, and, with sufficiently high degrees of metamerism, the frequency was always higher than for predominantly nonvegetated scenes. The higher metamerism associated with foliage may be due to the presence of chlorophylls and carotenoids, which provide multiple absorbance peaks in the visible spectrum.

B. Conditional probability of metamerism

As noted elsewhere,⁹ the significance of metamerism in natural scenes depends on the observer's task. Yet knowledge of the low frequency of metameric pairs in natural scenes may be less useful than it seems when attempting to estimate the chances of error in judging surface color. This is because there is an asymmetry in the conditional probabilities associated with distinguishable and indistinguishable pairs of surfaces under successive illuminants. Thus, as Table 2 shows, the relative frequency of pairs of surfaces whose color differences are subthreshold under the first illuminant appears also to be very low, between 10⁻⁴ and 10⁻³ (column with n = 0). This relative frequency sets an upper limit on the relative frequency of metameric pairs, since they are, by definition, a subset of subthreshold pairs under the first illuminant. Therefore, an observer viewing a natural scene under this illuminant can, in the absence of additional information, assume correctly that metamerism is very unlikely (this is true whether the illuminant change is from a daylight of correlated color temperature 25,000 K to one of 4000 K, or vice versa). Moreover, presented with a pair of surfaces that are distinguishable under the first illuminant, an observer can safely assume that they are very unlikely to become indistinguishable under the second illuminant.

The converse situation is more problematic. Presented with a pair of surfaces that are indistinguishable under the first illuminant, an observer cannot safely assume that they will remain indistinguishable under the second illuminant. Indeed, as Table 2 also shows, the conditional probability of their becoming distinguishable is quite high, with values ranging from about 0.3 to 0.6 (column with n = 1), depending on the type of scene and illuminant change. To be certain of the material identity of two surfaces, an observer would need to draw on evidence other than their color appearance. But the size of the sample from which the surfaces are drawn is critical. In information-theoretic terms, identifying surfaces on the basis of their color is, for samples somewhat smaller than those used here, a very effective strategy.⁴⁰

C. Generalized metamerism and surface-color judgments

The impact of metamerism may go beyond the failure of a small proportion of pairs of surfaces to maintain a match under a change in illuminant. As Fig. 5 shows, the median degree of metamerism was correlated over scenes with the median degree of generalized metamerism. Generalized metamerism applies, by definition, to pairs of surfaces that fail to maintain their color relationships under a change in illuminant. Since these failures are commonly misinterpreted by observers as being due to spectral-reflectance changes,⁴¹ it follows that scenes with high frequencies of metamerism may be associated with poorer surface-color judgments and consequently reduced color constancy,⁴² even when the surfaces being compared are not themselves metameric.

APPENDIX A: EFFECTIVE SPECTRA AND INDIRECT ILLUMINATION

The purpose of this appendix is to explain the assumptions of Subsections 2.A, 2.B, and 3.F concerning the use of effective spectral reflectances and illuminants with surfaces under direct and indirect illumination and the consequences of changing a global illuminant. The emphasis is on the information available to an observer, who is positioned on the same axis as the hyperspectral camera used to record the scene. The notation here differs slightly from that used in other, shorter accounts.^{42, 43}

First, consider the process of image acquisition. Let E(θ, ɸ; λ; x, y) be the incident radiance on the scene at a general point (x, y) in the direction ω = (θ, ɸ) at wavelength λ, where polar angle θ and azimuthal angle ɸ are defined with respect to a fixed directional coordinate system. Suppose, for the moment, that the illumination is direct, spatially uniform, and defined globally, so that E(θ, ɸ; λ; x, y) = E(θ, ɸ; λ). There is a physical correlate since scenes were recorded under a cloudless sky or under a sky with uniform cloud. Let R(θ₀, ɸ₀; θ, ɸ; λ; x, y) be the bidirectional reflectance function⁴⁴ at (x, y) for fixed viewing direction (θ₀, ɸ₀). This is a simplification of Ref. 44, where distinct (x, y) are defined for incidence and reflection. Then the color signal c(λ; x, y) defined by the reflected radiance in that direction at (x, y) is given⁴⁴ by c(λ; x, y) = ∫_2π​ E(θ, ɸ; λ)R(θ₀, ɸ₀; θ, ɸ; λ; x, y) dω. As noted in Subsection 2.A and in Refs. 14​, 17, the hyperspectral image, i(λ; x, y), say, of c(λ; x, y) was corrected for dark noise, spatial nonuniformities, and stray light. Any wavelength-dependent variations in registration were also corrected, but at a later stage.

An effective reflectance at each point of the scene and an effective global illuminant may be constructed as follows. Define the effective reflectance r(λ; x, y) at (x, y) by dividing i(λ; x, y) by the hyperspectral image i(λ; x_a, y_a) of the color signal c(λ; x_a, y_a) at a calibrated neutral reference surface a in the scene (also under direct illumination) and then multiplying by the known spectral reflectance r(λ; x_a, y_a) of a. Define the effective global illuminant e(λ) by taking the actual reflected spectrum at a, recorded with a calibrated telespectroradiometer^{14, 17} (see Subsection 2.A), and dividing by r(λ; x_a, y_a). For an observer, the color signal c(λ; x, y) at each (x, y) may be interpreted as the product c(λ; x, y) = e(λ)r(λ; x, y). This representation does not distinguish between changes in reflectance and changes in surface orientation, although for Lambertian surfaces, reflected radiance is independent of viewing direction.

Now suppose that the illumination at a particular point (x′, y′) in the scene is indirect, with local incident radiance E(θ, ɸ; λ; x′, y′) ≠ E(θ, ɸ; λ); for example, (x′, y′) might be in shadow or partly illuminated by reflection from another surface. Let R(θ₀, ɸ₀; θ, ɸ; λ; x′, y′) be the bidirectional reflectance function at (x′, y′), with respect to the same fixed coordinate system. Then the color signal c(λ; x′, y′) in the direction (θ₀, ɸ₀) at (x′, y′) is given by c(λ; x′, y′) = ∫_2π E(θ, ɸ; λ; x′, y′)R(θ₀, ɸ₀; θ, ɸ; λ; x′, y′) dω.

Under the assumption of spatially uniform illumination, this signal c(λ; x′, y′) may again be interpreted as a product c(λ; x′, y′) = e(λ)r(λ; x′, y′) of the original effective global illuminant e(λ) and an effective reflectance r(λ; x′, y′) at (x′, y′). The more accurate interpretation, as a product c(λ; x′, y′) = e′(λ)r′(λ; x′, y′) of a different effective illuminant e′(λ), corresponding to the illumination in the shadowed region, and reflectance r′(λ; x′, y′), is considered shortly. The relationship between r(λ; x′, y′) and R(θ₀, ɸ₀; θ, ɸ; λ; x′, y′) for indirect illumination at (x′, y′) is, of course, different from the relationship between r(λ; x, y) and R(θ₀, ɸ₀; θ, ɸ; λ; x, y) for direct illumination at (x, y). Notice that whether (x, y) is directly or indirectly illuminated, multiplying r(λ; x, y) by e(λ) recovers the true color signal c(λ; x, y) at each point in the scene. It is these effective reflectances r(λ; x, y) over the scene and illuminants e(λ) that were used in the main analysis.

Next consider the consequences of changing the effective global illuminant from, say, e₁(λ) to e₂(λ). The color signal at a directly illuminated point (x, y) changes from e₁(λ)r(λ; x, y) to e₂(λ)r(λ; x, y), representing a change in the incident radiance at (x, y) from E₁(θ, ɸ; λ) to E₂(θ, ɸ; λ), where E₂ (θ, ɸ; λ) = E₁(θ, ɸ; λ)k(λ) , and k(λ) = e₂(λ)/e₁(λ) (with e₁(λ) > 0 for all λ). Analogously, the color signal at an indirectly illuminated point (x′, y′) changes from e₁(λ)r(λ; x′, y′) to e₂(λ)r(λ; x′, y′). The more accurate interpretation is that the illuminant at (x′, y′) changes from, say, e′₁(λ) to e′₂(λ), so that e′₁(λ)r′(λ; x′, y′) changes to e′₂(λ)r′(λ; x′, y′), representing a change in the local incident radiance at (x′, y′) from E₁(θ, ɸ; λ; x′, y′) to E₂ (θ, ɸ, λ; x′, y′) . But, by definition, e′₁(λ)r′(λ; x′, y′) = e₁(λ)r(λ; x′, y′) and e′₂(λ)r′(λ; x′, y′) = e₂(λ)r(λ; x′, y′). Therefore e′₁(λ)/e′₂(λ) = e₁(λ)/e₂(λ). But e₁(λ)/e₂(λ) = k(λ), so E₂ (θ, ɸ; λ; x′, y′) = E₁(θ, ɸ; λ; x′, y′)k(λ) . That is, under the assumption of an effective global illuminant and an effective reflectance at each point, the change in incident radiance at (x, y) is precisely the same as the change in incident radiance at (x′, y′). Defining this change multiplicatively, by k(λ), rather than additively, is the natural choice in the analysis of surface-color perception under illuminant changes (Appendix 1 of Ref. 45).

It is emphasized that this is a device for calculation which ensures that all surfaces in the scene are treated in the same way. The color signals at the points (x, y) and (x′, y′), first under effective global illuminant e₁(λ) and then under effective global illuminant e₂(λ), represent the same change k(λ) in the true illuminants at the two locations, exactly as if the reflectance at (x′, y′) were indeed r(λ; x′, y′) and the illuminant there were indeed first e₁(λ) and then e₂(λ), as assumed in Subsections 2.A and 2.B.

In practice, the physical situation is necessarily more complicated. Changes in the position of the sun and in the amount and distribution of cloud lead to changes in the ratio of illuminant spectra within directly and indirectly illuminated regions of a scene and in the spatial distribution of shadows. But comprehensively representing such physical changes is not a prerequisite for estimating the frequency with which two surfaces drawn at random will match under one illuminant and not under another.

It is, however, reasonable to ask whether the assumption of an effective global illuminant e⁠(λ) and an effective reflectance r(λ; x′, y′) at each point (x′, y′) in indirectly illuminated regions biased the frequency estimates obtained here. This question is addressed experimentally in Subsection 3.F, where it is shown that the bias was in fact negligible: Frequency estimates were almost identical whether or not regions in shadow were excluded from each scene.

APPENDIX B: CHANGE IN THRESHOLD FOR METAMERISM

The purpose of this appendix is to show how an increase in nominal threshold ΔE^thr for the distinguishability of pairs of colored surfaces under each of two selected illuminants might lead either to an increase or to a decrease in the relative frequency of metamers, depending on the criterion degree of metamerism (Subsection 3.B).

Let g(x₂, x₁) be the joint probability density function of the color difference x₂ (i.e., ΔE₂) under the second illuminant and color difference x₁ (i.e., ΔE₁) under the first illuminant (the same color differences can come from many different pairs of surfaces). Let f(x₁) be the probability density function of the color difference x₁ under the first illuminant, that is, the marginal distribution of x₁, so that f(x₁)=∫₀^∞​ g(x₂, x₁) dx₂ . Suppose that the nominal threshold x (i.e., ΔE^thr) is increased by a small amount dx. Then the increase in the probability of subthreshold differences x₁ < x under the first illuminant is approximately f(x)dx, and, for a criterion degree of metamerism of n (where n = 1, …, 4), the increase in the probability of differences x₂ ≥ nx under the second illuminant is approximately [∫_nx^∞​ g(x₂, x) dx₂] dx . But there is also a decrease in this probability of approximately [∫₀^x​ g(nx, x₁) dx₁] ndx . Depending on the precise form of g, this loss can eventually exceed the gain at large n. That is, an increase in threshold may produce an increase in the relative frequency of metameric pairs with n = 1 and a decrease with n = 4, as was found here.