Abstract
Matching control selection strategies are often employed in PCOS case-control studies; however, they are infrequently used in an appropriate fashion. When properly applied, matching may offer improved study precision, but this is highly contingent on the causal pathway under consideration, strength of the associations between the matching variable and both the risk factor of interest and PCOS, and use of an appropriate stratified data analysis.
Variations in design, including strategies to consider suspected confounding variables, may be in part responsible for discrepancies among study results reported in the polycystic ovary syndrome (PCOS) literature (1). The case-control study design is frequently used to consider hypothesized risk factors for PCOS, with investigators often complementing this framework with a ‘matching’ strategy in which controls are selected for cases according to the distribution of suspected confounding variables among the latter (2). A recent PubMed search (i.e., on 6/14/06), using the search terms ‘polycystic ovary syndrome’ and ‘case-control studies’, limited to the English language and ‘published in the last 1 year’, generated 40 citations, 23 of which fell under the PCOS case-control rubric. Almost half of these 23 studies, 11 (48%), matched controls to cases by body mass index (BMI), age, or both, but only one (9%) analyzed the data appropriately for its matched nature. In a prior publication, we discussed the merits of the case-control design for studies of PCOS causal risk factors (3); however, the proper implementation of this design requires the appropriate consideration of which variables are suitable for matching and the proper analysis of data when matching is used.
Confounding, ‘mixing’ of associations of disinterest with one of interest, may result from the differential distribution of risk factors among cases and controls owing to variables other than the outcome under consideration (2). The confounding phenomenon is highly contingent on the proposed causal pathway between risk factor and outcome of interest, and thus adherence to blanket recommendations concerning adjustment for variables in PCOS studies appears misguided. Matching for potential confounding variables is advantageous under only limited circumstances and furthermore necessitates a tailored approach to analysis of the data, or bias and compromised study precision may result.
Traditional confounding definitions implicate variables causally associated with the outcome of interest, associated with the exposure of interest, conditional on other variables under consideration (4), and exclusive of the proposed causal pathway. More recent developments in causal graphing theory suggest that a variable must be causally associated with both the outcome and the risk factor of interest (5). Thus, a potential confounding variable must either temporally precede both the outcome and the risk factor or an unmeasured common cause precedes development of both the measured confounding variable and the risk factor of interest which occur concurrently (6).
The case-control study design has been described as efficient sampling from an underlying or ‘target cohort’, the joint source of cases and controls groups, that is truly of interest (7). Consequently, it is in this target cohort that confounding is resident (8) which may or may not be reflected in cases and controls participating in a study, depending on sampling variability. Alternately, sampling variability may lead to apparent or ‘pseudo-confounding’ not existing in the target cohort but suggested among the sample at hand (9). Ideally, an investigator has complete enumeration of the target cohort for a case-control study and can directly evaluate causal associations and identify potential confounding variables employing various statistical techniques, such as under the ‘nested’ case-control design (10). In reality, this occurs less frequently than desired, and thus potential confounding variables for a case-control study should be selected a priori using literature relevant to the target cohort, rather than by statistical criteria among participating cases and controls.
Inherent differences in matching selection strategies between the cohort and case-control study designs may be the source of the apparent confusion with regard to the purpose of matching control selection strategies. In cohort study designs, in which participants lacking a risk factor of interest are selected to the study on the basis of the distribution of a potential confounding variable among participants demonstrating the risk factor of interest, confounding is frequently eliminated as similar distributions of the potential confounding variable are generated between the groups (8). However, in case-control designs, participants lacking an outcome of interest (i.e., controls) are selected to the study on the basis of the distribution of a potential confounding variable among participants demonstrating the outcome of interest (i.e., cases). The requisite association between the potential confounding variable and the risk factor of interest (i.e., definition for a potential confounder) shifts or biases the distribution of the risk factor of interest among cases and controls. This ‘selection bias’ is introduced in lieu of confounding by the match and must be addressed during data analysis (2).
Although matching does not offer advantages over independent control selection with regard to study validity (i.e., confounding bias) under the case-control design, gains in study precision may be facilitated (11). Greater precision produces a smaller odds ratio variance, or analogously narrower confidence intervals, as the match facilitates the availability of controls for each or most case values of a matching variable during statistical adjustment. As certain cases may otherwise have been discarded during statistical adjustment for a potential confounder due to the unavailability of suitable controls under independent control selection, the matching strategy may translate into a more cost effective study in which a smaller sample size is required for sufficient power to generate adjusted effect estimates (12).
Matching may be conceptualized as stratified sampling (2) in that each matched case-control set comprises a distinct stratum with a uniform distribution of the matching variable (13). However, under proper data analysis, only those stratum in which case and control differ in terms of the risk factor of interest, ‘discordant cells’, contribute to effect estimates (12). If a misguided matching strategy forces similar risk factor distributions on the case and control groups, often due matching on variables with weak or null associations with the outcome of interest, but moderate or strong association with the risk factor of interest, the number of discordant cells are decreased and the number of ‘concordant’ cells are increased. The latter may effectively exclude a large proportion of the study sample from the analysis, reduce study precision, and obfuscate associations between the risk factor and outcome of interest, so called ‘over-matching’.
For example, consider Figure 1 in which a single realization of an artificially generated data set describing a series of imaginary case-control studies is demonstrated. Using both independent and matching control selection strategies 100 each PCOS cases and controls are considered with respect to insulin resistance as a hypothesized causal risk factor (14) and obesity (15) as a potential confounding variable. These date were generated using previously published formulae for expected values under independent and matched control selection strategies (16), with Excel 2003 (Microsoft Co., Redmond, WA), by varying the magnitude of the odds ratios between obesity and PCOS (OROb-PCOS) from 1.0 (i.e., no association) to 12.0 (very strong association) and obesity and insulin resistance (OROb-IR) from 1.0 to 7.4. Count data were subsequently analyzed with SAS v. 9.0 (SAS Institute, Inc., Cary, NC) to generate obesity adjusted odds ratios (17) and 95% confidence intervals for insulin resistance as a risk factor for PCOS (ORPCOS-IR). Stratified least squares regression lines were fit to the generated data describing OROb-IR as a predictor of the relative precision of the ORPCOS-IR (i.e., βOROb–IR)
Figure 1. Gains in precision of the obesity adjusted PCOS-insulin resistance odds ratio due to matching as a function of the obesity-insulin resistance odds ratio, stratified by the magnitude obesity-PCOS odds ratio.
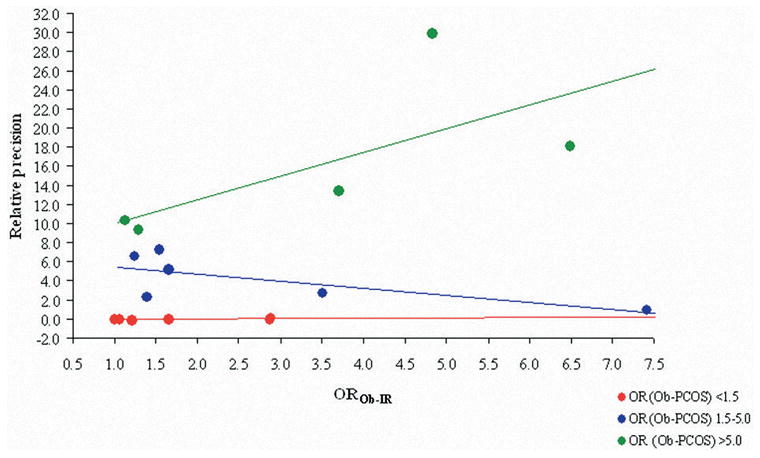
● OROb-IR: odds ratio between obesity and insulin resistance.
● OR (Ob-PCOS): odds ratio between obesity and PCOS.
Gains in ORPCOS-IR precision due to matching (i.e., positive slope) are demonstrated as a function of OROb-IR only in the Figure 1 stratum in which OROb-PCOS exceeds 5.0, (i.e., green plot): y = −0.1 + 0.0x (i.e., red plot, OROb-PCOS < 1.5), y = 6.3 − 0.8x (i.e., blue plot, OROb-PCOS 1.5–5.0), y =7.6 + 2.5x (i.e., green plot, OROb-PCOS >5.0). This suggests that matching only improves precision under those circumstances in which the matching variable is a strong cause of the outcome. Where OROb-PCOS is weak to moderate (i.e., <5.0) matching elicits no benefit (i.e., β 0 for the red plot) or even a slight detriment (i.e., β <0 for the blue plot) in ORPCOS-IR precision compared with independent control selection. These observations are consistent with patterns reported from statistical simulations of matching strategies (16, 18).
When conditions are favorable a stratified analysis addresses the aforementioned selection bias introduced by a matching control selection strategy (19, 20). A Mantel-Haenszel adjusted odds ratio stratified on the matching variable will accommodate the introduced selection bias, however many investigators employ logistic regression to generate odds ratios because of its widespread availability, among other advantages. However, the latter technique generates biased effect estimates using matched data (21) and an alternate procedure, conditional logistic regression, which generates unbiased estimates when using matched data (22), must be used in its stead.
Given the substantial public health impact of PCOS (23), inconsistency among reported study results, and frequent misapplication of matching strategies in PCOS case-control studies, we hope that greater consistency in regard to the appropriate application of epidemiologic methods will foster the elucidation of the causal factors. Investigators conducting case-control PCOS studies must carefully consider whether putative matching variables, such as age and BMI, are indeed potential confounders in the target cohort being sampled and furthermore strong causes of PCOS. If a matching strategy is considered advantageous only stratified procedures appropriate for matched data, such as the Mantel-Haenszel odds ratio or conditional logistic regression, should be employed during data analysis.
Acknowledgments
The authors would like to thank Neil Perkins for his insight and assistance in describing the matching precision rationale. This research was supported by the Intramural Research Program of the NIH, National Institute of Child Health and Human Development.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Michael S. Bloom, Postdoctoral Research Fellow, Epidemiology Branch, Division of Epidemiology Statistics and Prevention Research, National Institute of Child Health and Human Development, National Institutes of Health, U.S. Dept. of Health and Human Services, 6100 Executive Blvd., Rm. 7B03, MSC 7510, Bethesda, MD 20892, Phone (301) 496-5581, Fax (301) 402-2084, BloomM@mail.nih.gov
Enrique F. Schisterman, Investigator, Epidemiology Branch, Division of Epidemiology Statistics and Prevention Research, National Institute of Child Health and Human Development, National Institutes of Health, U.S. Dept. of Health and Human Services, 6100 Executive Blvd., Rm. 7B03, MSC 7510 Bethesda, MD 20892, Phone (301) 435-6893, Fax (301) 402-2084, SchisteE@mail.nih.gov
Mary L. Hediger, Investigator, Epidemiology Branch, Division of Epidemiology Statistics and Prevention Research, National Institute of Child Health and Human Development, National Institutes of Health, U.S. Dept. of Health and Human Services, 6100 Executive Blvd., Rm. 7B03, MSC 7510, Bethesda, MD 20892, Phone (301) 435-6897, Fax (301) 402-2084, HedigerM@mail.nih.gov
References
- 1.Escobar-Morreale HF, Luque-Ramirez M, San Millan JL. The molecular-genetic basis of functional hyperandrogenism and the polycystic ovary syndrome. Endocr Rev. 2005;26:251–82. doi: 10.1210/er.2004-0004. [DOI] [PubMed] [Google Scholar]
- 2.Rothman KJ, Greenland S. Modern epidemiology. Philadelphia, PA: Lippincott-Raven; 1998. [Google Scholar]
- 3.Bloom MS, Schisterman EF, Hediger ML. Selecting controls is not selecting “normals”: Design and analysis issues for studying the etiology of polycystic ovary syndrome. Fertility and Sterility. 2006;86:1–12. doi: 10.1016/j.fertnstert.2005.09.066. [DOI] [PubMed] [Google Scholar]
- 4.Fisher L, Patil K. Matching and unrelatedness. Am J Epidemiol. 1974;100:347–9. doi: 10.1093/oxfordjournals.aje.a112043. [DOI] [PubMed] [Google Scholar]
- 5.Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology. 1999;10:37–48. [PubMed] [Google Scholar]
- 6.Hill AB. The environment and disease: association or causation? Proc R Soc Med. 1965;58:295–300. doi: 10.1177/003591576505800503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wacholder S, McLaughlin JK, Silverman DT, Mandel JS. Selection of controls in case-control studies. I. Principles. Am J Epidemiol. 1992;135:1019–28. doi: 10.1093/oxfordjournals.aje.a116396. [DOI] [PubMed] [Google Scholar]
- 8.Miettinen OS, Cook EF. Confounding: essence and detection. Am J Epidemiol. 1981;114:593–603. doi: 10.1093/oxfordjournals.aje.a113225. [DOI] [PubMed] [Google Scholar]
- 9.Day NE, Byar DP, Green SB. Overadjustment in case-control studies. Am J Epidemiol. 1980;112:696–706. doi: 10.1093/oxfordjournals.aje.a113042. [DOI] [PubMed] [Google Scholar]
- 10.Wacholder S, Silverman DT, McLaughlin JK, Mandel JS. Selection of controls in case-control studies. III. Design options. Am J Epidemiol. 1992;135:1042–50. doi: 10.1093/oxfordjournals.aje.a116398. [DOI] [PubMed] [Google Scholar]
- 11.Greenland S, Morgenstern H, Thomas DC. Considerations in determining matching criteria and stratum sizes for case-control studies. Int J Epidemiol. 1981;10:389–92. doi: 10.1093/ije/10.4.389. [DOI] [PubMed] [Google Scholar]
- 12.Miettinen OS. The matched pairs design in the case of all-or-none responses. Biometrics. 1968;24:339–52. [PubMed] [Google Scholar]
- 13.Miettinen O. Confounding and effect-modification. Am J Epidemiol. 1974;100:350–3. doi: 10.1093/oxfordjournals.aje.a112044. [DOI] [PubMed] [Google Scholar]
- 14.Corbould A, Kim YB, Youngren JF, Pender C, Kahn BB, Lee A, et al. Insulin resistance in the skeletal muscle of women with PCOS involves intrinsic and acquired defects in insulin signaling. Am J Physiol Endocrinol Metab. 2005;288:E1047–E1054. doi: 10.1152/ajpendo.00361.2004. [DOI] [PubMed] [Google Scholar]
- 15.Salehi M, Bravo-Vera R, Sheikh A, Gouller A, Poretsky L. Pathogenesis of polycystic ovary syndrome: what is the role of obesity? Metabolism. 2004;53:358–76. doi: 10.1016/j.metabol.2003.10.005. [DOI] [PubMed] [Google Scholar]
- 16.Kupper LL, Karon JM, Kleinbaum DG, Morgenstern H, Lewis DK. Matching in epidemiologic studies: validity and efficiency considerations. Biometrics. 1981;37:271–91. [PubMed] [Google Scholar]
- 17.McKinlay SM. Pair-matching-a reappraisal of a popular technique. Biometrics. 1977;33:725–35. [PubMed] [Google Scholar]
- 18.Sturmer T, Brenner H. Degree of matching and gain in power and efficiency in case-control studies. Epidemiology. 2001;12:101–8. doi: 10.1097/00001648-200101000-00017. [DOI] [PubMed] [Google Scholar]
- 19.Miettinen OS. Matching and design efficiency in retrospective studies. Am J Epidemiol. 1970;91:111–8. doi: 10.1093/oxfordjournals.aje.a121118. [DOI] [PubMed] [Google Scholar]
- 20.Bross ID. How case-for-case matching can improve design efficiency. Am J Epidemiol. 1969;89:359–63. doi: 10.1093/oxfordjournals.aje.a120949. [DOI] [PubMed] [Google Scholar]
- 21.Kleinbaum DG, et al. Applied regression analysis and other multivariable methods. Pacific Grove: Duxbury Press; 1998. [Google Scholar]
- 22.Breslow NE, Day NE. Statistical methods in cancer research volume 1-the analysis of case-control studies. Lyon: International Agency For Research on Cancer; 1980. [PubMed] [Google Scholar]
- 23.Carmina E, Lobo RA. Polycystic ovary syndrome (PCOS): arguably the most common endocrinopathy is associated with significant morbidity in women. J Clin Endocrinol Metab. 1999;84:1897–9. doi: 10.1210/jcem.84.6.5803. [DOI] [PubMed] [Google Scholar]


