Design and Validation of a MR-Compatible Pneumatic Manipulandum

Introduction

While it is possible to study the activity of neural structures contributing to the control of movement in awake, behaving animals with microelectrodes (Evarts, 1968; Georgopoulos et al., 1982; Thach, 1978), it is not usually possible to do so in humans. Multi-unit recording techniques are limited due to the fact that distributed networks of brain regions are known to be involved in the control of goal-directed movements (including the primary sensorimotor, supplemental motor and premotor cortices, basal ganglia and cerebellum) and it is not practical to record from all involved regions simultaneously. Instead, indirect measures of neural activity such as functional magnetic resonance imaging (fMRI) have been used to study correlates of neural activity related to a variety of motor-related behaviors including the compensation for visuomotor perturbations (Imamizu et al., 2000), and regulation of force (Kawato et al., 2003; Peck et al., 2001; Vaillancourt et al., 2003). Imaging the neural mechanisms contributing to position regulation and the adaptive response to changing environmental loads using fMRI has been limited, however, since these tasks require devices able to perturb the subject's limb in a controlled manner (Milner, 2002; Scheidt et al., 2001; Shadmehr and Mussa-Ivaldi, 1994). The combination of MR-compatible robotic devices and fMRI promises to provide a noninvasive means to characterize and quantify how individual structures in the intact and impaired human central nervous system contribute to the planning, execution and learning of motor tasks.

The design of MR-compatible robots presents significant technical challenges including the satisfaction of several material, noise tolerance and size limitations imposed by current MRI technologies (Chinzei et al., 1999; Schenck, 1996). The large static magnetic fields generated by MR scanners preclude the use of ferromagnetic materials that would be attracted to the scanner, thereby compromising the safety of both subject and scanner. In addition, all actuators and sensors in the device must be impervious to the rapidly switching imaging gradients, and their operation must not cause disturbances in the homogeneity of the magnetic field, thus leading to image distortions. Finally, the device must also have a small form factor, capable of fitting inside the scanner bore without causing excessive discomfort to the subject during scanning. To date, a small number of MR-compatible manipulanda have been developed for use in neuroscience research or rehabilitation applications. One example is a haptic interface that perturbs the hand by using Lorentz coils to induce a force proportional to electrical current flow (Riener et al., 2005). Devices using this actuation method in the MR environment are limited in the magnitude of torque they can generate and in their placement within the scanner because current flowing through the coils creates a large magnetic field that can cause image artifacts. Another single degree-of-freedom device uses a traveling wave ultrasonic motor to impart torques about the wrist (Flueckiger et al., 2005), while yet another uses a hydrostatic, master-slave system to generate torques about the wrist (Gassert et al., 2006). While both of these devices use MR compatible sensors to monitor torque and motion, and both have been designed to facilitate expansion to multiple degree of freedom systems, a limitation is that they are not backdriveable which makes movements with rapid direction reversals awkward. Finally, a 2 degree-of-freedom device was developed by Diedrichsen, et al. for monitoring and perturbing whole-arm reaching movements during functional MR imaging (Diedrichsen et al., 2005). That system uses pneumatic servo valves and bi-directional pistons to generate torques about the elbow and shoulder. However; the application of perturbing forces to proximal limb segments requires special diligence in the prevention of stimulus correlated head motion artifacts (Diedrichsen and Shadmehr, 2005)

Here we describe the design and validation of a novel, MR compatible, 1 degree of freedom, pneumatically actuated robot. The advantages this device has over other such devices are that it is backdriveable (allowing the study of movements with rapid reversals) and that it limits motion to distal limb segments (reducing the occurrence of stimulus correlated head motion artifacts). We present the results of three separate experiments evaluating: 1) the device's ability to simulate spring-like (position-dependent) loads during point to point wrist flexion movements, 2) the MR compatibility of the device during scanning of a head phantom with concurrent robot actuation, and 3) the system's ability to record quality behavioral data and functional neuroimages during an experiment examining the neural correlates of point-to-point wrist flexion movements against position-dependent perturbations. Our aims were to create a device capable of both monitoring and perturbing wrist motion during fMRI scanning, and to demonstrate its safety and efficacy as a tool for use in motor control research on human subjects. The results demonstrate that the device possesses sufficient response time and bandwidth to accurately simulate position-dependent loads about the wrist (i.e. torsional spring-like loads) having variable gain. Both magnitude and phase images collected during echo planar imaging of a phantom show no distortions due to the operation of the robot during scanning. Likewise, scanning does not adversely effect measurements of position and actuator pressure recorded from the robot since signal-to-noise ratios are not different from those observed when the robot is operated outside the scanner environment. Finally, we show that the robot is indeed able to apply a wide range of torsional spring-like loads to the hand during wrist flexion movements, and that the brain regions activated by this task (and hemodynamic response functions measured using fMRI) are consistent with those previously reported from experiments wherein subjects manipulated a joystick or performed force matching tasks with the hand (cf. (Imamizu et al., 2000; Seidler et al., 2004; Vaillancourt et al., 2003)).

Materials and Methods

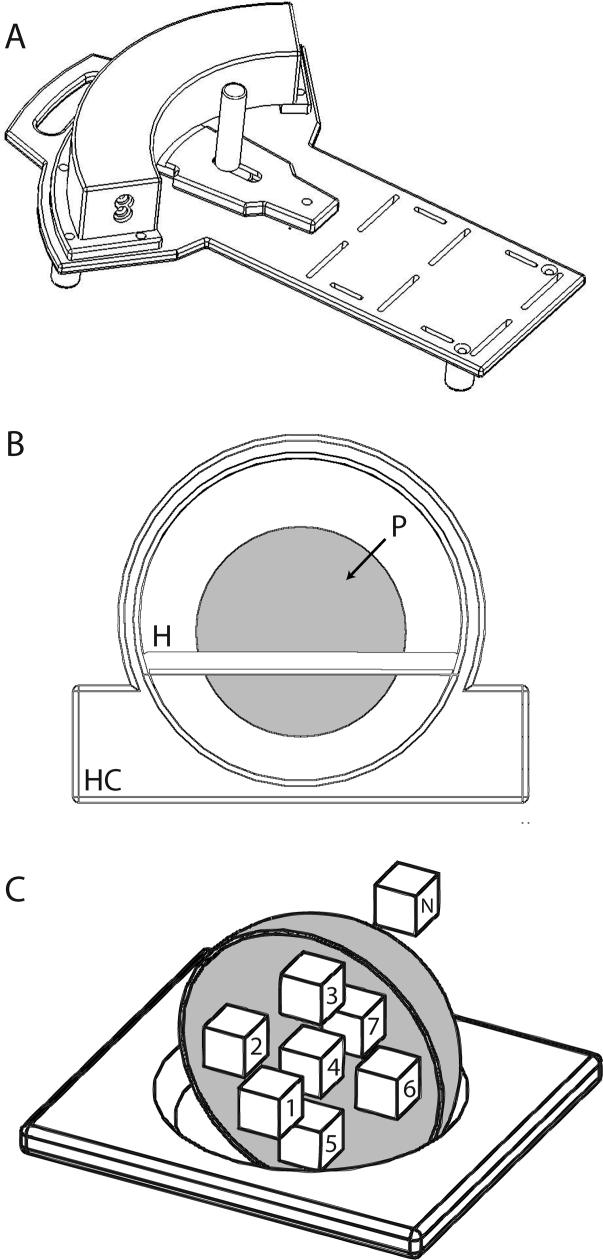
A MR-compatible manipulandum with integrated pneumatic actuator (Fig 1A) was developed to exert computer controlled torques about the wrist. A single-acting, bellows-type pneumatic actuator enclosed within a curved volume transmits force from compressed air to a wall rigidly attached to the device's handle. Pressurizing the actuator causes a force to be applied to the handle, thereby generating a torque about the subject's wrist. Local pressure and vacuum supplies are charged using separate, brushless DC compressors [part numbers H054−11 (pressure) and D736−22−02 (vacuum); Hargraves Technologies, Mooresville, NC], allowing the device to impart both extensor and flexor torques about the wrist. Air pressure within the actuator is sensed by a Honeywell 26PC series pressure transducer (Honeywell International, Inc., Morristown, NJ), amplified (gain = 25), low-pass filtered at a cutoff frequency of 20Hz, and digitized at 1000 samples per second with a National Instruments PCI-6036E multifunction data acquisition system (National Instruments Co., Austin, TX). Joint angle is sensed with an Agilent HEDM-6540, 3-channel, Mylar film optical encoder (Agilent Technologies, Inc., Palo Alto, CA) located on the underside of the device, and acquired with a Measurement Computing PCI-QUAD-04 incremental encoder driver (Measurement Computing Co., Middleboro, MA). The device monitors wrist position (within 0.05°) and actuator pressure (within 6.67×10⁻⁴ psi) Actuator pressure is converted into torque about the wrist according to the equation

$$\tau \left(t\right)=Lp\left(t\right)$$

where τ(t) is the torque generated by the device about the subject's wrist, p(t) is the pressure within the actuator, t is time, and L is a constant accounting for the geometry of the actuating system. Using this conversion factor, wrist torque is computed with a resolution better than 0.001 Nm.

Figure 1.

(A) Schematic representation of the one-degree of freedom pneumatic manipulandum. (B) Illustration of the set up of the head coil (HC), phantom holder (H), and phantom (P) used to validate the compatibility of the device. (C) Drawing of holder and phantom (cut away to show details of validation ROIs) including the ROIs used in the calculations of SNR and field homogeneity.

Only the manipulandum, pressure transducer, optical encoder, and necessary instrumentation are located with in the MR environment, while all control hardware, data acquisition, and computer components are located in the scanner control room. The manipulandum is designed to easily accommodate both right and left handed individuals providing a total of 60° range of motion at the wrist (30° flexion to 30° extension). Robot control is achieved using custom hardware and software designed to use the XPC™ target real-time operating system (the Mathworks Inc., Natick, MA). Pressure within the actuator is regulated by a Proportion Air QB3 electro-pneumatic pressure valve (Proportion-Air Inc., McCordsville, IN). Wrist angle and actuator pressure data are acquired at a rate of 1000 samples per second. Commands to the pressure valve are generated at the same rate. A Proportional-Integral-Derivative (PID) pressure controller was implemented to improve the performance of the system:

$$P_C\left(t\right)=K_{P}e\left(t\right)+K_I\int e\left(t\right)dt+K_D\stackrel{.}{e}\left(t\right)$$

where P_C(t) is the commanded actuator pressure in units of psi, e(t) is the difference between the measured and desired actuator pressure in units of psi, K_P is the proportional gain, K_I is the integral gain, and K_D is the derivative gain. Ziegler-Nichols tuning rules were used to tune the controller (Ziegler and Nichols, 1942), yielding the following gain values: K_P = 3.3 , K_I = 14, and K_D = 0.055.

Experiment 1 - Robot Validation

Performance of the system was quantified by comparing the step response under open- and closed-loop PID control conditions and by computing the frequency response with the device under PID control. Volume of the actuator was held constant during these tests by locking the handle of the device at a neutral wrist angle (angle represented in Fig 1A). Rise times (10−90% steady state), delay times (command onset to 10% steady state), and maximum overshoot were measured for rising and falling step changes in pressure of 1 and 2 PSI (above and below atmospheric pressure, respectively), while the frequency response of the system was obtained using a 1 PSI peak-to-peak, ‘chirp’ perturbation sweeping from 0 to 5Hz (Fig 3B, solid line). The frequency at which the system was unable to track commanded pressure changes within ±15% of peak pressure determined the system's bandwidth.

Figure 3.

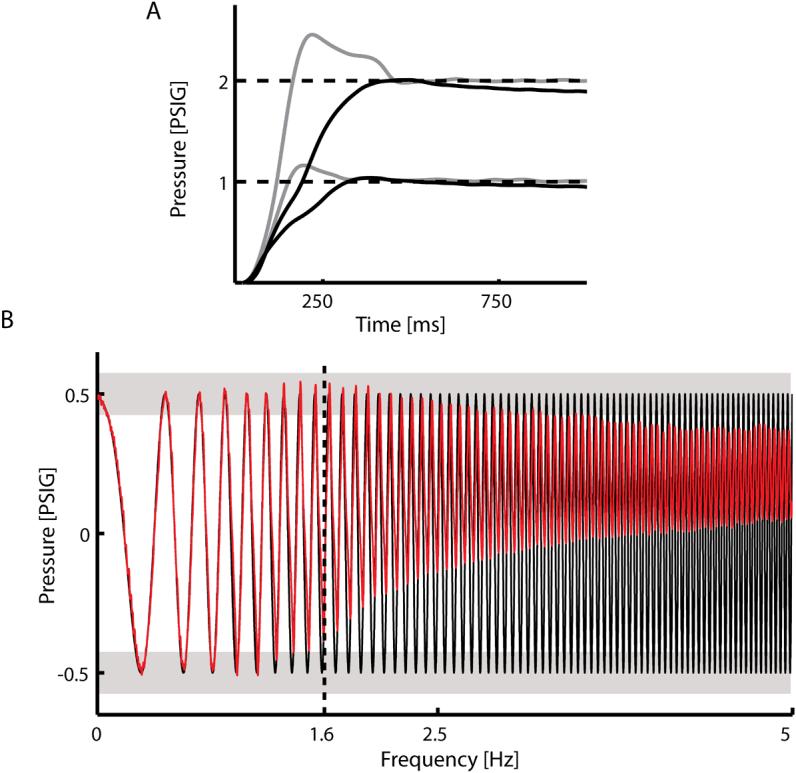
(A) Responses of the robot to 1 and 2 PSI step changes in pressure under open loop control (black lines) and closed loop PID control (gray lines). Response times decreased by 63% under PID control. (B) The frequency response of the system under closed loop PID control (red line) was identified by assessing the system's ability to track changes in commanded actuator pressure having a 1 PSI peak-to-peak ‘chirp’ profile sweeping from 0 to 5Hz (solid black line). The upper bound on the system's bandwidth was defined to be the frequency at which the controller was unable to regulate the actuator pressure within 15% of the peak commanded pressure (light gray bars). The system responses to the chirp perturbations revealed that the bandwidth of the device was at least 1.6 Hz under the simple PID controller described in the text.

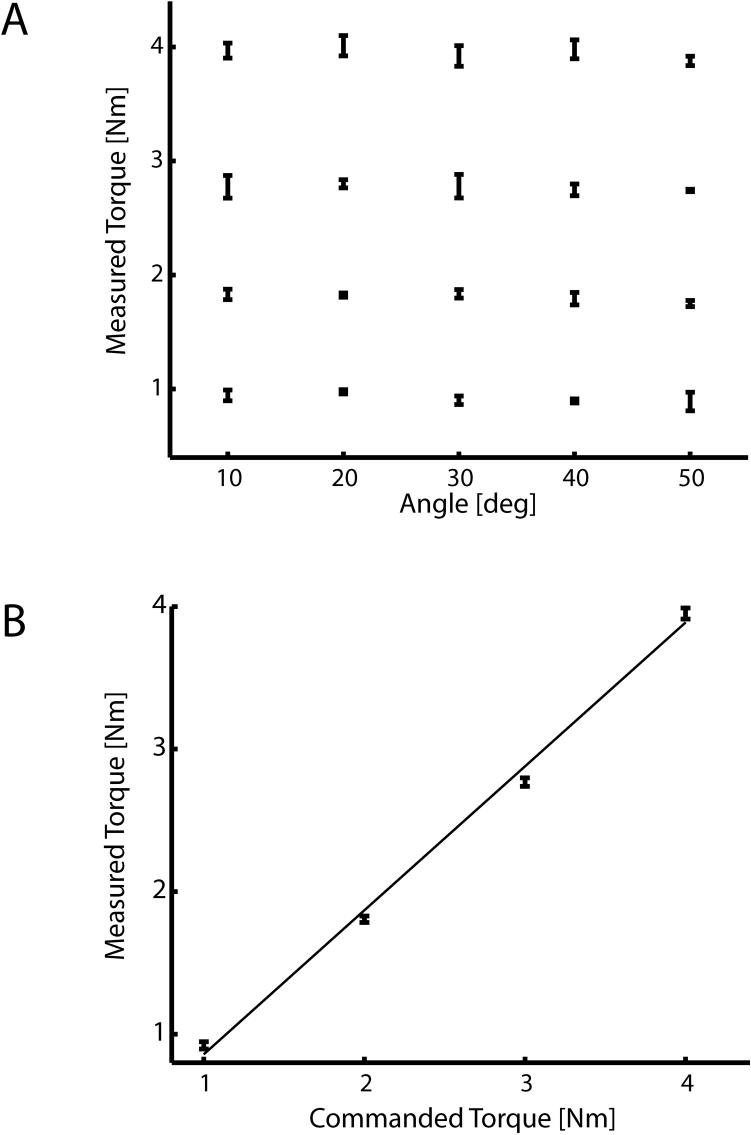
Next, we tested the device's ability to apply torques about the wrist uniformly across its workspace. We commanded the device to generate each of 4 desired torques (1, 2, 3, and 4 Nm) at each of 5 different joint angles (20° flexion to 20° extension in increments of 10°) and then measured the force applied by the robot at the handle with a Mark-10 BG Series force transducer (Mark-10, Copiague, NY). Torque output was calculated as the product of the measured force and the distance between the handle and the center of rotation of the joint. We performed separate one-way ANOVAs to determine if torque output varied as a function of joint angle.

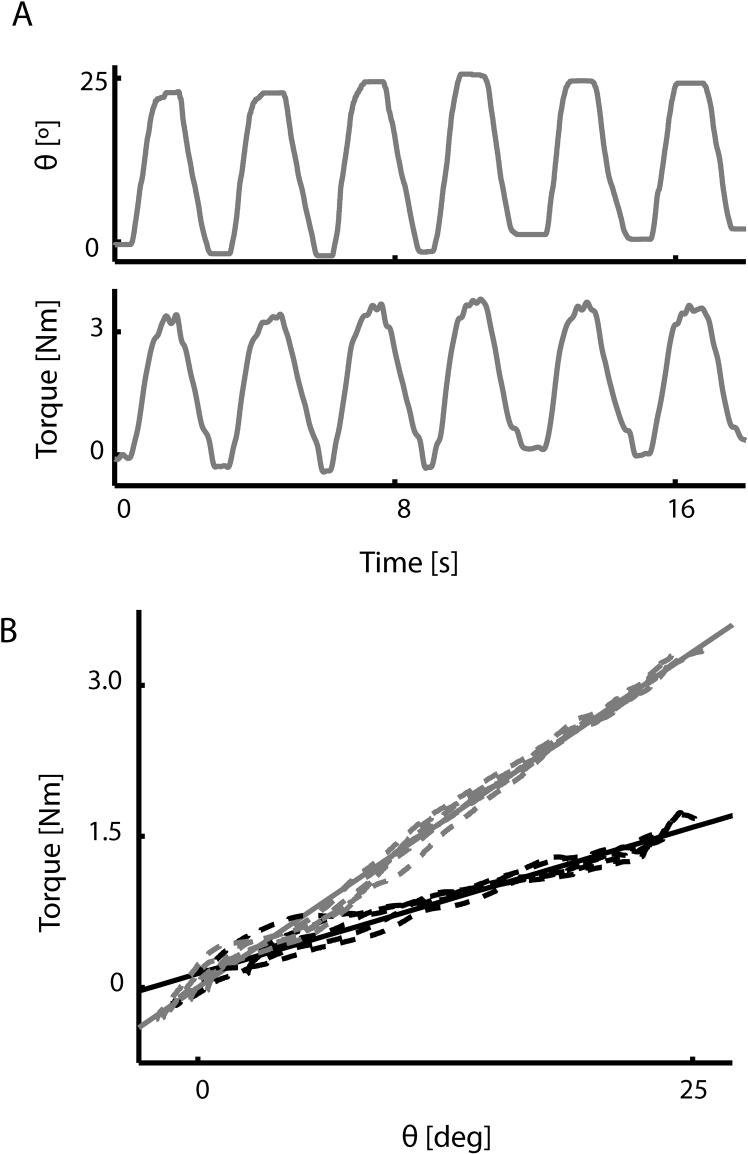
Finally, we implemented two position dependent, spring-like loads (0.075 and 0.15 Nm/deg) to verify that the device was able to apply controlled forces to the hand during flexion movements. Here, a subject made five 25° flexion movements in approximately 500ms traversing the center of the device's range of motion at each load magnitude to validate load production. A linear model was fit to the joint torque (computed from actuator pressure) and wrist angle data to quantify the realized spring constants during the flexion movements for comparison to the commanded values.

Experiment 2 - Compatibility Testing

To validate simultaneous acquisition of manipulandum data and scanner images, we scanned a phantom both with and without the device in a 3.0T GE Excite HD MR scanner (General Electric Healthcare, Milwaukee, WI), located at Froedert Hospital (Milwaukee, WI). A 3.0T spherical head phantom (Fig 1B, P; GE Model #: 2359877) was supported within a split transmit/receive quadrature head coil (Fig 1B, HC; GE Model #: 2376114) and imaged during validation testing. A gradient echo, echo planar (EP) imaging pulse sequence (29 contiguous sagittal slices; echo time (TE) = 25ms, interscan period (TR) = 2s, flip angle = 77°, field of view (FOV) = 24cm, 64 × 64 matrix; 3.75×3.75×6 mm spatial resolution) was used in order to verify that operation of the manipulandum during scanning does not induce significant artifacts in functional images, and to verify that the device could measure both pressure and joint angle without contamination from gradient switching noise during EP imaging. A field shim was performed with the phantom in the scanner only at the beginning of the experimental session, before the robot was introduced into the scanner environment.

Validation testing used a blocked experimental design (Duration = 270s). During “Motion” states, the computer cycled the device's handle through a sinusoidal trajectory (0.25 cycles per second) whereas the device remained motionless during “No Motion” states (50% duty cycle; period = 60s). Raw, complex k-space data (both I and Q channels) were collected during phantom imaging allowing analysis of both magnitude and phase MR images. We quantified the effects of simultaneous operation of the robot and scanner during both the “Motion” and “No Motion” states by imaging the phantom with the robot at 6 distances from the center of the imaging volume (0.25m, 0.50m, 0.75m, 1.0m, and 1.25m) as well as in a control condition with the robot operating outside the scanning suite (∞). The phantom was sampled using 7 equal volume (245 voxels; 20.6 cc) regions of interest (ROI) distributed within its spherical boundary to test for robot-induced spatial anisotropies in the magnitude and phase images (Fig 1C; ROIs 1−7).

Compatibility Testing Data Analysis and Statistical Inference

We used three measures to determine compatibility of the robot and MR scanner. Two measures were used to evaluate MR signal quality during robot operation during both “Motion” and “No Motion” states and the third to evaluate the effects of echo planar imaging on robot operation. First, we calculated the signal to noise ratio (SNR) within each ROI at each distance from the magnitude images:

$$SN{R}_{ROI}=\frac{{\mu }_{ROI}}{{0.665}^{\ast }{\sigma }_{noise}}$$

where μ_ROI is the time series average within a given ROI, and σ_noise is an estimate of noise in the magnitude images. The noise estimate was obtained by averaging the standard deviation of each voxel's time series in an identically sized ROI located outside the phantom (Fig 1C; ROI N). The scaling factor 0.665 was used to correct for changes in the statistical distribution of σ_noise caused by the calculation of the magnitude image from the original complex MR data (Haacke et al., 1999). Second, we used the phase images to quantify changes in magnetic field homogeneity induced by robot operation within the scanner suite. The average change in the magnetic field from baseline for each ROI (ΔB_ROI) was calculated (Haacke et al., 1999):

$$\Delta B_{ROI}=\frac{{\varphi }_{ROI}}{-\gamma T_E}$$

where, ϕ_ROI is the average change in each ROI's phase time series with respect to baseline (∞), γ is the gyromagnetic ratio, and T_E is the minimum full echo time of the EP imaging pulse sequence. The resultant change in the field was then normalized to the magnitude of the 3.0T static magnetic field (Bo) yielding a unitless quantity corresponding to the homogeneity of the magnetic field (ΔB/Bo) in parts per million. This normalization process allows a comparison between the field homogeneity and the bandwidth/voxel (39Hz or 0.32 ppm) of the EP imaging pulse sequence:

$$BW∕voxel{=}^{TS}{/}_{N_X{N}_Y}$$

where TS is the instantaneous sampling frequency of the MR scanner, N_X is the number of steps in the frequency encode direction, and N_Y is the number of steps in the phase encode direction. If introduction of the robot into the scanner environment disturbed the homogeneity of the magnetic field by more than 0.16 ppm (i.e. ½ voxel), the actual and measured location of a voxel in space would be inconsistent causing inaccuracy in the resultant images. Finally, we quantified the effects of echo planar imaging on robot operation while the computer drove the robot's handle through a sinusoidal trajectory by calculating SNR for the actuator pressure (SNR_P) and wrist angle (SNR_A) signals:

$$SNR={20}^{\ast }{\log }_{10}\left(\frac{RM{S}_{Signal}-RM{S}_{Noise}}{RM{S}_{Noise}}\right).$$

Root mean squared (RMS) values of actuator pressure and joint angle were calculated during “Motion” and “No Motion” states to approximate signal and noise respectively.

In both the “Motion” and “No Motion” conditions, we computed the average SNR magnitude within each ROI and distance condition. We performed a three-way ANOVA to compare SNR across ROIs, distance of robot from imaging volume, and motion condition. Post-hoc Dunnet's t-tests were used to compare SNR values at each distance and ROI with those obtained in the baseline condition, i.e. when the robot was outside the scanner suite. Next, to examine whether robot operation significantly disturbed field homogeneity, we performed one-sample, one-sided t-tests to determine if the field homogeneity (ΔB/Bo) was significantly greater than ½ voxel (0.16 ppm) in either of the motion states. Finally, one-sample, two-sided t-tests were performed to determine if SNR_P and SNR_A were statistically different from those measured when the robot was outside the scanner environment.

Experiment 3 - Psychophysical study

Twenty healthy volunteers participated in this study (6 female; mean age = 29 years, range: 19 to 46). All were strongly right-handed according to the Edinburgh Handedness Inventory (Oldfield, 1971). Subjects were excluded if they had significant neurological, psychiatric or other medical history, or were taking psychoactive medications. Additional exclusion criteria were specific to MR scanning: pregnancy, ferrous objects within the body, low visual acuity, and a history of claustrophobia. Written informed consent was obtained from each subject in accordance with institutional guidelines approved by the Medical College of Wisconsin and Marquette University in accordance with the Declaration of Helsinki.

Subjects rested supine in the scanner with their head constrained by foam padding to reduce head motion inside the head coil. With arms at their sides, subjects grasped the robot handle with their right hand. The handle's axis of rotation was aligned with that of the wrist, and the frame of the device was secured to the subject's forearm for support (Fig 2A). Visual stimuli were computer-generated and rear-projected on an opaque screen located at the subject's feet. The subject viewed the screen through prism glasses attached to the head coil. The sequence of trial events is displayed in Figure 2B. Prior to the start of a trial, subjects were instructed to relax and visually fixate on a central crosshair (Fig 2B, Relax) while the robot held the hand at the home position of 30° wrist extension (Fig 2B, “Relax”). Trials began with a “go” cue (Fig 2B, Go) signaling the subject to perform an out-and-back, 20° wrist flexion movement from the home position to the goal target (at 10° wrist extension) in 400 ms (± 25 ms). During the movement the robot applied perturbing forces to the hand which increased in proportion to movement displacement (i.e. a “spring-like” load). The magnitude of this perturbation was a random real value sampled from a uniform distribution between 0.045 and 0.21 Nm/deg such that the amplitude of the perturbation varied randomly from trial to trial. No visual feedback of position or velocity was provided during the wrist movement itself. Rather, the computer provided qualitative feedback of both the movement duration and the peak wrist flexion extent for approximately 1 second immediately after movement completion (Fig 2B, Feedback). Subjects were then instructed to relax and visually fixate while the robot moved the hand back to the initial starting location (Fig 2B, Relax) where they remained until the start of the next trial. Time between “go” cues varied randomly from 8 to 18 sec, with a mean of 10 sec. This variable inter-trial interval maximized the ability of the fMRI deconvolution analysis to extract hemodynamic response functions. An imaging run consisted of 50 trials, and a total of four imaging runs were conducted one after another (with 2 to 5 minute inter-run breaks) for a total of 200 trials. Total time to complete the 200 trials was approximately 35 minutes. The same sequence of perturbations (K) was used for each subject (Fig 2C). Just prior to beginning the imaging runs and while in the scanner, subjects performed 50 practice trials against a constant position-dependent load. This was done to familiarize subjects with the temporal and spatial accuracy requirements of the task. Initial practice trials were excluded from subsequent analyses.

Figure 2.

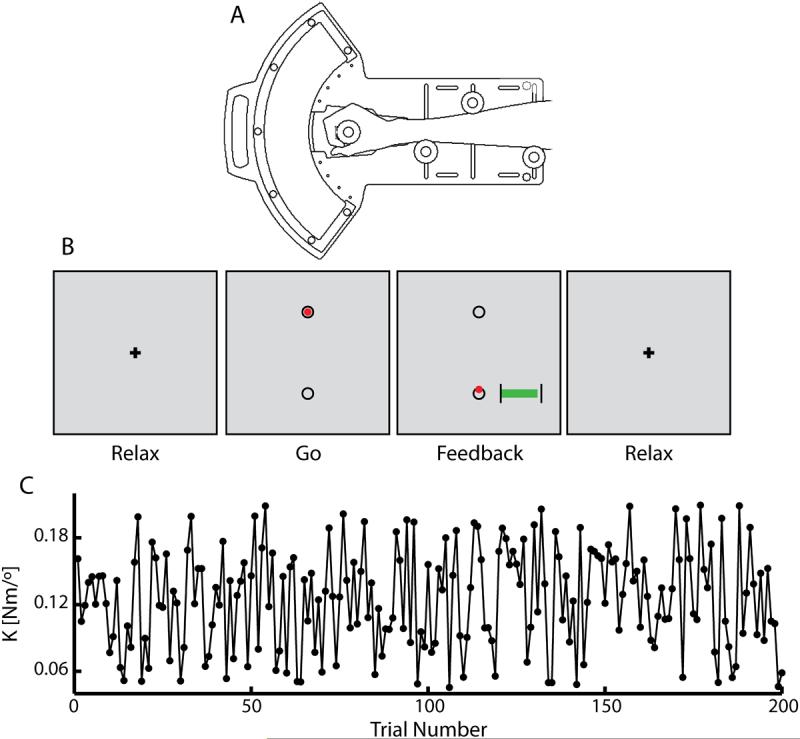
(A) Schematic representation of the one degree-of-freedom pneumatic manipulandum illustrating the subject's interaction with the device. (B) Subjects received instructions and feedback of performance via a visual display located at their feet which they viewed using prism glasses. Prior to the start of a trial, subjects were instructed to relax and visually fixate on the crosshair (Relax) while the robot held the hand at the home position. Trials began with the appearance of a red cursor within the top circle (the ‘GO’ cue) indicating that the subject was to perform a rapid, 20°, “out-and-back” wrist flexion movement. The cursor disappeared at movement onset, and reappeared at the location of peak movement extent after movement completion (Feedback). The computer also provided a graphical indication of movement time, showing whether the most recent movement was performed too fast (<375ms), too slow (>425ms), or just right. In this way, the computer provided qualitative feedback of both movement duration and end position. Finally, subjects were instructed to relax and visually fixate while the robot maintained the hand at the initial starting location (Relax). (C) The magnitude of the position-dependent perturbation, K, varied pseudo-randomly from trial to trial.

fMRI Scanning

Whole-brain imaging was performed using the MR scanner described in the Compatibility Testing section. EP images were collected using a single-shot, blipped, gradient echo EP pulse sequence (TE = 25ms, TR = 2s; FOV = 24cm; matrix 64 × 64). Thirty-five contiguous axial 4 mm thick slices were selected in order to provide coverage of the entire brain (3.75 × 3.75 × 4 mm typical voxel size). An additional 4 images were added to the beginning of the run to allow the fMRI signal to equilibrate, and 7 images were added to the end of the run to accommodate the delayed rise and fall of the hemodynamic response. Prior to functional imaging, we acquired 146 high-resolution spoiled GRASS (gradient-recalled at steady-state) axial anatomic images on each subject. These images allowed precise localization of functional activity and co-registration between subjects. That is, individual anatomical and functional images were linearly interpolated to volumes with 1 mm³ voxels, co-registered and converted to the Talairach stereotaxic coordinate space (Talairach and Tournoux, 1988). This procedure was used to compensate for subject-to-subject anatomical variation in group comparisons as described below.

Behavioral Data Analysis

Instantaneous wrist angle and actuator pressure were recorded at 1000 samples per second and low-pass filtered using a 4^th order, zero-lag, Butterworth filter with a cutoff frequency of 5Hz. We identified the maximum extent of each movement using an automated algorithm in the MATLAB computing environment. The maximum extent of movement on each trial was verified visually and manually adjusted if the algorithm erred. In addition, we calculated the joint torque generated by the subject on each trial from the actuator pressure measured at the point of maximum movement extent. Given that the trial series of movements generated by each subject may be considered a stochastic realization of a motor response to the perturbation sequence K, averaging across subjects reduces the effect of inter-subject execution variability on the performance analysis. Thus, we computed the across-subjects average of joint torque at maximum movement extent for each trial, and then performed a linear regression analysis to evaluate the linearity of the relationship between realized joint torque and specified perturbation strength for 20° wrist flexion movements.

fMRI Data Analysis

The raw fMRI signal data for each subject was converted to images using the Analysis of Functional NeuroImages software package(AFNI; (Cox, 1996)). The subjects' image time series were spatially aligned in three-dimensional space to minimize the effects of head motion using an interactive, linear, least squares method (AFNI program 3dVolreg; (Cox, 1996)) and blurred using a 6mm full width at half maximum filter to account for anatomical variability across subjects. Registration yielded 6 movement indices per functional imaging run (rotation in the superior-inferior, anterior-posterior, and left-right planes in degrees; translation in the superior-inferior, anterior-posterior, and left-right direction in mm). Mean displacement in mm was calculated for each subject as an index of head movement and ranged from 0.045 to 0.211 mm (mean = 0.099, SD = 0.046). No subjects were excluded from further analysis due to head motion (none averaged more than 0.36 mm displacement). These event-related fMRI data were analyzed using a deconvolution analysis (AFNI program 3dDeconvolve, (Cox, 1996)), in which the amplitude of the hemodynamic response (i.e., the BOLD component of the fMRI signal) was modeled using a single input reference function on a voxel-wise basis. The deconvolution estimated the time course of the BOLD signal's “impulse response” to the onset of the task relative to the resting baseline. The input reference function used in this analysis consisted of a binary time series having a value of 1 only at the onset of each individual wrist movement (i.e. the “go” cue) and 0 otherwise. This analysis made no prior assumptions regarding the shape, delay or magnitude of the impulse response function, aside from assuming that its duration was no longer than 20 seconds. For each imaging run, a 3^rd-order model of the resting fMRI baseline was included in the deconvolution analysis to account for any slow drift in the fMRI time series. Furthermore, the time series of head motion indices (obtained from the spatial registration process) were included in the model of resting baseline to reduce the potential for false positives due to stimulus correlated motion.

We calculated the change in the MR signal intensity, defined as the area under the curve (AUC) of the hemodynamic response function (HRF) estimated by the deconvolution analysis, for the images obtained 3 to 9 seconds post trial onset. The calculated AUC images were interpolated to obtain a volumetric grid having 1mm³ voxel volumes, coregistered, and then converted into the Talairach stereotaxic coordinate space (Talairach and Tournoux, 1988) to facilitate group analysis. Voxel-wise t-tests versus 0 (i.e. resting baseline) were performed using the AUC estimates to define functional regions of interest (fROI) for further analysis. fROIs were identified using both a statistical threshold (T₁₉ = 9.55, p<1×10⁻⁸) and a minimum cluster size (200μl ≈ 3.5 voxels). The threshold and cluster size values were chosen to maximize differentiation of regions, without sacrificing functional regions that might otherwise be included at a more liberal threshold. Average HRFs were then calculated for each of the fROIs for each subject and converted to percent signal change (PSC) according to the following equation:

$$PSC\left(t\right)={[\left(HRF\left(t\right)\right)∕Baseline]}^{\ast }100$$

where HRF is the hemodynamic response function averaged across all voxels contained in the fROI, and Baseline corresponds to the least squares estimate of the magnitude of the BOLD signal during periods of inactivity. This Baseline signal was estimated for each imaging run individually and then averaged across the runs yielding the measure used to compute PSC for each subject.

Finally, we calculated the average PSC across all subjects in the study. One-sample, one-sided t-tests were performed to determine if the magnitude of the population averaged PSC at each time point was significantly greater than zero (i.e. the baseline BOLD signal). The location of activated regions in functional ROIs was obtained using the Talairach atlas for cortical activations (Talairach and Tournoux, 1988) and the Schmahmann atlas (Schmahmann, 2000) for cerebellar functional ROIs. Activations were visualized using CARET (Van Essen et al., 2001); http://brainmap.wustl.edu/caret).

Statistical testing on MR compatibility and behavioral data was carried out within the Minitab computing environment (Minitab, Inc., State College, PA), whereas AFNI was used for statistical testing of fMRI data. In both cases, effects were considered statistically significant at the α = 0.05 level.

Results

Experiment 1- Robotic System Validation

The performance of the robotic system was quantified by characterizing its response to step changes in pressure under both open loop and closed loop PID control. For step changes of 1 and 2 PSI, open loop rise times were 218ms and 240ms, respectively (Fig 3A, black lines). No overshoot was observed in response to step changes in pressure in open loop conditions. Under PID control, rise times decreased by an average of 63% to 77ms and 90ms for 1 and 2 PSI step increases, respectively, with maximum overshoot averaged 19% (Fig 3A, gray lines). Rise times for 1 and 2 PSI step decreases were 93ms and 140ms, respectively. In both control conditions, we observed time delays due to propagation of air in the pneumatic system of 59ms and 65ms for the 1 and 2 PSI step increases, and 174ms and 151ms for the 1 and 2 PSI step decreases. The bandwidth of the closed-loop system was identified by assessing the system's ability to track changes in commanded actuator pressure having a 1 PSI peak-to-peak ‘chirp’ profile sweeping from 0 to 5Hz (Fig 3B top, black line). The device was able to track commanded pressure changes within 15% of the desired value up to 1.6 Hz under PID control (Fig 3B, red line). This limitation was asymmetric in that we did not observe severe degradation of positive pressure regulation at higher commanded frequencies. Asymmetries in the response times for 1 and 2 PSI step increases and decreases and the functional bandwidth of the system were mainly due to a smaller pressure differential between the vacuum supply and actuator pressure as compared to the pressure supply and actuator pressure, as well as an inability of the system to maintain a sufficient vacuum supply at higher commanded frequencies.

We then validated the system's ability to uniformly generate joint torque across its workspace. We measured the torque generated by the device at 5 joint angles in response to commanded torque values of 1, 2, 3, and 4 Nm (Fig. 4A). Separate one-way ANOVAs found that joint angle had no effect in the ability of the robot to generate torque (p = 0.121, p= 0.06, p = 0.768, and p = 0.203 for commanded loads of 1, 2, 3, and 4 Nm respectively). Next, we collapsed the measured torque values across joint angles and then fit a line to the desired vs. measured torque data. The resulting relationship was very linear (r² = 99%) with a slope of 1.01 indicating that the system accurately reproduced the desired torque across its workspace (Fig. 4B).

Figure 4.

(A) Validation of the system's ability to generate uniform torques across its range of motion. Measured torque generated by the device at in response to commanded torque values of 1, 2, 3, and 4 Nm did not vary as a function of joint angle. (B) The relationship between desired and measured torque was very linear (r² = 99%), having a slope of 1.01 indicating that the system accurately reproduced the desired torque across its workspace.

We then evaluated the system's ability to simulate spring-like loads about the wrist. Specifically, we estimated the realized spring constants for two simulated position-dependent loads (0.075 and 0.15 Nm/deg) by fitting a linear model to the joint torque-angle data collected during 25 degree flexion/extension movements (Fig 5A) as in Fig 5B. The estimated stiffness of the two spring-like loads generated by the device during wrist flexions were 0.059 and 0.134 Nm/deg, respectively, yielding an average error of 16%. In both cases, the torque-angle relationships were very linear, with r² values of the regressions exceeding 96% and 99% for the 0.075 and 0.15 Nm/deg loads respectively. Thus, the robot is quite effective in simulating torsional spring-like loads about the wrist.

Figure 5.

(A) Time courses of joint angle (top) and torque (bottom) during 25° wrist flexion movements while the robot simulated a 0.15 Nm/deg position-dependent load. (B) We estimated the realized spring constants for two simulated loads (0.075 and 0.15 Nm/degree; dashed black and gray lines respectively) by fitting a line to the joint torque and wrist angle data (solid lines). The realized stiffness of the two spring-like loads were 0.059 and 0.134 Nm/degree (average error: 16%; r² > 0.95 in both cases).

Experiment 2 - Compatibility Testing

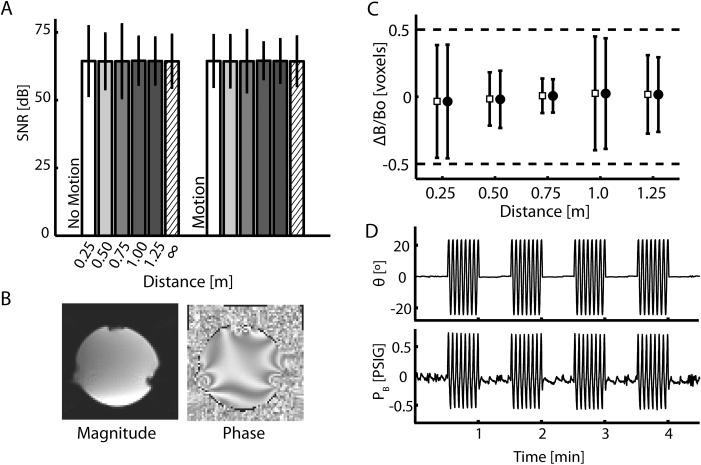
To evaluate the effect of robot operation on scanner performance, we computed SNR changes within 7 phantom ROIs caused by operating the robot at 5 distances from the center of the imaging volume relative to the control (∞) condition (Fig 6A). Values of SNR varied across the seven ROIs, but were relatively insensitive to robot placement distance within each individual ROI, as shown for a representative ROI (Fig 1C, ROI 3). ANOVA found significant main effects of both ROI (F_6,71 = 7635, p < 0.0005) and distance (F_5,71 = 7.73, p < 0.0005), but demonstrated that there was no effect of robot motion (F_1,71 = 0.01, p = 0.929). Comparison of SNR at the five distances to the control condition (∞) using Dunnet's post-hoc t-test revealed a small (0.64 and 0.90 dB) but significant increase in SNR at 1.0 m and 1.25 m as compared to control (p = 0.0008 and p = 0.008, respectively), but no change in SNR as compared to control at 0.75m, 0.5m, and 0.25m (p = 0.97, 0.97, and 0.7; respectively). Thus, there appears to be no systematic degradation of functional MR SNR as a function of robot distance from the imaging volume. The variation in SNR within the phantom volume with respect to ROI was clearly caused by local field artifacts induced by the phantom holder (Fig 1B; H) and boundary effects at the phantom's outer shell (Fig 6B), since these effects were observed even when the robot was not present.

Figure 6.

(A) Signal to Noise ratio (SNR) for phantom ROI 3 (see Fig 1C) plotted against device operating distance from the center of the imaging volume. The SNR measurements were calculated from magnitude images. Within ROIs, SNR measurements were similar, demonstrating little effect of the robot on scanner performance in both the “No Motion” and “Motion” states. Because we were interested in how the mean SNR changed with distance in this case, error bars in this panel represent 95% confidence intervals about the mean SNR at each distance (i.e. ±2 SEM). (B) Sagittal slice of the magnitude and phase images of the phantom. Notice the susceptibility artifact bilaterally in the lower portion of the image caused by the presence of the phantom holder. This artifact was seen in images both with and without the manipulandum in the scanner. (C) Estimate of field homogeneity in ROI 3 from phase data collected in the “No Motion” (open squares) and “Motion” (filled circles) states. Because we were interested in the distribution of homogeneity values, error bars in this panel represent ± 2 standard deviations about the mean homogeneity and thus 95% of the data lie within these bounds. All values of DeltaB/Bo are within expected ranges of field uniformity. (D) Representative measurements of wrist angle and bellows pressure taken during the validation experiment where the device was 0.50m from the imaging volume. Pressure and volume measurements are not adversely effected by the operation of the MR scanner.

Next, we computed the field distortion (ΔB/Bo) induced by the robot at each distance using imaging data acquired during both the “Motion” and “No Motion” states. As shown for a representative ROI (Fig 1C; ROI 3), field inhomogeneity induced by the robot (ΔB/Bo) was well below ½ voxel at each distance in the “No Motion” (Fig 6C; open squares) and “Motion” (Fig 6C; filled circles). A one-sided t-test rejected the hypothesis that the average magnitude of the field distortion exceeded 0.5 voxel in both the “No Motion” (T₃₅ = 189.6, p < 0.0005) and “Motion” (T₃₅ = 187.4, p < 0.0005) states. Thus image quality was not influenced by the device and its operation. Scanner operation also had minimal effects on manipulandum operation (Fig 6D). Neither joint angle nor pressure SNR varied systematically as a function of distance. No difference was observed in measurements of SNR_Angle (T₉ = 0.09, p = 0.934) or SNR_Pressure (T₉ = 0.39, p = 0.705) when compared to baseline measures obtained when the robot was operated outside scanner environment (∞). Neither image quality nor the robot performance was compromised by operation of the robot within the scanning environment during MR imaging.

Experiment 3 - Psychophysical study

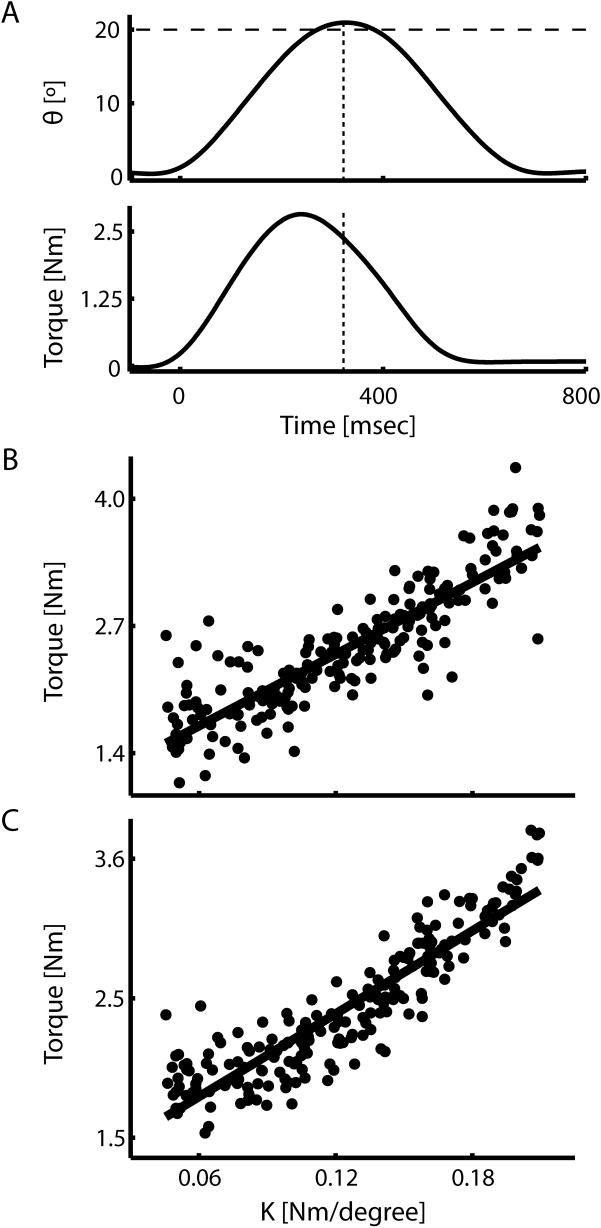
Subjects made smooth, accurate movements while being perturbed by the position dependent load (Fig 7A top, shown for a representative trial). Across subjects, movement time averaged 403.1 ± 23.1 ms (mean ± SD, both here and elsewhere) while the maximum movement extent averaged 19.81 ± 1.38 degrees demonstrating that subjects were successful in acquiring the target in the desired time period. As expected, joint torque increased in proportion to movement extent (shown for a representative trial in Fig 7A, bottom). The across subjects average torque equaled 2.49 ± 0.52 Nm at maximum movement extent (Fig 7A dashed lines), only 0.4% less than that specified by the mean perturbation magnitude. Joint torque at maximum movement extent was reasonably well-characterized as a linear function of commanded perturbation amplitude as demonstrated by separate within- and across- subject regression analyses (Fig 7B and C gray lines; r² = 76% and 82%; for a representative subject and the population, respectively). Thus, the device was effective in simulating spring-like loads over a wide range of magnitudes during point to point wrist flexion movements.

Figure 7.

Behavioral results of the psychophysical experiment. (A) Time series of wrist joint angle (top) and wrist torque (bottom) for a representative trial. The dotted vertical lines indicate the time at which maximum movement extent is achieved, while the dashed horizontal line indicates the target of the movement. (B and C) Scatterplots of individual trial joint torque values at maximum extent vs. perturbation strength for a representative subject (B) and averaged across all 20 subjects (C) were well-fit by a linear relationship (r² = 0.76 and 0.82 for a representative subject and the study population, respectively).

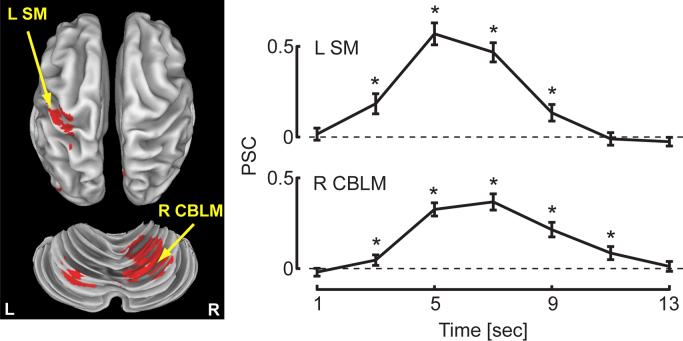
Changes in BOLD signal relative to rest correlated strongly with the onset of wrist motion in cortical and subcortical regions thought to contribute to the control of movement in the upper extremity (Table 1, p < 0.05, corrected for multiple comparisons; see Fig 8, left). Average across-subject hemodynamic response functions (HRF) extracted from the left sensorimotor cortex (Fig 8, right; L SM) and right cerebellum (Fig 8, right; R CBLM) demonstrate characteristic profiles with peaks in the BOLD response approximately 6 seconds after the “go” cue. One-sample t-tests found that the magnitude of the PSC value was significantly greater than baseline for four or five TRs in both fROIs (asterisks, Fig 8; p < 0.05).

Table 1.

Functional Regions of Interest Identified in Experiment 3

		Tailarach Coordinates
	Hem	X	Y	Z	Vol
Cortical
Precentral/Postcentral Gyrus (BA 2,3,4)	L	−36.2	−26.7	53.1	2538
Lingual Gyrus	B	0.8	−66	3.5	1124
Middle Occipital Gyrus (BA 19)	L	−38.9	−75.5	4.8	915
Medial Frontal Gyrus (SMA, BA 6)	L	−2	−18.9	47.6	724
Insula (BA 13)	L	−43.3	−29.8	22.1	377
Subcortcal
Cerebellum (Lobule IV,V,VI)	R	17.3	−55.6	−14.2	4694
Thalamus	L	−11	−18.3	10.1	1866
Thalamus	R	11.5	−14.7	14	913
Red Nucleus	B	1.9	−23.8	−4.9	750
Cerebellum (Lobule VI)	L	−19.2	−65.3	−19.5	684

Abbreviations: R = Right; L = Left; B = Bilateral

Figure 8.

Hemodynamic response functions (HRF) as a function of time following the movement ‘go’ cue extracted from functional ROIs in the left sensorimotor cortex (L SM) and right cerebellum (R CBLM) were robust and exhibited a characteristic profile. Asterisks indicate TRs where a one-sided, one sample t-test found a significant increase in the magnitude of the HRF compared to baseline (rest) at α = 0.05.

Discussion

We sought to design a robot able to both monitor and perturb wrist movements during FMRI scanning, and to demonstrate its efficacy as a tool to be used in motor control research involving human subjects. The pneumatic robot provides controlled flexion and extension torques about the wrist and monitors actuator pressure and joint angle via commercially available sensors. Performance and compatibility testing demonstrated that the device possesses sufficient bandwidth to apply spring-like loads to movements during imaging. Two measures of MRI signal quality were undisturbed by introduction of the robot into the scanner environment. Likewise, measurements of joint angle and actuator pressure were unaffected by FMRI scanning. In a final test of system efficacy, we scanned 20 human subjects as they made rapid, 20° wrist flexion movements against a wide range of spring-like loads. Peak torque scaled linearly with commanded load as desired. We expected this task to elicit BOLD activation in regions known to contribute to the control of movement. This was indeed the case, as hemodynamic response functions obtained from the left primary sensorimotor cortex and the right cerebellar cortex demonstrated robust BOLD responses to movement of the right wrist. These results show that neither image quality nor the performance of the robot is degraded by robot operation during MR imaging, and that regions activated by the wrist movement task are consistent with previous studies of goal-directed hand movements.

The one degree-of-freedom, MR-compatible manipulandum we have described compares favorably with other MR-compatible devices that have been developed by other groups for use in neuroscience research or rehabilitation applications. Whereas the devices developed by Hidler et al. (Hidler et al., 2006) and Khanicheh et al. (Khanicheh et al., 2005) can only monitor the torque/force generated by the subject, our device offers the ability to simulate dynamic environments by generating torque about the wrist. The ability to apply dynamic loads is also provided by MR-compatible actuators using Lorentz coils (Riener et al., 2005), ultrasonic motors (Flueckiger et al., 2005), or hydrostatic pistons (Gassert et al., 2006). In contrast to the device presented by Riener, et al., our device does not significantly degrade image quality when operated less that 1m from the scanner's isocenter. Because the devices presented by Flueckinger, et al. (Flueckiger et al., 2005) and Gassert, et al. (Gassert et al., 2006) are not backdriveable, they can not simulate realistic dynamic loads during movements requiring rapid changes in direction whereas our device is clearly able to do so. And while the two degrees of freedom device presented by Diedrichsen, et al. (Diedrichsen et al., 2005) offers the ability to perturb planar reaching movements of the arm, perturbation of proximal limb segments can lead to considerable head motion which must be accounted for during analysis of fMRI data (Diedrichsen and Shadmehr, 2005). In contrast, our current design limits motion to the wrist, which may lead to fewer head motion artifacts in the fMRI dataset.

Although the device and control scheme described here can generate wrist torques with sufficient bandwidth for simulating position dependent loads, the system's ability to simulate loads requiring a higher frequency response (eg. velocity- or acceleration-dependent loads) has yet to be demonstrated. Two approaches may be taken to improve system response. As demonstrated by Gassert and colleagues (Ganesh et al., 2004; Gassert et al., 2006), it is possible to develop MR compatible robots possessing bandwidth exceeding 20Hz using a hydrostatic, master-slave system (Ganesh et al., 2004; Gassert et al., 2006). That approach uses an incompressible medium and higher system pressures to generate greater bandwidth but also introduces the possibility of fluid leaks within the scanner environment if a component in the system fails. Similar performance enhancements have been demonstrated in a dual-acting pneumatic actuator by using a nonlinear mathematical model of the actuator system along with a sliding mode controller (Richer and Hurmuzlu, 2000a, 2000b). Using this last approach, we believe that the bandwidth of our system could be improved at least by a factor of 10.

Two considerations are of paramount importance in the design of a MR-compatible device. These are to ensure that the device is safe to operate within the MR environment by using MR-compatible materials and to demonstrate that neither image quality nor the performance of the device is degraded due to operation of the device The MR compatibility of materials and devices have been extensively investigated (Chinzei et al., 1999; Schenck, 1996) giving those developing devices guidance on which materials and components are safe to incorporate into their designs. In contrast, the methodology for demonstrating MR compatibility (i.e. operation of a device during imaging does not effect the MR images) has received little attention. A compatible device will not cause losses in magnetic field homogeneity or SNR due to its operation. In the majority of studies, compatibility is shown by collecting magnitude images of a phantom both with and without the device in the scanner and looking for changes (shifts or magnitude changes) in the subtraction of the two images (Flueckiger et al., 2005; Gassert et al., 2006; Khanicheh et al., 2005). In some cases the effects of device operation on scanner performance are also quantified as a function of distance (Khanicheh et al., 2005). Here, we explicitly looked at such effects on SNR and field homogeneity by collecting complex k-space data and then reconstructing the magnitude and phase images, allowing us to investigate the effects of robot operation on images both as a function of distance from the imaging volume and as a function of space within the phantom. We were able to detect local degradation of SNR and homogeneity caused by the presence of the phantom holder (but not the robotic device) that might have gone unnoticed by other methods, thereby increasing confidence that future neuroimaging studies using our system will not be confounded by signal artifact introduced by device operation within the scanning environment.

Phantom testing alone is not sufficient to demonstrate compatibility of the device because the quality of images generated by the scanner may change when it is loaded by a subject. Therefore, we scanned 20 human subjects as they made rapid, point-to-point, wrist movements while the robot simulated a position dependent load that varied in magnitude from trial-to-trial. We observed activations due to wrist movement in regions known to contribute to the control and execution of visuomotor tasks including the sensorimotor cortex, supplementary motor area, motor thalamus, and cerebellum (Diedrichsen et al., 2005; Imamizu et al., 2000; Vaillancourt et al., 2003). Average hemodynamic response functions extracted from sensorimotor cortex and the cerebellum demonstrate that movements perturbed by the position dependent loads elicit robust BOLD responses. We therefore conclude that the device is safe and effective for conducting future research exploring how individual structures in the intact and impaired human central nervous system contribute to the planning and execution of wrist movements.