Modeling river delta formation

Abstract

A model to simulate the time evolution of river delta formation process is presented. It is based on the continuity equation for water and sediment flow and a phenomenological sedimentation/erosion law. Different delta types are reproduced by using different parameters and erosion rules. The structures of the calculated patterns are analyzed in space and time and compared with real data patterns. Furthermore, our model is capable of simulating the rich dynamics related to the switching of the mouth of the river delta. The simulation results are then compared with geological records for the Mississippi River.

The texture of the landscape and fluvial basins is the product of thousands of years of tectonic movement coupled with erosion and weathering caused by water flow and climatic processes. To gain insight into the time evolution of the topography, a model has to include the essential processes responsible for the changes of the landscape. In geology, the formation of river deltas and braided river streams has long been studied, describing the schematic processes for the formation of deltaic distributaries and interlevee basins (1–5). Experimental investigation of erosion and deposition has a long tradition in geology (6). Field studies have been carried out for the Mississippi River delta (7–10), the Niger River delta (11–13), and the Brahmaputra River delta (14). Laboratory experiments have also been set up in the last decades for quantitative measurements (15–19). For instance, in the eXperimental EarthScape (XES) project, the formation of river deltas is studied on laboratory scale, and different measurements have been carried out (20–22).

Nevertheless, modeling has proven to be very difficult because the system is highly complex and a large range of time scales is involved. To simulate geological time scales, the computation power is immense and classical hydrodynamical models cannot be applied. Typically, these models are based on a continuous ansatz (e.g., shallow water equations), which describes the interaction of the physical laws for erosion, deposition, and water flow (23–28). The resulting set of partial differential equations are then solved with boundary and initial conditions using classical finite element or finite volume schemes. Unfortunately, none of these continuum models is able to simulate realistic land forms because the computational effort is much too high to reproduce the necessary resolution over realistic time scales. Therefore, in recent years, discrete models based on the idea of cellular automata have been proposed (29–34). These models consider water input on some nodes of the lattice and look for the steepest path in the landscape to distribute the flow. The sediment flow is defined as a nonlinear function of the water flow, and the erosion and deposition are obtained by the difference of the sediment inflow and outflow. This process is iterated to obtain the time evolution. In contrast to the former models, these models are fast and several promising results have been obtained; however, because they are only based on flow, a well defined water level cannot be obtained with this ansatz.

Here we introduce a model in which the water level and the landscape are described on a lattice grid coupled by an erosion and sedimentation law. The time evolution of the sediment and water flow is governed by conservation equations. The paper is organized as follows. After an overview on the different types of deltas and their classification, the model is introduced and discussed in detail. The analysis of the model results and a comparison with real landforms are provided. According to different parameter combinations, different delta types can be reproduced, and interesting phenomena in the time evolution of a delta, such as the switching of the delta lobe, can be observed. Finally, the scaling structure of the delta pattern is analyzed and compared with that obtained from satellite images.

Classification

The word “delta” comes from the Greek capital letter Δ and can be defined as a coastal sedimentary deposit with both subaerial and subaqueous parts. It is formed by riverborne sediment that is deposited at the edge of a standing water, in most cases an ocean, but some times a lake. The morphology and sedimentary sequences of a delta depend on the discharge regime, the sediment load of the river, and the relative magnitudes of tides, waves, and currents (35). Also, the sediment grain size and the water depth at the depositional site are important for the shape of the deltaic deposition patterns (1, 35–37). This complex interaction of different processes and conditions results in a large variety of different patterns according to the local situations. Wright and Coleman (1, 35, 38, 39) described depositional facies in deltaic sediments and concluded that they result from a large variety of interacting dynamic processes (climate, hydrologic characteristics, wave energy, tidal action, etc.) that modify and disperse the sediment transported by the river. By comparing 16 deltas, they found that the Mississippi River delta is dominated by the sediment supply of the river, whereas the Senegal River delta or the São Francisco River delta are mainly dominated by the reworking wave activities. High tides and strong tidal currents are the dominant forces at the Fly River delta.

Galloway (40) introduced a classification scheme where three main types of deltas are distinguished according to the dominant forces on the formation process: river-, wave-, and tide-dominated deltas. This simple classification scheme was later extended (36, 37, 41) to include grain size and other effects.

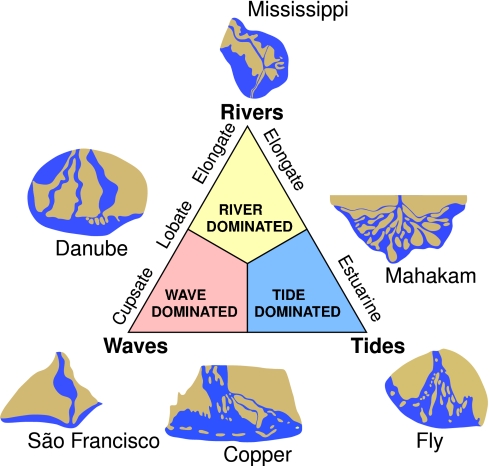
At the river-dominated end of the spectrum, deltas are indented and have more distributaries with marshes, bays, or tidal flats in the interdistributary regions. They occur when the stream of the river and the resulting sediment transport is strong and other effects, such as reworking by waves or tides, are minor (35, 38). These deltas tend to form big delta lobes into the sea, which may have little more than the distributary channel, and have a levee exposed above the sea level. Due to their similarity with a bird's foot, they are often referred to in the literature as a “bird-foot delta,” like in the case of the Mississippi River delta (35). When more of the flood plain between the individual distributary channels is exposed above the sea level, the delta displays lobate shape. Wave-dominated delta shorelines are more regular, assuming the form of gentle, arcuate protrusions, and beach ridges are more common (e.g., the Nile River delta or Niger River delta; refs. 12 and 42). Here, the breaking waves cause an immediate mixing of fresh and salt water. Thus, the stream immediately loses its energy and deposits all its load along the cost. Tide-dominated deltas occur in locations of large tidal ranges or high tidal current speeds. Such a delta often looks like a estuarine bay filled with many stretched islands parallel to the main tidal flow and perpendicular to the shore line (e.g., the Brahmaputra River delta). Using the classification of Galloway (40), the different delta types can be arranged in a triangle where the extremes are put in the edges (see Fig. 1).

Fig. 1.

The classification scheme after Galloway (40), where wave-, tide-, and river-dominated deltas are distinguished in the extremes of the triangle. By comparing 16 major river deltas, Wright and Coelman (38) concluded that, in the extremes, the Mississippi River delta is the most river-dominated delta and the São Francisco River delta is the most wave-dominated one. The delta of the Fly River in Papua New Guinea is mainly dominated by the tides.

The Model

The model discretizes the landscape on an rectangular grid where the surface elevation H_i and the water level V_i are assigned to the nodes. Both H_i and V_i are measured from a common base point, which is defined by the sea level. On the bonds between two neighboring nodes i and j, a hydraulic conductivity for the water flow from node i to node j is defined as

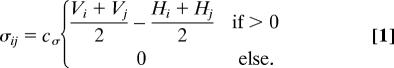Because only surface water flow is considered, σ_ij is set larger than zero only if the water level of the source node is larger than the topography, which means that water can only flow out of a node where the water level is above the surface. The relation between the flux I_ij along a bond and the water level is given by

Furthermore, water is routed downhill by using the continuity equation for each node

where the sum runs over all currents that enter or leave node i and V′_i is the new water level. The boundaries of the system are chosen as follows: On the sea side, the water level on the boundary is set equally to zero and water just can flow out of the system domain. On the land, the water is retained in the system by high walls or choosing the computational domain for the terrain such that the flow never reaches the boundary. Water is injected into the system by defining an input current I₀ at the entrance node.

The landscape is initialized with a given ground water table. Runoff is produced when the water level exceeds the surface. The sediment transport is coupled to the water flow by the rule that all sediment that enters a node has to be distributed to the outflows according to the strength of the corresponding water outflow. Thus, the sediment outflow currents for node i are determined via

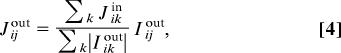where the upper sum runs over all inflowing sediment and the lower one over the water outflow currents. A sediment input current s₀ is defined in the initial bond.

The sedimentation and erosion process is modeled by a phenomenological relation that is based on the flow strength I_ij and the local pressure gradient imposed by the difference in the water levels in the two nodes V_i and V_j. The sedimentation/erosion rate dS_ij is defined through

where the parameters I* and V* are erosion thresholds and coefficients c₁ resp. c₂ determine the strength of the corresponding process. The first term, c₁(I* − |I_ij|), describes the dependency on the flow strength I_ij and is widely used in geomorphology (44), whereas the second term, c₂(V* − |V_i − V_j|), relates sedimentation and erosion to the flow velocity, which in the model can be described by I_ij /σ_ij ≈ |V_i − V_j|. The two terms of Eq. 5 are not linearly dependent on each other as one may think first by looking Eq. 2. In fact, due to Eq. 1, there is a nonlinear relation between V and I that leads to different thresholds in the pressure gradient and current.

The sedimentation rate dS_ij is limited by the sediment supply through J_ij; thus, in the case dS_ij > J_ij, the whole sediment is deposited on the ground and J_ij is set to zero. In the other cases, J_ij is reduced by the sedimentation rate or increased if we have erosion. The erosion process is also supply limited, which means that the erosion rate is not allowed to exceed a certain threshold T; so, if dS_ij < T, then dS′_ij = T. Note that, in the case of erosion, dS_ij is negative. Due to erosion or deposition, the landscape is modified according to

where the sediment deposits equally on both ends of the bond. The new topography is marked with H′_i. The same formulae (Eqs. 6 and 7) also hold in the case of erosion when dS_ij is negative.

Iterating Eqs. 1–7 determines the time evolution of the system. Finally, in a real system, subaqueous water currents lead to a smoothening of the bottom, which is modeled by the following expression

where ε is a smoothening constant determining the strength of the smoothening process. The sum runs over all nearest neighbors of node i.

Simulation

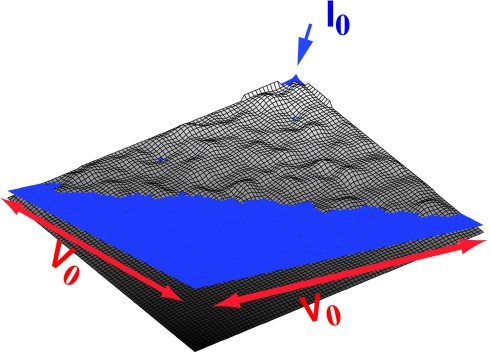
The simulation is initialized with a valley on a rectangular N × N lattice with equal spacing grid as shown in Fig. 2. The valley runs downhill with slope S along the diagonal of the lattice, and the hillslopes of the valley increase from the bottom of the valley sideward according to a power law with exponent α. In the simulation shown in Fig. 3, the value of α was chosen to be 2.0. Under the sea, the landscape is flat with a constant slope downhill. Furthermore, we assume the initial landscape to have a disordered topography by assigning uniformly distributed random numbers to H_i. This variable is then smoothed out according to Eq. 8. The water level V_i of the system is initialized with a given ground water table. In reality, the distance of the ground water to the surface is minimal on the bottom of the valley and increases uphill. This is obtained in the simulation by choosing the water level V_i in an incline plane δ below the bottom of the valley. The slope of the plane is the same as the slope of the valley S. This also keeps the river close to the bottom of the valley. Because we are only interested in studying the pattern formation at the mouth of the river, the braiding conditions of the upper river only determine the width of the delta front. On the seaside, when H_i ≤ 0, the water level is a constant and set to zero. A sketch of the initial landscape is shown in Fig. 2.

Fig. 2.

A sketch of the initial condition for a simulation. A water current I₀ is injected at the upper node and the water levels on the sea boundaries are kept constant (V₀ = 0). The landscape is initialized as an inclined plane with a disordered topography on the top. The water surface (blue) is parallel to the horizontal plane.

Fig. 3.

Time evolution of a bird-foot delta (from left to right). (a) The delta after 1.2 million time steps, where the main channel worked into the sea depositing sediment mainly on its levee sides. (b and c) After 2.5 million time steps, the main channel has split into two distributaries (b), whereas the smaller one becomes inactive after 5 million steps and a new channel breaks through the sidewalls (c). The main directions of the sediment flow are marked with the red arrows. The simulation was run on a 279 × 279 lattice, and the parameters for the water flow were I₀ = 1.7 × 10⁻⁴ and c_σ = 8.5. For the sedimentation and erosion, the constants were set to c₁ = 0.1 and c₂ = 0 with a sediment input current of s₀ = 0.00025. The erosion threshold I* was set to I* = 4 × 10⁻⁶, and the maximal erosion rate was set to |T| = 5 × 10⁻⁷. Smoothening was applied every 2,000 time steps with a smoothening factor of ε = 1 × 10⁻⁴. The initial depth of the water table at the bottom of the valley was set to δ = 0.0025.

An initial channel network is created by running the algorithm without sedimentation and erosion until the water flow reaches a steady state. Then, the sedimentation and erosion procedure is switched on, and the pattern formation at the mouth of the river is studied.

According to the dominance of the different processes, completely different coastline shapes can be observed. The smoothening procedure in Eq. 8 leads to the formation of an estuary by reworking the coastline at the river mouth, whereas the stream dominant erosion term c₁(I* − |I_ij|) in Eq. 5 favors the formation of river-dominated bird-foot-shaped delta. In contrast to this, the second term c₂(V* − |V_i − V_j|) in Eq. 5, which depends on the pressure gradient represented by the height difference of the water levels in the nodes i and j, produces more classical deltas with several islands and channels. These patterns are similar to the distributary structure of the Lena or Mahakam River deltas, which are more sea- or wave-dominated. This difference can be explained by the fact that the first term distributes sediments along the main current stream, whereas the second term distributes the sediment more equally to the neighboring nodes.

Fig. 3 a–c shows some snapshots of the time evolution of the simulation of a bird-foot delta (c₂ = 0). A map of the Mississippi River is given in Fig. 4 for comparison. In both cases, one can see how the main channel penetrated into the ocean depositing sediment mainly on its levee sides. When the strength of the main channel decreases, side channels start to appear; breaking through the sidebars as can be seen in the snapshots of Fig. 3 b and c. At the beginning of the delta formation process, the sediment transport is equally distributed among the different channels and leads to a broader growth of the delta front along the coast. With time, the side channels are gradually abandoned and the sediment is primarily routed through the main channel; thus, this dominant channel is growing faster than the others, forming the typical bird-foot-shaped deposits.

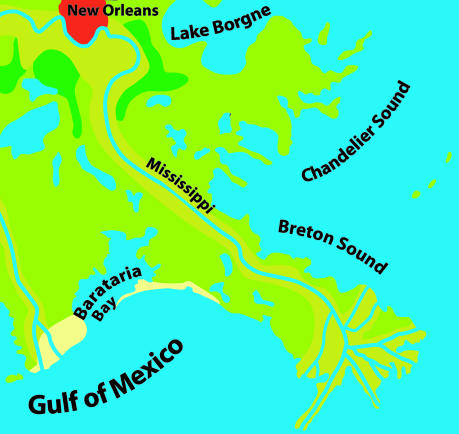
Fig. 4.

For comparison with the simulation results of Fig. 3, the figure shows part of a map of the mouth of the Mississippi River, where the bird-foot-shaped delta can be seen clearly. The colors indicate channel deposits (mustard), sand ridges (yellow), swamps (light green), and marshes (dark green). The figure was redrawn from ref. 35.

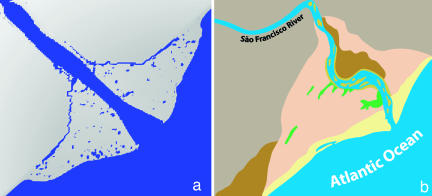
Fig. 5a shows another type of delta where the smoothening of the waves reworks the deposits at the river mouth and distributes it along the coast. Here, the river could built up only a slight protrusion in the immediate vicinity of the river mouth. The same happens in areas where the wave currents are dominant, and lead to the formation of wave-dominated deltas like the São Francisco River delta in Brazil or the Nile River delta. A map of the São Francisco River delta is also given in Fig. 5b for comparison. Here, the coast line has been straightened by the wave activities and consists almost completely of beach ridges that have the typical triangular shape inland. This flattened deposit can also be found in our simulation results. Because there is no evaporation included in the simulation, small ponds and abandoned channels remain in the sedimented zone instead of disappearing with time.

Fig. 5.

Comparison of the simulation results (a) with a real map (b). (a) Simulation of a wave-dominated delta. While the waves are reworking the coast at the mouth of the river to form an estuary, the river deposits sediment and forms large beaches. Because the simulation does not include evaporation, the ponds and inactive channels in the deposition zone do not disappear as in the map of the real river shown in b. The parameters in the simulation were n = 179, I₀ = 1.7 × 10⁻⁴, s₀ = 0.0015, c_σ = 8.5, c₁ = 0, c₂ = 0.1, and I* = 1.3 × 10⁻⁴. Smoothening was applied every 200 time steps with a smoothening constant ε = 0.01. (b) A map of the São Francisco River delta in southern Brazil, which is the most wave-dominated delta according to the classification of ref. 41. The colors in the map (b) indicate channel deposits (mustard), beach ridges (peach), eolian dunes (yellow), marsh-mangroves (green), the floodplain (brown), and the uplands (tan). The figure was redrawn from ref. 35.

Finally, if the term c₂(V* − |V_i − V_j|) dominates the sedimentation/erosion process, a half-moon-shaped delta with many small islands and channels appear. This delta type shows more activity in the channel network than the others. The channels split and come together, and when the main channel blocks its way due to sedimentation, the whole delta lobe switches to another place. This phenomenon is called delta switching. During the simulation, the switching of the delta occurred several times.

The best studied delta in the world is that of the Mississippi River, where the switching of the delta lobes was studied in detail (8). The switching of the Mississippi River delta during the last 4,000 years is well documented (7, 8, 44). The rich dynamics due to the switching phenomenon observed in the Mississippi can be also identified in our simulations. Three types of switching mechanisms are distinguished in the literature (35). The first type, referred to as switching type I, consists of a lobe switching in which the delta propagates in a series of distributary channels. After a certain time, the stream abandons the entire system close to the head of the delta and forms a new lobe in an adjacent region. Often, this lobe occupies an indentation in the coastline between previous existing lobes so that with time the sediment layers overlap each other. One can find this type of delta switching in areas where the offshore slope is extremely low and the tidal and wave forces are too small for reworking the lobe (35, 38, 40). In many cases, the delta lobes merge with each other, forming major sheet-type sand banks. This phenomena can be nicely observed when comparing the two images of the simulation in Fig. 6 a and b. This has happened several times in the past in the Mississippi River delta, and the different lobes have today different names. For example, type I shifts of the Mississippi River delta occurred 4,600 years B.P. between the Salé-Cypremort and the Cocodrie (4600–3500 B.C.) Lobe and when the St. Bernard lobe switched to the Lafourche Lobe at ≈1000 B.C.

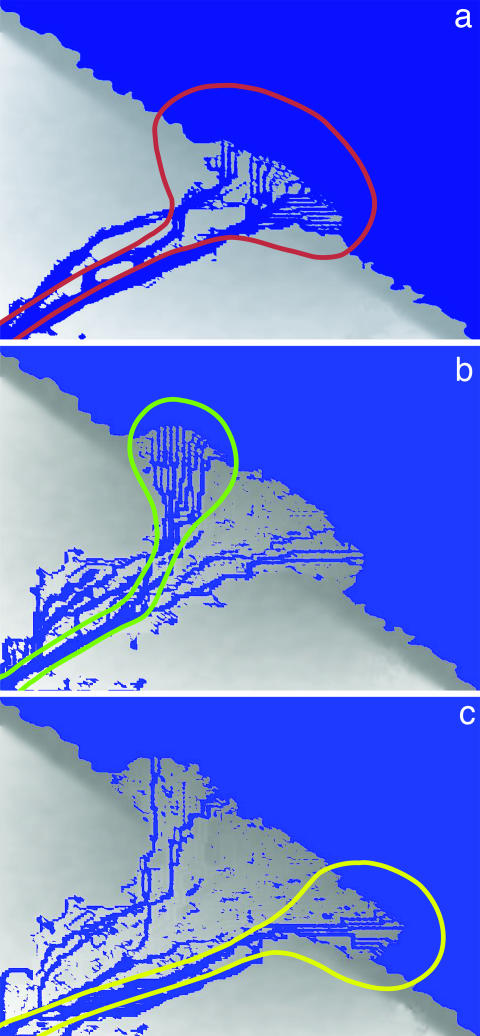
Fig. 6.

The switching of the delta lobe during the simulation. Comparing a and b, a type I switching can be identified where the main part of the delta lobe is abandoned close to the mouth of the river, just before the river splits into several distributaries and forms a new lobe beside. Another type of delta switching is shown comparing b and c, with two snapshots from the simulation. Here, the channel switches far upstream and takes a new course to the coast forming another delta lobe far away. This is referred as a switching of type II. The parameters for the simulation where I₀ = 1.7 × 10⁻⁴, s₀ = 5 × 10⁻⁵, c₂ = 0.0005, c₁ = 0, and I* = 3.3 × 10⁻⁴. The simulation was run on a 179 × 179 lattice with smoothening every 2,000 time steps and a smoothening constant of ε = 0.0001.

At ≈3500 B.C., the Mississippi River switched far upstream from the Cocodrie to the Teche stream, tailing a completely new course for the river and its delta. This type of switching is referred as type II switching (35) and can also be found in the simulation. When comparing Fig. 6 b and c, one can see a major shift of the channel far upstream in the deltaic plain, such that the river takes a completely different course and forms a new delta.

Type III delta switching is referred to as alternate channel extension in the literature (35). In this case, not the complete channel but the dominance of sediment flux in one or more distributaries is changing with time. This can be described as follows: two or more major channels split into several distributaries nearly at the same point at the head of the delta. Commonly, one of the distributaries is dominant, so it will carry most of the sediment and water discharge at any time. As a result, this active channel will rapidly propagate seaward, whereas the other channel will shrivel with time. At some point, the slope of the main active channel will decrease, and the discharge will seek one of the shorter distributaries. With the increased sediment flux downstream, the new channel will rapidly propagate into the sea. This switching process will repeat several times, forming a deltaic plain characterized by a series of multiple beach ridges. This switching can be best observed in the simulation of the bird-foot delta in Fig. 3 a–c, where the main path of the sediment flow is marked by the red arrows. One can see how side channels emerge and are abandoned after a certain time. Nevertheless, a major switching of the main channel could not be observed in the simulations. The average time between two lobe switchings was found to be ≈1,000 years for the Mississippi River (8, 35, 44).

At this point, we show that the river delta patterns generated from our simulations display geometric features that are statistically similar to real river delta structures. More precisely, we analyze the self-similar behavior of the real and simulated river deltas using the box counting algorithm (45). The box counting dimension is a quite common measure in geomorphological pattern analysis and has been used by many authors to characterize river basin patterns and coastlines (46–48).

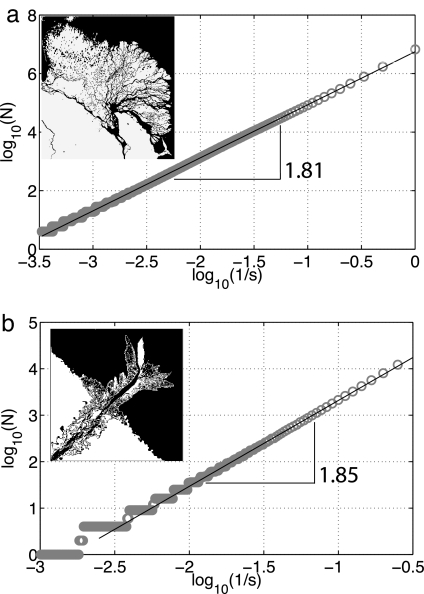
For the real satellite picture as well as for the simulated river delta, we show in Fig. 7 that the variation with the cell size s of the number of cells N covering the land follows typical power laws over more than three decades

where the exponent D is the fractal dimension. Moreover, the least squares fit of this scaling function to the data gives exponents that are strikingly close to each other, namely D = 1.81 ± 0.01 for the real Lena River delta and D = 1.85 ± 0.1 for the simulation.

Fig. 7.

Comparison of the fractal dimension of a real river delta pattern (a) with the simulation results (b). (a) The scaling behavior of the Lena River delta. On the y axis, we show the logarithm of the number of boxes N(s) of size s, which are necessary to cover the subaerial surface is plotted versus the logarithm of the inverse box size. The straight line is a power law fit N ≈ s^−D with exponent D = 1.81. (Inset) Satellite picture of the Lena River delta. (b) The scaling behavior of the bird-foot delta from the simulation (cf. Fig. 3) where the slope was calculated to be 1.85.

Conclusion

We have presented a model for simulating the formation process of river deltas. This model is based on simple conservation laws for water and sediment on a lattice grid, coupled by a phenomenological sedimentation/erosion law. Several interesting features of river deltas, like the different delta switching processes, could be found with the model and compared with real landforms.

Different delta shapes in the classification scheme of Galloway (40) could be reproduced by varying the model parameters and initial conditions. The pattern structure of the simulation has been analyzed and is in good agreement with real deltas. Furthermore, the delta-shifting phenomena could be observed in the simulation, and different types of delta shifting could be distinguished.