The structures of cyclic dihydronium cations

Abstract

Recent experimental discoveries have revealed the existence of hitherto unexpected cyclic hydronium di-cations trapped within crystal structures. The molecular formulas are (H₁₄O₆)²⁺, present as two isomers, four- and six-member cyclic structures, and (H₁₈O₈)²⁺, an eight-member cyclic structure. As these unprecedented hydronium species are stabilized by the crystal structures in which they are captured, the question arises whether they could be stable as independent species as, for example, in solution or gas phase. Quantum mechanical density functional theory calculations are used to investigate this question. We find these doubly charged cyclic hydronium structures to be energetically stable and, as between the four- and six-member structures, the former has more binding energy than the latter. We also determine the theoretically optimized structures for all three ions and give their calculated atomic charges for both their crystal and optimized geometries.

Recognition of the existence of hydrogen bonds was an early development in the chemistry of the 20th century. In ≈1920, the concept had been developed by Huggins, Latimer, and Rodebush and soon was elaborated on by others. Basically, the concept relied on the idea that an electron-rich atom (e.g., O, N, etc.) could donate a pair of electrons to an electron-poor atom (e.g., an H⁺) and form a stable bond. This concept was very useful in describing protonated species such as the NH₄⁺ cation. The same concept applies to the formation of BF₄⁻, where an F⁻ donates a pair of electrons to BF₃ and so on.

As crystallographic equipment, methods, and processing software became more sophisticated, reports began to be published in which a variety of species were found to contain a proton attached to one or more waters. Classically, these species were, invariably, linear or branched and having compositions H₃O⁺, H₅O₂⁺, H₇O₃⁺, and H₉O₄⁺. A recent review gives a rather complete description of all of these species, including color figures depicting their stereochemistry (1). Moreover, the review demonstrates that the hydronium cations described above, in some cases, can exist in isomeric forms, often because of changes in the species to which they are anchored. These changes in anchoring points cause asymmetry in such species as H₅O₂⁺, H₇O₃⁺ where, in some cases, the hydrogen bonds differ markedly whereas in others they are the same, or nearly so. For these and many other details please refer to the review (1).

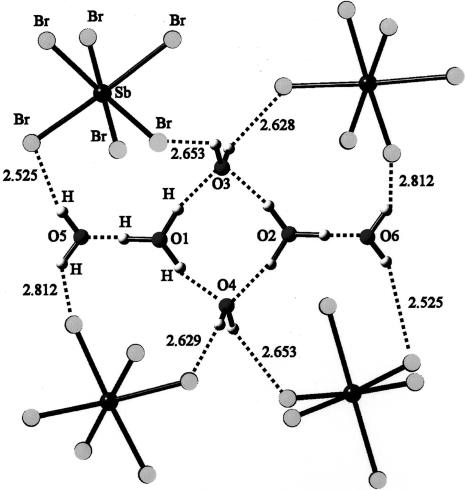
A unique species was described in a neutron diffraction paper (2), having the chemical composition H₁₄O₆²⁺. However, as the authors pointed out, a more accurate description of the di-cation is the dimeric species [(H₅O₂⁺)(H₂O)]₂ in which the two waters of hydration are attached to the two (H₃O⁺) cations in a terminal fashion (i.e., they are not part of the ring formation; shown in Fig. 1). Nonetheless, the species is a di-cation, and the first of its kind, as may be seen in the following.

Fig. 1.

The dihydronium cation of composition H₁₄O₆²⁺ described in ref. 2. It consists of a cyclic array of four waters that are protonated and two pendant (external) hydrogen-bonded waters. The species was trapped by a beautifully arranged array of four [SbBr₆]²⁻ anions whose structure is octahedral. The di-cation is shown in more detail in Fig. 5.

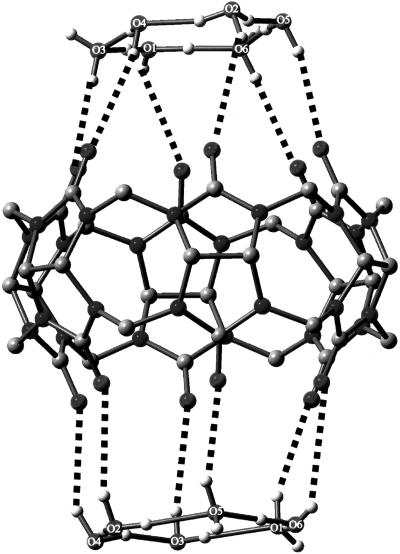
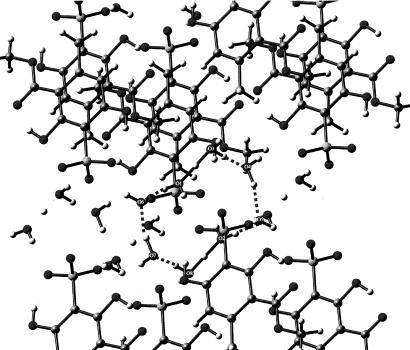
In 2005, Bernal et al. (3) demonstrated the existence of a cyclic, quasi-planar species of composition H₁₄O₆²⁺ that had been trapped by an organic substrate, as shown in Fig. 2. Interestingly, this compound and the compound of Henke and Kuhs (2) share the same composition and charge but have totally different structures. Finally, in another case of trapping by organic molecules having appropriate Lewis base donors [in this case, oxygen atoms of organic sulfonates (4)], the species of composition H₁₈O₈²⁺ was trapped, as shown in Fig. 3, by A. W. Hanson (5) but was insufficiently described then, probably because of the nature of the available graphics programs. Its proper description, including how it was trapped in crystals, is given in detail in ref. 4.

Fig. 2.

The cyclic hydronium di-cations trapped by the organic molecule cucurbituril. Their composition also is H₁₄O₆²⁺. The isolated molecule is shown in Fig. 6. The ring of six carbonyl oxygen atoms (CO) trapped the di-cations on the top and bottom of the molecule. A figure similar to this appeared in the review mentioned in ref. 1, and a somewhat different view appeared originally in ref. 3. Its REFCODE acronym in the Cambridge Structural Database is UCANOB (Cambridge Crystallographic Data Centre, www.ccdc.cam.ac.uk).

Fig. 3.

The environment of the eight-membered cyclic di-cation present in FEGTEQ (Cambridge Structural Database, Cambridge Crystallographic Data Centre, www.ccdc.cam.ac.uk). It is trapped by a complex set of hydrogen bonds in a lattice forming cylindrical cavities whose walls are formed by hydrogen-bonded sulfonate molecules. For details, consult ref. 5. Its REFCODE acronym in the Cambridge Structural Database is FEGTEQ (Cambridge Crystallographic Data Centre, www.ccdc.cam.ac.uk).

The three compounds mentioned above share a common, and most interesting, feature; namely, they are rings bearing a charge of 2+. Also, each one can be thought of as being made of two hydronium mono-cations strongly bonded to one another through a network of hydrogen bonds. The compound shown in Fig. 1 contains a four-water ring that can be viewed as being made up of a monohydrated pair of H₅O₂⁺ cations, as was suggested by Henke and Kuhs (2). The compound described in Fig. 2 contains a six-water ring that may be viewed as being made up of two strongly hydrogen-bonded H₇O₃⁺ hydronium species. Finally, the last compound, shown in Fig. 3, may be described as being composed of two hydrogen-bonded H₉O₄⁺ cations. However, given the fact that these three species certainly are held together by robust hydrogen bonds, the question that comes to mind immediately is: “How stable are they?” To answer that question, we decided to carry out the calculations described below.

Moreover, using theoretical calculations, it seemed desirable to ascertain the energetics of the two cyclic isomeric species in both their observed geometry within crystallographic structures and the ones obtained by calculated energy-minimization techniques. This determination now has been performed, and a comparison of the energies obtained is described below.

Results

There are three molecules of interest that we have studied with the density functional theory (DFT) calculations and basis set referred to below. These are two isomers of molecular formula H₁₄O₆²⁺ and one structure of formula H₁₈O₈²⁺. All three of these molecules have been discovered experimentally, and their geometries are known from solved x-ray crystal structures (2, 5, 6). In each case, these unusual doubly charged hydronium ions have been stabilized within crystal structures by hydrogen bonds anchoring them to the parent species of the lattice.

The dihydronium cation H₁₄O₆²⁺, displaying a cyclic array of four waters (protonated) and two pendant external hydrogen-bonded waters, is shown in Fig. 1. This dihydronium ion is trapped in the crystal by four [SbBr₆]²⁻ anions having an octahedral geometry. An isomer of the H₁₄O₆²⁺ dihydronium cation is pictured in Fig. 2 trapped in a crystal by the cucurbituril molecule. Rings of six carbonyl oxygen atoms (CO) trap pairs of di-cations at the top and bottom of the molecule. In Fig. 3, we show the dihydronium ion of formula H₁₈O₈²⁺ again entrapped within a crystal structure by a set of hydrogen bonds to sulfonate molecules. In each of these three cases, the dihydronium ions have been stabilized by the crystal structure that trapped them. But are they sufficiently stable on their own to enjoy an independent existence? Also, of the two isomers of molecular formula H₁₄O₆²⁺, which of them is relatively more stable? Again it is of interest to know how the theoretically optimized structures of the free molecules differ from the structures of the same molecules within their crystal environments. The calculations we carry out also produce the atomic charges of the molecules, both at their crystal geometry and as free molecules. All of these properties of the dihydronium ions are addressed by the calculations reported below.

In Table 1, we list the calculated energies for all three molecules. We consider each of the molecules at two different geometries. The first row of Table 1 gives their energies calculated at the crystal structure geometry. The second row of Table 1 refers to the geometries optimized by minimization of the energy. Consider the two isomers of the molecule H₁₄O₆²⁺. We find that the energy calculated at the crystal coordinates shows the four-member cyclic isomer (−457.118 a.u.) lower than the six-member cyclic isomer (−456.627 a.u.). At the optimized coordinates the situation is similar, and the four-member cyclic isomer (−457.163 a.u.) is of lower energy than the six-member isomer (−457.147 a.u.). In Table 1, the eight-member cyclic molecule of formula H₁₈O₈²⁺ has energies listed for both the crystal coordinates (−608.693 a.u.) and the energy-optimized coordinates (−609.402 a.u.).

Table 1.

The calculated crystal structure energies, the optimized geometry energies, and the binding energies of two isomeric H₁₄O₆²⁺ molecules and an H₁₈O₈²⁺ complex

	H14O62+ (four-cycle)	H14O62+ (six-cycle)	H18O82+ (eight-cycle)
Crystal energy	−457.118 a.u.	−456.627 a.u.	−608.693 a.u.
Optimized energy	−457.163 a.u.	−457.147 a.u.	−609.402 a.u.
Binding energy*	−0.199 a.u.	−0.183 a.u.	−0.294 a.u.

*Binding energy = optimized energy − (n E_H2O(opt) + m E_H3O⁺(opt)), where E_H2O(opt) = −76.0724587 a.u., E_H3O⁺(opt) = −76.3384031 a.u., n = number of H₂O, and m = number of H₃⁺.

The third row of Table 1 lists the binding energies for each of the three dihydronium ions. These binding energies are calculated at the optimized coordinates for the full molecular ions and the optimized coordinates for the free water (H₂O) and the free hydronium (H₃O⁺) ions (see Fig. 4). In each case, the binding energy is calculated according to the formula

where n and m count the number of waters [E_H2O(opt) = −76.0724587 a.u.] and hydronium ions [E_H3O⁺(opt) = −76.3384031 a.u.], respectively, that are contained in the full molecular ion. The binding energy in each case is negative, four-cycle (−0.199 a.u.), six-cycle (−0.183 a.u.), and eight-cycle (−0.294 a.u.), which implies stability for the full ionic molecules versus their separated fragments.

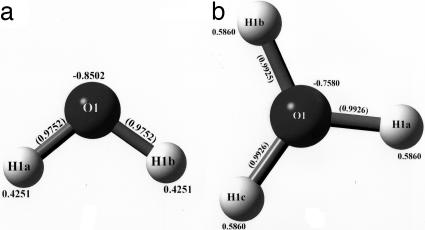
Fig. 4.

The calculated geometry and atomic charges of the free molecules H₂O (a) and the protonated species H₃O⁺ (b). The basis functions (DGDZVP) and DFT (SVWN) calculations used are the same as those discussed for the dihydronium ions. The optimized energies are E_H2O(opt) = −76.0724587 a.u. and E_H3O⁺(opt) = −76.3384031 a.u. The values in parentheses are the bond distances.

Thestructure of the three molecules studied are shown free of their crystal surroundings in Figs. 5–7, but they are drawn based on their coordinates within the crystal structure. The hydrogen bonds are shown as dashed lines. Bond distances and hydrogen bond distances are indicated,and the analogous bond distances for the theoretically optimized structures are given in parentheses. The same structure diagrams are used to indicate the atomic charges in Figs. 8–10, where, again, the values for the theoretically optimized structures are given in parentheses.

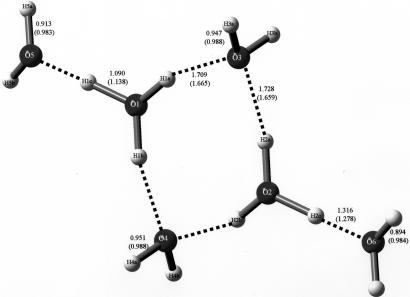
Fig. 5.

Bond distances of crystal structure and optimized structure (in parentheses) for H₁₄O₆²⁺, the four-membered cyclic molecule. The di-cation with composition H₁₄O₆²⁺ discovered by Henke and Kuhs and described in ref. 2 is shown. Note on left and right the di-protonated waters and the pendant (hydrogen-bonded) waters. Probably because of the primitive graphics available in 1987, the original paper failed to properly describe this beautiful species.

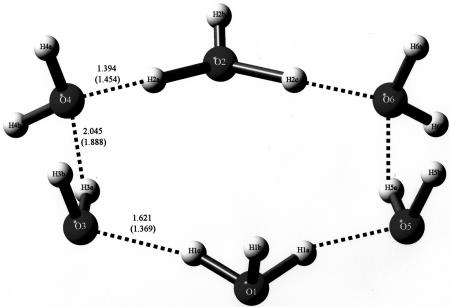
Fig. 7.

Bond distances of crystal structure and optimized structure (in parentheses) for H₁₄O₆²⁺, the six-membered cyclic molecule. The dihydronium cation trapped by cucurbituril is shown. One of the hydronium cations is shown at the bottom, and one is shown at the top.

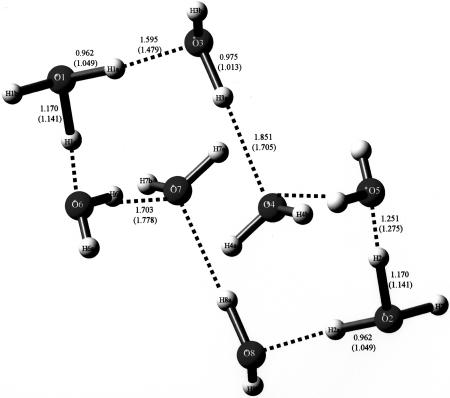
Fig. 7.

Bond distances of crystal structure and optimized structure (in parentheses) for H₁₈O₈²⁺, the eight-membered cyclic molecule. The dihydronium cation of composition H₁₈O₈²⁺ present in FEGTEQ (Cambridge Structural Database, Cambridge Crystallographic Data Centre, www.ccdc.cam.ac.uk) is shown. It also was trapped by an organic compound, as shown in Fig. 3.

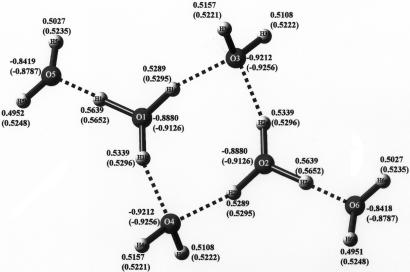
Fig. 8.

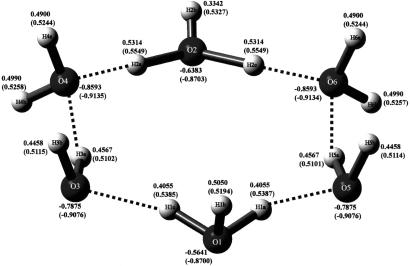
Atomic charges of crystal structure and optimized structure (in parentheses) for H₁₄O₆²⁺, the four-membered cyclic molecule.

Fig. 9.

Atomic charges of crystal structure and optimized structure (in parentheses) for H₁₄O₆²⁺, the six-membered cyclic molecule.

Fig. 10.

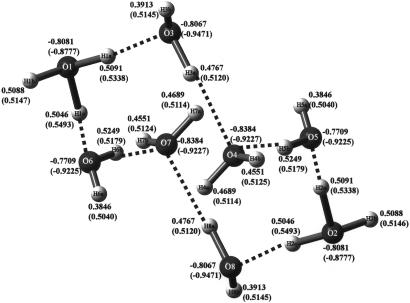
Atomic charges of crystal structure and optimized structure (in parentheses) for H₁₈O₈²⁺, the eight-membered cyclic molecule.

Discussion and Conclusions

We have noted that the three dihydronium molecular ions discussed in this article have an experimental existence within crystal structures (2, 5, 6). However, what we have been able to show by DFT quantum mechanical calculations is that all three also could exist as independent ions, free of the stabilization of the crystals in which they occur. This conclusion follows from the negative binding energies displayed for each case noted in Table 1. With regard to the relative stability of the free four-cycle and six-cycle isomers, as judged by their respective binding energies, Table 1 indicates that the former ion is slightly more stable and the total energy is slightly lower than the latter. The exact magnitude of the binding energies and molecular energies that we have calculated might be expected to vary somewhat if other quantum mechanical ab initio methods of calculation incorporating correlation energy were to be used. However, the overall conclusion that the dihydronium ions could show independent stability outside the crystals in which they have been captured is not expected to differ from our conclusions.

In Table 2, we list the Cartesian coordinates of all of the atoms for the three molecules we have studied. Table 2 includes both the coordinates within the crystal structure and those corresponding to the energy-optimized structures. In Table 3, we list the charges of the atoms associated with the three structures studied. The values associated both with the crystal coordinates and those for the optimized structures are given. In accordance with the relative electronegativities of the atoms involved, Table 3 shows that all of the molecular ions correspond to negatively charged oxygen atoms and positively charged hydrogen atoms, without exception. The general trend in going from the crystal case to the corresponding optimized case is that all of the oxygen atoms become more negative and the hydrogen atoms become more positive. This trend would add to the electrostatic stability of the molecular ions as the coordinates change from their values in the crystal case to their energy-optimized values.

Table 2.

The Cartesian coordinates for the crystal structures and optimized structures of four-member cyclic, six-member cyclic, and eight-member cyclic molecules

Label	H14O62+ four-member cyclic structure						H14O62+ six-member cyclic structure						H18O82+ eight-member cyclic structure
	Crystal			Optimized			Crystal			Optimized			Crystal			Optimized
	x	y	z	x	y	z	x	y	z	x	y	z	x	y	z	x	y	z
O1	2.670	−0.168	1.844	2.599	−0.214	1.819	0.000	11.381	11.908	−0.001	11.191	11.161	11.650	−0.891	3.927	11.495	−0.306	3.809
H1a	3.480	−0.220	1.315	3.438	−0.374	1.274	0.689	11.727	11.422	0.904	11.786	11.087	11.709	−0.272	4.661	11.780	0.295	4.620
H1b	1.896	0.124	1.309	1.872	0.220	1.260	0.000	12.034	12.620	−0.003	10.533	11.894	12.500	−1.138	3.558	12.238	−0.726	3.322
H1c	2.682	0.020	2.918	2.629	−0.037	2.943	−0.689	11.727	11.422	−0.905	11.790	11.087	11.042	−0.406	3.054	10.600	0.084	3.218
O2	2.677	0.168	−1.844	2.747	0.214	−1.819	0.000	13.092	6.458	0.000	12.806	6.868	8.309	4.491	3.228	8.464	3.906	3.346
H2a	3.450	−0.124	−1.309	3.474	−0.220	−1.260	−0.880	13.012	7.061	−0.944	12.912	7.359	8.250	3.872	2.494	8.179	3.304	2.536
H2b	1.867	0.220	−1.315	1.908	0.374	−1.274	0.000	13.631	6.128	0.000	13.079	5.920	7.459	4.738	3.597	7.721	4.326	3.833
H2c	2.665	−0.020	−2.918	2.717	0.037	−2.943	0.880	13.012	7.061	0.943	12.915	7.360	8.917	4.006	4.102	9.359	3.516	3.937
O3	4.529	−0.486	−0.007	4.458	−0.681	−0.006	−2.043	11.878	10.545	−1.929	12.641	10.768	11.873	0.654	5.950	11.809	1.222	5.771
H3a	5.346	0.000	0.000	5.298	−0.161	−0.004	−1.906	12.172	9.755	−2.268	12.644	9.837	12.113	1.544	5.632	12.444	2.011	5.784
H3b	4.798	−1.394	0.000	4.731	−1.630	−0.032	−2.337	12.628	10.928	−2.658	12.830	11.400	12.330	0.499	6.488	11.847	0.769	6.645
O4	0.817	0.486	0.007	0.888	0.681	0.006	−2.023	12.920	7.855	−2.263	12.931	7.971	12.202	3.222	4.856	12.802	3.647	5.464
H4a	0.000	0.000	0.000	0.048	0.161	0.004	−2.314	13.661	8.207	−2.728	13.796	7.858	12.539	3.142	4.079	13.592	3.849	4.911
H4b	0.549	1.394	0.000	0.615	1.630	0.032	−2.630	12.528	7.433	−2.850	12.249	7.559	12.570	3.796	5.246	12.875	4.235	6.252
O5	2.666	0.221	4.219	2.536	0.127	4.207	2.043	11.878	10.545	1.932	12.633	10.769	9.551	3.517	5.063	10.446	3.020	4.382
H5a	3.334	−0.093	4.757	3.025	0.818	4.708	1.906	12.172	9.755	2.269	12.640	9.837	9.305	2.931	5.374	10.453	2.269	5.038
H5b	1.898	0.091	4.657	2.325	−0.628	4.803	2.337	12.628	10.928	2.664	12.815	11.399	10.522	3.482	4.965	11.226	3.598	4.641
O6	2.680	−0.221	−4.219	2.810	−0.127	−4.207	2.023	12.920	7.855	2.261	12.936	7.972	10.408	0.083	2.093	9.513	0.580	2.773
H6a	2.012	0.093	−4.757	2.322	−0.818	−4.708	2.314	13.661	8.207	2.722	13.805	7.865	10.654	0.669	1.782	9.506	1.331	2.117
H6b	3.448	−0.091	−4.657	3.021	0.628	−4.803	2.630	12.528	7.433	2.853	12.260	7.557	9.437	0.118	2.190	8.733	0.001	2.514
O7	—	—	—	—	—	—	—	—	—	—	—	—	7.756	0.378	2.300	7.157	−0.048	1.692
H7a	—	—	—	—	—	—	—	—	—	—	—	—	7.420	0.458	3.076	6.366	−0.249	2.244
H7b	—	—	—	—	—	—	—	—	—	—	—	—	7.389	−0.196	1.910	7.084	−0.635	0.904
O8	—	—	—	—	—	—	—	—	—	—	—	—	8.086	2.946	1.206	8.150	2.378	1.384
H8a	—	—	—	—	—	—	—	—	—	—	—	—	7.846	2.056	1.523	7.515	1.589	1.372
H8b	—	—	—	—	—	—	—	—	—	—	—	—	7.629	3.101	0.667	8.111	2.831	0.510

The values of x, y, and z are in angstroms.

Table 3.

The charges for the crystal structures and optimized structures of four-member cyclic, six-member cyclic, and eight-member cyclic molecules

Label	H14O62+		H14O62+		H18O82+
	Four-member cyclic structure		Six-member cyclic structure		Eight-member cyclic structure
	Crystal	Optimized	Crystal	Optimized	Crystal	Optimized
O1	−0.8880	−0.9126	−0.5641	−0.8700	−0.8081	−0.8777
H1a	0.5289	0.5295	0.4055	0.5387	0.5091	0.5338
H1b	0.5339	0.5296	0.5050	0.5194	0.5088	0.5147
H1c	0.5639	0.5652	0.4055	0.5385	0.5046	0.5493
O2	−0.8880	−0.9126	−0.6383	−0.8703	−0.8081	−0.8777
H2a	0.5339	0.5296	0.5314	0.5549	0.5091	0.5338
H2b	0.5289	0.5295	0.3342	0.5327	0.5088	0.5146
H2c	0.5639	0.5652	0.5314	0.5549	0.5046	0.5493
O3	−0.9212	−0.9256	−0.7875	−0.9076	−0.8067	−0.9471
H3a	0.5157	0.5221	0.4567	0.5102	0.4767	0.5120
H3b	0.5108	0.5222	0.4458	0.5115	0.3913	0.5145
O4	−0.9212	−0.9256	−0.8593	−0.9135	−0.8384	−0.9227
H4a	0.5157	0.5221	0.4900	0.5244	0.4689	0.5114
H4b	0.5108	0.5222	0.4990	0.5258	0.4551	0.5125
O5	−0.8419	−0.8787	−0.7875	−0.9076	−0.7709	−0.9225
H5a	0.5027	0.5235	0.4567	0.5101	0.3846	0.5040
H5b	0.4952	0.5248	0.4458	0.5114	0.5249	0.5179
O6	−0.8418	−0.8787	−0.8593	−0.9134	−0.7709	−0.9225
H6a	0.5027	0.5235	0.4900	0.5244	0.3846	0.5040
H6b	0.4951	0.5248	0.4990	0.5257	0.5249	0.5179
O7	—	—	—	—	−0.8384	−0.9227
H7a	—	—	—	—	0.4689	0.5114
H7b	—	—	—	—	0.4551	0.5124
O8	—	—	—	—	−0.8067	−0.9471
H8a	—	—	—	—	0.4767	0.5120
H8b	—	—	—	—	0.3913	0.5145

To get a rough idea of the strength of the hydrogen bonds holding together the dihydronium ions we have studied, one may carry out the following calculation. Assume qualitatively that the binding energy of these molecules, as calculated by Eq. 1, is mainly attributable to the network of hydrogen bonds shown in Figs. 5–7. For each molecule, one then can approximate the average hydrogen-bond energy by dividing the total binding energy by the number of hydrogen bonds. This process results in an average hydrogen-bond energy of ≈83.68 kJ/mol for the two isomers (H₁₄O₆²⁺) and ≈96.23 kJ/mol for the third ion (H₁₈O₈²⁺); these are indeed strong hydrogen bonds holding these molecules together. There are important and practical issues raised by the possibility of the independent existence of doubly charged hydronium ions. Our calculations show that the ions are stable out of the crystals in which they have been discovered. Therefore, there must be at least a theoretical possibility for some range of physical conditions that might favor their existence in solution. An experimental investigation to confirm their presence in solution is indicated. If these ions were to be found to have such experimental existence, they possibly would be of importance to proton transport mechanisms, which play an important role in bioenergetics, environmental chemistry, and general acid–base reactions.

Method of Calculation

The Hartree–Fock method is perhaps the best known and most thoroughly understood type of ab initio quantum calculation. It is simple in that the Hartree–Fock wave function is a Slater determinant of orthonormal molecular orbitals whose molecular energy is a minimum. The energy error that is inherent to the independent particle Hartree–Fock model is called the correlation energy error, which in absolute terms is quite small, although it is nonetheless chemically important. We have used instead DFT, which in its modern form dates from the Hohenberg–Kohn theorem (7) and its numerical implementation in the Kohn–Sham equations (8). Here too the wave function is a single Slater determinant of orbitals, but these Kohn–Sham orbitals have the defining characteristic of delivering, in principle, the exact electron density. The Kohn–Sham equations are similar to the Hartree–Fock equations, but they are simpler because they contain only local potentials. The Kohn–Sham potential contains a representation of both the exchange and the correlation effects, of which the latter are inherently absent from the Hartree–Fock equations. Although the exact Kohn–Sham exchange correlation potential is unknown, in practice it is fitted to empirical data and theoretical constraints and is approximated rather successfully. Because of their simplicity and inclusion of correlation, DFT Kohn–Sham equations are the equations for the calculation adopted here.

These calculations were completed by using Gaussian 03 on a p670 IBM supercomputer running the AIX 5.2 IBM operating system. The DFT method used was the local density functional (SVWN), a combination of a Slater exchange functional and a uniform electron gas correlation functional (described in ref. 9), together with DGDZVP, a purely theoretical basis set. DGDZVP is a fairly large basis set, used in DGauss, including double-ζ valence plus polarization functions. It has been found to deliver fairly accurate energies when used together with DFT calculations (10, 11).

Abbreviation

DFT

density functional theory.