Hydrogen bond dynamics in aqueous NaBr solutions

Abstract

Hydrogen bond dynamics of water in NaBr solutions are studied by using ultrafast 2D IR vibrational echo spectroscopy and polarization-selective IR pump–probe experiments. The hydrogen bond structural dynamics are observed by measuring spectral diffusion of the OD stretching mode of dilute HOD in H₂O in a series of high concentration aqueous NaBr solutions with 2D IR vibrational echo spectroscopy. The time evolution of the 2D IR spectra yields frequency–frequency correlation functions, which permit quantitative comparisons of the influence of NaBr concentration on the hydrogen bond dynamics. The results show that the global rearrangement of the hydrogen bond structure, which is represented by the slowest component of the spectral diffusion, slows, and its time constant increases from 1.7 to 4.8 ps as the NaBr concentration increases from pure water to ≈6 M NaBr. Orientational relaxation is analyzed with a wobbling-in-a-cone model describing restricted orientational diffusion that is followed by complete orientational randomization described as jump reorientation. The slowest component of the orientational relaxation increases from 2.6 ps (pure water) to 6.7 ps (≈6 M NaBr). Vibrational population relaxation of the OD stretch also slows significantly as the NaBr concentration increases.

Water plays an important role in chemical and biological processes. In aqueous solutions, water molecules dissolve ionic compounds, charged chemical species, and biomolecules by forming hydration shells (layers) around them. Pure water undergoes rapid structural evolution of the hydrogen bond network that is responsible for water's unique properties (1). A question of fundamental importance is how the dynamics of water in the immediate vicinity of an ion or ionic group differ from those of pure water. For monatomic ions, molecular ions, charged groups of large molecules, or charged amino acids on the surfaces of proteins, the basic structure of hydration shells is determined by ion–dipole interactions between water molecules and the charged group (2, 3). Such ion–dipole interactions will influence both the structure and dynamics of water in the proximity of ions. Water dynamics in ion hydration shells play a significant role in the nature of systems such as proteins and micelles (3) and in processes such as ion transport through transmembrane proteins (4).

Over the last several years, the application of ultrafast IR vibrational echo spectroscopy (5, 6), particularly 2D IR vibrational echo experiments, (7, 8) combined with molecular dynamics (MD) simulations (9–12) have greatly enhanced understanding of the hydrogen bond dynamics in pure water. These experiments directly examine the dynamics of water rather than study the indirect influence of water dynamics on a probe molecule (13). The ultrafast 2D IR vibrational echo experiments on water (7, 8) and other hydrogen-bonded systems (14) build upon earlier IR pump–probe experiments that have been extensively used to study the vibrational population relaxation and orientational relaxation dynamics of pure water (15, 16), water in nanoscopic environments (17–19), and ionic solutions (20). Pump–probe experiments have also been used to investigate the hydrogen bond dynamics in aqueous solutions (20) and other hydrogen-bonded liquids (21).

Water molecules around monatomic ions provide the simplest system for the investigation of the dynamics of water in the presence of charges. Therefore, examining the dynamics of water in simple ionic solutions, such as sodium bromide (NaBr), can provide valuable insights that will increase understanding of chemical processes and biological systems that involve charged species in aqueous solutions. In pure water, water molecules are hydrogen-bonded to neighboring water molecules in a more or less tetrahedral geometry making an extended hydrogen bond network. Hydrogen bonds are continually breaking and reforming, and hydrogen bond lengths (strengths) are continually changing (9). The structure of water fluctuates on femtosecond to picosecond time scales (6, 9). The slowest component of the fluctuations is associated with the global structural rearrangement of the hydrogen bond network (7). As salt is dissolved in water, water molecules form hydration shells around ions, and consequently the local hydrogen bond network is perturbed.

In this paper, a very detailed study of the hydrogen bond dynamics of water in highly concentrated NaBr solutions is presented. Four experimental observables, which are based on measurements on the OD stretch mode of HOD in H₂O, were used. Ultrafast 2D IR vibrational echo experiments were used to measure spectral diffusion, which is directly related to the time evolution of the hydrogen bond structure. Polarization-selective IR pump–probe experiments were used to measure orientational relaxation dynamics of water, which is affected by the interactions of water molecules with their surroundings. The IR pump–probe experiments also were used to measure vibrational population relaxation dynamics of the OD stretch of HOD, which is very sensitive to the local environment. Finally, Fourier transform (FT) IR absorption spectra report on the overall effect of NaBr concentration on the OD stretch frequency.

In the experiments presented below, highly concentrated NaBr solutions are investigated. The number of water molecules per NaBr molecule ranges from 8 to 32. In low-concentration NaBr solutions, these numbers of water molecules would correspond to less than one hydration shell for each ion to approximately two hydration shells, respectively. By examining such highly concentrated NaBr solutions, all of water molecules are placed in close proximity to ions, and therefore, the influence of water–ion interactions is not diluted out by large quantities of bulk water that are not affected by the ions. Some limited initial vibrational echo experiments on highly concentrated salt solutions have been performed (22, 23). These experiments showed that the dynamics of water in concentrated salt solutions differ significantly from those of pure water, but not to the extent indicated earlier by less direct two-color pump–probe measurements (20). The results presented here confirm and extend earlier vibrational echo experiments. The surprising result is that even at the highest concentration with eight water molecules per NaBr (≈6 M solution) the time scale associated with the compete rearrangement of the hydrogen bond structure is slower than in pure water by only approximately a factor of three.

Results and Discussion

Linear FT IR Absorption Spectra.

NaBr solutions were chosen for study among aqueous halide salt solutions because the OD stretch band of HOD in aqueous NaBr solutions shows a reasonably large blue-shift in the FT IR spectrum compared with that of HOD in pure water, which suggests a large change in the hydrogen bond structure. The OD stretching band in halide salt solutions shifts more to the blue as the halide ion goes from F⁻ to I⁻. Subsequent experiments will examine other salt solutions.

All of the experiments were conducted on the OD stretch of 5% HOD in pure H₂O and aqueous NaBr solutions. The OD stretch of HOD in H₂O was examined for two reasons. First, it is a single local mode, which simplifies the absorption spectrum (24, 25). Second, of considerable importance for the time resolved experiments is the fact that measurements on the OD stretch of dilute HOD in H₂O eliminate vibrational excitation transfer (26). We are interested in the ground-state equilibrium properties of the aqueous solutions. H₂O or D₂O vibrational excitation transport interferes with measurements of spectral diffusion and orientational relaxation. MD simulations have shown that measurements on dilute HOD in H₂O yield the dynamics of water (7).

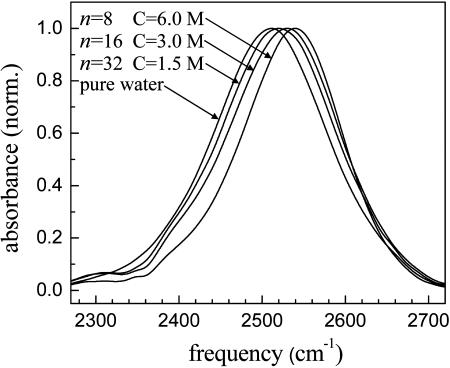
The H₂O background-subtracted FT IR spectra of the OD stretch are shown in Fig. 1. The curves are labeled by the number of water molecules per NaBr molecule, n. n = 8, 16, and 32 correspond to ≈6 M, 3 M, and 1.5 M NaBr solutions, respectively. The spectra are characteristically broad (25), and their peak positions are increasingly blue-shifted as the NaBr concentration increases. It is known for pure water that the broad spectrum is associated with different numbers and a wide range of strengths of the hydrogen bonds (27). For pure water, subensembles of water molecules with more and/or stronger hydrogen bonds have red-shifted absorptions, whereas subensembles with fewer and/or weaker hydrogen bonds are blue-shifted. In some other water systems, the blue-shift of the entire water spectrum has been interpreted as reflecting an overall weaker distribution of the hydrogen bonds (25, 28). However, this is not necessarily true. For example, it has been shown recently that the blue-shift of the water spectrum in small sodium bis(2-ethylhexyl)sulfosuccinate (AOT) reverse micelles is actually caused by the superposition of two distinct spectra of water molecules (18). One of the spectra is the bulk-like spectrum of water molecules in the core of the reverse micelle. The other is the substantially blue-shifted spectrum of water molecules associated with the ionic sulfonate head groups with sodium counter ions. Furthermore, a recent study showed that four distinct hydrogen-bonded systems containing water molecules could have essentially identical blue-shifted spectra of water molecules, although they had very different hydrogen bond dynamics (29). In the type of systems being considered here, in which the hydroxyl groups are as likely or more likely to be interacting with ions as with other water molecules, the blue-shift should not be interpreted as an indication of weakening of the hydrogen bond structure in aqueous solutions.

Fig. 1.

Linear FT IR spectra of the OD stretch of HOD in pure water and aqueous NaBr solutions (H₂O background subtracted). n = 8, 16, and 32 are the numbers of water molecules per NaBr, and correspond to ≈6 M, 3 M, and 1.5 M NaBr solutions, respectively. The peak positions (widths) of the OD stretch of HOD in pure water, n = 32, 16, and 8 are 2,509 cm⁻¹ (160 cm⁻¹), 2,519 cm⁻¹ (163 cm⁻¹), 2,529 cm⁻¹ (159 cm⁻¹), and 2,539 cm⁻¹ (141 cm⁻¹), respectively.

The width of the OD stretch band is relatively narrow in the n = 8 NaBr solution compared with pure water. In pure water, the hydroxyl group (OH and OD) is hydrogen-bonded only to the oxygen atoms in neighboring water molecules, making an extended hydrogen bond network leading to a broad distribution of the OD stretch frequencies as discussed above. On the other hand, in the n = 8 NaBr solution, there are four water molecules per ion on average. Given the fact that in dilute solutions the hydration numbers of Na⁺ and Br⁻ are 4 and 6, respectively (30, 31), Na⁺ and Br⁻ ions in the n = 8 NaBr solution are separated by a few water molecules. The detailed structure of such concentrated salt solutions is not known, but it is reasonable to assume that water molecules are bound to ions and are mainly interacting with ions rather than with a network of neighboring water molecules. At this high concentration, the hydrogen bond network of water is not only substantially disrupted but is unlikely to exist. There is nothing like bulk water at the highest concentration and even at the lower concentrations investigated here.

Water molecules in NaBr solutions can be hydrogen-bonded to ions by three different ion–dipole interactions in HOD–Br⁻, DOH–Br⁻, and HDO–Na⁺. The last two configurations may have less influence on the OD stretch frequency than the direct interaction of the OD groups with bromide ions. The broad line width for the n = 8 NaBr solution reflects the distribution of water–ion interactions rather than water–water interactions found in pure water. In the n = 16 NaBr solution with eight water molecules per ion, there are several extra water molecules beyond what would be the first hydration shells in dilute solution. The hydrogen bond structure of water in the n = 16 solution will still be substantially different from that of pure water. In the n = 32 solution, where there are 16 water molecules per ion, there are a significant number of water molecules beyond the first hydration shells. Nonetheless, the high concentration of ions should still have a substantial influence on many of water molecules. FT IR spectrum of the n = 32 solution is blue-shifted and broader than that of pure water (see Fig. 1). As discussed below, not only is the spectrum of the n = 32 NaBr solution different from that of pure water, but also all of the dynamic observables are different.

2D IR Vibrational Echo Spectroscopy.

2D IR vibrational echo spectroscopy is an ultrafast IR analog of 2D NMR, but it operates on time scales many orders of magnitude shorter than NMR. The 2D IR vibrational echo experiments measure the hydrogen bond dynamics of water through the time evolution of the hydroxyl stretch 2D IR spectra. In the experiment, there are three excitation pulses, ≈60 fs in duration, tuned to the OD stretch frequency. The short IR pulses have sufficient spectral bandwidth to span the entire OD stretch spectrum. The time between pulses 1 and 2 and between pulses 2 and 3 is called τ and T_w, respectively. The vibrational echo signal radiates from the sample at a time ≤τ after the third pulse. The vibrational echo signals are recorded by scanning τ at fixed T_w. The signal is spatially and temporally overlapped with a local oscillator for heterodyne detection, and combined pulse is dispersed although a monochromator onto an array detector. Heterodyne detection provides both amplitude and phase information. Taking the spectrum of the heterodyne-detected echo signal performs one of the two FTs and gives the ω_m axis (where subscript m stands for monochromator) in the 2D IR spectrum. When τ is scanned, temporal interferograms are obtained at each ω_m. The temporal interferograms are numerically Fourier transformed to give the other axis, the ω_τ axis. 2D IR spectra are obtained for a range of T_w values.

As T_w increases, the peak shapes in the 2D IR spectra change. These changes are directly related to the structural evolution of the water–ion system through the influence of the structural evolution on the OD stretch frequencies. Very qualitatively, the 2D IR experiment can be viewed as follows. The first and second pulses act to label the initial frequencies of the molecular oscillators. Between the second and third pulses, structural evolution causes the initially labeled frequencies to change (spectral diffusion). The third pulse ends the evolution period, and the vibrational echo signal reads out the final frequencies of the initially frequency-labeled molecular oscillators. As T_w increases, there is more time for structural evolution, and, therefore, larger frequency changes. The structural evolution (frequency changes) is reflected in the changes of peak shape of the 2D IR spectra. The 2D IR vibrational echo experiments have been reviewed recently (23, 32, 33).

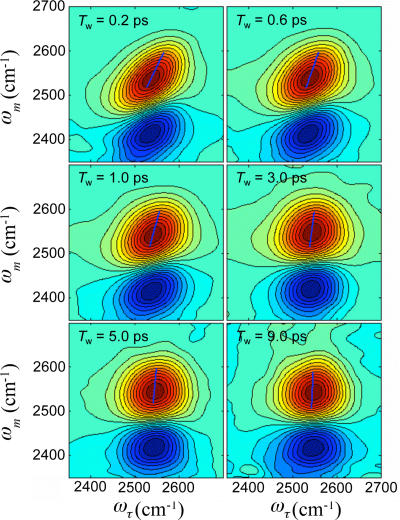
2D IR spectra of the OD stretch of HOD in the n = 8 NaBr solution are shown in Fig. 2 as a function of T_w. The red bands (on the diagonal) are positive-going and result from the transition between the ground and first excited vibrational states (0–1). The blue bands (off-diagonal) are negative-going and are associated with emission of the vibrational echo signal at the first overtone (1–2) transition frequency, which is shifted along the ω_m axis by the OD stretching mode anharmonicity. Focusing on the 0–1 transition (red positive band), a noticeable feature of 2D IR spectra is the change in peak shape as T_w increases. The red band is substantially elongated along the diagonal at T_w = 0.2 ps. As T_w increases, the peak shape becomes more symmetrical. This change is the signature of spectral diffusion. In the long time limit, all structural configurations are sampled and, consequently, all frequencies are sampled. In this limit, spectral diffusion is complete and the peak shape becomes completely symmetrical. However, because of the overlap with the negative-going peak that arises from emission at the 1–2 transition frequency, the bottom of the 0–1 transition band is eaten away. Spectral diffusion dynamics are obtained by analyzing the change of peak shapes as a function of T_w.

Fig. 2.

2D IR spectra measured with the n = 8 (≈6 M) NaBr solution. Red peaks (0–1 transition) are positive-going. Blue peaks (1–2 transition) are negative-going. The peak shape changes as T_w increases. The blue lines are the center lines.

The change of peak shapes in the 2D IR spectra with increasing T_w can be used to determine the time scales and amplitudes of various contributions to the structural evolution of the water–ion systems using methods based on diagrammatic perturbation theory (34). The frequency–frequency correlation function (FFCF) connects the experimental observables to the underlying dynamics. The FFCF is the probability that an oscillator with a given initial frequency still has the same frequency at time t later, averaged over all starting frequencies. Once the FFCF is known, all linear and nonlinear optical experimental observables can be calculated by time-dependent diagrammatic perturbation theory (34). Conversely, the FFCF can be extracted from 2D IR spectra with additional input from linear FT IR absorption spectra. In general, to determine the FFCF from 2D IR and linear FT IR spectra, full calculations of linear and nonlinear third-order response functions are performed iteratively until the calculation results converge to the experimental results (7).

Here, we used the center line slope (CLS) method (23, 35). The CLS method is a new approach for extracting the FFCF from the T_w dependence of the 2D IR spectra that is accurate and much simpler to implement numerically than iterative fitting methods with calculations of all response functions based on time-dependent diagrammatic perturbation theory. Furthermore, the CLS provides a more useful quantity to plot for visualizing differences in the dynamics as a function of the NaBr concentration than a series of full 2D IR spectra (23, 35). In the CLS method, frequency slices through the 2D IR spectrum parallel to the ω_τ axis at various ω_m values are projected onto the ω_τ axis (35). These projections are a set of spectra with peak positions, ω_τ^max, on the ω_τ axis. The plot of ω_τ^max vs. ω_m form a line called the center line. Center lines are shown in Fig. 2. In the absence of a homogenous contribution to the 2D IR spectrum, the peak shape in the 2D IR spectrum at T_w = 0 ps would be essentially a line along the diagonal at 45°. The slope of this center line would be 1. At very long time, the peak shape in the 2D IR spectrum becomes symmetrical, and the center line is vertical (slope is infinite). The change in the slope of the center line with increasing T_w can be seen in Fig. 2. It has been shown theoretically that the normalized FFCF is equal to the T_w dependence of the inverse of the slope of the center line (35). For simplicity, the inverse of the slope of the center line is called the CLS. Therefore, the CLS will vary from a maximum value of 1 at T_w = 0 ps to a minimum value of 0 at a sufficiently long time. It has also been shown theoretically that combining the analysis of the CLS with the linear FT IR absorption spectrum, the full FFCF can be obtained, including the T_w independent homogenous component (35).

A homogenous contribution to the peak shape in the 2D IR spectra and to the line shape of the linear FT IR absorption spectra can arise from three sources: very fast structural fluctuations that produce a motionally narrowed contribution to the FFCF (7, 36), vibrational population relaxation, and orientational relaxation. Both vibrational population relaxation and orientational relaxation times were measured independently using polarization-selective IR pump–probe experiments. However, these contributions are quite small compared with the main homogeneous contribution for the water systems studied in this paper, which is the motionally narrowed component. Motional narrowing occurs when there is some portion of the structural fluctuations that are extremely fast, such that Δτ ≪ 1, where τ is the time scale of the fast fluctuations and Δ is the amplitude of the associated frequency fluctuations. Motionally narrowed fluctuations produce a Lorentzian contribution to both the 2D IR spectrum and the linear FT IR absorption spectrum. The T_w-independent homogeneous contribution manifests itself by broadening the 2D IR spectrum along the ω_τ axis even at T_w = 0 ps. This broadening reduces the initial value of the CLS to a number <1.

A multiexponential form of the FFCF, C(t), was used to model the multitime scale dynamics of the structural evolution of the water systems. This form has been used previously for the analysis of pure water (7) and nanoscopic water pools in AOT reverse micelles (22, 37). The FFCF has the form

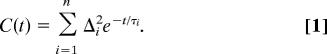The Δ_i and τ_i terms are the amplitudes and correlation times, respectively, of the frequency fluctuations induced by water–ion structural fluctuations. τ_i reflects the time scale of a set of structural fluctuations and the Δ_i is the range of the OD stretch frequency sampled due to the structural fluctuations. In the motionally narrowed limit (fast modulation limit) with Δτ ≪ 1, Δ and τ cannot be determined independently but Δ²τ = 1/T*₂ is obtained as a single parameter describing the motionally narrowed Lorentzian contribution. T*₂ is called the pure dephasing time. The Lorentzian contribution to the 2D IR spectrum also has contributions from lifetime (T₁) and orientational relaxation (T_or). The total homogeneous (Lorentzian) contribution, T₂, is given by 1/T₂ = 1/T*₂ + 1/(2T₁) + 1/(3T_or), where T₂ is determined from the CLS combined with the linear FT IR absorption spectrum (23, 35), and T₁ and T_or are measured by polarization-selective IR pump–probe experiments. The total homogeneous line width is Γ = 1/(πT₂). Γ is dominated by the pure dephasing, T*₂.

The CLS procedure is well defined and reliable. However, for water systems, it has been shown that there are non-Condon effects; that is, the transition dipole moments are frequency dependent, which influence the vibrational echo observables to some extent (11, 38). The non-Condon effects have been included in MD simulations of pure water, and they have some influence on the calculation of experimental observables (11, 38). However, there is no direct method for going from the experimental observables to the FFCF that includes non-Condon effects. Therefore, as with all current methods when applied to water, the FFCFs obtained using the CLS must be considered approximate to some extent. Nonetheless, the FFCFs are very useful for comparing the influence of NaBr concentration on the dynamics of water. Furthermore, the FFCFs obtained with the CLS can be used in calculations to reproduce the experimental results, and then any theoretical method can be used for additional analysis.

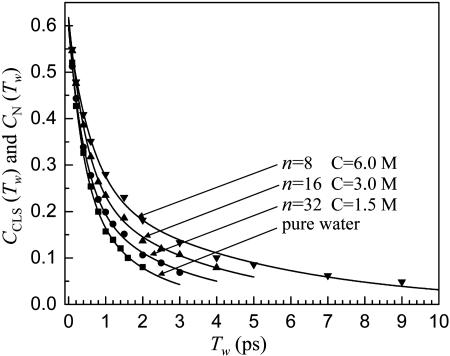
Fig. 3 shows the T_w-dependent CLS, C_CLS(T_w), and the normalized FFCF, C_N(T_w). The points are the experimental data obtained from 2D IR spectra. As the NaBr concentration increases, the vibrational lifetime of the OD stretch also increases (see the next section), which permits the 2D IR spectra to be taken out to longer times. The solid lines are the normalized FFCF, C_N(T_w), determined from the CLS and the FT IR absorption spectrum. As the NaBr concentration increases, the decays of C_N(T_w) get slower. The hydrogen bond dynamics slow as the NaBr concentration increases. The decrease in value of C_N(T_w = 0 ps) from 1 is indicative of a homogeneous contribution to the FFCF.

Fig. 3.

The inverse of the slope of the center line (CLS), C_CLS(T_w), obtained from 2D IR spectra of pure water and aqueous NaBr solutions. The lines through the data are the normalized FFCF, C_N(T_w), determined from the 2D IR spectra and linear FT IR spectra. As the NaBr concentration increases, the dynamics of water slow.

Quantitative information on the differences in the hydrogen bond dynamics in NaBr solutions is given in Table 1. To fit the data and obtain the lines through the data shown in Fig. 3, three terms are used in Eq. 1. One of the components of the FFCF is motionally narrowed for each sample. For this component, the homogeneous line width, Γ = 1/(πT₂) is reported because the Δ and τ values are not independently determined. For the other two exponential components, both the Δ and τ values are given. The values for pure water are almost identical to those reported previously, although the methodology has been improved, and therefore, the current values are used for comparison with the NaBr solutions.

Table 1.

FFCF parameters

Sample	Γ, cm−1	Δ1, cm−1	τ1, ps	Δ2, cm−1	τ2, ps
Water	76 ± 14	41 ± 8	0.38 ± 0.08	34 ± 11	1.7 ± 0.5
n = 32	78 ± 9	43 ± 5	0.43 ± 0.06	34 ± 7	2.6 ± 0.5
n = 16	74 ± 6	41 ± 3	0.49 ± 0.05	34 ± 4	3.5 ± 0.5
n = 8	67 ± 6	35 ± 3	0.63 ± 0.09	30 ± 4	4.8 ± 0.6

Examining Table 1, it is seen that the major change with increasing NaBr concentration is in the slowest time constant, τ₂, of the FFCF. The homogeneous line widths, Γ, of pure water and the n = 32 and n = 16 NaBr solutions are identical within experimental error. Only for the n = 8 NaBr solution is Γ slightly smaller, and this value is within the error bars of the others. The Δ values, which give the amplitudes of the fluctuations on different time scales, are again very similar, with the n = 8 NaBr solution being slightly smaller, but on the edge of the error bars. The time constants, τ₁ and τ₂, show a systematic trend, both become longer as the NaBr concentration increases. Although the error bars for successive values overlap, the trend is clear. τ₁ increases by a factor of ≈1.66, whereas τ₂ increases by ≈3.

To understand the trends in the FFCF, we can draw on MD simulations of pure water that have been used to model previous 2D IR vibrational echo experiments (7). The simulations used a number of standard water models, such as SPC/E and SPC-FQ, to calculate the FFCF of a quantum OD oscillator of HOD embedded in the simulations. The FFCFs were then used to calculate the 2D IR spectra, which were compared with the experimental results (7). Although the agreement between the simulation results and 2D IR experimental results was not quantitative and varied depending on which water model was used, the simulation results were sufficiently close to the experimental results to provide understanding of the nature of the fluctuations that occur on different time scales. The FFCFs produced from the simulations are functions that can be well approximated as a triexponential function like that given by Eq. 1. The simulations produce a motionally narrowed component on a subpicosecond time scale and then a T_w-dependent spectral diffusion on a slower time scale, which is captured by the two terms in our model FFCFs that are not motionally narrowed.

The simulations of pure water show that the motionally narrowed component arises from extremely fast (tens of femtoseconds), very local fluctuations mainly in the hydrogen bond length. These exceedingly fast fluctuations amount to overdamped oscillations of single hydrogen bonds. There is some experimental evidence that the strongest hydrogen bonds (red side of the absorption spectrum) are slightly underdamped (6, 38). However, these ultrafast motions do not change the global structure of hydrogen bond networks. The slowest time (1.7 ps) is associated with the final complete reorganization of hydrogen bond structure. This is the time scale for global rearrangement of hydrogen bond networks, and it requires breaking and reforming hydrogen bonds as well as reorienting and switching hydrogen bond partners. The complete structural reorganization means that the OD stretch oscillators will have sampled all structures and, therefore, all vibrational frequencies. This slowest decay time is the time scale on which spectral diffusion is complete, and all frequencies under the inhomogeneously broadened absorption spectra have been sampled. The ≈400-fs time scale is a transition between the strictly local hydrogen bond length fluctuations and the final complete structural reorganization. The intermediate and slowest time scale components in the FFCF should not necessarily be viewed as distinct processes.

It is useful to take the results from the MD simulations of pure water and carry them over to understanding the FFCFs obtained from highly concentrated NaBr solutions. It is reasonable to assume that ultrafast motionally narrowed contribution to the FFCF still arises from very local hydrogen bond length fluctuations. However, in highly concentrated NaBr solutions, the hydrogen bonds are no longer among water molecules but rather between water molecules and ions. At the highest concentration, n = 8, most of the OD groups will be hydrogen bond donors to Br⁻ ions. This change in the nature of the OD hydrogen bond length fluctuations may be manifested in the reduction in Γ seen in Table 1. As mentioned above, the slowest component of the FFCF displays the largest change with increasing NaBr concentration. The slowest component slows by almost a factor of three going from pure water to the n = 8 NaBr solution. Therefore, as more and more hydrogen bonds are made to Br⁻ ions rather than among water molecules, the rate of global structural rearrangement slows. The structural randomization is only a factor of three slower than in pure water even when the number of water molecules is less than would be required to make single hydration shells in dilute aqueous solutions.

IR Pump–Probe Experiments.

Polarization-selective pump–probe experiments were used to measure the vibrational population relaxation and the orientational relaxation of the OD stretch in aqueous NaBr solutions. The parallel (S_‖) and perpendicular (S_⊥) components of the pump–probe signal measured with two beam polarization configurations are given by

and

where P(t) is the population relaxation, and C₂(t) = 〈P₂[μ(t)·μ(0)]〉 is the second-order Legendre polynomial describing transition dipole orientational correlation function (orientational relaxation).

Vibrational population relaxation, P(t), is obtained from

Orientational relaxation dynamics are determined from the anisotropy decay, r(t), which is calculated from the parallel and perpendicular components of the pump–probe signals (18).

In water systems, vibrational population relaxation is followed by the deposition of heat into the solution, which produces a long-lived orientationally isotropic signal (16). This long-lived isotropic signal, which decays on thermal diffusion time scales, is caused by the temperature dependence of the water spectrum. The magnitude of the temperature change in these experiments is small (a fraction of 1 K). The pump–probe signals and local heating effects scale equivalently with laser intensity. The heating effects are well understood and are subtracted from the pump–probe signals using the standard procedure (16, 39).

Orientational relaxation.

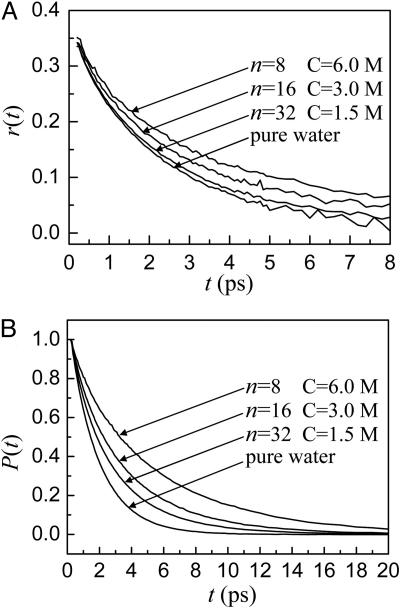
Fig. 4A displays the anisotropy decays, r(t), for pure water and aqueous NaBr solutions. As the NaBr concentration increases, the orientational relaxation slows. The anisotropy decays do not begin at the maximum value of 0.4 (see Eq. 5) because of an ultrafast inertial component that occurs on a tens-of-femtoseconds time scale (17, 40, 41). For times <100 fs, when the pump and probe pulses are overlapped in time, there is a very large nonresonant signal that obscures the inertial component. The difference in the amplitude of the measured anisotropy decay and 0.4 gives a measure of the amplitude of the inertial component. In the following text, only the anisotropy decay after the inertial component is discussed.

Fig. 4.

Results of pump–probe measurements. (A) Anisotropy decays, r(t), of the OD stretch of HOD in pure water and aqueous NaBr solutions. As the NaBr concentration increases, the orientational relaxation slows. (B) Population relaxation, P(t), of the OD stretch of HOD in pure water and aqueous NaBr solutions. As the NaBr concentration increases, the population relaxation slows.

The anisotropy decay of HOD in pure water is a single exponential with a time constant of 2.6 ps (18, 41). However, the anisotropy decays in aqueous NaBr solutions are clearly not a single exponential and are fit very well by a biexponential function of the form

where τ_or2 > τ_or1. Experiments on HOD in water nanopools in small AOT reverse micelles (18) and in nanoscopic water channels in Nafion fuel cell membranes (19) also displayed biexponential decays of the anisotropy. Both of these systems have interfacial layers composed of sulfonate head groups with associated sodium counter ions. The nanoscopic environment of water modifies the nature of the hydrogen bond network and alters both spectral diffusion (18) and orientational relaxation (18, 19). In the nanoscopic water systems, the fast component of the biexponential decay of the anisotropy was analyzed by using a wobbling-in-a-cone model based on restricted orientational diffusion (18, 19, 42).

The orientational relaxation is modeled as two processes (17). The motions at short times are restricted by the boundary condition of a cone, and orientational diffusion occurs by the wobbling motion of water within a cone of semiangle of θ_c. After the initial wobbling period, a longer time decay of the anisotropy is associated with complete orientational randomization. The essential idea is that, on a time scale short compared with the rearrangement of hydrogen bond structure (breaking and reforming hydrogen bonds), the OD bond vector, which is essentially the transition dipole vector, can sample a restricted range of orientations but cannot be completely randomized. In the wobbling-in-a-cone model, the orientational correlation function is given by

where S (0 ≤ S ≤ 1) is the generalized order parameter that describes the degree of restriction of the orientational motion, τ_w is the time constant of the wobbling-in-a-cone motion, and τ_l is the time constant for the complete orientational relaxation (18, 19, 42). By comparing Eqs. 6 and 7, τ_w = (τ_or1⁻¹ − τ_or2⁻¹)⁻¹, τ_l = τ_or2, and $S=\sqrt{a_2}$. The cone semiangle θ_c is obtained from the generalized order parameter S = 0.5 cosθ_c(1 + cosθ_c).

The parameters from fitting the anisotropy decays with Eqs. 6 and 7 are given in Table 2. In the absence of the ultrafast inertial component, a₁ + a₂ = 0.4. The decrease from 0.4 gives the amplitude of the inertial component. For the three NaBr solutions, the wobbling time constant τ_w and cone semiangle θ_c are identical within experimental error. However, the long time constant, τ_l, increases as the NaBr concentration increases. In the n = 8 NaBr solution, τ_l is almost three times longer than in pure water. Like the slowest component of the spectral diffusion (see Table 1), the complete randomization of the OD orientation requires a global reorganization of the hydrogen bond structure. Although the FFCF and the orientational correlation function cannot be directly compared, the slowest component of each requires rearrangements of the hydrogen bond structure. It is interesting to compare the effect of NaBr concentration on the slowest components of the FFCF and orientational correlation function shown in Tables 1 and 2, respectively. This can be done by taking the ratios, R, of the time constants of the slowest components for NaBr solutions with respect to the value for pure water. For the FFCF, R_FFCF = 1.5, 2.1, and 2.8 going from low concentration to high concentration. For the orientational correlation function, R_or = 1.5, 2.0, and 2.6. These trends support the picture that the slowest components of both experimental observables are closely related to the global rearrangement of the hydrogen bond structure by breaking and reforming of the hydrogen bonds.

Table 2.

Orientational relaxation parameters

Sample	a1	τw, ps	θc, °	a2	τl, ps
Water				0.35 ± 0.01	2.6 ± 0.1
n = 32	0.16 ± 0.02	1.7 ± 0.2	38 ± 4	0.21 ± 0.03	3.9 ± 0.3
n = 16	0.17 ± 0.03	1.6 ± 0.1	38 ± 2	0.21 ± 0.01	5.1 ± 0.2
n = 8	0.17 ± 0.01	1.6 ± 0.1	38 ± 2	0.21 ± 0.01	6.7 ± 0.3

Recently, Laage and Hynes (12, 43) have shown that the orientational relaxation of water molecules in pure water and ionic solutions is described by a jump reorientation model rather than Gaussian orientational diffusion. This model was recently applied to nanoscopic water in Nafion fuel cell membranes (19). Water molecules undergo complete randomization of their orientations by switching their hydrogen bond partners in a concerted manner, which involves large angular jumps. The decay time τ_l is related to the jump reorientation time constant, τ_j by Ivanov's jump reorientation model (44)

where τ_j is the average delay time between jumps, and θ_j is the jump angle. On a time scale that is short compared with τ_j, the orientational motion is restricted by the intact hydrogen bonds and the angular motion is described by the wobbling-in-a-cone model. In MD simulations of water, one of the characteristics used to define the existence of a hydrogen bond is the angle between the O–D bond and the O–O axis being <30° (12). This definition permits a significant amount of orientational space to be sampled without breaking hydrogen bonds. Here, there are both water–water and water–ion hydrogen bonds. In aqueous NaBr solutions, it is reasonable to assume that, over some range of angles, the orientational motion of the OD bond will be caused by fluctuations of the intact hydrogen bond network and will be diffusive in nature within a cone.

From the measurement of τ_l, it is not possible to independently determine τ_j and θ_j. It has been found from MD simulations of an aqueous 1 M NaCl solution that the jump angles of water molecules are 63° and 70° for switching their hydrogen bond partners from water to water and from Cl⁻ to water, respectively (12, 43). For θ_j = 63°, τ_l = 1.17τ_j, and for θ_j = 70°, τ_l = 1.03τ_j. If θ_j = 72°, τ_l = τ_j. Therefore, the measured τ_l is closely related to τ_j.

Vibrational population relaxation.

Fig. 4B displays P(t), vibrational population relaxation of the OD stretch in pure water and aqueous NaBr solutions at the peak of their absorptions. As the NaBr concentration increases, population relaxation becomes significantly slower. In pure water, P(t) is a single exponential decay with a lifetime T₁ = 1.8 ps. However, P(t) for the NaBr solutions are biexponential decays:

where T_1f is the fast decay time constant and T_1s is the slow decay time constant. Table 3 lists the population relaxation parameters.

Table 3.

Population relaxation parameters

Sample	A	T1f, ps	1 − A	T1s, ps
Water	1.0	1.81 ± 0.003
n = 32	0.32 ± 0.01	1.19 ± 0.02	0.68	3.21 ± 0.02
n = 16	0.27 ± 0.01	1.20 ± 0.03	0.73	3.99 ± 0.03
n = 8	0.19 ± 0.01	1.21 ± 0.04	0.81	5.74 ± 0.02

The biexponential decays indicate that there are two distinct OD environments. Biexponential decays have been observed for vibrational population relaxation of water in nanoscopic environments of AOT reverse micelles (18) and Nafion membranes (19). Detailed analysis of linear FT IR absorption spectra, spectral diffusion, orientational relaxation, and vibrational population relaxation of water molecules in small AOT reverse micelles have demonstrated that the vibrational population relaxation is very sensitive to the immediate local environment (18). In contrast, spectral diffusion and orientational relaxation depend on the dynamics of the hydrogen bond network. The hydrogen bond network couples the different environments so that the structural dynamics of the hydrogen bond network are not separable despite the system having different local structures (18). It has been demonstrated that a system with two distinct orientational relaxation times associated with two independent environments does not give rise to a biexponential decay of the orientational correlation function (18). Therefore, the vibrational population relaxation reports on local structural differences, whereas the spectral diffusion and orientational relaxation measure global hydrogen bond network dynamics.

It has been shown that in HOD–D₂O systems, the HOD bend overtone (≈2,900 cm⁻¹) is coupled to the OH stretch mode (≈3,400 cm⁻¹) and provides an efficient relaxation pathway for the OH stretch (45). The broad bandwidths of these transitions leads to substantial overlap of the spectra, which results in efficient wavelength-dependent relaxation of the OH stretch. As a result, the lifetime of the OH stretch of HOD in D₂O (T₁ = 0.7 ps) is shorter than that of the OD stretch of HOD in H₂O (T₁ = 1.8 ps). The HOD bend overtone is not an efficient relaxation pathway for the OD stretch (≈2,500 cm⁻¹), because it is uphill and the bands do not overlap. For the OD stretch of HOD in H₂O, the OD stretch lifetime is not wavelength-dependent (16). It seems unlikely that the relatively small shift of the OD spectrum with NaBr concentration is by itself responsible for the change in the vibrational population relaxation with concentration.

The rate of vibrational population relaxation will depend on the strength of the coupling to intramolecular molecular modes, the continuum of low-frequency modes of the environment, and a density of states factor (46). In Table 3, it is seen that the fast decay time (T_1f) for the NaBr solutions is shorter than that of pure water and is constant with NaBr concentration. However, its amplitude decreases as the NaBr concentration increases. The slow decay time (T_1s) is significantly longer than that of pure water and becomes increasingly long as the NaBr concentration increases. The implication is that there is one environment that does not change with NaBr concentration, but the probability that the OD oscillator is in that environment decreases with increasing NaBr concentration. The other environment increases in probability, and its nature also changes as the NaBr concentration increases. Vibrational population relaxation is exceedingly sensitive to small changes in the energy levels of accepting modes and the continuum density of states. In contrast to orientational relaxation and spectral diffusion, it is much more difficult to ascribe changes in vibrational population relaxation to specific variations in the systems. One possibility is that the fast vibrational population relaxation (T_1f) comes from the OD being hydrogen-bonded to the oxygen atom of another water molecule, but the coupling and/or density of states are modified by the ionic environment, resulting in a decay time that is somewhat faster than in pure water. The slow vibrational population relaxation (T_1s) could arise from the OD hydrogen-bonded to Br⁻ ions. As the NaBr concentration increases, the probability of the OD being hydrogen-bonded to Br⁻ ions increases, and there is an increasing probability that the oxygen atom and the OH group are interacting with ions as DOH–Br⁻ and HDO–Na⁺. If the oxygen atom and the OH group are interacting with ions rather than with water molecules, the change in these interactions could lengthen the lifetime of the OD stretch.

Concluding Remarks

In liquid water, water molecules can form up to four hydrogen bonds in an approximately tetrahedral geometry forming an extended hydrogen bond network. The hydrogen bond network evolves continuously, breaking and reforming hydrogen bonds as well as reorienting and switching hydrogen bond partners. In aqueous NaBr solutions, the hydrogen bond network of water is partially or completely disrupted depending on the concentration of NaBr salt. The HOD molecules in highly concentrated NaBr solutions studied here are hydrogen-bonded to ions as HOD–Br⁻, DOH–Br⁻, and HDO–Na⁺ and form partial or complete hydration shells around the ions. As a consequence, the structural evolution of the water–ion network is very different from the evolution of the hydrogen bond network in pure water.

The FFCFs extracted from 2D IR vibrational echo experiments and the anisotropy decays measured with polarization-selective IR pump–probe experiments as a function of ion concentration in aqueous NaBr solutions were compared with those for pure water (see Tables 1 and 2). The slowest time components of both the FFCFs and the anisotropy decays demonstrate that the time scale for complete rearrangement of the hydrogen bond structure increases with NaBr concentration. At the highest concentration with eight water molecules per NaBr molecule (≈6 M NaBr), the evolution of the hydrogen bond structure is slower than in pure water by a factor of three.

Previously, two-color IR pump–probe experiments were performed by pumping the OH stretch of HOD in D₂O salt solutions (6 M NaCl, NaBr, or NaI) near the center of the OH stretching band and measuring vibrational population relaxation at different frequencies (20). The results were interpreted as spectral diffusion and were analyzed in terms of a correlation time constants τ_c. The correlation times were reported to be 20 to 50 times longer than those of pure water. MD simulations on halide–water systems suggested that the very long correlation times measured by two-color pump–probe experiments were similar to residence times of water molecules in the first hydration shells of halide anions in dilute solutions (30, 47–49). However, there is no bulk water in the highly concentrated salt solutions, and, as shown in previous studies of various water systems (5–, 18), the FFCFs of water are nonexponential in nature and decays on multiple time scales. A model with two subsets of water molecules, water bound to ions and bulk water, seems to be insufficient to describe the hydrogen bond dynamics of water in the very highly concentrated salt solutions.

The very long correlations times obtained from two-color pump–probe experiments are in contrast to the results obtained here from direct measurements of spectral diffusion dynamics using the 2D IR vibrational echo experiments for the 6 M NaBr and are supported by the anisotropy decays occurring on similar time scales. Recently, MD simulations performed on ionic-solution, hydrogen-bond lifetime correlation functions were calculated (48, 49). These simulations show that the lifetime of water–Br⁻ hydrogen bonds is a few picoseconds and is somewhat longer than that of water–water hydrogen bonds (49). The results presented in this paper indicate that the global rearrangement of the hydrogen bond structure in aqueous NaBr solutions is associated with breaking and reforming hydrogen bonds between water molecules and ions in a manner analogous to that of pure water. The time scales of hydrogen-bond lifetime correlation functions are qualitatively in accord with the results presented here.

Perhaps the most significant result to emerge from this work is that the time scale for the structural evolution of the hydrogen bonds in the presence of ions is longer, but not vastly longer, than that of pure water. In the ≈6 M NaBr solution, there are only eight water molecules per NaBr. In this solution, water molecules must be closely associated with ions, but the time scale for spectral diffusion and orientational relaxation is only a factor of three longer than that of bulk water. These results have implication for the nature of water dynamics in other aqueous systems with charged species, such as at the surfaces of biological membranes or in the vicinity of charged amino acids on the surfaces of proteins.

Materials and Methods

Samples.

n = 8, 16, and 32 NaBr solutions were prepared by mixing 0.1, 0.05, and 0.025 mol of NaBr with 0.8 mol of 5% HOD in H₂O, respectively. The samples were placed in a cell with two 3-mm-thick CaF₂ windows and a 6-μm path length to give a maximum absorbance of the OD stretch of ≈0.3 including the H₂O background absorption.

2D IR Vibrational Echo Experiments.

The experimental details of 2D IR vibrational echo spectroscopy are described in ref. 23 and briefly in the text. The vibrational echo signal emitted in a unique phase-matched direction is spatially and temporally overlapped with a local oscillator and is dispersed through a monochromator onto a 32 MCT array detector with frequency resolution of ≈6 cm⁻¹. A range of 2,340–2,700 cm⁻¹ is measured in the experiments.

Pump–Probe Experiments.

The pump–probe setup is similar to an experimental setup described previously (19). The pump and probe beams with a relative intensity of 9:1 are focused onto the sample. The probe beam is dispersed through a monochromator onto the array detector. The measurements are performed with two polarization configurations, i.e., the probe beam is parallel or perpendicular to the pump beam polarization.

Abbreviations

MD

molecular dynamics

FT

Fourier transform

AOT

sodium bis(2-ethylhexyl)sulfosuccinate

FFCF

frequency–frequency correlation function

CLS

center line slope.