Reorientional dynamics of water molecules in anionic hydration shells

Abstract

Water molecule rotational dynamics within a chloride anion's first hydration shell are investigated through simulations. In contrast to recent suggestions that the ion's hydration shell is rigid during a water's reorientation, we find a labile hydration sphere, consistent with previous assessments of chloride as a weak structure breaker. The nondiffusive reorientation mechanism found involves a hydrogen-bond partner switch with a large amplitude angular jump and the water's departure from the anion's shell. An analytic extended jump model accounts for the simulation results, as well as available NMR and ultrafast spectroscopic data, and resolves the discrepancy between them.

Ion hydration shell dynamics are critical for aqueous chemical reaction mechanisms (1, 2). They are also key for transport of ionic solutes in water; ionic mobility, for example, cannot be simply related to the ion size because of the important role of hydration shell structure and lability (3, 4). Further, ionic hydration dynamics play a central role in several physiological contexts such as ion transport through membranes, where the hydration shell reorganizes in the initial and final stages of the membrane-crossing mechanism (5). However, despite their importance, microscopic-level information concerning ionic hydration shell dynamics has been lacking.

A new experimental window on hydrogen (H)-bond dynamics in ionic hydration shells has been opened recently by femtosecond infrared spectroscopy (fsIRS) (6–10). Interpretation of these results for aqueous halide anions has given a picture where the ion's first hydration layer behaves as a rigid shell, which rotates concertedly around the ionic solute and reorients more slowly than does a water molecule in the bulk (7, 9). However, the dominance of such a mechanism for the reorientation can be doubly questioned: first, it requires the energetically costly cleavage of many H-bonds between the first and second hydration layers; second, it contradicts numerous viscosity (4, 11), NMR (12, 13), and neutron scattering (14) studies, which indicate that among the halides, I⁻, Br⁻, and to a lesser extent Cl⁻ are structure breakers, accelerating orientational relaxation with respect to bulk water. An alternate mechanism in which the first shell is instead labile is suggested by the case of neat water, in which individual water molecules were recently argued to reorient mainly through a molecular jump mechanism consisting of sudden large-amplitude angular jumps (15). Here we investigate, through molecular simulations and an extended jump model, how the water orientational dynamics are modified by the presence of an anionic solute, which can serve as a paradigm system for water dynamics in an inhomogeneous environment. We focus on aqueous Na⁺Cl⁻ solutions, which have been extensively studied experimentally (3, 7–10, 12, 13).

Results and Discussion

Classical molecular dynamics simulations are an incisive tool for this study, because they provide a molecular picture of the mechanism while giving results that can be compared with experimental measurements. To account for the polarization of the surrounding waters by the chloride anion charge and its impact on the dynamics, we employ the state-of-the-art polarizable and flexible Amoeba force field, which quantitatively describes ion solvation thermodynamics (16) and diffusion (see Methods). Solutions with 1 and 3 M salt concentrations are simulated to reproduce the experimental conditions (see Methods) (7–10, 12, 13).

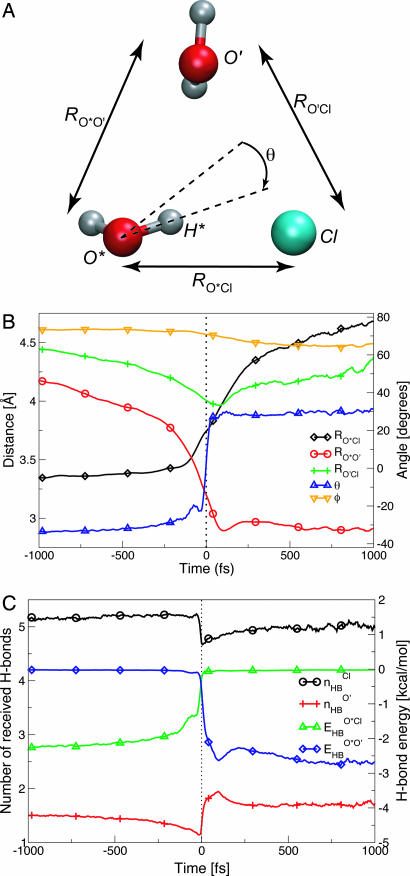
To identify the reorientation mechanism around the anion, we follow a procedure inspired by one that proved successful for neat water (15). Along a trajectory, we collect all of the times a water OH that was initially H-bonded to a Cl⁻ ion forms an H-bond with a different acceptor, which in the dilute 1 M solution is most likely a water molecule. For each switch event, we examine the sequence preceding it when OH is H-bonded to the anion, and the sequence following it when OH is H-bonded to a new partner, before any subsequent switch occurs. We calculate the time evolution of several key quantities during the switch, in particular the distances R_O*Cl and R_O*O′, where O* is within the reorienting water and O′ is the new H-bond acceptor, and the angle θ between the O*H* vector and the ClO*O′ bisector plane (Fig. 1A). More than 4,000 switch trajectories are collected and averaged with a common time origin at the instant when θ = 0°.

Fig. 1.

Time evolution, centered on the H-bond switching event, of the geometric parameters defined in A and presented in B, together with C, which represents the change in the number of H-bonds received by the different partners in A. (A) Geometric coordinate definitions: R_O*Cl and R_O*O′ are the oxygen–chloride and oxygen–oxygen distances between the rotating water and its initial and final partners, and R_O′Cl is the distance between initial and final partners; θ is the angle between the rotating O*H* bond and the bisector plane of the ClO*O′ angle φ. (B) Time evolution of these geometric quantities, averaged over 4,279 switch events. (C) nHBCl and nHBO′ are the number of H-bonds accepted, respectively, by Cl⁻ and O′ (see Methods); E HBO*Cl and E HBO*O′ are the O*H*···Cl⁻ and O*H*···O′ H-bond energies (see Methods).

This results in an average path for the switch event, which should provide a useful characterization, although individual trajectories can sometimes deviate significantly from this mean (see below). The average trajectory starts with O* H-bonded to Cl⁻, while the future partner O′ lies in the second shells of both Cl⁻ and O* (Fig. 1B). The number of H-bonds received by the Cl⁻ and O′ acceptors are equal to their equilibrium values, 〈n_HB^Cl〉 ≈ 5 and 〈n_HB^O′〉 ≈ 1.8 (Fig. 1C). Next, because of fluctuations in the solution H-bond network, Cl⁻ becomes overcoordinated, whereas O′ becomes undercoordinated (Fig. 1C). This facilitates the motion of O*-H* away from the overcoordinated initial acceptor Cl⁻ and toward the undercoordinated future partner O′. By analogy with the proton coordinate in proton transfer reactions (17), the θ angular coordinate can be considered as a fast coordinate responding to the reorganization of the slower environment (including H-bond lengths), which is the reaction coordinate: the angular jump occurs when the O*H* orientation toward O′ is as favored as it is toward Cl⁻. The transition state (TS) environment configuration therefore corresponds to a situation where the O*H* bond is equally stabilized whether it points toward the initial Cl⁻ partner or toward the new O′ partner, i.e., when the O*-H*···Cl⁻ and O*-H*···O′ bond energies (see Methods) are equal (Fig. 1C). In contrast to pure water (15), this corresponds to a structure where O* and H* are not equidistant from the initial and final H-bond acceptors: the exchange is asymmetric, replacing an energetically weaker (8) and longer (3, 14, 16) O*H*···Cl⁻ bond by an energetically stronger and shorter O*H*···O bond. The TS saddle point on the free energy surface is the structure from which trajectories with random Boltzmann-distributed velocities lead to configurations bonded to Cl⁻ or to O′ with equal probabilities; this is found for the θ = +3° O*H* bond orientation (see Methods).

The average jump amplitude can be estimated as 70° from the angle between the initial average OH direction, the O*···Cl⁻ axis, and the new O*···O′ direction, i.e., the (Cl⁻O*O′) angle (Fig. 1A), when the jump occurs. [The jump angle distribution is peaked at 55° and is characterized by a 18° mean square deviation and a 1.2 positive skewness (18), reflecting a tail for larger jump angles.] The OH-bond angular jump interchanges the undercoordination and overcoordination defects between Cl⁻ and O′, which subsequently relax through H-bond network fluctuations (Fig. 1C). Because O* and Cl⁻ are then no longer H-bonded, the reorientation process ends with O* leaving the anion first shell and forming an H-bond with O′ in the second anion hydration shell (Fig. 1B).

These results depict a nondiffusive jump-reorientation mechanism of water next to chloride, schematized in Fig. 2. This differs qualitatively from the small angular step, rotational diffusion mechanism typically assumed (12, 13). To further assess the jump mechanism's validity, we now construct an analytic kinetic model to connect it to the orientational time correlation function (tcf), accessible both from experiments and simulations,

where P₂ is the second-rank Legendre polynomial and u is the OH-bond direction vector. After a short transient period, the tcf is commonly modeled by a monoexponential decay characterized by the reorientation time τ₂, measured experimentally through NMR (12, 13), fsIRS (9, 10), and depolarized Rayleigh scattering (19).

Fig. 2.

Schematic representation of the successive steps in the molecular jump mechanism for the reorientation of a water away from a chloride anion determined from the simulations. The green sticks represent H-bonds within the reactive trimer, and the blue sticks are H-bonds involving molecules in the surrounding solution (data not shown). H-bond network fluctuations first lead to an overcoordinated Cl⁻ ion and an undercoordinated second shell water, facilitating the reorienting water's motion away from Cl⁻ and toward its future partner. The O*-H* bond then switches abruptly from one acceptor to the other, with a TS structure of an asymmetric bifurcated H-bond configuration with the O*H*···Cl⁻ bond longer than the O*H*···O′ bond. The reorientation product results from the rotating water's departure from the Cl⁻ hydration shell and its arrival in the new water partner first shell, eventually stabilized by H-bond network relaxation. The total water exchange mechanism around Cl⁻ involves the superposition of this mechanism for a coordination water departure with the reverse of this mechanism for the arrival of a new different water. The observed Cl⁻ overcoordination in the H-bond exchange process supports an associative water exchange mechanism (ref. 40 and references therein), in which the arrival of a new water molecule precedes the departure of the initial water molecule.

Two possible states I and W are assumed for any water OH-bond in the ionic solution, H-bonded either to the Cl⁻ ion or to water, respectively. (Because this modeling is relevant for longer timescales, transient H-bond breakings do not appear.) The interconversion rate constants between these states are k₊ and k₋ in the reaction scheme

with the equilibrium constant K = k₊/k₋. We focus on the behavior within the time range where the orientational correlation vanishes, i.e., within ≈8 ps. Therefore, the W state corresponds essentially to the ion second hydration shell, and slower diffusive effects due to the further water departure beyond the second shell need not be considered. The resulting equilibrium constant K thus reflects the equilibrium between the ion H-bonded waters and the ion second hydration shell, which is smaller than the equilibrium constant with the bulk in its totality. The resulting probabilities p_I(t) and p_W(t) to belong to each state are

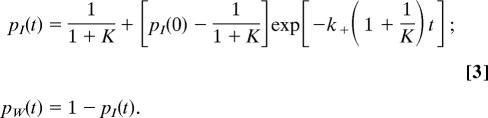(Including diffusive effects would lead to an additional much slower exponential decay term.) These populations are obtained from the simulations without any timescale restriction; fitting them on the 0- to 8-ps interval with the above analytic forms then provides the equilibrium constant K and the forward rate constant k₊ which is the H-bond switch rate constant starting from an O*H*···Cl⁻ H-bond (Table 1) (20).^¶ The reorientation times are different in each state and we now determine them.

Table 1.

Extended jump model parameters to describe the different reorientation processes in a 1 M NaCl aqueous solution

State	W			I
Possible jumps	W → W		W → I	I → W
Jump amplitude Δθ, °	63		70	70
Jump rate constant inverse τ0, ps	3.4		23.4	3.2
τ2jump, ps	4.2		24.1	3.3
τ2frame, ps		8.7		6.2
τ2W,I, ps		2.6		2.2
α, °		30		30
τlib, ps		–		0.15

The W → W jump parameters are recalculated in neat water (15), by using the Amoeba polarizable force field (16), following the same procedure as around the anion and with results comparable with our previous study (15). The other parameters are obtained from the present 1 M NaCl solution simulations. The τ₀ jump values are determined from a fit of the simulated populations p_I,W(t) in the 0–8 ps interval. (τ ₀^I→W and τ ₂^{I frame} increase slightly to 3.6 and 10 ps at 3 M, compared with the 1 M values in this table.) The τ ₂ values are determined from Eq. 4.

A water molecule in either state can reorient either via large amplitude jumps when it switches H-bond acceptors, or less importantly via slow rotation of the H-bond axis between two switches (15). Focusing first on the jump contributions, in state I the only possible H-bond switch in dilute solutions converts the molecule to state W. For a jump instead originating in state W, the OH can end in donating an H-bond either to another water or to a Cl⁻ anion: the water–water jump has already been characterized (15), and the water–ion jump is the reverse process of the switch studied here. Finally, the slow local frame reorientation between jumps is known in state I from the present simulations (Fig. 3A) and has already been determined for pure water (15). The reorientation times for the two states are therefore (15)

Each jump reorientation time is calculated by using Ivanov's jump model (21)

where Δθ is the angular jump amplitude. Here τ₀ is the average delay between jumps converting OH bonds from state I to state W and reciprocally; these τ₀ jump times are the jump rate constant inverses, τ₀^W→I = 1/k₋ and τ₀^I→W = 1/k₊, and their ratio is the equilibrium constant τ₀^W→I/τ₀^I→W = K. The parameters' values, all determined from the simulations or prior work (15), are summarized in Table 1.

Fig. 3.

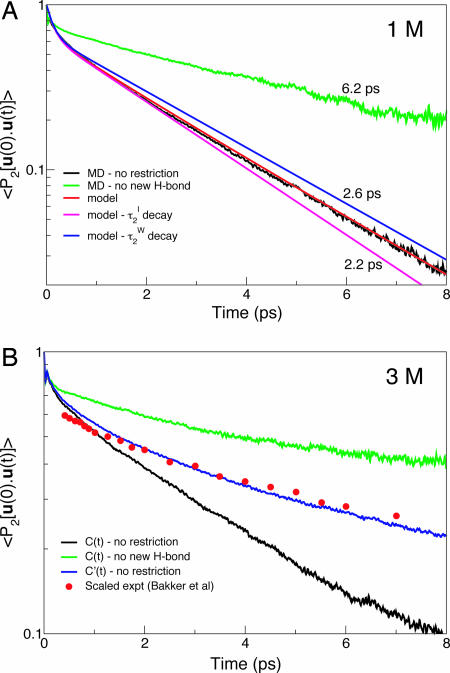
Orientational tcfs. (A) C(t) (Eq. 1) for all water OH bonds initially H-bonded to a Cl⁻ anion from the 1 M molecular dynamics simulation (which is nearly identical to the simulated 0.2 M function; see Methods) and from the molecular jump model (Eq. 7). Also shown is the C(t) tcf for the subensemble of OH bonds never donating an H-bond to an acceptor other than the initial Cl⁻, providing the frame reorientation time τ ₂^{I, frame}. As with the experimental results (9), reorientation times are determined through a monoexponential fit in the 2- to 6-ps range. (B) 3 M simulation C(t) (Eq. 1) for all water OH bonds initially H-bonded to a Cl⁻ and for all OH bonds never donating an H-bond to an acceptor other than the initial Cl⁻, C′(t) tcf (Eq. 8), evaluated as described in the text and including the T₁ vibrational lifetime [2.7 and 0.8 ps for Cl⁻ and O H-bond acceptors (7)], and from ultrafast IR spectroscopy (9); because the experimental probe frequency is on the absorption spectrum's red-side selecting stronger H-bonds with a smaller initial librational decay (22), the experimental values are scaled by 0.8 to be compared with the simulated C′(t).

To predict the orientation tcf from the above model, two further considerations are necessary. First and most importantly, because the reorientation rates are different in the I and W states, the orientational tcf depends on the times t_I and t_W spent by the OH bond in each state, which are determined as

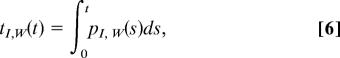together with Eq. 3. Second, the initial short time decay of the tcf, although not the main focus, needs to be accounted for; it is due to the OH librations within a cone whose axis is the H-bond direction and whose semiangle is denoted α (22). Although this initial decay is mainly inertial and nonexponential, it can be satisfactorily modeled for present purposes by an exponential with an effective timescale τ_lib. The full orientational tcf at both short and long delays is then described by

where C_lib = [1/2 cos(α)(1 + cos(α))]² (22). The τ 2I,W values come from the jump characterizations Eq. 4; the librational cone angle α is determined from a local frame orientational tcf (22), and the effective librational decay time τ_lib is obtained by fitting the tcf initial decay (Eq. 1). When the parameters are inserted in this model tcf, it compares extremely well with the simulation result (Fig. 3A), without any adjustment. Even after the initial inertial decay the relaxation is not monoexponential because of the involvement of two processes: the relaxation results initially from the OH-bond rotation away from an anion and later from jumps between two waters, with respective times τ ₂^I and τ ₂^W.

To compare the above reorientation results with the available experimental τ₂ data, we first need to discuss those experiments. When measuring reorientation dynamics, all experimental techniques face the difficulty of distinguishing the anion shell water's contribution from that of the bulk, i.e., C(t) should be averaged only over the system OH-bonds initially H-bonded to a chloride ion. In NMR spectroscopy (12, 13), this is achieved by measuring τ₂'s dependence on the salt concentration. This thus provides reliable estimates of the reorientation times, even though these techniques are not time-resolved and measure a behavior averaged over many exchanges between the anion shell and the bulk. For fsIRS, advantage is taken of the vibrationally excited OH stretch lifetime T₁ being longer for H-bonding to a chloride anion than to a water (8). After a few picoseconds, the measured signal is therefore expected to come mainly from OH-bonds within the anion's first hydration shell. Whereas fsIRS measures a reorientation time of 9.6 (9) to 10 (10) ps, which is constant in the 1–5 M salt concentration range (10), NMR yields a constant time of 1.7 (13) to 2.3 (12) ps in infinitely dilute solution, with a small increase for NaCl concentrations beyond 1 M (12). The marked disparity between these results has not yet been satisfactorily explained, and we now address it.

NMR measures the full time integral of the tcf Eq. 1. [We have verified that the 1 M simulation result is the same as that for a lower 0.2 M concentration (see Fig. 3 legend), consistent with the NMR results.] NMR determines the reorientation component proportional to the salt concentration. Because of the librational component, this time integral is not τ 2I, which is defined in terms of an exponential decay after a brief librational transient (15); it is instead from Eq. 7 (1 − C_lib)/(1/τ_lib + 1/τ 2I) + C_libτ 2I, which is 1.5 ps in the 1 M solution from our model (see Table 1), in reasonable agreement with the experimental 1.7 (13) to 2.3 (12) ps value. Further, the ratio between the reorientation times around the ion and in bulk water is τ 2I/τ2W ≈ 0.8 from our model, comparable with the NMR value of 0.9 (12) and in agreement with the weak structure-breaker character for Cl⁻ (4, 11–14).

FsIRS measures a reorientation time (9, 10) markedly longer than NMR and the present results. However, as noted above, this technique follows the reorientation of vibrationally excited OH stretches, whose lifetime T₁ is finite and changes with the H-bond acceptor [2.7 ps with Cl⁻ and 0.8 ps with O (7)]; the experimental results therefore are biased in favor of the longer-lived excited species, here the waters H-bonded with Cl⁻ (7). This can be accounted for by considering the modified orientational tcf

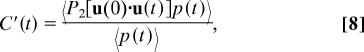where p(t) is the probability that the OH vibration is excited. Within our model, this probability can be factored as

where t_I,W(t) are the cumulated times (Eqs. 6 and 3) during which the OH is H-bonded to a chloride ion or to a water, respectively, and T₁^I,W are the respective vibrational lifetimes. However, the orientational relaxation was measured by fsIRS on a concentrated 3 M NaCl solution (9, 10), where the influence of nearby Na⁺ counterions on the waters in the neighborhood of a Cl⁻ can no longer be safely neglected. At such a high concentration, our detailed model should still describe the water dynamics qualitatively, but it need no longer apply quantitatively because it was developed, and shown to be successful, for the more dilute situation of salt concentrations of ≈1 M or less (see Fig. 3A).

To understand the experimental results, we have simulated a 3 M NaCl solution, because any Na⁺ counterion effects are automatically included in the molecular dynamics and, as described below, have used the ideas of the model, in particular Eqs. 4, 6, and 9, without however using the detailed model prescription appropriate for lower concentrations. First, the tcf C(t) is calculated without any inclusion of the differing vibrational lifetimes of water in its different environments (and without the use of the model Eq. 7); Fig. 3B shows that C(t) decays more rapidly than the relaxation measured by fsIRS. Next, we have included the different vibrational lifetimes by calculating C′(t) according to Eqs. 8, 9, and 6, but using a p(t) probability based on t_I,W(t) times numerically accumulated along the trajectory rather than through the model Eq. 3, and with the T₁ vibrational lifetimes determined experimentally (7). Fig. 3B shows that the relaxation of C′(t) from our 3 M simulation follows the fsIRS decay and exhibits a biexponential behavior, which is observable in the fsIRS data (9, 10). The difference between vibrational lifetimes lengthens the observed reorientation relaxation because at long delays, only the water OH bonds that remain H-bonded to Cl⁻ persist in the excited state; this is the fraction that has not experienced an exchange of H-bond acceptor with its associated jump reorientation and has only reoriented by slow rotation of the OH···Cl⁻ H-bond axis, a concept consistent with Eq. 4 of the model. This subensemble's reorientation time is τ₂^{I frame}, which is determined to be 10 ps from our 3 M simulations (Fig. 3B) and which agrees with the 9.6- to 10-ps fsIRS result (9, 10). In the 1 M solution, although the fsIRS orientational decay is not shown, the estimated 10-ps relaxation time (10) corresponds here as well to the frame component, determined to be 8.7 ps in our simulations. FsIRS for Cl⁻ therefore measures selectively the frame component of the reorientation mechanism followed by water molecules around the ion but remains insensitive to the H-bond exchange component: the main component is the exchange, reflected in C(t) in Fig. 3B, and fsIRS measures only the slower frame reorientation, reflected in C′(t) in Fig. 3B. Thus, the results from NMR and fsIRS are not in conflict because different components of reorientation dynamics are measured, and these are all satisfactorily reproduced by our simulations and model.

The extended molecular jump mechanism and model (15), which recently have been confirmed experimentally for pure water (23), have been shown here to describe the orientational dynamics in a chloride anion hydration shell, which are thus nondiffusive. The first hydration shell is very labile, is in fast exchange with the second shell, and is not rigid as has been recently suggested (7, 8, 24). This model could be further generalized to account, e.g., for a distribution of jump angles and a distribution of times between jumps; however, the current model has been shown to already provide a satisfactory description of the reorientation dynamics and to capture both the NMR- and fsIRS-probed components.

The present study can be extended to anions (such as I⁻ or F⁻) long considered to be strong structure breakers or makers (4, 11) to help resolve the recent controversy (6) on the very existence of such structural effects. Examination of multiply charged ions (3, 25) is also of interest, because for these cases the ion–water attraction is very strong, and the frame reorientation likely will dominate the jump reorientation component of the reorientation time, leading to a rotational “solventberg” picture in analogy to that of ion transla-tional mobility discussions (26, 27). Indeed, there is a clear reorientation–translation coupling because the reorienting water goes from the first to the second hydration shell (28)^‖in the jump component of the reorientation, and the jump and frame component perspective may prove useful in describing aspects of ionic mobility (3, 4, 29, 30).^†† Finally, the success of the mechanism and model in the present paradigm system for water in inhomogeneous asymmetric environments is encouraging for the challenging study of detailed water H-bond dynamics in the hydration shells of (usually charged) biomolecules, where both experiments and simulations point to a dynamical regime noticeably different from the bulk, with implications in protein recognition and drug binding (31–33).

Methods

Molecular Dynamics Simulations.

We used the state-of-the-art polarizable and flexible Amoeba force field (16), as implemented in the Tinker package (34). The trajectory was propagated with a Better Beeman (35) integrator with a 0.5-fs timestep. We employed periodic boundary conditions, and long-range coulombic interactions were calculated by Ewald summation (36). The system was first equilibrated for 50 ps at 300 K in the canonical ensemble by using a Berendsen coupling (36) with a 10-fs relaxation time. The trajectory was then propagated in the microcanonical ensemble. Three salt concentrations were simulated. The first is a 1 M solution, which is the only concentration for which both NMR (12, 13) and fsIRS (10) results are available. This concentration represents a close-to-dilute solution: NMR results have indeed shown that the water reorientation time is similar in the 1 M case and at infinite dilution (12, 13). The second is a more dilute 0.2 M benchmark simulation to verify that the C(t) correlation function (Eq. 1) determined in the 1 M solution is similar to the one calculated in this dilute solution. Third, we also simulated a concentrated 3 M solution to reproduce the experimental conditions used in refs. 7–9. The 1 M solution is modeled by a 24.65-Å-wide cubic simulation box containing 9 Cl⁻ anions, 9 Na⁺ cations, and 479 water molecules, corresponding to a 1.01 g·liter⁻¹ density. This system was propagated for 750 ps. The benchmark 0.2 M solution was modeled by a 19.67-Å-wide cubic simulation box containing a single Cl⁻ ion and 253 water molecules, corresponding to a 1.00 g·liter⁻¹ density. This system was propagated for 300 ps. The 3 M solution was modeled by a 24.65-Å-wide cubic simulation box containing 27 Cl⁻ anions, 27 Na⁺ cations, and 443 water molecules, corresponding to a 1.06 g·liter⁻¹ density. This system was propagated for 150 ps. The simulated densities are comparable with, although slightly lower than, the experimental densities (37).

Chloride Diffusion Constant in Water.

The chloride ion translational diffusion constant D in water was calculated from our simulations through the ion mean-square displacement D = lim_t→∞1/(6t)〉|r(t) − r(0)|²〉. The simulations with the Amoeba polarizable and flexible force field (16) lead to a diffusion coefficient D = 1.8 10⁻⁵ cm²·s⁻¹ in a 1 M NaCl solution. This is in good agreement with the experimental value of D = 1.66 10⁻⁵ cm²·s⁻¹ (38).

Definitions of the OH···O and OH···Cl⁻ H-Bonds.

A first definition for the H-bond was used to determine the number of H-bonds accepted by initial Cl⁻ and final O′ partners along the average switch trajectory (Fig. 1C). These were calculated with a geometric H-bond definition involving the donor–acceptor and hydrogen–acceptor distances, and the angle between the donor–hydrogen and donor–acceptor vectors. We adopted widely used OH···O bond conditions, R_OO <3.5 Å, R_HO < 2.45 Å, and θ_HOO < 30°, and their generalizations to the OH···Cl⁻ bond, R_OCl < 4.1 Å, R_HCl < 3.0 Å, and θ_HOCl < 30°, based on radial distribution functions (16). As expected, these H-bond numbers were lower than the coordination numbers (3, 14) which consider only the donor–acceptor distance. A second H-bond definition relies on energetic criteria and was used to illustrate that the angular jump occurs when the O*-H*···Cl⁻ and O*-H*···O′ bond energies are equal (Fig. 1C). There is no explicit H-bond energy term in the Amoeba force field (16). However, the H-bond free energies can be calculated from the two-dimensional potential of mean force obtained from the radial distribution functions g_OO(r_OO, θ_HOO) and g_OX(r_OX, θ_HOX) as E_OO,OX^HB(r, θ) = −k_BT Ln[g_OO,OX(r, θ)] where k_B is the Boltzmann constant. These E_OO,OX^HB(r, θ) potentials of mean force then were fitted by an analytic form combining a Morse potential with an ad hoc angular dependence E_OO,OX^HB(r, θ) = D_OO,OX{[1 − exp[a_OO,OX(r − r_OO,OX)]]² −1}cos⁸θ. The parameters are listed in Table 2 and correspond to an OH···Cl⁻ bond weaker and longer than the OH···O bond, as observed experimentally (8, 14).

Table 2.

Parameters of the OH···O and OH···Cl⁻ H-bonds energetic definitions

H-bond	D, kcal/mol	a, Å−1	r0, Å
OH···O	4.0	2.36	2.78
OH···Cl−	3.7	2.06	3.20

TS Determination from Reactant/Product Committors.

A characteristic feature of the TS is that trajectories initiated with random Boltzmann-distributed velocities from that configuration have equal probabilities to reach the reactant and the product. The reactant and product committors then were defined for each point in configuration space by the probability that a trajectory initiated with random momenta from that point “commits” itself to the reactant or product basin respectively (see, for example, ref. 39). Along the average switch trajectory, we focused on the time interval close to the angular jump, and for each range of θ values, we selected 30 uncorrelated configurations and started 4 short trajectories with random Boltzmann-distributed velocities from each configuration. The θ = +3° ± 0.5° range led to an equal partitioning of the trajectories and was identified as the TS structure.

Abbreviations

fsIRS

femtosecond infrared spectroscopy

tcf

time correlation function

TS

transition state.