Recent LTR retrotransposon insertion contrasts with waves of non-LTR insertion since speciation in Drosophila melanogaster

Abstract

LTR and non-LTR retrotransposons exhibit distinct patterns of abundance within the Drosophila melanogaster genome, yet the causes of these differences remain unknown. Here we investigate whether genomic differences between LTR and non-LTR retrotransposons reflect systematic differences in their insertion history. We find that for 17 LTR and 10 non-LTR retrotransposon families that evolve under a pseudogene-like mode of evolution, most elements from LTR families have integrated in the very recent past since colonization of non-African habitats (≈16,000 years ago), whereas elements from non-LTR families have been accumulating in overlapping waves since the divergence of D. melanogaster from its sister species, Drosophila simulans (≈5.4 Mya). LTR elements are significantly younger than non-LTR elements, individually and by family, in regions of high and low recombination, and in genic and intergenic regions. We show that analysis of transposable element (TE) nesting provides a method to calculate transposition rates from genome sequences, which we estimate to be one to two orders of magnitude lower than those that are based on mutation accumulation studies. Recent LTR integration provides a nonequilibrium alternative for the low population frequency of LTR elements in this species, a pattern that is classically interpreted as evidence for selection against the transpositional increase of TEs. Our results call for a new class of population genetic models that incorporate TE copy number, allele frequency, and the age of insertions to provide more powerful and robust inferences about the forces that control the evolution of TEs in natural populations.

Retrotransposons are a taxonomically widespread class of transposable elements (TEs) that transpose via an RNA intermediate and comprise significant fractions of most multicellular eukaryotic genomes. Much is known about the molecular mechanisms governing the retrotransposition cycle (transcription, reverse transcription and insertion) because they were among the very first eukaryotic DNA sequences to be characterized at the molecular level (1). However, as with most kinds of mobile DNA, less is known about the evolutionary mechanisms that control their abundance, distribution, and diversity. A more detailed understanding of these mechanisms will provide insight into the causes and consequences of retrotransposition, one of the major forces that shape eukaryotic genome organization and evolution.

In Drosophila melanogaster, as in other metazoans, retrotransposons can be subdivided into two major subclasses that are based on the presence or absence of LTRs. LTR and non-LTR (or LINE-like) retrotransposons share many basic structural features, such as encoding a reverse transcriptase gene and the use of internal, TATA-less RNA polymerase II promoters (1). However, there are important differences among them as well, most notably in their mechanisms of reverse transcription and insertion, which may lead to differences in the evolutionary history of TE sequences recorded in the genome. Aspects of this prediction have been confirmed by analyses of TEs in the D. melanogaster genome sequence, which have revealed that LTR elements are more abundant in both number and amount of DNA, have higher numbers of distinct families, and are less likely to be found in particular genomic regions (such as on the small “dot” fourth chromosome) (2–4). An important unresolved question is whether differences in historical activity may affect observed patterns of retrotransposon abundance or whether the static representation encoded in the genome sequence truly represents the long-term equilibrium processes that control retrotransposon abundance in D. melanogaster.

To address the question of whether systematic differences in age structure exist between retrotransposon subclasses in D. melanogaster, we analyzed patterns of substitution that occur in the pseudogene-like phase of molecular evolution after retrotransposon insertion and subsequent nonfunctionalization. To do this, we took advantage of the fact that a genomic DNA copy of an RNA-mediated retrotransposon is itself unable to transpose (unlike genomic copies of DNA-mediated transposons) and upon insertion effectively becomes a genomic relic evolving under the absence of selective constraint, unless it is otherwise recruited for some function by the host genome. Because domestication of TEs in D. melanogaster is rare (5), analysis of substitutions inferred to have occurred after retrotransposon copies integrate in the genome should therefore provide an accurate means to estimate the age structure of retrotransposon families. This approach has been used in the past to yield basic insights into the evolutionary history and mutational properties of non-LTR elements and their host genomes in Drosophila and other species (6–9). In principle, the same approach can be extended to LTR elements as well, because after insertion they too are effectively unconstrained from the standpoint of the genomic DNA sequence, even if an individual copy may be capable of expressing a functional RNA for some period. Thus, contrasting the pseudogene-like phase of LTR and non-LTR element evolution offers a means to address how the timing of insertion events affects differences in the abundance and diversity between these subclasses of retrotransposons in the absence of confounding effects of selective constraint.

Results

The Majority of Both LTR and Non-LTR Retrotransposon Families Show a Pseudogene-Like Mode of Evolution.

A necessary condition for the use of retrotransposon families as pseudogene-like sequences is to demonstrate that purifying selection has not operated on the terminal branch substitutions inferred to occur since retrotransposon insertion (6, 7). This condition can be established by testing the ratio of point substitution across codon positions in retrotransposon-coding fragments: this ratio is expected to be ≈1:1:1 for first:second:third codon positions under no selective constraint but can vary slightly because of missing data, incomplete/overlapping ORFs, deletions, and nonunique variant sites. No significant deviation from the expected ratio indicates that the majority of terminal branch substitutions observed are unlikely to have occurred under the constraints of purifying selection to maintain a functional ORF sequence. Conversely, an excess of third (and first) position substitutions indicates that purifying selection acted for some period on the terminal branch of one or more genomic copies in the family. The expected pattern of unconstrained terminal branch substitution has been shown for the non-LTR retrotransposon Helena in both the Drosophila virilis and D. melanogaster groups (6, 7, 10) and reported for four additional non-LTR families in D. melanogaster (8). The generality of this pattern, however, has not yet been established for all non-LTR families, and a pseudogene-like mode of evolution of terminal branch substitution has not thus far been reported for any LTR family in Drosophila.

We curated an initial data set of 46 retrotransposon families (27 LTR, 19 non-LTR) that had sufficient data for evolutionary inference from ref. 3. In these 46 families, we found an excess of unique third (and first) position substitutions in 10 of 27 LTR (37%) and 9 of 19 non-LTR (47%) families. The proportion of constrained families does not differ between LTR and non-LTR elements (Fisher's exact test, P = 0.55). For these families, the most parsimonious interpretation is that a large fraction of substitutions unique to individual genomic copies in fact occurred on internal branches of active lineages rather than on terminal branches after insertion. This signal of constraint could result simply from sparse sampling whereby other copies that potentially share these internal branch substitutions are not observed by chance; however, this explanation seems unlikely given that the median sample size and length of constrained (n = 10; 4,710 bp) and pseudogene-like (n = 10; 4,406 bp) families do not differ significantly (Wilcoxon tests, P = 0.81, P = 0.12). Constrained “families” may actually derive from multiple “subfamilies,” with genomic copies arising from transposition events separated by appreciable divergence on functionally active lineages. This possibility is consistent with the fact that constrained families typically have a larger number of unique variant sites (Wilcoxon test, P = 0.02) and with the fact that TEs can insert into other copies of the same family (4), which can occur if transposition occurs over multiple periods of time. Inclusion of constrained families significantly biases the ratio of unique point substitutions totaled across all families for both LTR and non-LTR elements [Table 1 and supporting information (SI) Table 2], underscoring the need to establish a pseudogene-like mode of evolution for individual families in genome-wide analyses of retrotransposon demographics. This result also demonstrates that previous results concerning the ages of retrotransposon families in D. melanogaster on the basis of average pairwise distance of all elements within a family (3, 11) or average pairwise distance of all elements from a consensus sequence (12, 13) are likely to be biased because of the influences of selective constraint.

Table 1.

Summary of LTR and non-LTR families analyzed in this study

Subclass	No. of families	n	Total bp surveyed	First	Second	Third	Total substitutions	P(Ho)
All LTR	27	385	1,973,013	677	603	1,120	2,420 (20)	2.18E-44
ψ LTR	17	279	1,491,867	272	267	307	851 (5)	0.159
All non-LTR	19	377	836,819	1,515	1,424	1,917	4,884 (28)	3.56E-24
ψ non-LTR	10	158	336,748	791	746	781	2,341 (23)	0.192
Grand total	46	762	2,809,832	2,192	2,027	3,037	7,304 (48)	5.18E-61
Total ψ	27	437	1,828,615	1,063	1,013	1,088	3,192 (28)	0.060

Columns provide information on the following: subclass (LTR or non-LTR); the number of copies sampled; total amount of genomic sequence surveyed; the number of unique substitutions in first, second, and third codon positions; the total number of unique substitutions (numbers in parentheses indicate the number in regions of overlapping ORFs); and the P value under the null hypothesis that point substitutions occur at equal rates across codon positions for all families and those exhibiting a pseudogene-like (ψ) mode of evolution. See SI Table 2 for details on individual families.

Nevertheless, the expected pattern of pseudogene-like evolution is observed for the majority (27 of 46, 59%) of both LTR and non-LTR retrotransposon families. This result demonstrates that most LTR elements (like their non-LTR counterparts) evolve under a pseudogene-like mode of evolution subsequent to insertion and that this abundant subclass of elements can be used to estimate rates and patterns of substitution in genome sequences. Total numbers of unique substitutions for these 27 families showed no residual evidence of purifying selection (Table 1 and SI Table 2). Thus, we conclude the 1.83 megabases (Mb) of DNA included in these 437 (279 LTR, 158 non-LTR) retrotransposons evolves under a pseudogene-like mode of evolution. In total, we infer that 3,192 unique point substitutions occurred in unconstrained, pseudogene-like retrotransposon sequences. Remarkably, 72% of these point substitutions are observed in non-LTR elements, even though non-LTR sequences only account for 18% of the genomic sequence surveyed. Because there is no evidence for purifying selection acting on these substitutions, we rescaled numbers of unique substitutions by the number of positions in which unique substitutions could be observed to estimate terminal branch lengths as a proxy for time since insertion into a particular genomic location. In the analyses below, we converted branch lengths to absolute time under the standard assumptions of a molecular clock by using a neutral mutation rate of 0.0111 point substitutions (subs) per base pair per million years (Myr) (14). In parentheses, we also show the corresponding estimates that are based on faster neutral mutation rates reported in the literature of 0.016 subs per bp/Myr (15) and 0.058 subs per bp/Myr (16).

LTR Elements Are Systematically Younger Than Non-LTR Elements.

Overall, we find that the distributions of terminal branch lengths differ significantly between LTR and non-LTR elements (Kolmogorov–Smirnov test, P < 10⁻¹⁶) (SI Fig. 2), with a tendency for LTR elements to be younger on average than non-LTR elements across the genome (Wilcoxon test, P < 10⁻¹⁶). LTR elements have a single mode of extremely young elements, with the longest terminal branch observed having 0.02853 subs per bp or an estimated age of insertion 2.6 (1.8/0.5) Myr, roughly half the divergence time since speciation with D. simulans. Most LTR-terminal branch lengths are in fact much shorter, with a median length of 0.0001639 subs per bp or 14,800 (10,200/2,800) years ago. Ninety percent of all LTR elements inserted less than 92,600 (64,200/17,800) years ago. Our results based on unconstrained terminal branch substitutions broadly support previous conclusions of recent LTR insertion in D. melanogaster on the basis of intra-element LTR–LTR divergence (ref. 11; SI Fig. 3); however, our estimates of LTR age are much younger than those of Bowen and McDonald (11) even when we use the same molecular clock. This discrepancy may result from the exclusion of all zero values in age estimates that are based on intra-element LTR–LTR divergence or the use of unfinished Release 2 sequences in the previous study (11). In fact, we find that age estimates that are based on terminal branch lengths are highly correlated with age estimates that are based on intra-element LTR–LTR divergence in our data set (SI Fig. 4), mutually reinforcing both methods as accurate means to date LTR insertion. Our results indicate that most LTR elements have inserted since the colonization of Europe by cosmopolitan populations of D. melanogaster ≈16,000 thousand years ago (17–19), even when we use age estimates that are based on the slowest, most conservative molecular clock. Thus, unlike single nucleotide variation for which cosmopolitan populations of D. melanogaster are thought to harbor a subset of variation found in African populations, our results predict that the majority of LTR insertion variants will not be shared with African populations. This prediction is compatible with the observation that derived non-African populations of D. melanogaster have a higher TE copy number than ancestral African populations (20).

In contrast, non-LTR elements have a more complex distribution of terminal branch lengths, with branch lengths up to 0.1194 subs per bp or 10.8 (7.4/2.1) Myr, nearly twice the estimated divergence between D. melanogaster and D. simulans (14). The median terminal branch length of non-LTR elements is 0.0086850 subs per bp or 782,400 (542,800/149,700) years ago, >50-fold greater than that for LTR elements. This median age predicts that many non-LTR elements inserted in ancestral populations of D. melanogaster in Africa and, like SNP variation, will be shared by both African and non-African strains of D. melanogaster. Further evidence for more recent insertion of LTR relative to non-LTR elements based on patterns of TE nesting can be found in SI Text. Despite being systematically older than LTR elements, only 12.7% of non-LTR elements have estimated ages older than the divergence time from D. simulans. Insertion since speciation for the majority of both LTR and non-LTR elements is consistent with observations that D. melanogaster is known to have a higher TE copy number relative to its sister species D. simulans (21), and most TE insertions in D. melanogaster are not shared by closely related species (22).

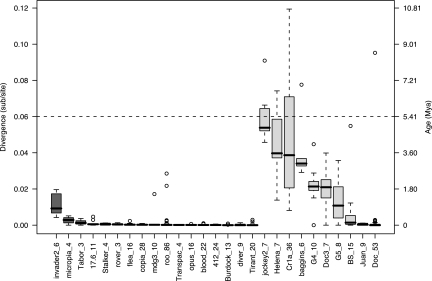
Each family of retrotransposon may have its own unique demographic history, as has been shown for five D. melanogaster non-LTR families that each exhibit quite distinct distributions of terminal branch lengths (8). To address whether the relative antiquity of non-LTR elements observed here is simply the result of just one or a few old non-LTR families, we analyzed terminal branch lengths on a family-by-family basis for both LTR and non-LTR elements. As shown in Fig. 1, the vast majority of LTR families have tight distributions of short terminal branch lengths, all at the same approximate time horizon. Families of non-LTR elements show an entirely different picture of broad, overlapping waves of insertion, which together form the complex age distribution shown in SI Fig. 2. LINE-1 subfamilies in the human genome show a similar pattern of overlapping waves of activity (23), perhaps suggesting a common mechanism controlling the activity of multiple non-LTR families. Median values of terminal branch lengths for each family are significantly lower for LTR elements than non-LTR elements (Wilcoxon test, P < 10⁻¹⁶), indicating that the majority of families contribute to the overall trend observed between the two subclasses of retrotransposons.

Fig. 1.

Age distribution of 27 pseudogene-like retrotransposon families in D. melanogaster. Terminal branch lengths (measured as the number of substitutions per site) are shown as box plots for 17 LTR families (dark gray) and 10 non-LTR families (light gray) ranked by decreasing median age. Numbers after family names indicate sample sizes of sequences in our alignments. Rectangles indicate the 25th and 75th percentiles, with the horizontal lines representing the median age, whiskers representing 1.5 times the interquartile range, and circles representing outliers beyond this range. The horizontal dashed line represents the estimated divergence time since the split of D. melanogaster and D. simulans from their common ancestor by using the molecular clock estimate in ref. 14.

To further demonstrate a categorical difference in the age of LTR and non-LTR retrotransposons, we developed a linear mixed effects model (24, 25) that accounts for the nonindependence of transposable elements that belong to the same family by treating family as a random effect while accounting for the fixed effects of recombination rate and transcription. Using this model, we find that non-LTR elements are older than LTR elements irrespective of recombination rate or transcription of a particular genomic region (F_1,25 = 28.0, P < 0.0001) but that TEs are older in low recombination regions regardless of whether these are LTR or non-LTR elements (linear mixed-effects model, F_1,407 = 28.8, P < 0.0001) (8). We find no general difference in the age of TEs in regions that are transcribed compared with those that are not (F_1,407 = 3.2, P = 0.08). However, we do find that genic TEs are younger than intergenic TEs in high recombination regions but less so in low recombination regions, leading to a significant interaction between recombination rate and transcription in our linear mixed-effects model (likelihood ratio = 6.0, df = 1, P = 0.015). Details of the effects of recombination rate and transcription on retrotransposon age can be found in SI Text and SI Fig. 5.

Estimating the Total Genomic Transposition Rate by Using Sequence Data.

The rate of transposition is a fundamental parameter for our understanding of TE evolution but has only been estimated from a limited number of labor-intensive mutation accumulation experiments (16, 26–31). Using our large data set of terminal branch lengths for pseudogene-like sequences together with information on the number of TE insertions nested within these pseudogene-like targets, we can derive estimates of the rate of transposition by using genomic data only. This approach to estimate transposition rates is similar to that used in the past to estimate rates of small-scale insertion and deletion events relative to that of point substitution (6, 8, 32). Out of a total of 326 primary nesting events in the genome with retrotransposons as the outer component, we can only estimate the age of eight nests that have pseudogene-like TEs as outer components. These eight nests include a total of 15 primary nesting events with inner TEs of all major classes, including pseudogene-like and constrained retrotransposons as well as DNA-based transposons. Six TE nests are simple two-component nests (hopper → Doc, blood → Doc, FB → jockey2, 1360 → jockey2, copia → mdg3, hobo → roo) and two are complex multicomponent nests: in the first case, five separate TEs (gypsy12, BS, F, 1731, Dm88) have inserted into one roo element; in the second case, four TEs (297, G6, Stalker, GATE) have inserted into one roo element. We note that an additional two TEs (roo, blood) have inserted into the 297 element of this latter nest, but because these are secondary nesting events that do not insert directly into the outer roo element whose age we can estimate, we have discounted them in the following calculations. As expected, if TE insertion is a function of time, the 8 pseudogene-like retrotransposons that have additional TEs nested within them are older than the 429 that do not (Wilcoxon test, P = 0.04). Scaling these 15 transposition events relative to 3,192 point substitutions in our set of pseudogene-like sequences, we obtain a relative rate of 0.0047 TE insertions per point substitution, with a 95% confidence interval (C.I.) of 0.0025–0.0072 TE insertions per point substitution under the standard assumption that mutation occurs as a Poisson process. Thus, in contrast to previous estimates (33), we estimate that point substitution occurs in unconstrained regions of the D. melanogaster genome at a rate >200 times greater than transposition per bp.

To compare this genomic estimate of transposition rate with previous estimates based on mutation-accumulation studies, we converted our relative rate to absolute time and extrapolated to the entire euchromatin. Given a point mutation rate of 0.0111 per bp/Myr (14), we estimate a rate of 5.22 × 10⁻⁵ (95% C.I.: 2.78 × 10⁻⁵ − 8.00 × 10⁻⁵) transposition events per bp/Myr combined across all families in the genome. Assuming 10 generations per year, we estimate a total genomic transposition rate of 5.22 × 10⁻¹² (95% C.I.: 2.78 × 10⁻¹² − 8.00 × 10⁻¹²) transposition events per base pair per generation, or a total of 6.26 × 10⁻⁴ (95% C.I.: 3.34 × 10⁻⁴ − 9.60 × 10⁻⁴) transposition events per genome per generation across 120 megabases (Mb) of euchromatin, which corresponds to approximately one transposition event every 1,600 generations (160 years). This estimate of the total genomic transposition rate is two to three orders of magnitude lower than previous estimates that are based on mutation accumulation experiments (16, 30, 33). Given that there are ≈530 full-length TE copies in the D. melanogaster genome potentially capable of producing new copies (4), we estimate the per-element transposition rate to be 1.18 × 10⁻⁶ (95% C.I.: 6.30 × 10⁻⁷ − 1.81 × 10⁻⁶) per generation. This estimate of the rate of transposition per element is one to two orders of magnitude lower than previous estimates obtained from mutation accumulation studies (26–28, 30, 31, 33).

Discussion

The mechanisms that control the abundance and distribution of TEs in D. melanogaster have been the subject of substantial theoretical and empirical investigation (reviewed in refs. 34–36). Given the fact that transposition rates are typically assumed to exceed excision rates, models that propose an equilibrium copy number of TEs require some deterministic force (either negative selection or self-regulated transposition) to control the unchecked, unidirectional accumulation of TEs in the genome. In the absence of evidence for self-regulation (as is the case for retrotransposons), negative selection is typically invoked as the deterministic force leading to copy-number equilibrium. Under the transposition-selection balance paradigm, our results minimally require that LTR and non-LTR families cannot be treated as one homogeneous set in equilibrium models. Recent LTR insertion, however, requires us to reexamine the widely held view that TEs in D. melanogaster are at copy number equilibrium (and the predictions of any models that require this assumption), because the vast majority of studies testing models of TE evolution in the last 20 years have used LTR elements (37). For example, eight of nine known TE families used in the studies of Charlesworth and colleagues (30, 31, 38–41) that established much of the current paradigm for TE evolution were LTR elements. Likewise, the original test for the reduction in TE abundance on the X chromosome predicted by the deleterious insertion model used only three families of elements (297, 412, and roo), all of them LTR families (42). Nonequilibrium conditions for the majority of LTR elements may explain why no single selective mechanism appears to be sufficient to explain the distribution of all LTR families (43). Recent LTR insertion may also explain the observation that levels of nucleotide diversity within full-length LTR elements are much lower than expected (44) relative to predictions of models that assume copy number and coalescent equilibrium (45, 46).

Whether our observation that almost all LTR elements in the sequenced strain are <100,000 years old is compatible with TEs in D. melanogaster being at copy number equilibrium depends critically on the per-element transposition rate, which we have shown here (10⁻⁶) may be lower than has previously been estimated from mutation accumulation data (10⁻³ to 10⁻⁵). This discrepancy between laboratory and genomic estimates of the transposition rate deserves further investigation, especially considering that the results of mutation accumulation studies are known to conflict with inferences based on evolutionary studies for other types of molecular variation (16, 47). One possibility is that our genomic estimates may rely on an incorrectly calibrated molecular clock of 0.0111 subs per Myr (14). However, if we use the faster molecular clocks of 0.016 (15) or 0.058 (16) subs per Myr, estimates of the per-element transposition rate based on genomic data increase (1.70 × 10⁻⁶ or 6.17 × 10⁻⁶, respectively) but remain lower than the range that is based on mutation accumulation experiments. If our interpretation that there has been a recent increase in the number of LTR insertions in D. melanogaster is correct, it would imply a recent increase in the transposition rate, thus providing an explanation for lower genomic estimates (which are rates averaged over longer periods of time) and higher laboratory estimates (which reflect the current rate). Estimates of transposition rates from mutation accumulation studies could be upwardly biased because of inbreeding in laboratory culture or because transposition is a self-accelerating process (33). Alternatively, transposition into other TEs in nature may occur at a lower frequency than unique DNA and therefore may not reflect the genome-wide rate. Another possibility is that there is a distribution of selection coefficients on the direct effect of TE insertions, and thus our genomic estimate represents the unconstrained “neutral” transposition rate (omitting strictly and slightly deleterious mutations), whereas laboratory estimates represent the “nearly neutral” rate (including slightly deleterious insertions that would otherwise be purged in nature). This latter possibility is likely for two reasons: first, mutation accumulation studies deliberately reduce the effects of selection through the use of small population sizes; and second, our genomic estimates of the transposition rate come from unconstrained regions of the genome, whereas laboratory estimates are based on events in normal euchromatin in which selective constraint in Drosophila is rampant (48). Thus, the “realized” transposition rate that leads to observable TE insertions in nature may be substantially lower than the maximal transposition rate that can be observed in the laboratory.

Simplistically assuming no excision and exponential growth of TE copy number from a single ancestral element, a family of LTR elements would have >22,000 copies in 100,000 years of unchecked growth at a rate of 1 × 10⁻⁵ per element, but only three copies growing at a rate of 1 × 10⁻⁶ per element. Thus, if transposition rates are on the order of 1 × 10⁻⁵ or greater, there has been more than sufficient time (based on the range of observed ages of LTR elements) for copy number to have exceeded the current number of LTR elements in the genome [n = 1,321 (4)] and to have been brought into check by natural selection. However, if transposition rates are on the order of 1 × 10⁻⁶ or lower, then the time horizon of observed LTR ages would not be sufficient for LTR copy number to have come to transposition-selection equilibrium. Likewise, if we use the fast molecular clock estimate that generates a more recent time horizon of 17,800 years for insertion of 90% of all LTR elements and the correspondingly higher transposition rate estimated from genomic data (6.17 × 10⁻⁶), there still has not been sufficient time to exceed the total number of LTR elements in the genome. It is unlikely that the differential age structure of LTR and non-LTR elements results simply from rampant elimination of older LTR elements by intra-element LTR–LTR recombination, because few solo LTRs are present in the D. melanogaster genome (3, 13). It is also difficult to envision why selection would purge LTR elements so much more than non-LTR elements, especially because they do not exist in significantly different family sizes (Wilcoxon test, P = 0.11), but it is clear that the mutational mechanisms which give rise to LTR and non-LTR elements differ fundamentally (1). Although the estimate of transposition rate that is most relevant for understanding the evolution of TE dynamics still remains to be determined, the potential for low transposition rates in nature, coupled with a lack of old LTR elements in the genome, raises the possibility that LTR element may not be at copy number or coalescent equilibrium in D. melanogaster (44).

One “sure fact” of TE evolution in D. melanogaster is the classical observation that the frequency of TE insertions at a given genomic location is typically very low in natural populations (36), typically being observed only once in a sample of 10–20 individuals (34). This observation has typically been interpreted as evidence for negative selection against TE insertions and is expected under a model of transposition-selection balance with relatively high rates of transposition. However, if LTR elements are not at equilibrium, low population frequencies observed in nature may simply reflect the recent age of LTR insertions, rather than the effects of natural selection. Given an effective population size (N) of 1 × 10⁶, as is typically assumed for D. melanogaster (49), if we conservatively estimate that the vast majority of LTR elements inserted in the last 100,000 years (1 × 10⁶ generations), their current low frequencies are compatible with evolution under genetic drift, because for new mutations arising with an initial frequency of 1/2N, the expected time to reach a frequency of only 10% is on the order of N generations (50). Thus, tests of selection that are based on differential site frequencies between TE insertions and SNPs (51) may be rendered invalid because, under the recent insertion hypothesis, different frequencies of SNPs and TE insertions may result from differences in the ages of alleles in the same genomic region, rather than differences in selection coefficients. Given the inherent mobility of TEs and the different mutation processes creating these two types of variants, there is no reason to assume that TE variants should have an age distribution that is comparable to SNPs in their flanking regions. Unfortunately, the TE families presumed to cause large insertion polymorphisms in RFLP surveys have only rarely been directly assayed (51–53); however, it is safe to assume that the majority of randomly sampled, anonymous TE insertions are LTR elements because they are the most abundant type of element in the genome (3, 4). We also note that the low frequency of TE insertions is not a universal trend in the genus Drosophila. In D. simulans, which (like its sister species D. melanogaster) has recently colonized worldwide habitats from Africa, TE insertions are typically found at low frequency (54), whereas TE insertions in endemic species with stable ranges such as Drosophila affinis, Drosophila algonquin, Drosophila heteroneura, and Drosophila sylvestris are typically found at high frequencies (55, 56).

It is important to clarify that we do not claim that there is no evidence for negative selection on TE insertions; on the contrary, negative selective is clearly evident from the facts that many visible mutations are caused by TE insertions (34), that TEs are rare in exons and introns (2, 3, 5), and that TEs accumulate in regions of low recombination where selection is less effective (2, 4, 57). Rather, we argue that the assumption of copy number equilibrium and low population frequency may no longer be used to unambiguously support the action of natural selection on LTR element insertions. Furthermore, the fact that subclasses and families of retrotransposons have distinct demographic histories requires that the age of TE insertions based on molecular evolutionary data must be accounted for in population genetic tests for selection acting on TEs. Unlike SNPs for which estimated age of a mutation and its population frequency are intimately linked, TE insertions offer two independent sources of evolutionary information about their history within species: their frequency based on population genetic data and their age since insertion based on molecular evolutionary data. We suggest that a new class of models that incorporate both these sources of information about TE history may provide more powerful and robust inferences about the evolutionary forces that control the evolution of TEs in natural populations, as well as more general inferences about the mechanisms of molecular evolution that cannot otherwise be obtained from the analysis of simple point mutations.

Materials and Methods

Sequences, annotations, and multiple alignments were obtained from (3). ORFs and LTRs were extracted from version 7.1 of the Berkeley Drosophila Genome Project (BDGP) transposon sequence set, modified to correct errors, and added to multiple alignments. Genomic copies in multiple alignments were then updated to: (i) join fragments of the same element in TE nests split by the insertion of another TE, (ii) omit unfinished or potentially misassembled TEs (58), (iii) omit TEs with no ORF sequence, and (iv) omit TEs attributed to the wrong family that are members of newly identified families in version 9.0 of the BDGP transposon sequence set. Entire families were excluded from the analysis if they did not contain three or more TE sequences (excluding copies in segmental duplications) over some region of ORF, a necessary condition to assign polarity to substitutions.

Substitution events were studied only where ancestral states could be inferred with respect to the functional ORF. We used the unique-substitution approach of ref. 32 to infer terminal branch substitutions, which has been shown to give equivalent results to phylogeny-based methods for Drosophila retrotransposons (10). For older TE insertions, the method of unique substitutions may slightly underestimate ages because of multiple hits; however, we note that this bias is weak for the divergence times considered here and is conservative with respect to the conclusion that non-LTR elements are older than LTR elements. Terminal branch lengths were estimated as the number of unique substitutions rescaled by the number of positions in the TE fragment at which unique substitutions could be observed, accounting for both deletion and nonunique variant sites. χ² tests of deviation from the expected ratio of point substitution across codon positions in retrotransposon coding fragments were conducted at the 0.05 level, with no correction for multiple testing. This cutoff is conservative from the standpoint of excluding potentially constrained sequences, because lower α-levels corrected for multiple testing allow inclusion of more constrained families into the pseudogene-like set of sequences. This test has high power to detect deviation from even substitution across codon positions, with only three substitutions (0:0:3) yielding P < 0.05.

Boundaries between “high” and “low” recombination rate regions of the genome (59) were estimated using the “cytolocation” search in FlyBase gbrowser. Ranges of cytological divisions were grouped into genome coordinates following ref. 2, with “reduced” and “null” recombination rates being considered together here as “low” recombination rates. Release 3 coordinates of high and low recombination rate regions were operationally defined for the major chromosome arms as proximal to bands 19D3 on chromosome arm X (20,231,085), 38A1 on chromosome arm 2L (19,625,057), and 77E1 on chromosome arm 3L (20,529,509), the distal to bands 42F3 on chromosome arm 2R (2,206,426), and 84B1 on chromosome arm 3R (2,811,680) and all of chromosome 4.

Analyses were conducted using the R statistical computing language. We investigated the joint effects of the factors of subclass (LTR or non-LTR), transcription (genic or intergenic), and recombination rate (high or low) on terminal branch length, while accounting for the nonindependence of TEs that belong to the same family by using a linear mixed-effects model (24, 25). Subclass, transcription, recombination rate, and their two-way interactions were included as fixed effects, and TE family was included as a random effect. The response variable, terminal branch length, was square-root transformed so that the error structures of these data would better approximate a normal distribution. To account for the effects of TE fragment length, estimates of variance for terminal branch lengths were weighted by 1/L of each transposable element fragment (where L is the fragment length) (25). The model with these weights applied [Akaike information criterion (AIC) = −1,871] was better than the unweighted linear mixed effects model (AIC = −1,573), and the relationship between standardized residuals and fitted values showed a better fit to the assumptions of the linear mixed-effects model in the case of the weighted model (results not shown).

We fit the linear mixed effects model by maximizing its log-likelihood by using the lme function in the R package (24, 25). We did not use the default method for a linear mixed-effects model in R, which maximizes the restricted log likelihood, but instead we chose to maximize the log likelihood because this allows the subsequent comparison of nested models with different fixed effects (as recommended in ref. 24). The full linear mixed-effects model was therefore simplified by using likelihood ratio tests to test the effects of stepwise removal of the least significant terms until we arrived at the minimal adequate model. In this way, we were able to reduce the full model to the main effects of subclass, transcription, and recombination rate plus the two-way interaction of transcription and recombination rate.

Abbreviations

C.I.

confidence interval

Myr

million years

subs

substitutions

TE

transposable element.