Insights into the Mechanism of Flavoprotein-Catalyzed Amine Oxidation from Nitrogen Isotope Effects on the Reaction of N-Methyltryptophan Oxidase

Abstract

The mechanism of N-methyltryptophan oxidase, a flavin-dependent amine oxidase from Escherichia coli, was studied using a combination of kinetic isotope effects and theoretical calculations. The ¹⁵(k_cat/K_m) kinetic isotope effect for sarcosine oxidation is pH-dependent with a limiting value of 0.994–0.995 at high pH. Density functional theory (DFT) calculations on model systems were used to interpret these isotope effects. The isotope effects are inconsistent with proposed mechanisms involving covalent amine-flavin adducts but cannot by themselves conclusively distinguish between some discrete electron-transfer mechanisms and a direct hydride-transfer mechanism, although the latter mechanism is more consistent with the energetics of the reaction.

Flavin-dependent amine oxidases and dehydrogenases catalyze the oxidative deamination of primary amines and the oxidative dealkylation of secondary amines. These enzymes are ubiquitous in nature and are involved in a myriad of biological activities. For example, glycine oxidase is involved in thiamin biosynthesis in microorganisms (1), while the recently discovered lysine-specific histone demethylase is involved in regulation of transcription in humans (2). The ubiquity and functional diversity of this family of enzymes underlie its importance and have prompted many structural and biochemical studies. To date, flavoenzymes that catalyze amine oxidations have fallen into two structural groups. One class includes D-amino acid oxidase (3), monomeric sarcosine oxidase (MSOX)1 (4) and glycine oxidase (1), with monoamine oxidase (MAO) B (5) polyamine oxidase (6), lysine-specific demethylase-1 (7) and L-amino acid oxidase (8) forming a separate structural class. While a number of these enzymes have been the subject of kinetic, spectroscopic, and structural studies, only in the case of D-amino acid oxidase have mechanistic (9) and structural studies (3) led to a consensus that the reaction involves hydride transfer. The chemical mechanism of the remaining amine oxidases is still debated.

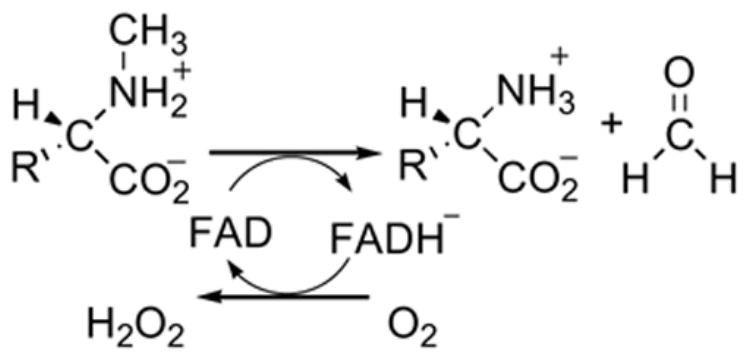
N-Methyltryptophan oxidase (MTOX) catalyzes the oxidative demethylation of N-methyl amino acids (Scheme 1), with a preference for bulky hydrophobic substrates such as N-methyl-L-tryptophan (10). Although the three dimensional structure of MTOX is unavailable, it shares 41% sequence identity with MSOX and the active site residues are conserved, establishing that it can be assigned to the same structural class. As shown in Scheme 2, a variety of mechanisms have been proposed for substrate oxidation by MTOX (11). Similar mechanisms have been proposed for other flavin-dependent amine demethylases and for flavin-dependent amine oxidation in general (for recent reviews, see references (12) and (13)). Therefore, investigation of the chemical mechanism of MTOX should aid in understanding a number of important flavoenzymes.

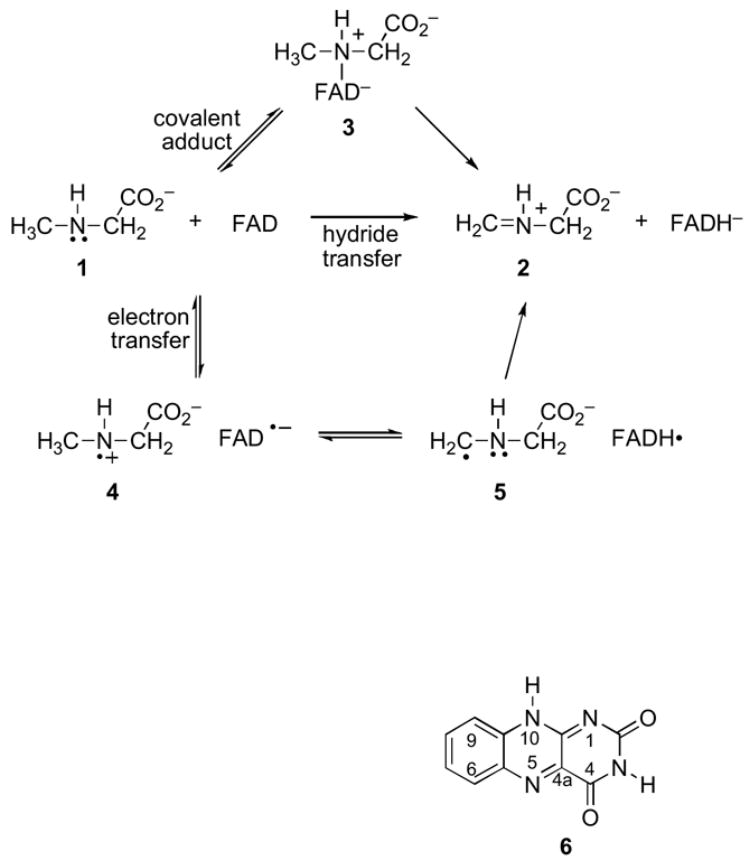
The simplest mechanism in Scheme 2 is a one-step hydride transfer from the methyl group of the substrate 1 to the flavin to form iminium product 2 directly. In a second possibility, the substrate nitrogen attacks the flavin cofactor at C^4a or N⁵ to form a covalently bound flavin adduct 3. This is followed by the loss of a proton from the substrate methyl carbon and elimination to give the final products. In a variation of this mechanism, the addition and elimination occur in a single step (14). A third possible mechanism involves two separate one-electron transfer steps. The initial transfer of an electron to the flavin from 1 forms a flavin semiquinone and aminium cation radical 4, which is then further oxidized by separate proton and electron transfers via 5. In variations of the electron-transfer mechanism, proton and electron transfers are combined into a single hydrogen transfer step, either forming 5 directly from 1 or forming 2 directly from 4.

We have previously used deuterium kinetic isotope effects to show that CH bond cleavage is fully rate-limiting for sarcosine turnover by MTOX (15). Moreover, no intermediate flavin species is observable when the reduction of the flavin in MTOX is monitored using a stopped-flow spectrophotometer. These results are fully consistent with the hydride-transfer mechanism and put limitations on the covalent-adduct and electron-transfer mechanisms, each of which involve an intermediate flavin species prior to CH bond cleavage. If an intermediate flavin species is indeed formed, it must be formed reversibly and it must be significantly higher in energy than its precursor, so that less than 5% of the enzyme is in the form of the postulated intermediate species at any time in the reaction.

Although the previous results are consistent with a hydride-transfer mechanism, they do not by themselves rule out the alternative mechanisms. In the present study, ¹⁵N isotope effects and model theoretical calculations have been utilized to further probe the mechanism of sarcosine oxidation by MTOX. The results firmly exclude mechanisms involving covalent adducts.

EXPERIMENTAL PROCEDURES

Materials

Sarcosine (N-methylglycine) was purchased from Sigma Chemical Company (St. Louis, MO) or ACROS Organics (Morris Plains, NJ). MTOX was purified on a HiTrap Chelating HP column as previously described (15).

Sample preparation

Sarcosine consumption reactions were run over a pH range of 7.5 to 9.8. Starting conditions were typically 0.2 M sarcosine and 100 μg mL⁻¹ catalase in 10 mL. Samples were buffered using potassium phosphate (pH 7.5), potassium pyrophosphate (pH 8–9) or sarcosine (pH > 9). A significant decrease in the sample pH typically occurred as the reaction progressed. Therefore, the pH was frequently monitored and adjusted with potassium hydroxide as necessary. The samples were generally kept within 0.1 pH units of the desired value. Additional MTOX was added periodically to keep the reaction progressing. Reactions were stirred in the dark at 25 °C with wet 100% oxygen blowing over the surface. Reaction progress was monitored by HPLC as follows: A 100 μL sample was withdrawn and mixed with 500 μL of 50 mM monobasic potassium phosphate in 50 % MeCN. Protein was removed by either filtering the sample through a 0.20 km nylon filter or by centrifugation for 20 min at 21000 × G. The sample was then loaded onto a Waters μBondapak-NH2 column (3.9 × 300 mm) with a 100 μL loop and eluted isocratically with 77 % MeCN, 5 mM potassium phosphate, pH* 7.2, at 3 mL min⁻¹. Sarcosine, glycine, and formaldehyde were detected by monitoring the absorbance at 210 nm. The fractional consumption of sarcosine was determined by comparing the peak areas of sarcosine and glycine to standard curves prepared using commercially available compounds. When sufficient sarcosine had been oxidized, reactions were quenched by the addition of hydrochloric acid to yield a pH below 1. Protein was then removed by centrifugation. Samples were dried using a rotary evaporator and resuspended in 4 to 5 mL of water. Acetonitrile was added to yield 40 to 50%, and the pH was adjusted to pH* 7. Samples (1 mL) were loaded onto a preparative Waters μBondapak⁻NH₂ column (7.8 × 300 mm) and eluted at 4 mL min⁻¹ with 77 % MeCN, 2.5 mM potassium phosphate, pH* 7.2 while collecting 8 mL fractions. The sarcosine and glycine fractions were separately pooled, dried on a rotary evaporator, resuspended in water, lyophilized, and submitted for isotopic ratio mass spectrometry (IRMS) analysis.

IRMS analysis

Quartz tubes (0.9 cm o.d. × 0.7 cm i.d. × 24 cm long) were charged with the sample of interest (either 8–10 mg of sarcosine or 6–8 mg of glycine), diatomaceous earth (100 mg), CuO (3–4 g), and Cu (500 mg). The tubes were placed under vacuum, flame sealed, and combusted at 850 °C. The N₂ produced was distilled on a high vacuum line through two −78 °C traps and one −196 °C trap, and then trapped on molecular sieves at −196 °C. The isotopic composition of the N₂ was determined using a Finnegan delta E isotope ratio mass spectrometer.

Data analysis

The observed ¹⁵N isotope effects were calculated from equations 1 and 2, where f is the final fractional consumption of sarcosine, R₀ is the abundance of ¹⁵N in sarcosine prior to enzyme addition, and R_P and R_S are the abundances of ¹⁵N in the enzymatically formed glycine and remaining sarcosine respectively. The pH dependence of the observed ¹⁵N effects was fit to equation 3 using KaleidaGraph (Synergy Software, Reading, PA). Here, the pK_a is for the sarcosine amine, ¹⁵K_eq is the equilibrium effect for amine deprotonation, and ¹⁵k is the intrinsic, pH-independent isotope effect.

$${\hspace{0.17em}}^{15}({\text{k}}_{\text{cat}}/{\text{K}}_{\text{m}})=\frac{log(1-f)}{log[(1-f)(R_S/R_0)]}$$ (1)

$${\hspace{0.17em}}^{15}({\text{k}}_{\text{cat}}/{\text{K}}_{\text{m}})=\frac{log(1-f)}{log(1-f{R}_P/R_0)}$$ (2)

$${\hspace{0.17em}}^{15}{({\text{k}}_{\text{cat}}/{\text{K}}_{\text{m}})}_{\text{obs}}{=}^{15}{\text{k}}^{\ast }[1+{(}^{15}{\text{K}}_{\text{eq}}-1)/(1+{10}^{\text{pH}-\text{pKa}})]$$ (3)

Theoretical calculations

The mechanisms of Scheme 2 were explored using the parent alloxazine 6 as a model for FAD and using dimethylamine as a model for the N-methyl amino acid substrates of MTOX. (The pKa’s of the Me₂NH₂⁺ and MeNH₂⁺CH₂CO₂− are 10.64 and 10.01, respectively, and the calculated methyl-group C-H bond strengths for Me₂NH and sarcosine are 88.6 and 89.2 kcal/mol, respectively.) Ground-state and transition structures were fully optimized in B3LYP/6-31+G** calculations using Gaussian 03 (16). Unrestricted calculations (UB3LYP) were employed for odd-electron species. A vibrational frequency analysis was performed on all stationary points. To allow for solvation effects, structures were also optimized using an Onsager solvent model for water (17) with single-point energies calculated using a PCM solvent model (18) and Bondi atomic radii (19). Equilibrium and kinetic isotope effects were calculated based on the Onsager solvent-model structures from the scaled (0.9614) frequencies at 25 °C using the statistical mechanics/conventional transition state theory formulation of Bigeleisen and Mayer (20, 21). Tunneling corrections were applied using the one-dimensional Wigner model (22).

RESULTS

¹⁵N Isotope Effects

To determine ¹⁵N isotope effects for MTOX, sarcosine solutions were oxidized by the enzyme to 30–50 % conversion, yielding a mixture of sarcosine, glycine, and formaldehyde. The sarcosine and glycine were separated by HPLC and analyzed for their ¹⁵N/¹⁴N content using IRMS. Sarcosine consumption reactions were conducted over a pH range of 7.5 to 9.8, with enzyme instability prohibiting reactions at higher pH. The observed ¹⁵N isotope effects were calculated using equations 1 and 2, as described above.

As shown in Table 1, the observed isotope effects are pH-dependent, starting at a value greater than 1 and then decreasing with increasing pH. The pH dependence of the observed isotope effects is not due to changes in either the rate-limiting step or the transition state structure, as the observed deuterium kinetic isotope effect is pH-independent (15). It can therefore be attributed to the ¹⁵N equilibrium isotope effect on sarcosine deprotonation (see below).

Table 1.

Observed and corrected ¹⁵(k_cat/K_m) values.^a

pH	15KIEobs,S	15KIEobs,G	15kS	15kG
7.5	1.0185	1.0166	0.9960	0.9942
7.5	1.0180	1.0168	0.9955	0.9943
8.0	1.0172	1.0157	0.9948	0.9933
8.5	1.0180	1.0157	0.9958	0.9935
8.5	1.0171	1.0166	0.9949	0.9944
8.5	1.0171	1.0168	0.9950	0.9946
9.0	1.0165	1.0154	0.9950	0.9940
9.0	1.0166	1.0151	0.9951	0.9937
9.5	1.0141	1.0129	0.9945	0.9934
9.5	1.0140	1.0130	0.9944	0.9934
9.7	1.0128	1.0122	0.9946	0.9940
9.7	1.0137	1.0123	0.9955	0.9941
9.8	1.0129	1.0117	0.9955	0.9944
9.8	1.0132	1.0117	0.9958	0.9943
average			0.9952 ± 0.0005	0.9940 ± 0.0004

^aThe ¹⁵N abundances were determined as described in the Experimental Procedures and used in equations 1 and 2 to calculate the observed isotope effects for sarcosine (¹⁵KIE_obs,S) and glycine (¹⁵KIE_obs,G), respectively. Fitting the data to equation 3 using a ¹⁵K_eq of 1.0226 ± 0.0001 (31–33) yields the pH-independent isotope effects shown as ¹⁵k_S and ¹⁵k_G for sarcosine and glycine, respectively.

For each sarcosine consumption reaction, ¹⁵(k_cat/K_m)_obs values were obtained independently from the sarcosine remaining and from the glycine produced. A comparison of the two values serves as an internal control for any artifactual ¹⁵N fractionation that may result from sample preparation. As shown in Table 1, the isotope effect calculated from the residual sarcosine was always slightly higher than that calculated from the product glycine at any given pH. The first reaction at pH 8.5 showed the largest difference in ¹⁵(k_cat/K_m)_obs values (0.0023). Therefore, a second reaction was run at the same pH which yielded a much smaller difference in ¹⁵(k_cat/K_m)_obs values (0.0004). Importantly, the averages of the isotope effects determined from substrate and product are nearly identical for both reactions (1.0168 and 1.0169). These observations are inconsistent with random errors in measuring ¹⁵N fractionation. Random ¹⁵N fractionation should affect the two determinations of ¹⁵(k_cat/K_m)_obs independently and would therefore alter the measured average isotope effects. Furthermore, random errors are unlikely to result in a consistent increase of one value relative to the other. Instead, a small systematic error in the determination of the percent conversion from either the substrate or the product is consistent with the above observations. Most importantly, the differences between the values calculated from sarcosine and glycine are small enough that mechanistic conclusions are the same using either the sarcosine or the glycine-derived values or their averages.

Theoretical Mechanisms

No simple theoretical model can adequately represent the energy surface for the enzymatic reaction in solution. Instead, our goal was to calculationally explore a range of mechanistic models for the amine oxidation mechanisms of Scheme 2 in order to interpret the experimental ¹⁵N kinetic isotope effect. This by itself is complicated due to the involvement of charged intermediates. Gas-phase calculations on mechanistic steps involving charge separation or annihilation are dominated by Coulombic effects, distorting the calculated transition structures for such steps. To mitigate this problem, the calculational models here employ either cationic species (avoiding zwitterionic charge separation), an implicit solvent model, or a combination of the two. The calculational models cannot mimic the specific interactions employed by the enzyme in promoting the reaction, but should serve as a guide for interpreting the isotope effects.

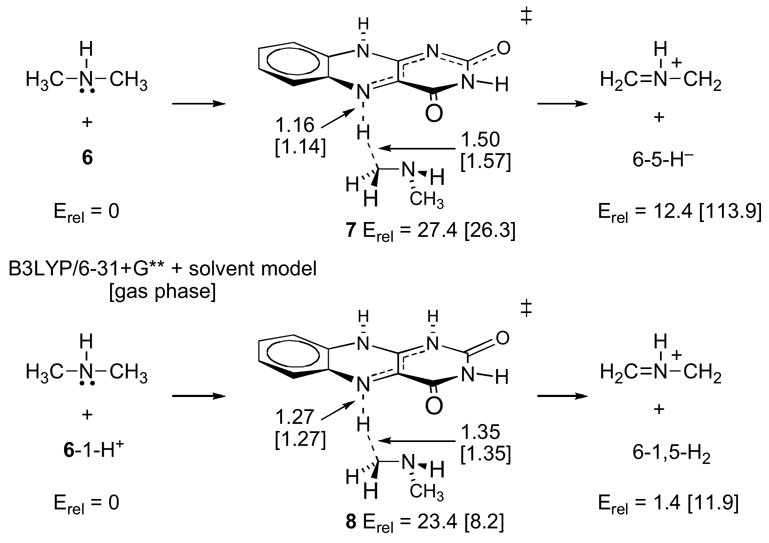
Scheme 3 shows the calculational model reactions for direct hydride transfer. Relative energies (kcal/mol versus starting materials) and selected interatomic distances (in Å) are shown in the scheme for the structures obtained employing a solvation model (PCM/B3LYP/6-31+G**//Onsager/B3LYP/6-31+G** + zpe), along with corresponding energies and distances in brackets obtained with gas-phase calculations. Transition structure 7 was located for the transfer of a hydride from dimethylamine to the neutral FAD model 6, affording a complex of the N-methyliminium cation with 6-5-H⁻ (the model for FADH⁻). The favored orientation shown minimizes charge separation between the incipient ions and leads to a very tight anion-cation complex. Pulling apart these ions in the gas phase is prohibitively uphill (accounting for most of the ≈114 kcal/mol to form separate gas-phase product ions), but the barrier for hydride transfer to form an ion pair is only 26.3 kcal/mol (B3LYP/6-31+G** + zpe). When an implicit solvent model for water is incorporated, the hydride transfer is predicted to be much less endothermic, with the separate ions only 12.4 kcal/mol uphill from 6/dimethylamine (PCM/B3LYP/6-31+G**//Onsager/B3LYP/6-31+G** + zpe), and the transition structure shifts earlier as expected from Hammond’s postulate.

An alternative calculational model for the hydride transfer starts with a 1-protonated FAD model 6-1-H⁺, and proceeds to form FADH₂ model 6-1,5-H₂ via transition structure 8. The discrete protonation of FAD prior to subsequent steps is probably unrealistic due to its low basicity, but protonation at N¹ could reasonably occur as the reaction coordinate for hydride transfer to N⁵ proceeds. Weighing against any concerted hydride transfer / proton transfer mechanism is the lack of a solvent isotope effect on the k_cat/K_m value for sarcosine (15). Because the hydride transfer from dimethylamine to 6-1-H⁺ is more nearly thermoneutral than hydride transfer to 6, the transition structure 8 is earlier than 7. Interestingly, the barrier for hydride transfer to 6-1-H⁺ is increased by about 15 kcal/mol in the PCM solvent model compared to the gas phase, and this barrier in solution is predicted to be fairly similar to the barrier for hydride transfer to 6 in solution. (Similar results were obtained using an IPCM solvent model for water.) The increased barrier with 6-1-H⁺ in free solution may be understood by considering that the starting cation 6-1-H⁺ is more stabilized by solvent than the more charge-delocalized transition structure 8.

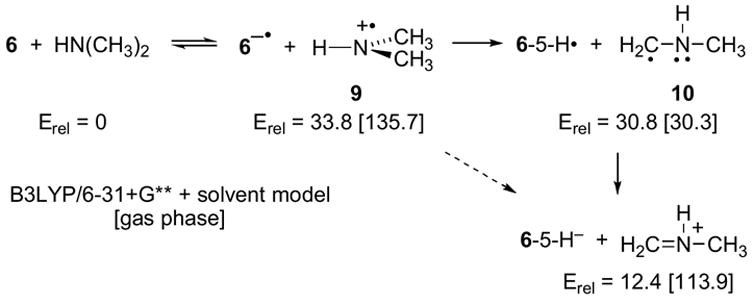
The ion pair that would result from electron transfer between adjacent flavin and amine molecules is an electronic excited state, and is not readily modeled computationally. For this reason, the computational exploration of the electron-transfer mechanism was limited to separate discrete flavin and amine oxidation states as shown in Scheme 4. Electron transfer between dimethylamine and 6 to afford separate 6^−• and aminium cation radical 9 in free solution is predicted to be quite uphill at 33.8 kcal/mol (PCM/UB3LYP/6-31+G**//Onsager/UB3LYP/6-31+G** + zpe). This is in reasonable agreement with an approximate separation of 1.7 V (39 kcal/mol) between the oxidation potential of secondary amines (23) and the reduction potential of FAD (24). Electron transfer between flavin and amine in the enzyme could of course be much less unfavorable than this calculation suggests, owing to the possibility of flavin distortion or specific solvation by the enzyme, or ion pairing, depending on the distance between resulting ions. However, the active site of MTOX is identical to that of MSOX and the structure of the latter enzyme with dimethylglycine bound (25) shows no negatively charged residue in the active site which could form such an ion pair.

Proton transfer between 6^−• and 9 affords neutral radicals 6-5-H• and 10. The overall formation of 6-5-H•/10 from 6/dimethylamine is predicted to be uphill by 30.8 kcal/mol, and because the two radicals are neutral, solvation by the enzyme is less likely to be able to avoid this barrier. However, the high-energy radical pair could be avoided by direct hydrogen transfer between 6^−• and 9 to afford 6-5-H⁻/N-methyliminium cation, which can also result from a notably downhill proton transfer between 6-5-H• and 10.

Mechanisms involving a covalently bound flavin adduct could potentially occur in two ways, either by addition of the amine to C^4a or by addition to N⁵ (26–30). From our previous observation of a large deuterium kinetic isotope effect of 7.2 ± 1.0 in this reaction (15), the formation of a discrete adduct would have to be reversible and followed by a rate-limiting elimination step. Alternatively, a concerted addition/elimination process as proposed by Miller and Edmondson (14) could account for the deuterium isotope effect. For the purpose here of interpreting the ¹⁵N kinetic isotope effect, the exploration of each of these mechanisms focused on the possible rate-limiting steps.

Scheme 5 outlines the model mechanism involving formation of adduct 11 by addition of the amine to C^4a of 6, followed by an E2 elimination to afford the 6-1,5-H₂ and N-methylformaldimine. The adduct 11 is predicted to be uphill from 6/dimethylamine, consistent with the failure to observe adducts in simple flavin/secondary amine reactions (27). The key elimination step was modeled in two ways, using either methoxide anion to model a relatively early, tight transition state (12a) or methylamine to model a relatively late, loose transition state (12b). In either case, the elimination requires protonation at N¹ to proceed, as the FADH⁻ model 6-5-H⁻ is a poor leaving group. Even after protonating at N¹, the elimination in free solution would be extremely difficult; 12b is uphill by 59.7 kcal/mol from 6/dimethylamine/MeNH₃⁺ (PCM/B3LYP/6-31+G**//Onsager/B3LYP/6-31+G** + zpe).

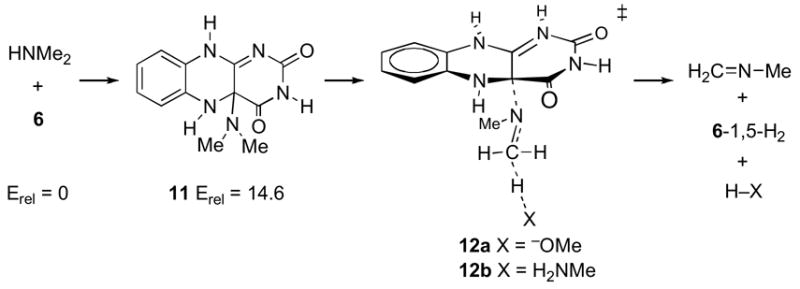
No transition structure could be located for an intramolecular elimination from the C^4a adduct. However, an intramolecular elimination process becomes possible if adduct formation occurs by addition of the amine to N⁵ to afford adduct 13, followed by proton transfer from ammonium 13 to N⁵ (Scheme 6). The elimination transition structure 14 is predicted to be quite high in energy in free solution at 45.7 kcal/mol, and would initially afford the 4,5-H₂ flavin tautomer.

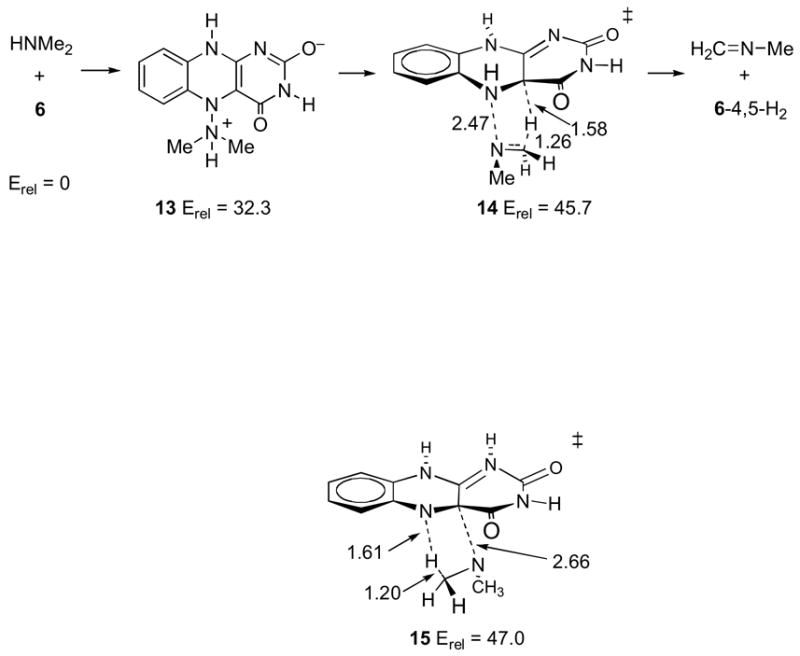
Finally, transition structure 15 was located as a model for the concerted addition/elimination process proposed by Miller and Edmondson (14). The location of a transition structure of this type requires the combination of protonation at N¹ and deprotonation of the nitrogen of the attacking amine (presumably as the process ensues); otherwise, there is no attraction of the amine to C^4a, and the resulting transition structures approach 7 or 8. Structure 15 is predicted to be 47.0 kcal/mol above 6/dimethylamine in free solution.

Predicted Isotope Effects

The calculated structures in the previous section provide a series of models for the prediction of the ¹⁵N isotope effect for various mechanistic possibilities. For the various hydride-transfer and elimination mechanisms, isotope effect predictions were obtained by applying conventional transition state theory to the discrete transition structures 7, 8, 12a, 12b, 14, and 15. The isotope effects associated with possible electron-transfer mediated mechanisms could not be modeled in this way due to the absence of electronically ground-state transition structures. An approach to predicting these isotope effects is described in the Discussion section, but a first step toward a prediction is the calculation of the equilibrium isotope effects for formation of either cation-radical 9 or radical 10/6-5-H•. These equilibrium isotope effects should be a poor model for the primary deuterium isotope effect in this reaction, but may approximate the secondary ¹⁵N isotope effect. Equilibrium predictions do not include a tunneling correction.

In predicting the isotope effects for the calculational models, a choice must be made of the starting material reference state between neutral dimethylamine and the protonated dimethylammonium ion. For comparison with the limiting pH-independent ¹⁵N isotope effect at high pH, dimethylamine was chosen as the reference state. This has the advantage of easing the qualitative understanding of the isotope effect predictions, without their being masked by a normal isotope effect for ammonium deprotonation. However, the choice makes no real difference in how closely predictions match with experiment. This is because the calculated equilibrium isotope effect for deprotonation of the dimethylammonium ion matches the experimental equilibrium ¹⁵N isotope effect (1.0226 ± 0.0001) (31–33) used to arrive at the experimental high-pH limiting ¹⁵N isotope effect. Dimethylammonium ion was used as the starting material reference state for the prediction of deuterium isotope effects since sarcosine would be predominantly protonated under the conditions used to measure the experimental isotope effect.

The results are summarized in Table 2. A key observation in these results is that the mechanisms involving either intramolecular or intermolecular elimination reactions as the rate-limiting step are predicted to result in ¹⁵N isotope effects significantly greater than unity. The equilibrium ¹⁵N isotope effect associated with possible intermediates in an electron-transfer mechanism are slightly inverse. More substantially inverse ¹⁵N kinetic isotope effects are predicted for the hydride transfer transition structures 7 and 8.

Table 2.

Predicted ¹⁵N (k_15N/k_14N, high-pH limit) or deuterium (k_H/k_D) kinetic isotope effects at 25 °C.

Structure	15N isotope effect	2H isotope effecta	15N isotope effect/Wigner correction	2H isotope effect/Wigner correction
7	0.9921	4.00	0.9927	4.77
8	0.9932	4.71	0.9942	6.17
9	0.9978b	1.38b	----	----
10/6-5-H•	0.9962b	1.22b	----	----
12a	1.0116	6.69	1.0130	9.20
12b	1.0223	4.16	1.0250	4.29
14	1.0139	4.07	1.0151	4.45
15	1.0197	3.24	1.0203	3.34

^aThe ²H isotope effect was calculated for a trideuterated methyl group, in keeping with experimental studies which used a trideuterated methyl group on sarcosine. The predicted ²H isotope effect thus represents the product of a primary and two secondary isotope effects.

^bThe isotope effects predicted for 9 and 10 are equilibrium isotope effects, not kinetic isotope effects.

DISCUSSION

Isotope effects

Previous analyses of the primary deuterium isotope effect on the MTOX-catalyzed reaction have established that cleavage of the sarcosine CH bond is rate-limiting for turnover (15). The observation that the intrinsic deuterium isotope effect is expressed in the k_cat/K_m value for sarcosine establishes that CH bond cleavage occurs during the first irreversible step in catalysis. While the presence of a primary deuterium isotope effect has thus proven exceedingly useful in identifying rate-limiting hydrogen transfer, the magnitude of a primary deuterium isotope effect is less useful in deciding among competing mechanisms that all involve rate-limiting hydrogen transfer. A key problem is that primary deuterium isotope effects are not readily predicted accurately due to tunneling and variational transition state effects (34). The deuterium isotope effects predicted from conventional transition state theory in Table 2 are a lower bound, as tunneling will generally increase the deuterium isotope effect. The predictions using a one-dimensional Wigner tunneling correction are also likely to underestimate the isotope effect, as this correction is minimal. Because of this, comparison of the predicted deuterium isotope effects with the experimental deuterium isotope effect of about 7.0 (15) does not distinguish among the various mechanisms. The use of heavy-atom isotope effects in concert with calculational studies has the substantial advantage that tunneling plays a much smaller role. As a result, heavy-atom isotope effects are often accurately predicted when the theoretical mechanism is correct (35–38). Here, such predictions allow a detailed interpretation of the experimental ¹⁵N isotope effect.

While the proposed chemical mechanisms in Scheme 2 involve substrate with a neutral nitrogen, the zwitterionic form of sarcosine predominates over the pH range accessible for mechanistic study. Deprotonation of the substrate nitrogen is affected by the isotopic content of the nitrogen, such that there is a measurable ¹⁵N effect on the equilibrium constant for deprotonation. Because k_cat/K_m values reflect the reaction of the free substrate and enzyme, they will include this ¹⁵K_eq, and the measured ¹⁵(k_cat/K_m) values must be corrected to obtain the ¹⁵N isotope effect on catalysis. The decrease in the measured isotope effects in Table 1 with increasing pH reflects this equilibrium isotope effect, in that the fraction of the substrate in the zwitterionic form decreases with increasing pH. The accuracy of correction of the measured values to obtain the high-pH isotope effect for the reaction of the anionic substrate is obviously affected by the accuracy of the equilibrium ¹⁵N isotope effect for sarcosine protonation which is used. While the ¹⁵N isotope effect for sarcosine protonation has not been measured, we have calculated the equilibrium ¹⁵N isotope effect for dimethylamine/dimethylammonium ion (Onsager/B3LYP/6-31+G**) as 1.0226. This is identical to literature values for measured equilibrium ¹⁵N isotope effects for deprotonation of glycine, alanine, and phenylalanine (31–33), so that it is likely to be quite reliable. Consequently, this value was used to correct the observed ¹⁵(k_cat/K_m) values, yielding the pH-independent values in the last two columns in Table 1. As noted above, the ¹⁵(k_cat/K_m) values determined from sarcosine are consistently slightly greater than those determined from glycine, reflecting a systematic but unidentified experimental error. Still, the average ¹⁵N effects for oxidation of anionic sarcosine calculated independently from the residual sarcosine and the glycine product (Table 1) are much closer than the isotope effects for several of the different mechanisms under consideration. Even with the caveats above, it is clear that the ¹⁵N isotope effect for the N-demethylation of sarcosine by MTOX is significantly inverse (less than unity), with a limiting value of 0.994–0.995 at high pH. This value can be used for comparison with values for the isotope effect calculated for the different proposed mechanisms in Scheme 2.

Covalent adducts and concerted addition/elimination

The possibility of a C^4a adduct was supported in model reaction studies done by Mariano (27, 28). However, the observable amine adducts in the Mariano work were stabilized by a combination of N⁵ alkylation and amine deprotonation. In the absence of such stabilization, formation of a C^4a adduct is energetically unfavorable. Thus, calculational model 11 is 14.6 kcal/mol above starting materials, and there is no energy minimum in calculations for the zwitterionic adduct that would result from attack of dimethylamine at C^4a of 6. Addition at C^4a would need to be aided by flavin distortion (39, 40) or deprotonation of the amine as it attacks C^4a, or a combination of the two. Deprotonation of the amine probably cannot occur by direct transfer from the amine to N⁵ during addition — the required four-membered-ring transition state would be expected to be high in energy and was not locatable calculationally. Calculations were also unable to locate a transition state for unimolecular elimination of N-methylformaldimine from 11. These observations suggest that both the formation of the C^4a adduct and the subsequent elimination step (as in 12) would require an as yet undefined catalytic base. While the crystal structure of MTOX is not available, a catalytic base in MSOX (sharing 41% sequence identity) has not been identified (41).

The alternative possibility of an N⁵ adduct is favored in calculations by greater electrophilicity at N⁵. While zwitterionic adduct 13 would be high in energy in free solution, it is at least a local energy minimum, unlike the analogous adduct resulting from attack at C^4a. Elimination from an N⁵ adduct could also avoid the need for an external base, with imine being formed directly via a transition state resembling model 14. However, the barrier associated with 14 in free solution is very high, and the overall neutrality of this cyclic transition structure would make it difficult for an enzyme to electrostatically catalyze the elimination.

In a study of the oxidation of benzylamine analogues by MAO A, Miller and Edmondson made the intriguing observation that the reaction was accelerated by electron-withdrawing groups (14). From a ρ of ≈2.0, a deuterium isotope effect in a range of 6 to 13, and the lack of observable flavin intermediates, they proposed a concerted addition/elimination mechanism. This unusual process can be modeled as in transition structure 15 with the proviso that the amine is deprotonated.

The ¹⁵N isotope effect results strongly weigh against any of these mechanisms. For these mechanisms involving elimination reactions as the rate-limiting step, the various calculational models lead to high-pH limit ¹⁵N isotope effects of 1.012–1.022. The predictions of normal isotope effects in these cases are readily understandable and expected on a qualitative basis. The mechanisms all involve transition states in which the nitrogen atom is undergoing a σ-bonding change, so that a primary ¹⁵N isotope effect should be observed. The observed absence of a primary ¹⁵N isotope effect would be conventional qualitative evidence against these mechanisms, and the calculated isotope effects strongly support the conventional interpretation.

One complicating factor in this interpretation is that the ¹⁵N isotope effect could be decreased if the amine nitrogen were protonated at the transition state. None of the elimination transition structures 12a, 12b, 14, and 15 involve protonated amine nitrogens. However, this is because these elimination steps are not viable when the amine is protonated. This may be understood at an electron-pushing level by considering that any of these eliminations involve pushing electrons away from the amine nitrogen, which is much more difficult when the nitrogen is protonated. As a result, when high-level calculations search for elimination transition structures in protonated analogs of 12a, 12b, 14, and 15, alternative processes intervene.

It should be noted that the barriers associated with 14 and 15 in free solution are very high, and the overall neutrality of the transition structures makes it difficult to envision how an enzyme could catalyze these cyclic elimination steps. The calculated energetics thus support the conclusion from the ¹⁵N isotope effect that mechanisms of this type are not viable.

Single electron transfer

Electron-transfer mechanisms have been frequently proposed for flavin-dependent amine oxidations (reviewed in (42)). Support for these mechanisms comes primarily from oxidation studies of cyclopropyl or cyclobutyl compounds that act as mechanism based inhibitors for MAO ((12) and references therein) and for MSOX (43, 44). However, it is important to note that a cyclopropyl group blocks hydride transfer, as cyclopropylidene imines are very strained, and facilitates electron transfer, as cyclopropyl groups greatly stabilize adjacent positive charge. Less strained cyclic substrates and inhibitors have failed to give the ring opening products (45–47). With the latter compounds, the lack of the ring-opening product is consistent with a non-radical mechanism.

To date, monitoring flavin reduction by substrate has failed to show any visible flavin radical spectrum in MTOX (11, 15), MSOX (41, 48), trimethylamine oxidase (49), lysine-specific histone demethylase-1 (50), MAO (14, 51), or any of the flavin-dependent amine oxidases. In many of these cases, deuterium isotope effects have shown that CH bond cleavage is partially or completely rate-limiting. Therefore, if an aminium radical is utilized, its formation must be reversible and energetically unfavorable, but not rate-limiting.

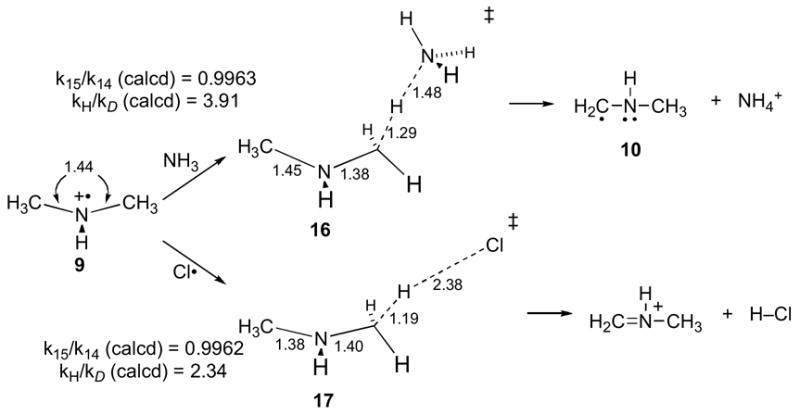
Neither proton nor hydrogen transfer from 9 to 6^−• can be modeled computationally as these would involve electronic excited states, so theoretical calculations cannot directly calculate a ¹⁵k value. To get around this problem, some simpler reactions of 9 not complicated by electronic excited states were studied. To model proton transfer from 9, the reaction of 9 with ammonia was chosen, and transition structure 16 was located (Onsager/UB3LYP/6-31+G**) for the formation of 10/NH₄⁺. It is unclear how closely 16 would resemble a transition structure for proton transfer from 9 to 6^−• (or sarcosine cation radical to flavin semiquinone), but 16 has the virtue of being a tractable model that could also model proton transfer from 9 to an active-site base. Modeling hydrogen transfer from 9 is more difficult, and can only be done with a radical that is sufficiently electronegative to maintain radical character in the presence of 9. For this purpose, a chlorine atom was chosen, and transition structure 17 was located for the hydrogen transfer affording N-methyliminium cation/HCl. This transition state is notably early, as would also be expected for the downhill hydrogen transfer from 9 to 6^−•.

For the calculated transition structures 16 and 17, the predicted ¹⁵N kinetic isotope effect (including a tunneling correction) was 0.9963 and 0.9962, respectively. These modestly inverse isotope effects may be understood as resulting from a strengthening of bonding to the nitrogen atom as proton or hydrogen transfer proceeds, as evidenced by an overall decrease in the C-N bond distances. Multiplying these kinetic isotope effects by the predicted equilibrium isotope effect for formation of 9 from Table 2 gives 0.9941 and 0.9940, respectively. Despite the simplicity of the models, both are in remarkable agreement with experiment.

An analogous analysis can be carried out for the deuterium isotope effect. Combining predicted H/D isotope effects for 16 and 17 of 4.02 and 2.38, respectively (including the Wigner tunneling correction), with the equilibrium isotope effect of 1.38 for formation of 9 gives 5.55 and 3.28, respectively. As discussed above, these predictions with a minimal tunneling correction are likely lower bounds and cannot be considered inconsistent with the experimental H/D isotope effect of about 7.0.

An occasionally proposed mechanism, related to the electron-transfer mediated mechanisms, is rate-limiting abstraction of a hydrogen atom from the substrate, forming a carbon radical (42, 52). This mechanism is not directly calculable because the product is an electronic excited state; in the calculational model, it is downhill from 6-5-H• + 10 to 6-5-H⁻ + N-methyliminium cation, and a combined ground-state calculation must give the latter as a hydride transfer instead of a hydrogen transfer. To model this process, a transition structure was located for hydrogen abstraction from dimethylamine by methyl radical (see the Supporting Information). The predicted ¹⁵N and H/D isotope effects for this process are 0.9985 and 8.98, respectively. Both isotope effects are somewhat higher than observed experimentally, and the lower-bound nature of the H/D isotope effect prediction adds significance to its being larger than that observed experimentally. While the simplicity of the calculational model in this case makes it difficult to reach a firm conclusion on the direct hydrogen-transfer mechanism, the isotope effects cannot be said to provide support for the mechanism as in the cases above. In addition, considering the energetic preference for 6-5-H⁻ + N-methyliminium cation over 6-5-H• + 10, and a presumed greater difficulty for the enzyme to stabilize the latter neutral molecules over the former charged species, the calculated energetics add weight against a direct hydrogen transfer from starting amine.

Overall, this analysis of the isotope effects and the close correspondence of predicted and experimental ¹⁵N kinetic isotope effects would appear to support rate-limiting proton or hydrogen transfer after an initial electron-transfer. However, it will be seen that the results provide equal support for a hydride-transfer mechanism.

Hydride transfer

A concerted hydride transfer is the simplest proposed mechanism for flavin-dependent amine oxidation, and is frequently accepted as the chemical mechanism for the thoroughly studied D-amino acid oxidase (13). This mechanism is most consistent with the lack of visible intermediate flavin species during sarcosine oxidation (15), as it requires no intermediates. The absence of an observable intermediate does not exclude covalent-adduct and electron-transfer mechanisms, as intermediates could be too short-lived to be observed, but it does weigh against such mechanisms, particularly since the mechanisms involve intermediate flavin species prior to the rate-limiting CH bond cleavage.

The evaluation of the hydride-transfer mechanism here is based on the comparison of the experimental ¹⁵N isotope effect of 0.994–0.995 versus those predicted for model transition structures 7 and 8. The ¹⁵N isotope effects predicted for 7 and 8 are notably inverse at 0.992 and 0.993, respectively. At first glance, these inverse isotope effects may seem surprising, since the nitrogen is undergoing a substantial bonding change in the process. However, heavy-atom isotope effects associated with π-bonding changes depend on the nature of the bonding change. When there is little change in total π-bond order, the isotope effect is very small. For example, the central carbons of a diene in a Diels-Alder reaction do not exhibit a significant ¹³C isotope effect (53). In reactions of O₂, the direction of the isotope effect can be associated with the direction of change in the O₂ bond strength - a weakening of the O–O bond leads to a normal isotope effect, while a strengthening leads to an inverse isotope effect (54). In 7 and 8, there is a shortening of the C–N bond as the hydride is transferred, leading to a tighter potential energy well around the nitrogen atom, leading to the inverse isotope effects.

The agreement of the predicted ¹⁵N isotope effects for hydride-transfer mechanisms with experiment is striking. Considering the experimental uncertainty discussed above, the agreement must be considered at least as good as that for the electron-transfer mechanisms. It may be argued that the agreement is of greater significance in the case of the hydride-transfer mechanisms, as 7 and 8 are straight-forward models for hydride transfer while the prediction of isotope effects for electron-transfer mechanisms was necessarily a contrived process. However, the observed ¹⁵N isotope effect can clearly be taken as supporting either mechanism.

Although the energetics for the calculational model mechanisms are not directly related to those for possible enzyme-catalyzed mechanisms, some comment can be made on the energetic feasibility of the hydride transfer versus alternative possibilities. The barriers associated with 7 and 8 in free solution are 10–15 kcal/mol higher than those for the enzymatic reaction, but a direct uncatalyzed hydride transfer should occur at an observable rate at ambient temperature and should be reasonably facile at elevated temperature. The hydride transfer should be readily catalyzed by an enzyme by hydrogen bonding or proton transfer to N¹, and the greatly decreased gas-phase barrier for 8 suggests that proton transfer ought to be most effective in a non-polar pocket. Consistent with such a model, many flavoproteins oxidases have a positively charged residue or the positive end of a helix near the flavin N¹ (55, 56). The enzyme could also ease the hydride transfer by electrostatically stabilizing the incipient iminium ion. Alternatively, if the flavin is distorted away from planarity by the enzyme, this should facilitate the hydride transfer, just as it facilitates electron transfer. In products 6-5-H⁻ and 6-1,5-H₂, the flavin rings are bent approximately 20° from planarity (the C⁴–N⁵–C⁶ angles are approximately 160°) while the starting flavin is planar, so enzymes that pre-bend the flavin will lower the barrier to hydride transfer. Overall, the calculated facility of the reaction in free solution and the expected ease of its catalysis support the viability of the hydride-transfer mechanism.

Electron transfer to form 6^−•/9 is predicted to have a higher barrier in free solution than hydride transfer. In the actual mechanism, this electron transfer would necessarily precede a yet higher barrier for rate-limiting proton or hydrogen transfer to account for the observed primary deuterium isotope effect. The combination of the calculated energetics and the primary H/D isotope effect thus adds to an energetic argument against the electron-transfer mechanism. However, it is impossible to dismiss the electron-transfer mechanism on this basis, as MTOX might promote electron transfer either by electrostatic stabilization of the charged intermediates or by flavin distortion.

CONCLUSIONS

The computational predictability of heavy-atom kinetic isotope effects has often allowed their detailed interpretation beyond conventional qualitative considerations. In the case of sarcosine oxidation by MTOX, the interpretation of the observed ¹⁵N kinetic isotope effect of approximately 0.994 based on calculated isotope effects is not unique. Both a direct hydride-transfer mechanism and reversible electron transfer followed by rate-limiting proton or hydrogen transfer can account for the observed isotope effect. However, the isotope effects predicted for models of mechanisms involving covalent adducts or concerted addition/elimination are significantly different from the experimental value and thus strongly disfavor these mechanisms. In concert with the absence of observable intermediates and the poor calculated energetics for these mechanisms, we conclude that their consideration for sarcosine oxidation by MTOX can be discounted. The calculated energetics for model reactions add some support for the hydride-transfer mechanism, as the enzyme need only modestly lower the barrier for the reaction versus that in free solution. The electron-transfer mechanisms in contrast would require somewhat greater energies, and it would be surprising if this left a proton or hydrogen transfer step as rate-limiting.

Scheme 1.

Scheme 2.

Scheme 3.

Scheme 4.

Scheme 5.

Scheme 6.

Scheme 7.

Abbreviations

MTOX

N-methyltryptophan oxidase

MSOX

monomeric sarcosine oxidase

MAO

monoamine oxidase

DFT

density functional theory

IRMS

isotopic ratio mass spectrometry

PCM

polarizable continuum model

IPCM

isodensity-surface polarized continuum model