Abstract
A simple model is formulated for analyzing the coupled folding-unfolding equilibrium present in a unique class of molecular switch proteins. We previously fused two single-domain proteins, barnase and ubiquitin, such that the free energy stored in the folded structure of one subunit is used to drive unfolding of the other. Here, we present a thermodynamic test of that mechanism. The antagonistic interaction is represented by a coupling free energy term ΔGX. ΔGX is the penalty imposed on folding of one domain by the native structure of the other. If ΔGX = 0, then neither domain senses the other and they fold and unfold independently. If ΔGX > 0, then destabilizing one domain will stabilize the other, and vice versa. In the limit where ΔGX is greater than the intrinsic stability of either protein, then only one domain can be folded at any given time. We estimate ΔGX by measuring stability parameters for a series of mutants which destabilize either the barnase or ubiquitin domains. Fitting the data to the model leads to a ΔGX value of ~ 4 kcal·mol−1. ΔGX is proposed to depend on both the length of the linker peptides used to join the two proteins, and on the inherent structural plasticity of each domain. We predict that shortening the linkers from their current lengths of two and three amino acids will increase structural and thermodynamic coupling.
Multidomain proteins are most often comprised of two or more subunits connected in an end-to-end fashion1. When these chimeras are created in the laboratory, the objective is usually for each domain to retain its original structure, stability and function, and to perturb the other as little as possible. For example, proteins are frequently tagged in this fashion to aid in their purification, crystallization, or detection. We previously took the opposite approach and fused two single-domain proteins so that they fold antagonistically 2; 3. The goal is to create a bifunctional protein in which folding of one domain is coupled to unfolding of the other. According to this molecular switching mechanism, dubbed “mutually exclusive folding”, the molecule converts between two partially folded forms. The position of the switch, and hence the overall function of the protein, is controlled by factors that affect stability of the individual domains; for example, ligand binding, temperature, or pH.
In our first study, we inserted human ubiquitin (Ub, 76 amino acids) between residues 66 and 67 of the bacterial ribonuclease barnase (Bn, 110 amino acids), at the tip of a solvent exposed loop (Fig. 1) 2. In another study, the DNA binding domain from yeast GCN4 (56 amino acids) was grafted into the same site in Bn 3. The coupled folding-unfolding equilibrium is established by a distance incompatibility: the amino to carboxy terminal lengths of Ub and GCN4 (when bound to its cognate DNA sequence) are 38 Å and 75 Å, respectively, while the distance between the ends of the Bn surface loop is only ~10 Å. The folded structures of Ub or GCN4 will therefore stretch Bn, splitting it in two if the amino to carboxy terminal distance is sufficiently long. The native form of Bn will compress and similarly destabilize Ub and GCN4. In this way, the free energy stored in the native state of one domain is used to mechanically unfold the other, and vice versa.
Figure 1.
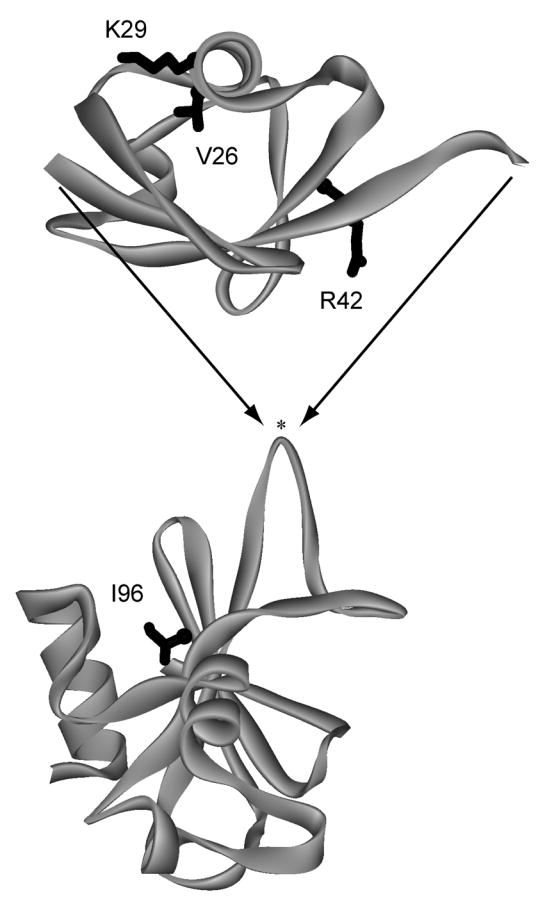
Design of the BU fusion protein. Ub (top) was inserted into a surface loop of Bn (bottom) between residues 66 and 67 (indicated by asterisk). Locations of mutated residues are shown in black. BU variants were cloned, expressed, and purified as described previously 2.
Here, we test the mutually exclusive folding mechanism by determining the extent to which the folding free energies of the Ub and Bn domains are coupled, in the barnase-ubiquitin fusion protein (BU) previously described 2. Known destabilizing mutations are introduced into one domain, and the change in stability of the other is determined by guanidine hydrochloride (GdnHCl) denaturation experiments. We chose to mutate Ub and observe Bn because the conformational state of Bn can be monitored readily by Trp fluorescence (all three Trp residues in BU are in the Bn domain). Results are interpreted using a minimal four-state model in which coupling is described by an energetic penalty that is imposed on the folding of one domain by the folded structure of the other. The model predicts that destabilization of one domain will stabilize the other, and vice versa. This relationship is expected to produce unusual behavior. For example, placing a helix-breaking mutation into an alpha helix may cause a distant region of the molecule to fold. Conversely, introducing a stabilizing interaction in one part of the protein may induce unfolding of another portion. Previous studies have used a similar mechanism to model mutual stabilization of domains by favorable binding interactions 4. To our knowledge, however, there has been no corresponding analysis of antagonistic folding.
An additional motivation for this study arises from the observation that domains are comprised of non-sequential parts of the polypeptide chain in ~25 % of naturally occurring multidomain proteins 1; 5. This finding suggests that these proteins may have evolved by inserting one domain into a loop of another domain, as we have done here. It has been shown that proteins are generally tolerant to insertions of polypeptide sequences—even long ones—into loops, provided that the inserted sequences are unstructured 6; 7; 8; 9; 10; 11. The energetic and structural consequences of inserting folded domains into loops are less well known 12; 13. Our results may help to understand how proteins adapt to domain insertions and provide guidance for rational design of allosteric protein chimeras in the future 14.
Choice of mutations
To retain consistency with the original literature, mutations are numbered according to the sequence of the parent protein in which they are found. Mutations V26A, V26G, K29N, K29Q and R42E are in the Ub domain. Val26 is one of the most highly buried side chains in the hydrophobic core of Ub. The V26A and V26G mutations were reported to reduce the folding free energy of free Ub by 3.3 kcal·mol−1 and 6.3 kcal·mol−1, respectively 15. Lys29 is located on the surface where it participates in favorable electrostatic interactions 16. The K29Q and K29N mutations were found to reduce stability of free Ub by 1.5 kcal·mol−1 and 1.7 kcal·mol−1, respectively 16. Arg42 is also on the surface, but it is involved in unfavorable charge-charge interactions. The R42E mutation reverses the charge and was shown to stabilize free Ub by 1.6 kcal·mol−1 16. The I96V and I96A mutations are in the Bn domain. Ile96 is buried in the hydrophobic core. I96V and I96A were reported to be less stable than free WT Bn by 0.95 kcal·mol−1 and 3.3 kcal·mol−1, respectively 17.
Model and simulations
The minimal folding mechanism is shown in Eq. 1, where underlined letters and non-underlined letters denote folded and unfolded domains, respectively.
| (1) |
ΔGU and ΔGB are folding free energy changes of the Ub and Bn domains when the other is unfolded. Physically, this scenario corresponds to Ub folding with unstructured polypeptides at both ends, and Bn folding with an extended surface loop. The stabilities of the domains decrease with denaturant according to the linear extrapolation equation (Eqs. 2 and 3):
| (2) |
| (3) |
ΔGBH2O and ΔGUH2O are the values in the absence of denaturant, and m is proportional to the difference in accessible surface are between folded and unfolded states of each domain. mB and mU are expected to be close to the values measured for the respective free proteins. ΔGx is assumed to remain constant as a function of denaturant. The fraction of each species is given by Eqs. 4–7, where Ki = exp(−ΔGi/RT):
| (4) |
| (5) |
| (6) |
| (7) |
ΔGx represents the energetic penalty that is imposed on the folding of one domain by the native structure of the other, according to the distance metric described above. If very long linker peptides are used to join the two proteins, then neither domain will be able to sense whether the other is folded or unfolded. In this case, ΔGX = 0, and each domain folds independently. As the linker peptides shorten, ΔGX is expected to increase. If ΔGx exceeds ΔGU and ΔGB, then both domains cannot exist simultaneously in their native states, and mutual exclusivity is attained. The linkers used in this study consist of Gly-Thr and Gly-Ala-Ser at the N and C-termini of Ub, respectively. We surmise that ΔGx depends not only on distance considerations, but also on the properties of the native and unfolded states. It may contain information on the inherent plasticity of the folded domains, i.e., the degree to which they can distort without unfolding. It is also important to recognize that the unfolded states produced by mechanical disruption and by chemical denaturation may be quite different. For example, when the nested Ub domain unfolds in the presence of folded Bn, its ends remain fixed in close proximity. The reduced entropy is expected to raise the free energy of unfolded Ub, relative to the unfolded conformation that would exist if the Bn domain were itself unstructured. On the other hand, forcing the termini together may not require Ub to unfold completely. One can envision partially folded or molten globule-like structures that are compatible with shorter N and C-terminal distances.
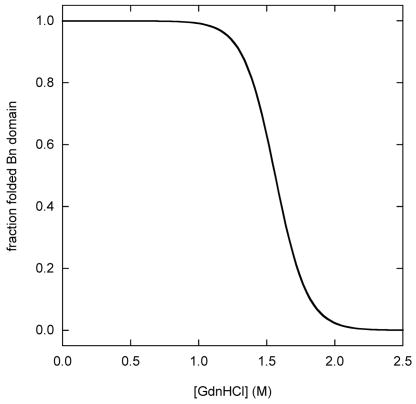
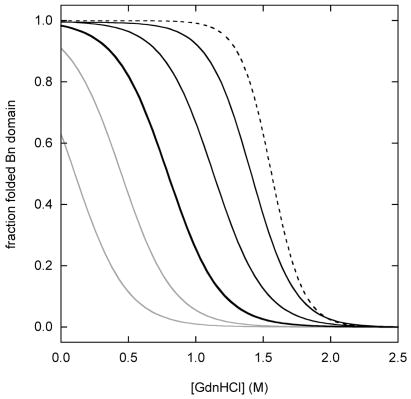
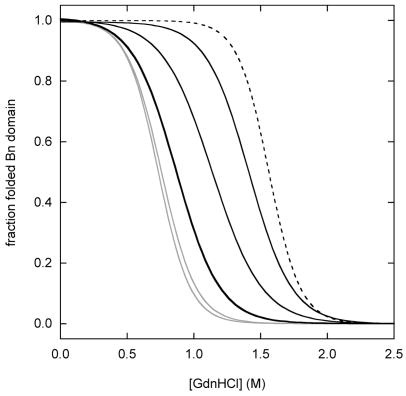
Figure 2 simulates fluorescence-monitored unfolding curves for three representative cases: zero coupling (ΔGx = 0), strong coupling (ΔGx > ΔGBH2O, ΔGUH2O), and intermediate coupling (0 < ΔGx < ΔGBH2O, ΔGUH2O). The fraction of folded Bn domain (f(bu) + f(bu)) is plotted on the y-axis. The simulations employ parameters determined experimentally for WT BU (ΔGBH2O = 7.5 kcal·mol−1, mB = 4.8 kcal·mol−1·M−1, ΔGUH2O = 5.2 kcal·mol−1, mU = 1.8 kcal·mol−1·M−1; see next section). Results are shown for WT BU, and for a series of mutants in which the Ub domain is either stabilized or destabilized by 1 kcal·mol−1 and 2 kcal·mol−1.
Figure 2.
Simulated Bn domain unfolding curves for three representative coupling regimes: (A) zero coupling (ΔGX = 0), (B) strong coupling (ΔGX = 20 kcal·mol−1), (C) intermediate coupling (ΔGX = 4 kcal·mol−1). WT BU is depicted by the heavy black line. Variants in which the Ub domain is stabilized are shown in gray. Gray curves to the immediate left and far left of WT are mutants stabilized by 1 kcal·mol−1 and 2 kcal·mol−1, respectively. Variants in which the Ub domain is destabilized are shown in black. Black curves to the immediate right and far right of WT are mutants destabilized by 1 kcal·mol−1 and 2 kcal·mol−1, respectively. Free Bn is indicated by the dashed line. Curves are generated from the model in Figure 2 using the following parameters: ΔGB = 7.5 kcal·mol−1, mB = 4.8 kcal·mol−1·M−1, ΔGU = 5.2 kcal·mol−1 (WT), mB = 1.8 kcal·mol−1·M−1. Panel D shows the dependence Bn domain stability on Ub domain stability, as gauged by Cm values. The zero, strong, and intermediate coupling cases are represented by gray, solid black, and dashed black lines, respectively. Bn domain Cm values are derived from fitting the data in panels A–C to the two-state linear extrapolation equation. ΔCm and ΔΔGH2O values on the x-axes are relative to WT Ub.
In the zero coupling limit, the Bn and Ub domains denature independently (Fig. 2A). The observed Bn unfolding transition corresponds to bu ↔ bu (for stable Ub variants) or to bu ↔ bu (for unstable Ub variants). In either case, the fitted parameters (ΔGappH2O and mapp) are simply equal to ΔGBH2O and mB, respectively. The stability of the Bn domain is not connected to that of the Ub domain, as evidenced by the fact that WT and mutant unfolding curves are identical.
In the strong coupling threshold (Fig. 2B), state bu is never populated. The observed transition is described by bu ↔ bu for all but the most destabilized Ub mutants. Ub folding now accompanies Bn unfolding. A direct result is thatΔGappH2O = ΔGBH2O − ΔGUH2O and mapp = mB − mU. Stabilizing or destabilizing the Ub domain therefore produces an equal but opposite effect on the stability of the Bn domain. As in the zero coupling case, the Bn unfolding transition for highly unstable mutants corresponds to bu ↔ bu, and ΔGappH2O and mapp approach their maximum values of ΔGBH2O and mB.
More complex behavior is observed in the intermediate coupling regime (Fig. 2C). ΔGX is low enough so that, for relatively stable Ub mutants, bu is the species most populated in the absence of denaturant. The Bn unfolding transition for WT BU is thus attributed largely to bu ↔ bu. Mutations that further stabilize the Ub domain have little effect on Bn unfolding, as they stabilize both bu and bu to comparable extents. Mutations that destabilize Ub, however, stabilize Bn significantly. The reason is that these mutations raise the free energy of bu but not that of bu. Consequently, bu becomes more populated than bu in the absence denaturant. The observed transition switches to bu ↔ bu, as observed for the strong coupling condition. Finally, a third transition, bu ↔ bu, is observed for extremely unstable Ub mutants, as in the previous two cases.
We now consider how to best quantitate stability changes in order to test the model. It is clear from the shift in the midpoints of denaturation (Cm) that, when ΔGX > 0, stabilizing or destabilizing the Ub domain produces the opposite effect on the Bn domain (Figs. 2B and 2C). However, up to three two-state reactions can contribute to the observed Bn unfolding transition. The individual reactions are not differentiated by Trp fluorescence: all data are fit well by the two-state linear extrapolation equation, as evident from the simulations. ΔGappH2O and mapp values can oscillate as a consequence. For example, in the intermediate coupling regime (Fig. 2C), mapp drops from mB to mB–mU, then rises again to mB as the Ub domain is progressively destabilized by mutation. ΔGappH2O fluctuates correspondingly. ΔGappH2O is therefore not a suitable parameter for gauging stability of BU (although it is appropriate in the case of free Bn and free Ub, which unfold in a two-state manner). We instead use Cm, as it exhibits a consistent and predictable dependence on stability of the Ub domain in all coupling regimes (Fig. 2D). Cm can also be determined with greater accuracy and precision than ΔGappH2O. Accordingly, we express the change in stability of mutants as ΔCm rather than ΔΔGappH2O.
Comparison with experimental results
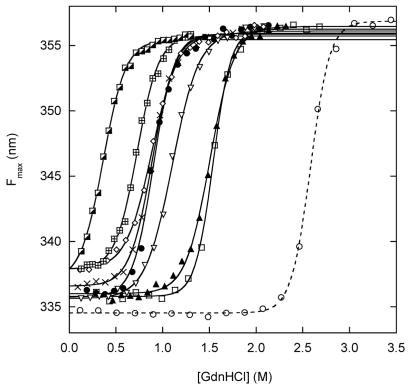
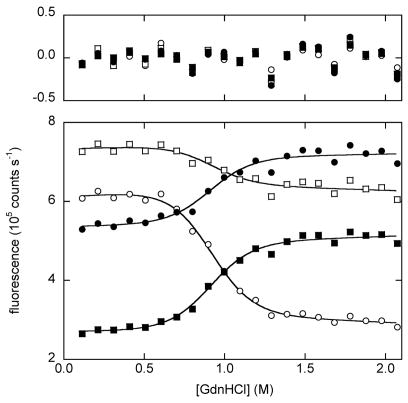
Figure 3 shows GdnHCl denaturation curves for BU and free Bn. The conformational state of the Bn domain is assessed by fluorescence spectra of the three Trp residues of BU, all of which are located in the Bn portion of the molecule. Folded Bn is identified by a maximum emission wavelength (Fmax) value near 336 nm. Plotting Fmax as a function of denaturant reveals a cooperative transition to a final value of 356 nm for unfolded Bn (Fig. 3A). Fmax is an effective means for ascertaining relative stabilities of BU variants from the primary data, but it is not ideal for obtaining thermodynamic parameters. For that purpose, we fit fluorescence intensities from the full Trp emission spectra. Multi-wavelength analysis is expected to provide better estimates of ΔGappH2O, mapp and Cm, as well as identify intermediates that may not be detected by the Fmax method. Each wavelength from 305–405 nm was fit to the two-state linear extrapolation equation 18 using the IGOR Pro software package (WaveMetrics, Inc.). ΔGappH2O and mapp values were linked and fluorescence intensities of native and unfolded states (as well as baseline slope parameters) were allowed to float independently. Satisfactory fits are obtained for all BU variants, and plotting the residuals finds no systematic deviation at any wavelength. Several representative wavelengths are shown in Fig. 3B. This result confirms that Bn unfolding is adequately described by a two-state transition by fluorescence, despite the possibility that multiple individual reactions may be present.
Figure 3.
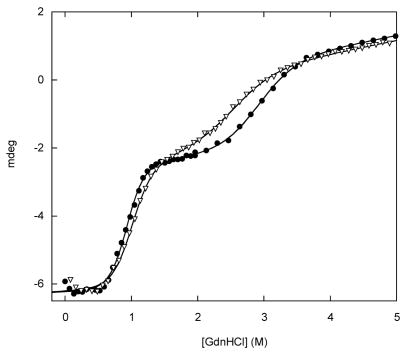
(A) GdnHCl-induced unfolding curves for BU variants, monitored by Trp fluorescence maximum. Fmax values were calculated using the DATAMAX software package (Jobin-Yvon/SPEX). Lines are best fits to the linear extrapolation equation. Symbols are as follows: filled black circles, WT; crosses, R42E; diamonds, K29Q; inverted triangles, K29N; filled triangles, V26A; squares, V26G; crosshatched squares, I96V; half-filled squares, I96A; open circles and dashed line, free WT Bn. (B) GdnHCl-induced unfolding of K29N BU monitored by fluorescence intensity at 320 nm (open circles), 340 nm (open squares), 360 nm (closed circles), 380 nm (closed squares). Lines are best fits to the linear extrapolation equation, as determined by multi-wavelength fits of Trp emission spectra from 305–405 nm. Curve-fit residuals are shown in the upper panel. (C) CD spectra of WT BU (solid line) and V26G BU (dashed line). (D) GdnHCl-induced unfolding of WT (closed circles) and K29N (inverted triangles) BU monitored by circular dichroism signal at 230 nm. Lines are best fit to the three-state linear extrapolation equation. Sample conditions are listed in Table 1.
To characterize unfolding of the entire BU molecule, we employed circular dichroism (CD) spectroscopy. CD spectra of WT and V26G BU are depicted in Fig. 3C. Ellipticity at 230 nm reveals two distinct transitions for WT BU (Fig. 3D). Fitting the data to a three-state unfolding mechanism yields ΔGappH2O = 3.7 kcal·mol−1, mapp = 4.3 kcal·mol−1·M−1, Cm = 0.87 M for the first transition. These values agree with those determined from fluorescence-monitored denaturation experiments (Fig. 3A and Table 1), thus; the first CD transition corresponds to the coupled Bn unfolding/Ub folding reaction. The second CD transition is assigned unambiguously to the bu ↔ bu equilibrium, as it occurs at GdnHCl concentrations beyond the midpoint of Bn domain unfolding. Fitting the second transition as above yields ΔGUH2O = 5.2 kcal·mol−1 and mU = 1.8 kcal·mol−1·M−1. By comparison, free WT Ub exhibits ΔGappH2O and mapp values of 6.9 kcal·mol−1 and 1.9 kcal·mol−1·M−1, respectively (Table 1). The presence of unfolded Bn fragments at both ends destabilizes Ub by 1.7 kcal·mol−1 and reduces Cm by 0.74 M.
Table 1.
Thermodynamic parameters for unfolding of free Ub, free Bn, and the Bn domain of BU. Bn and BU parameters are determined from multi-wavelength fits of fluorescence data. Ub parameters are obtained from fitting CD ellipticity at 230 nm. Sample conditions are 1–2 μM protein, 10 mM sodium acetate (pH 5.0), 0.1 M NaCl, 10 °C. Reported values are the averages of three measurements. Standard deviations are typically ± 0.2–0.4 kcal·mol−1 (ΔGappH2O), ± 0.1–0.3 kcal·mol−1·M−1 (mapp), ± 0.01–0.02 M (Cm).
| Protein | Variant | ΔGappH2O (kcal·mol−1) | mapp (kcal·mol−1·M−1) | Cm (M) |
|---|---|---|---|---|
| Ub | WT | 6.9 | 1.9 | 3.63 |
| Ub | R42E | 7.2 | 1.8 | 4.00 |
| Ub | K29Q | 6.7 | 1.8 | 3.72 |
| Ub | K29N | 5.7 | 1.9 | 3.00 |
| Ub | V26A | 4.4 | 2.1 | 2.10 |
| Ub | V26G | 1.8 | 2.5 | 0.72 |
|
| ||||
| Bn | WT | 11.8 | 4.6 | 2.58 |
| Bn | I96V | 8.9 | 3.8 | 2.38 |
| Bn | I96A | 8.7 | 4.5 | 1.96 |
|
| ||||
| BU | WT | 3.8 | 4.3 | 0.87 |
| BU | R42E | 3.7 | 4.2 | 0.87 |
| BU | K29Q | 3.6 | 4.0 | 0.90 |
| BU | K29N | 4.0 | 3.8 | 1.04 |
| BU | V26A | 7.3 | 4.6 | 1.57 |
| BU | V26G | 7.5 | 4.8 | 1.56 |
| BU | I96V | n.d.a | n.d. | 0.72b |
| BU | I96A | n.d. | n.d. | 0.35b |
Not determined due to insufficient native baseline.
Obtained from constrained fits of Fmax values (see text).
To test the mechanism of Eq. 1, we introduced stabilizing and destabilizing mutations into the Ub domain of BU and monitored unfolding of the Bn domain. The model holds that destabilizing Ub will stabilize Bn. This prediction is supported by the primary CD data. Figure 3D shows that the K29N mutation shifts Cm of the Bn and Ub unfolding transitions to higher and lower denaturant concentrations, respectively. This trend continues so that for V26A and V26G only a single transition is observed (data not shown). Moreover, multi-wavelength analysis of CD data is made largely ineffective by the absorptivity of GdnHCl, which blocks wavelengths below ~215 nm. For these reasons, we used fluorescence data exclusively to obtain thermodynamic parameters. As expected, insertion of Ub strongly destabilizes Bn. Cm of the Bn domain of WT BU is lower than that of free Bn by 1.7 M (Table 1). The stability of Ub variants follows the order R42E > WT > K29Q > K29N > V26A > V26G. Figure 3A and Table 1 show that Cm values of the Bn domain increase with the opposite rank order. The stability of the Bn domain is inversely proportional to the stability of the Ub domain, and the zero coupling condition (Fig. 2A) can be excluded.
We applied the following strategy to estimate ΔGX. The V26G mutation lowers the stability of free Ub to 1.8 kcal·mol−1 and its Cm to 0.72 M (Table 1). Figure 3D suggests that the presence of Bn will further decrease these values by approximately 1.7 kcal·mol−1 and 0.74 M, respectively. The Ub domain of V26G BU is therefore predicted to be intrinsically unstable in the absence of denaturant. Consequently, the observed unfolding transition of V26G BU should closely approximate bu ↔ bu. ΔGBH2O and mB can thus be assigned to the ΔGappH2O (7.5 kcal·mol−1) and mapp (4.8 kcal·mol−1·M−1) values measured for V26G BU. Bn appears to be destabilized by 4.3 kcal·mol−1 by the presence of unfolded Ub (Table 1). This value is considerably greater than the amount that Ub is destabilized by unfolded Bn (1.7 kcal·mol−1). The result is expected because in the former case, Bn folding requires closing of a lengthy, unstructured surface loop. The decrease in entropy associated with loop closure can be approximated by Eq. 8:
| (8) |
where a is related to the distance between ends of the closed loop (−2 to −8 cal·mol−1·K−1) and N is the number of amino acids in the loop 8; 19. The observed decrease in ΔGappH2O falls within the range of TΔS values defined by Eq. 8.
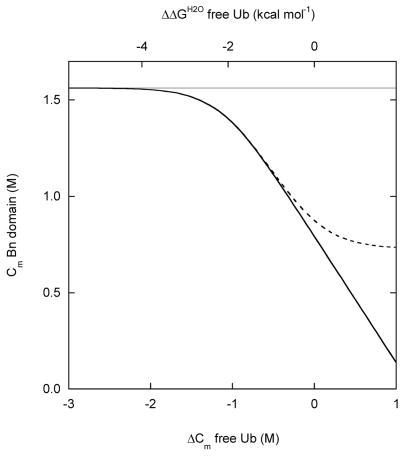
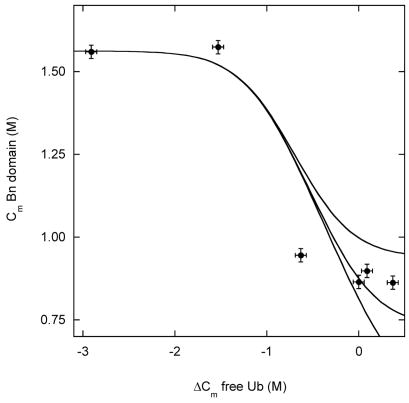
We then plotted experimental Cm values of the Bn domain against the change in stability of the Ub domain, expressed as ΔCm (Fig. 4A). The latter quantity was determined by separate experiments on the same mutants in free Ub (Table 1). ΔGUH2O (5.2 kcal·mol−1) and mU (1.8 kcal·mol−1·M−1) were obtained from Fig. 3D as described. ΔGX was then adjusted manually, and theoretical Cm values were calculated from simulated BU unfolding curves such as those in Fig. 2. The lines in Fig. 4A are the results of simulations using ΔGX values of 3, 4 and 5 kcal·mol−1.
Figure 4.
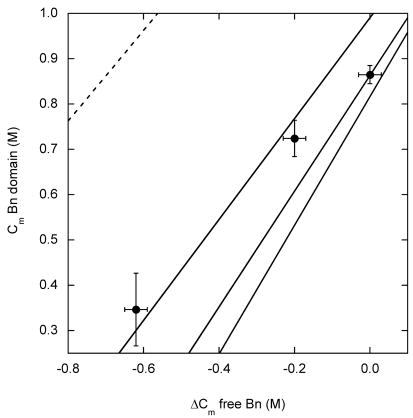
(A) Stability of the Bn domain of BU, reported by Cm values, as a function of the change in stability of free Ub, determined by ΔCm values. ΔCm is relative to free WT Ub. Circles represent the following variants, from left to right: V26G, V26A, K29N, K29Q, WT, R42E. Lines are simulated results using ΔGX values of 3 kcal·mol−1, 4 kcal·mol−1 and 5 kcal·mol−1(from upper to lower curves); see text for other parameters. (B) Stability of the Bn domain of BU as a function of the stability of free Bn. ΔCm is relative to free WT Bn. Data points are, from left to right: I96A, I96V, WT. Solid lines are simulated results for ΔGX values of 3 kcal·mol−1, 4 kcal·mol−1 and 5 kcal·mol−1 (from left to right). Dashed line is the simulated result for ΔGX = 0.
A reasonable fit is obtained with ΔGX ~ 4.0 kcal·mol−1 (Fig. 4A). All values of ΔGX shown in the figure are able to reproduce the behavior of the most unstable Ub variants. To determine ΔGX more accurately, it is necessary to extend the data set to the regime where Ub is stabilized relative to WT. Unfortunately, few such variants have been reported. The R42E mutation stabilizes WT Ub by 1.6 kcal·mol−1 when measured by urea denaturation 16. GdnHCl appears to screen the favorable effect of charge reversal, however, and R42E Ub is only 0.3 kcal·mol−1 more stable than WT in our experiments (Table 1). An alternate approach is to measure the extent to which mutations destabilize the Bn domain of BU relative to free Bn. We introduced the I96V and I96A mutations into BU and free Bn and repeated the analysis of Fig. 4A. Because native baselines are not well defined for these unstable mutants, ΔGappH2O and mapp values could not be determined confidently by the procedure used for the other mutants. Cm values, however, could be obtained reasonably accurately by fitting Fmax data while constraining the native Fmax to the average value of the other variants (337 nm) (Fig. 3A). The results (Fig. 4B) confirm that a ΔGX value of 3–4 kcal·mol−1 fits the data adequately.
In our earlier paper we concluded that Bn and Ub domain folding are mutually exclusive in WT BU 2. That deduction was drawn from variable temperature CD experiments. As temperature increased from 5–50 °C, a cooperative positive shift in the 230 nm peak was observed, signifying Bn unfolding (the 230 nm minimum arises from Trp94 of Bn and is diagnostic of folded Bn structure 20). The 208 nm peak showed a corresponding negative change and an isodichroic point was noted at 223 nm. Since the molar ellipticity of Ub at 208 nm is more negative than that of Bn, those findings argue that the Ub domain is unfolded at temperatures below 30 °C, and that it folds as Bn is denatured by heat or GdnHCl. The current results, however, place ΔGX is in the intermediate range which implies that folding is not fully exclusive. For example, ΔGX values of 3–5 kcal·mol−1 predict that 98-58 % of the WT protein exists in conformation bu in the absence of denaturant. Which view is correct?
As a first test we compared CD spectra of WT and V26G BU (Fig. 3C). If Bn folding causes Ub to unfold completely, then the two spectra should be identical. The region below 200 nm is particularly diagnostic of unfolded structure. The ellipticity of V26G is markedly lower at those wavelengths, indicating a greater amount of random coil conformation. The more positive signal observed above 205 nm is also consistent with a lower α-helix and/or β-sheet content in V26G. We attempted to estimate secondary structure content using the SELCON3 21 and CONTIN/LL 22; 23 programs. Both methods agree that V26G contains a greater percentage of unfolded structure compared to WT (7–15 % increase, using the SDP42 reference protein set). This figure should be considered as only a rough estimate, as agreement between experimental and theoretical data is poor above ~205 nm (presumably due to the anomalous minimum at 230 nm arising from Trp94). Nevertheless, CD results suggest that the Ub domain is folded in a fraction of WT BU molecules.
A second test is provided by mapp values. The model holds that mapp of BU variants with unstable Ub domains (e.g. V26G) should be similar to mapp of free Bn. That result is indeed found (Table 1). If Bn and Ub folding are completely exclusive in WT BU, then mapp is expected to decrease by the full value of 1.8 kcal·mol−1·M−1 observed for free Ub. mapp of WT BU is smaller than that of V26G, but only by 0.5 kcal·mol−1·M−1. Thus, CD and thermodynamic data together suggest that both domains are folded in a measurable percentage of WT BU molecules. Denaturing the Bn domain by GdnHCl or temperature appears to allow the fraction of unfolded Ub domains to refold, which forms the basis of our earlier conclusion.
We now turn the discussion to limitations of the model. Although it reproduces the important trends in the experimental data, it does not capture some details. The dependence of Cm on Ub stability appears to be steeper and more cooperative than the model predicts (Fig. 4A). In addition, while Bn mapp values exhibit the expected dependence on Ub stability (a decrease then an increase as the Ub domain is progressively destabilized), the experimental figures exceed theoretical values by 0.2–0.4 kcal·mol−1·M−1 for most mutants. One reason may be that the four-state model neglects the possibility of the two domains associating in their folded states. Additional molecular surface could be buried as a result of such an interaction. A related assumption is that the individual domains unfold in a two-state manner, i.e., that the unfolded states produced by mechanical disruption and by GdnHCl denaturation are structurally and energetically equivalent. This is most likely not the case, as pointed out earlier. The unfolded conformations of the Ub domain in bu (populated in the absence of GdnHCl) and bu (present in high GdnHCl concentrations) are different, if for no other reason than the termini of Ub are constrained in the former. There may also be a significant amount of residual structure present in mechanically disrupted Ub. These issues can be addressed by incorporating additional states into the folding model. Such a mechanism would contain too many parameters to be characterized by the present data set. It may be possible, however, to test it using higher resolution structural techniques such as nuclear magnetic resonance studies of BU variants in different concentrations of denaturant.
In conclusion, we have established a thermodynamic framework for analyzing the coupled folding-unfolding equilibrium of the new class of bi-functional molecules exemplified by BU and barnase-GCN4. The coupling free energy of ~ 4 kcal·mol−1 is less than or comparable to ΔGBH2O and ΔGUH2O values of most mutants, suggesting that coupling is in the intermediate regime. Surprisingly, the model predicts that both domains are folded in a significant fraction of WT BU molecules. We propose that shortening the linker peptides from their current lengths of two and three amino acids will intensify the strain that the folded structures of Bn and Ub impose on each other, and thus increase ΔGX. We are currently testing that hypothesis by experimental and computational studies of BU variants with progressively shortened linkers.
Acknowledgments
We thank Drs. James S. Butler and Jeung-Hoi Ha for discussions. This work was supported by N.I.H. Grant R01GM069755.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Jones S, Stewart M, Michie A, Swindells MB, Orengo C, Thornton JM. Domain assignment for protein structures using a consensus approach: characterization and analysis. Protein Sci. 1998;7:233–242. doi: 10.1002/pro.5560070202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Radley TL, Markowska AI, Bettinger BT, Ha JH, Loh SN. Allosteric switching by mutually exclusive folding of protein domains. J Mol Biol. 2003;332:529–536. doi: 10.1016/s0022-2836(03)00925-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ha JH, Butler JS, Mitrea DM, Loh SN. Modular enzyme design: regulation by mutually exclusive protein folding. J Mol Biol. 2006;357:1058–1062. doi: 10.1016/j.jmb.2006.01.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brandts JF, Hu CQ, Lin LN, Mas MT. A simple model for proteins with interacting domains. Applications to scanning calorimetry data. Biochemistry. 1989;28:8588–8596. doi: 10.1021/bi00447a048. [DOI] [PubMed] [Google Scholar]
- 5.Holm L, Sander C. The FSSP database of structurally aligned protein fold families. Nucleic Acids Res. 1994;22:3600–3609. [PMC free article] [PubMed] [Google Scholar]
- 6.Ferraro DM, Hope EK, Robertson AD. Site-specific reflex response of ubiquitin to loop insertions. J Mol Biol. 2005;352:575–584. doi: 10.1016/j.jmb.2005.07.012. [DOI] [PubMed] [Google Scholar]
- 7.Ferraro DM, Ferraro DJ, Ramaswamy S, Robertson AD. Structures of ubiquitin insertion mutants support site-specific reflex response to insertions hypothesis. J Mol Biol. 2006;359:390–402. doi: 10.1016/j.jmb.2006.03.047. [DOI] [PubMed] [Google Scholar]
- 8.Scalley-Kim M, Minard P, Baker D. Low free energy cost of very long loop insertions in proteins. Protein Sci. 2003;12:197–206. doi: 10.1110/ps.0232003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ladurner AG, Fersht AR. Glutamine, alanine or glycine repeats inserted into the loop of a protein have minimal effects on stability and folding rates. J Mol Biol. 1997;273:330–337. doi: 10.1006/jmbi.1997.1304. [DOI] [PubMed] [Google Scholar]
- 10.Nagi AD, Regan L. An inverse correlation between loop length and stability in a four-helix-bundle protein. Folding Design. 1997;20:67–75. doi: 10.1016/S1359-0278(97)00007-2. [DOI] [PubMed] [Google Scholar]
- 11.Doi N, Itaya M, Yomo T, Tokura S, Yanagawa H. Insertion of foreign random sequences of 120 amino acid residues into an active enzyme. FEBS Lett. 1997;402:177–180. doi: 10.1016/s0014-5793(96)01522-0. [DOI] [PubMed] [Google Scholar]
- 12.Collinet B, Hervé M, Pecorari F, Minard P, Eder O, Desmadril M. Functionally accepted insertions of proteins within protein domains. J Biol Chem. 2000;275:17428–17433. doi: 10.1074/jbc.M000666200. [DOI] [PubMed] [Google Scholar]
- 13.Betton JM, Jacob JP, Hofnung M, Broome-Smith JK. Creating a bifunctional protein by insertion of β-lactamase into the maltodextrin-binding protein. Nature Biotechnol. 1997;15:1276–1279. doi: 10.1038/nbt1197-1276. [DOI] [PubMed] [Google Scholar]
- 14.Ostermeier M. Engineering allosteric protein switches by domain insertion. Protein Eng Des Sel. 2005;18:359–364. doi: 10.1093/protein/gzi048. [DOI] [PubMed] [Google Scholar]
- 15.Khorasanizadeh S, Peters ID, Roder H. Evidence for a three-state model of protein folding from kinetic analysis of ubiquitin variants with altered core residues. Nature Struct Biol. 1996;3:193–205. doi: 10.1038/nsb0296-193. [DOI] [PubMed] [Google Scholar]
- 16.Loladze VV, Ibarra-Molero B, Sanchez-Ruiz JM, Makhatadze GI. Engineering a thermostable protein via optimization of charge-charge interactions on a protein surface. Biochemistry. 1999;38 doi: 10.1021/bi992271w. [DOI] [PubMed] [Google Scholar]
- 17.Kellis JT, Nyberg K, Fersht AR. Energetics of complementary side-chain packing in a protein hydrophobic core. Biochemistry. 1989;28:4914–4922. doi: 10.1021/bi00437a058. [DOI] [PubMed] [Google Scholar]
- 18.Santoro MM, Bolen DW. Unfolding free energy changes determined by the linear extrapolation method. 1 Unfolding of phenylmethanesulfonyl alpha chymotrypsin using different denaturants. Biochemistry. 1988;27:8063–8068. doi: 10.1021/bi00421a014. [DOI] [PubMed] [Google Scholar]
- 19.Chan HS, Dill KA. Intrachain loops in polymers. J Chem Phys. 1988;90:492–509. [Google Scholar]
- 20.Vuilleumier S, Sancho J, Loewenthal R, Fersht AR. Circular dichroism studies of barnase and its mutants: characterization of the contribution of aromatic side chains. Biochemistry. 1993;32:10303–10313. doi: 10.1021/bi00090a005. [DOI] [PubMed] [Google Scholar]
- 21.Sreerama N, Woody RW. A self-consistent method for the analysis of protein secondary structure from circular dichroism. Anal Biochem. 1993;209:32–44. doi: 10.1006/abio.1993.1079. [DOI] [PubMed] [Google Scholar]
- 22.Sreerama N, Woody RW. Estimation of protein secondary structure from circular dichroism spectra: comparison of CONTIN, SELCON, and CDSTTR methods with an expanded reference set. Anal Biochem. 2000;287:252–260. doi: 10.1006/abio.2000.4880. [DOI] [PubMed] [Google Scholar]
- 23.Provencerh SW, Glockner J. Estimation of globular protein secondary structure from circular dichroism. Biochemistry. 1981;30:33–37. doi: 10.1021/bi00504a006. [DOI] [PubMed] [Google Scholar]