The function of inter segmental connections in determining temporal characteristics of the spinal cord rhythmic output

Abstract

Recent renewed interest in the study of rhythmic behaviors and pattern-generating circuits has been inspired by the currently well-established role of oscillating neuronal networks in all aspects of the function of our nervous system: from sensory integration to central processing, and of course motor control. An integrative rather than reductionist approach in the study of pattern-generating circuits is in accordance with current developments. The lamprey spinal cord, a relatively simple and much studied preparation, is a useful model for such a study. It is an example of a chain of coupled oscillatory units that is characterized by its ability to demonstrate robust coordinated rhythmic output when isolated in vitro. The preparation allows maximum control over the chemical (neuromodulators and hormones) as well as neuronal environment (sensory and descending inputs) of the single oscillatory unit - the pattern-generating circuit. The current study made use of recently developed tools for nonlinear analysis of time-series, specifically neurophysiological signals. These tools allow us to reveal and characterize biological-functional complexity and information capacity of the neuronal output recorded from the lamprey model network. We focused on the importance of different types of inputs to an oscillatory network and their effect on the network's functional output. We show that the basic circuit, when isolated from short and long-range neuronal inputs, demonstrates its full potential of information capacity: maximal variation quantities and elevated functional complexity. Morphological and functional constraints result in the network exhibiting only a limited range of the above. This constitutes an important substrate for plasticity in neuronal network function.

Introduction

Central pattern generating circuits (CPG) constitute a unique type of neuronal network characterized by the ability to generate rhythmic motor patterns in the absence of timing cues from sensory or extrinsic inputs (Marder and Bucher, 2001; Kiehn, 2006). There has been a resurgence of interest in CPG with the growing recognition that rhythmic activity patterns are widespread in the brain and play an important role in all aspects of the function of our nervous system, from sensory integration to central processing and motor control (Laughlin and Sejnowski, 2003; Buzsaki and Draguhn, 2004; Sejnowski and Paulsen, 2006; Kahana, 2006). Yuste et al. (2005) have recently suggested profound similarities between simple pattern generating networks and other circuits, namely neocortical networks. These similarities reflect basic organization or rules common to circuits that generate robust and spatially patterned rhythmic activity on different timescales.

The lamprey spinal cord, a relatively simple and much studied preparation, is a useful model for the study of oscillatory circuits and specifically CPG. The lamprey, a representative of a group of early vertebrata, swims using undulatory movements of its eel-like body. These movements are generated and coordinated by oscillatory neural networks repeated along the approximately 100 spinal cord segments (Cohen and Wallen, 1980; Sigvardt, 1989; Grillner et al., 1998). The lamprey locomotor pattern is activated by descending inputs from reticulospinal neurons in the brainstem. However, in an isolated piece of spinal cord the same basic pattern can be activated by bath application of excitatory amino acids such as D-glutamate (Poon, 1980; Wallen and Williams, 1984). The intact spinal cord can be isolated and kept in oxygenated Ringer solution in vitro for days and its activity can be monitored by extracellular recording from spinal ventral roots (Rovainen, 1979).

Much effort has been focused on the neural circuitry of the oscillatory mechanism in lampreys (Grillner, 2003). The acquired information has been incorporated into various CPG models of varying complexity. However, these occasionally fail to reproduce experimental results beyond those used during the models' development (Parker, 2006). This may at least partly be due to inadequate emphasis on the functional role of circuit interconnections and on inputs to the CPG network. The anatomy of the system supports the presence of both short as well as long-distance inter segmental connections (Rovainen, 1983; Buchanan and Kasicki, 1999, and references within). The vast majority of research into these connections was aimed at elucidating their role in determining and controlling the inter segmental phase lags appropriate for forward swimming (Cohen, 1987; Williams et al., 1990; Williams, 1992; Cohen and Kiemel, 1993; Miller and Sigvardt, 2000). However, the functional coupling that determines phase appears to extend over a much more limited range than the full projection range of 30–50 segments reported for some interneurons (Rovainen, 1974; Cohen, 1987; Williams et al., 1990; Williams, 1992; Cohen and Kiemel, 1993; Miller and Sigvardt, 2000). Thus, it has been suggested that the interneurons that comprise a segmental oscillator act not only to generate the local rhythm but also project to, and influence, rhythm generation in other nearby or distant segments (see Hill et al., 2003, and references within). These effects can in turn take part in shaping the distinct temporal characteristics of the networks' motor output - the information sent to and read by the muscles, resulting in the animal's behavior.

Buchanan and Cohen (Buchanan and Cohen, 1982) and others have demonstrated that lamprey slow muscle fibers respond to the precise temporal structure of the motor output (Fig. 1; Buchanan and Cohen, unpublished results). In the lack of a detailed study of the dynamic properties of the lamprey swim muscles, we can only speculate on the behavioral significance of the rhythmic bursts' temporal characteristics or their information capacity.

Figure 1.

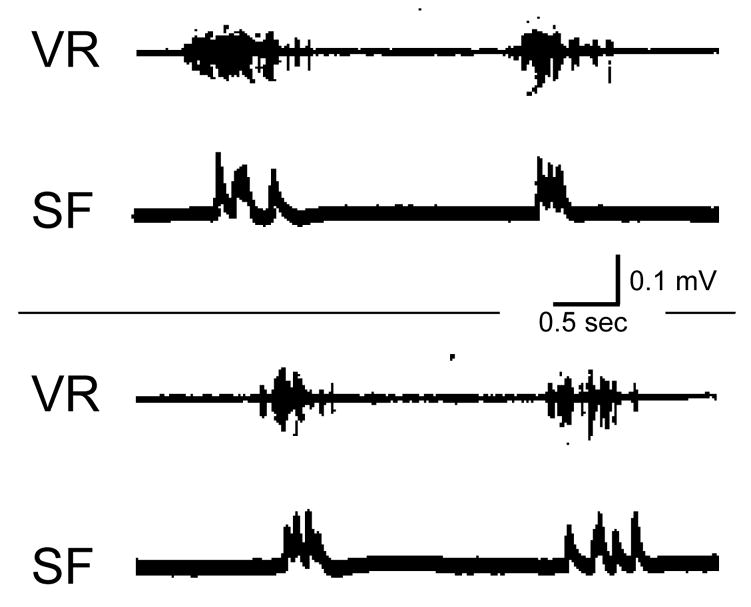
Two examples of an extracellular recording from a lamprey spinal cord ventral nerve root and a simultaneous recording of slow muscle fibers junction potentials reveal the strong dependence of the muscle response on the distinct temporal pattern of the burst of activity in the nerve.

The current study was aimed at investigating fundamental principles in circuit dynamics, namely the functional role of oscillator coupling and neuronal inputs to a pattern generating network. We took advantage of the well-established lamprey model system, and recently developed analysis tools, including clustering algorithms and functional biological complexity analysis (Hulata et al., 2004; Segev et al., 2004). We investigated temporal motifs seen in the CPG output and constructed tests to extract the maximal information on the sequence temporal ordering. Our results shed light on the neural mechanisms underlying behavior in this motor system and potentially also on oscillatory and rhythmic pattern generating systems in general.

Experimental Procedures

Animals and in vitro preparation

Adult lampreys, Ichthyomyzon unicuspis, were obtained from a commercial supplier and kept in tanks at 5°C. Experimental animals were anesthetized by immersion in a buffered solution of 0.18g/L MS222. After inhibition of all reflex and breathing was ensured, animals were decapitated and transferred to a chilled surgical dish. Next, animals were eviscerated, their skin and muscle removed from around the spinal cord, and the membranes overlying the spinal cord were removed. In all experiments 50 of the roughly 100 total spinal cord segments were exposed, retaining the support of the notocord, which was split and pinned down.

Electrophysiology

The nerves that exit the spinal cord along the notochord were cleared for recording. In lamprey, the muscles and sensory nerves are separate at this point, so one can record from the muscle nerve alone using a loosely fit suction electrode. D-glutamate was added to the saline bath to induce fictive swimming motor output (Poon, 1980); Cohen and Wallen, 1980). Analog voltage was sampled at 5 kHz using a 4-channel differential amplifier (Model 1700, A-M Systems, USA) and stored on the computer in real time using an A-D board (National Instruments) and VI-Logger software (National Instruments, USA).

Data Analyses

Initial event detection was carried out using threshold recognition (DataView; W. Heitler, Univ. St. Andrews, UK). All recorded signals were transformed into ordinary binary time sequences whose “1”s mark detected action potentials (spike sequences). Next, we evaluated for each such time sequence of spikes its corresponding sequence of neuronal bursting events (bursts of action potentials). The bursts' time positions and time widths were evaluated (burst sequences).

Burst classification and correlation analysis

This method followed in general that reported by Segev et al. (2004). In short, for each recorded sequence, a time window T was selected that included each of the N bursts of action potentials. This time window (constant for all bursts) was divided into time bins of 2 msec. A matrix A of N rows (analyzed bursts) and T/2 columns (time bins) was composed. Each row represents the activity of all the neurons firing throughout the burst. In most cases (if not stated otherwise) N = 200 randomly selected bursts were analyzed. We defined A_i,j =1 if an action potential was fired in the i-th burst during the j-th time bin, and zero otherwise. In order to obtain a smooth representation of the burst activity profile the activity vectors were then convolved with a normalized Gaussian. Next, the cross-correlation between the n-th and the m-th convoluted bursts (n,m =1,2…N) was computed using a standard algorithm under a MatLab environment (The MathWorks Inc. USA). We then found the maximum value of the cross-correlation to obtain R(n,m), the time invariant correlation between the two bursts . For visualization, a color code was assigned to R(n,m) according to the Jet color map, where blue represents the lowest correlation and dark red the highest (The MathWorks Inc. USA). In the final color cross-correlation matrices, by definition, R(n,m)= R(m,n) and R(n,n)=R(m,m)=1.

We then reordered each recorded sequence so that bursts with higher correlations were closely positioned; namely, we applied a hierarchical clustering algorithm (dendrogram) to identify clear groups in the matrix. Block partitioning in the matrix indicates non-random variation, i.e. that a recorded burst sequence is composed of subgroups of distinct bursts with mixed temporal order of appearance. In order to determine whether bursts that belong to one group or in a specific experimental condition differ from others, we applied a similar cross correlation procedure to all bursts from different groups and conditions.

Representation in the time-frequency domain, best tiling and complexity

Neuronal information is expected to be encoded both in activity rates and in their relative temporal location. Signals of complex temporal nature, characterized by large local and global temporal variations, demonstrate large frequency variations at each temporal location when looking at time windows of different widths. These local variations also vary from one time to another place to place along the sequence. Hence a proper method of characterizing and quantifying signal dynamics would be to use the sequence representation in a time-frequency plane.

The algorithm used for analyzing signal complexity was fully described by Hulata et al. (2004). We first transformed each sequence of events into a representation in its corresponding time-frequency domain. Utilizing the wavelet packet decomposition (MatLab, The MathWorks Inc. USA), the domain was tiled (partitioned) into N rectangles, each with its own height Δf and width Δt representing the relative “energy” (q_n) of the frequency range f in the time window Δt. Each tiling (a combination of non-overlapping rectangles covering the time-frequency domain) served to represent the recorded sequence. We used the Thiele-Villemoes algorithm (Thiele and Villemoes, 1996) to construct the best tiling: that which extracts maximal information about the sequence temporal ordering (the tiling that maximizes the global information measure M ≡ − Σq_n Log q_n).

The structural complexity of a sequence is associated with the plane local (intra segment) and global (inter segment) variability. We began by segmenting the sequence into words and quantifying the amount of variation factor (VF) within each word l to be:

$${VF}_l=(\frac{N_E(l)-\overline{N_E}}{\overline{N_E}})\frac{{\sum }_{n,m}\mid R_n-R_m\mid \cdot \mathrm{\Theta }(q_n\cdot q_m)}{{\sum }_{n,m}\mathrm{\Theta }(q_n\cdot q_m)}$$

where the sum is over all neighboring rectangles n,m. NE(l)is the number of events detected within the l -th word, and $\overline{N_E}$ is an average over different words of the same length as the l -th one. Θ(x) , is the heavy-tail function; Θ(0) and Θ(x≠0) = 1. The global variability was then quantified using the variance of the variation factors between the sequence words. For a sequence segmented into N_w words, we will thus define the observable structural complexity (SC) as:

$$SC\equiv var(VF)\equiv \frac{1}{N_w}\sum _{l=1}^{N_w}{(V{F}_l-\overline{VF})}^2$$

The above was conducted for the time sequence of action potentials within bursts as well as for the sequence of burst events.

Experimental procedures: differentially manipulating inputs to an oscillatory unit

The presentes results are based on overall 16 different preparations (animals). It was not possible however to go through all the experimental procedures described below with each preparation. Thus, each experimental group (different manipulation) comprised of 4-7 independent repetitions (Fig 2). The experimental bath was divided into three chambers (Rostral, Medial and Caudal; 15, 20 and 15 segments respectively; Fig 2) by carefully sealed Vaseline partitions. The activity of a selected range of adjacent segments within one chamber was silenced by bathing the segments in a D-glutamate-free, low calcium solution. This procedure inhibited all oscillatory activity in, and consequently all output originating from, the selected segments (in practically all cases the blocked region showed no spiking activity whatsoever). Thus spinal cord segments in the neighboring or distal chambers were deprived of short-range or long-range inputs respectively. Such blocking of the medial region of the spinal cord did allow long-range connections between the rostral and caudal chambers.

Figure 2.

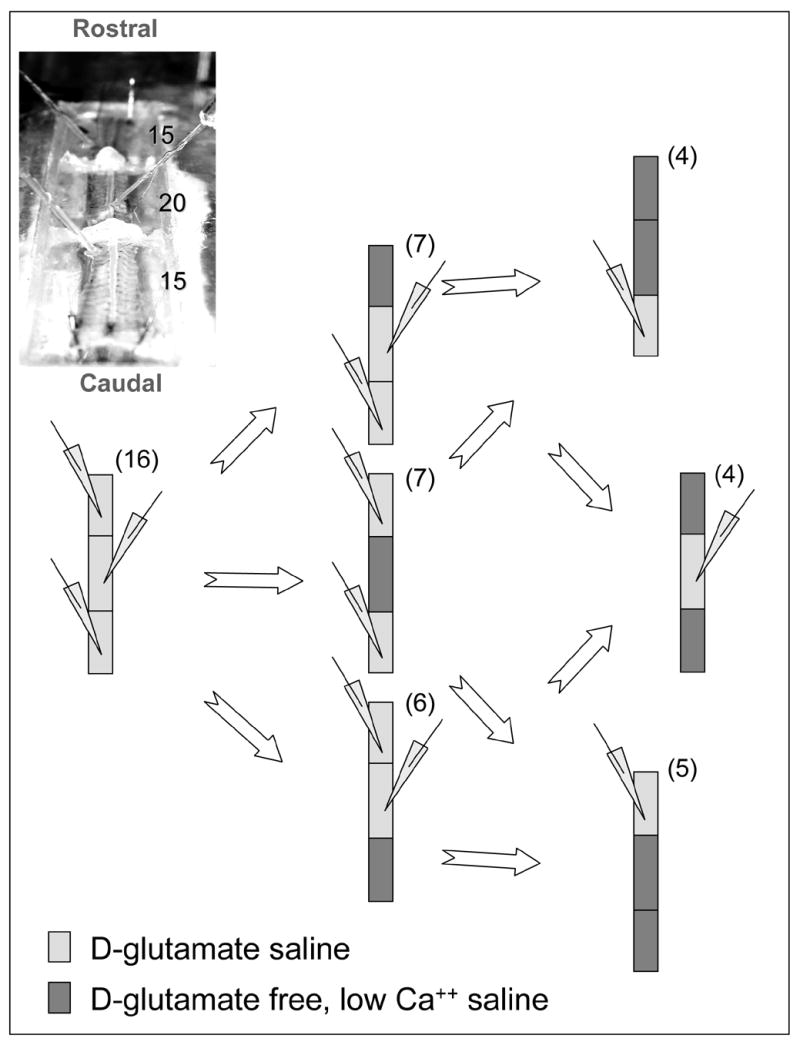
The experimental preparation was composed of 50 spinal cord segments divided into three chambers as shown (top left, number of segments indicated). Loosely fit suction electrodes were used to record the D-glutamate-induced fictive swimming motor pattern from the ventral nerve roots in the three locations along the preparation. The different experimental manipulations are shown; blocking activity in selected chambers and testing for the effects of depriving short-range or long-range inputs to a selected range of segments whose activity was monitored. (1 mM D-Glutamate, or Glutamate free, low Ca2+ saline were used to induce or block activity respectively)

The above described analysis methods were used to characterize the neuronal output of the spinal chord oscillatory network, first under control conditions with all chambers in the same D-glutamate solution. Next, activity in one or more of the chambers was blocked according to one or several of the routes in figure 2 and the same analysis was applied. Thus we conducted a comparative study of the role of the different inputs in shaping the temporal characteristics of the motor output of spinal cord pattern generating circuits and their information capacity.

Further data for analysis were kindly supplied by Dr. Guan Li. These comprised recordings from a selected range of distal segments in similar preparations as above, under control conditions and also after long-range inputs had been differentially omitted by applying two hemisections halfway down the length of the spinal cord: first on one side, and then on the other, five segments apart (described in (Kiemel et al., 2003). Practically no long-range fibers transverse the five segments separating the two hemisections (Rovainen, 1983, Kiemel et al., 2003).

Results

Figure 3 shows a typical simultaneous spinal cord ventral root recording at three locations along the spinal cord (each at one of the three experimental chambers, left or right sides and segment number are indicated). This figure also shows the accepted statistics used to characterize rhythmic patterns including cycle period, burst duration and inter-burst intervals.

Figure 3.

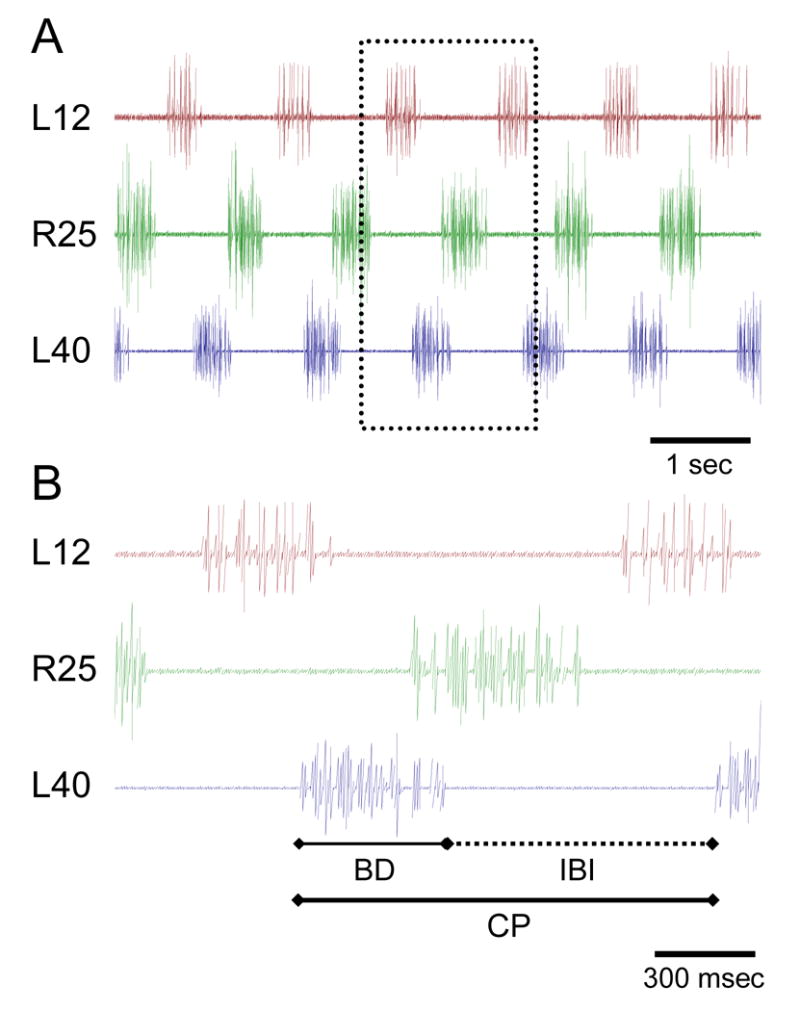
An example of a simultaneous recording of ventral nerve roots as shown in figure 2. A. A robust fictive swimming motor pattern is shown with both left-right alternation and consistent phase lag from head to tail. L- Left or R- right side of the body and the position of the recording are noted (segment number out of a total of 50, 0 being the most rostral). The segments in the isolated spinal cord preparation are numbered 1–50 from rostral to caudal. B. Commonly used statistical parameters are noted on a short time window shown in higher time resolution. CP, cycle period; BD, burst duration; IBI, inter-burst interval.

The basic and most consistent result demonstrated in all the different experimental protocols described in figure 2 was that of increased variation in the temporal parameters of the rhythm with the elimination of rhythmic inputs (short range and/or long range) to any spinal cord region. This was clear in all preparations when comparing either burst duration, cycle period, or inter-burst intervals (n=16 different preparations, 4–7 in each experimental group). For example, the average cycle period calculated for the rhythmic bursting activity recorded from a distal region of the spinal cord (rostral or caudal) under control conditions (1 mM D-Glutamate) was 1.61±0.47 sec. Blocking the middle and opposite distal regions of the cord and thus practically all inputs to the recorded segments resulted in a general slowing: i.e. the cycle period increased to 2.66±1.46 sec (n = 7). This represents a 1.7-fold increase in cycle period, while comparing the average coefficient of variation calculated for the above two conditions yielded a four-fold increase in variation (0.11 vs. 0.44 for the control and “all inputs blocked” conditions respectively). Similarly, the corresponding burst durations changed from 0.55±0.20 sec in control to 0.83±0.50 sec in the fully blocked preparation (both short and long-range inputs blocked) while the average coefficient of variation was again more than tripled (from 0.22 to 0.71 respectively).

Not all kinds of manipulations, however, resulted in such dramatic effects. Blocking only long-range inputs to a distal region, for example, usually resulted in no significant change in burst duration and only a minor effect on cycle period. Similarly, when monitoring the middle segments, blocking the first neighboring (distal) region had practically no effect on burst duration and only a minor effect on cycle period. However, changes in the above statistics, or lack thereof, may not fully reflect the functional consequences of blocking inputs. Thus we went on to investigate changes in the information capacity of the recorded time sequences, e.g. the within-burst temporal structure, when we differentially blocked short and long range, descending or ascending inputs.

Figure 4 shows a typical example of an experiment in which the rostral segments of the spinal cord were monitored (recordings made 10 segments from the rostral end of the preparation) while eliminating first the long range, and then also the short-range inputs to the recorded region. The dendrograms shown in figure 4A are the results of hierarchical clustering analysis based on cross correlation of 200 randomly selected bursts out of the 1000–1500 bursts recorded for each experimental condition. As can be seen, already after blocking activity in the distal chamber (thus eliminating long-range inputs) the rather uniform temporal structure of the control bursts changed to reveal heterogeneity and some partitioning. This was in spite of the fact that the frequency of the recorded rhythmic activity (Fig 4B), as well as the burst duration in this example, were practically unchanged.

Figure 4.

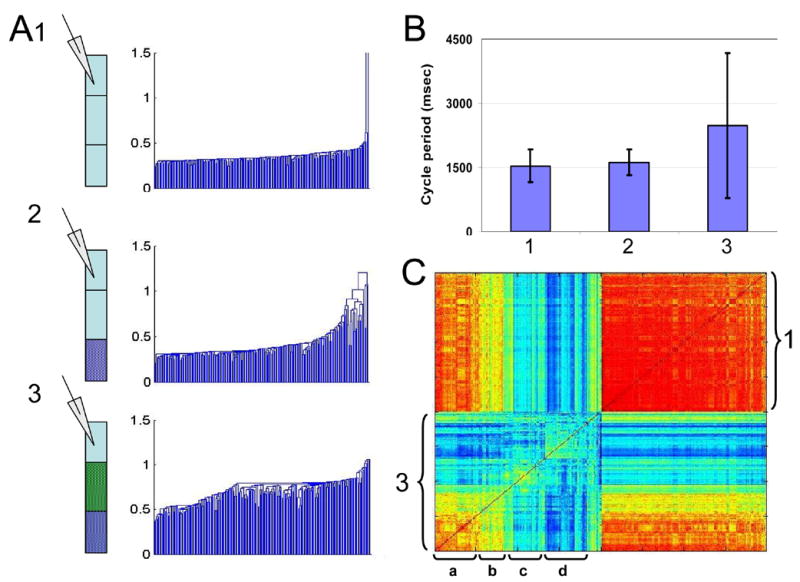
A1-3. Three examples of the results of a hierarchical clustering algorithm (dendrogram) applied to the outcome of the inter-burst cross-correlation analyses of 200 randomly selected bursts recorded from a single preparation in each of the different, illustrated, experimental conditions. The dendrograms clearly demonstrate the change from the rather homogenous highly correlated activity in control (top, low and uniform branch length) to the more variable and partitioned picture induced by blocking inputs. The effect is clear already after blocking long-range inputs (A2) although this can not be seen by comparing a traditional descriptive of rhythmic activity such as cycle periods (B, numbers correspond to experimental conditions as in A). C. The reordered cross-correlation matrices based on the clustering analysis conducted for conditions 1 and 3 (indicated) were subjected to a second round of analysis showing the correlation between the bursts recorded under the two conditions. As can be seen, out of the emerged subgroups or types of bursts in condition 3 some show rather high or medium similarity of temporal structure to the control bursts (indicated by a and b respectively, yellow to cyan colors in the between-conditions correlation area). Other bursts seem to be completely new types (indicated by c, dark bluish color in the cross correlation matrix).

The large assembled cross-correlation matrix shown in figure 4C is a combined sorted matrix of the bursts under control and under the fully-blocked conditions (based on the dendrograms shown in 4A1 and 3). As indicated by the rather uniform shades of red, the correlation or similarity of the control bursts to each other is high (top right, marked 1). Blocking both types of inputs to the recorded region resulted in a general decrease in similarity, as is evident by the appearance of bluish shades in the cross-correlation matrix (bottom left, marked 3). The introduced variation, which in this case was also reflected in cycle period (Fig 4B), is not random however, as distinct clusters or types of bursts are clearly seen. The temporal structures of some of these bursts were somewhat similar to the control bursts (indicated by 'a' in Fig 4C). Other bursts were less similar to control (indicated by 'b'), while others still were completely new types of bursts (indicated by 'c' and 'd' in Fig 4C). For further clarity, we show in figure 5 raw data from a similar experiment. A change in the temporal pattern of activity as inputs are blocked is clear though more difficult to fully appreciate without analysis.

Figure 5.

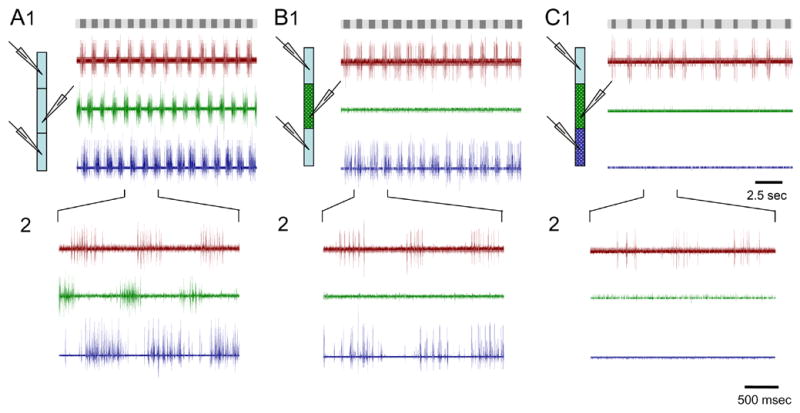
A second example of the results of the experimental manipulation used for the data presented in figure 4. Simultaneous recording of the ventral nerve roots on the left side of segment 11, the right side of segment 21 and the left side of segment 30 in a 40 segments preparation. Control conditions are shown in A. B and C show the effects of blocking first short-range, and then also long-range inputs to the continuously monitored rostral segments. Grey bars on top indicate the time and duration of the rostral bursts of action potentials (dark) in the different conditions demonstrating the increase in variation from A through B to C. The lower panels (2) show a 2.5 sec trace from each experimental condition in greater resolution.

Monitoring activity of the caudal region of the spinal cord while successively blocking inputs resulted in a similar picture: a consistent trend of increased non-random variation, i.e. appearance of partitions in the correlation matrixes (Fig 6). The data in figure 6 were also used to further demonstrate that new types of bursts were indeed emerging. Average burst profiles were generated from 50 control bursts and 50 bursts comprising a clear new correlation cluster after blocking short and long-range inputs (Fig. 6B, I and II respectively as marked). To emphasize the point, a third 50-burst average profile was constructed from a region not different from control (III from Fig 6A2).

Figure 6.

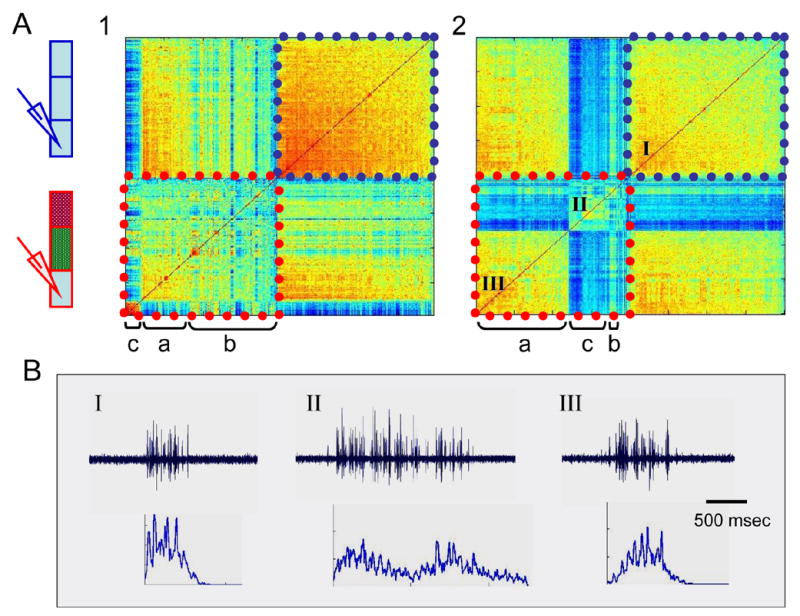
A. Two examples of the results of blocking both short and long-range inputs to a caudal region of spinal segments. As in figure 4C, matrices shown include the results of the inter-burst correlation of 200 randomly selected bursts recorded under control and under the fully blocked conditions (indicated by blue or red dashed lines respectively), as well as the cross correlation between the two experimental conditions. Thus, again, while control bursts are rather homogenous, fairly similar as well as clearly new types of bursts can be seen after manipulating the inputs (a, b or c respectively). B. An example of one burst as well as the average burst profile of 50 bursts (bottom) from the areas indicated in A2: I, control bursts; II, a new type of burst, compared to a rather similar group of bursts in III.

We calculated the structural complexity for the time series recorded for all experimental conditions (sequences of 500–2000 bursts), following the different manipulations of inputs to a monitored region of spinal segments. The measure of complexity in figure 7 is shown relative to that calculated for control in the specific experimental protocol (indicated by a dashed line in all panels). As can be seen, this kind of information capacity analysis corroborates the trend of increase in non-random variability with elimination of inputs demonstrated by our cross correlation analysis. Though the differences are not always significant, they are strongly supported by the fact that they repeat in every single experiment and under all the different manipulations. Furthermore, when pulling data from the upper and lower panels (monitoring the rostral or caudal regions), a two way ANOVA shows a significant effect of blocking short range inputs as well as short and long range inputs (for analysis of spike or burst sequences).

Figure 7.

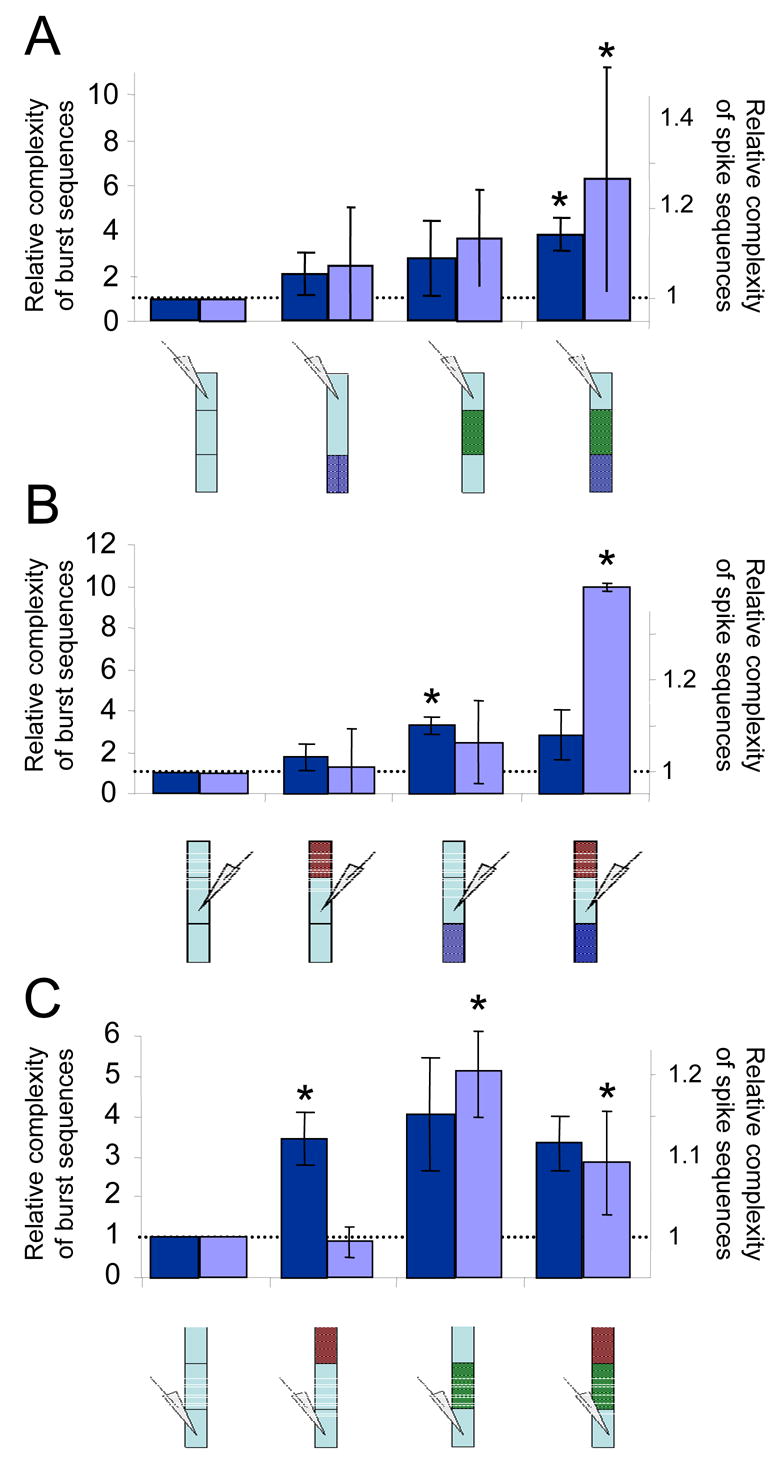
Structural complexity (see details in Method section) computed for the sequences of spike or burst times recorded in the different experimental conditions reveals a similar trend of increase in non-random variability with elimination of inputs. A, B, C show results of analyses conducted on all recordings obtained from the rostral, middle or caudal regions of spinal segments respectively. Data shown as change from control; statistical significance is indicated. Analysis of spike or burst sequences are shown in dark and light bars respectively.

While blocking a region of the spinal cord distal to the recording site (more than 20 segments away) eliminates long-range inputs, it may also have indirect effects via short-range connections to the adjacent non-blocked middle region. To verify the distinct effects of blocking long-range inputs, we analyzed additional data, obtained before and after applying two hemisections at the middle region of the cord (see Experimental Procedures; Kiemel et al., 2003). As can be seen in figure 8, results of the hemisection experiments confirm a clear effect of blocking long-range inputs; a general decrease in similarity is reflected by the appearance of more greenish and bluish shades in the cross-correlation matrix. The introduced variation is not random, as evident from the distinct clusters or types of bursts, some of which have little or no similarity to the control bursts. Our analysis may suggest that the rostral part of the cord is more sensitive to elimination of the long-range connections (compare Fig. 8A and 8B), but the data are not conclusive at this stage (this point is being specifically addressed in a current follow-up study).

Figure 8.

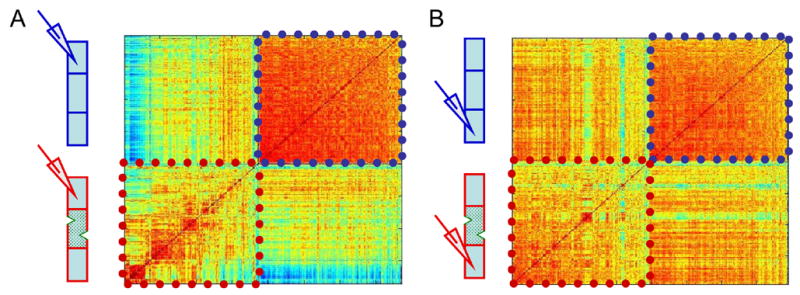
Inter-burst cross-correlation matrices similar to those shown in figures 4C and 5A. Bursts are compared within and between control conditions and after applying two hemisections, 5 segments apart, in the middle region of the spinal cord. Two examples are shown of data recorded from rostral (A) or caudal (B) segments of the cord.

In order to further demonstrate the functional relevance of our findings to neural mechanisms for animal behavior, we conducted a similar analysis as above on time series recorded from the lamprey spinal cord after bath application of an endogenous modulator; 5HT (n=2 preparations, 2 different concentrations each). Here, instead of directly manipulating the inputs to a recorded set of spinal segments, we manipulated its neuromodulatory state which, among other things (e.g. presynaptic inhibition of neurotransmitter release; Schwartz et al., 2005, segmental premotor interneurons; Biró et al., 2006), may affect the inter-segmental connections. As previously reported, 5-HT reduces the frequency of ventral root bursting during fictive locomotion (see above references). In accordance with these reports, we found cycle period to be increased from 0.95±0.23 sec in control conditions to 3.64±0.84 and 10.63±3.26 sec under 10⁻⁶ M and 10⁻⁵ M 5HT respectively (n=500–1000 cycles in 2 preparations). A similar effect on the duration of the burst resulted in a minor (though statistically significant) change in duty cycle (burst duration divided by cycle period): from 0.22±0.06 in control to 0.25±0.12 under 10⁻⁵ M 5HT. As mentioned earlier these statistics carry no information regarding the within-burst temporal structure Thus we further analyzed the time sequences recorded with and without the modulator. Figure 9A shows data similar to those seen in figure 4C. Again, a large cross-correlation matrix is shown which includes sorted correlation results (based on the corresponding dendrograms). The region of the matrix showing control conditions is again characterized by relative uniformity and high levels of correlation (shades of red) compared to the bursts recorded in the presence of the modulator. Moreover, distinct types of bursts can be seen in the 5HT data, some of which are somewhat similar to control bursts (indicated by 'a' in Fig 9A ) while others are clearly new, modulator-induced types of bursts (indicated by 'b'). Furthermore, increased non-random variability, as indicated by a relatively low correlation and somewhat clustered matrix, could already be seen following application of the low dose of the modulator (Fig 9B). As in figure 6, average burst profiles are shown, each calculated for 50 bursts from the region of the cross-correlation matrixes indicated by I (control), II (10⁻⁵ M 5HT) and III (10⁻⁶ M 5HT).

Figure 9.

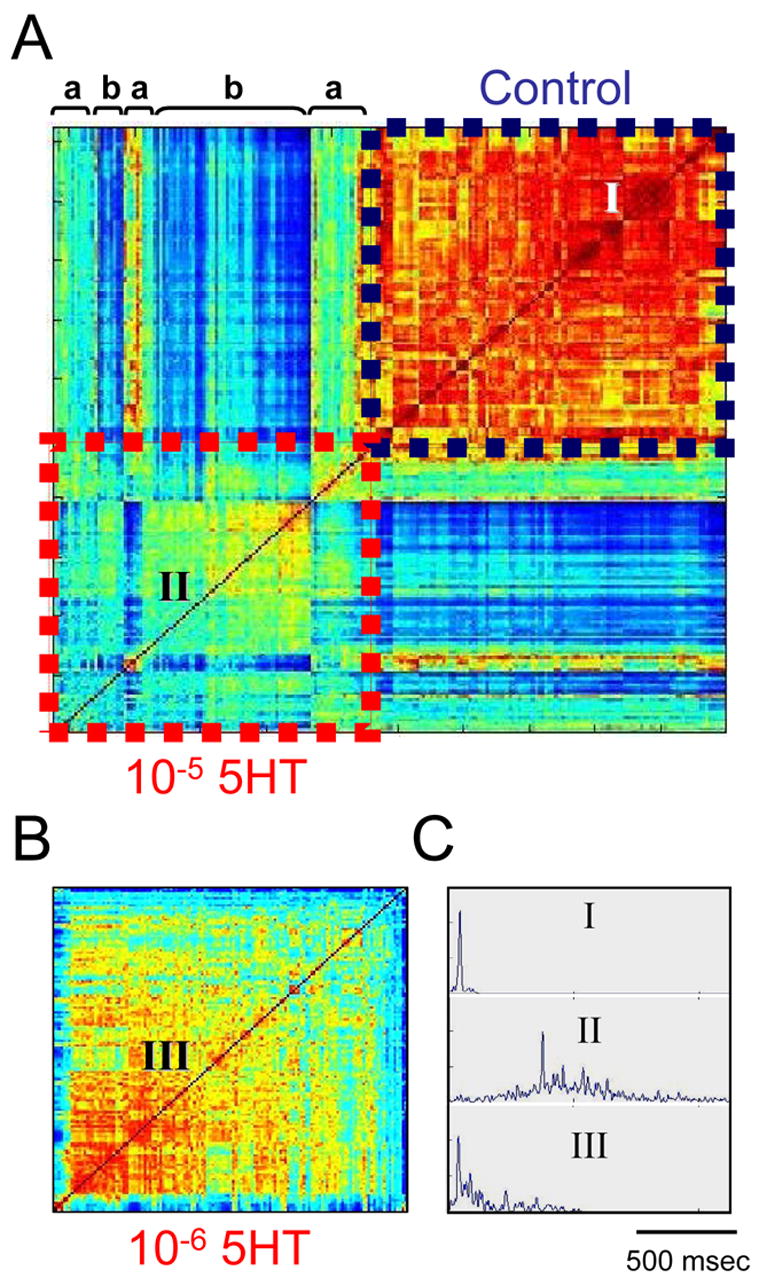
The results of applying a modulator to the spinal cord are reminiscent of the results of eliminating input to a distinct region of spinal segments. A. A correlation matrix composed for bursts recorded in control and after bath application of 10⁻⁵ M 5HT shows that the modulator induces the appearance of somewhat different or new types of bursts (indicated by a and b respectively). B. Variation is induced already after application of 10⁻⁶ M 5HT. C. An average burst profile calculated for groups of 50 bursts recorded in control conditions (I) or after application of the different doses of the modulators (II and III). The areas of the cross correlation matrixes representing the bursts used for calculating the averages are indicated in A and B.

Discussion

The current results have direct implications for our understanding of the lamprey spinal cord as a model for the study of mechanisms of locomotory behavior. Oscillator coupling and intersegmental neuronal inputs have an important functional role in shaping the temporal characteristics of the rhythmic motor output and in stabilizing it. Thus these connections should be important components of any proposed computational model of the system.

Our results show first that short-range coupling has the dominant role in stabilizing cycle frequency and burst properties. Second, long range connections have an additive influence on burst properties, but not cycle frequency, as is evident from the appearance of hidden correlations in the correlation matrix (distinct and new types of bursts not seen in control) already after blocking regions of the cord separated by more than 20–30 segments from the recording site, as well as by the results of the hemisections experiments. Segev et al. (2004) have reported on hidden neuronal correlations in cultured neuronal networks. Using multi-electrode array technology for simultaneous recording of many neurons in vitro, these authors were able to show that in a cultured network system the appearance of distinct burst types (or hidden correlations) was a reflection of different neuronal populations taking part in generating the different bursts. There is no direct way to extrapolate from the culture system to the spinal cord. Yet, in our system also, it may well be that the inputs to an oscillator unit serve to choose a subpopulation of interneurons (and follower motorneurons) to take part in generating the burst. Eliminating inputs or applying a modulator, in this respect, changes the active neuronal populations. Biró et al. (2006) have suggested that 5HT modulation of different types of segmental premotor interneuron types can partially account for the observed effects of 5-HT on the swim pattern in lamprey. In the neonatal mouse spinal cord, Zhong et al. (2006) report that 5HT modulates the properties of ascending commissural interneurons and propose that these may be component neurons in the locomotor CPG. Similarly, in the lamprey the input interneurons may be both modulated by 5HT and important components of the CPG.

The spinal chord is very often referred to as a homogenous chain of coupled oscillators. To what extent is functional rostral - caudal asymmetry imbedded in the intrinsic structure of the spinal chord, the inter- and intra-connections of the spinal cord pattern generating networks, is a question that was not yet fully addressed. The current results may offer some insights into this question. The data presented in figure 7 suggest differences between the effects of a caudal vs. a rostral short-range blockade. When directly tested by comparing the relative change from control of the complexity value when caudal or rostral segments were blocked the result was a consistently though non-significantly larger effect of blocking the caudal segments (p=0.1). In a future study (already underway) we intend to focus on this question as part of a larger effort to reveal endogenous functional rostral-caudal asymmetry in the lamprey spinal cord.

As mentioned, the lamprey spinal cord serves as a model for systems of coupled oscillators and moreover can also serve as a model for systems generating rhythmic output in general. For controlling motor behavior, CPGs must act in a highly coordinated and self-regulated mode in order to demonstrate flexible modulation without losing their essential stability (Harris-Warrick and Marder, 1991; Marder and Bucher, 2001; Nusbaum and Beenhakker, 2002). An important factor allowing the nervous system in general and specifically modular ensembles of neurons such as the CPG the plasticity needed to generate continuously adjusting behavior, is that of the endogenous capacity of their singular unit to show very large variations in output. The unit may be the single neuron or a small sub-network in a simple invertebrate pattern generating circuit, or it may be an oscillatory unit in the vertebrate spinal cord, or a complex microcircuit in our central nervous system.

In accordance with this hypothesis, Ayali et al. (2004) recently reported that self-assembled in-vitro networks, obtained from a relatively simple invertebrate ganglion, the locust frontal ganglion, show very rich spontaneous electrical activity. By characterizing the activity of a distinct population of neurons under progressive levels of structural and functional constraints- self-formed networks of neuron clusters in-vitro, isolated ex-vivo ganglia, in-vivo task-free, and in-vivo task-forced neuronal activity in the intact animal - Ayali et al. demonstrated common motifs and identified trends of increasing self-regulated complexity with decreasing constraints

This important principle is supported and may even be better demonstrated by the current results. The motor output of single unit oscillator in a complex system of coupled oscillators, the lamprey spinal cord, is characterized by high information capacity, i.e non-random variability or self regulated complexity. This endogenous high capacity is not evident however under normal (control) conditions, as it is restricted by morphological and functional constraints. In the in vitro system these constraints are the short-range coupling and long-range inputs from nearby or remote oscillatory networks. The constraints are more elaborate in the intact animal, including descending and sensory inputs, and interactions with the rest of the body and the environment. Glimpses of this vast potential can be experimentally revealed by blocking inter segmental connections or by the appropriate modulatory conditions.

The overall result of the above is the animal's ability to demonstrate stereotyped, consistent, or stable behavior that can, nonetheless, show large context-dependent variability and rich behavioral plasticity.