HYPOTONIC SWELLING OF SALICYLATE-TREATED COCHLEAR OUTER HAIR CELLS

Abstract

The outer hair cell (OHC) is a hydrostat with a low hydraulic conductivity of P_f = 3×10⁻⁴ cm/s across the plasma membrane (PM) and subsurface cisterna (SSC) that make up the OHC's lateral wall. The SSC is structurally and functionally a transport barrier in normal cells that is known to be disrupted by salicylate. The effect of sodium salicylate on P_f is determined from osmotic experiments in which isolated, control and salicylate-treated OHCs were exposed to hypotonic solutions in a constant flow chamber. The value of P_f = 3.5±0.5 ×10⁻⁴ cm/s (mean ± s.e.m, n = 34) for salicylate-treated OHCs was not significantly different from P_f = 2.4±0.3 ×10⁻⁴ cm/s (mean ± s.e.m, n = 31) for untreated OHCs (p=.3302). Thus P_f is determined by the PM and is unaffected by salicylate treatment. The ratio of longitudinal strain to radial strain ε_z/ε_c = −0.76 for salicylate-treated OHCs was significantly smaller (p = .0143) from −0.72 for untreated OHCs, and is also independent of the magnitude of the applied osmotic challenge. Salicylate-treated OHCs took longer to attain a steady-state volume which is larger than that for untreated OHCs and increased in volume by 8-15% prior to hypotonic perfusion unlike sodium α-ketoglutarate treated OHCs. It is suggested that depolymerization of cytoskeletal proteins and/or glycogen maybe responsible for the large volume increase in salicylate-treated OHCs as well as the different responses to different modes of application of the hypotonic solution.

INTRODUCTION

Outer hair cells (OHCs) are mechanosensitive cells located in the mammalian cochlea. The OHC possesses a hydraulic skeleton, i.e. the OHC wall is supported by a positive intracellular (turgor) pressure which helps to maintain its cylindrical shape (Brownell, 2006; Brownell et al., 2001). The hydraulic skeleton is necessary for electromotility (Brownell, 1990), which was first reported by Brownell et al. (1985). Electromotility is believed to be the basis of the active process within the cochlea proposed by Gold (1948) resulting in the fine frequency selectivity and sensitivity of mammalian hearing (Brownell, 1999; Dallos, 1992; Patuzzi, 1996).

The cell's ability to maintain a positive intracellular pressure may be related to the hydraulic conductivity of the OHC wall. The OHC hydraulic conductivity (P_f), which is a measure of the rate at which water crosses the OHC wall, may be obtained by analyzing OHC shape changes in response to an osmotic challenge. We have analyzed the OHC volume response to a hypotonic solution with an osmotic difference of −45 mOsm and obtained P_f = 3 × 10⁻⁴ cm/s for the OHC hydraulic conductivity using a mathematical model of osmotic water transport (Ratnanather et al., 1996b). This value is on the low side of values reported for different lipid bilayers and is 2 orders of magnitude lower than the hydraulic conductivity of red blood cells. The low conductivity may help to maintain the intracellular pressure necessary for cell function.

The low OHC hydraulic conductivity may be attributed to either the plasma membrane (PM) or the other components of the highly specialized lateral wall. Beneath the PM lies a flattened unfenestrated cylindrical sac called the subsurface cisterna (SSC) (Slepecky et al., 1992). In the space between the SSC and PM (defined as the extracisternal space, ECiS) is the cortical lattice that is believed to supply the mechanical reinforcement of the wall (Holley, 1996). The micropillars, which form part of the cortical lattice, extend radially across the ECiS from the SSC to the PM. Water transport into and out of the cell must cross the PM. Water movement inside the cell may be across the SSC or exclusively within the ECiS moving towards the basal and apical ends.

In addition, we have used data from OHC shape changes in response to osmotic challenge of different magnitudes (−17, −30 and −45 mOsm) to assess the mechanical properties of the OHC (Ratnanather et al., 1996a). The ratio of the longitudinal strain to the circumferential strain was found to be −0.72 and independent of the magnitude of the osmotic challenge, and was used by Spector et al. (1998) along with other data to estimate the in-plane and bending stiffnesses of the OHC wall.

Salicylate, which is a by-product of aspirin metabolism, is known to result in reversibly elevated threshold of hearing, decreased speech discrimination, tinnitus and altered cochlear function (Mongan et al., 1973; Myers et al., 1965; Stypulkowski, 1990). The effect of salicylate on biomechanical properties of the OHC has been the focus of several studies as summarized in table 1 of Snyder et al. (2003); see also Brownell (2006). Briefly, sodium salicylate permeates the OHC presumably in the uncharged form of salicylic acid and then dissociates to acidify the cell cytoplasm with about 0.6 μM in the undissociated form (Kakehata et al., 1996; Tunstall et al., 1995). One notable effect of salicylate (at 10 mM concentration levels) on OHCs is the reversible disruption of the SSC (Dieler et al., 1991) together with reduction in turgor pressure (Shehata et al., 1991), longitudinal stiffness (Russell et al., 1995) and active force generation (Hallworth, 1997), suggesting that the OHC is a likely target of salicylate ototoxicity.

Thus we examine the effect of salicylate on both the hydraulic conductivity and mechanical properties of the OHC. In this paper, we analyzed the response of salicylate-treated OHCs to osmotic challenges of different magnitudes and calculated the rate of water flow into the cell. Then we compared these rates with those obtained by analyzing those for untreated OHCs. We also analyzed the longitudinal and circumferential strains of salicylate-treated OHCs and compared them with the previously reported strains for untreated OHCs.

MATERALS and METHODS

A complete description of the experimental method may be found in Chertoff and Brownell (1994) and Ratnanather et al. (1996a; 1996b). A brief summary follows.

OHC isolation

200-300g pigmented guinea pigs were sedated in a 100% carbon dioxide chamber and decapitated. Temporal bones were removed from the skull and the bulla opened to expose the cochleae, which were then placed into standard medium (solution 1, see below). The OHCs were isolated from the cochlea using standard techniques. The OHCs were gathered in 1 ml syringe, injected into a rectangular chamber (Chertoff et al., 1994), which was placed onto the stage of an inverted microscope (Zeiss Axiovert 35) and allowed to settle to the bottom of the chamber. An oil immersion 63 X objective lens (NA 1.4) was used to image the cell. The cell was monitored on a television screen (final magnification 1500 X) and recorded on tape with a video cassette recorder (Panasonic AG-1830, S-VHS). Time and date were imposed on the video image with a time-date generator (Panasonic WJ-810).

Solutions

We used the following solutions. Isotonicity was defined as a final osmolarity of 293-297 mOsm. Hypotonicity was defined as a solution which differed from the isotonic solution by ΔC = −17, −30 and −45 mOsm (Ratnanather et al., 1996a) and was made by diluting the isotonic solution with distilled water. Four types of solutions were made: phosphate buffered saline (PBS), salicylate, salt and ketoglutarate.

1. Isotonic-PBS solution (Delbeco's) supplemented with 1.5 mM CaCl₂, 1.5 mM MgCl₂ and 10 mM D-glucose;

2. Hypotonic-PBS solution which differed in osmolarity from solution 1;

3. Isotonic-salicylate solution (solution 1 + 10 mM sodium salicylate + distilled water to maintain isotonicity);

4. Hypotonic-salicylate solution which differed in osmolarity from solution 3;

5. Isotonic-salt solution (solution 1 + 10 mM NaCl + distilled water);

6. Hypotonic-salt solution which differed in osmolarity from solution 5;

7. Isotonic-ketoglutarate solution (solution 1 + 10 mM sodium α-ketoglutarate + distilled water);

8. Hypotonic-ketoglutarate solution which differed in osmolarity from solution 7.

All solutions were adjusted with HCl or NaOH to a final pH value of 7.3-7.4 at room temperature. The osmolarity of each solution was measured by placing a 2 ml sample in a freezing point osmometer (Osmette A). Ketoglutarate was used as a control for salicylate because it has a similar molecular weight (Shehata et al., 1991).

Experimental procedure

After the cell attached to the bottom of the chamber, it was perfused at a rate of 247 μl/min with solutions in the following sequence:

• untreated cells: 15 min. with isotonic-PBS (solution 1) followed by 15 min. with hypotonic-PBS (solution 2) followed by 15 min. with isotonic-PBS.

• treated cells: there were two treatments - salicylate and α-ketoglutarate. The first treatment involved exposure for 30 min. to isotonic-salicylate (solution 3) followed by 15 min. with hypotonic-salicylate (solution 4) followed by 30 min. with isotonic-salt (solution 5) followed by 15 min. with hypotonic-salt (solution 6). The ketoglutarate treatment used isotonic-and hypotonic-ketoglutarate (solution 7 and 8) instead of the corresponding salicylate solutions.

Data analysis

A detailed morphometric analysis was used to measure the spatial changes in response to the hypotonic challenge. Since the video images were recorded continuously, the spatial information about the cells could be obtained at any time during the experiment. This analysis assumed that the cross-section of the cell remained circular throughout the experiment (Chertoff et al., 1994). There was a dead time of about 3 min. for the perfusate to reach the cell (Chertoff et al., 1994; Ratnanather et al., 1996a; Ratnanather et al., 1996b). Video images were digitized at intervals (see for example the error bars in fig. 1c). At each time, the outline of the cell was traced 4-5 times and the pixel coordinates of the outline of the OHC were collected using the image analysis software SEMPER (Synoptics, Cambridge, MA). The resulting pixel files were then analyzed using a set of programs written in MATLAB (The Mathworks, Natick, MA). From the MATLAB analysis, the temporal changes in radius, length and volume were obtained.

Fig. 1.

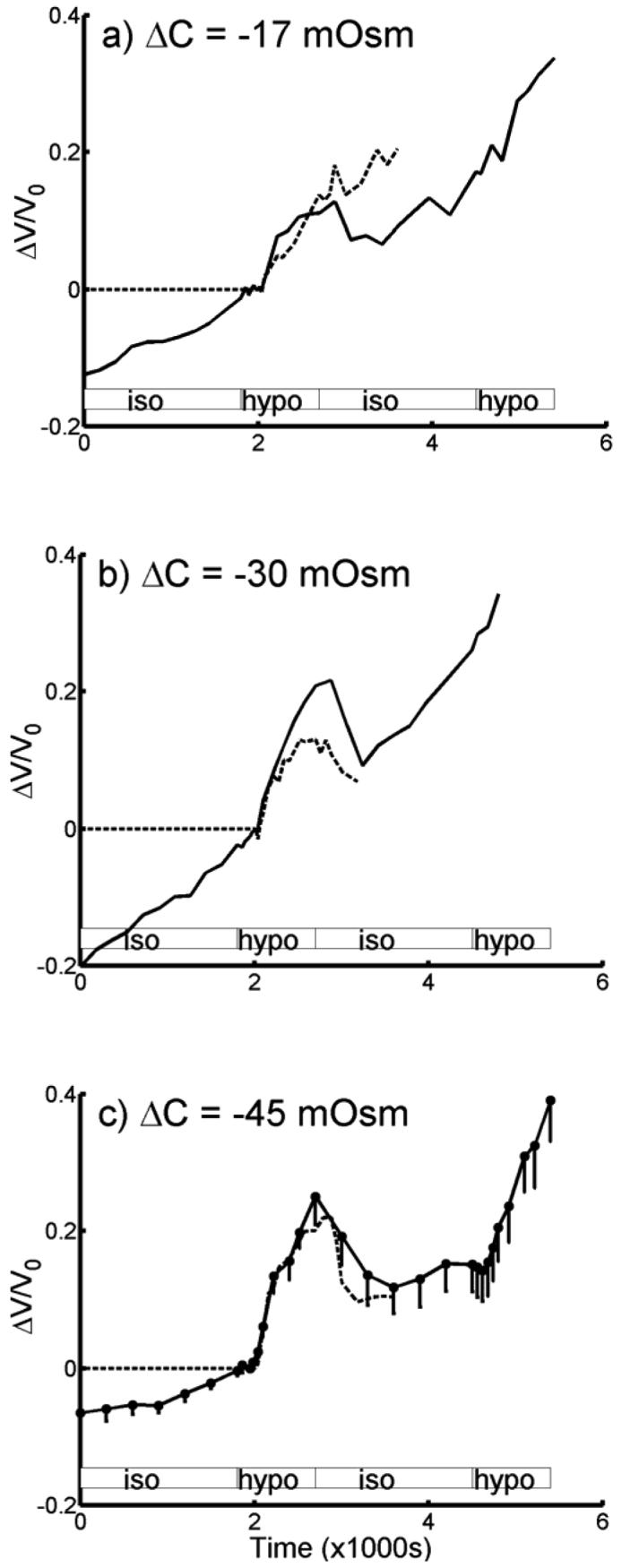
Relative volume change averaged from salicylate-treated OHCs (—) and compared with untreated OHCs (- - -). Volume change has been normalized with respect to volume at start of hypotonic perfusion at 2010 s. a) ΔC = −17 mOsm (treated, n = 10; untreated, n = 9), b) ΔC = −30 mOsm (treated, n = 8; untreated, n = 10) and c) ΔC = −45 mOsm, (treated, n = 13; untreated, n = 15). For clarity, half-error bars in s.e.m. are only shown in (c). The change in volume response for untreated cells prior to hypotonic perfusion is negligibly small and assumed to be zero (ref. 4; see also ketoglutarate treated cells in fig. 3). Shaded boxes indicate duration of perfusion of the different solutions (isotonic and hypotonic solutions); note the dead time of approximately 210s.

The care and use of animals reported on this study were approved by the Johns Hopkins University School of Medicine Animal Care and Use Committee (protocol number GP2M334).

RESULTS AND ANALYSIS

Fig. 1 shows the averaged change in volume for a population of salicylate-treated OHCs that were exposed to hypotonic solutions of concentrations ΔC = −17, −30 and −45 mOsm. The change in volume was normalized with respect to the time when the cells began to respond to the hypotonic solution at 2010 s (i.e. 210 s after the start of perfusion of the hypotonic solution). Superimposed on each graph is the response of untreated OHCs to hypotonic solutions; the ΔC = −45 mOsm data for untreated OHCs was previously reported (Ratnanather et al., 1996b).

For ΔC = −17 mOsm, the initial length of 10 salicylate-treated cells varied from 61 to 80 μm with a mean of 72±2 μm and that of 9 untreated cells varied from from 27 to 74 μm with a mean of 56±6 μm; for ΔC = −30 mOsm the initial length of 8 salicylate-treated cells varied from 44 to 77 μm with a mean of 65±5 μm and that of 10 untreated cells varied from from 28 to 78 μm with a mean of 60±5 μm; for ΔC = −45 mOsm, the initial length of 13 salicylate-treated cells varied from 45 to 78 μm with a mean of 63±3 μm and that of 15 untreated cells varied from from 37 to 79 μm with a mean of 60±3 μm. The initial length for untreated cells is slightly different from that reported in Ratnanather et al. (1996b) because a different reference point was used.

We have previously shown that osmotic induced OHC volume change can be described by (Ratnanather et al., 1996b):

$$\frac{V-V_0}{V_0}=a(1-e^{-\mathit{bt}})$$ (1)

where V is the OHC volume, V₀ is the initial OHC volume at the start of the hypotonic perfusion, and a and b are constants. For small t, the right hand side of Eq. 1 can be expressed as abt. Thus ab is the initial rate of normalized change in OHC volume and may be used to determine the hydraulic conductivity of the OHC wall, P_f (Ratnanather et al., 1996b):

$$P_f=\frac{50{\mathit{abr}}_0}{V_w\Delta C}$$ (2)

or

$$\frac{50r_0}{V_w}\mathit{ab}=P_f\Delta C$$ (3)

where r₀ is the initial OHC radius and V_w = 18×10⁻⁶ m³/mol is the molar volume of water. We included the ΔC = −45 mOsm untreated data from Ratnanather et al. (1996) for comparison.

Eq. 3 describes a linear relationship between the initial rate of normalized change in OHC volume and the magnitude of the applied osmotic challenge. The product ab for each cell is determined from an exponential fitting procedure based on the Nelder-Meade simplex algorithm (MATLAB). To test the linear relationship, the flux, 50r_oab/V_w, in response to ΔC was analyzed using parametric tests, non-parametric tests and a linear model.

Brown-Forsythe tests of homogeneity of variances (HOV) (Manly, 1994) indicated that variances of fluxes between concentration levels within untreated and treated sets were not significantly different (p=.2169 and p=.9071, respectively). Hence, the variation in flux was not affected by ΔC for both treated and untreated data. Nevertheless, nonparametric tests were appropriate since normality failed for at least one group. For example, fluxes for untreated OHCs at ΔC = −17, and treated OHCs at ΔC = −17 and −30 were significantly non-normal (p=.0120, p=.0341, and p=.0095, respectively) based on Lilliefor's test (Thode Jr., 2002). Therefore, Kruskal-Wallis test (Zar, 1984) for multi-group comparisons and Wilcoxon rank sum test (Zar, 1984) with Holm's correction (Holm, 1979) for pairwise comparisons were used. There were group differences within the untreated set (p=.0002).

Pairwise comparisons of fluxes for ΔC levels were performed. Fluxes at ΔC = −17 were significantly less than those at ΔC = −30 (p=.0028), those at ΔC = −17 were significantly less than those at ΔC = −45 (p≤.0001), and those at ΔC = −30 were significantly less than those at ΔC = −45 (p=.0204). There was no evidence of group differences within the treated set (p=.1709) and thus no need for pairwise comparisons. Fluxes at ΔC = −17 were almost (or marginally) significantly less than those at δC = −45 level (p=.0876). Furthermore, when ΔC levels were ignored, the comparison of the untreated and treated groups by Wilcoxon rank sum test yielded no significant difference (p=.6382). Likewise for comparison of treated versus untreated data at concentration levels ΔC = −30 and ΔC = −45 (p=.4013 and p=.3814, respectively), but untreated fluxes were significantly less than treated fluxes at ΔC = −17 (p=.0330). Kolmogorov-Smirnov tests for cumulative distribution functions (cdfs) (Zar, 1984) for untreated OHCs at ΔC = −45 were significantly smaller than those for ΔC = −30, whose cdfs were significantly smaller than those for ΔC = −17 (p=.0128, p=.0016, respectively); thus cdf at ΔC = −45 was significantly smaller than that at ΔC = −17 (p=.0030). In other words, it was more likely for fluxes at ΔC = −45 to be larger than those at ΔC = −30 whose fluxes were more likely to be larger than those at ΔC = −17 as might be expected from Eq. 3.

The linear model described by Eq. 3 was fitted using regression. Note that Eq. 3 implies that (i) concentration levels should be considered as numerical measurements, rather than factors (or categories) and (ii) the y-intercept is zero. First, we checked whether considering the concentration levels as factors would have gained any power in the statistical analysis. So, we ran two models, one with ΔC as factors, and one with ΔC as numbers. In both cases, the residuals of the fitted models were significantly non-normal (Shapiro-Wilks test), but removing a few outliers resolved this issue, thereby yielding insignificant departure from normality in each model. Then, for untreated OHCs, using ANOVA F-test (Zar, 1984), there was no significant improvement in considering concentration levels as categories compared to assuming them as numerical (p=.3908); similarly, for treated OHCs, p=.5691. Therefore, for both treated and untreated data, we assumed the concentration levels to be numerical. For untreated data, the y-intercept was estimated as −.0027 (with s.e. = 0.0023) which was not significantly different from 0 (p=0.2340); for treated data, the estimated y-intercept was 0.0026 (s.e.= 0.0024) which was not significantly different from 0 also (p= 0.2856).

Thus the estimated model based on Eq 3. yielded P_f = 2.6×10⁻⁴ cm/s and 2.4×10⁻⁴ cm/s for untreated and treated OHCs (adjusted R² =.8141 and .7692) respectively. To test for difference, we use ANCOVA methods (Zar, 1984) for the following model

$$\frac{50{\mathit{abr}}_0}{V_W}={\beta }_1\Delta C+{\beta }_2{I}_{\mathit{ut}}\Delta C+{\mu }_1+{\mu }_2{I}_{\mathit{ut}}+\epsilon$$ (4)

where I_ut is the indicator function (1 if untreated, 0 if treated) and β₁ is P_f for treated group, while β₁ + β₂ is for untreated group; μ₁ is the mean influence due to existence of treatment and μ₁ + μ₂ is when there is no treatment, and ε is the error term. So if β₂ = 0 then, the two lines should be identical, i.e. P_f should be the same for both treated and untreated groups. Similarly if μ₂ = 0 , there should be no mean influence difference between treatment or no treatment. There was no interaction between ΔC and treatment (p=.0863), i.e., no slope difference (or β₂ = 0 ) thus interaction was removed from the model. There were significant differences at concentration levels (p < 0.0001) but no significance with respect to treated or untreated labels (p=.9963). Thus the lines in Fig. 2 are parallel with no significant separation, reducing the model to 50abr₀ /V_W = P_fΔC + ε . Linear regression yielded P_f =2.5 ×10⁻⁴ cm/s for the common slope for treated and untreated data with adjusted R² = 0.7968.

Fig. 2.

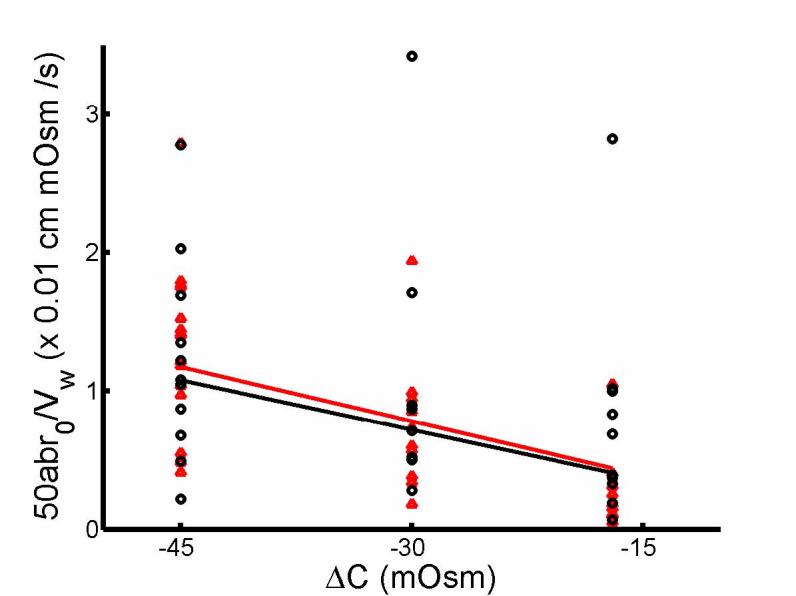
Linear relationship between initial rate of change in OHC volume, 50abr₀/V_w, and magnitude of osmotic challenge, ΔC. ab and r₀ are obtained from exponential fitting of OHC volume change in response to hypotonic solution and the initial radius respectively for salicylate-treated (black) and untreated (red) cells. Linear regression of the two straight lines yielded P_f = 2.6 × 10⁻⁴ cm/s (R² = 0.814) and P_f = 2.4 × 10⁻⁴ cm/s (R² = 0.769) for untreated and treated OHCs respectively.

An alternative calculation of P_f is to use Eq. 2 for each individual cell. Lilliefor's test for normality suggested that the ΔC = −17 untreated set and ΔC = −30 treated set were significantly non-normal (p=.0183 and p=.0024, respectively). Hence, non-parametric tests were more appropriate although Brown-Forsythe tests for HOV suggested that variances of treatment groups within untreated and also within treated sets were not significantly different (p=.9691 and p=.1502, respectively). There was evidence of significant group differences within untreated OHCs (by Kruskal-Wallis tests, p=.0170) but not for treated OHCs (p=.4694). Untreated OHCs at ΔC =−17 are not significantly different from those at ΔC =−30 (p=.1070), which are not significantly different from those at ΔC =−45 (p=.2609). But, untreated OHCs at ΔC =−17 were significantly less than those at ΔC =−45 (p=.0134). There was no overall differences between treated and untreated OHCs when treatment levels were ignored (Wilcoxon rank signed sum test, p=.3302). Additionally, treated and untreated OHCs were not significantly different at each concentration levels (p=.1605 at ΔC =−17, p=.7618 at ΔC =−30, and p=.5474 at ΔC =−45).

Further Kolmogorov-Smirnov tests for cdfs showed no significant differences in the distributions of P_f values for untreated and treated OHCs, although cdf of OHCs at ΔC = −17 was larger than that at ΔC = −45 with marginal significance (p=.0522). Thus for untreated OHCs, P_f = 2.9±0.1 ×10⁻⁴ cm/s (mean ± s.e.m., ΔC = −45 mOsm, n = 15), P_f = 2.5±0.5×10⁻⁴ cm/s (ΔC = −30 mOsm, n = 10), P_f = 1.5±0.6 ×10⁻⁴ cm/s (ΔC = −17 mOsm, n = 9). For salicylate-treated OHCs, P_f = 2.4±0.4 ×10⁻⁴ cm/s (ΔC = −45 mOsm, n = 13), P_f = 3.6±1.2 ×10⁻⁴ cm/s (ΔC = −30 mOsm, n = 8), P_f = 4.7±1.2 ×10⁻⁴ cm/s (ΔC = −17 mOsm, n = 10). Combining the data, P_f = 3.5±0.5 ×10⁻⁴ cm/s (n = 34) and P_f =2.4 ±0.3 ×10⁻⁴ cm/s (n = 31) for untreated and salicylate-treated OHCs respectively, giving an overall value of P_f =2.9±0.3 ×10⁻⁴ cm/s (n = 65).

Fig. 3 shows that ketoglutarate-treated OHCs (n=9) did not increase in volume prior to perfusion of hypotonic solutions. We also obtained P_f = 3.7±2.9 ×10⁻⁴ cm/s (ΔC = −45 mOsm, n = 4).

Fig. 3.

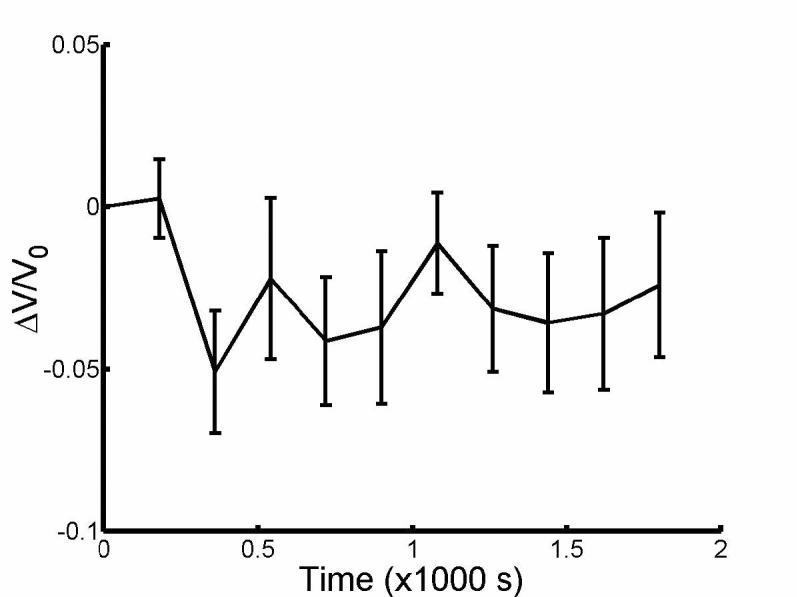
Relative volume change averaged from cells perfused with isotonic sodium α-ketoglutarate (n=9) prior to exchange of solutions from isotonic to hypotonic at 1800s. Error bars in s.e.m.

Fig. 4 shows the adjusted volume response to hypotonic perfusion obtained by subtracting the linear fit of the response up to the start of the hypotonic perfusion. When we analyzed the modified response of the salicylate-treated OHCs, statistical analysis showed that HOV was not violated (p=.2875), but not normality (p=.0146 for ΔC = −30). Still there was no difference between the three groups (Kruskal-Wallis, p=.6615). Thus P_f = 2.6±0.5 ×10⁻⁴ cm/s (ΔC = −45 mOsm, n = 13), P_f = 3.3±1.2 ×10⁻⁴ cm/s (ΔC = −30 mOsm, n = 8), P_f = 4.3±1.1 ×10⁻⁴ cm/s (ΔC = −17 mOsm, n = 10), giving an overall mean of P_f = 4.3±0.6 ×10⁻⁴ cm/s (n=31). Both fig. 1 and fig. 4 show that the averaged response of salicylate-treated OHCs did not reach a steady state by 15 min. of hypotonic perfusion unlike untreated OHCs. Fig. 5 shows that averaged modified response of salicylate-treated OHCs (ΔC = −45 mOsm, n = 7) attained a steady state after 30 min. of hypotonic perfusion.

Fig. 4.

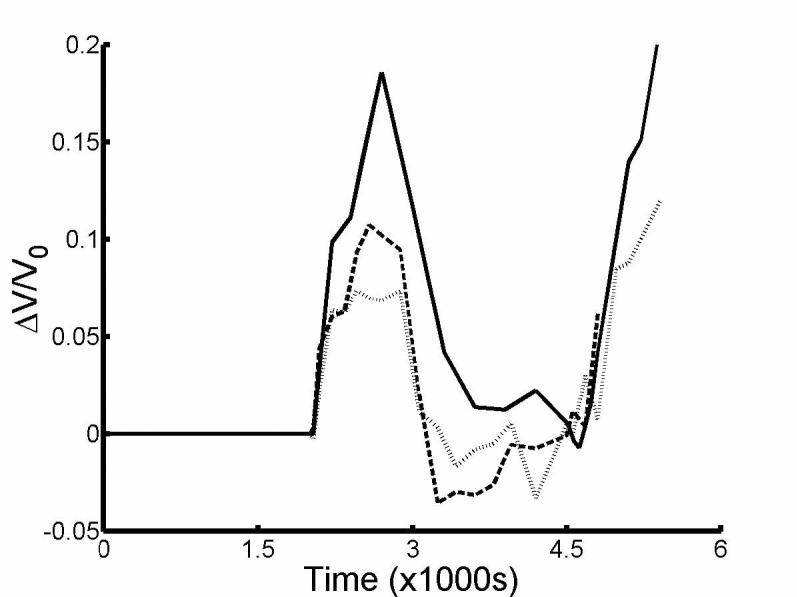
Averaged volume response to hypotonic perfusion modified by subtracting the linear volume response prior to hypotonic perfusion of solutions with ΔC = −45 mOsm (—, n = 9), −30 mOsm (---, n = 6) and -17 mOsm (⋯, n = 8).

Fig. 5.

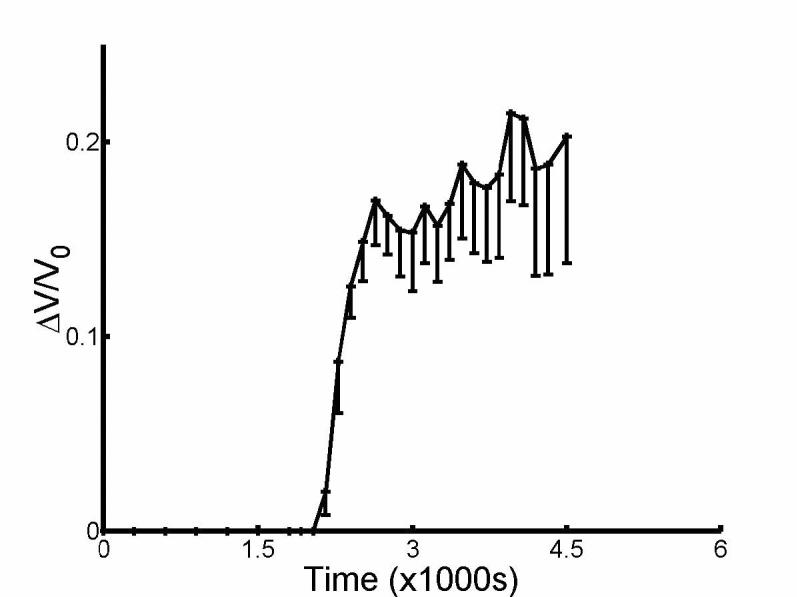
Modified averaged volume response to hypotonic perfusion for 30 min. for ΔC = −45 mOsm (n=7).

For an OHC of length, l₀, and radius, r₀, in the reference state (at the start of hypotonic perfusion), the OHC deformation can be characterized by longitudinal and circumferential strains, ε_z = (l − l₀) / l₀ and ε_c = (r − r₀ ) / r₀, respectively where l and r are the length and radius of the OHC in the deformed state. Following Ratnanather et al. (1996a), the strains for each treated cell,ε_z and ε_c, were calculated at the data points indicated by the error bars in fig. 1c and then averaged. Fig. 6 combined these averaged values in response to the three hypotonic solutions. Lilliefor's tests indicated problems with normality in ε_z and ε_c values so non-parametric tests were used although Brown-Forsythe tests for HOV were not rejected. Kruskal-Wallis tests indicated no differences between concentrations for ε_c (p=.4439) and ε_z (p=.5645). Overall, Wilcoxon signed rank test indicated that ε_c > −ε_z (p<.0001). Kolmogorov-Smirnov tests showed no differences in cdfs of ε_z and ε_c at each concentration for both groups. Finally, linear regression analysis gave a slope of ε_z/ε_c = −0.79 (R² = 0.98); however, since the residuals were significantly autocorrelated, an autoregression model of order 1 (Box et al., 1994) yielded ε_z/ε_c = −0.76. This slope was significantly different from −0.72 for untreated OHCs obtained by Ratnanather et al. (1996a) with p=.0174 (Zar, 1984).

Fig. 6.

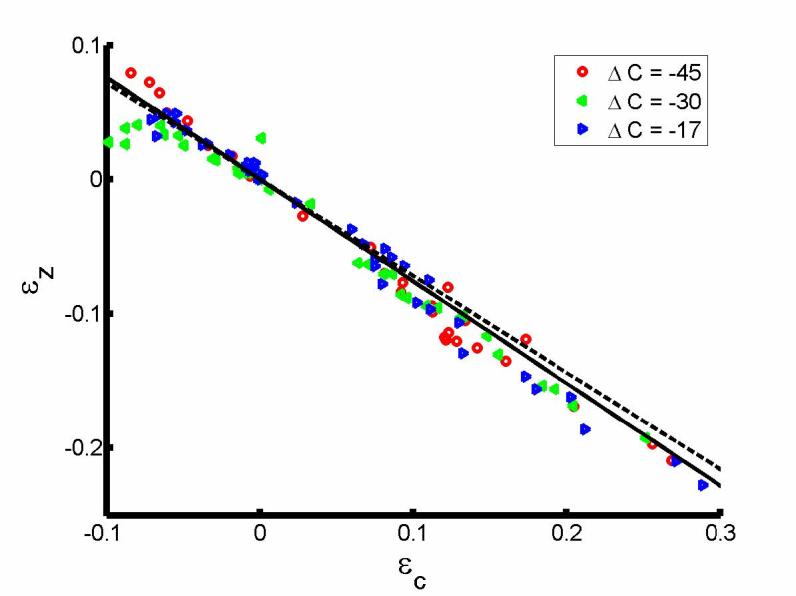
Plot of ε_z against ε_z for salicylate-treated OHCs. Linear regression of the solid line (—) through the origin gave a slope of −0.76. Also shown is the dashed line for untreated OHCs with slope of −0.72 (--, Ratnanather et al., (1996a)).

DISCUSSION

The aim of the present study was to determine the hydraulic conductivity and the mechanical properties of the lateral wall of salicylate-treated OHCs by examining their response to hypotonic solutions. The OHC hydraulic conductivity, P_f = 3×10⁻⁴ cm/s, was unaffected by salicylate (Fig. 2). Salicylate-treated OHCs were more elongated and narrower than untreated OHCs yielding ε_z/ε_c = −0.76 (Fig. 6). Both values were found to be independent of the size of the osmotic challenge. Salicylate-treated OHCs took longer to attain a steady-state volume which is larger than that for untreated OHCs (Figs. 1, 4, 5) and increased in volume by 8-15% prior to hypotonic perfusion (Fig. 1) unlike sodium α-ketoglutarate treated OHCs (Fig. 3). The implications of these findings are discussed below.

Plasma membrane dominates resistance to water movement across OHC lateral wall

Although the nature of water movement across the OHC lateral wall has not been determined, water is likely to move through the PM and into the cell core via either the extracisternal space (ECiS) pathway or across the SSC or both. If the hydraulic conductivities of the PM, SSC and ECiS are given by P_PM, P_SSC and P_ECiS respectively, then the hydraulic conductivity of the OHC wall is (cf. Krylov et al., 2001):

$$\frac{1}{P_f}=\frac{1}{P_{\mathit{PM}}}+\frac{1}{P_{\mathit{SSC}}+P_{\mathit{ECiS}}}$$ (5)

Since the SSC is a flattened unfenestrated cylindrical sac beneath the PM, it can be regarded as a double-layered membraneous system which probably does not possess water channels. This suggests that the SSC is relatively impermeable to water compared to the PM. Using this first approximation, Ratnanather et al. (2000) used a hydrodynamic model of the ECiS to show that P_ECiS is several orders of magnitude larger than those for lipid bilayers and biological membranes. Thus from Eq. 5, P_f ≈ P_PM suggesting that the resistance to water movement across the OHC lateral wall is dominated by the PM and is not affected by salicylate.

SSC disruption affects osmolyte generation and regulation in salicylate-treated OHCs

The volume increase prior to hypotonic perfusion is probably caused by intracellular osmolytes which both do not affect P_f even after factoring out preperfusion effects and influence the long-time response as predicted (Ratnanather et al., 1996b). Treated OHCs, when adjusted, showed a volume change plateau but with a longer time course (fig 5). Despite having similar molecular weight as salicylate, sodium α-ketoglutarate contains 2 charged carboxyl groups which lack salicylate's aromatic character, making it impermeant to biological membranes absent specific transporters. Since sodium α-ketoglutarate does not disrupt the SSC (Dieler et al., 1991), it is a useful control that does not generate intracellular osmolytes prior to hypotonic perfusion.

The large volume increase during hypotonic perfusion suggests that intracellular osmolytes may be caused by depolymerization of cytoskeletal filaments and glycogen. The dilation and fenestration of the SSC (Dieler et al., 1991; Pollice et al., 1993) results in a change of the nanoenvironment of the ECiS. The efficiency of membrane associated small GTPases that regulate the polymerization of cytoskeletal proteins will thus be affected (for discussion see Brownell, 2006; Kakehata et al., 2000). A plausible outcome is that the one or more of the long chain cytoskeletal proteins in the cortical lattice will depolymerize increasing the osmolarity of the cytoplasm. In addition, glycogen concentrations in the OHC are greater than in liver cells. Glucose-6-phosphatase is found in the SSC (Brownell, 1982) and plays a role in glycogenlysis. The depolymerization of glycogen could also contribute to an increase in cytoplasmic osmolarity.

Passive and jet flows result in different mechanisms of osmotic-induced water transport

A wide range of P_f values for OHCs (Belyantseva et al., 2000; Morimoto et al., 2002; Ratnanather et al., 1996b) reflects different mechanisms of osmotic-induced water transport across the PM. Belyantseva et al. (2000) obtained values of P_f =9.7×10⁻³ cm/s (adult rats) and P_f =11.1×10⁻³ (adult guinea pigs) with puff pipettes of radius R=0.5-1 μm placed at a distance of H=25-30 μm applying an osmotic challenge of ΔC= −5mOsm for 20s. Appendix A.1 reevaluated data by Morimoto et al. (2002) in the range 1.5-2×10⁻³ cm/s for untreated and salicylate-treated OHCs with R=2.5 μm, H=10 μm and ΔC= −45mOsm for 20-25s. Following the discovery that the motor mechanism underlying OHC electromotility involves the membrane protein prestin which is a member of the SLC26 family of anion transporter proteins (Zheng et al., 2000), Chambard and Ashmore (2003) obtained P_f=2×10⁻⁴ cm/s from prestin-transfected HEK-293 cells with R=0.5-1 μm, H=100-200 μm and ΔC=−5mOsm for 200s.

These differences may be explained by a model of a viscous jet impinging on a planar wall (Davis, Ceritoglu and Ratnanather, in preparation) which suggests that the wall pressure and wall shear stress away from the point of impact is influenced by H/R. When H/R=100-400 in Chambard and Ashmore (2003), the flow near the OHC lateral wall is similar to a constant pressure-gradient flow in a channel in this study. In contrast, when H/R = 4-60 in Belyantseva et al. (2000) and Morimoto et al. (2002), the wall pressure and wall shear stress changes rapidly within a concentrated region of about 3R. Indeed, Morimoto et al. (2002) suggested that such strain-dependent osmotic water transport may occur via selective mechano-sensitive pores observed in the membrane of the OHC (Le Grimellec et al., 2002). Aside, Belyansteva et al. (2000) suggested that low P_f values were caused by a regulatory volume decrease (RVD) mechanism (Crist et al., 1993) which is not possible since P_f is independent of osmolytes that might be generated by RVD (Ratnanather et al., 1996b). Although the density of prestin in OHC is much higher than in transfected cells, the similar modes of perfusion gave similar conductivities suggesting that dominant water pathway is across the PM.

Passive and jet flows result in different mechanical properties of the cortical lattice

Fig. 6 suggests a mechanical origin for the strains. ε_z/ε_c, is −0.76 for salicylate-treated OHCs in contrast with −0.72 for untreated OHCs (Ratnanather et al., 1996a). The steeper slope may reflect the contribution of the SSC to the OHC's longitudinal stiffness. The contribution that the intact SSC makes to the longitudinal stiffness could be removed by its disruption by salicylate. The longitudinal stiffness γ_a of a typical OHC of radius r₀ and length l₀ is πr₀ (2+ε_z/ε_c)(2 −ν₁)C_zz/2l₀ where ν₁ is the Poisson ratio that corresponds to the lateral deformations in the circumferential direction and C_zz is the in-plane longitudinal stiffness (Spector et al., 1998). For salicylate-treated OHCs, 2 +ε_z/ε_c is reduced. According to Spector et al. (1998), C_zz is a monotonic decreasing function of γ_a and ν₁ is a monotonic increasing function of γ_a ; also for fixed γ_a , both ν₁ and C_zz decrease with respect to K_s that is the stiffness parameter determined from the micropipette aspiration experiment. Lue and Brownell (1999) showed that K_s is reduced with 10 mM salicylate probably via its effect on the SSC-cortical lattice complex which contributes to 80% to K_s (Oghalai et al., 1998). Hallworth (1997) found that the compliance 1/γ_a was reduced with 10mM salicylate but it did not change much with 5mM salicylate in contrast with reduced γ_a observed by Russell and Schauz (1995); the discrepancy data maybe due to different modes of delivery of the drug (Hallworth, 1997). Further, the little change in stiffness observed by Hallworth (1997) is consistent with the results of Ermilov et al. (2005) that suggest that 10mM salicylate has less effect on the mechanics of the PM than on competing with the anions involved in electromotility. Thus the principal contributions to the longitudinal stiffness may be affected by the different competing and possibly dose-dependent changes in ε_z/ε_c, ν₁ and C_zz related to SSC disruption.

Analysis of data from Morimoto et al. (2002) in Appendix A.2 showed that when subject to a puff pipette, untreated and salicylate treated OHCs yielded ε_z/ε_c = −0.58 and −0.45 respectively. These values are different from −0.76 and −0.72 obtained in this study and in Ratnanather et al. (1996a) (p<<0.0001) suggesting that the opposite effect on ε_z/ε_c may be due to the different mechanical stimulus acting on the PM mentioned above. The undulating PM may be characterized as having an outer leaflet and inner leaflet (Raphael et al., 2000). After permeating the PM and acting as a competitive antagonist at the anion-binding site (Oliver et al., 2001), salicylate intercalates the outer leaflet causing outward membrane bending and thus differential membrane tension (Morimoto et al., 2002) while reducing membrane mechanical stiffness (Raphael et al., 1999; Zhou et al., 2005). These changes may be correlated with those in ε_z/ε_c, ν₁ and C_zz due to a resultant effect from competing differential tensions caused by the formation of the mechano-selective pores (Brownell et al., 1994), opening and closing of transporters (Brownell, 2002), salicylate-induced membrane crenation (Morimoto et al., 2002), stretch-activated channels (Ding et al., 1991; Iwasa et al., 1991; Rybalchenko et al., 2003; Spector et al., 2005) or increase in spontaneously formed meta-stable water defects (Marrink et al., 2001).

The differences in mechanical properties due to the passive and jet flows suggest greater depolymerization of the roughly longitudinally-oriented spectrin and the circumferentially-oriented actin respectively. Further these differences are consistent with permeability changes that allow calcium into the ECiS which would interfere with the homeostasis of long chain cytoskeletal proteins of the cortical lattice but in a manner different from SSC disruption by the membrane associated small GTPases.

Loss of turgor pressure does not affect OHC hydraulic conductivity

Although it has not been observed in electrophysiological experiments, a small volume increase may be associated with loss of turgor pressure in salicylate-treated OHCs and would be much smaller than that observed in this study. The rapid action of salicylate on prestin may reduce the transmembrane induced membrane tension (Ermilov et al., 2005), thus allowing turgor pressure to dissipate via elongation and the apparent volume increase. Alternatively, if PM folding is maintained in part by voltage-induced high curvature and salicylate causes a reduction in curvature then the cell elongates and less of the cell volume is “hidden” in the folding. Since wall pressure difference does not affect P_f (Ratnanather et al., 1996b), referencing to the start of hypotonic perfusion ensures that loss of turgor pressure does not affect the OHC's hydraulic conductivity.

Summary

OHC hydraulic conductivity is unaffected by salicylate but salicylate-treated OHCs are more elongated and narrower than untreated OHCs. The biophysical basis for the large salicylate-induced volume change may be the result of the depolymerization of cytoskeletal proteins and/or glycogen but further experiments, well beyond the original intent of this study, are required to test these hypotheses.

APPENDIX A

In this appendix, we obtained estimates of P_f in cm/s units and of ε_z/ε_c from Morimoto et al. (2002) which subjected untreated and treated OHCs to an osmotic challenge via a puff pipette.

A.1 Hydraulic conductivity

Data was taken at intervals of 5s from t=0 to 25s. For each cell, the reference time at which the volume started to increase was noted (generally at t=0, or 5 or 10s). Linear fitting of the volume increase was used. Since the concentration of the solutions were not noted, it was assumed that ΔC =−35 or −45 mOsm. For untreated OHCs, P_f = 1.6±0.1–2.0±0.1 (×10⁻³) cm/s (mean ± s.e.m., n=9); for salicylate-treated OHCs, P_f = 1.4±0.1–1.8±0.1 (×10⁻³) cm/s (n=8) which is higher than that derived from Morimoto et al. (2002) when converted by a factor of 100RT/V_w.

A.2 Ratio of longitudinal strain to radial strain

For each group, the strains in radius and length at t=0,5,10,15,20,25s were averaged. Regression through the origin (Student's t-test, Zar, 1984, p. 284) yielded values of ε_z/ε_c = −0.58 (R² = 0.99), −0.45 (R² = 0.99) respectively for untreated and salicylate-treated OHCs which are significantly different (p < 0.0001) (Zar, 1984, p. 300) but not the same as −0.72 or −0.76 (p < 0.0001).