Abstract
Computer-aided detection (CAD) has been attracting extensive research interest during the last two decades. It is recognized that the full potential of CAD can only be realized by improving the performance and robustness of CAD algorithms and this requires good evaluation methodology that would permit CAD designers to optimize their algorithms. Free-response receiver operating characteristic (FROC) curves are widely used to assess CAD performance, however, evaluation rarely proceeds beyond determination of lesion localization fraction (sensitivity) at an arbitrarily selected value of non-lesion localizations (false marks) per image. This work describes an FROC curve fitting procedure that uses a recent model of visual search that serves as a framework for the free-response task. A maximum likelihood procedure for estimating the parameters of the model from free-response data and fitting CAD generated FROC curves was implemented. Procedures were implemented to estimate two figures of merit and associated statistics such as 95% confidence intervals and goodness of fit. One of the figures of merit does not require the arbitrary specification of an operating point at which to evaluate CAD performance. For comparison a related method termed initial detection and candidate analysis (IDCA) was also implemented that is applicable when all suspicious regions are known, no matter how low the degree of suspicion (or confidence level). The two methods were tested on seven mammography CAD data sets and both yielded good-excellent fits. The search model approach has the advantage that it can potentially be applied to radiologist generated free-response data where not all suspicious regions are reported, only the ones that are deemed sufficiently suspicious to warrant clinical follow-up. This work represents the first practical application of the search model to an important evaluation problem in diagnostic radiology. Software based on this work is expected to benefit CAD developers working in diverse areas of medical imaging.
Keywords: CAD evaluation, free-response, FROC curves, lesion localization, search model, maximum likelihood, figure of merit, imaging system optimization
1. Introduction
Computer-aided detection (CAD) has been attracting extensive research interest during the last two decades. Many studies indicate that radiologists are not perfect in lesion detection tasks. For example, it is difficult for radiologists to detect cancers at screening mammography where a large number of images have to be read to find a small number of cancers (there are approximately 3–6 cancers per 1,000 patients). As a result 10% to 30% of breast cancers that are retrospectively visible are missed by radiologists 1,2. Missed cancers are not uncommon in CT or radiograph interpretation for lung nodules 3,4,5,6. In CT colonography it has been reported that approximately 17%–21% of false-negative polyp diagnoses are due to perceptual errors 7. One possible solution to reduce perceptual misses in radiological interpretation tasks is to perform double reading 8,9. However, double reading is expensive since it essentially doubles the demand on radiologists’ time. CAD has been proposed as an alternative to double reading. A CAD algorithm is intended to assist the radiologist by showing suspicious regions that may be otherwise overlooked. CAD systems have been developed to assist radiologists in a number of tasks, including the detection of masses and microcalcifications on mammograms, detection of lung nodules in thoracic CT volumes and chest radiographs, and detection of polyps in CT colonography.
Historically, mammography has been the most widely-researched area in CAD. Commercial CAD systems are being routinely used in a large number of medical centers to assist radiologists interpreting screening mammograms, and mammography CAD is rapidly becoming accepted clinical practice 10. Commercial CAD systems are also available for lung cancer detection on chest radiographs and CT images. In all of these application areas the full potential of CAD systems in the clinical environment can only be realized by improving the performance and robustness of CAD algorithms 2,11,12,13. This requires accurate and precise evaluation methodology that would permit CAD designers to optimize CAD systems.
In a general sense CAD could be regarded as an algorithmic observer for medical imaging tasks. The receiver operating characteristic (ROC) method is the most common way of evaluating observer performance in imaging tasks 14. In the ROC method the observer classifies each image as normal or abnormal. A correct classification of an abnormal case is termed a true positive and an incorrect classification of a normal case is termed a false-positive. The ROC curve is defined as a plot of true positive fraction, TPF, relative to the total number of abnormal cases, vs. false positive fraction, FPF, relative to the total number of normal cases. A pair of TPF and FPF values defines an operating point on the curve. By changing the confidence-level for rendering an abnormal classification, the operating point can be moved along the ROC curve. TPF is synonymous with sensitivity and FPF is the complement of specificity. Observer performance can be quantified by the area Az under the ROC curve. Software is available that allow one to estimate Az and associated statistics and analyze more complex ROC-based study designs 14.
Because of incompatibility in the data-structures ROC methodology is rarely used to assess CAD performance. [Note that CAD in this work refers to the detection / localization task. Algorithms, termed CADx, that determine if an already detected lesion is malignant or benign, are appropriately assessed by the ROC method.] The ROC data-structure consists of a single numerical rating per image, expressing the degree of confidence that the image is abnormal. In contrast, CAD algorithms yield a variable number (0, 1, 2, …) of mark-rating pairs per image. A mark is the physical location of a suspicious region identified by CAD and the rating is the degree of suspicion that the region is a lesion. This data-structure is identical to the free-response paradigm 15,16,17,18. Because of the identical data structures, the free-response method is widely used to assess CAD algorithms 19,20,21. Although the CAD outcome could be converted into an ROC data structure by using the highest rating in a case (or an image) as the confidence that the case is abnormal, studies have shown that one pays a price in terms of reduced statistical power18,22.
Before free-response data can be analyzed each mark has to be classified as lesion localization (LL) or non-lesion localization (NL). [In the context of free-response studies we avoid usage of the terms true and false positives, true and false negatives, sensitivity, specificity and detection, as these terms are widely used in ROC methodology where no location information is collected and the data structures are incompatible.] The LL / NL classification necessitates the adoption of a proximity criterion that determines how close a marked region has to be to an actual lesion in order to be classified as lesion localization. Alternatively, an overlap criterion between the computer-detected and truth panel indicated regions can be used 23. According to the proximity or overlap criteria, if a mark is close to a true lesion it is scored as lesion localization and otherwise it is scored as NL. An FROC curve is defined as the plot of lesion localization fraction, LLF, relative to the total number of lesions, vs. the non-lesion localization fraction, NLF, relative to the total number of images. It is a graphical summary of the information in a free-response data set.
For a particular image set the CAD designer knows the locations of all regions that were tagged as suspicious by the algorithm and the associated degrees of suspicion (i.e., ratings). The number of suspicious regions is typically large and the ratings are finely spaced, allowing a quasi-continuous FROC curve to be plotted. We refer to this type of detailed data, available only to the CAD designer, as designer-level data. In clinical applications of CAD only marks with degrees of suspicion exceeding a preset designer-specified cutoff are shown (or “cued”) to the radiologist, typically 0.5 to 3 marks per view for mammography CAD, and one is interested in measuring performance of the radiologist with and without CAD assistance. Because radiologists mark even fewer locations than are cued by CAD and cannot provide finely spaced ratings data, clinical free-response studies generally yield a limited number (typically 3–5) of operating points 16,24. We refer to this type of data observed in clinical studies as clinical-level data.
A prerequisite for comparing CAD algorithms is definition of a figure of merit (FOM) that rewards an observer for marking lesions while penalizing the observer for marking non-lesions. A commonly used figure of merit is the lesion localization fraction LLFα at a specified value α of NLF and other figures of merit involving the slope of the curve at a specified α, the average LLF over the range NLF = α1 and NLF = α2 have also been proposed 25,26. Parametric and non-parametric approaches 27,28,29 have been described for estimating some of these figures of merit. These methods appear to have been developed for designer-level data. We are not aware of any applications of these methods to clinical free-response studies. There is no consensus on the optimal α-value, or range of values, at which to report CAD performance. One designer may state performance at α= 0.5 while another designer may state performance at α= 1.0, and it is difficult to compare them even if the algorithms were evaluated on the same reference data set. A method of comparing CAD systems that is independent of α and can be applied to clinical-level data is desirable. Software implementations of the methods described above are not readily available, and most, if not all, CAD optimization research to date has used empirical (e.g., graphical or interpolation) methods to estimate LLFα and compare different algorithms. The jackknife free-response receiver operating characteristic (JAFROC) method 18 has been used to compare human observer free-response performance 24,30 where the number of marks per view is relatively small. JAFROC ignores all NLs on abnormal images and all but the highest rated NL on normal images but nevertheless has superior power to ROC 18. However use of JAFROC for CAD evaluation is questionable, since at the designer-level there are more marks per view and JAFROC cannot predict an FROC curve and LLFα, which are of most interest to CAD designers.
The approach taken in this paper builds on the initial detection and candidate analysis (IDCA) method 29 of fitting designer-level FROC data. While this method has been informally used by some CAD designers 21,31 to draw smooth FROC curves through data points, the contribution of the IDCA work was to provide a theoretical foundation for the ad-hoc procedure. Aims of this study were: (1) to examine the assumptions underlying IDCA that limit it to designer-level data and develop a software implementation of this method, including quantitative fit statistics that would make it more useful to CAD designers, which to our knowledge is currently unavailable. (2) To develop a method that relaxes the assumptions and is not only applicable to designer-level data but is potentially applicable to clinical-level data. The method is based on a psychophysical model of visual search 32,33,34 that closely parallels the approach used in the design of CAD algorithms. (3) To develop a method for analyzing CAD data that does not require specification of an arbitrary operating point or α-value. The organization of the paper is as follows: introductory material is presented to define the CAD designer-level free-response data structure and to establish the notation and the plotting of FROC data points. Descriptions of IDCA and the search model and corresponding expressions for fitted FROC curves are given and two figures of merit are defined, one of which does not require specification of an arbitrarily chosen operating point. The IDCA and search model maximum likelihood estimation procedures are described as well as calculation of relevant statistics such as confidence intervals and goodness of fit. Practical details of CAD data sets, in particular case-based vs. view-based scoring, are reviewed. Results of applications of both methods to 7 CAD designer-level data sets are presented and discussed, as well as differences between IDCA and the search model, their relationship to JAFROC, and avenues for further research are indicated.
2. Methods
2.1 FROC and pseudo-ROC operating points
CAD identifies regions suspicious for lesions and for each region, or decision site, it calculates a decision variable z related monotonically to the estimated probability that a lesion is present. It is assumed that the truth regarding these regions is known to the designer and higher values of z correspond to higher probabilities. N′ regions corresponding to non-lesions are termed noise-sites and U′ regions corresponding to lesions are termed signal-sites. The primes are needed to distinguish between these integers that are known to the algorithm designer, and are specific to a particular CAD data set, from similar numbers in the search model, described below, that are unknown. A cutoff variable ζ determines if a suspicious region is marked, if z > ζ, or not marked, if z ≤ζ. Marked regions corresponding to lesions are classified as lesion localizations (LLs) and all other marked regions are classified as NLs. Let F(ζ) and T(ζ) denote the numbers of NL and LL marks, respectively, where both are functions of ζ. The ordinate of the FROC operating point corresponding to cutoff ζis y(ζ) = T(ζ)/NL, where NL is the total number of lesions in the data set. The corresponding abscissa is x(ζ) = F(ζ)/NI, where NI is the total number of images. Considering the N′ and U′ regions as normal and abnormal “cases”, respectively, in a pseudo-ROC study, the cutoff yields F(ζ) “false-positives” and T(ζ) “true-positives”. The ordinate of the pseudo-ROC operating point is T(ζ) / U′ and the corresponding abscissa is F(ζ) / N′. If ζis now gradually lowered, it will eventually drop below the z-sample(s) of the next-most suspicious region(s), until now unmarked, and these region(s) will be marked. This will result in an upward-right jump to the next FROC and pseudo-ROC operating points. The FROC and pseudo-ROC operating points have a one-to-one correspondence. The staircase like FROC plot resulting from this procedure is often referred to as the “raw” FROC curve. The FROC curve starts at (0, 0) corresponding to ζ= ∞ when no regions are marked and F(ζ) = T(ζ) = 0. It ends at (λ′, ν′) where λ′ = F(−∞)/NI = N′/NI and ν′ = T(−∞)/NL = U′/NL, when all regions being marked. The corresponding pseudo-ROC curve starts at (0, 0) and ends at (1, 1).
2.2 IDCA
Fig. 1 illustrates the IDCA approach to fitting FROC operating points. IDCA regards the lesion and non-lesion localization counts as arising from normal and abnormal “cases” in a pseudo-ROC study. The counts are analyzed by ROC curve-fitting software yielding the fitted curve shown in the upper panel. The FROC curve, shown in the lower panel, is obtained by a mapping operation indicated by the arrow, consisting of a point-by-point multiplication of the pseudo-ROC curve along the y-axis by ν′, and along the x-axis by λ ′, where (λ′, ν′) are the coordinates of the observed end-point of the FROC curve, i.e., the point farthest from the origin. Therefore the corner (1, 1) of the pseudo-ROC curve maps to the end-point (λ′,ν′) and each pseudo-ROC point maps to a unique FROC point. Four pseudo-ROC and four FROC operating points and the corresponding cutoffs ζi (i = 1, 2, 3, 4) are shown in Fig. 1. The ROC fitting procedure is based on a probabilistic model for the ratings, most commonly the binormal model 35, but other models 36,37,38,39 can be used. Let xROC(ζ), yROC(ζ) denote the coordinates of a particular operating point on the fitted pseudo-ROC curve and let x(ζ), y(ζ) denote the coordinates of the corresponding point on the fitted FROC curve. The observed end-point is reached by including all suspicious regions in the NL and LL counts,
Figure 1.
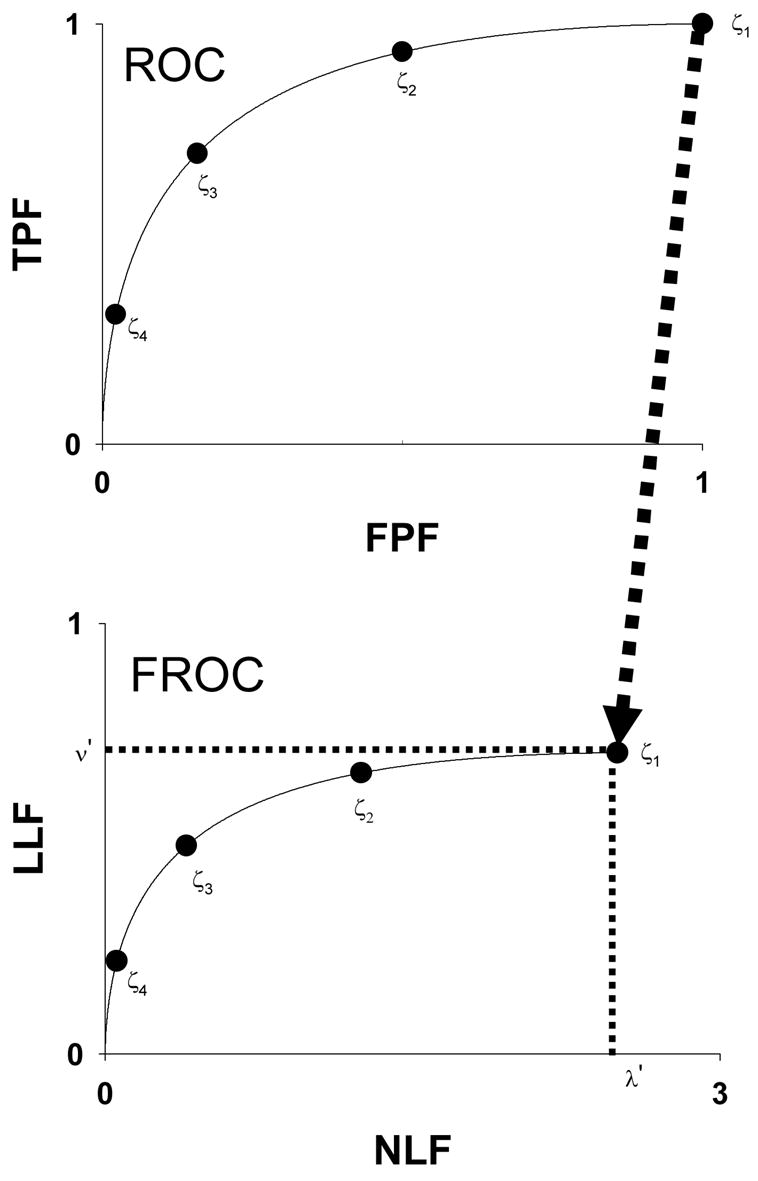
This figure illustrates the IDCA approach to fitting FROC operating points. IDCA regards the lesion and non-lesion localization counts as arising from normal and abnormal “cases” in a pseudo-ROC study. The counts are analyzed by ROC curve-fitting software yielding the fitted curve shown in the upper panel. The FROC curve, shown in the lower panel, is obtained by a mapping operation indicated by the arrow, consisting of a point-by-point multiplication of the pseudo-ROC curve along the y-axis by ν′, and along the x-axis by λ′, where (λ′,ν′) are the coordinates of the observed end-point of the FROC curve. Therefore the corner (1, 1) maps to the end-point (λ′,ν′) and each pseudo-ROC point maps to a unique FROC point. Four pseudo-ROC and four FROC operating points and the corresponding cutoffs ζi (i = 1, 2, 3, 4) are shown.
| Eqn. 1 |
According to IDCA the fitted FROC curve is obtained by scaling the pseudo-ROC curve as follows:
| Eqn. 2 |
If the binormal model is used to fit the pseudo-ROC data points then
| Eqn. 3 |
where Φ(ζ) is the cumulative distribution function corresponding to the zero-mean unit-variance normal distribution and a and b, the parameters of the binormal model 35, can be calculated by available software (e.g., ROCFIT or RSCORE-II, links to which are to be found at http://www.mips.ws).
Consider an R-rating free-response study where the decision variable z is binned into one of R bins labeled 1, 2, …, R, with higher bin labels corresponding to higher probability that a lesion is present (R= 4 in the example shown in Fig. 1). The R bins correspond to R ordered cutoffs ζi (i = 1, 2, …, R), see Figs. 2 (a) and (b). For convenience define dummy cutoffs ζ0 = −∞ and ζR+1 = ∞. The cutoff vector is defined as and the binning rule is that if ζi < z < ζi+1 then the corresponding decision site is marked and rated in bin “i”, and if z < ζ1 then the site is not marked, and by definition these belong to the default bin “0”. The NL ratings vector is and the LL vector is , where Fi is the sum over all images of NLs rated in bin “i” and Ti is the corresponding number for LLs. The pseudo-ROC and FROC operating points corresponding to bin j (j = 0, 1, …, R) are defined by
Figure 2.
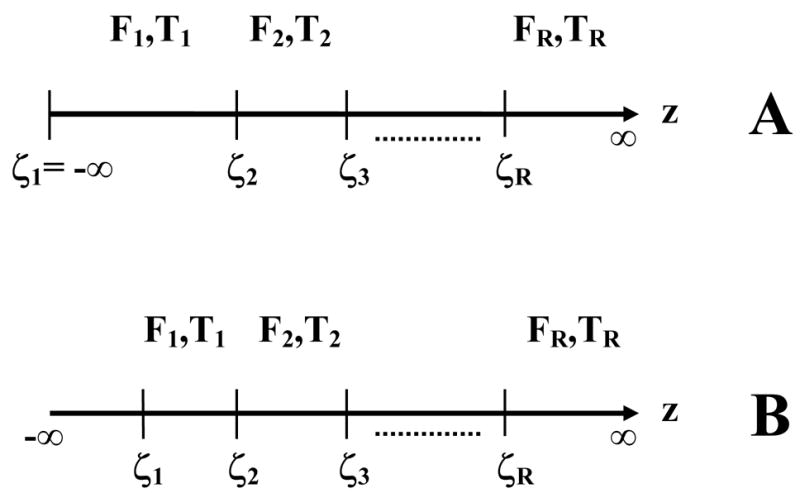
This figure compares the cutoffs implicit in the two models; panel (a) corresponds to IDCA and panel (b) corresponds to the search model. For an R-rating free-response study there are R ordered cutoffs ζi (i = 1, 2, …, R). The observed non-lesion and lesion localization counts are Fi and Ti, respectively. Since the pseudo-ROC point corresponding to the lowest bin is (1, 1), the corresponding cutoff ζ1 is negative infinity and no counts are possible below it, whereas in the search model ζ1 is finite and an unknown number of counts are possible below it. It is this difference that makes search model parameter estimation more difficult.
| Eqn. 4 |
| Eqn. 5 |
IDCA assumes that all decision sites are known to the investigator and each one is marked and rated. The binning assures that each mark is binned into a non-default bin, i.e., each mark is explicitly rated 1 or higher. Therefore F0 = T0 = 0 and and . This implies , in other words the most-lax pseudo-ROC operating point, corresponding toζ1, is at the upper-right corner. The upper-right corner of an ROC plot is known to correspond to a cutoff at negative infinity. Therefore the IDCA assumption is equivalent toζ1 = −∞, see Fig. 2 (a). Since the (1, 1) point on the pseudo-ROC curve point is mapped to λ′,ν′ on the FROC curve, it follows that the observed end-point of the FROC curve also corresponds to a cutoff at negative infinity. Since the cutoff is at its lowest limit the observer cannot move past the observed end-point, i.e., have an operating point that is upward-right with respect to the observed end-point. Fig. 2 (b) shows the cutoffs ζi(i = 1, 2, …, R) necessary to model an R rating free-response study according to the search model. Note that in this case the lowest cutoff is not at negative infinity – a crucial difference from IDCA that necessitates a more complex estimation procedure as will be shown below. The numbers of unmarked suspicious regions with z-samples below ζ1 are unknown to the investigator. Therefore N and U are unknown and must be treated as non-negative random integers. In IDCA the number of unmarked regions is assumed to be known, specifically it is assumed to be zero, therefore N′, U′ are known, and hence the notational distinction between primed and unprimed variables.
The claim that ζ1 = −∞ for IDCA may appear surprising since the smallest z-sample for a particular CAD data set is some finite number , not negative infinity, and therefore, on the face of it, should equal this number. Here r is the replication or “realization” index, r = 1, 2, ....., corresponding to different dataset realizations from an underlying population of datasets, all analyzed by the same CAD algorithm. The apparent paradox is resolved if one bears in mind that a smaller theoretical cutoff will also result in the same observed numbers of counts, and therefore cannot be ruled out. Moreover, the fact that for every realization r there are zero counts below implies that the true lowest cutoff for each realization must be at negative infinity. It may be noticed that in IDCA cutoffs ζ0 and ζ1 are both equal to −∞. To describe the IDCA model we need not have introduced the dummy cutoff ζ0. However ζ0 is needed when one cannot assumeζ1 = −∞, as in the search model.
2.3 Figure of merit
A commonly used figure of merit in CAD algorithm optimization is the LLF at a specified value αof NLs per image (i.e., NLF = α). This quantity is denoted LLFα and one expects that LLFα = LLF (a,b,λ′,ν′,α). The value of α depends on the CAD application. For example, for lesion detection on mammograms, typical values of α currently lie in the range of 0.5 to 3.0, while for lung nodule detection on radiographs or CT volumes typical values of α are usually higher. LLF α was computed by solving
| Eqn. 6 |
for ζα. Then
| Eqn. 7 |
The IDCA parameters a, b,λ′,ν′,ζ2,…,ζR were estimated as described in Ref. 29. Note that since IDCA assumes ζ1 = −∞ this parameter is absent from the parameter list. Methods for calculating relevant statistics, including asymmetric 95% confidence interval for ν′ and LLFα, and the χ2 goodness of fit statistic, are described in Appendix A.
2.4 Search model
Medical images are interpreted by radiologists who do not report all suspicious regions, only those considered sufficiently suspicious to warrant clinical action. The observed end-point for radiologists cannot correspond to ζ1 = −∞. For this reason it would be incorrect to apply the IDCA procedure to radiologist free-response data, a possibility noted in the IDCA publication. We will shortly describe a method by which a theoretical FROC curve can potentially be fitted to either clinical-level data or designer-level CAD data. The method 40,41 is based on a two-stage cascaded visual interpretation model 32,33,34 that closely parallels the approach used in the design of CAD algorithms (see Discussion). The first stage identifies suspicious regions that need further examination and decision making. At the second stage the observer calculates a decision variable (or z-sample) for each suspicious region that was identified at the first stage. A region is marked if the z-sample exceeds the observer’s lowest reporting cutoff ζ1 and the rating assigned to the mark depends on how the z-sample is binned. Regions identified at the first stage that correspond to non-lesions are termed noise-sites and regions corresponding to lesions are termed signal-sites. Signal and noise sites are collectively referred to as decision sites. The number n of noise-sites on an image is modeled by a Poisson process 42 with mean λ. The number u of signal-sites on an abnormal image is modeled by a Binomial process 42 with success probability ν and trial size s, where s is the number of lesions in the image. The lowercase variables n and u pertain to individual images and the uppercase variables N and U denote the corresponding quantities summed over all images. Let NN and NA denote the number of normal and abnormal images, respectively, and let k denote the image index, i.e., k = 1, 2,…, NN+NA and NI = NN+NA. Since n, u and s depend on the image, they are denoted nk, uk and sk. Then
| Eqn. 8 |
| Eqn. 9 |
and
| Eqn. 10 |
Noise-site z-samples are obtained by sampling from the zero mean unit variance normal distribution and signal-site z-samples are obtained by sampling from the unit variance normal distribution with mean μ.
2.5 Search model predicted FROC curves
The probability that a noise site z-sample exceeds ζ is
| Eqn. 11 |
Here Φ(ζ) is the cumulative distribution function corresponding to the zero mean unit variance normal distribution. Because of the assumed Poisson process the mean number of noise-sites on an image is λ and therefore the mean number of NLs per image, i.e., the FROC x-coordinate is
| Eqn. 12 |
The probability that a signal site z-sample exceeds ζ is
| Eqn. 13 |
Because of the assumed Binomial process, the expected number of signal-sites on an image is siν, where si is the number of lesions in the ith abnormal image. Therefore the expected number of LLs in the ith abnormal image is si ν(1 − Φ(ζ − μ)). The y-coordinate of the FROC curve is obtained by summing this quantity over all images and dividing by the total number of lesions, i.e.,
| Eqn. 14 |
2.6 Figure of merit
The figure of merit LLFα = LLFα(μ, λ, ν, α) for the search model was computed by solving
| Eqn. 15 |
for ζα. Then
| Eqn. 16 |
2.7 An alternate figure of merit
A quantity θ where 0 ≤ θ ≤ 1 was defined 40 as the probability that the highest z-sample on an abnormal image exceeds that on a normal image. For normal images the highest z-sample is necessarily from a noise site but for an abnormal image it could be either from a noise site or a signal site, whichever has the greater z-sample. Assuming the highest z-sample on an image is used as the single “ROC-like” z-sample for the image, it was shown 41 that θ is identical to the area under the search model predicted ROC curve. This curve is not to be confused with the pseudo-ROC which was defined by treating the noise and signal sites as “images” and N′ and U′ are treated as fixed and known integers. One has where denotes the vector of numbers of lesions in the abnormal images. [The figure of merit LLFα does not depend on the vector ] As shown earlier 40 and as expected on physical grounds, increases as the number of lesions per image increases. To remove this dependence, which would bias the measurement in favor of observers or CAD algorithms evaluated with lesion-rich image sets, we propose as the free-response figure of merit the area under the search model predicted ROC curve for a hypothetical data set where every abnormal image has 1 lesion, namely, . The fitting algorithm function takes into account the actual vector but the figure of merit corresponds to .
2.8 Estimating the search model parameters
Maximum-likelihood (ML) is a common method of estimating the parameters of a statistical model 43. Let denote the R+3 dimensional vector of search model parameters. The log likelihood function for the search model is given in Appendix C. Maximizing LL is equivalent to minimizing −LL. The following algorithm was used. One regards ζ1 as a deterministic function of λ instead of as an independent parameter and the new parameter vector is ξ̂′ = (μ, λ ν ζ2,..., ζR). The relation between ζ1 and λ is
| Eqn. 17 |
where λ′ is the abscissa of the observed end-point. A value for λ was selected and the corresponding ζ1 determined by solving the above equation. Next −LL was minimized with respect to the remaining parameters ξ̂″ = (μ, ν ζ2,..., ζR). The method of simulated annealing 44 as implemented in the GNU library 45 was used to find the minimum value of −LL, namely −LLλ(λ). The parameter λ was varied until a global minimum of −LLλ(λ) was found. Since 0 ≤ 1 ≤ Φ(ζ1) ≤ 1, Eqn. 17 implies a constraint on λ, namely λ ≥ λ′. Methods for calculating statistics for the search model, including asymmetric 95% confidence interval for ν′, LLFα and θ1, and the χ2 goodness of fit statistic, are described in Appendix A.
2.9 Case-based vs. view-based analysis
So far we have implicitly assumed that each image corresponds to a different patient (or case) so that the number of images and cases are equal. In practice there could be more than one image per case. In mammography usually there are four views per case: two views per breast (craniocaudal and mediolateral) and two breasts per case. Depending on the slice reconstruction interval, in CT screening for lung cancer there could be several hundred slices per case 46. Therefore new definitions are needed to account for the distinction between cases and views. Define and the numbers of normal and abnormal cases, respectively, and NN and NA the numbers of normal and abnormal views, respectively. A normal view is defined as one in which no lesions are visible to the truth panel, i.e., the radiologist(s) who specify the locations of lesions. For each abnormal case the contralateral breast may contribute 2 normal views, if they are lesion free, and if a lesion is only visible on one view of the affected breast, the other view would be counted as normal. Assuming each case contributes the same number NV of views, the total number of views is .
It is necessary at this point to distinguish between case-based and view-based methods for calculating LLF, as both methods are used and this distinction affects the analysis. Calculation of NLF is the same for either method – the denominator is always the total number of views. Essentially the two methods employ different definitions of NL and what constitutes lesion localization. In the case-based method LL is defined as localization of any lesion in an abnormal case. In the event of multiple LLs on a case the highest rated one is used. Multiple LLs could represent localizations of the same lesion visible on both views and / or localizations of multiple lesions in a view. Therefore in the case-based method the denominator for LLF is the number of abnormal cases . Defining a general lesion count NL as the relevant denominator for calculating LLF, for the case-based method one has . In the view-based method each LL is counted individually and the relevant denominator is the total number of lesions, , where si is the number of lesions on the ith abnormal view. For either method if multiple marks occur near the same lesion the highest rated mark is used. For either case-based or view-based method the fitting algorithm requires appropriate values for LL and NL counts, and appropriate values for calculating the denominators of LLF and NLF. Since the highest rating is used it may be seen that the figure of merit for case based analysis will exceed that for view-based analysis.
The CAD designer chooses a cutoff ζ for displaying marks and only marks with decision variable greater than ζ are shown. This determines the average number of NLs that are marked per image α = x(ζ) and the corresponding ordinate LLFα = y(ζ) of the FROC curve. The choice of α is a compromise between cuing more lesions, which favors large α, and not cuing too many non-lesions, which favors small α. The proximity or overlap criteria, namely how close a mark had to be to a lesion in order to be counted as LL, were specific to the different data sets.
The decision variable data (sometimes referred to as the “raw data”) was binned into R categories. Starting with a high value for cutoff (20) the cutoff was gradually lowered until both LLs and NLs counts in the highest bin exceeded 5, thereby determining the highest cutoff. Next the cutoff was lowered from the previous value until both LLs and NLs counts in the next-highest bin exceeded 5. The procedure was repeated until all marks were exhausted. The number of bins identified as described above equals R and the bin index runs from 1 to R. Since they do not generate marks, the counts in the “0” bin, that is how many z-samples were below the lowest cutoff are unknown. The minimum bin-count (5) ensured that we could calculate a valid chi-square statistic 42. Both IDCA and search model fits were calculated for each data set. For the IDCA fits all counts Ti and Fi (i = 0, 1,…, R) are regarded as known. Specifically the counts in the “0” bin are assumed to be zero. This follows from the assumption that the lowest cutoff is negative infinity. For the search model fits the counts T0 and F0 are regarded as unknown non-negative random integers. [If there were more than 19 bins, the minimum bin-count was incremented from 5 to 6, and the procedure was repeated until the total number of bins was 19 or less. The restriction to 19 bins is so that we did not have to estimate a large number of cutoffs. A similar restriction to 20 or less bins is performed in LABROC to convert quasi-continuous rating data to a form amenable to ML analysis 47.]
2.10 CAD data sets used in this work
Table 1 summarizes the relevant characteristics of the 7 mammography CAD data sets used in this work. Data sets CAD_A, CAD_B, CAD_C and CAD_D represent case based analysis. The task was the detection of masses. All cases in CAD_A and CAD_B had four views (i.e., NV = 4). These data sets consisted of the same 1800 views (or 450 cases) that were processed by two CAD versions and 250 cases each had one malignant mass. Therefore and . Of the 250 masses 236 were visible on both views and 14 were visible only on one view. Therefore NA = 2 × 236 + 14 = 486, and NN = 1800 − 486 = 1314. CAD_D (CAD_C) included 195 (111) abnormal cases, in which 185 (106) masses were visible on both views. The remaining 10 (5) masses in these two data sets were visible only on one view. These values can be used to verify the values of NA listed in Table 1. A few cases had only two views and the rest had 4 views, therefore for these data sets . The same CAD version used for data set CAD_A was applied to process CAD_C and CAD_D.
Table 1.
The characteristics of the mammography CAD data sets used in this work: NV is the number of views per case, is the number of normal cases, is the number of abnormal cases, NN is the number of normal views, NA is the number of abnormal views, and NL is the relevant denominator for calculation of LLF (see text). N′ and U′ are the observed numbers of NLs and LLs, respectively, and R is the number of discrete ratings. The quantity α is the x-coordinate of the operating point at which the CAD algorithm is to be used in the clinic. C and V denote the case-based and view-based methods, respectively.
| Data set | Task | NV | Cases | Views | NL | N′ | U′ | R | α | Analysis Method |
|---|---|---|---|---|---|---|---|---|---|---|
| NN / NA | ||||||||||
| CAD_A | Mass | 4 | 200 / 250 | 1314 / 486 | 250 | 5014 | 234 | 20 | 0.48 | C |
| CAD_B | Mass | 4 | 200 / 250 | 1314 / 486 | 250 | 4447 | 233 | 19 | 0.68 | C |
| CAD_C | Mass | 4* | 0 / 111 | 195 / 217 | 111 | 1139 | 95 | 17 | 0.59 | C |
| CAD_D | Mass | 4* | 0 / 195 | 342 / 380 | 195 | 2029 | 189 | 18 | 0.46 | C |
| CAD_E | Micro | 2 | 71 / 96 | 142 / 192 | 218 | 2048 | 202 | 18 | 1.0 | V |
| CAD_F | Mass | 2 | 0 / 58 | 0 / 116 | 116 | 465 | 101 | 12 | 2.0 | V |
| CAD_G | Micro | 2 | 71 / 96 | 142 / 192 | 96 | 2048 | 96 | 12 | 1.0 | C |
a few cases had only 2 views
For CAD_E, CAD_F and CAD_G there were two views per breast (i.e., NV = 2). CAD_E and CAD_G illustrate the difference between the view-based (CAD_E) and case-based (CAD_G) methods. They represent the same data set with different definitions for NL and what constitutes LL. The task was the detection of microcalcification clusters. Each abnormal case ( ) contained at least one microcalcification cluster and there were normal cases. A total of 104 clusters were visible on both mammographic views, while ten were visible only on one view. Therefore the total number of microcalcification cluster locations marked by the radiologists was 218 and NL = 218. Since each abnormal breast in case-based CAD_G counts as one lesion, NL = 96. The task in dataset CAD_F was the detection of masses. The view-based data set contained 58 malignant masses, all of which were visible on both views, therefore and NL = 116.
N′ ranged from 465 to 5014 NL marks and U′ ranged from 95 to 234 LL marks. The average number of marks per view ranged from 2.5 to 4 for all data sets except CAD_F, for which it was 6.2. Values for NL, the total number of lesions, ranged from 96 to 250. As explained above NL depends on the analysis method. For case-based analysis and for view-based analysis . In all cases U′ ≤ NL, since a lesion can only be localized once, but N′ is unrestricted (possible upper limits on F(ζ) are discussed later). The number of categories R ranged from 12 to 20, with the smaller numbers corresponding to the smaller data sets (view based CAD_E allowed more bins than CAD_G since there were more abnormal views than abnormal cases). The α-values as suggested by the algorithm designers ranged from 0.46 to 2.0 NLs per view. Note that three of the data sets, CAD_C, CAD_D and CAD_F, had no normal cases, i.e., .
3. Results
A typical plot of −LLλ(λ) vs. λ for data set CAD_B is shown in Fig. 3 where the ordinate is the value of −LL(μ,λ,ν,ζ1,…,ζR) after it has been minimized with respect to all parameters except λ. It is seen that −LLλ(λ) has as a minimum as a function of λ, and in this case the minimum occurs at λ = 14.6. A unique minimum was found for all data sets used in this work (uniqueness was tested by using different starting values for the parameters to be estimated). This figure is shown to demonstrate that −LLλ(λ) indeed has a minimum. Initially we had some doubts whether the parameters of this model were estimable since one can argue that the parameters ζ1 and λ are degenerate, with an increase in ζ1 being compensated by an increase in λ, to preserve the observed total numbers of NLs. A similar degeneracy is possible between ζ1 and ν. It appears that the constraint Eqn. 17 resolves this degeneracy.
Figure 3.
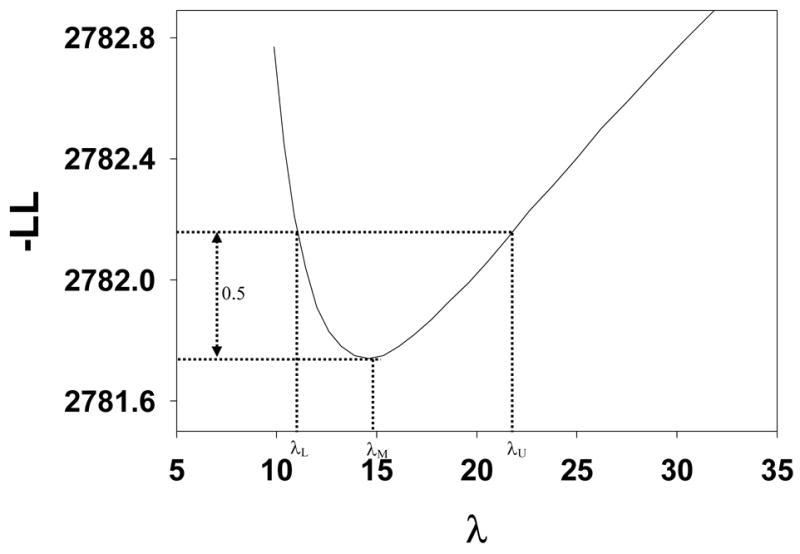
A typical plot of −LLλ (λ) vs. λ, where the ordinate is the value of the negative of the log likelihood after it has been minimized with respect to all parameters except λ. It is seen that −LLλ (λ) has as a minima at λ = λM and [λL,λU ] illustrates the construction of an asymmetric confidence interval for λ, see text.
Fig. 4 shows IDCA (upper panel) and search model (lower panel) fits to data set CAD_A and Figs. 5 and 6 show corresponding plots for data set CAD_B and CAD_F, respectively. Shown are the raw data, showing the expected staircase pattern, the operating points used in the fitting algorithm and the fitted curve. Note that the operating points are constrained to lie exactly on the raw data plot. Also shown are 95% confidence intervals for an intermediate operating point calculated by the method described in Ref. 29 with a modification to account for expected asymmetry in the intervals. For example, the y-confidence interval cannot include values greater that 1.
Figure 4.
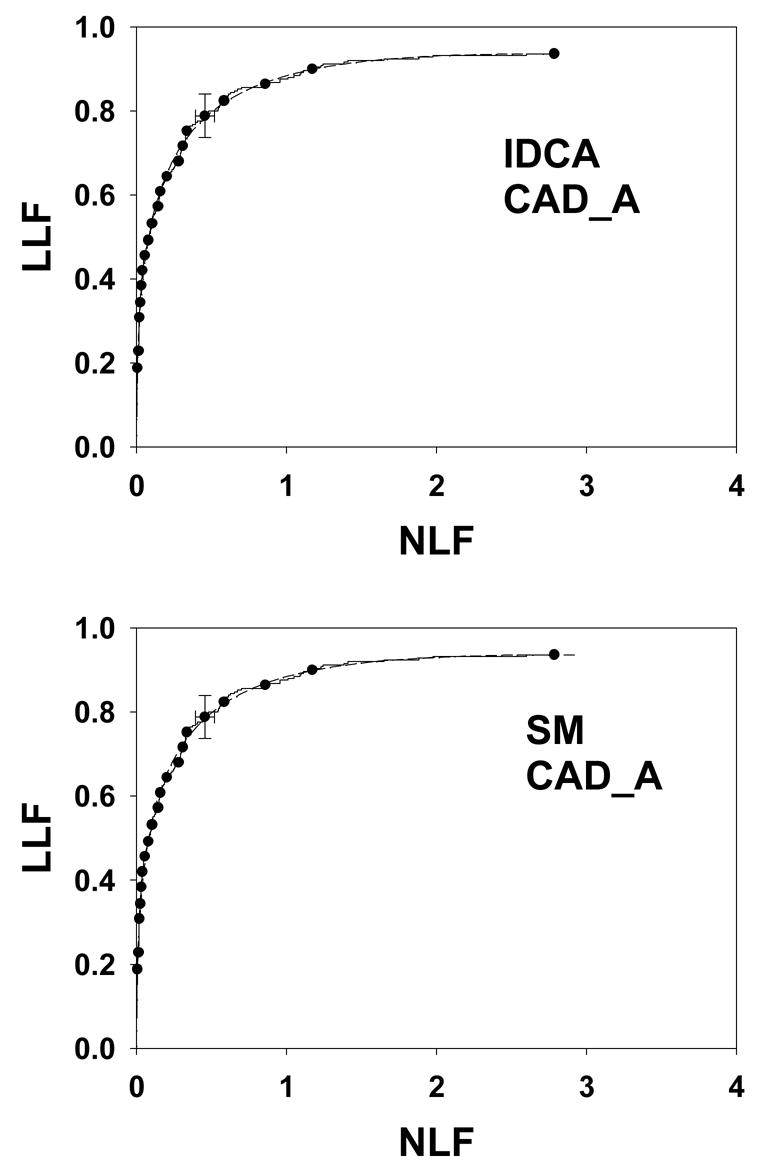
IDCA (upper panel) and search model (lower panel) fits to data set CAD_A. The dashed curves correspond to the model fits (IDCA – upper panel, or search model – lower panel) and the solid curves are the raw data (the same raw data is plotted in the upper and lower panels). Since the fits are close to the raw data it is difficult to distinguish between them – the “staircase” pattern corresponding to the raw data may be helpful. The solid circles are operating points resulting from binning the data, and the binned data was used by the fitting procedures. They are constrained to lie exactly on the raw curve. Shown are 95% confidence intervals for an intermediate operating point. Both fits are visually excellent although the statistical measures of quality of fit are not as good (p-values 0.0074 and 0.0073, see text for more discussion of this aspect).
Figure 5.
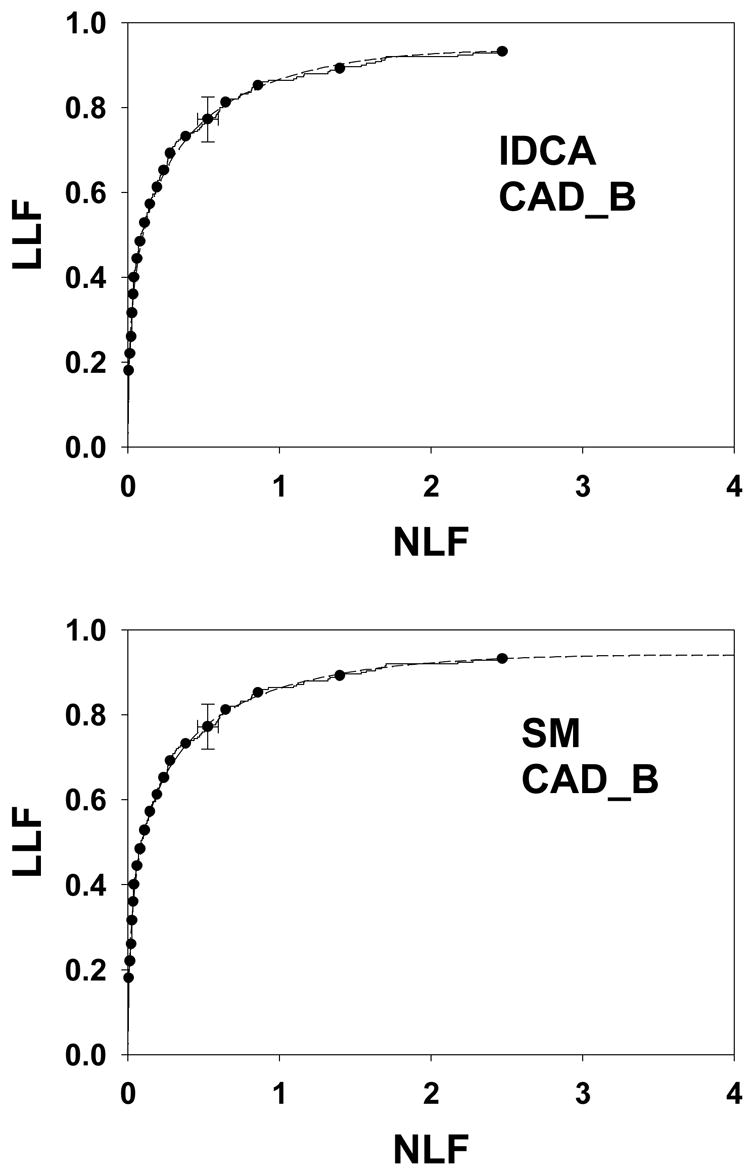
As in Figure 4, except this is for data set CAD_B. Both fits are excellent (p-values 0.36 and 0.44).
Figure 6.
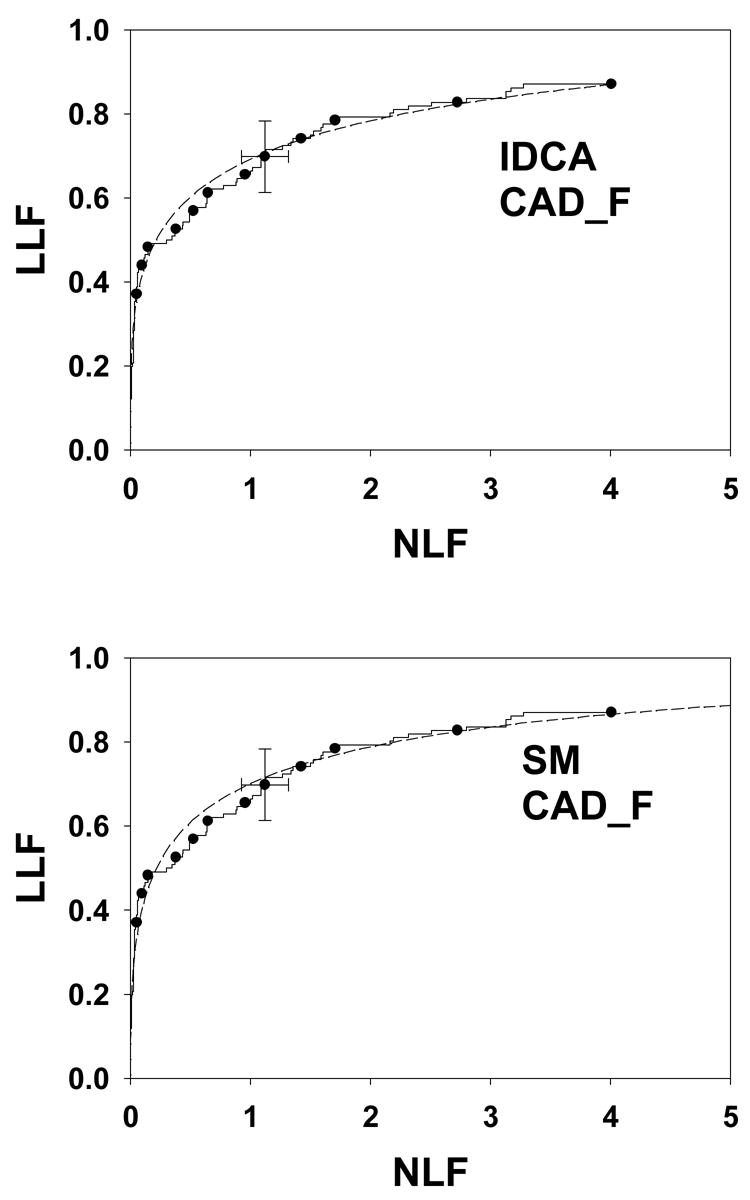
As in Figure 4, except this is for data set CAD_F. Both fits are excellent (p-values 0.28 and 0.21).
Table 2 lists the results of IDCA analyses of the data sets. The μ′ and σ′ parameters refer to the mean and standard deviation of the Gaussians of the binormal model. They are related to the a and b parameters of the binormal model by μ′ = a / b and σ′ = 1 / b. The x and y coordinates of the observed end-point are identical to the corresponding IDCA estimates λ′ and ν′, respectively. The quantities in parentheses are asymmetric 95% confidence intervals. The figure of merit LLFα using the α values listed in Table 1 ranged from 0.554 to 0.942. The p-value is an indicator of the quality of the fit, with larger p-values corresponding to better fits. With the exception of CAD_A, p-value = 0.0074, all fits are statistically acceptable. Further details for this data set are provided below. For our data sets the average reported number of NLs was 2.5 to 6.2 per view, as reflected in the IDCA estimates of the λ′ parameter in Table 2. Table 3 lists the results of search model analyses of the data sets. The parameter estimates μ, λ and ν and their 95% confidence intervals (in parentheses) are listed. For the search model the estimated end-point (λ, ν) does not, in general, coincide with the observed end-point (λ′, ν′). Since the search model is allowing for unobserved counts below ζ1 one expects λ ≥ λ′, and ν ≥ ν′, as observed in Tables 2 and 3 and as is evident from Figs. 4, 5 and 6. In other words λ and ν resulting from SM analysis lie to the upper-right of the observed end-point, λ′ and ν′.
Table 2.
This shows the results of IDCA analyses. The μ′ and σ′ parameters refer to the mean and standard deviation of the Gaussian from which the signal-site decision variables are sampled, λ′ and ν′ parameters are the x and y coordinates of the observed end-point, and quantities in parentheses are 95% confidence intervals. The figure of merit LLFα, evaluated at the α values shown in Table 1, is commonly used by CAD designers to evaluate CAD performance. The p-value is an indicator of the quality of the fit.
| Data set | σ′ | μ′ | λ′ | ν′ | LLFα | p-value |
|---|---|---|---|---|---|---|
| CAD_A | 1.02 (0.882,1.15) | 1.98 (1.82,2.13) | 2.79 (2.71, 2.86) | 0.936 (0.900,0.962) | 0.791 (0.775,0.806) | 7.35E-3 |
| CAD_B | 1.09 (0.954,1.24) | 1.85 (1.69,2.01) | 2.47 (2.40, 2.54) | 0.932 (0.895,0.959) | 0.814 (0.800,0.828) | 0.360 |
| CAD_C | 1.14 (0.929,1.35) | 1.17 (0.918,1.42) | 2.57 (2.41, 2.72) | 0.856 (0.782,0.915) | 0.554 (0.524,0.585) | 0.247 |
| CAD_D | 1.18 (0.996,1.36) | 1.83 (1.63,2.04) | 2.60 (2.49, 2.72) | 0.969 (0.937,0.988) | 0.755 (0.736,0.774) | 0.541 |
| CAD_E | 0.928 (0.764,1.09) | 2.15 (1.96,2.34) | 6.13 (5.86,6.40) | 0.927 (0.886,0.957) | 0.830 (0.816,0.845) | 0.821 |
| CAD_F | 1.47 (1.10,1.85) | 1.89 (1.49,2.28) | 4.01 (3.64,4.38) | 0.871 (0.801,0.925) | 0.783 (0.755,0.810) | 0.282 |
| CAD_G | 0.958 (0.704,1.21) | 2.40 (2.13,2.67) | 6.13 (5.86, 6.40) | 1.0 (1.00,1.00) | 0.930 (0.921,0.939) | 0.324 |
Table 3.
This shows the results of search model analyses. The μ parameter refers to the mean of the Gaussian from which the signal-site decision variables are sampled (the standard deviation is assumed to be unity) and λ and ν parameters are the x and y coordinates of the true end-point. In addition to LLFα, which depends on the choice of α, the search model provides a second figure-of-merit which is independent of α. NA: confidence interval cannot be calculated due to floating point overflow.
| Data set | μ | λ | ν | LLFα | θ1 | p-value |
|---|---|---|---|---|---|---|
| CAD_A | 2.00 (1.82,2.45) | 2.92 (2.79, 5.79) | 0.936 (0.900,0.970) | 0.792 (0.761,0.807) | 0.747 (0.722,0.778) | 7.33E-3 |
| CAD_B | 2.06 (1.68,2.57) | 4.02 (2.47, 10.7) | 0.941 (0.895,0.989) | 0.814 (0.781,0.840) | 0.736 (0.706,0.768) | 0.440 |
| CAD_C | 1.49 (0.924,2.66) | 5.33 (2.57, 37.5) | 0.925 (0.782,1.00) | 0.560 (0.528,0.594) | 0.624 (0.585,0.706) | 0.226 |
| CAD_D | 2.16 (1.60,2.80) | 5.96 (2.60, 17.4) | 0.992 (0.937,1.00) | 0.763 (0.734,0.790) | 0.737 (0.696,0.783) | 0.573 |
| CAD_E | 2.19 (2.02,2.55) | 6.13 (6.13,9.06) | 0.927 (0.886,0.958) | 0.822 (0.799,0.835) | 0.821 (0.796,0.847) | 0.757 |
| CAD_F | 2.84 (NA) | 95.6 (4.64,1096) | 1.00 (NA) | 0.789 (NA) | 0.771 (NA) | 0.210 |
| CAD_G | 2.42 (2.17,3.04) | 6.13 (6.13, 14.8) | 1.00 (1.00,1.00) | 0.925 (0.894,0.932) | 0.833 (0.793,0.877) | 0.303 |
Two figures of merit, namely LLFα(for the same α values in Table 1) and θ1 are listed in Table 3. The figure of merit LLFα ranged from 0.567 to 0.923 and θ1 ranged from 0.624 to 0.833. The values of LLFα for the two methods are in good agreement (the correlation coefficient was 0.93). For the data sets CAD_E and CAD_G which used the same mark-rating data, thereby permitting such comparisons, for both IDCA or search model analysis the case-based figures of merit were larger than the corresponding view based quantities. In terms of p-values, the search model yielded similar fits as IDCA for all data sets. The parameter estimates for CAD_F had large variability, e.g., λ was essentially indeterminate. The IDCA and search model fits to this data set are indistinguishable, see Fig. 6, and statistically both are good fits to the data. IDCA or search model based estimates of the variability of the ordinate of an operating are expected to be smaller than that predicted by binomial statistics, since the latter does not use all the data, only the portion that is below (in the FROC plot) the chosen operating point. According to binomial statistics the standard deviation of y is σ = √ [y(1 − y)/NL]. For CAD_B at operating point (0.860, 0.852) the width of the search model based confidence interval (4σ) for y = 0.852 was 0.0565, and the corresponding binomial estimate was 0.0898.
In Fig. 3 the minimum occurs at λ = 14.6, which is 4 times the value of λ listed in Table 3. The ML analysis treats λ as the mean number of noise sites per case, but in keeping with current convention, in the FROC plot the x-axis is defined per view. For this data set there were 4 views per case. For data sets CAD_E, CAD_F and CAD_G the difference is a factor of two, as there were 2 views per case.
4. Discussion
The search model used in this study was introduced to model lesion and non-lesions localizations and the corresponding z-samples (decision variables) generated in a free-response study 40. It was compared to other models, the figure-of-merit was defined and its dependence on model parameters was analyzed. Assuming the highest rating on an image is reported as the equivalent single “ROC” rating for that image, search model predicted ROC curves were described 41. However, the model was not previously used to fit FROC data. In this study, we have described a search model based technique for analyzing free-response data generated by CAD algorithms. The method yields the lesion localization fraction LLFα at a specified value of α, the number of NLs per image. The figure of merit LLFα, widely used by CAD designers, can be utilized to optimize algorithms. The search model allows the calculation of an alternate figure of merit measuring the ability of the CAD system to discriminate between normal and abnormal images in a hypothetical data set where each abnormal image contains one lesion. This figure of merit does not require specification of α. Since there is no consensus on what value of α to use, the alternate optimization scenario of maximizing θ1 may be advantageous. Alternative α–based figures of merit 26,28 can be calculated from the search model.
Unlike IDCA the search model approach is applicable not only to designer-level data but potentially to clinical-level data. This is because IDCA assumes that the lowest cutoff ζ1 = − ∝, i.e., all suspicious regions are reported. The search model treats ζ1 as a free parameter to be estimated from the data. This more closely models the clinical task since radiologists do not report every region that was deemed suspicious, only those meeting their criterion for clinical reporting. The essential difference between IDCA and the search model is this: IDCA does not permit the fitted curve to extend beyond the uppermost observed operating point. This fact is evident in all IDCA fits shown in this paper. Consider a human observer study involving a single reader reading thousands of images (to eliminate sampling variability) and assume that the reader is infinitely reproducible (to eliminate that source of variability). If this study was repeated with the observer using a laxer criterion, i.e., reporting more suspicious regions, then some of the new operating points would be to the upper-right of the end of the IDCA-fitted curve based on the first reading. IDCA may yield a good fit to the first study but it would not be able to fit all operating points in the second study. By assuming that the lowest cutoff in the first study is negative infinity, the observer who re-reads the images is not permitted to adopt an even lower criterion (nothing is smaller than negative infinity). In contrast the search model curve does not end at the uppermost observed operating point but generally extends beyond it. This is evident in all search model fits shown in this paper and is obvious in Figs. 5 and 6. This allows the search model to better fit all acquisitions using the same reader, not just the first. We have conducted preliminary studies showing the feasibility of the search model approach using simulated clinical data 48 but estimation of search model parameters from clinical-level data is outside the scope of this work.
The IDCA implementation described in this work includes an algorithm for calculating the figure of merit LLFα, its 95% confidence interval, and a measure of quality of the fit. Both IDCA and the search model methods involve maximum-likelihood estimation. Likelihood functions corresponding to the two methods are compared in Appendix C where it is shown that in the limit ζ1 = −∞ they are identical. IDCA assumes that N′ and U′, the numbers of noise sites and signal sites, respectively, equal the observed numbers of NLs and LLs, respectively. This allows λ′ and ν′ to be readily estimated, see Eqn. 1. For the search model N and U are regarded as unknowns (random) and the estimation procedure is necessarily more complex. The IDCA procedure uses a two parameter model (unequal-variance binormal, or perhaps a proper-ROC model) to describe z- sampling, whereas the search model uses one parameter μ, equivalent to an equal-variance binormal model. However, both models involve identical numbers of parameters. The extra z-sampling parameter in IDCA is balanced by the fact that it assumes the lowest cutoff ζ1 = −∞ and does not need to be estimated. Either method can be used to compare different CAD algorithms applied to the same of cases and where the marks are scored using the same proximity criterion. To our knowledge no method exists that can compare CAD performance on different case sets and using different proximity criteria, although a method for dealing with the arbitrary proximity criteria issue has recently been suggested 49.
Both methods involve parametric models and independence assumptions and differ substantially from the quasi non-parametric JAFROC 18 method (JAFROC assumes normal distributions at the analysis of variance step). However, unlike JAFROC, parametric models use all the data and predict FROC curves. JAFROC is unable to analyze data sets with no normal images (CAD_C, CAD_D and CAD_F) but this is not a problem for IDCA or the search model methods. Both IDCA and the search model assume Poisson sampling. This permits large values of n, the numbers of noise sites per image. In reality the anatomic area to lesion area ratio places a geometric upper limit on these numbers. Therefore the Poisson assumption may not be valid for some CAD data. [A binomial distribution for n, currently under investigation, may be a better sampling model.] Based on simulation work in the ROC context 50, failure of the Gaussian assumption may not be critical but this needs to be tested. Failure of the independence assumption is expected to result in underestimation of confidence intervals. For modality comparisons the independence issue can be resolved using resampling schemes 51, e.g., jackknifing 18,52 and bootstrapping 53. In the jackknife method, for each modality, reader and case, one removes all responses pertaining to the case, re-computes the figure of merit and calculates a pseudovalue. The array of pseudovalues is analyzed by analysis of variance 52. When resampling methods are used the parametric assumptions needed to compute a figure of merit may not be significant limitations. In other words, we are suggesting the use of a parametric model to compute the figure of merit (FOM) and performing resampling analysis using this FOM to infer inter modality differences. An advantage of this procedure over other suggested non-parametric methods 27,28 is that unlike them it uses all the data, not just the data below NLF = α.
An implication of the search model is that the actual number of decision sites on an image may exceed the observed number in a designer-level data set. A typical CAD algorithm has a pre-screening step at which some regions are identified as potential lesions, and a false-positive reduction or feature analysis step in which one focuses attention to only the identified regions. The pre-screening step might start with the application of a spatial filter that preferentially enhances regions that resemble the type of lesions that the algorithm is expected to find. For example, a microcalcification detection algorithm might apply a band-pass filter to the image to enhance regions that might contain small objects with high contrast. A cutoff and other rules may then be applied to the filtered image to select any region that may match the lesion criteria. Therefore, the prescreening step typically produces a relatively large number of candidate regions, but ideally misses relatively few lesions. Some CAD systems reduce the number of candidate regions in two ways. First, an overlap criterion may be used to eliminate regions that substantially overlap with each other. Second, the number of candidate regions per image (or case) may be further limited to a specified maximum number. In IDCA terminology prescreening step described above yields the initial detections. The false-positive reduction or feature analysis step represents the candidate analysis, which yields the z-samples. Since in effect multiple cutoffs are being applied prior to identification of the initial detections, the reported number N′ is expected to be smaller than the true N, where “true” is the effective number of regions that are considered by the CAD algorithm as possible candidates. The qualifier “effective” allows for the fact that N is expected to be smaller than the number of regions exhibiting the lesion criteria.
As noted previously, the CAD_A fits shown in Fig. 4 had the smallest p-values, representing the worst statistical fits, yet both are seen to be excellent visual fits to the data. The small p-values (large chi-square statistics) resulted from a few neighboring bins where the expected and observed counts differed significantly but in opposite directions (i.e., in one bin the expected count was larger than the observed count, but in the adjacent bin it was smaller). If these bins were combined, the expected and observed counts were in closer agreement and the p-value improved markedly. For example, using 17 bins (instead of 20) the p-value of the search model fit to CAD_A improved to 0.241 (the other estimated quantities were essentially unaffected).
The search model λ and ν parameter estimates for CAD_F are unreasonable. This may be due to the significant linear portion of the raw data plot which is inconsistent with the search model. To accommodate a linear portion one needs mixture distributions for both signal and noise, specifically probability density functions with significant components centered at a common value between 0 and μ. [A mixture distribution for signal with a component centered at the origin is used in the contaminated binormal model to predict an ROC curve with a linear portion39.] However, the search model confidence interval for λ is very large, which is due to a quasi-flat likelihood function −LLλ (λ) vs. λ plot. Limitations of floating point arithmetic prevented us from calculating confidence intervals for the remaining quantities for this data set. Nevertheless in the common range (i.e., not extending beyond the observed end-point) both IDCA and search model yielded excellent and essentially indistinguishable fits for all data sets.
If interest is in comparing designer-level CAD algorithms data using LLFα, and a common α can be agreed upon and which is in the accessible range of all algorithms being compared, then either IDCA or the search model could be used. The search model allows calculation of an additional figure of merit that is independent of α. The distinction between FROC curve comparisons based on (α, LLFα) and that based on is analogous to ROC curve comparisons based on (specificity, sensitivity) and that based on area under the ROC curve. In ROC applications usually the latter method is preferred. This does not invalidate designer-level CAD optimization using LLFα but evaluation of clinical-level CAD is best performed, in our opinion, using a figure of merit like θ1 that is independent of any specific operating point on the FROC curve.
5. Conclusion
We have described two methods of fitting FROC curves and obtaining figures of merit and their confidence intervals. One method is termed IDCA and the other is based on a recently introduced search model. Both methods closely parallel the approach used in the design of CAD algorithms. The IDCA method is applicable to designer-level CAD data where one knows all locations that were considered suspicious, not just the ones that were actually marked. The search model method is potentially applicable to clinical-level CAD data and to human observers where only a small fraction of all suspicious regions that are found are actually reported. Both methods yielded excellent fits to seven designer-level CAD data sets and either of them could be used to evaluate a CAD algorithm at the designer-level. A new figure of merit is proposed for CAD evaluation that does not depend on arbitrary selection of an operating point on the FROC curve.
Acknowledgments
This work was supported in part by NIH grants R01 EB005243 and R01 EB006388 (DPC), R01 CA101733 (BZ) and R01 CA095153 (BS). The authors are grateful to Drs. Heang-Ping Chan and Sophie Paquerault for a portion of the CAD datasets, and to Dr. Andrei Bandos for assistance with the confidence interval calculations.
Appendix A
IDCA confidence intervals
The R+3 parameters of the IDCA model are denoted by the vector . The IDCA likelihood function29 is the sum of three terms corresponding to three independent sampling processes, Poisson for the number of noise sites, Binomial for the number of signal sites, and Binormal for the z-sample. Therefore the covariance of λ′ and ν′ is zero as are the covariances of λ′ and ν′ with each of the remaining parameters a, b,ζ2,…,ζR. The variances of λ′ and ν′ are given by29
| Eqn. A1 |
The 95% confidence interval for ν′ is ν′ ± 2σ (ν′) and similarly for λ. When ν′ is close to unity, the above procedure can result in an interval that is partially outside the allowed range 0 ≤ ν′ ≤1. To circumvent this ν′ was transformed to the unconstrained variable νt according to
| Eqn. A2 |
where −∞ < νt < ∞. The variance of νt was calculated from
| Eqn. A3 |
The symmetric confidence interval for νt, namely νt ± 2σ (νt), was inverse-transformed to an asymmetric confidence interval for ν′ which was always inside the allowed range 0 ≤ ν′ ≤1. The covariance matrix of the parameters a, b,ζ2,…,ζR, denoted COV′, is calculated by standard ROC software. Regarding LL as a function of the full covariance matrix is given by
| Eqn. A4 |
where the inner matrix (i.e., excluding the first two rows and columns of COV) is COV′. A similar procedure to that described above for ν′ was used to calculate the asymmetric confidence interval for LLFα. LLFα was transformed to an unconstrained variable ; the variance of was calculated by the multivariate delta method 54 according to:
| Eqn. A5 |
In the above expression is the R+3 dimensional column vector of the derivatives of with respect to the parameters, and T denotes the transpose. Since does not depend on the cutoffs the derivative vector has only 4 non-zero elements, namely those with respect to λ′, νt, a and b. The symmetric 95% confidence interval for is . This was inverse-transformed to obtain the asymmetric confidence interval satisfying 0 ≤ LLFα ≤1.
Search model confidence intervals
The procedure for calculating search model confidence intervals was different from that described above. The search model expression for −LL (see Eqn. C6 vs. Eqn. C8 in Appendix C) was different and the minimization process was significantly different. As noted earlier, it involved two stages. In the first stage one selects λ, calculates ζ1 (Eqn. 17), and minimizes with respect to all other parameters. The minimum value of the negative log likelihood is −LLλ (λ) and, as described above, the first stage minimization determines the parameter estimates and the confidence intervals. These are expected to be underestimates since they do not take into account the variability of λ. [The uncertainty of λ can be appreciated from the fact that the minimum in Fig. 3 is not infinitely sharp. Since ζ1 is regarded as a deterministic function of λ, its uncertainty is completely determined by that of λ and therefore does not introduce additional uncertainty in the estimates of the other parameters.] In the second stage λ was varied until a global minimum of −LLλ (λ) was found (see Fig. 3). Let λM denote the corresponding value of λ. More realistic confidence intervals for μ, ν, LLFα and θ1 were constructed using the following ad-hoc procedure. [We are not aware of any method for estimating confidence intervals for the two stage minimization approach and the asymmetric −LLλ (λ) function.] The 95% confidence interval for λ, namely [λL,λU], corresponds to the increment (or decrement) of λ that results in −LLλ (λ) increasing by one-half 55. Since the lower limit cannot be smaller than λ′ (see Eqn. 17) if it was, it was replaced with λ′, i.e., λL = max(λL,λ′). We illustrate this procedure for μ (analogous procedures were used for the other quantities). Let denote the confidence interval for μ as determined by the minimization performed at the first stage. Here L and U denote lower and upper bounds, respectively, and the superscript emphasizes that the confidence interval is for a specific value of λ, namely λM. The above procedure was repeated for λ = λL and λ = λU. This resulted in two additional confidence intervals for μ, namely and . The final confidence interval for μ was assumed to be , which amounts to a worst case scenario.
Goodness of fit statistic
The statistical validity of the IDCA model was assessed by computing the Pearson goodness of fit 42 statistic χ 2 :
| Eqn. A6 |
The expected value of Fi and Ti for IDCA and for the search model are derived in Appendix B. The number of degrees of freedom df associated with χ 2 is df = 2R − (3+R) − 1, i.e., df = R − 4. The χ2 statistic is valid if the expected number of counts in each bin is at least five 42, which condition was assured by the cutoff selection procedure described previously. Define χ2df as the chi-square distribution pdf for df degrees of freedom 42. Then, at the α level of significance, the null hypothesis that the estimated parameter values are identical to the true values is rejected in favor of the hypothesis that at least one of them is different if χ2 > χ21−α,df, where χ21−α,df is a value such that the integral of χ2df from 0 to χ21−α,df equals 1−α. The observed value of χ2 can be converted to a significance value (p-value) from χ2 = χ21− p,df. At the 5% significance level, one concludes that the fit is not good if p < 0.05 (poor fits lead to small p-values). [In practice one occasionally accepts p > 0.001 44 before completely abandoning a model. It is known that adoption of a stricter criterion (e.g., p > 0.05) can occasionally lead to rejection of a retrospectively valid model. An example is shown in Fig. 4. This is believed to be due to departures from the Gaussian assumption on which the Pearson goodness-of-fit statistic depends 44.]
Appendix B
Expected values for NL and LL counts
Let N (μ,1) denote the Gaussian distribution with mean μ and unit variance. The probability density and cumulative distribution functions are
| Eqn. B1 |
For an R-rating free-response study define the cutoff vector where ζ0 = −∞ and ζR+1 = +∞, as shown in Fig. 2 (b). The area under N (μ,1) between neighboring cutoffs ζi and ζi+1 (i = 1, 2, …, R) and the abbreviations pi and qi are defined by
| Eqn. B2 |
In the following all uppercase variables refer to the whole image set and lowercase variables refer to individual images. Define the NL ratings vector , where Fi is the observed number of NLs rated in bin “i”. NLs can occur on normal and abnormal images. The total number of NLs over all images is . Since N is the total numbers of noise-sites, the number of noise-sites that were not marked is F0 = N − F. Using the logic leading to Eqn. 12 and Eqn. 13 the expected values of Fi and Ti are
| Eqn. B3 |
for IDCA, and the corresponding search model values are
| Eqn. B4 |
The above equations look similar, but there is a difference. For IDCA
| Eqn. B5 |
since the probabilities sum to unity (because ζ1 = −∞). However, for the search model
| Eqn. B6 |
since the probabilities sum to less than unity due to the missing areas to the left of ζ1 ≠ −∞.
Appendix C
Search model likelihood function
The Poisson and Binomial density functions are defined by
| Eqn. C1 |
Given N noise-sites and cutoff vector the probability of observing the NL ratings vector is
| Eqn. C2 |
The sampling distribution of N (defined over all images) is given by the Poisson distribution with mean NIλ, namely Poi( N | NI λ). [The distribution of n (defined for an image) is given by the Poisson distribution Poi(n | λ) with mean λ.] To obtain , the probability for given λ and that one will observe the NL ratings vector , one multiplies the above equation by Poi(N | NI λ) and sums over all values of N ≥ F:
| Eqn. C3 |
The lower limit on N is due to the fact that for an image set with F observed NLs, N must be at least F. This expression can be evaluated in closed form using Maple (Maple 8.00, Waterloo Maple Inc.).
Define the LL ratings vector , where Ti is the observed number of LLs rated in bin “i”. LLs can occur only on abnormal images. The total number of LLs on all images is . Since U is the total numbers of signal-sites, the number of signal-sites that were not marked is T0 = U −T. Given U signal-sites and the cutoff vector the probability of observing the LL ratings vector is
| Eqn. C4 |
Multiplying by Bin(U | NL,ν ), the binomial density function with mean ν and maximum number of successes NL, and summing over all values of U ≥ T, one obtains for the likelihood function for the signal-sites
| Eqn. C5 |
The lower limit on U is due to the fact that on an image set with T lesion localizations, U must be at least T. The net likelihood is the product of the two likelihood functions derived above, namely Eqn. C3 and Eqn. C5. Let LL denote the logarithm of the net likelihood. Using Maple it can be shown that
| Eqn. C6 |
where terms independent of the parameters are not shown.
Comparison to IDCA likelihood function
Define
| Eqn. C7 |
where a and b are the parameters of the binormal model. The expression for is different from Eqn. B2 (hence the prime) since the IDCA z-sampling allows unequal variances for the signal and noise distributions (this is commonly referred to as the “binormal” model) whereas in the search model they are equal (i.e., equal-variance binormal model). In our notation and dropping terms that are independent of parameters, the IDCA likelihood function is
| Eqn. C8 |
If one makes the IDCA assumption ζ1 = −∞ and furthermore sets b = 1 and a = μ in order to make the two z-sampling models identical, then expressions Eqn. C6 and Eqn. C8 become identical. In the search model analysis one does not assume ζ1 = −∞ and therefore the additional terms shown in C6 are needed.
References
- 1.Brake GM, Karssemeijer N, Hendriks JH. Automated detection of breast carcinomas not detected in a screening program. Radiology. 1998;207:465–471. doi: 10.1148/radiology.207.2.9577496. [DOI] [PubMed] [Google Scholar]
- 2.Birdwell RL, Ikeda DM, O’Shaughnessy KF, et al. Mammographic characteristics of 115 missed cancers later detected with screening mammography and the potential utility of computer-aided detection. Radiology. 2001;219:192–202. doi: 10.1148/radiology.219.1.r01ap16192. [DOI] [PubMed] [Google Scholar]
- 3.White CS, Romney BM, Mason AC, et al. Primary carcinoma of the lung overlooked at CT: analysis of findings in 14 patients. Radiology. 1996;199:109–115. doi: 10.1148/radiology.199.1.8633131. [DOI] [PubMed] [Google Scholar]
- 4.Kakinuma R, Ohmatsu H, Kaneko M, et al. Detection failures in spiral CT screening for lung cancer: analysis of CT findings. Radiology. 1999;212:61–66. doi: 10.1148/radiology.212.1.r99jn1461. [DOI] [PubMed] [Google Scholar]
- 5.Forrest JV, Friedman PJ. Radiologic errors in patients with lung cancer. Western Journal of Medicine. 1981;134:485–490. [PMC free article] [PubMed] [Google Scholar]
- 6.Muhm JR, Miller WE, Fontura RS, et al. Lung cancer detected during a screening program using four-month chest radiographs. Radiology. 1983;148:609–615. doi: 10.1148/radiology.148.3.6308709. [DOI] [PubMed] [Google Scholar]
- 7.Fletcher JG, Johnson CD, Welch TJ, et al. Optimization of CT colonography technique: Prospective trial in 180 patients. Radiology. 2000;216:704–711. doi: 10.1148/radiology.216.3.r00au41704. [DOI] [PubMed] [Google Scholar]
- 8.Thurfjell EL, Lernevall KA, Taube AAS. Benefit of independent double reading in a population-based mammography screening program Radiology 1994; 191:241–244. Radiology. 1994;191:241–244. doi: 10.1148/radiology.191.1.8134580. [DOI] [PubMed] [Google Scholar]
- 9.Wormanns D, Ludwig K, Beyer F, et al. Detection of pulmonary nodules at multirow-detector CT: effectiveness of double reading to improve sensitivity at standard-dose and low-dose chest CT. Eur Radiol. 2005;15:14–22. doi: 10.1007/s00330-004-2527-6. [DOI] [PubMed] [Google Scholar]
- 10.Gur D, Sumkin JH, Rockette HE, et al. Changes in breast cancer detection and mammography recall rates after the introduction of a computer-aided detection system. J Natl Cancer Inst. 2004;96:85–190. doi: 10.1093/jnci/djh067. [DOI] [PubMed] [Google Scholar]
- 11.Khoo LA, Taylor P, Given-Wilson RM. Computer-aided detection in the United Kingdom National Breast Screening Programme: prospective study. Radiology. 2005;237:444–449. doi: 10.1148/radiol.2372041362. [DOI] [PubMed] [Google Scholar]
- 12.Summers RM, Jerebko AK, Franaszek M, et al. Colonic polyps: Complementary role of computer-aided detection in CT Colonography. Radiology. 2002;225:391–399. doi: 10.1148/radiol.2252011619. [DOI] [PubMed] [Google Scholar]
- 13.Awai K, Murao K, Ozawa A, et al. Pulmonary Nodules at Chest CT: Effect of Computer-aided Diagnosis on Radiologists’ Detection Performance. Radiology. 2004;230:347–352. doi: 10.1148/radiol.2302030049. [DOI] [PubMed] [Google Scholar]
- 14.Metz CE. Receiver Operating Characteristic Analysis: A Tool for the Quantitative Evaluation of Observer Performance and Imaging Systems. J Am Coll Radiol. 2006;3:413–422. doi: 10.1016/j.jacr.2006.02.021. [DOI] [PubMed] [Google Scholar]
- 15.Bunch PC, Hamilton JF, Sanderson GK, et al. A Free-Response Approach to the Measurement and Characterization of Radiographic-Observer Performance. J of Appl Photogr Eng. 1978;4(4):166–171. [Google Scholar]
- 16.Chakraborty DP, Breatnach ES, Yester MV, et al. Digital and Conventional Chest Imaging: A Modified ROC Study of Observer Performance Using Simulated Nodules. Radiology. 1986;158:35–39. doi: 10.1148/radiology.158.1.3940394. [DOI] [PubMed] [Google Scholar]
- 17.Chakraborty DP. Maximum Likelihood analysis of free-response receiver operating characteristic (FROC) data. Med Phys. 1989;16(4):561–568. doi: 10.1118/1.596358. [DOI] [PubMed] [Google Scholar]
- 18.Chakraborty DP, Berbaum KS. Observer studies involving detection and localization: Modeling, analysis and validation. Medical Physics. 2004;31(8):2313–2330. doi: 10.1118/1.1769352. [DOI] [PubMed] [Google Scholar]
- 19.Sahiner B, Chan HP, Hadjiiski LM, et al. Joint two-view information for computerized detection of microcalcifications on mammograms. Med Phys. 2006;33:2574–2585. doi: 10.1118/1.2208919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zheng B, Leader JK, Abrams GS, et al. A multi view based computer aided detection scheme for breast masses. Medical Physics. 2006;33(9):3135–3143. doi: 10.1118/1.2237476. [DOI] [PubMed] [Google Scholar]
- 21.Bellotti R, Carlo FD, Tangaro S, et al. A completely automated CAD system for mass detection in a large mammographic database. Med Phys. 2006;33:3066–3075. doi: 10.1118/1.2214177. [DOI] [PubMed] [Google Scholar]
- 22.Chakraborty DP. Statistical power in observer performance studies: A comparison of the ROC and free-response methods in tasks involving localization. Acad Radiol. 2002;9(2):147–156. doi: 10.1016/s1076-6332(03)80164-2. [DOI] [PubMed] [Google Scholar]
- 23.Petrick N, Sahiner B, Chan HP, et al. Breast Cancer Detection: Evaluation of a Mass-Detection Algorithm for Computer-aided Diagnosis—Experience in 263 Patients. Radiology. 2002;224(1):217–224. doi: 10.1148/radiol.2241011062. [DOI] [PubMed] [Google Scholar]
- 24.Penedo M, Souto M, Tahoces PG, et al. Free-Response Receiver Operating Characteristic Evaluation of Lossy JPEG2000 and Object-based Set Partitioning in Hierarchical Trees Compression of Digitized Mammograms. Radiology. 2005;237(2):450–457. doi: 10.1148/radiol.2372040996. [DOI] [PubMed] [Google Scholar]
- 25.Bornefalk H. Estimation and Comparison of CAD System Performance in Clinical Settings. Acad Radiol. 2005;12:687–694. doi: 10.1016/j.acra.2005.02.005. [DOI] [PubMed] [Google Scholar]
- 26.Gurcan MN, Chan HP, Sahiner B, et al. Optimal neural network architecture selection: Improvement in computerized detection of microcalcifications. Academic Radiology. 2002;9:420–429. doi: 10.1016/s1076-6332(03)80187-3. [DOI] [PubMed] [Google Scholar]
- 27.Bornefalk H, Hermansson AB. On the comparison of FROC curves in mammography CAD systems. Med Phys. 2005;32(2):412–417. doi: 10.1118/1.1844433. [DOI] [PubMed] [Google Scholar]
- 28.Samuelson FW, Petrick N. presented at the 2006 IEEE International Symposium on Biomedical Imaging: From Nano to Micro; Arlington, VA; 2006. unpublished. [Google Scholar]
- 29.Edwards DC, Kupinski MA, Metz CE, et al. Maximum likelihood fitting of FROC curves under an initial-detection-and-candidate-analysis model. Med Phys. 2002;29(12):2861–2870. doi: 10.1118/1.1524631. [DOI] [PubMed] [Google Scholar]
- 30.Zheng B, Chakraborty DP, Rockette HE, et al. A comparison of two data analyses from two observer performance studies using Jackknife ROC and JAFROC. Medical Physics. 2005;32(4):1031–1034. doi: 10.1118/1.1884766. [DOI] [PubMed] [Google Scholar]
- 31.Zheng B, Shah R, Wallace L, et al. Computer-aided detection in mammography: an assessment of performance on current and prior images. Acad Radiol. 2002;9:1245–1250. doi: 10.1016/s1076-6332(03)80557-3. [DOI] [PubMed] [Google Scholar]
- 32.Kundel HL, Nodine CF. A visual concept shapes image perception. Radiology. 1983;146:363–368. doi: 10.1148/radiology.146.2.6849084. [DOI] [PubMed] [Google Scholar]
- 33.Kundel HL, Nodine CF. Modeling visual search during mammogram viewing. Proc SPIE. 2004;5372:110–115. [Google Scholar]
- 34.Nodine CF, Kundel HL. Using eye movements to study visual search and to improve tumor detection. RadioGraphics. 1987;7(2):1241–1250. doi: 10.1148/radiographics.7.6.3423330. [DOI] [PubMed] [Google Scholar]
- 35.Dorfman DD, Alf E. Maximum likelihood estimation of parameters of signal-detection theory and determination of confidence intervals - rating method data. J Math Psychol. 1969;6:487–496. [Google Scholar]
- 36.Pan X, Metz CE. The “proper” binormal model: parametric receiver operating characteristic curve estimation with degenerate data. Academic Radiology. 1997;4(5):380–389. doi: 10.1016/s1076-6332(97)80121-3. [DOI] [PubMed] [Google Scholar]
- 37.Dorfman DD, Berbaum KS, Metz CE, et al. Proper Receiving Operating Characteristic Analysis: The Bigamma model. Acad Radiol. 1997;4(2):138–149. doi: 10.1016/s1076-6332(97)80013-x. [DOI] [PubMed] [Google Scholar]
- 38.Metz CE, Pan X. “Proper” Binormal ROC Curves: Theory and Maximum-Likelihood Estimation. J Math Psychol. 1999;43(1):1–33. doi: 10.1006/jmps.1998.1218. [DOI] [PubMed] [Google Scholar]
- 39.Dorfman DD, Berbaum KS. A contaminated binormal model for ROC data: Part II. A formal model. Acad Radiol. 2000;7(6):427–437. doi: 10.1016/s1076-6332(00)80383-9. [DOI] [PubMed] [Google Scholar]
- 40.Chakraborty DP. A search model and figure of merit for observer data acquired according to the free-response paradigm. Phys Med Biol. 2006;51:3449–3462. doi: 10.1088/0031-9155/51/14/012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chakraborty DP. ROC Curves predicted by a model of visual search. Phys Med Biol. 2006;51:3463–3482. doi: 10.1088/0031-9155/51/14/013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Larsen RJ, Marx ML. An Introduction to Mathematical Statistics and Its Applications. 3. Prentice-Hall Inc; Upper Saddle River, NJ: 2001. [Google Scholar]
- 43.Stuart A, Ord K, Arnold S. Kendall’s Advance Theory of Statistics: Classical Inference and the Linear Model, Vol 2A. 6. Oxford University Press; New York: 2004. [Google Scholar]
- 44.Press WH, Flannery BP, Teukolsky SA, et al. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press; Cambridge: 1988. [Google Scholar]
- 45.Galassi M, Davies J, Theiler J, et al. GNU Scientific Library Reference Manual. 1.6. Network Theory Limited; Bristol, UK: 2005. [Google Scholar]
- 46.Yuan R, Vos P, Cooperberg PL. Computer-aided detection in screening CT for pulmonary nodules. American Journal of Roentgenology. 2005;186:1280–1287. doi: 10.2214/AJR.04.1969. [DOI] [PubMed] [Google Scholar]
- 47.Metz CE, Herman BA, Shen JH. Maximum-likelihood estimation of ROC curves from continuously-distributed data. Stat Med. 1998;17:1033. doi: 10.1002/(sici)1097-0258(19980515)17:9<1033::aid-sim784>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 48.Chakraborty DP. presented at the SPIE Medical Imaging, Image Perception, Observer Performance, and Technology Assessment; San Diego. 2007. unpublished. [Google Scholar]
- 49.Chakraborty DP, Yoon HJ, Mello-Thoms C. Spatial localization accuracy of radiologists in free-response studies: inferring perceptual FROC curves from mark-rating data. Acad Radiol. 2007;14:4–18. doi: 10.1016/j.acra.2006.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Hanley JA. The Robustness of the “Binormal” Assumptions Used in Fitting ROC Curves. Med Decis Making. 1988;8(3):197–203. doi: 10.1177/0272989X8800800308. [DOI] [PubMed] [Google Scholar]
- 51.Efron B. The Jackknife, the Bootstrap and Other Resampling Plans. Capital City Press; Montpelier: 1982. [Google Scholar]
- 52.Dorfman DD, Berbaum KS, Metz CE. ROC characteristic rating analysis: Generalization to the Population of Readers and Patients with the Jackknife method. Invest Radiol. 1992;27(9):723–731. [PubMed] [Google Scholar]
- 53.Beiden SV, Wagner RF, Campbell G. Components-of Variance Models and Multiple-Bootstrap Experiments: An Alternative Method for Random-Effects, Receiver Operating Characteristic Analysis. Academic Radiology. 2000;7(5):341–349. doi: 10.1016/s1076-6332(00)80008-2. [DOI] [PubMed] [Google Scholar]
- 54.Lehmann EL, Casella G. Theory of Point Estimation. 2. Springer-Verlag; New York: 1998. [Google Scholar]
- 55.Brandt S. Data Analysis: Statistical and Computational Methods for Scientists and Engineers. 3. Springer-Verlag; New York: 1999. [Google Scholar]


