Partial Field-of-View Spiral Phase-Contrast Imaging Using Complex Difference Processing

Abstract

Rapid flow imaging was achieved with a partial field of view (pFOV) spiral motion-encoded technique. The FOV and the acquisition time were reduced by a factor of 2 by undersampling k-space. The pFOV spiral k-space trajectory aliased signals from outside a circular ring whose radius was inversely proportional to the distance between adjacent spirals in k-space. In this study the FOV was adjusted so that all of the moving spins were located inside the inner half circle of the full FOV. Complex subtraction of two differentially flow-encoded images was used to remove the spurious phase sources and provide an accurate measurement of flow. The complex subtraction process also serves to eliminate aliasing artifacts that are generated by static tissue from outside the reduced FOV. Experiments in a flow phantom and volunteers showed that the flow estimates obtained by pFOV spiral motion encoding are in good agreement with the estimates reconstructed using complex difference processing.

MRI methods can measure blood flow within the cardiovascular system by using the first moment of bipolar gradients to encode motion of the nuclear spins into the phase of the magnetization (1-6). PC MRI and complex difference processing are two methods that are based on this principle. The PC-MRI method encodes motion into the phase of the magnetization and ultimately into the image phase. In addition to motion information, there is residual image phase information from radiofrequency (RF) receiver coils and off-resonance that are commonly compensated for in PC-MRI by acquiring two flow-encoded images with two different first-moment encoding gradients. Subsequently the images are phase-subtracted from each other to generate a final image in which the blood velocity is proportional to the image phase. Complex difference reconstruction of the PC data is an alternative to phase difference processing, in which the image reconstruction is accomplished by subtracting the complex MR raw signals from two differentially encoded image sets (6). This technique was originally proposed for MR angiography (MRA) applications because of its excellent suppression of stationary tissue, but contrast-enhanced angiography proved to be faster and more robust for such applications (7). The complex difference technique has the advantage of eliminating the partial volume effects from voxels that contain both flowing and stationary components (6). The ability of complex difference processing to eliminate aliased signals from stationary tissues has been illustrated with as few data as a single projection (8). However, this extreme approach relies on the absence of overlapping vessels in the field of view (FOV), which is not practical for imaging of the great vessels.

Spiral data acquisition patterns can be used to sample k-space in a motion-encoded study (9-11). Early sampling of the center of k-space reduces the intrinsic sensitivity to motion, which reduces the generation of flow-related artifacts (12). To obtain the temporal resolution required for imaging cardiovascular blood flow, the spiral sampling can be segmented over multiple heartbeats in which one spiral interleave is acquired repeatedly during each heartbeat (13). There is always a trade-off between the total acquisition time or breath-hold length and the temporal resolution, and temporal resolution is often compromised to ensure a sufficiently short breath-hold duration. Fractional k-space acquisitions (14-17) are an attractive option for reducing the duration of the image acquisition or increasing the temporal resolution that can be achieved in a given breath-hold. However, since the image-phase information is lost during the reconstruction, they are incompatible with methods that encode motion in the phase.

In this study we propose a partial FOV (pFOV) complex difference technique that reduces the acquisition time by factor of at least 2, while maintaining the spatial resolution, temporal resolution, and FOV required to image the blood flow within the cardiovascular system. In this technique the image information lost by undersampling is not synthesized; rather, the aliasing effects from undersampling are eliminated by subtracting out the aliased signals.

MATERIALS AND METHODS

The primary sideband of the spatial point spread function (PSF) of spiral k-space sampling has a circular ring with radius equal to the imaging FOV. Acquiring every alternate spiral interleave from a fully sampled k-space trajectory will result in a circular PSF with a half-FOV radius but with the same spatial resolution. This PSF suggests that an aliasing artifact will appear in the reconstructed image that originates from the objects located outside the circular region in the image. The total received MR signal S(t) from an excited plane can be expressed as

$$S\left(t\right)=\iint \kappa (x,y)M(x,y)e^{i\theta (x,y)}\mathit{dxdy}$$ [1]

where κ(x,y) is the receiver coil sensitivity map, M (x,y) is the excited transverse magnetization weighted by the imaging parameters (such as the TR, TE, and spin relaxation parameters), and θ (x,y) is the accumulated phase of the transverse magnetization at each location. Ignoring the phases from the imaging gradients, the θ(x,y) phase in a PC experiment is the sum of background phases (φ_b) and velocity encoded phase (φ_v):

$$\theta (x,y)={\phi }_b(x,y)+{\phi }_v(x,y)={\phi }_b(x,y)+\gamma M_{1\mathrm{r}}{v}_{\mathrm{r}}(x,y)$$ [2]

where M_1r is the encoded first moment, v_r (x,y) is the velocity of the spin in the direction of r, and γ is the gyromagnetic ratio. The background phase is a combination of the RF coil phase offset, off-resonance phase, Maxwell terms, and unbalanced gradient phases due to the eddy currents. The acquired MR raw data S(t) consist of signal components originating from static and dynamic spins located in the inner or outer regions of the circular FOV in image space:

$$S\left(t\right)=S_{(\mathit{or},d)}+S_{(\mathit{or},s)}+S_{(\mathit{ir},d)}+S_{(\mathit{ir},s)}$$ [3]

in which S_or, S_ir, S_s, and S_d represent the signals originating from outer and inner regions and the static and dynamic magnetization spins, respectively. If the imaging FOV is prescribed such that the dynamic portion is contained within inner region (S_{(or, d)} = 0), there will be no aliased signal from the dynamic components from the outer region of the image. However, the signals originating from static object outside the circular FOV will alias back into the image, resulting in severe aliasing artifacts in the image. The aliased signal in a bipolar gradient motion-encoded experiment can be removed by subtracting the complex MR raw data acquired from two encoding steps S¹ and S²:

$$\Delta S\left(t\right)=S_{(\mathit{ir},d)}^2-S_{(\mathit{ir},d)}^1$$ [4]

The subtracted raw signal ΔS(t) is alias-free data that contains only the signals originating from the dynamic magnetization spins. The subtracted 2D complex k-space can be used to calculate a velocity map across the vessels. In particular, the subtracted 2D raw image can be expressed as

$$\Delta S\left(t\right)=\kappa (x,y)M(x,y)(e^{i{\theta }_2(x,y)}-e^{i{\theta }_1(x,y)})$$ [5]

where θ₁ and θ₂ are the transverse magnetization phases from the two bipolar encoding PC experiments. Using Eq. [2], the raw image can be simplified to

$$\Delta S\left(t\right)=\kappa (x,y)M(x,y)e^{i{\phi }_b(x,y)}\left\{2i\sin \left(\frac{\pi v_r(x,y)}{2V_{\mathit{enc}}}\right)\right\}$$ [6]

where V_enc is the velocity-encoding strength. The velocity map in the image can be calculated by

$$v_r(x,y)=\frac{2V_{\mathit{enc}}}{\pi }\arcsin \left(\frac{\mid \Delta S(x,y)\mid }{\mid 2\kappa (x,y)M(x,y)e^{i{\phi }_b(x,y)}\mid }\right)$$ [7]

where |x| is the absolute value of x. To calculate the velocity map v_z(x,y), an aliase-free calibration image κ(x,y)M(x,y)e^iφb(x,y) is required. This image is reconstructed adaptively from the imaging data set by an acquisition scheme previously proposed by Sedarat et al. (18). The spiral interleaves for reconstruction of an image with a given resolution are grouped into even or odd groups, and each group is acquired in different cardiac phases. By combining the data from consecutive cardiac phases, a fully sampled image can be reconstructed that can be used to extract the calibration image. The sign of the PC image reconstructed from this image is used to determine the direction of the flow in the complex difference processing.

Imaging Sequence

The spiral PC pulse sequence was developed by the addition of a bipolar gradient after the slice-rephasing gradient in a 2D spiral sequence, as shown in Fig. 1. A balanced flow-encoding scheme with equal and opposite first moments, ±M_1z, was used. A time-shifting bipolar gradient was used for motion encoding in all of the studies. The time-shifting approach for encoding the two bipolar motion-encoding steps (as opposed to variations in gradient amplitude) ensures that the bipolar gradients have the same shape, and thus minimizes the eddy and Maxwell phase differences between the two encoding steps (8). The introduced delay maintains the balanced first moment ±M_1z in the two encoding steps, and the duration of the delay is determined by the slice-selective gradient area and the desired V_enc. All MR experiments were performed on a GE Signa Excite 1.5T MRI system (GE, Waukesha, WI, USA) with Twin gradient (maximum gradient of 4 G/cm, maximum slew rate of 150 G/cm/ms) using an eight-channel cardiac phased-array coil (Nova Medical, Wilmington, MA, USA) for signal detection.

FIG. 1.

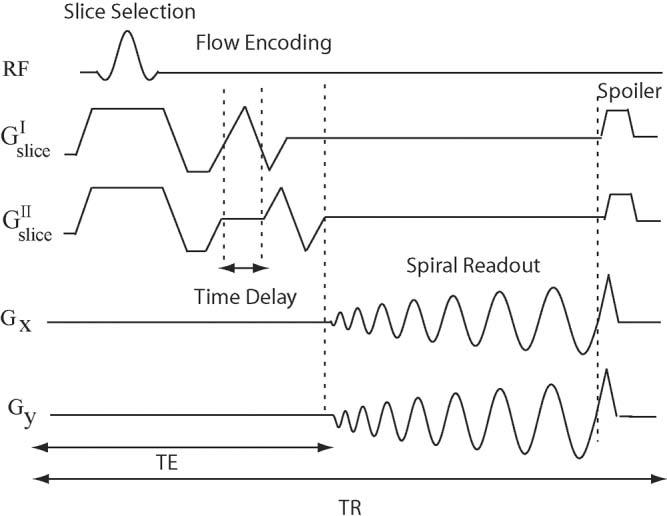
Spiral PC sequence. The slice-selective RF pulse is followed by a bipolar gradient and spiral readout, and a spoiler gradient is used at the end of each TR. A time-shifted bipolar gradient scheme is used to encode different first moments in the two motion-encoding steps of the sequence.

Phantom and In Vivo Validation

For the flow validation experiments, through-plane flow velocity was measured in a constant flow rate tube phantom with inner diameter of 1 cm. Two tubes were placed among three stationary phantoms that covered the entire imaging FOV. The solution in the tube system was water doped with Gd-DTPA (Magnevist, Berlex; 0.05 mmol/L) to approximate the T₁ of blood at 1.5T. Experiments were performed with five flow rates ranging from 6.28 ml/s to 18.59 ml/s. The imaging parameters were as follows: TR = 25.4, V_enc = 80 cm/s, θ = 30°, slice thickness = 3 mm, FOV = 40 cm, BW = ±125 kHz, 4096 readout points, and 32 spiral interleaves. For pFOV reconstruction, data were subsampled by using only even spiral interleaves.

Motion-encoded studies were performed on five normal volunteers (all males, average age = 29 years) with no known history of cardiovascular disease. Written informed consent was obtained from all participants, and the protocol was approved by the NHLBI IRB. Through-plane flow images were acquired in an axial slice superior to the aortic valve with a fully sampled k-space. All studies were breath-held and ECG-gated. The imaging parameters were as follows: TR = 23.6 ms, V_enc = 150 cm/s, θ = 30°, FOV = 30 cm × 30 cm, BW = ± 125 kHz, slice thickness = 6 mm. A total of 16 spiral interleaves of 4096 samples with an image reconstruction matrix of 256 × 256 was used to sample the k-space. A spatial resolution of 1.06 mm × 1.06 mm was achieved. A single interleaf per segment was used to achieve a temporal resolution of 47.2 ms for acquisition of both bipolar encoding steps in each heartbeat. The pFOV images were obtained from the eight even spiral interleaves.

Statistical analysis using the Bland-Altman method (19) was performed on flow velocity measurement from a region of interest (ROI) within the ascending aorta. In addition to this analysis, a signal-to-noise ratio (SNR) measurement was performed using the noncalibrated complex difference data to quantify the SNR loss for the pFOV reconstruction. The mean signal from an ROI in the ascending aorta and the standard deviation (SD) of the noise outside the vessels in air were used for SNR calculation.

RESULTS

For the phantom studies we calculated the average through-plane flow velocity by averaging the velocities in the lumen of the tube. We performed a linear correlation analysis by comparing the mean velocities calculated from a full FOV and the pFOV complex difference technique for four different flow rates. The average flow velocities measured from the fully-sampled and pFOV complex difference approaches yielded r > 0.9988 and a slope of 0.9921.

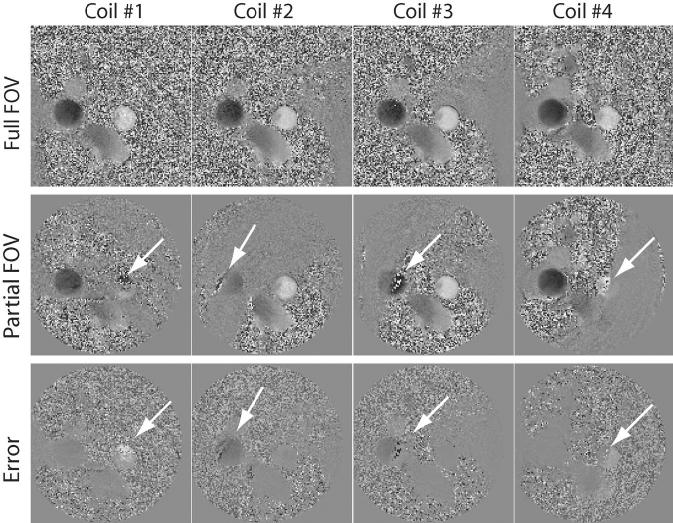
Figure 2 shows the conventional phase difference (PC-MRI) reconstruction for fully sampled (top row) and pFOV images reconstructed from even spiral interleaves (middle row) of four coil elements (different columns), and shows considerable aliasing artifacts. The bottom row images show the error difference between the two reconstructions. The results show significant aliasing artifacts in the flow images (indicated by arrows) that cause significant errors in flow quantifications. Figure 3 shows the corresponding complex difference images reconstructed from a fully sampled acquisition (top row), a pFOV image reconstructed from even spiral interleaves (middle row), and the image difference (bottom row). There is no visual aliasing artifacts in the pFOV reconstructed with the complex difference, as shown in the image difference; however, there is an increase in the noise level. Note that the complex difference images shown are not calibrated for the flow quantification to better visualize the artifact level in the image reconstruction.

FIG. 2.

Phase difference processing of a fully sampled acquisition (first row), a half-sampled acquisition (second row), and the image difference that is calculated by subtraction of the two reconstructed images (third row) for different coil elements (different columns). The arrows point to significant aliasing artifacts in phase difference reconstruction of pFOV.

FIG. 3.

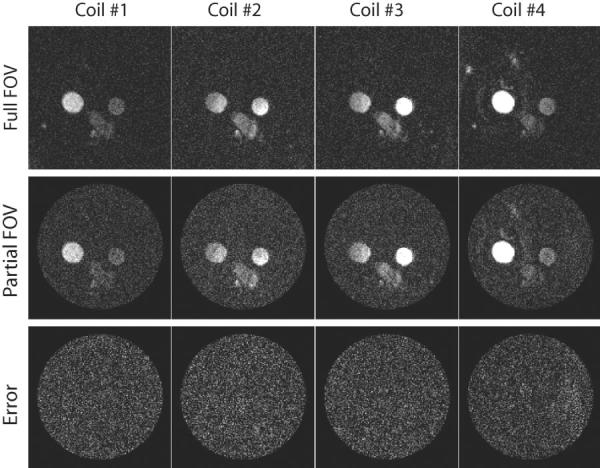
Complex difference images reconstructed from a fully sampled acquisition (first row), a pFOV acquisition (second row), and the image difference (third row) for different coil element (columns). There are no aliasing artifacts in the pFOV images reconstructed with the complex difference; however, there is an increase in the noise level. The difference images confirm the excellent agreement between the two methods.

Figure 4 shows the quantitative analysis of the blood flow within an ROI in the ascending aorta over a cardiac cycle. The velocity curves in Fig. 4a show the mean blood flow velocity across the aorta measured from the velocity map reconstructed with complex difference using a fully and partially acquired k-space data in addition to the conventional phase difference processing using a fully sampled data set. The results show a good agreement between the velocities calculated. Figure 4b shows the Bland-Altman plot of flow measurements in the ROI in the ascending aorta of a normal volunteer using the data from all of the coils over one cardiac cycle. The mean difference between the two techniques is 2.58 cm/s with a 95% confidence interval (CI) of 2.02–3.14 cm/s. The SD of the mean difference is 3.2 cm/s, and most of the data points (>96%) lie in the mean difference ± 1.96 times the SD of the differences, which implies that the two techniques can be used interchangeably. An SNR analysis showed a 30% SNR decrease in the pFOV acquisition compared to a fully sampled acquisition, which is the direct consequence of reducing the total readout acquisition time by a factor of 2.

FIG. 4.

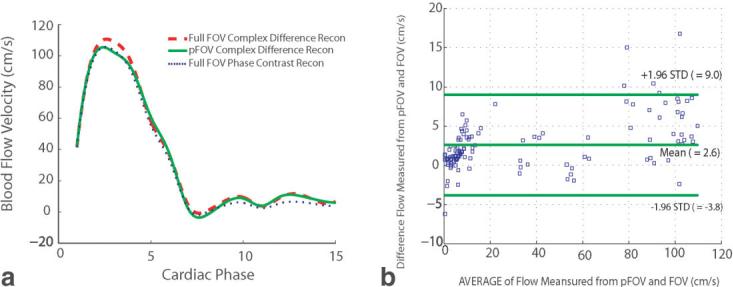
Blood flow velocity through the ascending aorta. a: Comparison of the mean blood flow velocity measured in an ROI within the ascending aorta calculated from a partial vs. full acquisition, and the corresponding phase difference reconstruction from a fully sampled acquisition. b: Bland-Altman graph of the mean velocity measured from full FOV and pFOV reconstructed with complex difference over one cardiac cycle.

DISCUSSION

Phantom and in vivo studies demonstrate that the acquisition time of a flow imaging study can be reduced by a factor of 2 using complex difference processing, while maintaining the accuracy of the measured velocity and flow values. The advantage of complex-difference processing with a pFOV acquisition is that it effectively reduces the object size by eliminating signal from static tissue, and thus eliminates the aliasing signal source. While only a factor of 2 reduction in FOV, and thus scan time, was achieved in this study, the use of higher reduction factors is limited only by the minimum FOV that contains moving spins. Note that the improvements in efficiency can alternatively be used to increase the temporal resolution while maintaining the total scan duration.

Spectral-spatial RF pulses are commonly used in spiral imaging to excite only water spins and hence remove the blurring effects introduced in the image from off-resonance spins, such as from fat. These pulses are significantly longer, which reduces the efficiency of acquisition. However, in complex difference processing, the signals from fat are removed by subtracting the two complex signals, so there is no need to use spectral-spatial pulses.

A potential limitation of the complex difference approach is the saturation of the longitudinal magnetization by the application of multiple RF pulses, which causes a corresponding reduction in the acquired signal. Polzin et al. (20) derived an expression describing the relationship between the amount of saturation and the blood velocity and pulse sequence parameters. The ideal conditions are a complete refreshment of the blood in the slice every TR, for which there is no saturation. For example, for a TR of 25 ms and slice thickness of 0.5 cm, a velocity of only 20 cm/s is required for complete refreshment every TR. Even with only partial refreshment, for velocities less than 20 cm/s, and a reduced flip angle, it is possible to retain almost 100% efficiency (8). The long TR values that are intrinsic to the spiral pulse sequence allow for this minimal loss of blood signal due to saturation. Another limitation of such reconstruction is the SNR loss, which is the consequence of the reduction in acquisition time. Further investigation is warranted concerning the performance of this technique in images acquired with low SNR.

CONCLUSIONS

In this study we propose a new technique for imaging and reconstruction of pFOV flow blood velocity images. Flow phantom and in vivo flow images are presented to show the efficacy of this technique. The results show the total suppression of the aliasing artifacts in flow images reconstructed using only half of the raw data, assuming that all of the vessels of interest are located within the center half of the FOV.