Ghost Artifact Cancellation Using Phased Array Processing

Abstract

In this article, a method for phased array combining is formulated which may be used to cancel ghosts caused by a variety of distortion mechanisms, including space variant distortions such as local flow or off-resonance. This method is based on a constrained optimization, which optimizes SNR subject to the constraint of nulling ghost artifacts at known locations. The resultant technique is similar to the method known as sensitivity encoding (SENSE) used for accelerated imaging; however, in this formulation it is applied to full field-of-view (FOV) images. The method is applied to multishot EPI with noninterleaved phase encode acquisition. A number of benefits, as compared to the conventional interleaved approach, are reduced distortion due to off-resonance, in-plane flow, and EPI delay misalignment, as well as eliminating the need for echo-shifting. Experimental results demonstrate the cancellation for both phantom as well as cardiac imaging examples.

Phased array reconstruction (1), which employs coil sensitivity (B₁) maps as weights for phased array combining, has been shown to optimize SNR and, in addition, provide a degree of artifact suppression for alias ghosts. In this article, we formulate how phased array combining may be used to cancel ghosts caused by a variety of distortion mechanisms. This method is based on a constrained optimization, which optimizes SNR subject to the constraint of nulling ghost artifacts at known locations. The resultant technique is similar to the method known as sensitivity encoding (SENSE); however, in this formulation it is applied to full field-of-view (FOV) images. The SENSE technique (2), which also performs phased array combining, is typically used to accelerate imaging by acquiring a reduced FOV in the phase encode direction. In this case, ghost images caused by the intentional aliased acquisition are then removed by phased array processing. We present a general formulation to eliminate ghosts, which applies “SENSE” directly to the full k-space reconstruction. Furthermore, the method is applicable to the case of space variant ghost distortion, which commonly arises due to effects such as off-resonance or flow.

Application of SENSE (3) and SMASH (4) to EPI ghost elimination was described in which odd and even lines were processed separately and noncoherently combined. In our method, in which “SENSE” is applied directly to the full k-space reconstruction, we reconstruct images weighted by each value of the point spread function, rather than by their Fourier coefficients. These component ghost images may be combined either coherently, using a complex weighted sum if the point spread function is known, or noncoherently, using the root-sum-of-squares method. We show that an estimate of the space variant “point spread function” may be derived as a by-product of the reconstruction. As in the conventional application of SENSE for partial FOV accelerated imaging, the phased array method for ghost cancellation incurs a similar loss in SNR due to the ill-conditioning of the inverse solution. However, in this full FOV imaging application there is no additional loss in SNR due to acceleration.

Adaptive phased array combining (5) has been formulated in which the complex weights are derived using sample correlation estimates, based on a stochastic signal model. This adaptive method has been further applied to ghost cancellation (5), by using sample “noise” statistics measured near the source of the artifact, which serves to null the artifact as well as nulls the region of the desired image that corresponds to the source of the artifact. However, in this method the extent of the spatial null is fairly broad.

While the theoretical formulation presented in this article may be generalized to shows that distortion with quite general point spread function may be eliminated by the phased array artifact cancellation method, the performance of phased array processing, which depends on the number of coils and sensitivity maps, poses practical limitations on which type of distortion may be cancelled effectively. Typical surface coils have relatively slow spatial variation. Therefore, deblurring, in which case point spread values are closely spaced, is not practical since the inverse solution is correspondingly ill-conditioned. However, widely spaced ghost artifacts may be readily cancelled, as demonstrated experimentally.

Echo-planar imaging (EPI) is widely used for ultrafast imaging. A number of techniques (7-15) are used to minimize distortion and ghost artifacts, which result from phase and amplitude errors between echoes. The phased array processing method for ghost cancellation adds yet another tool which may be incorporated to further mitigate EPI distortion and artifacts. Application to multishot EPI with noninterleaved phase encode acquisition order is described. Cancellation of ghosts by means of phased array processing makes noninterleaved phase encode acquisition order practical, and has a number of benefits such as reduced distortion due to off-resonance, in-plane flow, and EPI delay misalignment, as well as eliminating the need for echo-shifting. Incorporating this phased array method for ghost cancellation may result in greater flexibility in designing acquisition strategies.

We present experimental results that demonstrate ghost artifact cancellation of EPI ghosts for a phantom as well as for cardiac imaging. In both of these examples, the ghost artifacts were spatially varying.

METHODS

Theory

Consider the case of ghost artifacts occurring in the phase encode dimension. The reconstructed image, g_i(x,y), for the i-th coil may be written as:

$$g_i(x,y)=\sum _{k=0}^{N_g}{s}_i(x,y-kD)h_k(x,y-kD)f(x,y-kD)+n_i(x,y)$$ [1]

where f(x,y) is the desired (magnetization) image, s_i(x,y) is the complex field sensitivity for the i-th coil, N_g is the number of ghosts (N_g + 1 superimposed images) with spacing D, h_k(x,y) is the complex weight of the k-th ghost arising from the signal at (x,y), n_i(x,y) is the observation noise, and (x,y) variables are assumed to be discrete as a result of image reconstruction from a finite set of periodic k-space samples. As a result of periodic k-space sampling with spacing Δk_y between phase encode lines, f(x,y) = f(x,y-FOV_y), where FOV_y = 1/Δk_y is the full FOV in the phase encode direction. Equation [1] may be used to model a wide range of ghost mechanisms caused by k-space weightings and space variant distortion due to flow or local off-resonance from chemical shift or field inhomogeneity. Throughout the article, h_k will be referred to as a “point spread function” (PSF), even though it is understood that it is a function of (x,y) and, therefore, is actually space variant. For reception with N_c coils, Eq. [1] may be written in matrix form as:

$$\left[\begin{array}{c}\hfill g_1(x,y)\hfill \\ \hfill ⋮\hfill \\ \hfill g_{N_c}(x,y)\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill s_1(x,y)\hfill & \hfill \cdots \hfill & \hfill s_1(x,y-N_{g}D)\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill s_{N_c}(x,y)\hfill & \hfill \cdots \hfill & \hfill s_{N_c}(x,y-N_{g}D)\hfill \end{array}\right]\times \left[\begin{array}{c}\hfill h_0(x,y)f(x,y)\hfill \\ \hfill ⋮\hfill \\ \hfill h_{N_g}(x,y-N_{g}D)f(x,y-N_{g}D)\hfill \end{array}\right]+\left[\begin{array}{c}\hfill n_1(x,y)\hfill \\ \hfill ⋮\hfill \\ \hfill n_{N_c}(x,y)\hfill \end{array}\right],$$ [2]

or more compactly as:

$$\mathbf{g}(x,y)=\mathbf{S}(x,y)\tilde{\mathbf{f}}(x,y)+\mathbf{n}(x,y),$$ [3]

where the matrix and vectors in Eq. [3] are in direct correspondence with Eq. [2].

Equation [3] becomes overdetermined (more equations than unknowns) when the number of coils, N_c, is greater than the number of superimposed signals, N_g + 1, and can be “solved” in the least-squares sense for an estimate of f̃(x, y), given estimates for the complex coils sensitivities (B₁ maps) s_i(x,y), as well as knowledge of the number of ghosts N_g and spacing D. The weighted least-squares estimate $\widehat{\tilde{\mathbf{f}}}$ of f̃(x,y), which optimizes SNR, may be written as:

$$\widehat{\tilde{\mathbf{f}}}(x,y)={\left[\mathbf{S}{(x,y)}^{\mathrm{H}}{\mathbf{R}}_{\mathit{n}}^{-1}\mathbf{S}(x,y)\right]}^{-1}\mathbf{S}{(x,y)}^{\mathrm{H}}{\mathbf{R}}_{\mathit{n}}^{-1}\mathbf{g}(x,y)=\mathbf{U}(x,y)\mathbf{g}(x,y)$$ [4]

where Rn is the noise covariance matrix, the superscript ^H denotes the conjugate transpose or Hermitian operator, and the “unmixing” matrix U defined by this equation is N_g + 1 rows by N_c columns. The k-th component of the vector $\widehat{\tilde{\mathbf{f}}}$(x,y) is an estimate of h_k(x,y-kD)f(x,y-kD), a weighted and shifted version of the image f(x,y). Define the vector f̂(x,y) of estimates with all the components properly y-aligned:

$$\widehat{\mathbf{f}}(x,y)=\left[\begin{array}{c}\hfill h_0(x,y)f(x,y)\hfill \\ \hfill ⋮\hfill \\ \hfill h_{N_g}(x,y)f(x,y)\hfill \end{array}\right]+{\mathbf{n}}^{\prime }(x,y),$$ [5]

where n′(x,y) represents the noise after array processing and perfect artifact cancellation is assumed (i.e., U(x,y) · S(x,y) equals the identity matrix). The individual component ghost images of f̂ (x,y) may be combined to gain an improved estimate of the desired image f(x,y). It is not necessary to know the space variant “point spread function” h_k(x,y) in order to cancel the ghosts. However, estimates of the complex PSF may be used to optimize SNR when combining the individual estimates, as described in the Appendix.

A block diagram showing the above signal processing steps for artifact cancellation is shown in Fig. 1. Note that the (N_g+1) × N_c unmixing matrix U may either be applied to the N_c × 1 image vector g explicitly, as formulated, and then each component image of $\widehat{\tilde{\mathbf{f}}}$ is (x,y) aligned to create the N_g × 1 image vector f̂, or alternatively, as shown in the implementation of Fig. 1, the shifting of components is performed prior to array combining. In this case, shown by rewriting Eq. 1 for g_i(x,y-kD), the array combiner weights (for all components) are simply the first row of the matrix U. The sample images illustrate the case of N_c = 4 coils and N_g = 1 ghost with D = FOV/2, which is described in greater detail below.

FIG. 1.

Block diagram for artifact cancellation using phased array processing method (illustration for N_c = 4 coils and N_g = 1 ghost artifact with D = FOV/2).

The individual component ghost images, weighted by complex PSF values h_k(x,y), may be combined either coherently or noncoherently (see Appendix). In this context, coherent combining refers to the complex weighted sum which preserves phase, while noncoherent combining refers to the (positive real) weighted sum of magnitudes or root sum of weighted squared magnitudes. For applications that require phase-sensitive detection it is essential to combine coherently in order to preserve the phase. Likewise, in order to perform partial-Fourier acquisition such as partial-NEX, it is necessary to perform the homodyne reconstruction prior to magnitude detection. In this case, coherent combining is desirable to gain an improved estimate of background phase prior to homodyne detection.

In applications such as real-time or retrospective cine imaging, for which a series of image frames are acquired, it is possible to use multiple image frames to estimate smoothed matched filter coefficients directly from the series of point spread weighted images, provided that any temporal variation in point spread values is slow relative to the amount of temporal smoothing. One such method for estimating the matched filter coefficients is described in the Appendix.

This solution (Eq. [4]) has been shown (2,6) to optimize the SNR. In the case of Cartesian sampling, this formulation may be recognized as a generalized form of the SENSE method (2) for reduced FOV imaging, which is a special case. In the case of accelerated imaging using SENSE, the alias ghosts are caused by the k-space sampling function (intentional undersampling), whereas in this formulation the distortion arises from continuous amplitude or phase errors, including space variant distortion. Phased array combining which optimizes SNR subject to nulling constraints is also known as the generalized sidelobe canceller (6). Phased array combining for optimized SNR without nulling constraints has been shown (1) to provide a degree of artifact suppression for aliasing when the ghost spacing D is large relative to the effective width of the individual coil sensitivity profile (such as in a linear array). However, without nulling constraints phased array combining optimized strictly for SNR provides very little ghost suppression for the general case where coils have significant overlap in field sensitivity and ghosts are more closely spaced.

Application to Ghost Artifacts in EPI

Ghosts artifacts result from periodic phase and amplitude errors between lines of k-space (echoes). In applications such as EPI, widely used for ultrafast imaging, examples of errors that cause ghost artifacts include EPI phase or delay misalignment and phase errors due to motion or flow. In general, ghost artifacts are a spatial variant distortion, since the values depend on local effects such as flow or off-resonance due to chemical shift or susceptibility variation. A number of techniques (7-15) are used to minimize distortion and ghost artifacts. The phased array processing method for ghost cancellation adds yet another tool, which may be incorporated to further mitigate EPI distortion and artifacts.

Application to multishot EPI with both interleaved and noninterleaved phase encode acquisition order is considered for cardiac imaging. In applications such as in cardiac imaging where the T* ₂ value is relatively short, images are typically acquired using multiple shots with relatively short echo-trains. To avoid ghost artifacts, images are frequently acquired using an interleaved phase encode order (8,9), although interleaved phase encode order has several drawbacks. Drawbacks of this approach are the geometric and intensity distortion caused by off-resonance phase errors due to chemical shift or susceptibility variation (7), distortion due to in-plane flow, increased echo train length, which results when echo shifting is employed, and distortion due to echo delay misalignment. Using a noninterleaved phase encode order with an echo train length, ETL, will cause N_g=ETL - 1 ghosts spaced D = FOV/ETL, and, therefore, has not been considered viable. A noninterleaved phase encode acquisition order has benefits if the ghosts may be eliminated. Cancellation of ghosts by means of phased array processing makes noninterleaved strategies possible. In this case, the drawbacks cited above for interleaved acquisition are traded for widely spaced ghosts, which in turn are cancelled by phased array processing. In addition, the time ordering of shots may be designed to optimize the k-space weighting due to T₁-recovery for applications such as contrast enhanced imaging.

In the case of noninterleaved acquisition, pixels with an off-resonance frequency of Δf lead to a periodic k-space (phase) weighting, with period ETL Δk_y, where Δk_y is the spacing between phase encode lines. The complex k-space weights (ignoring a constant phase factor), due to off-resonance at a pixel (x,y), are H_m (x,y) = e ^j[mΔφ, where Δφ = 2π Δf(x,y) ΔTE, ΔTE is the echo spacing, m = 0,...,ETL - 1 is an integer index corresponding to k_y = mΔk_y repeating with period ETL Δk_y. The corresponding values of the discrete point spread function h_m(x,y) (space variant) are derived from the (N_g + 1)-point discrete Fourier transform, i.e., h_m(x,y) = DFT{H_m(x,y)}.

Experimental Parameters

Experiments were performed using a phantom to demonstrate the artifact cancellation method and validate SNR. Cardiac imaging was performed to further demonstrate the technique and illustrate some of the unique benefits of this approach.

A cylindrical phantom was constructed using oil and water to demonstrate space variant ghosts that arise from off-resonance when imaged using a short echo-train and noninterleaved phase encode order. The phantom consisted of vegetable oil in a plastic tube surrounded by saline in a concentric cylindrical container. The inner diameter of oil was approximately 2.5 cm and the outer diameter of water was approximately 11 cm. The saline was doped with gadopentetate dimeglumine (Magnevist) at a concentration of 0.1 mM to reduce the T₁ relaxation to approximately 800 msec.

Imaging was performed using a GE Signa CV 1.5 T MR Imager. A real-time fast gradient recalled echo train (FGRE-ET) pulse sequence (14,15) was used, modified to acquire in noninterleaved, as well as conventional interleaved, phase encode order. Data was reconstructed offline using the method described.

A four-element cardiac phased array coil was used. The design of this array is not optimized for the SENSE processing application. Individual coils were rectangular with dimension of approximately 11.5 × 19 cm each, with the four-coil array consisting of two overlapped coils (2 cm overlap along shorter side) on the top and similarly two overlapped coils for the bottom pair. The top and bottom coils were spaced approximately 13 cm apart for this oil/ water phantom. This spacing is less than the nominal design separation and a small degree of inductive coupling between top and bottom coils was observed. The axis of the cylindrical phantom was along the main field, with the baseline for individual elements of each pair of coils in the perpendicular direction (left/right).

Axial slices of the phantom were imaged using the following parameters. Echo train lengths (ETL) of 1, 2, 3, and 4 echoes were used with ±62.5 kHz bandwidth, with the repetition interval TR in the range 5.4 and 9.8 msec for the various ETLs. The flip angle was 20°, with a slice thickness of 10 mm. The field-of-view was 120 × 120 mm with an image matrix of 128 frequency encodes × 128 phase encodes for ETL = 1, 2, and 4. For ETL = 3, the phase FOV was reduced to 3/4, resulting in a matrix size of 128 × 96 (thereby divisible by 3). The echo spacing was approximately 1.4 msec.

A pulse sequence designed for cardiac cine application was used which acquired a series of images in a gated segmented manner (16 views per segment for ETL =1, 2, and 4, and 12 views per segment for ETL = 3). The number of cardiac phases acquired was 10, 19, 27, and 22 for ETL = 1, 2, 3, and 4, respectively. The phantom images shown in the figures were averaged (over all cardiac phases) to improve the SNR. Reference images were acquired with the same spatial resolution using ETL = 1 to produce artifact-free images for estimating the complex coil sensitivity profiles (B₁ maps). The raw sensitivity estimates were calculated from the reference image by normalizing with the magnitude image (square root of the sum of the squares) rather than using a body coil reference. Spatial smoothing over a small region (3 × 3) was performed. The noise correlation matrix was estimated from the sample covariance matrix calculated in noise-only regions of the images.

Cardiac cine imaging of a single slice, short axis view of the heart was performed using a gated (ECG trigger) segmented acquisition of k-space over several heartbeats during a single breath-hold. The pulse sequence used FISP (16) implemented with an echotrain ETL = 2. Data was acquired using interleaved, with and without echo-shifting, and noninterleaved phase encode orders. The imaging parameters used in this experiment were as follows. The bandwidth was ±125 kHz bandwidth and the repetition interval was approximately TR = 5.1 msec without echoshifting and TR = 6 msec with echo-shifting. The flip angle was 60°, with a slice thickness of 10 mm. The FOV was 360 × 270 mm (3/4 phase FOV) with an image matrix of 128 frequency encodes × 96 phase encodes. The echo spacing was approximately 0.9 msec. There were 12 views (six TRs) per segment acquired over eight heartbeats resulting in acquisition of between 30 -36 cardiac phases (images), depending on the heart rate, which varied between 46 -55 bpm for different breath-hold acquisitions. A 15% trigger window was used for the ECG R-wave trigger. All individuals in this study were normal, healthy volunteers. This study was approved by the Institutional Review Board of the National Heart, Lung, and Blood Institute.

The cardiac images shown in the results were not averaged. Reference images were acquired with the same spatial resolution using the interleaved echo-shifted data to produce artifact-free images for estimating the complex coil sensitivity profiles (B₁ maps). The raw sensitivity estimates were calculated from the reference image by normalizing with the magnitude image (square root of the sum of the squares). Spatial smoothing over a small region (3 × 3) was performed. The noise variance for each coil was measured during a prescan calibration, and the off-diagonal terms in the noise correlation matrix were ignored. The four surface coil cardiac array described above was used. The baseline for individual elements of each pair of coils was in the left-right direction. The slice was doubly oblique to image the short axis view of the heart.

RESULTS AND DISCUSSION

Oil and Water Phantom

Images of an axial slice of the oil and water phantom are shown in Fig. 2. Figure 2a,b illustrates ghost artifacts that arise using a noninterleaved phase encode order with echo-train length ETL = 2. In Fig. 2a the individual coils are combined noncoherently using the root sum of squares method, while Fig. 2b uses B₁-weighted complex phased array combining optimized for SNR. In this particular case, the B₁-weighted image of Fig. 2b is virtually the same as the root sum of squares method of Fig. 2a in the phantom region, since there is significant overlap of the coil sensitivities at the ghost spacing FOV/2. Furthermore, the rootsum of squares method has artifact suppression when the relative magnitude of the point spread values (|h₀|and |h₁|) are not equal. Of course, the B₁-weighted image of Fig. 2b suppresses artifact outside the phantom region since the estimate of coil sensitivity outside the phantom is effectively noise (thresholding was not used).

FIG. 2.

Images of oil and water phantom: (a,b) images with off-resonance ghost artifacts using multishot EPI (ETL = 2) with noninterleaved phase encode acquisition order with individual coil images combined using (a) root sum of squares and (b) B₁-weighted to optimize SNR, (c) reference image of oil and water phantom without ghost artifacts obtained using a single echo per shot (ETL = 1), (d,e) aligned images after phased array ghost cancellation processing weighted by point spread coefficients, h₀(x,y) and h₁(x,y), respectively, (f) ghost-cancelled image calculated using root sum of squares combining (ETL = 2), (g,h) images after SENSE processing weighted by DFT of point spread coefficients H₀(x,y) and H₁(x,y), respectively, (i) image from ETL = 2 interleaved acquisition with echo-shifting showing slight geometric distortion in the phase-encoding direction.

The magnitude of the ghost in the oil region is much greater than that of the water, due primarily to the chemical shift off-resonance phase of the oil. The water ghost is caused primarily due to off-resonance phase errors caused by field inhomogeneity (shimming error). The reference image for this slice without ghost artifacts is shown in Fig. 2c (using ETL = 1). Phased array ghost cancellation processing produced the image vector f̂ comprised of two images weighted by the complex space variant point spread values, in this case h₀(x,y) and h₁(x,y), per Eq. [5]. The magnitude of these two images is shown in Fig. 2d,e, with the same grayscale (window and level) used for both images. These images may be transformed (2-point DFT of each pixel) to display the images corresponding to SENSE processing of even and odd k-space lines (3), weighted by even and odd k-space coefficients H₀ and H₁, as shown in Fig. 2g,h, respectively. In this example, with an echo-spacing of 1.4 msec, the off-resonance phase for oil is approximately 108°, corresponding to a PSF with nominal magnitudes of |h₀| = 0.58 and |h₁| = 0.82 in the oil region.

Noncoherent combining (square root of the sum of squares) of the images in Fig. 2d,e is shown in Fig. 2f. Noncoherent combining of the images in Fig. 2g,h is essentially the same. The ghost artifact is effectively removed by means of this phased array processing technique. For comparison, an image acquired using interleaved acquisition with echo-shifting is shown Fig. 2i. Without echo-shifting (8,9) there would be considerable artifact due to phase discontinuities in φ(k_y). Echo-shifting eliminates this artifact at the expense of a slightly longer repetition interval, TR; however, geometric, as well as amplitude, distortion remains. Chemical shift distortion in the phase encode direction, clearly evident in Fig. 2i, has been eliminated by this phased array processing method.

The measured SNR for an artifact-free image (single image frame without averaging) varied in the range 30-60 (higher in proximity to surface coils). The SNR for images with artifact cancellation was compared to that of ghost-free reference images. An estimate of the SNR was made for each pixel by calculating the sample mean and variance over a number of time frames (32 images acquired). The SNR loss (due to ghost cancellation) is spatially varying (Eq. [A-4]), with up to 25% loss in the center of the image, as expected for this coil array with N_g = 1.

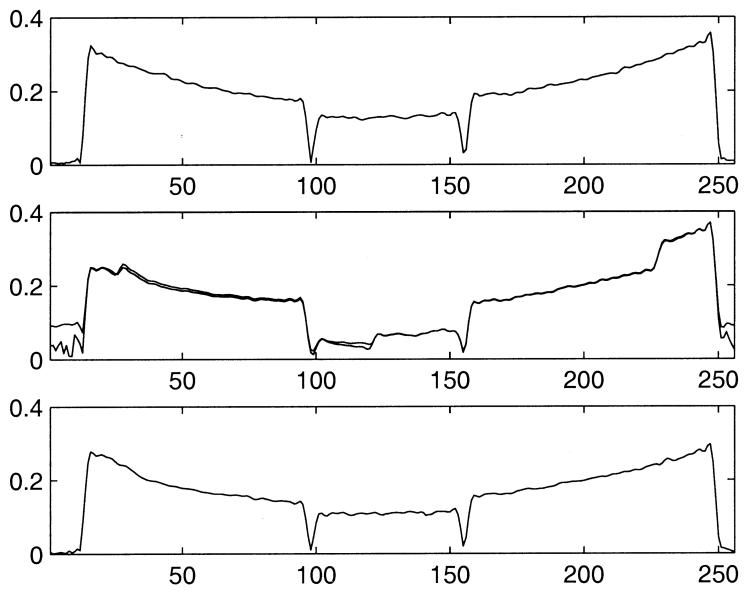
A plot of the magnitude for a single line of the image (vertical line through the center) is shown in Fig. 3 for several cases. The plot in Fig. 3a is for the artifact-free (reference) image with ETL = 1, corresponding to Fig. 2c. The plots in Fig. 3b are for the ETL = 2 noninterleaved acquisition image with artifact, corresponding to Fig. 2a,b, which are virtually identical inside the phantom region, as described earlier. The plot in Fig. 3c is for the ETL = 2 noninterleaved acquisition image with artifact cancelled, corresponding to Fig. 2f. The magnitude of the ETL = 2 image is slightly smaller than the ETL = 1 image (approximately 20%) due to T* ₂ effect, and there is a slight variation in magnitude across the image due to variation in T* ₂ caused by susceptibility variation due to shimming errors, particularly at the edges. Therefore, the ETL = 1 reference in Fig. 3a and ETL = 2 artifact cancelled image in Fig. 3c cannot be compared directly by subtraction to measure artifact suppression. However, since the artifact (not evident in Fig. 3c) is suppressed below the noise, the artifact suppression, for this example, is estimated to be at least 40:1 (locally at the edge) by measuring the artifact-to-noise ratio of the step in the right-hand side of Fig. 3b.

FIG. 3.

Magnitude plots along vertical line through center of oil/water phantom images for (a) artifact-free reference image (Fig. 2c), (b) images with artifacts (Fig. 2a,b), and (c) artifact-cancelled image (Fig. 2f).

Using the four-coil GE cardiac phased array, it is possible to cancel up to N_g = 3 ghosts corresponding to ETL = 4 noninterleaved acquisition. An example image for ETL = 3 with two ghosts is shown in Fig. 4a, using root sum of squares combining. Ghost cancellation was achieved, although the resultant image (using root sum of squares combining) shown in Fig. 4b is quite noisy. Increased noise is evident in regions that correspond to a large SNR loss factor (see Appendix), giving the appearance of residual ghost artifact. With this array, the SNR loss factor for processing of N_g = 2 ghosts was quite large, with a maximum value estimated to be as high as 10. With a greater number of coils designed for this application, it should be practical to work with ETL = 4. As the number of ghosts increases and their spacing decreases correspondingly, a larger number of coils, where the relative sensitivity profiles between coils contains greater spatial variation, are required.

FIG. 4.

Images from noninterleaved phase encode acquisition order using ETL = 3, (a) with ghost artifacts, and (b) after phased array processing to eliminate ghosts.

Cardiac Images

Short axis images of the heart are shown in Fig. 5 for a single cardiac phase during mid-systole. Ghost artifacts that arise using a noninterleaved phase encode order with ETL = 2 are evident in Fig. 5a,b, which combine individual coil images using the root sum of squares method in Fig. 5a, and using complex B₁-weighted combining optimized for SNR in Fig. 5b. The phase encode direction is left-right in these figures. In addition to the ETL = 2 ghosts, there is aliasing (wrap) within the FOV. In this particular case, the level of artifacts is comparable for Fig. 5a,b. The image in Fig. 5c without artifacts is acquired using ETL = 2 with interleaved phase encode order and echo-shifting. This image was acquired during a different breath-hold than the other images; nevertheless, the spatial registration is quite good.

FIG. 5.

Short axis heart images using multiecho FISP with ETL = 2: (a,b) images with artifacts using noninterleaved phase encode acquisition order with individual coil images combined using (a) root sum of squares, and (b) B₁-weighted to optimize SNR, (c) image without ghost artifacts obtained with an interleaved acquisition with echo-shifting, (d,e) aligned images after phased array ghost cancellation processing weighted by point spread coefficients, h₀(x,y) and h₁(x,y), respectively, (f) ghost-cancelled image calculated using root sum of squares combining.

The primary artifacts in Fig. 5a,b are due to off-resonance. The strongest artifacts are due to fat, most distinct in the chest and back walls. The back wall artifact in Fig. 5a is indicated by the label A. The artifact labeled B is a due to in-plane flow and is apparent only during the midsystole phase of the cycle. The flow artifact which is a ghost in Fig. 5a,b using noninterleaved acquisition order creates slight distortion using interleaved acquisition, indicated by label C in Fig. 5c. This distortion is apparent only during the time that there are flow ghosts, as expected.

The magnitude of the two images with phased array ghost cancellation, weighted by h₀(x,y) and h₁(x,y), are shown in Fig. 5d,e, respectively, with the same grayscale (window and level) used for both images. The h₁-weighted image of Fig. 5e is primarily due to the fat and, therefore, it is possible to simply use the magnitude image of Fig. 5d, which will provide a slight fat suppression and slight increase in SNR (particularly in low SNR regions). The image of Fig. 5f is the root sum of squares combination of Fig. 5d,e. The ghost artifacts due to both off-resonance and in-plane flow are effectively removed by means of this phased array processing technique. Furthermore, using the noninterleaved acquisition the repetition time TR is reduced significantly by eliminating echo-shifting. In comparison, the “fat suppressed” h₀-weighted image calculated by this method is equivalent to the sum of H₀ and H₁ weighted images (h₀ = H₀+H₁) calculated using the method (3) which applies SENSE to the images reconstructed from even and odd k-space lines.

General Discussion

The phased array method for ghost artifact cancellation may be used to reconstruct complex images. In comparison, the method (3) uses noncoherent combining of the separate images reconstructed from even and odd EPI-acquired k-space lines, which are weighted by H₀ and H₁ for even and odd images, respectively. This method, which was used for single-shot EPI, is similar to the method described in this article, except for the weighting and combining, and, of course, different implementation. For noncoherent, magnitude squared combining with uniform weighting both methods result in equivalent images, since Σ|h_k|² = Σ|H_k|² by Parseval’s theorem. In general, these methods differ in cases where specific weighting and combining is considered. In comparison with the method (4) based on SMASH, which is implemented on separate reconstruction of even and odd lines similar to (3), this method is implemented in the k-space domain and, therefore, only cancels ghosts caused by global errors in k-space, and does not treat the more general case of space variant distortion such as caused by local flow or off-resonance. Ghost cancellation methods, which are based on k-space weighting (equalization), for example, phase compensation, have similar limitations.

There are practical limitations to the effectiveness of this method, which are imposed by the number of coils and the acceptable loss in SNR. When the nonzero point spread values are closely spaced, the inverse solution, which depends on the coil sensitivity profile, becomes ill-conditioned, with correspondingly high loss in SNR. Additionally, errors in the estimate of coil profiles will reduce the artifact suppression, particularly in regions of ill-conditioning which are more sensitive to errors. For application to cancellation of ghosts with relatively few widely spaced point spread values, the solution has much better conditioning, since the relative coil sensitivities vary considerably at these wider distances. While the theoretical formulation is quite general (and may even be further generalized to 2D distortion), the performance of phased array processing poses practical limitations on the number and spacing of nonzero point spread values that may be cancelled by this method. In other words, to gain increased spatial resolution by phased array processing, the relative sensitivity profiles must have reasonably high spatial frequency.

This method requires estimates of the coil sensitivities, which are typically derived from reference images. It is necessary to acquire the reference images without distortion. There are numerous applications, such as cine imaging, for which the reference image may be acquired with little or no increase to the overall acquisition time.

CONCLUSION

A method for cancellation of ghosts artifacts based on phased array processing using constrained optimization has been formulated and demonstrated. This array processing technique optimizes SNR subject to the constraint of nulling ghost artifacts at known locations. The nulling constraints incur a penalty in SNR, as compared to the optimum SNR without constraints, which results in a spatially varying amplification of noise due to ill-conditioning of the inverse solution. The number of coils and specific sensitivity profiles dictate the performance in terms of number and spacing of ghosts. For the case of Cartesian sampling, this method can be seen as a more general formulation of the sensitivity encoding technique (SENSE) used for accelerated imaging.

The method reconstructs intermediate images for each ghost, weighted by the complex space variant point spread function, which are combined to produce a final image with ghosts artifacts cancelled. The intermediate ghost images may be combined in a coherent manner using complex weights derived from estimates of the point spread function. Coherent combining preserves phase and, therefore, permits partial-Fourier homodyne demodulation or more general phase-sensitive image reconstruction.

Application of this phased array ghost cancellation method to noninterleaved multishot EPI ghosts was demonstrated experimentally with phantom as well as cardiac imaging. Incorporating this phased array method for ghost cancellation may result in greater flexibility in designing acquisition strategies. Cancellation of ghosts by means of phased array processing makes noninterleaved phase encode acquisition order practical and permits a reduction in repetition time, TR, by eliminating the need for echo-shifting. Noninterleaved phase encode order has benefits of reduced distortion due to off-resonance, in-plane flow, and EPI delay misalignment. Ghosts caused by amplitude or phase variation during the approach to steady state may also be cancelled. Noninterleaved phase encode order might also be desirable in contrast-enhanced imaging in order to optimize the k-space weighting due to T₁ recovery by proper time ordering of noninterleaved shots. Although not demonstrated experimentally, this technique is applicable to cancellation of ghosts arising from other mechanisms such as motion during cine imaging even with single echo.

In theory, the general formulation presented shows that phased array processing may be used for quite general distortion, including local blurring; however, the ability to use this method to improve spatial resolution places demands on the coil sensitivity profile which are currently not deemed practical.

APPENDIX

The desired image f(x,y) can be estimated from the solution vector f̂ defined by Eq. [5]. In the case where the point spread function h(x,y) is known, or can be estimated adaptively, the SNR of the estimate f̂(x,y)of f(x,y) is maximized by matched filtering:

$$\widehat{f}(x,y)=\mathbf{h}{(x,y)}^{\mathrm{H}}\cdot \widehat{\mathbf{f}}(x,y).$$ [A-1]

The estimate of the image is weighted by the squared norm ||h||² = h^H · h, which in many cases is approximately constant. If, instead, the matched filter coefficient vector is first normalized to have unity norm (i.e., h/||h||), then the resultant image is weighted by ||h||. Alternatively, in cases where h is unknown, the image magnitude may be estimated noncoherently as the square root of the sum of the squares:

$$\widehat{f}(x,y)=\sqrt{\widehat{\mathbf{f}}{(x,y)}^{\mathrm{H}}\cdot \widehat{\mathbf{f}}(x,y)}.$$ [A-2]

The matched filter coefficients may be estimated from the images themselves. In situations where multiple images are acquired, smoothing may be employed to reduce the error due to noise. For this case, one method which estimates the normalizes coefficients (within a constant phase offset) is to form the time averaged (or temporally low-pass filtered) sample covariance matrix for each pixel,

$$\mathbf{R}(x,y)=\sum _t\widehat{\mathbf{f}}(x,y,t){\widehat{\mathbf{f}}}^{\mathrm{H}}(x,y,t),$$ [A-3]

where the variable t represents a time index and averaging is performed over a number of frames during which h(x,y,t) has small time variation. An estimate of h(x,y)/ ||h(x,y)|| may be obtained by using the eigenvector of R(x,y) with maximum eigenvalue. The relative phase between components is preserved. For phase-sensitive reconstruction, the same matched filter coefficients must be applied to the reference and desired images.

The inverse solution (Eq. [4]) amplifies the noise causing a loss in SNR which is spatially varying. The loss in SNR relative to the artifact-free image, i.e., h(x,y) δ(x,y) (discrete delta function), is calculated as (2):

$${\mathit{SNR}}_{\text{loss}}=\frac{1}{\sqrt{{\left({\mathbf{S}}^{\mathrm{H}}{{\mathbf{R}}_{\mathit{n}}}^{-1}\mathbf{S}\right)}_{(1,1)}^{-1}{\left({\mathbf{S}}^{\mathrm{H}}{{\mathbf{R}}_{\mathit{n}}}^{-1}\mathbf{S}\right)}_{(1,1)}}},$$ [A-4]

where the subscript (1,1) denotes the index of the matrix (first diagonal element). The spatially varying denominator of Eq. [A-4] is also referred to as the geometry factor G. This is derived by noting that the SNR loss of each component of the properly aligned image vector f̂ relative to the SNR of h_k(x,y)f(x,y) is given as SNR_loss (Eq. [A-4]). The individual noise components of the vector f̂(x,y) are independent since the full FOV acquisition results in spatially white noise over the full FOV. Thus, the net loss in SNR for the final matched filter estimate f̂₍ x,y) (Eq. [A-1]) relative to the SNR of f(x,y) is simply SNR_loss (Eq.[A-4]).