An interpretation of fluctuations in enzyme catalysis rate, spectral diffusion, and radiative component of lifetimes in terms of electric field fluctuations

Abstract

Time-dependent fluctuations in the catalysis rate (δk(t)) observed in single-enzyme experiments were found in a particular study to have an autocorrelation function decaying on the same time scale as that of spectral diffusion δω₀(t). To interpret this similarity, the present analysis focuses on a factor in enzyme catalysis, the local electrostatic interaction energy (E) at the active site and its effect on the activation free energy barrier. We consider the slow fluctuations of the electrostatic interaction energy (δE(t)) as a contributor to δk(t) and relate the latter to δω₀(t). The resulting relation between δk(t) and δω₀(t) is a dynamic analog of the solvatochromism used in interpreting solvent effects on organic reaction rates. The effect of the postulated δE(t) on fluctuations in the radiative component (δγ_r⁻¹(t)) of the fluorescence decay of chromophores in proteins also is examined, and a relation between δγ_r⁻¹(t) and δω₀(t) is obtained. Experimental tests will determine whether the correlation functions for δk(t), δω₀(t), and δγ_r⁻¹ are indeed similar for any enzyme. Measurements of dielectric dispersion, ε(ω), for the enzyme discussed elsewhere will provide further insight into the correlation function for δE(t). They also will determine whether fluctuations in the nonradiative component γ_nr⁻¹ of the lifetime decay has a different origin, fluctuations in distance for example.

Single-molecule experiments on proteins have revealed novel phenomena, including fluctuations in the rates of enzyme catalysis (1–3), on–off blinking behavior in proteins (4–6), and oscillations under a near-denatured condition of a green fluorescent protein (7). The on–off blinking behavior of proteins and the fluctuations in the enzyme catalysis rate in the experiments were interpreted in terms of fluctuations of the protein/enzyme between various conformational substates (2, 3). The rates of enzyme-catalyzed reactions themselves occur typically on the milliseconds-to-seconds time scale, and the millisecond dynamics of enzymes are believed to contribute to the “functional dynamics” of the enzyme (8). Single-molecule enzyme experiments on cholesterol oxidase revealed an autocorrelation function of the rate of catalysis that decayed on a time scale about the same as that for the decay of the autocorrelation function of the spectral diffusion of a chromophore in the same enzyme in the absence of the substrate (1), thus suggesting a common origin for the two fluctuations.

Significant insight into the functioning of enzymes has been achieved by using computer simulations (9–11) and empirical valence bond (9) and hybrid quantum mechanical/molecular mechanics (10) methods, among others. In these studies the catalysis is affected by several factors: electrostatic effects of the enzyme on the substrate (9) and coupling of protein fluctuations with motions of the substrate–coenzyme pair in the transition state (e.g., ref. 8). Electrostatic effects have been seen to be significant in enzymatic catalysis (9, 12–25). Direct molecular dynamics simulations of protein dynamics are typically restricted to tens of nanoseconds, and so a detailed dynamical analysis of the observed millisecond rate fluctuations via an integration of the equations of motion of the atoms is presently beyond the scope of such simulations. Simulations with bias potentials using methods such as accelerated molecular dynamics (26), which allow long-time-scale trajectories up to milliseconds, have not yet been performed to study the equilibrium conformational fluctuations in enzymes.

Spectral diffusion of a chromophore has been interpreted as due to transitions of the molecule between different chromophore conformations (27) or in terms of the density fluctuations of the dielectric matrix leading to polarization fluctuations (28). Previous studies of a different nature have included the role of the electric field on time-dependent vibrational Stark shift at the heme site of myoglobin (29) and of the nitrile stretching mode in human aldose reductase (30), both in the picosecond regime. Considering the importance of electrostatics in enyzme catalysis (9, 12–25) and in spectral diffusion (δω₀(t)), we explore the possibility that δk(t) and δω₀(t) may be related to each other via the time-dependent fluctuations in the local electrostatic interaction energy, δE(t).

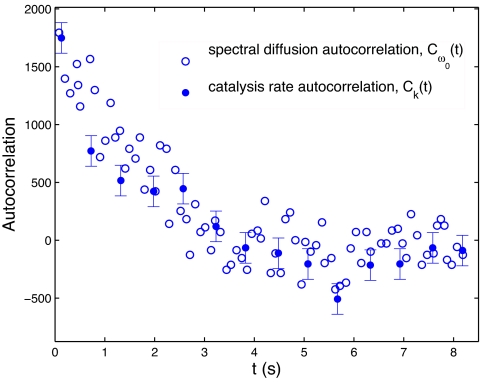
The present work on correlation functions of different enzyme properties was prompted by an experimental observation of the autocorrelation functions of catalysis rate of oxidation of cholesterol (C_k(t)) and the spectral diffusion (C_ω0(t)) for cholesterol oxidase (1). The two autocorrelation functions are compared in the present Fig. 1. The C_ω0(t) in figure 2 of ref. 1 has a fast initial decay followed by a slow decay. The fast initial decay is attributed to the noise in the spectral means and/or fluctuations on a time scale faster than the experimental resolution (31). In the present Fig. 1, only the slow decay component is shown by excluding the data point at t = 0. The result is seen to have the same functional form as the C_k(t). To compare the time behavior of these two different physical measurements, the absolute value of C_k(t) from ref. 1 was rescaled to match that of C_ω0(t). The comparison in Fig. 1 highlights a similarity of the decay of the two autocorrelations with time. By examining the reduced autocorrelation functions, such as 〈δω₀(t) δω₀(0)〉/〈δω₀(0)²〉, the focus is on the time scale rather than on absolute values.

Fig. 1.

Comparison of the decay of autocorrelations of catalysis rate fluctuations [C_k(t) in s⁻²] and spectral diffusion [C_ω0(t) in cm⁻²] from figures 4A and 5C of ref. 1. C_k(t) is rescaled to account for the difference in normalization factors for both of these autocorrelations. The abscissa for C_k(t) is given in number of turnovers, converted to time units by using ≈600 ms per turnover (1). The point value for C_ω0(t) at t = 0 is excluded as discussed in the text.

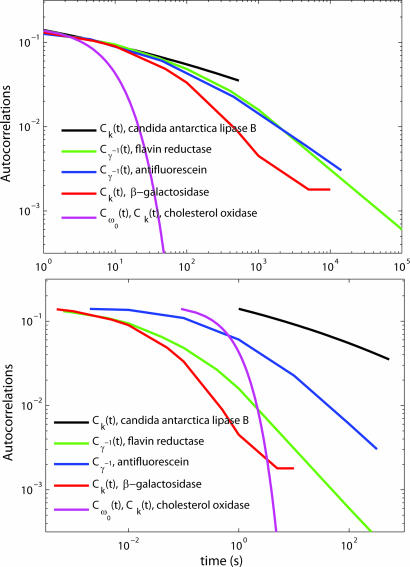
Fig. 2.

Comparison of the fits to experimental autocorrelation functions C_γ⁻¹(t), C_k(t), and C_ω0(t) from three different enzymes. The autocorrelation functions are scaled to the same value at short time for comparison. (Upper) The autocorrelation functions were shifted horizontally in the log–log plot to make the comparison of their behavior as a function of time easier. (Lower) The same data without this shift. The measurements are from the following sources: candida antarctica lipase B, ref. 2; flavin reductase, ref. 32; antifluorescein, ref. 33; β-galactosidase, ref. 3; and cholesterol oxidase, ref. 1.

With a common theme of fluctuations in the local electrostatic interaction energy, three different observables are examined: catalysis rate fluctuations (δk(t)), spectral diffusion (δω₀(t)), and fluctuations in the radiative component of fluorescence decay (δγ_r⁻¹). In the following analysis, the δk(t) and δω₀(t) are first related to the fluctuations local electrostatic interaction energy (δE(t)) and then to each other. These fluctuations, δE(t), are used later to describe δγ_r⁻¹ by relating it to δω₀. Experimental tests are suggested for exploring the suggested relationships between the three quantities. A quantity not specifically treated but discussed later is the fluctuation in the nonradiative component γ_nr⁻¹ of the lifetime decay of a fluorescing protein, which may have a different origin as studied by Xie and coworkers (32, 33). These two components of fluorescence decay, γ_r and γ_nr, can be distinguished by an experiment suggested later in the article to be performed in the total absence in the enzyme of any fluorescence quencher that is responsible for the nonradiative fluorescence decay, γ_nr, by electron transfer.

Enzyme Fluctuations

Fluctuations in Catalysis Rate and in Local Electrostatic Interaction Energy.

The autocorrelation function C_E(t) of the fluctuations in local electrostatic interaction energy at the active site, δE(t), can be defined as

Experimentally, the catalysis rate, k, is obtained by averaging the turnover times from several cycles of the enzyme (1), over which the enzyme is assumed to be in the same conformation. We assume that there is some slow protein coordinate, X(t), representing this conformation and that the local electrostatic interaction energy at the active site, E, depends on this X, and because X varies with t, we write the slowly fluctuating E(X(t)) as E(t). Fluctuations in the catalysis rate (δk(t)) depend, among other factors, on these slow fluctuations in the electrostatic energy (δE(t)) occurring on the time scale of the order of the reciprocal of the rate constant for the hydride (or other) transfer within the bound substrate and enzyme complex. We write δk(δE(t)) as δk(t).

Fluctuations of k with time, δk(t), around a mean value k₀, are related to the time-dependent fluctuations in E, δE(t), around a mean value E₀. The relation can be regarded as occurring via a dependence of the activation free energy on E(t) through the dipole moment difference (Δμ_r) of the transition state and the reactants. We assume for simplicity that fluctuations in X mainly affect those in E rather than those in Δμ_r. The approximate relationship can be written as

where the notation

is used for convenience and A is a proportionality factor that can depend on other factors affecting the reaction rate. Assuming the fluctuations δu(t) are Gaussian about a mean value 〈δu〉 = 0, using a cumulant expansion (34), and neglecting the terms beyond the quadratic, the following relation can be obtained

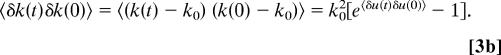It was seen in ref. 1 that the ratio of the catalysis rate maximum to minimum was about a factor of 10. The root mean square fluctuation of k is much less, perhaps a factor of 2, as in figure 5C of ref. 3. These results mean that the catalysis rate fluctuates from the mean by a factor of ≈3 (≈$\sqrt{10}$), so in Eq. 2b, δu(t) ranges from approximately ≈1.09 to 1.09, and the variance, 〈δu(0)²〉, is ≈0.3. With this variance for δu, the following approximation can be made:

After normalization by division by the appropriate factors 〈δk(t) δk(0)〉 and 〈δu(0) δu(0)〉, the autocorrelation function C_k(t) is approximated to that of δu(t). We thus have

Using Eqs. 2b and 4, we have

Thereby, the fluctuations in the catalysis rate of the enzyme are interpreted in terms of the fluctuations in the local electric field.

Spectral Diffusion and Fluctuations in Electrostatic Energy.

The emission spectrum was obtained by collecting fluorescence emissions of photons for ≈100 ms (1) at different time intervals. The spectral mean of broad emission spectrum is calculated by averaging over the spectrum. The spectral mean so obtained undergoes fluctuations, namely, spectral diffusion (1). To relate the fluctuations in local electrostatic interaction energy to spectral diffusion in enzymes and so relate the latter to catalysis, we note that, to first-order in δE, the change in emission frequency, δω₀, of the chromophore is given as

In this case of spectral diffusion, the electrostatic interaction energy, δE(t), depends on Δμ, the change in dipole moment of the chromophore upon electronic excitation. The autocorrelation function of the spectral diffusion is

Using Eqs. 6 and 7a, we have

where the equality between C_E and C_ω0 in Eq. 7b follows from Eqs. 6 and 7a. Comparing Eqs. 5 and 7b, we then have C_k(t) = C_ω0(t).

Fluctuations in Radiative Component of the Fluorescence Decay Rate.

Fluorescence decay lifetime (γ⁻¹) was obtained experimentally by averaging the delay times between the excitation of the chromophore and emission of photons (32), and fluctuations in γ⁻¹ were observed (32, 33). The fluorescence decay lifetime of a chromophore in the protein, γ⁻¹, depends on the rate constants of radiative (γ_r) and nonradiative (γ_nr) components, with possible fluctuations in either or both of these quantities:

Eq. 8 with a single exponential decay of fluorescence intensity was assumed in refs. 32 and 33. The decay of fluorescence intensity of the chromophore on the nanosecond time scale could in principle be a multiexponential. However, in the current absence of detailed studies of single molecules on nanosecond time scales showing evidence to the contrary (a point we discuss further below), a single exponential decay is assumed, as in refs. 32 and 33. We examine now a modeling of fluctuations in the radiative component of the fluorescence decay lifetime (δγ_r⁻¹) of a chromophore in the protein in terms of δE(t). γ_r⁻¹ and the spectral frequency (ω₀) are related by (28)

This relation also was observed experimentally in ref. 35, with a mostly linear relation between the δγ_r and δω₀ over the observed range, δω₀, of spectral diffusion.

The variations in the observables k, ω₀, and γ⁻¹ can be discussed using either the standard deviation of their distribution or the variation between the maximum and minimum of the observable (amplitude). Here, we refer to the latter extreme variation (amplitudes) in all of these observables, unless we explicitly mention that it is the root mean square deviation. For a spectral diffusion between the extreme values of 550 nm and 580 nm for carbocyanine dye molecules in a polymeric matrix, a purely radiative decay coupled to the environmental fluctuations can explain the maximum fluctuations of lifetime approximately ±0.5 ns, an ≈2-ns fluorescence lifetime (35). In other experiments with chromophores embedded in polymeric matrix, a maximum variation in spectral diffusion between 650 nm and 670 nm for sulforhodamine 101 (27) and fluorescence lifetime between 2 ns and 4 ns for the chromophore 1,10-dioctadecyl-3,3,30,30-tetramethylindodicarbocyanine (28) were observed. For the entire range of spectral diffusion between 520 nm and 535 nm observed in cholesterol oxidase-flavin adenine dinucleotide complex in ref. 1, a nearly linear relation between δγ_r⁻¹ and δω₀ is valid because δω₀/ω₀ = ±0.015.

From Eqs. 7b and 10, the autocorrelation function of the radiative component of the lifetime is

We then have from Eqs. 5, 7b, and 11

If other contributions to the radiationless transitions are minor, the autocorrelation of γ_r⁻¹ can be obtained from single-molecule experiments for mutated Tyr-35 flavin reductase. This autocorrelation function of γ_r⁻¹ does not appear to have been given explicitly in ref. 32. If, for that system, the fluctuations in γ_r⁻¹ prove to be negligible, then the fluctuations in γ⁻¹ in refs. 32 and 33 are solely due to nonradiative fluorescence decay, γ_nr⁻¹. Fluctuations in γ_nr⁻¹ have been treated in terms of fluctuations in donor–acceptor distance δr_DA for quenching of fluorescence by electron transfer (32, 33). Only if δr_DA and δE have a common origin, for example, due to conformational fluctuations of the enzyme, could one then write C_γ⁻¹(t) = C_γr⁻¹(t) = C_γnr⁻¹(t) = C_E(t), and, hence, C_k(t) = C_ω0(t) = C_γ⁻¹(t).

Discussion

Different facets of enzyme catalysis have been examined previously (8, 9). For example, Warshel et al. (9) discussed the role of electrostatics at the active site in affecting the activation barrier for the reaction and Agarwal et al. (11) discussed statistical correlations of the dynamics of the different residues of the enzyme by mapping out the network of correlated motions using NMR. These discussions have not yet been applied to time-dependent fluctuations of the enzymatic catalysis rate observed in refs. 3 and 36, as noted earlier. Catalysis rate fluctuations have been interpreted qualitatively as due to conformational fluctuations of the enzyme, each rate corresponding to a different conformation (2, 3). Similarly spectral diffusion was attributed to different conformations of the enzyme (1).

The dynamics in proteins happens on multiple time scales from tens of femtoseconds to hundreds of seconds (37). Each motion in protein is associated with a typical time scale, for example, the vibrations are on the hundreds of femtoseconds and large motions, such as domain movements in proteins, are on the milliseconds time scales (37). The electric field fluctuations can arise from any or all of these different dynamics and so can last over the whole dynamic range of proteins from femtoseconds to seconds. The experimental techniques used in refs. 1, 3, 30, and 31 focus on the slow dynamics on millisecond to second time scales. The dynamics faster than this are averaged over in the observations. One feature of formulating the fluctuations of observables, sometimes termed dynamic disorder (38), in terms of fluctuations in electrostatic interactions is seen from a method of computing the autocorrelation function, C_E(t), discussed elsewhere (39), in terms of a measurable frequency-dependent dielectric dispersion (ε(ω)) of the protein. In that formalism, the dielectric constant varying in the frequency range of kilohertz to hertz provides an estimate of the electric field fluctuations on the desired milliseconds-to-seconds time scale.

The experimentally observed similarity in the time scale for decay of the autocorrelation function of catalysis rate fluctuations and the autocorrelation function of spectral diffusion seen in ref. 1 in the absence of the substrate also recalls the empirical relation (40) between organic reaction rates and electric field effects on spectra in different solvents. In the latter formalism, the solvatochromic shift of the spectral frequency of a dye in a solvent indicates the degree of polarity of the solvent and is empirically found to be proportional to the decrease in the activation free energy (ΔG^≠) for the reaction, expressed in terms of the logarithm of the rate constant. The present model with fluctuations is a dynamic analog of solvatochromism. Although the proportionality constant to ΔG^≠ will depend on the chromophore and the polarity of transition state relative to the reactants, it can be ≈1 in an order of magnitude estimate (40). With this approximation, the reduction in the activation free-energy barrier for a reaction is equal to the shift in energy levels of a chromophore placed in the same environment, the enzyme in the present case. The spectral frequency emitted by the chromophore in the enzyme may be different for every photon. Over a short time (milliseconds), the change in the frequency is due to the homogeneous broadening of the emission because of dynamics happening on time scales faster than nanoseconds. At times longer than a hundreds of milliseconds, as the slow conformational changes of the enzyme happen, the new enzyme environment leads to a new emission spectrum, and the shift in the spectral mean is used to interpret the conformational dynamics. It should be noted that the width of the homogeneous broadening is much higher than the shift in the spectral mean (figure 5 A and B of ref. 1). Therefore, broadening introduced in the emission may be interpreted only by studying the single molecules, because these small changes may not be noticeable in ensembles.

One can estimate the standard deviation of the fluctuations in enzymatic rate constant k from the standard deviation of the spectral diffusion. Using k = k₀ exp(−δu), and 〈k〉 = k₀ exp(−〈δu²〉) from the cumulant expansion, we have

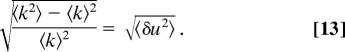The standard deviation of spectral diffusion in cholesterol oxidase as seen from figure 5C in ref. 1, after excluding the first data point, which can be because of noise as noted earlier, is 46 cm⁻¹ (≈0.13 kcal·mol⁻¹). It corresponds to $\sqrt{\langle \delta u^2\rangle }$ ≈ 0.13 kcal·mol⁻¹/k_BT = 0.22. This $\sqrt{\langle \delta u^2\rangle }$ using Eq. 13 leads to a predicted fluctuation in k of a factor of 0.22. The standard deviation of k in β- galactosidase from figure 5C of ref. 3 is ≈60 s⁻¹ from mean value of k, 170 s⁻¹. This gives a variation of 60 s⁻¹/170 s⁻¹, which is ≈0.35 and therefore is larger though comparable with that predicted from spectral diffusion for a different enzyme, cholesterol oxidase. If both spectral diffusion and catalysis rate fluctuation measurements are made on the same enzyme, it will be possible to test the validity of the prediction of the catalysis rate based on the spectral diffusion found by using the electrostatics arguments. Such studies will determine the agreement or disagreement of the measurements with the predictions and will help clarify the relative role of electrostatics as a possible common origin for these experimental observables. Depending on the specific properties of the chromophore and the polarity of the reaction, the fluctuations between the extreme values can vary by a factor different from this estimated value of 0.22. The simulations of human aldose reductase (hALR2) containing the inhibitor IDD743 show a distribution of electric fields corresponding to various orientations of the side chains, ranging between extreme values separated by ≈3 k_BT/eA (= 7.7 MV/cm), 5 k_BT/eA (= 12.9 MV/cm) for the wild-type and V47D enzymes (figure 3C of ref. 30). In the introduction to this study by Boxer and coworkers (30), an electric field of 9 MV/cm was estimated to stabilize the transition state with a typical charge separation of 1 Å by 2.3 kcal/mol. Using this estimate of 1.8 kcal/mol, the catalysis rate can fluctuate by a factor of exp(−1.8 kcal·mol⁻¹/k_BT) ≈ 20. The latter is approximately on the order of the observed fluctuation of a factor of 10 between the extreme values of k seen in figure 5 of English et al. (3) for β-galactosidase. Therefore, the magnitude of fluctuations in electrostatic interaction energy in proteins are significant enough to be a possible origin of the observed fluctuations in k. Had root mean square values been available, as they were in the previous paragraph, those quantities could also have been compared.

Fluctuations in γ_r⁻¹ due to electric field fluctuations may be related in the model to catalysis rate fluctuations, C_k(t) = C_γr⁻¹(t) in Eq. 12. The relation can be explored experimentally by comparing the two autocorrelation functions, analogous to the comparison of C_k(t) and C_ω0(t) pointed out in ref. 1. The experimental fluorescence lifetime autocorrelation function, C_γ⁻¹(t), reported in the literature (32, 33) for flavin reductase and the fluorescein–antifluorescein complex were interpreted, as noted earlier, in terms of the nonradiative lifetime fluctuations δγ_nr⁻¹ due to fluctuations in an electron donor–electron acceptor distance coordinate, r_DA (32). To relate γ_nr⁻¹ fluctuations to δk(t), one then uses information on how r_DA is related to k. The present fluctuation in γ_r⁻¹ follows instead from the hypothesis of fluctuations in electrostatic interaction energy, which in turn can used to interpret the fluctuations in catalysis rate.

The ensemble data on the enzymes (figure 1 of ref. 32) shows a multiexponential decay of fluorescence intensity. This multiexponentiality can arise from the enzyme fluctuating between different conformations, each with a different single exponential decay. Alternatively the fluorescence decay can be multiexponential in each of these conformations. As we noted earlier, the data on the delay times for fluorescence emission thus far (32) do not distinguish between single and multiple exponential decay on a nanosecond time scale. Because of the very small intensity of the fluorescence, it was necessary to accumulate delay times for ≈1 ms to calculate the approximate fluorescence lifetime. Despite the long binning time, the number of photons collected were not enough to distinguish a single exponential from a multiexponential on a nanosecond time scale.

Assuming a single-exponential decay for each enzyme conformation as in Eq. 8, we have the fluctuations in the total radiative lifetime γ⁻¹ as

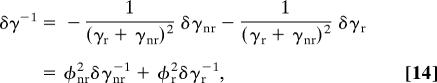where φ_nr and φ_r are the quantum yields of nonradiative and radiative fluorescence decays, respectively, γ_nr/(γ_r + γ_nr) and γ_r/(γ_r + γ_nr). In the single-molecule experiments (32, 33), the multiexponentiality in the fluorescence decay was interpreted as being due to a distribution of conformations. In these experiments, the fluctuations in total fluorescence lifetime δγ⁻¹ were reported, rather than the individual components δγ_r⁻¹ and δγ_nr⁻¹. To study the fluctuations in the purely radiative component in the enzyme environment from a single-molecule experiment, the contribution of the nonradiative effect on the fluorescence decay must be reduced. Ensemble fluorescence decay on flavin reductase performed with and without Tyr-35 responsible for fluorescence quenching by electron transfer is available (figure S3 of ref. 32). However, data on single-molecule fluorescence lifetime fluctuations in the absence of a quencher are currently not available.

The radiative component we refer to is the radiative component of fluorescence decay of the chromophore in the enzyme environment. The single-molecule fluctuations of fluorescence decay of a chromophore embedded in a gel in the absence of a quencher was studied (figure S5 of ref. 32). There was no slow component in the decay in the autocorrelation function of that system. However, what would be particularly interesting is the measurement of the lifetime fluctuation autocorrelation function of the chromophore in the enzyme in the absence of a quencher: The slow motion (millisecond) in enzymes may not have a counterpart in gels.

When single-molecule data without Tyr-35 become available, it will be possible to test Eq. 12 using spectral diffusion data for the same enzyme. If the experiments thus performed by eliminating quencher show an autocorrelation function (C_γr⁻¹(t)) similar to that with the quencher (C_γ⁻¹(t)), the result may indicate a common origin for the fluctuations δγ_r⁻¹ and δγ_nr⁻¹ in terms of protein conformations. Molecular dynamics simulations were performed (41) on flavin reductase, an enzyme used in the single-molecule experiments on fluctuations in γ⁻¹ (32). The distribution of electron transfer donor–acceptor distance fluctuations in these simulations ranging from femtoseconds to nanoseconds was found to be similar to that in the experiments. The next question in using these simulations to interpret the δγ_nr⁻¹ fluctuations is to see what molecular aspects of the motions of the protein are preserved between the experimentally observed time scales of milliseconds to seconds and the fast motions accessible to simulations.

The experimental autocorrelations from the observables C_γ⁻¹(t), C_k(t) and C_ω0(t) from the enzymes antifluorescein (33), candida antarctica lipase B (2), β-galactosidase (3), and cholesterol oxidase (1) are compared in Fig. 2. In Fig. 2 Upper, the experimental data were shifted in the log–log plot to make the comparison of the decay pattern of the autocorrelations easier. To compare the inherent time scales in different enzymes, Fig. 2 Lower shows no shift in time. The experimental data on C_ω0(t) and C_k(t) from cholesterol oxidase (1) show the same normalized autocorrelation function after eliminating the data point at t = 0 from the C_ω0(t) data as noted earlier. The autocorrelation functions from different enzymes in Fig. 2 Lower (no scaling in time) are different from one another. Whether the differences in Fig. 2 are due to differences in properties of the observables or to differences in enzymes remains to be determined by future experiments. It would be helpful to test the proposed relations between the C values to see whether different C values from the same enzyme fall on the same plot and whether the differences in Fig. 2 are because of the different enzymes used in the experiments. One feature of the present formulation as given in Eq. 12, if it is borne out by further experiments, is that it may also serve as a guide in further theoretical analyses. It also reduces the number of necessary independent properties to be evaluated from the computational or other theoretical studies.

Experiments Suggested by the Analysis

Several experimental measurements can serve to explore the consequences of the present equations and test equations such as Eq. 12. These tests involve quantitative comparisons of catalysis rate correlation C_k(t) and spectral diffusion C_ω0(t) similar to the study in ref. 1 and new measurements to compare them with fluctuations in the radiative component of fluorescence decay C_γr⁻¹(t).

1. A comparison of the autocorrelation function C_ω0(t) and C_k(t) can be made from experimental data and the validity of Eq. 12 can be tested, if possible over a time range longer than the one order of magnitude in ref. 1.

2. The two different measurements for a chromophore in an enzyme, C_ω0(t) and C_γr⁻¹(t), do not appear to have been made for the same enzyme in the absence of the quencher (so reducing the value of γ_nr). The measurements of these two autocorrelation functions provide a test of Eq. 12. GFP is another possible candidate for the test. Recent experiments have shown a spectral diffusion in GFP (41). Because the fluorescence quantum yield of GFP is very high, ≈0.8, it might be a useful system to study the fluctuations in γ_r⁻¹ in a way less affected by the γ_nr⁻¹ contributions.

3. The fluctuations in fluorescence lifetime γ⁻¹ are attributed to γ_nr⁻¹ through electron transfer (32). A comparison of δγ_nr⁻¹ and δγ_r⁻¹ for a given system can be obtained most clearly by performing the control experiments with the nonradiative pathways reduced. In flavin reductase, experiments show that Tyr-35 is the primary quencher responsible for the electron transfer process (32). If the autocorrelation function measurements can be performed by mutating Tyr-35, so as to eliminate the quenching by electron transfer (and removing less important quenchers), the fluctuations in γ_r⁻¹ would become more evident and, thus, the data can be used to test Eq. 12.

Conclusion

A mechanism involving local electrostatic interaction energy fluctuations was explored to interpret an experimentally observed similarity (1) of time scale for spectral diffusion and fluctuations in catalysis rate. A theoretical relation between the two quantities arises if both fluctuations reflect the fluctuations in local electrostatic interaction energy. It can be regarded as a dynamical analog of the solvatochromism used in the catalysis of organic reactions by different solvents. The formalism also was extended to fluctuations of the radiative component γ_r⁻¹ of the fluorescence decay lifetime, information on which can be obtained when nonradiative pathways, such as quenching of fluorescence by electron transfer, are reduced. The various tests may help provide a broader framework for relating fluctuations in physical quantities to each other and to enzyme kinetics.