A mechanobiochemical mechanism for monooriented chromosome oscillation in mitosis

Abstract

During mitosis, the condensed chromosomes undergo a series of spectacular oscillations after they are captured in an end-on manner by kinetochore microtubules (KMT) emanating from the spindle poles. Such oscillations are commonly attributed to tug-of-war-like mechanisms, where the mechanical force imbalance alone drives the chromosome movement. However, a large portion of the force imbalance upon the chromosome is absorbed by the kinetochore and may not drive chromosome movement directly. Mounting evidence suggests that such resistance by the kinetochores regulates the chemical reactions of KMT plus-end growth and shrinkage, which have been shown as the determinant of the chromosome antipoleward (AP) and poleward movements. Here we incorporate this important regulatory feature, propose a mechanobiochemical feedback mechanism, and apply it to the monooriented chromosome oscillation, the early stage of the series of observed chromosome oscillations. In this model, the mechanical movement of the chromosome and the local biochemical reactions at the attached kinetochore region form a feedback loop that drives the oscillation. The force imbalance exerted on the chromosomes provides a bias (via mechanically sensitive proteins) on the local biochemical reactions controlling the KMT plus-end dynamics, and the movement of the chromosome in turn changes the forces exerted on it through the experimentally supported gradient in AP force. The proposed feedback mechanism can generate oscillatory behavior that depends on the topology of the feedback loop but is largely independent of the detailed molecular mechanism. We suggest potential molecular players, whose perturbation may allow direct experimental tests of the model.

During mitosis the replicated parental chromosomes are condensed and precisely partitioned into two daughter cells. The centromere regions of chromosomes build kinetochores, which act as the primary chromosomal attachment sites for spindle microtubules in an end-on manner (1). Kinetochore–spindle interactions eventually result in biorientation, where sister chromatids are connected to opposite spindle poles. The transition to anaphase is triggered only after all sister chromatids are properly bioriented on the spindle. The path to biorientation involves a monooriented intermediate state during which the kinetochore of one chromatid is attached to a spindle pole and the other kinetochore is waiting to be captured by the opposite pole. For mitotic vertebrate cells, monooriented as well as bioriented chromosomes exhibit regular oscillatory movements while remaining attached to spindle microtubules (2). The magnitude of the oscillation is normally ≈3–4 μm and the period is ≈5 min (3, 4). The switch in direction during such oscillations is very abrupt, and this regular oscillatory behavior has been termed “directional instability” (3, 4). The existence of oscillations on monooriented chromosomes indicates that they arise from intrinsic changes in activity of kinetochores attached to the spindle. The regularity of oscillations makes them unlikely to stem from stochastic fluctuations such as those in yeast (5). Moreover, movements of individual chromosomes in the same cell are independent of each other (3, 4), suggesting that global changes in cellular state are unlikely to be involved.

The mechanism for chromosome oscillation remains largely a matter of speculation. It is commonly accepted that a tug-of-war-like mechanism is responsible for the oscillations (6–12). In this model, the antipoleward (AP) ejection force from chromokinesin motor proteins antagonizes the poleward (P) pulling force from kinetochore microtubules (KMT) (6–12). However, such a mechanism is likely to be only a part of the story, because the chromosome attaches end-on to the KMT plus-end, and whenever it moves poleward, KMT plus-ends must shrink to allow its movement (9, 13); conversely, when the chromosome moves in the AP direction, the KMT plus-ends must grow to pave its way (9).

A recent theoretical paper described a model of how a pure mechanical tug-of-war mechanism might generate oscillations (14). In this model, KMT plus-end dynamics was not taken to be a limiting factor of chromosome motility, and it was assumed to grow or shrink passively following the direction of the dominating mechanical force exerted on the chromosome. However, experimental evidence suggests that KMT plus-end dynamics does limit and control chromosome movement: For instance, the typical speed of chromokinesins is ≈10 μm/min (15), which is ≈5 times that of the chromosome oscillation speed (3, 4). Moreover, chromosome movement is largely stopped by low doses of microtubule-stabilizing drug treatment, such as Taxol, which stops KMT plus-end dynamics (7). These observations clearly cannot be accounted for by a simple mechanical tug-of-war (11, 12, 14). Furthermore, from a mechanical perspective, the imbalance between the P and AP forces (>1 pN) that drives chromosome movement is not entirely balanced by viscous drags (≈0.1 pN) (9, 13). Instead, a large portion of it is resisted by the kinetochore because of the strong end-on binding between the chromosome and the KMT plus-end (3, 4, 6–10), which we term “kinetochore resistance.” Thus, the mechanical forces postulated to drive chromosome oscillation have to be coordinated somehow with the local chemical reactions that control the shrinkage and the growth of the KMT plus-end (5, 7, 9, 12). The origin of such local mechanobiochemical coordination remains largely unexplored and is the main focus of this study.

Here we propose a feedback mechanism between local biochemical reactions at the attached kinetochore and chromosome movement that can give rise to monooriented chromosome oscillations. Such feedback has been suggested by many experimental studies. In particular, evidence for mitotic kinase-dependent activation of chromokinesins that exert AP ejection force and kinase-dependent inhibition of KMT plus-end shrinkage at the kinetochore has been reported (15–18). Moreover, there is evidence that mitotic kinase activity can be regulated by a postulated kinetochore-localized sensor (19–26), which itself is modulated by the kinetochore resistance. Local kinetochore resistance is modulated by the direction of chromosome movement (27) and may also depend on chromosome position. The latter is plausible because kinetochore resistance to P pulling is reduced by AP ejection force, which is expected to have an increasing P gradient due to the astral distribution of spindle microtubules (4). Finally, the proteins involved in the above regulatory pathways are highly localized at the kinetochore region (19, 20, 28–30) and not limited by their rapid diffusion. Taken together, feedback between chromosome movement and the local biochemical reactions could generate oscillatory behavior, which would be uncorrelated between individual chromosomes in the same cell, as observed in vivo.

Below, we first describe qualitatively the basis and structure of our mechanobiochemical model. We next formulate the model in mathematical terms and discuss features that are critical for the emergence of oscillatory behavior. To facilitate experimental investigations, we suggest in Summary and Perspectives molecular components that could potentially represent the model components. However, we stress at the outset that the goal of this paper is not to pinpoint a specific molecular mechanism, but rather to suggest the potential of robust oscillations generated by this mechanobiochemical control mechanism.

Model

Qualitative Model.

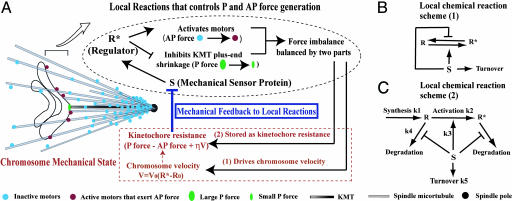
Our model is schematized in Fig. 1. In the model, we propose the following:

1. There is a regulator (R) localized at kinetochores, which is likely to be a mitotic kinase. When activated (R*), this regulator inhibits KMT plus-end shrinkage and promotes AP movement by activating the AP ejection force (Fig. 1A, black portion).

2. The local amount of R* is determined by the balance between synthesis of R, R → R* activation, R* → R deactivation, and degradation of R, R*. Two possible scenarios are sketched in Fig. 1 B and C.

3. The AP ejection force possesses a P-increasing gradient, in addition to being activated by R* (Fig. 1A).

4. R → R* activation, the deactivation reaction, and R/R* degradation are modulated by the “sensor” protein S (Fig. 1 B and C).

5. Kinetochore resistance reduces the local level of the sensor protein S (Fig. 1A).

Fig. 1.

Schematics of local reaction networks coupled with monooriented chromosome movements.

Although an imbalance between the P force and the AP force drives chromosome movement, it is ultimately controlled by R*, i.e., the chromosome velocity is controlled by the activated regulator R*, instead of directly by unregulated mechanical forces. This is the key feature distinguishing our model from a simple tug-of-war mechanism. As only a part of the force imbalance is accounted for by the viscous drag arising from chromosome velocity, a large portion of this force imbalance is stored as kinetochore resistance, which depends on both the chromosome position and chromosome velocity (see Fig. 1A, and also Mathematical Formulation below).

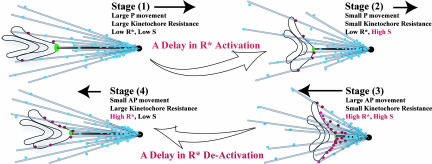
Within our model, oscillations in chromosome movement can be qualitatively described as follows: When a chromosome moves poleward (Fig. 2, stages 1 and 2), the kinetochore experiences resistance and the ability of S to promote R* formation is decreased. As the chromosome gets closer to the pole, the increase in AP ejection force relieves kinetochore resistance, which in turn enhances the ability of S to promote R*. The increase in R* further activates the AP force and decreases KMT P pulling (Fig. 2, stage 2 to 3). Conversely, as the chromosome moves away from the pole, the AP ejection force fades away, effectively increasing kinetochore resistance, thereby reducing the ability of S to activate R and promote P movement (Fig. 2, stage 4 to 1). Because of the multiple steps in the feedback loop, there is a delay in the effect of chromosome movement on the local chemical reaction, and vice versa (Fig. 2, stage 1 to 2 and stage 3 to 4). This delay is important to the oscillatory behavior observed. As we show below, under extended parameter regime, the oscillation generated by this mechanobiochemical model is similar to that observed in vivo. The key hypothesis generated from this theoretical exploration is that oscillations can arise from a feedback between local regulatory pathways and the mechanics of the kinetochore–spindle microtubule interface.

Fig. 2.

Schematics for monooriented chromosome oscillation. Delays in the mechanobiochemical feedback mechanism give rise to oscillation.

Mathematical Formulation.

To formulate the above qualitative model in quantitative terms, it is necessary to adopt specific regulatory molecules and mechanisms. The mathematical model developed below is based on the feedback scheme of Fig. 1 (A and C), wherein Cdk1 is taken as the regulator R and spindle checkpoint proteins are taken as the sensor S. One reason we choose to illustrate the model with these molecules is that many of the associated kinetic parameters have been measured, and hence quantitative results may be derived. But we stress again that the existence of generic oscillatory behavior is not limited to this choice. For example, we show in the supporting information (SI) Appendix (Section IV) that the feedback scheme of Fig. 1 A and B (which would necessarily involve different regulatory molecules) yields similar oscillatory behavior.

In our description, chromosome movement is characterized by its position x and velocity V. x = 0 is taken to be the equator of the cell, and x < 0 is defined to be the P direction, such that V > 0 correspond to the leftward AP movement in Fig. 1A. In the simplest scenario, the chromosome velocity is proposed to be linearly controlled by the activated regulator R*, i.e.,

In this equation, V₀ is a parameter describing the rate of chromosome velocity activation by the regulator; it is related to the intrinsic strength of the relevant molecules to depolymerize or polymerize the attached kinetochore microtubule plus-end. R₀ describes the regulator amount that changes chromosome movement direction. As we will show below, R₀ sets the scale of the number of regulatory molecules, R*. Because the typical amount of each protein at the kinetochore region is ≈500–5,000 molecules (31). We set R₀ to be 500 molecules; this value can be shown not to affect the behavior of the system. To simplify the description, we express the levels of all molecular species below in unit of R₀ and set it dimensionless, i.e., with R₀ = 1.

Next, we describe the local chemical reactions involving the regulator. These include the synthesis, degradation, and activation of R/R*, as well as the protection of their degradation by the sensor protein S. Eqs. 2 and 3 represent the simplified version of the complete set of reactions where R is taken to be Cdk1 (see refs. 32–35 and also SI Appendix, Section I):

Here k₁ is the synthesis rate, k₂ + k₃S is the sensor-dependent activation rate, and k₄ is the degradation rate. The degradation machinery could include APC/C-Cdc20 complex, which is inhibited by the sensor through a conjugation reaction that is assumed to reach equilibrium instantaneously with the equilibrium constant K_C (see SI Fig. 5 in the SI Appendix).

Then, the local sensor level S is modulated by its turnover (k₅), recruitment (k₇), and the local kinetochore resistance Γ,

where k₆ is the force response rate of S, and the resistance is expressed in the dimensionless scale.

Finally, the local kinetochore resistance Γ(x, t) is reduced by the AP ejection force and modulated by the viscous drag on the chromosome, which is modulated by the chromosome position and the regulator R* activation. This effect is captured by the equation

where Γ₁ is the P-pulling force arising from KMT plus-end shrinkage, (A + Bx)R* is the AP force that is activated by R* and has an increasing P gradient (A + Bx), and ηV is the viscous drag from chromosome movement with η the viscous drag coefficient. As V = V₀(R* − R₀), the kinetochore resistance can be represented as Γ = (A − ηV₀)(Γ₀ − (1 + αx)R*), where

Γ₀ describes the residual kinetochore resistance arising from the intrinsic KMT plus-end shrinkage, and (1 + αx) describes the postulated space-dependent AP ejection force along the spindle axis, with α < 0 for x < 0. This form gives an increasing P profile that is taken as a fixed background field, i.e., it is assumed to be not perturbed by chromosome movement.

Combining Eqs. 4 and 5, we have

Here, the constant (A − ηV₀) is absorbed into k₆. And f₀ = k₇ − k₆Γ₀ is a constant. In the following, we will take f₀ = 0 unless otherwise mentioned. The effect of f₀ on chromosome dynamics will be explored later in the text. Note that R, R*, and S in Eqs. 1–6 refer to the local amount of proteins at the attached kinetochore. This assumes that the protein level travels with the moving chromosome, without being limited by their diffusion (19, 20, 28–30).

Results and Discussions

In this section, we first integrate Eqs. 1–3 and 6 over time numerically to study the full coupled mechanobiochemical dynamics of the system. Subsequently, we characterize the system dynamics for a variety of different parameters to explore the robustness of the behavior. The kinetic parameters involved in Eqs. 1–6 are listed in Table 1 with references. If not otherwise mentioned, the parameters used in the model are as follows: k₁ = 0.1 nM·min⁻¹, k₂ = 0.06 min⁻¹, k₃ = 0.02 nM⁻¹·min⁻¹, k₄ = 0.25 min⁻¹, k₅ = 3.33 min⁻¹, k₆ = 3.33 min⁻¹, K_C = 0.2 nM⁻¹, V₀ = 20 μm·min⁻¹, α = −0.01 nm⁻¹, and f₀ = 0. The SI Appendix describes the analysis of a simplified model, its implication, and the linear stability analysis of the full model, and provides further details on model assumptions, parameter estimations, and their justifications.

Table 1.

Kinetic parameters in the model

Parameter	Description	Values	Ref.
k1	Synthesis rate of R per kinetochore region	≈0.1 nM·min−1	29, 32–34
k2	Bare activation rate of R	≈0.05–0.07 min−1	32, 35
k3	Rate of R activation by S	≈0.02 nM−1·min−1	32, 34
k4	Bare rate of R degradation	≈0.2–0.25 min−1	32, 34, 35
KC	Equilibrium constant of Cdc20 and S conjugation	≈(5 nM)−1	36–38
k5	Rate of S turnover	≈2.0–3.0 min−1	39
k6	Response rate of S to force	≈k (estimated)
α	Effective AP force gradient	≈−0.01 nm−1 (estimated)
f0	External AP pushing force	≈0 (estimated)
V0	Chromosome velocity response rate upon activation of R*, ensuring chromosome velocity V < 5 μm·min−1		40
R0	The threshold value, above which R* reverse chromosome movement from P to AP	≈1

Monooriented Chromosome Oscillation.

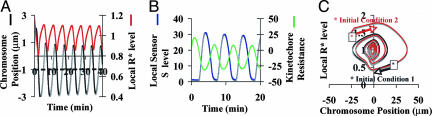
Fig. 3A is a plot of the chromosome position x (black line) and the active R* (red line) as a function of time starting from an arbitrary initial condition at t = 0. (We have tried a variety of initial conditions, and the same type of oscillation is obtained.) In Fig. 3A, the equator of the cell is at x = 0 by definition, and the negative x is the direction of the pole to which the monooriented chromosome is attached. The figure shows that the chromosome could oscillate stemming from the proposed feedback mechanism, with an amplitude of ≈4 μm and a period of ≈5 min. Such movement yields an average chromosome velocity (P or AP) of ≈1.6 μm/min, consistent with experimental observations (3, 4). The steady-state position of the chromosome is indicated by the dashed line at x ≈ −1 μm. Such an oscillation allows the chromosome to go ≈2 μm beyond the steady-state position toward the other pole. The local regulator level R* also oscillates along with the chromosome, in accordance with the concept that kinetochore phosphorylation level controls chromosome motility (41). Other components in the model also oscillate accordingly. For instance, Fig. 3B shows that the local sensor level S (blue line) is strongly anticorrelated with kinetochore resistance, Γ(x, t) = Γ₀ − (1 + αx)R* (green line). Fig. 3A further shows that there is a lag between the R* increase and the chromosome P movement, which is necessary to allow the chromosome to move poleward beyond its steady state position and hence set in the oscillation (Fig. 3A). Qualitatively, such a lag comes from the delay in the effect of mechanical movements on the local biochemical reactions due to the multiple steps along the feedback loop (Fig. 2). In contrast, if the dynamics of sensor protein S becomes much faster than those of R and R*, i.e., k₅ and k₆ ≫ k_i (i = 1–4), then the effect of the chromosome movement can immediately feedback to R*. Effectively, the whole system is at steady state; consequently, the oscillation largely disappears from the same initial condition as shown in Fig. 3A (data not shown).

Fig. 3.

Chromosome oscillation generated by the mechanobiochemical model. (A) Monooriented chromosome oscillation. The dashed line represents the steady state chromosome position determined by Eqs. 1–6. (B) Local kinetochore resistance Γ vs. sensor level S, where Γ₀ is neglected in the plot. (C) Phase plot (x vs. R*): starting from different initial conditions, the dynamic trajectory of the system always falls in the same limit cycle.

Another important aspect of the oscillation concerns its robustness. Fig. 3C is a phase plot of the chromosome position x vs. the active regulator level R* starting from different initial conditions (the arrow represents the direction of the dynamic trajectory over time). It shows that the oscillation behavior from our proposed mechanism is largely insensitive to initial conditions. Now, what if the topology of the local reaction network is simplified, e.g., there is just a single protein that is both a tension-sensor and a regulator for the chromosome movement? Will the chromosome oscillation persist robustly?

For this simpler scenario, we can show that the oscillation will critically depend on initial conditions (see SI Appendix, Section II), because the delay along the feedback loop for this single-component scenario is qualitatively less robust than those with multiple steps, i.e., the effect of chromosome movement can immediately feedback to the tension-sensor level. Thus, it appears that our proposed mechanism, i.e., the central scheme in Fig. 1A, could be the simplest case that reproduces oscillation robustly (also see SI Appendix, Section IV).

Phase Diagrams for Monooriented Chromosome Oscillation.

The oscillatory behavior in Fig. 3 results from one set of the kinetic parameters in the model and is shown to be insensitive to its initial conditions. Next, we explore how sensitive the oscillation is with respect to parameter variations within the feedback mechanism. In the following, we will report the nature of monooriented chromosome motility according to the model, by varying pairs of parameters while fixing the others. The results, summarized as “phase diagrams,” not only provide quantitative conditions for monooriented chromosome oscillation but also yield a qualitative criterion for the occurrence of oscillation. Additional phase diagrams are presented in SI Appendix, Section III.

Requirement of AP Ejection Force Gradient and Positive Feedback Between the Regulator R* and Chromosome AP Movement.

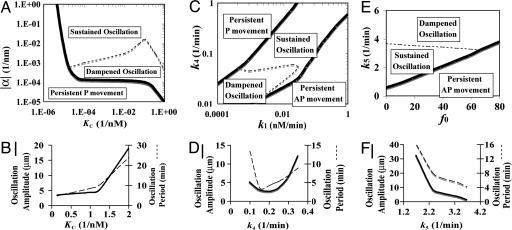
Fig. 4A is a phase diagram for chromosome motility, where K_C represents the ability of the sensor to prevent R* degradation/inactivation, and α is the effective AP ejection force gradient. For any value of K_C, the model predicts that the chromosome could undergo sustained oscillation only if |α| is larger than a threshold value (dashed line). Therefore, maintaining a relatively large AP ejection force gradient is necessary for oscillation under the proposed mechanism. This result is in accordance with the loss of oscillations observed after chromokinesin inhibition (4, 10). For α → 0, the stimulation of the sensor by R* has no sense of chromosome position. Although the local biochemical reactions at the attached kinetochore still control chromosome velocity (Eq. 1), they no longer get feedback from chromosome movement. Without the influence of chromosome movement, the local R* and S will simply reach their steady states. For the given kinetic parameters in the model, the steady state of R* is less than R₀, leading to persistent P movement without oscillation (SI Fig. 8A in the SI Appendix). Thus, the positive feedback between R* and chromosome AP movement is in part governed by the AP force gradient α.

Fig. 4.

Parameter dependences of chromosome oscillations. (A, C, and E) Phase diagram of monooriented chromosome oscillations. (B, D, and F) The dependence of oscillation characteristics (amplitude and period) on kinetic parameters in the model.

For intermediate range of |α| (between the solid and dashed lines), the feedback between chromosome movement and the local biochemical reactions is sufficiently strong, such that the AP ejection force counterbalances the tendency of the chromosome to move poleward. In this regime, we expect the chromosome to undergo dampened oscillation, eventually becoming stationary with R* → R₀ (SI Fig. 8B in the SI Appendix). The steady state is stable upon perturbations and is verified by linear stability analysis (see SI Appendix, Section IV). Note that because the chromosome oscillates only for approximately three to four oscillation periods in vivo, dampened oscillation might not look much different from sustained oscillation over such a short timescale.

The behavior of the model is also strongly influenced by the sensor “strength” parameter K_C. According to the model, a chromosome will experience more AP ejection force close to the pole (Eqs. 3–5), which relieves kinetochore resistance and enhances the sensor level. Through the activation and the protection by the sensor, chromosome AP movement modulates R*. Thus, K_C represents part of the positive feedback strength between the regulator R* and chromosome AP movement. Fig. 4A shows that, monooriented chromosome oscillation generally requires a relative large K_C, i.e., a strong positive feedback between R* and chromosome AP movement. (A similar requirement also applies to the activation rate k₃ of the regulator R* by the sensor and the activation rate of the sensor by AP ejection force k₆. The oscillation can exist even if the bare activation rate k₂ = 0, see SI Appendix, Section III). Fig. 4B shows that both the amplitude and the period of the chromosome oscillation increase with K_C. Oscillation characteristics have qualitatively similar dependence on α (data not shown).

Requirement of the Local Amount of the Regulator R* Around the Threshold Level R_0.

Fig. 4C is a phase diagram of monooriented chromosome motilities characterized by the synthesis rate k₁ and the degradation rate k₄ of the regulator. Fig. 4C shows that chromosome oscillation is only possible when the regulator synthesis rate and degradation rate are comparable in a sense that the local amount of R* can be maintained ≈ R₀. When the synthesis rate is too low, there will not be enough R* to activate the AP ejection force (R* < R₀); hence, chromosome P movement will persist. On the contrary, when the synthesis rate is too high, there will be plenty of R* to push the chromosome toward the middle ground (i.e., x → 0, see SI Fig. 12). Once the chromosome reaches the other half of the cell, there is no AP ejection force gradient anymore (Eqs. 4 and 5). Like the α → 0 case in Fig. 4A, the local biochemical reactions will no longer be able to couple to chromosome movement. Then the regulator level will reach its steady state determined by the degradation rate k₄ (if all other kinetic parameters are fixed). Thus, k₄ is below a certain threshold, the R* steady state level will become greater than R₀ (SI Fig. 8C), thereby pushing the chromosome in the AP direction without oscillation (SI Fig. 8C). Fig. 4D shows that both the amplitude and period of the oscillation reach their respective minimums for an intermediate range of degradation rate k₄.

Note that both the persistent P and the AP movements (without oscillation) will be limited by the cell boundary and many other constraints in vivo. Furthermore, the monooriented chromosome cannot move in the AP direction forever, because the microtubules from the other spindle pole will capture the chromosome if it is nearby, beyond which point the chromosome is bioriented and the mechanism of its subsequent movement would be different. For simplicity, we did not include these effects in the model and restricted our analysis to the monooriented state.

Requirement for Limiting Additional AP Pushing Force and an Intermediate Sensor Turnover Rate.

In vivo, certain kinesin motors, e.g., CENP-E (42–44), can exert AP pushing force at centromeres of monooriented chromosomes to help congression to the equator. In our model, an AP ejection force that is independent of the local reactions and the spatial gradient could be represented by f₀ > 0. As f₀ increases, it reduces kinetochore resistance and hence increases the local sensor level according to Eqs. 4 and 5. Such elevation in the sensor level stimulates R*, which in turn promotes the tendency of AP movement. As shown in Fig. 4E, monooriented chromosome oscillation remains robust to small f₀. However, as f₀ increases beyond a certain threshold (solid line), the intrinsic oscillation from the coupled mechanobiochemical feedback system becomes enslaved to the position-insensitive AP force, and the chromosome is predicted to move persistently in the AP direction.

For a fixed f₀ (Fig. 4E), chromosome oscillation is possible only for an intermediate range of the sensor turnover rate k₅. Fig. 4F shows that, both the amplitude and the period of the oscillation decrease with k₅. Interestingly, within the physiological range (k₅ ≈ 2–3 min⁻¹) (39), such a decrease is marginal.

Summary and Perspectives

During mitosis, after a chromosome is captured by one spindle pole, it rapidly forms an end-on attachment with spindle microtubule plus-ends at its kinetochore (1, 2, 9). The monooriented chromosome oscillation that ensues is much slower than the typical velocity of dynein and kinesin transport along the microtubule (3, 4, 9, 15). The slowness of chromosome movement makes it unlikely to be a simple result of a “tug of war” between dyneins and kinesins (11, 12, 14). Rather, due to the strong attachment between the chromosome and the KMT plus-end (9, 13), the underlying microtubule needs to “chew” its way toward the pole or “pave” its way from the pole (7, 13) whenever the chromosome moves P or AP, respectively. Therefore, we expect the dynamics of the KMT plus-end to be a key determinant of the observed chromosome oscillation. We suggest that the dynamics of the KMT plus-end is regulated by the same mitotic kinases as those that govern the AP ejection force (15–18). This forms the basis for our proposal that the mechanical force generation and the local biochemical reactions at the kinetochore form a feedback loop that generates oscillations.

In this study, we explored such a mechanobiochemical model of chromosome oscillation. The key feature of our model is that the KMT plus-end dynamics, and hence the chromosome velocity, is controlled by the local level of the active regulator R*. In our model, the forces impinging on the chromosome is not entirely balanced by the viscous drag arising from chromosome movement. Instead, a large portion of it is resisted by the kinetochore and stored as kinetochore resistance. Such resistance diminishes the level of a kinetochore-localized sensor protein S, which in turn promotes R*. In this way, a feedback loop between the chromosome movement and the local reactions is realized. We showed that oscillation in chromosome movement could arise, in ways largely insensitive to the initial conditions (Fig. 3), due to the delays that are built in to the multiple steps along the proposed feedback loop. Explorations of our model (e.g., the phase diagrams in Fig. 4) suggest the following as key ingredients for robust oscillation: (i) a relatively large increasing P gradient in the AP ejection force; (ii) a strong positive feedback between the regulator that activates AP ejection force and the chromosome AP movement; (iii) maintenance of active regulator in the kinetochore region around the threshold level necessary to produce changes in chromosome direction; and (iv) any additional AP pushing force that is spatially invariant has to be relatively small.

In vivo, monooriented chromosome oscillation could be complicated by many additional factors. To capture the simplest scenario, we also investigated the effect of a position-insensitive constant AP pushing force on chromosome oscillation. This constant AP pushing force may be generated from certain kinesins independent of the local reaction loop and the spatial gradient (42–44). As this AP pushing force increases, our model predicts that the monooriented chromosome would progressively undergo sustained oscillation, damped oscillation, and directed AP movement (without oscillation). Although not included in the model, it is conceivable that the stochastic nature of kinesin molecules getting on/off the KMT and the chromosome might cause uncorrelated oscillations of the different chromosomes within the same cell, as well as variations of the oscillation characteristics for the same monooriented chromosome over time.

In the numerical analysis, we took Cdk1 as an example of the regulator in the model, primarily because of measured parameters. However, we note that Aurora B kinase is another plausible candidate, given in vivo data (45–49). In terms of the model, the degradation of R* (represented by the k₄ term) may instead be an inactivation reaction, or simple dissociation from the attached kinetochore region, neither of which are explicitly considered. Any protein could serve as the sensor if it promotes the local R* level and is modulated by kinetochore resistance at the same time. The AP ejection force spatial gradient α could stem from the distribution of the spindles engaged by the chromokinesins. It may also originate from the distribution of the depolymerases or polymerases that control KMT plus-end dynamics and modulate kinetochore resistance. The kinetochore-localized, length-dependent depolymerases may contribute to such a P gradient (50).

The functional role of monooriented chromosome oscillation is not clear. It could represent a byproduct of the local interactions at the chromosome. Alternatively, it could help chromosome biorientation by moving monooriented chromosomes close to the other pole. A simple way to push the chromosome toward the other pole is to have high R*. However, the cell has to sharply switch regulatory states of mitotic kinases, such as Cdk1, at metaphase/anaphase transition, and hence the R* level cannot be too high. Monooriented chromosome oscillation facilitates biorientation because it allows the chromosome to take an excursion of several microns closer to the other pole than its steady state position (dash line in Fig. 3A). It should be pointed out that oscillations may be just one of the many modes that the cell can exploit to get its chromosomes bioriented. For instance, the kinesin CENP-E could independently push the monooriented chromosome in the AP direction processively by walking along other bioriented chromosomes (42).

In conclusion, our model provides a theoretical framework for monooriented chromosome oscillations in vertebrate cells. More generally, this work illustrates how nontrivial dynamics could be generated from coupling a molecular reaction network to cytoskeleton dynamics.

Abbreviations

KMT

kinetochore microtubule

P

poleward

AP

antipoleward.