Confined Animal Feeding Operations as Amplifiers of Influenza

Abstract

Influenza pandemics occur when a novel influenza strain, often of animal origin, becomes transmissible between humans. Domestic animal species such as poultry or swine in confined animal feeding operations (CAFOs) could serve as local amplifiers for such a new strain of influenza. A mathematical model is used to examine the transmission dynamics of a new influenza virus among three sequentially linked populations: the CAFO species, the CAFO workers (the bridging population), and the rest of the local human population. Using parameters based on swine data, simulations showed that when CAFO workers comprised 15-45% of the community, human influenza cases increased by 42-86%. Successful vaccination of at least 50% of CAFO workers cancelled the amplification. A human influenza epidemic due to a new virus could be locally amplified by the presence of confined animal feeding operations in the community. Thus vaccination of CAFO workers would be an effective use of a pandemic vaccine.

INTRODUCTION

A human influenza pandemic is likely to occur when a novel zoonotic influenza A virus becomes transmissible from person-to-person. The H5N1 avian influenza virus that has recently spread rapidly to several continents and infected millions of wild birds and domestic poultry has the potential to become the next pandemic strain. Fortunately, thus far only about 240 humans are known to have been infected. However, it has been suggested that the virus only needs to slightly change to become communicable among humans. The numerous cases of H5N1 avian influenza infection in avian species provide many opportunities for H5N1 to mutate, recombine, or reassort with other influenza viruses to make that change.

With so much attention upon H5N1 infections among avian species, it is easy to forget that swine may play a role in pandemic influenza strain generation and transmission. Such was the case during the 1918-1919 pandemic when there were numerous accounts of a farmer developing influenza from his swine or swine developing influenza after farmers were infected (Crosby 2003, Easterday 2003). Since then human-to-swine and swine-to-human influenza cases have been well documented (Kimura et al. 1998, Dacso et al. 1984, de Jong et al. 1988, Hinshaw et al. 1978). Today many millions of susceptible pigs and poultry are housed in confined animal feeding operations (CAFOs) in the United States and in other countries. Not only is this crowding growing more intense for the swine, but also the industries are being consolidated in specific geographical areas. Often the swine or poultry industry is the chief employer in some rural communities.

The crowding of swine and poultry in CAFOs increases the transmission of influenza viruses. Occupational exposure to pigs has been shown to increase the risk of swine influenza virus infection in humans (Myers et al. 2006, Olsen et al. 2002). Thus, CAFO workers could serve as a bridging population for transmission of an influenza virus between a local human population and animals in CAFOs. Amplification occurs if the size of the epidemic in humans is increased due to transmission of the influenza virus into the CAFO species which leads to an epidemic in the CAFO species, and subsequent transmission back to the local human population. This is similar to amplification of the West Nile virus epidemic by alligators (Klenk et al. 2004).

Here we use mathematical modeling and simulations to assess the potential amplification of a new influenza virus by domestic birds or animals raised in CAFOs. It is assumed that the new influenza virus is transmissible in humans and in the CAFO species. This new influenza virus may be the product of reassortment or mutation, but more important is the assumption that it is both intra- and interspecies communicable. The model considers a local human population that is connected epidemiologically to the CAFO species by CAFO workers. We consider pre-epidemic vaccination of the CAFO workers as an intervention measure. Several vaccines against H5N1 influenza virus are being tested (Stohr and Esveld 2004, Treanor et al. 2006) and may be available in case of an epidemic, but a low efficacy is expected since it could poorly match the emergent strain (Longini et al. 2005). Swine in CAFOs are chosen for our simulations, since data were available to estimate parameter values, but a similar reasoning would apply in the case of confined poultry. Note that highly pathogenic forms of avian influenza might quickly destroy domestic chickens, alerting CAFO workers of a problem. However, domestic chickens previously vaccinated against that strain may show few signs of infection and highly pathogenic forms of avian influenza may cause mild or no clinical signs among swine or domestic ducks (Choi et al. 2005, Songserm et al. 2006), prolonging undetected human exposure.

METHODS

A multiple host model is used for the dynamics of the transmission of the influenza virus (Dobson 2004, Hethcote 1978, 1996, Hethcote and Van Ark 1987, Hethcote and Thieme 1985). The sequentially linked host populations are the CAFO species, the CAFO workers, and the rest of the local human community. It is assumed that each host population is divided into three epidemiological classes: susceptibles, infectives, and recovered individuals, so that an SIR epidemic model is used (Anderson and May 1991, Hethcote 2000). Thus susceptible individuals become infected and then recover with permanent immunity. The latent period for influenza is very short, so it is not included in the model. The human influenza mortality rate during the 1918 influenza pandemic was less than 1% in the United States (Crosby 2003). The infection-related mortality rate in swine is also estimated to be less than 1% (Richt et al. 2003). Since the infection-related mortality rates in humans and swine are small for influenza, they are neglected in our model. For avian strains like H5N1, where the case-fatality rate is high, the model could be modified to include infection-related deaths. However, this modification would not have much effect on the infection dynamics and subsequent amplification, since infection-related deaths commonly occur near the end of or after the individuals’ infectious period, for example, the median number of days from onset of symptoms until death was 9 days for the H5N1 avian influenza infection in humans (WHO 2006).

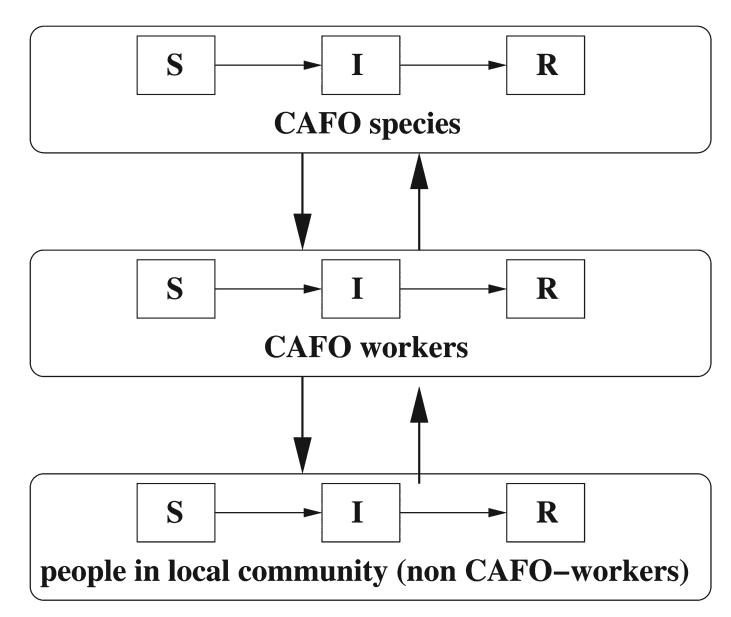
The transmission terms in the model are defined so that there are no direct contacts between CAFO species and non CAFO-workers. Figure 1 shows the interactions between the three groups. The groups considered in the model are the CAFO species (s), the CAFO workers (w), and the rest of the people in the local community (n). Pre-epidemic vaccination of the CAFO workers is also evaluated. It is assumed that a fraction of the CAFO workers are successfully vaccinated before the beginning of the epidemic. The percentage successfully vaccinated is the product of the vaccination coverage percentage and the vaccine efficacy. CAFO workers are selected as the target group since vaccination of this bridging population would have the biggest impact. Since a newly emergent influenza strain is considered, it is assumed that every individual is susceptible at the beginning of the epidemic (with the exception of those starting the epidemic and those successfully pre-vaccinated). Details of the mathematical model are given in the Appendix.

FIG. 1.

Transmission dynamics between the CAFO species, CAFO workers, and the rest of the local community. In each group, susceptibles (S) become infected (I) and then removed (R) after recovery.

Parameter estimates for the model

The basic reproduction number R₀ is defined as the average number of secondary infections that occur when one infective is introduced into a completely susceptible host population (Anderson and May 1991, Hethcote 2000). For a single species SIR epidemic model, the basic reproduction number is R₀ = β/γ, which is the daily contact rate β times the average length 1/γ of the infectious period in days (Hethcote 2000), so that β = γR₀. The average infectious period 1/γ for human influenza has been estimated to be about 4 days (Stöhr 2004), so this is used as the baseline value (thus γ_w = γ_n = 1/4). The average infectious period 1/γ_s for swine influenza has been estimated to be 5-7 days (Richt et al. 2003, Hinshaw et al. 1981) and 7-10 days (Brown 2000), so that the value of 7 days is used as the baseline value (thus γ_s = 1/7).

Estimates of R₀ for past human influenza epidemics are 2 < R₀ < 3 for the 1918 Spanish influenza A (H1N1) in US (Mills et al. 2004), 1.33 < R₀ < 2.6 for the 1957 Asian influenza A (H2N2) (Longini et al. 2005, Burnett and White 1974), and 1.4 < R₀ < 1.89 for the 1968 Hong Kong influenza A (H3N2) (Evans 1982). A newly emergent influenza strain would initially not be well adapted for transmission among humans, so that its R₀ would be less than 2 and probably just above 1 (Antia et al. 2003). Thus $R_0^H=1.2$ is selected as the baseline value of the basic reproduction number in humans of the new influenza strain. This $R_0^H$ comprises the basic reproduction number for both CAFO workers and non CAFO-workers as members of a community.

For the swine the approximation R₀ = ln(S₀/S_∞)/(S₀ - S_∞) is used, where S₀ and S_∞ are the susceptible fractions before and after the epidemic, respectively (Hethcote 2000). The percentage of swine in a CAFO infected during a swine influenza outbreak in north-central US was 51% (Brown 2000) and is often nearly 100% (Richt et al. 2003). The baseline value selected is 80%, so that S₀ = 1 and S_∞ = 0.2. These values in the formula above lead to $R_0^S=2$ for the swine in a CAFO, which is used as the baseline value. Sensitivity analysis is done to consider other fractions S_∞ of infected animals at the end of a swine influenza epidemic.

The formula β = γR₀ implies that the daily contact rate for humans is β_H = (1/4) × 1.2 = 0.30 and the daily contact rate for swine is β_S = (1/7) × 2 = 0.2857. For humans (CAFO workers and non CAFO-workers together), the average number of adequate contacts β_ij is assumed to be a multiple of the parameter β_H, with constant of proportionality equal to the fraction of individuals in group j. Thus, if the fraction of CAFO workers in the community equals θ, then the contact rates with infected workers (w) are β_nw = β_ww = θβ_H and the contact rates with infected non CAFO-workers (n) are β_nn = β_wn = (1 - θ)β_H, so that β_nn + β_nw = β_H and β_ww + β_wn = β_H. Notice that this assumption implies that the basic reproduction number for the CAFO workers’ group equals $R_0^w=\theta R_0^H$, while the basic reproduction number for the non CAFO-workers is $R_0^n=(1-\theta )R_0^H$.

The swine to swine contact rate is β_ss = β_s. In order to estimate the contact rate β_ws of infected swine with CAFO workers, an SIR epidemic model is used, in which the swine virus is only spread by the swine (among themselves and to the CAFO workers). This agrees with the usual dynamics of swine influenza viruses in humans (Kimura et al. 1998, Dacso et al. 1984). The total fractions of people in the swine industry infected with a single strain of the swine influenza virus have been recorded in several studies with values given by 20% (Schnurrenberger et al. 1970), 23% (Olsen et al. 2002), and 79% (Ayora-Talavera et al. 2005). We selected 50% as the baseline percentage of infected CAFO workers. Thus the contact rate of infected swine with CAFO workers β_ws is set to cβ_ss and we adjust c to 0.43 in the simulations to obtain the 50% baseline percentage.

Due to the high number of hogs compared to the number of CAFO workers in the same facility, it is assumed that it is much more likely that the confined swine transmit the virus to a CAFO worker than the CAFO workers transmit it to an individual hog. Thus, the contact rate of infected workers with swine β_sw is set to dβ_ws, and we select d = 0.01 as the baseline value. The sensitivity to the choices of c and d is considered below. The baseline values of the parameters are summarized in Table 1.

Table 1.

Baseline Values Of Parameters

Parameter	Baseline value
γs	1/7
γw, γn	1/4
R0H	1.2
R0S	2
θ	0-0.45
βH	0.30
βww, βnw	θβH
βwn, βnn	(1 - θ)βH
βss	0.2857
βws	0.43βss
βsw	0.01βws

RESULTS

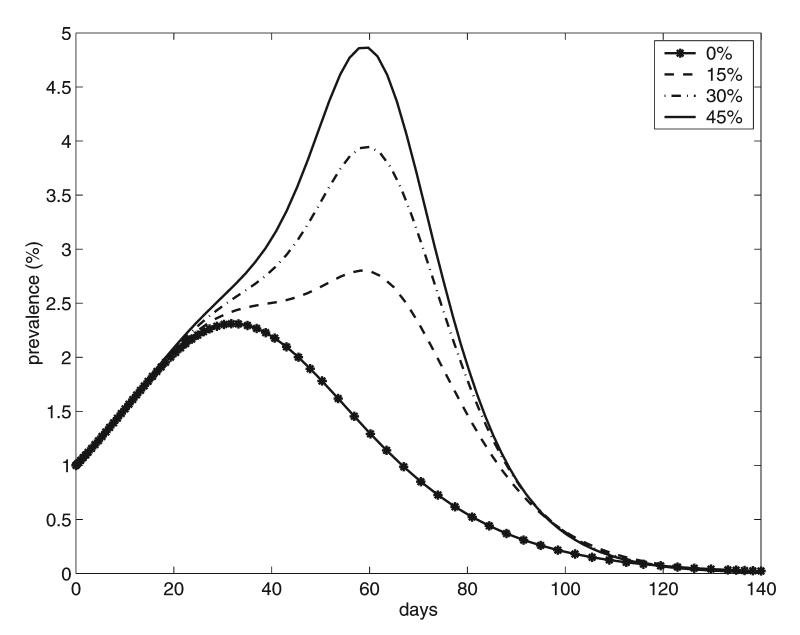
The following results are based on numerical simulations of the model equations in the Appendix using the baseline parameter set. We assume that the new influenza virus would be already adapted for transmission in humans, so it is started in the human population with 1% of the humans initially infected, proportionally distributed among CAFO workers and the general population. Communities in which 0%, 15%, 30%, and 45% of the population are CAFO workers are considered. Figure 2 shows the simulated epidemic prevalence curves for humans (both CAFO workers and the general population). Note that the presence of CAFO workers increases dramatically the size of the epidemic and that these effects are greater as the percentage of CAFO workers increases. The peak of the epidemic is delayed and is approximately doubled when the percentage of CAFO workers is increased from 0% to 45%. This epidemic delay reflects the time that it takes for transmission of the infection into the swine followed by an outbreak in the swine and then transmission back to the local population.

FIG. 2.

Epidemic prevalence curves for humans corresponding to different percentages of CAFO workers in the community.

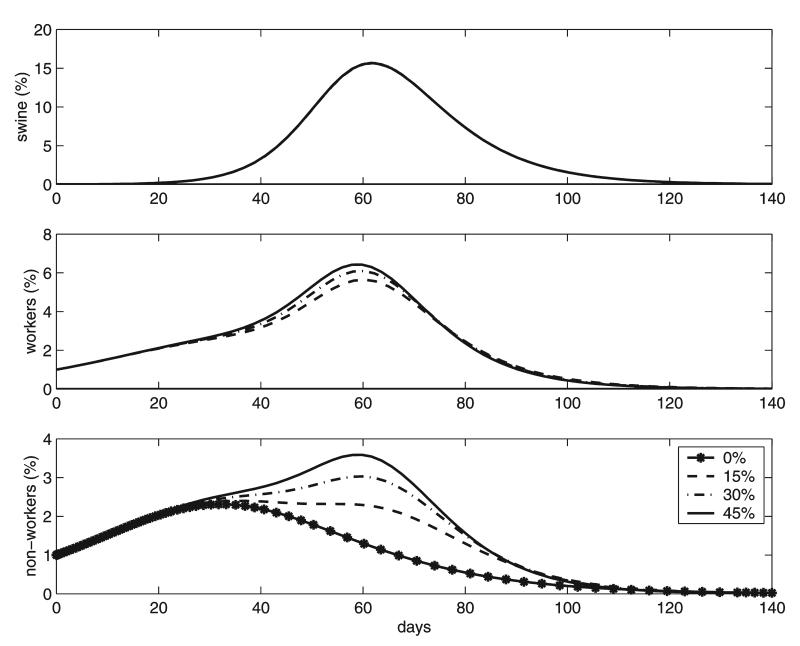
The bottom graphs in Figure 3 show how the increase in the epidemic curves for the local population coincides with the epidemic in swine. Notice also that the swine epidemic curve is independent of the percentage of CAFO workers in the community, since the majority of the new cases in hogs are due to contacts with other hogs. The peak in the CAFO workers epidemic coincides with the swine epidemic peak due to their close interaction with the confined species and is almost independent of the percentage of CAFO workers.

FIG. 3.

Epidemic curves showing the prevalences for the confined species, CAFO workers, and local population. Local communities consisting of 0%, 15%, 30%, and 45% CAFO workers are considered in each case.

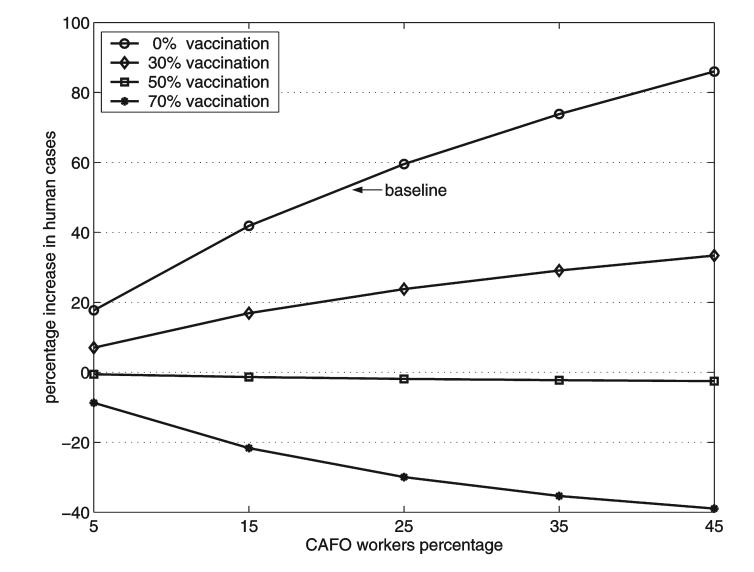
Another way to evaluate the impact that the CAFO species, through the CAFO workers, might have on the influenza epidemic is by the percentage of seropositive individuals in the community at the end of the epidemic. Figure 4 shows the percentage increases in the total number of humans infected compared to the situation when no other species are present. For the baseline case (no vaccination) the total number of infected persons is increased by 42% and 86% when the CAFO workers represent 15% and 45% of the local population, respectively.

FIG. 4.

Percentage increases in the final size of the human influenza epidemic as a function of the percentage of CAFO workers in the community. The curves correspond to pre-epidemic successful vaccination of 0% to 70% of the CAFO workers. Local communities with 5%, 15%, 25%, 35%, and 45% of CAFO workers are considered.

Figure 4 shows that when vaccination of CAFO workers is included in the simulations, the impact of the CAFO species is reduced. When 30% of the CAFO workers are successfully vaccinated prior to the epidemic, the percentage increase of human cases is reduced by more than half. Successful vaccination of 50% of the CAFO workers approximately cancels the amplification. The decrease in the number of human cases is even larger when 70% of the CAFO workers are successfully vaccinated.

Sensitivity analysis

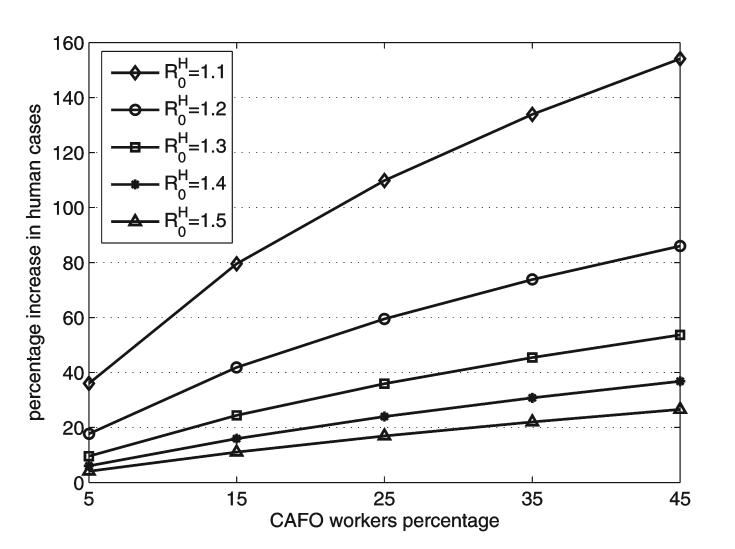
Figure 5 shows the impact of $R_0^H$ in humans on the percentage increase in human cases. The effect of the CAFO species is much larger when $R_0^H$ decreases to 1.1 from its baseline value of 1.2. Even with 5% of CAFO workers in the community the percentage increase in cases is 38%. There would be a 154% increase, if 45% of the local population worked in a CAFO. The impact of CAFOs becomes more significant as $R_0^H$ is decreased from its baseline value of 1.2. As the value of $R_0^H$ decreases, the increase in amplification may be explained by the relative increase of $R_0^S$ with respect to $R_0^H$, so that the role of the CAFO species becomes more important in the epidemic dynamics.

FIG. 5.

Percentage increases in the final size of the epidemic as a function of the percentage of CAFO workers in the community with $R_0^H=1.1$, 1.2, 1.3, 1.4, and 1.5. CAFO workers are 5%, 15%, 25%, 35%, and 45% of the local population.

To consider the sensitivity of the basic reproduction number $R_0^S$ in swine, we varied the total fraction S_∞ of infected swine at the end of a swine epidemic in our model from 50% to 95%. Our simulations showed no change in the percentage increase of human cases. This occurs because as the total percentage of infected swine is varied, the parameter β_ws changes so that 50% of CAFO workers are infected.

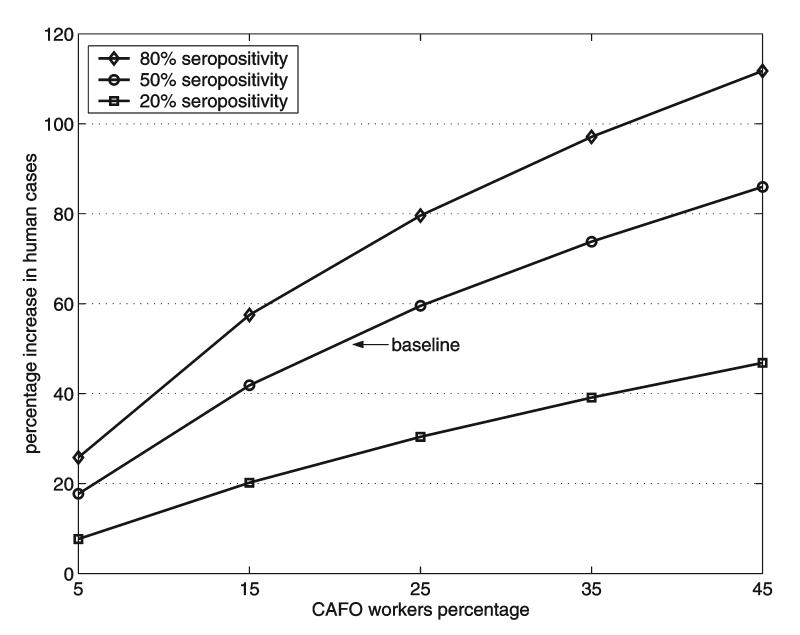
Figure 6 shows the increase in the percentage of total human cases as a function of the percentage of CAFO workers, when the total fraction of CAFO workers infected (with a swine influenza virus) varied from 20% to 80%. The parameter c in β_ws = cβ_ss increases as the total fraction of infected CAFO workers increases. Higher seropositivity percentages of CAFO workers to swine influenza strains lead to larger increases in human cases.

FIG. 6.

Percentage increases in the final size of the human epidemic as a function of the percentage of CAFO workers in the community. The contact rate β_ws is based on data in which 20-80% of CAFO workers were seropositive to specific strains of swine influenza.

Variation of the value of d in β_sw = dβ_ws does not change the amplification of the epidemic, but does change the epidemic duration. For the baseline value d = 0.01, the duration of the epidemic was 110 days and the maximum size of the epidemic was reached at 60 days (Fig. 3). When the value of d is increased to d = 0.2, the epidemic lasts around 90 days and the peak of the epidemic is at 40 days, but for d = 0.002 the epidemic lasts about 125 days with the peak at 75 days. Sensitivity analyses of the infectious periods were not done because consistent estimates for them exist in the literature.

DISCUSSION

We have investigated the impact of a pandemic influenza virus upon multiple species in the modern agriculture industry, where industry workers care for thousands of animals living in efficient, but crowded conditions. As in the 1918 pandemic experience we have assumed that the emergent human influenza virus would be efficiently transmitted among both humans and domestic animals. We have used swine as the CAFO species in our model simulations, because we live in Iowa (the largest producer of hogs in the United States) and we were able to estimate the transmission parameters using CAFO swine. However, the model and the concept of local amplification by a CAFO species would also be applicable to domestic poultry. Recent H5N1 epidemics in the domestic poultry industry in Thailand, Nigeria, and France have illustrated the explosive outbreaks that may occur in CAFOs (OIE 2006). Birds may show few signs of infection if the outbreaks occur among previously vaccinated flocks. The recent detection of likely subclinical H5N1 infections among domestic swine in Indonesia and Vietnam show the potential for CAFO transmission, should the virus change and move more efficiently among swine.

The model developed for the transmission dynamics of this novel influenza virus considered three sequentially linked populations: a CAFO species, the CAFO workers, and the rest of the local human community. The CAFO workers serve as the bridging population for interspecies transmission, in the sense that only CAFO workers can infect and be infected by both humans and the CAFO species. We used a system of simultaneous, nonlinear differential equations for an SIR disease. Data on human and swine influenza epidemics and the extent of transmission from swine to humans were used to estimate parameter values. Epidemics of the new influenza virus were investigated in a local community, in which 5-45% of the population were CAFO workers. Simulations of epidemics in the local community were obtained by numerical solutions of the differential equation model. Using the baseline parameter set, we found that the extent of the influenza epidemic in humans was amplified by 42-86% as the percentage of CAFO workers in the local community varied from 15% to 45%. The amplification results are sensitive to changes in the basic reproduction number $R_0^H$ in humans and the extent of the transmission of influenza viruses from swine to swine workers, but not to changes in other parameter values.

It is known that CAFO workers are important transmitters of human influenza viruses to swine in CAFOs, so that it is recommended that CAFO workers get yearly influenza vaccinations and remain at home when they are ill (Olsen 2004). Similarly, vaccination of CAFO workers could be used to reduce or prevent the local amplification of a new human influenza by a CAFO species. Figure 4 shows the effects of vaccinating CAFO workers against the new influenza virus in our transmission model. Notice that the amplification is cancelled out when about 50% of CAFO workers are successfully vaccinated, and higher successful vaccination levels lead to decreases in the size of the human epidemic. Thus vaccination of CAFO workers would be an effective use of a vaccine against a new influenza virus.

While it is possible that a new influenza pandemic will not occur in the near future, many public health officials believe that an influenza pandemic is likely to occur in this century. The ongoing pandemic of H5N1 avian influenza in wild and domestic birds worldwide is providing many opportunities for the virus to change into a form that might move more efficiently among both humans and animals.

APPENDIX

The three groups considered in the model in Figure 1 are the CAFO species (s), the CAFO workers (w), and the rest of the people in the local community (n). In group i, the variables X_i, ${\mathsf{Y}}_i$, and Z_i denote the numbers of susceptibles, infectives, and recovered individuals, respectively. The parameter γ_i represents the rate at which infective individuals in group i recover from the disease. The factor F_i gives the average number of adequate contacts with infectious individuals per unit time of one susceptible from group i. Thus, F_iX_i denotes the incidence of the disease, which is the number of new cases per unit time in group i. The differential equations for the epidemiological dynamics of the new influenza virus are

$$\begin{array}{c}\frac{d{X}_i}{dt}=-F_i{X}_{\mathrm{i}},\hfill \\ \frac{d{\mathsf{Y}}_i}{dt}=F_i{X}_{\mathrm{i}}-{\gamma }_i{\mathsf{Y}}_i,\hfill \\ \frac{d{Z}_i}{dt}={\gamma }_i{\mathsf{Y}}_i,\hfill \end{array}$$ (1)

where i = s, w, or n.

The frequency-dependent incidence term for the CAFO species is given by $F_s{X}_s=({\beta }_{ss}{\mathsf{Y}}_s∕N_s+{\beta }_{sw}{\mathsf{Y}}_w∕N_w)X_s$, where β_ij denotes the average number of adequate contacts per unit time of a susceptible individual in group i with individuals in group j (an adequate contact is an encounter which is sufficient for transmission of infection if the group i individual is susceptible and the group j individual is infectious) and N_i denotes the constant number of individuals in group i (Hethcote et al. 2005). The incidence term for the people in the community (non CAFO-workers) is given by $F_n{X}_n=({\beta }_{nn}{\mathsf{Y}}_n∕N_n+{\beta }_{nw}{\mathsf{Y}}_w∕N_w)X_n$. CAFO workers are assumed to be the bridge for the transmission of the influenza virus between the confined species and non CAFO-workers, so that all of the species affect the incidence of the disease for the CAFO workers. Thus, this incidence term has the form

$$F_w{X}_{\mathrm{w}}=({\beta }_{ww}{\mathsf{Y}}_w∕N_w+{\beta }_{ws}{\mathsf{Y}}_s∕N_s+{\beta }_{wn}{\mathsf{Y}}_n∕N_n)X_w.$$

Using the change of variables X_i = S_iN_i, ${\mathsf{Y}}_i=I_i{N}_i$, Z_i = (1 - S_i - I_i)N_i, system (1) becomes system (2) below. The new variables S_i and I_i represent the proportions of susceptibles and infectious individuals in group i, respectively, with respect to the total population size of group i. system (2) is given by:

$$\begin{array}{c}\frac{d{\mathcal{S}}_i}{dt}=-f_i{\mathcal{S}}_{\mathrm{i}},\hfill \\ \frac{d{I}_i}{dt}=f_i{\mathcal{S}}_{\mathrm{i}}-{\gamma }_i{I}_i,\hfill \end{array}$$ (2)

where i = s, w, or n, and

$$\begin{array}{c}{f}_s{S}_s=({\beta }_{ss}{I}_s+{\beta }_{sw}{I}_w)S_s,\hfill \\ f_w{S}_w=({\beta }_{ww}{I}_w+{\beta }_{ws}{I}_s+{\beta }_{wn}{I}_n)S_w,\hfill \\ f_n{S}_n=({\beta }_{nn}{I}_n+{\beta }_{nw}{I}_w)S_n.\hfill \end{array}$$

In order to consider pre-epidemic vaccination in the model, it is assumed that a fraction of the CAFO workers are successfully vaccinated before the beginning of the epidemic.