Biodiversity and ecosystem functioning: A mechanistic model

Abstract

Recent experiments have provided some evidence that loss of biodiversity may impair the functioning and sustainability of ecosystems. However, we still lack adequate theories and models to provide robust generalizations, predictions, and interpretations for such results. Here I present a mechanistic model of a spatially structured ecosystem in which plants compete for a limiting soil nutrient. This model shows that plant species richness does not necessarily enhance ecosystem processes, but it identifies two types of factors that could generate such an effect: (i) complementarity among species in the space they occupy below ground and (ii) positive correlation between mean resource-use intensity and diversity. In both cases, the model predicts that plant biomass, primary productivity, and nutrient retention all increase with diversity, similar to results reported in recent field experiments. These two factors, however, have different implications for the understanding of the relationship between biodiversity and ecosystem functioning. The model also shows that the effect of species richness on productivity or other ecosystem processes is masked by the effects of physical environmental parameters on these processes. Therefore, comparisons among sites cannot reveal it, unless abiotic conditions are very tightly controlled. Identifying and separating out the mechanisms behind ecosystem responses to biodiversity should become the focus of future experiments.

The relationship between biodiversity and ecosystem processes has emerged as a major scientific issue today (1–3). Recent experiments have provided evidence that loss of biodiversity may impair the functioning and sustainability of ecosystems (3–11). The interpretation of these experiments is still debated (12–16), however, and there is some experimental evidence that not all ecosystem processes are improved by enhanced species richness (5, 6, 17). As experiments progress, there is a growing need for adequate theories and models to provide robust generalizations, predictions, and interpretations of experimental results. But theoretical models that attempt to link community and ecosystem processes explicitly are still very few (18, 19).

Here I present a mechanistic model of a spatially structured ecosystem in which plants compete for a limiting soil nutrient. The model is kept as simple as possible to remain analytically tractable, but it is realistic enough to be applicable to actual experimental situations. I use this model to explore the effects of plant species richness on aggregated ecosystem stocks and processes, in particular plant biomass, primary productivity, and nutrient retention.

Current experiments and theories are focused on the effect of biodiversity on ecosystem processes. But there is a long tradition in ecology of considering the opposite effect, i.e., how species diversity is affected by abiotic factors, hence indirectly by ecosystem processes, in particular productivity (20–23). It is important to separate the two effects and understand their interaction, not only because of the scientific interest of the issue per se, but also because changes in abiotic factors may confound biodiversity field experiments. I also use the present model for doing this.

The Model

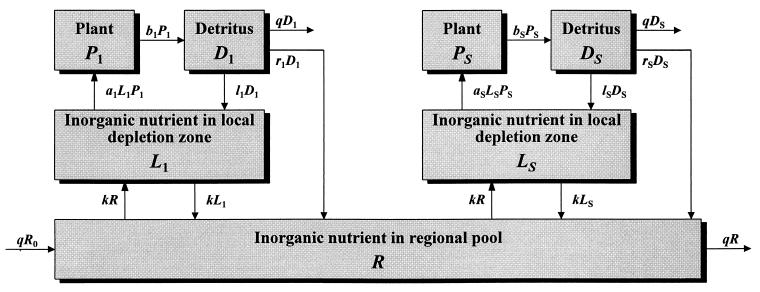
The present ecosystem model is built on an individual-based approach to resource competition in a heterogeneous environment (18, 24). Plant nutrient uptake is considered to decrease the soil concentration of a limiting nutrient in the immediate vicinity of the rooting system, thus creating a local resource depletion zone around each plant (25). Variation in the rate of nutrient physical transport between these and the regional soil nutrient pool determines the degree to which plants interact competitively through their indirect effect on the shared nutrient pool.

A regional soil inorganic nutrient pool (R, of volume V_R) supports a number of plants (P_i) with their associated detritus (D_i) and soil inorganic nutrient in local resource depletion zones (L_i, of volume V_i) (Fig. 1). Because the ecosystem is assumed to be limited by a single nutrient, all compartment sizes and fluxes correspond to nutrient concentrations and fluxes. For simplicity’s sake, plants are lumped by species, numbered from 1 to S. Nutrient in inorganic form flows through the ecosystem at a rate q per unit time; R₀ is the inflowing nutrient concentration. Nutrient is transported by physical processes between the local and regional pools at a rate k per unit time. Plants from species i take up nutrient at a rate a_i per unit time per unit nutrient concentration, and release it at a rate b_i per unit time into the local detritus pool. Nutrient is recycled both locally and regionally, at rates l_i and r_i per unit time, respectively.

Figure 1.

Flow diagram of the model ecosystem.

The diagram of Fig. 1 translates into dynamical equations simply by setting the time derivative of compartment size equal to the sum of inflows minus the sum of outflows for each compartment:

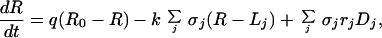1

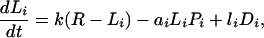2

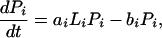3

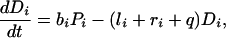4

where σ_i = V_i/V_R is the relative volume of the total resource depletion zone of plants from species i. At equilibrium, the time derivatives in Eqs. 1-4 vanish; in other words, inflows balance outflows for each compartment. Solving these mass-balance equations provides the equilibrium nutrient concentrations and fluxes. More details and a more general version of this model can be found elsewhere (18).

Here I focus on the relationship between plant species richness and ecosystem processes. For the sake of simplicity and clarity, higher trophic levels are omitted, and plants will be assumed to have identical parameters, except for the relative volume they occupy in the soil, σ_i, and their resource-use intensity, as inversely measured by the equilibrium level of their resource, L^*_i = b_i/a_i. As is well known, the lower this equilibrium level, the higher a species’ competitive ability (26).

Because the model is based on the concept of local interactions of individual plants with their environment and interactions between plants are indirect, aggregated ecosystem stocks and processes are obtained in a straightforward way by summation over all individuals and species. Assuming that plant biomass and productivity are proportional to plant nutrient stock and inflow, respectively, the average nutrient concentration in the local resource depletion zones (i.e., in the rooting zone), L^*_σ, the nutrient concentration in the regional pool (i.e., below the rooting zone), R*, the total plant biomass, B*, and primary productivity, Φ*, at equilibrium are found to be:

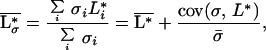5

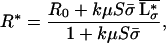6

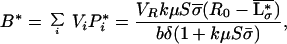7

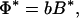8

where μ = (r + q)⁻¹, δ = (l + r + q)⁻¹, and 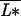and σ̄ are the average values, taken over all species, of the plants’ resource-use intensity and occupied space.

Effect of Plant Diversity on Ecosystem Processes

I first consider how the stocks and processes of the above ecosystem (Eqs. 5–8) are affected by plant species richness, S, as the single independent variable, as in recent experiments. The outcome depends critically on the way the space occupied by the plants, σ_i, and their resource-use intensity, L^*_i, vary with diversity. As regards occupied space, reality is expected to lie generally somewhere between the following two limiting cases. At one extreme, if plants from all species have the same root geometry and potentially occupy identical resource depletion zones, an increase in the number of species, S, can only be achieved by a corresponding reduction in the average occupied space per species, σ̄, so that the total occupied space, Sσ̄, is constant. I call such species “redundant,” because they occupy the same spatial niche and thus fulfill the same functional role, even though their resource-use intensities may differ. At the other extreme, if plants from different species have very different root geometries and occupy nonoverlapping spaces (for instance, because they take up nutrient at different depths in the soil), these are not affected by the presence of other species, so that the average occupied space per species, σ̄, is constant. I call such species “complementary,” because they occupy distinct spatial niches and thus fulfill complementary functional roles.

Now suppose ideally that the average resource-use intensity, 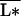, and its covariation with σ are not affected by diversity. In an experimental setting, this may be achieved, at least initially, by avoiding any sampling bias in the establishment of diversity treatments. It is then easy to see from Eqs. 5–8 that in the “redundant species” case none of the ecosystem stocks and processes is affected by diversity, whereas in the “complementary species” case plant biomass and productivity increase with diversity while nutrient concentration below the rooting zone decreases, similar to results reported in some recent field experiments (7, 10).

In real situations, however, the average resource-use intensity 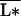may vary with diversity for various reasons, one of them being the “sampling effect” (14, 19). This effect arises because high-diversity plots have a higher probability of containing the most competitive species from the species pool, and these tend to have a dominant effect on total productivity in each plot. This acts to generate a positive correlation between average resource-use intensity and diversity. How do such correlations affect ecosystem processes? To explore a few extreme scenarios, suppose, for simplicity’s sake, that the various plant species all occupy the same relative volume σ, and their resource-use intensities follow a regular distribution, defined by the relation

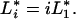9

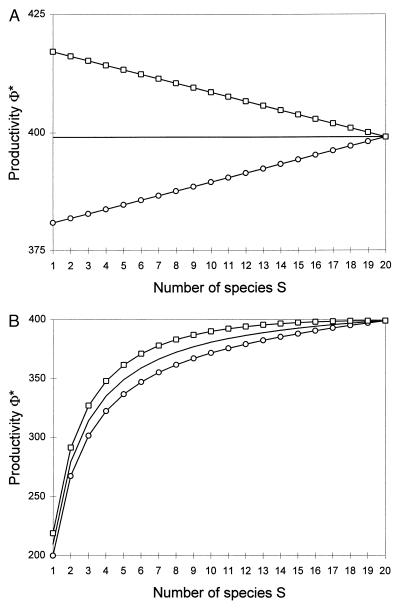
In this distribution, a species’ resource-use intensity is inversely proportional to its competitive rank, i. In one scenario, assume that species are added in increasing order of resource-use intensity; in another scenario, assume they are added in decreasing order of resource-use intensity. These two scenarios are contrasted in Fig. 2 against the “null” scenario where the average resource-use intensity 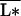does not change with diversity. In the “redundant species” case, primary productivity either can increase or decrease with diversity, depending on whether high-diversity treatments comprise more relatively good or poor competitors. On the other hand, in the “complementary species” case, productivity always increases to saturation with diversity, changes in the mean competitive ability only affecting the steepness of the response. It is easily seen from Eqs. 6–8 that plant biomass has the same response to diversity as does productivity, whereas nutrient concentration below the rooting zone has an inverse response.

Figure 2.

Primary productivity as a function of species richness, in the two cases of “redundant” species (total occupied space constant, A) and “complementary” species (average occupied space constant, B). Scenario 1 (continuous line), average resource-use intensity independent of species richness; scenario 2 (circles), species added in increasing order of resource-use intensity; scenario 3 (squares), species added in decreasing order of resource-use intensity. Resource-use intensities are assumed to follow a regular distribution, L^*_i = iL^*₁. All other parameters are identical for all species. Parameter values: R₀ = 220, L^*₁ = V_R = kμ = 1, δ = 0.5, Sσ = 20 in A, and σ = 1 in B.

These results do not hinge on the particular scenarios chosen. Any positive or negative correlation between mean competitive ability and species richness among treatment levels will have the same qualitative effects as do the above scenarios in both cases, the only difference being the form of the response curves obtained. Thus, this model shows that plant diversity does not necessarily enhance ecosystem processes. It does so under two types of circumstances: (i) when species occupy complementary spaces and (ii) when there is a positive correlation between mean competitive ability and diversity. These two types of circumstances have different implications for the understanding of the relationship between biodiversity and ecosystem functioning (see Discussion).

Direct and Indirect Effects of Abiotic Factors

The foregoing treats ecosystem processes as a function of biodiversity, as in recent experiments. On the other hand, it is well known that natural species diversity itself is determined by ecosystem processes such as productivity or, more exactly, by abiotic factors that also affect these processes (20–23). What is less clear, however, is how these effects interact to explain the observed relationships between diversity and ecosystem processes in among-site comparisons. When both species diversity and ecosystem processes are affected by variations in abiotic factors, is the effect of diversity on ecosystem processes still detectable, or is it negligible compared with the abiotic control of these processes? I now use the above model to address this question.

In this model ecosystem, persistence of plant species i requires (18):

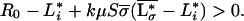10

There is a limit to species richness imposed by the constraint that the poorest competitor has to meet inequality 10. Using the above assumptions of a regular distribution of resource-use intensities (Eq. 9) and otherwise identical species, the maximum number of species able to coexist is then found to be:

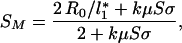11

and

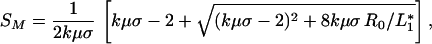12

in the respective cases of “redundant” and “complementary” species.

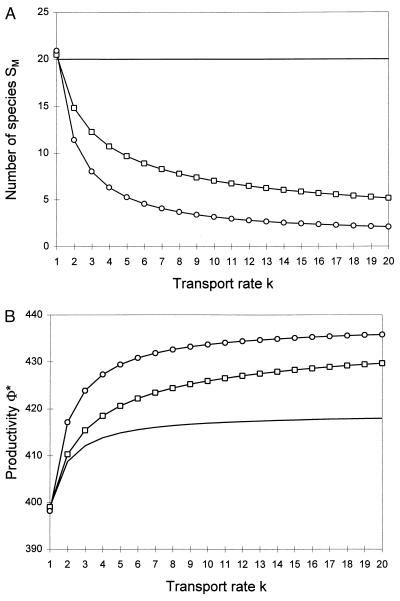
Abiotic nutrient flux parameters have the same qualitative effect on maximum species richness, S_M, in the two cases. The inflowing nutrient concentration, R₀, and the throughflow rate, q, both contribute to an increase in maximum species richness, because they contribute to increasing the amount of resources available to the community and the control of external (versus internal, competitive) processes on the dynamics of the shared nutrient pool, respectively. In contrast, the transport rate, k, contributes to a decrease in maximum species richness, because it enhances plant access to the shared nutrient pool and hence increases competitive interactions. These physical factors sometimes have contradictory direct and indirect effects on ecosystem processes. The transport rate, k, for instance, has a direct positive effect on plant biomass and productivity, as appears from Eqs. 7 and 8 when the number of species is held fixed. But it also has a negative effect on the maximum number of species able to coexist. Because, in the case of “complementary” species, species richness has a positive effect on plant biomass and productivity, the transport rate thus has a negative indirect effect on these ecosystem properties. The net result, however, is an overall positive effect (Fig. 3).

Figure 3.

Net effects of the nutrient transport rate k on the species richness at saturation (A) and the corresponding primary productivity (B), in the cases of “redundant” (circles) and “complementary” (squares) species. The continuous line shows the direct effect of k on primary productivity when the number of species is held constant. Resource-use intensities are assumed to follow a regular distribution, L^*_i = iL^*₁. All other parameters are identical for all species. Parameter values: R₀ = 220, L^*₁ = V_R = μ = 1, δ = 0.5; Sσ = 20 (circles), σ = 1 (squares), or S = 20 and σ = 1 (continuous line).

A systematic study of partial derivatives of ecosystem stocks and processes with respect to abiotic parameters shows that the direct effect prevails over the indirect effect in all cases (Table 1). When these effects are contradictory, this tends to generate negative correlations between species richness and ecosystem properties. Thus, if the transport rate is variable among several sites, sites of higher diversity also will be less productive (Fig. 3), as often is observed over part of the natural productivity range (20–22). This occurs despite the fact that diversity may be intrinsically beneficial to productivity (Fig. 2B). In conclusion, any effect of diversity on productivity or other ecosystem processes tends to be masked by the effects of environmental parameters when these vary among sites.

Table 1.

Effects of abiotic nutrient flux parameters on soil nutrient concentration below the rooting zone (R^*), plant biomass (B^*), and primary productivity (Φ^*) at equilibrium

Effect of	Type of effect
	Indirect	Direct	Net
R0 on R*	−	+	+
R0 on B* or Φ*	+	+	+
q on R*	−	+	+
q on B* or Φ*	+	− (if k low)	− (if k low)
		+ (if k high)	+ (if k high)
k on R*	+	−	−
k on B* or Φ*	−	+	+

Effects are given qualitatively by the sign of the partial derivative of the ecosystem stock or process with respect to the abiotic parameter considered. Direct effects are the effects obtained when the number of species is held fixed in Eqs. 6–8. Indirect effects are the effects mediated by changes in maximum species richness (Eq. 11 or 12), assuming that species richness acts to increase plant biomass, primary productivity, and nutrient retention, as in the “complementary species” case. Net effects are the effects obtained when the number of species is at its maximum, that is, when Eq. 11 or 12 is substituted into Eqs. 6–8. The signs of the effects are identical in the two cases of “redundant” and “complementary” species. Note that the net effect always has the sign of the direct effect; only the k values required for the transition from a negative to a positive effect of q on plant biomass and productivity differ. 

Discussion

The strength of the present model is that it is both simple enough to be tractable analytically and realistic enough to be applicable to actual experiments. In contrast to more conceptual models highlighting a single isolated factor (19), it allows one to explore several factors in combination and describe a variety of relationships between biodiversity and ecosystem processes. This model shows first that plant diversity does not necessarily enhance ecosystem processes, but it identifies two types of circumstances leading to such a positive effect: (i) when species occupy complementary spaces in the soil and (ii) when there is a positive correlation between mean resource-use intensity (which measures exploitation-competitive ability) and diversity. In both types of circumstances, it predicts that plant biomass, primary productivity, and nutrient retention all increase with diversity, similar to results reported in some recent field experiments (7, 10).

The model also shows that variation in abiotic factors that control nutrient flux rates can significantly alter our understanding of the relationship between biodiversity and ecosystem functioning. The effect of species richness on productivity or other ecosystem processes is masked systematically by the effects of environmental parameters on these processes. Therefore, comparisons among sites cannot reveal it, unless abiotic conditions are very tightly controlled. In particular, negative relationships between diversity and productivity do not allow any inference to be drawn on the specific effect—whether positive, neutral, or negative—of diversity.

As with any model, this one is a simplification of reality and thus also has limitations that must be borne in mind to avoid improper generalizations (18). In particular, the only limiting factor considered is a single nutrient, which does not allow humped-shaped relationships between species richness and productivity (20–22) to be obtained in among-site comparisons. If light is considered as a second limiting factor that acts mainly when plant biomass and thus nutrient supply are high, a unimodal relationship is easily obtained (24). However, the model then loses its analytical tractability, and explanation of this unimodal relationship—which is still debated (23)—was not the objective of this work. Thus, the present model applies to ecosystems in which the nutrient supply is low enough for light or other factors not to become major limiting factors of plant growth.

The model also ignores the spatial dynamics of colonization and development of local resource depletion zones; it assumes that the plants’ spatial distributions and the volumes of their depletion zones are given (i.e., σ_i is treated as a parameter). Clearly, different dynamics of space occupancy will lead to different species compositions and distributions. This long-term perspective is not the focus of the present model; the model inquires into the outcome of nutrient exploitation competition once a given species composition and distribution has been established. As such, it applies well to biodiversity experiments that run over relatively short periods of time. In the long run, the original diversity treatments cannot be maintained any more in the experiments than in the model.

The two types of factors identified by the model that lead to a positive effect of species richness on ecosystem processes have very different implications for the understanding of the relationship between biodiversity and ecosystem functioning. The first factor—complementarity among species in the space they occupy—is a biological factor that is both predictable from the individual species’ traits and has a consistent effect on ecosystem processes. It may have a general effect independent of species identity if there is a wide enough variation among species for traits such as root geometry. This should be more likely among species from different taxonomic or functional groups. Recent experimental evidence does suggest that the diversity of functional groups significantly affects ecosystem processes (10), although their composition may be as or more important (10, 11).

The second factor—positive correlation between average resource-use intensity and diversity—may arise as a result of various statistical and biological effects, the significance of which may vary depending on the kind of system or the time scale considered, as well as the scientist’s or the manager’s objectives. The “sampling effect” hypothesis (19) is a particular case, in which the average resource-use intensity increases with diversity because high-diversity plots have a higher probability of containing the most competitive species from the species pool. Although this effect may be important to explain short-term responses in randomized manipulative experiments (7, 19), its relevance in a broader and longer-term perspective is more problematic. Natural and, above all, managed communities are not random samples from a species pool, and the “sampling effect” is not sustainable as a biodiversity effect because initial diversity decreases until all habitats become monocultures on this hypothesis (19), at least in a constant environment. This type of effect may, however, be more critical in fluctuating environments (S. Yachi and M.L., unpublished results). Although they are not described explicitly in the model, direct neighborhood interactions, either negative (interference) or positive (facilitation), may act to modify the species’ exploitation-competitive ability. Thus, interspecific facilitation is another factor that might lead to a positive correlation between average resource-use intensity and diversity. However, direct neighborhood interactions are likely to be highly species-specific; there is currently no evidence that direct interspecific facilitation (i.e., other than indirect effects because of resource-use complementarity) among plants generally increases with species diversity.

Considerable progress would be achieved in biodiversity experiments if these not only recorded ecosystem responses to species diversity but also attempted to separate out the various factors at work in these responses. In particular, sampling effects could be controlled for by suitable experimental designs or data analyses (8, 14, 17, 27, 28). Complementarity in space occupation could be assessed by suitable comparative measurements among diversity treatments and supplementary experiments. The present model brings out complementarity in below-ground space occupation as a mechanism for biodiversity effects in nutrient-limited ecosystems. One may expect complementarity in above-ground space occupation to play a similar role when light is a limiting factor. In this respect, it is encouraging that in one experiment, greater light interception because of better space-filling canopies was suggested as a mechanistic explanation for biodiversity effects (5, 6). Greater emphasis on ecological mechanisms, notably on below-ground processes, is highly desirable in future experiments.