Automation of Random Conical Tilt and Orthogonal Tilt Data Collection using Feature Based Correlation

Abstract

Visualization by electron microscopy has provided many insights into the composition, quaternary structure, and mechanism of macromolecular assemblies. By preserving samples in stain or vitreous ice it is possible to image them as discrete particles, and from these images generate three-dimensional structures. This ‘single-particle’ approach suffers from two major shortcomings; it requires an initial model to reconstitute 2D data into a 3D volume, and it often fails when faced with conformational variability. Random conical tilt (RCT) and orthogonal tilt (OTR) are methods developed to overcome these problems, but the data collection required, particularly for vitreous ice specimens, is difficult and tedious. In this paper we present an automated approach to RCT/OTR data collection that removes the burden of manual collection and offers higher quality and throughput than is otherwise possible. We show example datasets collected under stain and cryo conditions and provide statistics related to the efficiency and robustness of the process. Furthermore, we describe the new algorithms that make this method possible, which include new calibrations, improved targeting and feature-based tracking.

Introduction

The Initial Model Problem

Single particle reconstruction is a technique used to create three-dimensional structures of samples that have been preserved in stain or vitreous ice. When a sample has been prepared properly and is examined using a transmission electron microscope (TEM) the result is an image containing particles of unknown orientations distributed across the field-of-view. The primary challenge of a single-particle reconstruction is to determine the orientation of these particles relative to one another so that they may be transformed properly into a three-dimensional volume. Due to the low signal-to-noise ratio in the raw images, having an initial model is an invaluable tool in determining particle orientations. By comparing each particle with projections generated from the initial model, a good first guess of the orientations can be used to bootstrap iterative refinement. For some samples a suitable starting model is known a-priori from previous structural work, but for many samples lack of an initial model may become a formidable roadblock to structural investigation. The requirement of a starting model to create a first approximate structure from new data is termed the initial model problem, and is the Catch-22 of structural EM work. An excellent overview and detailed description of single particle methods is given by Joachim Frank in his book, (Frank, 2006).

Another large problem commonly faced by investigators using single-particle methods is the presence of conformational variability in their samples (Orlova and Saibil, 2004). Conformational variability greatly complicates single-particle analysis since particles must not only be assigned correct orientations, but they must also be sorted by their conformational state. Given the poor quality of raw data, this is an extremely difficult task, and as a result the most common solution is to simply ignore the problem. Sometimes this works, for example when one conformational state is dominant and drives the reconstruction, but when it doesn’t, the results can be reduced resolution, structural artifacts and failure to converge to a final structure. ‘Standard’ single-particle data is collected with the sample oriented perpendicular to the microscope’s optical axis; an arrangement referred to as 0° tilt. Based on this observation, approaches that attempt to solve the initial model problem can be classified into two groups- those that perform specialized post-processing on 0° data, and those that use data collected at tilts other than 0°.

The post-processing approach attempts to determine particle orientations by exploiting a characteristic present in the data called ‘common-lines’. Theoretically, the Fourier transform of any two projections contain one-dimensional lines, termed common lines, whose profiles match exactly (barring the effects of noise). By finding these common lines the angular relationship between particles can be established so that they may be recombined to create a three-dimensional volume. The use of two-dimensional classification, averaging, and common lines to create an initial three-dimensional structure is termed angular reconstitution (Van Heel, 1987), and is an elegant approach that is often difficult to implement in practice. Angular reconstitution is reliant on the correct classification of particles; and the common lines, which are theoretically perfect matches, are frequently far from perfect in reality and do not differentiate the handedness of structures.

The second approach to overcome the initial model problem is to collect a second tilted image for every image originally collected. Since the particles in these image pairs are related by a known rotation this provides an additional constraint that can be used to roughly determine the particle orientations. In cases of conformational variability this also allows the creation of multiple starting models that can be used to sort conformational states and perform multiple reconstructions. The original method proposed by Michael Radermacher (Radermacher, 1988) suggested that one collect an image at as high a tilt as possible (for example 60°) and a second image of the same view at 0° tilt. This method of data collection was termed random conical tilt (RCT) and was devised to deal with particles that adopted preferred orientations and required tilted data to generate a three-dimensional structure. The drawback of RCT is that image pairs are not collected orthogonal to one another resulting in cone-shaped pieces of missing data referred to as ‘missing cones’. These missing cones generate artifacts in the structures that can confuse and complicate correct interpretation. A recently proposed amendment to the RCT method was to take images at a 90° angular difference to remove the missing cones in the collected data (Leschziner and Nogales, 2006). While it is impossible to tilt the stage from 0° to 90° in the microscope, it is possible to tilt from +45° to -45°, in effect achieving orthogonal coverage as long as the particles do not show a preferred orientation at 0°. This method was termed orthogonal tilt reconstruction (OTR) combining the data collection schema with the act of reconstruction. For the purposes of this paper OTR refers only to the automation of orthogonal data collection and not the processing required to reconstruct this data.

In theory RCT or OTR provide tools for reconstructing a 3D map of any sample, including those lacking initial models or exhibiting conformational variability. The critical factors in RCT/OTR data acquisition are the speed at which image pairs can be acquired, the overlap between the image pairs, and the quality of the acquired images in terms of the defocus, dose, drift and charging. The combination of these factors is what determines the overall throughput (or perhaps more accurately, output) of these methods. In practice, the use of RCT/OTR has remained somewhat marginal due partly to the difficulty of satisfying these requirements. This includes the burden of performing and maintaining microscope calibrations critical for efficient data collection; the constant correction of sample movements caused by specimen tilting and drifting; and the onerous bookkeeping required to correctly pair tilted images. Maintaining accuracy and consistency is further complicated since corrections are often made away from actual imaging areas to reduce sample dose.

When collecting tilted pairs of images a decision must be made whether to tilt the stage after each image acquisition, or whether to collect many images at one tilt before returning to collect the same field of views at a second tilt. For human operators it is much easier to tilt between every image since this simplifies the task of correcting instrument conditions and organizing image pairs. Conversely, it is very difficult for humans to accurately track previously imaged areas during tilting unless they are centered on distinctive landmarks. This makes the task of collecting multiple images at each tilt manually a visually challenging and inaccurate process. Furthermore, tilting can cause specimen drift, sample movement, and focus changes that delay image acquisition until drift is reduced to tolerable levels, the defocus is corrected, and the field of view is re-centered. In vitreous ice specimens, in fact, there may be such an increased overhead from tilting excessively that it becomes impractical to do so between every image pair.

Finally, there are factors that affect the quality of tilted images that are difficult to control without trial and error. Specimen charging is an effect commonly seen when samples preserved in vitreous ice are imaged at high tilt (Brink et al., 1998). It causes portions of images, especially over vitreous ice, to appear as if they are moving under the influence of the beam and can be mistaken for specimen drift. It is not usually seen at 0° because when the electron beam is perpendicular to the sample charging causes small defocus changes rather than image movements. An example of an image exhibiting charging can be seen in Figure 4A compared to its uncharged tilted pair in 4B. Part of the difficulty in providing a uniform and predictable solution to charging is the large number of factors that influence its magnitude. It is therefore greatly beneficial to have the ability to adapt settings, such as pre-exposure, on the fly in response to current imaging conditions, making the use of a CCD for data collection critical.

Figure 4.

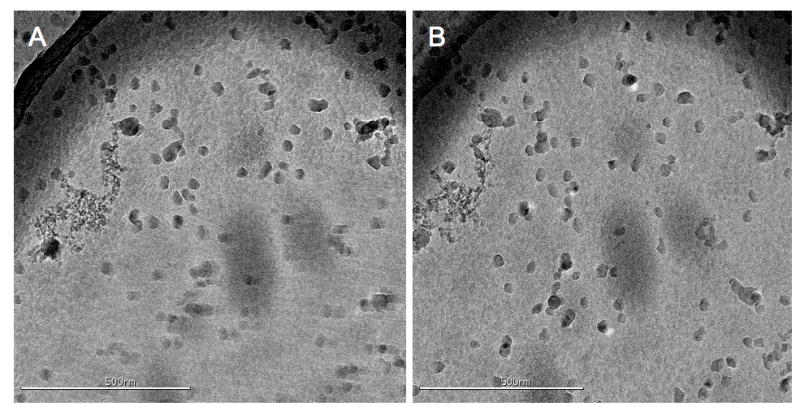
An example OTR image pair taken from the COPII vitreous ice dataset. In panel A is the first tilt image of a pair, taken at -45°, showing considerable charging towards the bottom half of the image. The charging resembles drift except that the effect is localized to only a portion of the image. In panel B is the second image (at 45°) taken 30 minutes later showing little evidence of the previous charging. The image overlap for this pair was ~90%. This image pair was taken before the use of a pre-exposure timing on the camera shutter.

Automated EM Data Collection

Automated TEM data collection can increase the number of images acquired, improve the consistency and quality of images, and provide an abstraction to microscope control that makes the technique more accessible to novice users. Over the past several years a number of automated data acquisition packages have been developed such as GRACE (Oostergetel et al., 1998), Leginon I (Potter et al., 1999), AutoEM (Zhang et al., 2003), AutoEMation (Lei and Frank, 2005), TOM (Nickell et al., 2005), and our own software package Leginon II(Suloway et al., 2005), which we have now extended to include acquisition of tilted image pairs and sequences. Leginon consists of a series of python programs, called ‘nodes’, that are connected together in ‘applications’ to perform the task of operating the microscope, finding targets, focusing, compensating for drift, acquiring images, etc. The most commonly used Leginon application is the multi-scale imaging (MSI) application, which uses different magnification levels to successively evaluate regions of interest until a final magnification is reached. This addresses the vast scale differences that make it unfeasible and extremely inefficient to automatically image an entire sample area at high magnification.

Using Leginon it is now possible for someone with relatively little training to oversee their data collection remotely and collect large datasets by running in single, continuous stretches that would tax the endurance of a human operator controlling the microscope manually (Stagg et al., 2006). Additional advantages of automated data collection include the possibility of extending EM maps to higher resolution, as well as the ability to deal with structurally uncharacterized samples or those exhibiting conformational variability.

Feature Based Image Processing

An important part of any undertaking to automate RCT or OTR data collection requires the efficient and accurate tracking of targets during stage tilting. Due to its various advantages we decided to utilize a feature-based correlation approach for tracking rather than a cross-correlation based one. Cross correlation, a method used commonly in the EM field for tracking tilt changes during tomographic data collection (Zheng et al., 2007b), works well with noisy images, but requires accurate foreknowledge of the image transformations caused by tilting. Previous work automating random conical tilt (Zheng et al., 2007a) has used cross-correlation to track tilting in a manner similar to the automated collection of tomography datasets.

Feature based techniques have become quite popular in the field of computer vision and are used for object recognition (Obdrzálek and Matas, 2005), stereo matching (Matas et al., 2002), automated panorama stitching (Brown and Lowe), and many other tasks. The term ‘feature’ refers to things such as edges, corners and blobs, and often corresponds with things a human might identify as interesting by eye. Various feature detection techniques exist with different propensities for the kinds of features they find and their ability to provide different levels of invariance (Mikolajczyk et al.). Examples include the Harris corner detector (Harris and Stephens), the Difference of Gaussian (DoG) detector (Lowe, 2004) and the Maximally Stable Extremal Region (MSER) detector (Matas et al., 2002) which can provide invariance to rotation, rotation and scale, and affine transformation respectively. Feature-based correlation works by using the features found in two images to determine the relationship between them, in a manner that is similar to how a human might intuitively perform such a task. The human brain is in fact so good at this, that at very small angles, such as the spacing between eyes, it continuously (and quite accurately) creates three-dimensional conceptualizations of the world before us.

A correlation technique based on features can be implemented so that it does not require foreknowledge of the geometric transformations between images, and can maintain accuracy in complicated imaging circumstances. The downside is that feature-based methods typically have poorer performance in low-signal-to-noise environments; a realm in which whole image techniques such as cross-correlation dominate. Fortunately the targeting images used in automated EM data collection are usually down-sampled, acquired at low magnification, and high defocus. These factors create images where the signal-to-noise ratio is very high and well within the realm of a feature-based approach.

In this paper we present an automated approach to RCT and OTR data collection built within the Leginon framework. To demonstrate the efficiency and robustness of the technique we have collected various datasets, both in stain and in vitreous ice, and have tabulated the results. We also discuss the design and capabilities of the calibration and tracking algorithms we have implemented.

Methods

Data were acquired on two FEI Tecnai F20 Twin transmission electron microscopes; one equipped with a Gatan Ultrascan 4k X 4k CCD camera, and the other with a Tietz F415 4k X 4k CCD camera, at accelerating voltages of 120KeV and 200KeV. The details of each dataset, such as magnification, dose and defocus, are shown in Table 1. The use of a 4K camera over a 2K camera is highly recommended, but not necessary, since it increases both the number of particles collected in each image, and the amount of useable overlap between image pairs. The GroEL vitreous ice specimen was imaged on a new substrate, created by Protochips Inc., called CryoMesh™. These new grids are designed and manufactured by Protochips using a novel process, and semiconductor materials rather than carbon, to improve the mechanical stability and conductivity of the substrate. A full discussion of their properties and performance will be the subject of a future paper. For the vitreous ice samples a side-entry Gatan 626 stage was used to maintain the temperature of the specimen below -170°C.

Table 1.

Datasets collected using our automated RCT/OTR application and their associated acquisition details.

Sample Type	CCD Camera	Type of Data Collection	Substrate Type	Electron Dose (per image)	Voltage KeV	Normal Defocus	Magnification	Tilt Pairs Collected
N-ethylmaleimide-sensitive fusion protein (NSF)	Gatan	RCT	Thin Carbon Negative Stain	20e-/Å2	120	-2μm	50,000X (2.26Å/pixel)	88
GroEL chaperone complex	Tietz	OTR	CryoMesh™ Vitreous Ice	15e-/Å2	120	-3μm	29,000X (2.85Å/pixel)	56
CopII (Sec13/31) Cages	Tietz	OTR	Thin Carbon Negative Stain	20e-/Å2	120	-3μm	29,000X (2.85Å/pixel)	275
CopII (Sec13/31) Cages	Tietz	OTR	Quantafoil™ R2/4 Vitreous Ice	20e-/Å2	200	-4μm	29,000X (2.85Å/pixel)	79

Leginon Automated RCT/OTR Application

A Leginon RCT/OTR data acquisition session begins by deciding the magnification that will be used for targeting and the magnification that will be used for final imaging. The targeting and final magnifications are selected so as to ensure they both use the microscope’s objective lens. This increases the stability and consistency of image shift alignments between magnifications, which degrade if the objective lens is shut down and allowed to ‘cool’. For the Tecnai F20 microscope series we typically use a targeting magnification of 1,700X and a final magnification between 29,000X and 50,000X.

The user begins the data collection process by selecting the location at which to begin targeting. A z-height correction and optical axis correction are performed at this selected location and an image is acquired using the targeting magnification. Targets for high magnification imaging are then selected on this image either manually (using mouse input), or automatically using one of various automated targeting capabilities available within Leginon. The selected targets are tracked to the first desired tilt angle before each is centered on the CCD and imaged at the final magnification. Once this is complete the targets are tracked to the next tilt angle and each is centered and imaged again. A focus correction and drift check is done once at the beginning of each of these tilt changes. Image pairs can be examined using a web-based viewer connected to the Leginon database to visually assess the image quality and extent of overlap. Once all the image pairs have been collected a new location is selected and the process is repeated. An overview of the entire process, as experienced by the user, is shown in Figure 1.

Figure 1.

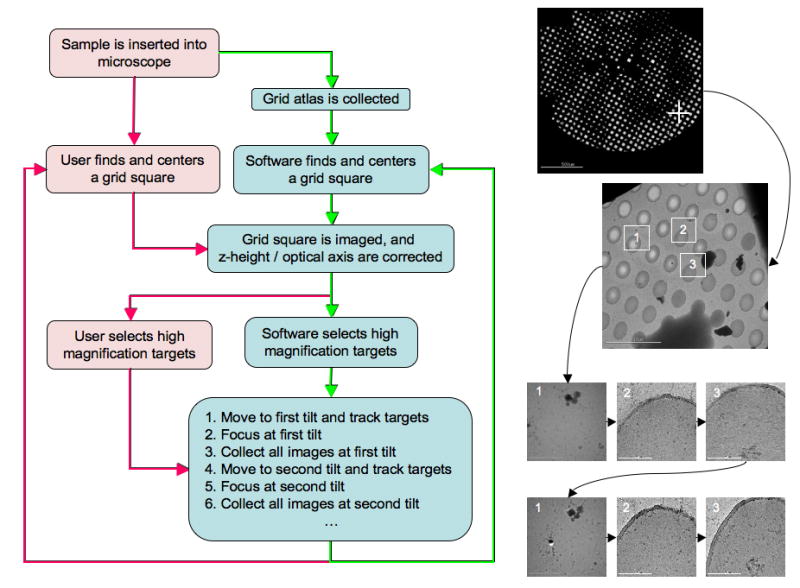
An overview of automated RCT/OTR data collection as experienced by the end user. The boxes in red depict actions a user must perform while the boxes in blue depict functions performed by Leginon. The red arrows denote the semi-automated approach where a user must select the regions they are interested in imaging and the software handles the rest. The green arrows depict the fully automated approach where Leginon determines the regions of interest automatically. The images on the right provide a visual example of each step in the process and demonstrate the order in which images are collected.

Optical Axis Correction and Iterative Targeting

The RCT/OTR application requires additional calibrations during the Leginon set-up process, the most critical of which is an alignment between the microscope optical axis and the specimen tilt axis (illustrated in Figure 2). Z-height correction is part of the optical axis alignment and serves to bring the sample close to the correct focal plane and minimize image translation during tilting. To correct the z-height we measure the image displacement observed when the stage is tilted to either side of zero degrees by an equal amount, typically 5-10°. Once the z-height has been corrected, a second measurement is taken of the image displacement between a tilted (10°-30°) and un-tilted image. This displacement is caused by the misalignment between the optical axis and specimen tilt axis, and if left uncorrected can result in drastic defocus changes during tilting. This second measurement is used to calculate an image shift correction that centers the tilt axis on the CCD. Once the z-height and optical axis have been set correctly any subsequent movement using the goniometer will move the sample through the correct focal plane regardless of the tilt angle. This greatly simplifies the task of maintaining focus during the acquisition of tilted targets. The entire procedure described above is now automated and performed by the Leginon focusing node.

Figure 2.

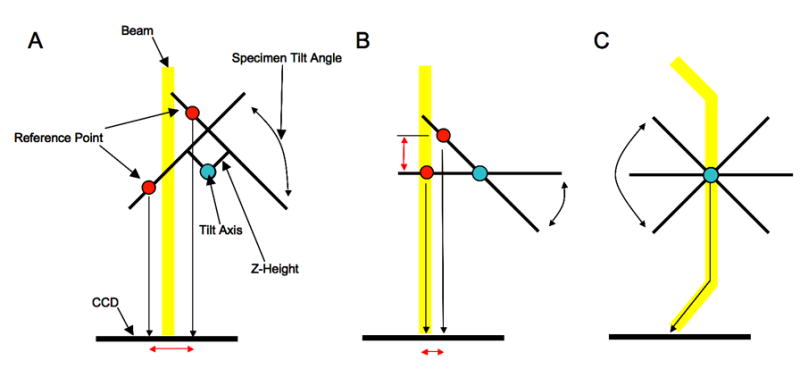
The three panels illustrate the microscope z-height and optical axis alignment that is performed prior to automated collection of RCT or OTR data. Panel A shows the image translation (red arrow) seen when the microscope z-height is set incorrectly and the stage is tilted to either side of 0°. By measuring this displacement it is possible to correct the z-height regardless of the position of the optical axis. Panel B shows the microscope when the z-height is set correctly but the tilt axis is misaligned with the optical axis. This misalignment manifests itself, as shown, as another image displacement and defocus change when the stage is tilted away from 0°. Since this alignment has no effect when the stage remains at 0° it is commonly ignored in standard data collection. Fortunately it can be corrected electronically by using an image shift adjustment to compensate. Panel C shows the final aligned state where sample remains within a consistent focal plane regardless of tilt angle or stage movement (stage movements translate the specimen along the tilt plane).

Another important requirement for collecting tilted image pairs is accurate target centering on the CCD. Accurate centering directly affects the efficiency of RCT/OTR data collection by increasing the overlap between image pairs. An error of a single pixel when centering a target at low magnification (1,700X bin by 4) can translate into an error of greater than a hundred pixels at high magnification (50,000X bin by 1). Unfortunately, two factors preclude the use of image shift adjustments to center targets accurately; the required movements are often beyond the range of image shift alone (~5μm) (Suloway et al., 2005), and the image shift has already been set so as to align the optical axis. The accuracy of our goniometer when returning to a pre-defined location is rated as <100nm, but this accuracy is worse, by up to an order of magnitude, when attempting to reach a new location unless the non-linear behavior of the goniometer has been modeled (Pulokas et al., 1999). To further improve the reliability of goniometer movements we implemented an iterative procedure that measures the error after each movement and attempts to re-center the target until a specified level of accuracy is achieved. The amount of error between moves is measured using cross-correlation, and to account for the possibility that these repeated attempts may result in an infinite loop, there is a conditional that stops the process if the error ever worsens rather than improves. Using this simple approach we typically achieve a goniometer accuracy of ~30nm in one to three moves depending on the quality of the goniometer calibrations and the distance traveled.

Target Tracking using Feature Detection

Our feature based matching algorithm proceeds via three stages; the first is a detection stage that finds ‘features’, the second is a descriptor stage that describes the features so that they may be compared, and third is a matching stage where corresponding features are found so that the relationship between two images can be determined. For feature detection we opted to use the affine-invariant MSER technique (Matas et al., 2002) over the scale-invariant SIFT DoG detector (Lowe, 2004). We implemented and tested both detectors using images acquired at a variety of magnifications and a range of tilt angles. In most circumstances the MSER method resulted in a higher number of correct matches than the DoG detector but the DoG detector was often able to find indistinct features more consistently. We have retained the option to use both detectors concurrently if the need should arise.

The MSER method works efficiently by first sorting image pixels by their values using binsort (Sedgewick) and then performing union-find operations (Sedgewick) on each pixel and its neighboring pixels. The end result of these union find operations is that regions form and grow as pixels on their borders are added to them. The size of each region at each pixel value is recorded and regions that show little growth over long pixel value spans are selected as ‘stable’. One can manually enter the thresholds for which regions are determined as stable, i.e. the percent growth rate, but instead we have these values determined from the images themselves. As a result our feature detector tries harder to find features in images where they are not as obvious, and thereby maintains more consistency during the tracking process than we observe using fixed thresholds. Once stable regions have been found their borders are extracted using isocontour navigation (Kirk) and approximated using a direct linear least-squares ellipse fitting (Fitzgibbon et al.). The image information within this elliptical region is then transformed to a circle with a radius of 20 pixels. The transformation of all features to this standard reference (41X41 pixels) provides affine invariance; an example of the entire process is illustrated in Figure 3.

Figure 3.

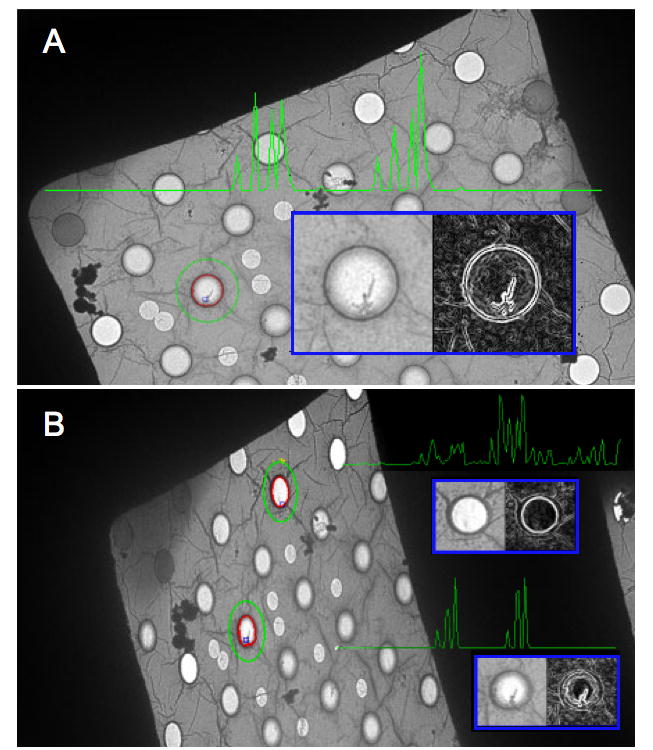
Shown, is an overview of feature detection and matching. Panel A is a view of a grid square at 0° tilt. The border of a region (in this case a hole in the carbon) found using MSER is shown in red, and around it, in green, is the ellipse that has been fitted to the border (the ellipse radii are multiplied by 2). In the blue inset is the normalized feature (using the fitted ellipse parameters), on the left, and its derivative image, on the right. The green graph, superimposed in the panel, represents the PCA-SIFT descriptor for this feature, and is composed of the 36 principal components derived from the derivative image. Panel B shows two features found in an image of the same grid square tilted to 55°. Of note is that the fitted ellipses are now eccentric, and when normalized, the features become circular. This illustrates the reason why the MSER detector is affine invariant. The PCA-SIFT descriptors for two features in Panel B are also shown, and as expected, the feature that corresponds to the one in panel A has a very similar descriptor, while the other does not. The fact that the descriptors do not match perfectly has several potential sources, i.e. noise, detector instability, and the fact that an EM image is created by projection rather than reflection. Reasonable differences between correctly matched descriptors are fairly common in feature tracking, where the most important criterion is generally not how perfect a correct match is, but how well it compares to all the incorrect matches.

Once features have been found they must be converted to a form that allows them to be easily compared. Most often this entails reducing image information so as to retain discriminatory ability while reducing the influence of noise and other destabilizing effects. The most robust descriptors to date belong to a group commonly referred to as the SIFT-based descriptors (Mikolajczyk and Schmid, 2004). These operate by taking the image derivative around the feature and summing the gradient values into positional and directional bins. This methodology provides invariance to linear illumination changes, reduces the effects of noise, and provides additional invariance to affine deformations. One method, PCA-SIFT (Ke and Sukthankar, 2004), does not use a predefined binning strategy, but instead performs principal component analysis on a large set of training features. Using the principal vectors determined from this training set, all future features are then projected into the same space to reduce their dimensionality. Using PCA-SIFT, we reduce each 41X41 pixel image patch obtained from the MSER detector, to its 36 principal components. The size of the image patches and the number of principal components were chosen based on the results of the original PCA-SIFT paper (Ke and Sukthankar, 2004).

The last step in feature-based image correlation is to find correspondences between the features in two different images so that an accurate global transformation can be calculated. Matches in our tracking routine are found by calculating the vector distance between every descriptor in one image against descriptors in another and keeping those whose shortest distance is at least 5% shorter than the second-shortest distance. This methodology is simple and widely used, but generates many false positives so a robust outlier removal algorithm is required. To this end, initial correspondences are filtered using RAndom SAmple Concensus (RANSAC) (Fischler and Bolles, 1981), to find the largest set of geometrically consistent feature correspondences. In RANSANC three correspondences are selected at random and a tentative affine transform is generated from them. All matches that agree with this affine transform (error of less than a pixel) vote for it, and the process is repeated with the starting assumption that 95% of the matches are correct and the terminating assumption that 1% are correct. Using MSER, PCA-SIFT, and RANSAC we typically find that tracking works reliably even when the percentage of correct matches falls as low as 8%, though it is often above 50%. The feature-tracking algorithm generally takes 1-15 seconds for each correlation between images depending on factors such as the number of features, the percentage of correct matches, the size of the images, and the speed of the computer. This is fast enough that it only adds a minimal amount of overhead to the entire process of automated data collection; but it could certainly be improved through optimization, particularly during region selection and descriptor matching. We also would like to mention that this tracking works without modification even if the image size, magnification, and rotation are different between images. The feature detection, descriptor creation, and matching code was written in C and wrapped in a Python object before being integrated into the Leginon acquisition node.

Results

In this section we discuss the performance of our automated RCT/OTR acquisition program. To assess the efficiency and consistency of automated RCT/OTR data collection we collected two large datasets in stain and two smaller datasets in vitreous ice. From these datasets we were able to assess the overlap between image pairs, the defocus consistency, and the efficiency of the entire process. The information related to the acquisition of these datasets is shown in Table 1.

Automated OTR Data Acquisition Results

Example RCT/OTR image pairs collected using our application are shown in Figure 5. The four datasets collected were GroEL in vitreous ice, COPII in vitreous ice, COPII in negative stain and NSF in negative stain. The details for each of these data acquisition sessions are shown in Table 1. Overall we collected 528 image pairs in stain and 134 image pairs in vitreous ice, and the approximate collection rate was 1.3 minutes per pair in stain and 2.2 minutes per pair in ice. These timings do not include the time taken to set Leginon up, which typically varies from 30 minutes to 2 hours depending on the state of microscope calibrations. The quality of target tracking and centering was quantified by measuring the degree of overlap between image pairs. Figure 6 shows percent number of images versus percent image overlap. It also graphs the number of images as a cumulative sum to provide a better idea of the amount of useable overlap, i.e. over 50% of the image pairs taken have an overlap of ~90% or better and 90% of the images have an overlap of ~70% or better.

Figure 5.

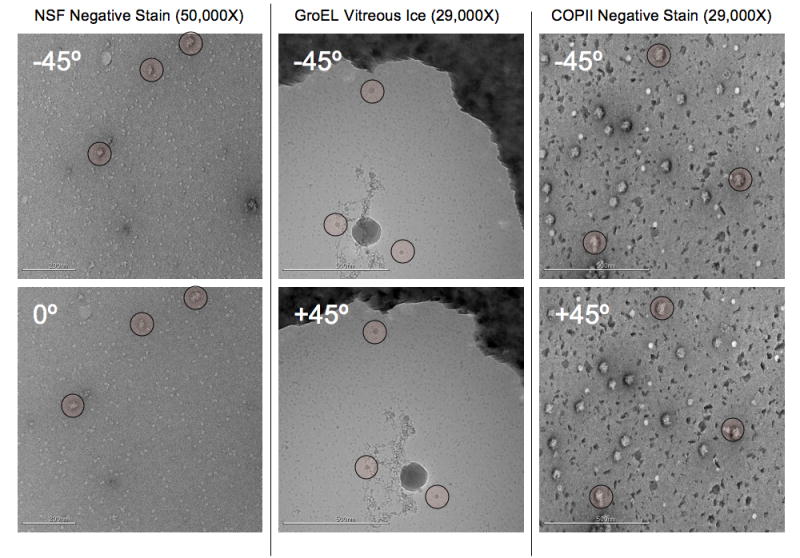
Example tilt pairs taken from the NSF negative stain, GroEL in vitreous ice, and COPII in negative stain datasets, these images are representative of most images in the dataset. An example of the COPII dataset was shown in Figure 4. Landmarks have been highlighted to make the image overlap easier to assess by eye. The tilt axis in these images largely runs along the y axis, though there is a small rotational component of about 5-10° in the orientation of the tilt axis between each pair. This is an example of a difference that is automatically incorporated when using feature based tracking. Note that in comparison to the vitreous ice tilt pair shown in Figure 3, the GroEL (on CryoMesh™) image pair shows no sign of charging in either image even without the use of pre-exposure.

Figure 6.

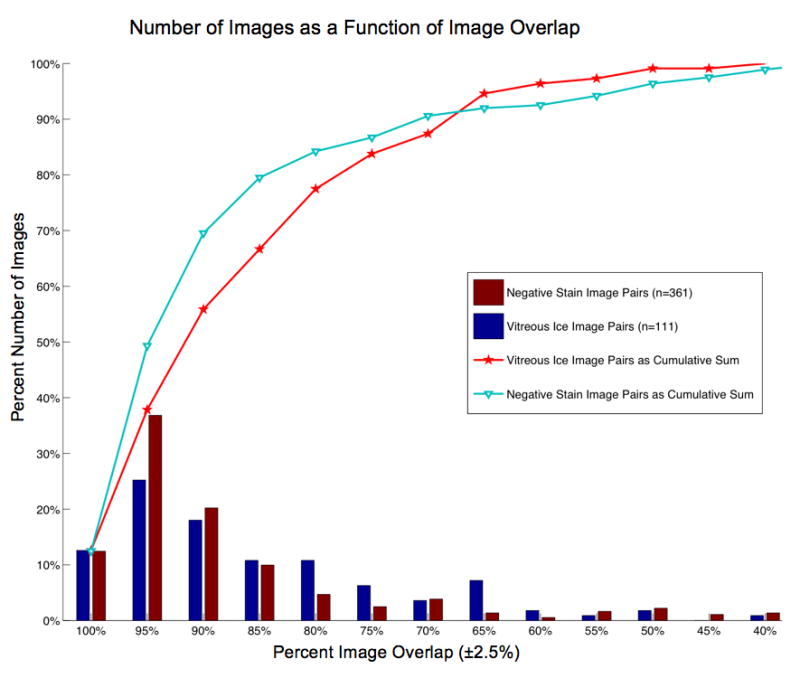
A histogram that plots the number of images (as a percent of the total number) vs. the percent image overlap between tilt pairs. For example, ~38% of the negative stain image pairs, and ~25% of the vitreous ice image pairs, have an overlap of 95% ± 2.5%. The line graphs represent the cumulative sum of these distributions and are included to aid in an alternate assessment of the image overlap. For example, ~80% of the vitreous ice image pairs have an overlap greater than, or equal to, 77% and ~80% of the negative stain image pairs have an overlap of greater than, or equal to, 85%.

The program ACE (Mallick et al., 2005) was used to measure the defocus of the datasets so that we could determine the accuracy and consistency of defocus during automated data collection. The result of plotting the deviation of the measured defocus from the nominal (set) defocus can be seen in Figure 7, and indicates that the final images fell within a suitable defocus range. The vitreous ice images have a larger distribution of defocus values than the negative stain datasets due to a small error in the alignment of the optical axis to the tilt axis, likely caused by performing the optical axis alignment right after stage insertion when the specimen was still drifting. Since most of these vitreous ice images (66%) fall within a ±0.792μm range of the nominal defocus, we still consider them suitable for low-resolution initial model work, and if required, a tighter defocus distribution could be achieved by verifying the result of the initial optical axis correction and repeating it if necessary. The accumulated dose for each image pair was estimated by adding the dose at high magnification to the dose accumulated from low magnification images. It ranged from ~30 e^-/A² to ~32 e^-/A², with at most ~6% of the dose attributed to the overhead of tilt tracking and target centering. The actual overhead dose of many images, however, is far below 6%, as that constitutes a high upward estimate. For many of the vitreous ice image pairs collected (~75%) the dose from overhead is less than 2%.

Figure 7.

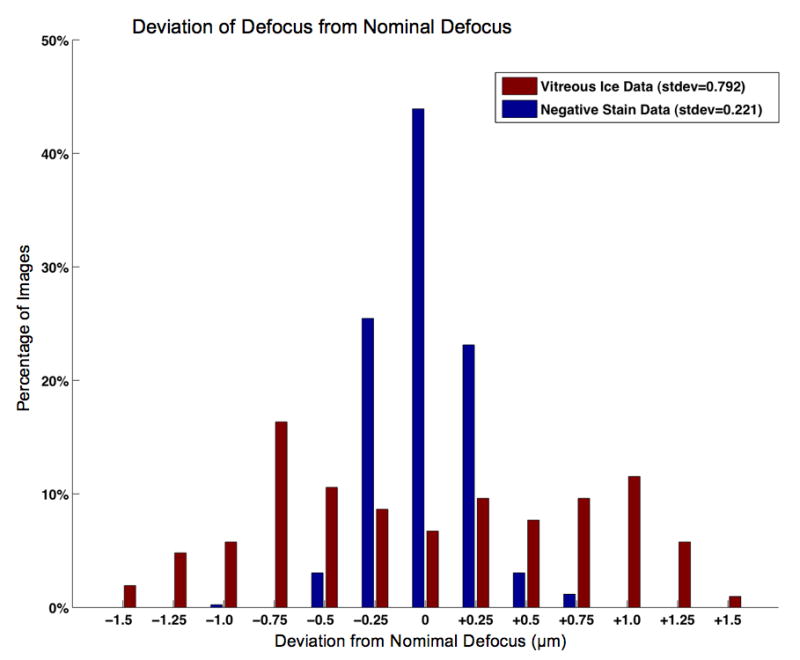
A bar graph showing the deviation between the measured defocus and the nominal defocus for the image pairs collected. As can be seen the negative stain dataset is very tightly clustered around the desired defocus, while the ice datasets, are not as tightly clustered, but fall within a useable range of defocus values.

As mentioned in the introduction, a serious limitation of tilted image acquisition over vitreous ice is the image deterioration caused by charge buildup from the electron beam (Glaeser and Downing). We observed this charging effect in 49% of the COPII images collected using C-Flat™ grids under cryo conditions. Interestingly, charging was usually seen only in the first (tilted) image of each pair despite the long time delay (up to 29 minutes) between collection of the first and second tilt images (example, Figure 4). To eliminate the possibility that charging in the first image was due to the tilt direction, half the COPII OTR ice dataset was collected using an initial tilt of 45° and the other half using -45°. This had no discernible effect on the observation of charging in the first image. Conversely, the use of a camera pre-exposure set to 100ms appeared to abolish the effect of charging but at the cost of 20% of the total specimen dose. We also note that the effect of charging appeared greatly reduced on the prototype CryoMesh™ grid we tested, but we reserve making definitive and quantitative statements on this result as the topic of a future paper.

Discussion

Alignments

Efficient collection of tilted image pairs requires more fastidious microscope alignment than is usually necessary since stage tilting can both translate the sample and move it away from the focal plane. During our early testing we found that our tracking routine could track the position of targets even with large optical axis and z-height misalignments but the autofocus routine could not compensate adequately for the changes in focus. Additionally we found that using image shifts to move to targets, a common practice when collecting standard 0° data, complicated matters by actively misaligning the optical axis. This is unfortunate since image shifts are very accurate and correctly centering targets is an important criterion when trying to achieve better overlap between image pairs. Although it would have been feasible to use image shifts for targeting, it would have required a complex focusing scheme and occasional z-height corrections- essentially replacing one inaccurate mechanical movement (goniometer position) with another (goniometer height).

Instead we decided to set the image shift and z-height once and gain the advantage that stage movements would automatically move the sample into the correct focal plane. On a reasonably flat substrate this means that only one focusing step is necessary to set the defocus of all images acquired within the same grid square, and target centering only requires a goniometer movement rather than a change in z-height, image shift, and focus. The relative inaccuracy of goniometer movement compared to image shift is compensated by our iterative movement routine, which works well in practice since stage movement error is proportional to the distance traveled (Pulokas et al., 1999). One disadvantage of iterative stage targeting is an increase in the dose accumulated by the specimen as a result of the images acquired during this procedure. However the total dose accrued at the targeting magnification is on the order of < 0.01 e^-/A² and thus a very large number of targeting images can be taken before they become a significant percentage of the total dose.

Proceeding directly from a very low magnification targeting image directly to the high magnification image removes an intermediate magnification step that is commonly used in standard 0° MSI Leginon runs. This intermediate magnification serves two purposes, it provides a step between inaccurate stage movements and accurate image shifts and it provides a higher magnification image from which it may be easier to distinguish areas that contain good ice or well-distributed sample. With more experience it has become apparent that the quality of the ice can often be judged at low magnification, and while the sample distribution cannot be as easily assessed, the grid can instead be rapidly screened for desirable sample distribution prior to the start of automated data collection.

Feature Detection and Correlation

Feature based tracking offers the advantage of being able to provide an affine relationship between two images without a priori knowledge of the imaging conditions and in the presence of complications such as occlusion. As a result, it provides the ability to track targets not only across tilts, but also through translations, rotations, and scale changes without modification to the underlying algorithm. When using cross-correlation to track tilt changes it is necessary to explicitly provide several variables, including the tilt angle of both images and the position and orientation of the tilt axis in both images. The tilt angle is used to compensate for image compression and should be accurate (not relative) since the compression seen when going from -4° to 51° is not the same as the compression seen when going from 0° to 55°. Another easily overlooked factor is the image rotation that may be introduced while tilting due to mechanical peculiarities in the goniometer (for our Tecnai F20 this can be 10° when going to -45° to 45°). If any of these factors are unaccounted for they can lead to systematic tracking errors.

When tilting the specimen stage at low magnifications we also commonly observe many large, non-planar image changes that complicate tracking. These include the grid square profiles, pieces of contamination, and the carbon surface, which translate separately due to different heights. The effect is most clearly seen by observing how holes in the carbon surface disappear, or appear, behind grid bars. Feature based correlation using RANSAC does a good job of dealing with these occlusions by voting for the affine transformation with the largest number of correspondences. Since the carbon surface always has the most features (cracks, markings, holes, grains, etc.) the correlation is very strongly biased towards tracking the carbon surface.

Automation of RCT/OTR Data Collection

Images collected using the automated RCT/OTR application are of consistently high quality (excepting cases of charging) and the defocus values fall within a range reasonable for low-resolution initial model construction. The most serious problem affecting the quality of the data is the effect of charging when imaging tilted specimens in vitreous ice. Our example datasets showed that if no steps are taken to avoid charging, up to half the images can exhibit the effect, and unfortunately, this half almost exclusively consists of the first image of each pair, making the useable throughput very low. Fortunately, various solutions to this problem exist, such as the use of pre-exposure, carbon sandwiching (Gyobu et al., 2004), and new grid substrates. Of these methods we tested the use of pre-exposure, and did preliminary evaluations of a new grid substrate, CryoMesh™. The use of pre-exposure removed the effect of charging at the expense of increased dose, but charging in an area would not recur if it had been previously exposed, even after a significant period of time (30 minutes). This leads us to believe that only the first image of each tilt pair, rather than every image, requires the use pre-exposure making the added dose requirement more bearable. Likewise, the use of the new CryoMesh™ substrate seemed to greatly reduce the effect of charging. These two observations, along with the results reported for the carbon sandwich technique, lead us to conclude that while RCT/OTR data collection in vitreous ice may be more difficult than it is in stain, it is still made accessible and efficient using an automated method.

The Leginon RCT/ORT application considerably improves the throughput of tilt pair data acquisition and automates a process that is difficult and tedious to do by hand. The usual rate of data acquisition when using Leginon is on the order of 1000 high magnification 4K CCD frames every 24 hours (Stagg et al., 2006). Our results show that we can now achieve a similar rate of data acquisition even when acquiring tilted pairs of images. The principal reasons that RCT/ORT application is competitive with standard Leginon MSI data acquisition is that the overhead of tilting is minimized, focus corrections are performed less frequently, and intermediate targeting steps have been eliminated.

The value of automated RCT/OTR data collection is two-fold. Now that it is more accessible it is our wish to use it routinely prior to, during, or after, standard data collection. This will hopefully provide a useful springboard from which to deal with new samples that are structurally uncharacterized or that have multiple conformations. The second benefit is that we can now undertake a much more systematic evaluation of the factors that affect tilted data collection, such as charging, drift, defocus, etc. This can be used to optimize parameters that will improve the quality and efficiency of tilted data collection in the future.