Concentration-Effect Relationship of Ceftazidime Explains Why the Time above the MIC Is 40 Percent for a Static Effect In Vivo

Abstract

Growth-kill dynamics were characterized in vitro, and the parameter estimates were used to simulate bacterial growth and kill in vivo using both mouse and human pharmacokinetics. The parameter estimates obtained in vitro predicted a time above the MIC of between 35 and 38% for a static effect in mice after 24 h of treatment.

For beta-lactam antibiotics, the most important pharmacokinetic-pharmacodynamic index correlating with in vivo efficacy has been shown to be the duration that the unbound concentration of an antibiotic remains above the MIC as a percentage of the dosing interval (%fT_>MIC) (1, 4, 5). Typically, in animal experiments, the %fT_>MIC is correlated with the change in CFU after 24 h of exposure compared to that of the initial inoculum. The in vivo static effect then corresponds to no net CFU change after 24 h of treatment. Although it is sometimes believed that the %fT_>MIC needed to obtain an in vivo static effect would be close to 100%, results from several animal models show that this value is 35 to 40% fT_>MIC for cephalosporins (3). One of the explanations could be that the MIC is a hybrid parameter (12), being the net result of the concentration effect over time after 18 h of incubation (10). From the results of time-kill curves, one can conclude that although the concentration-effect relationship of beta-lactams is relatively concentration “independent,” there is a range of one to four times the MIC where the effect increases, while at slightly lower concentrations, some effect is still observed (2, 6, 10, 14, 16, 17, 19). Since concentrations during intermittent infusion do fluctuate, the in vivo static effect could be considered to be the net result of killing over time, with incremental killing at concentrations up to around four times the MIC. The net result thereof is not necessarily equal to the MIC in vitro. Here, we sought to explain whether concentration-effect relationships of ceftazidime could explain this seeming discrepancy between the MIC and static effects in vivo by characterizing growth-kill kinetics in vitro and to subsequently use the parameter estimates to simulate growth and kill kinetics in vivo.

(Parts of these data were presented at the 46th Interscience Conference on Antimicrobial Agents and Chemotherapy, San Francisco, CA, 27 to 30 September 2006.)

The MIC of ceftazidime was determined for Pseudomonas aeruginosa ATCC 27853 by microdilution according to standard procedures (13) and by Etest (AB Biodisk, Solna, Sweden). Time-kill curves in Mueller-Hinton were determined in duplicate in twofold dilutions from 0.0625 to 64 mg/liter by taking samples every 0.5 h up to 3 h, 4 h, 6 h, and 24 h. Growth rates (GRs) and kill rates (KRs) were obtained by linear regression to change in ln CFU over 1 to 4 h. The Hill equation was fit to the KRs versus concentrations using Graphpad Prism 3.0 (Graphpad Inc., San Diego, CA). The net maximum KR was determined by correcting the observed maximum KR with the observed GR (8). Subsequently, the estimated parameters were used to simulate bacterial kill over time during dosing regimens of 1 mg every 2 h up to 256 mg every 8 h using pharmacokinetic parameters observed for mice and humans and the following equation for bacterial growth and killing, as described previously (11):

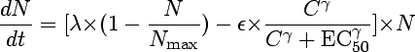(1)

where λ represents the GR, ɛ represents the maximum KR, C represents the concentration of antibiotic, EC₅₀ represents the 50% effective concentration, γ represents the Hill coefficient, N represents the number of viable bacteria, and N_max represents the maximum number of bacteria. A computer program was developed and validated for that purpose. Briefly, the program determines dN/dt over time intervals of 0.01 h using the concentration obtained from simulated concentration-time profiles using a one-compartment open model with first-order absorption and elimination (15). It then numerically integrates these effects over 24 h. The pharmacokinetic parameter values were obtained from previous studies of infected mice (5): a volume of distribution (V_c) of 0.5 liters/kg, an elimination rate constant (k_el) of 1.96 h⁻¹, an absorption rate constant (k_a) of 15 h⁻¹, bioavailablity (F) of 1.0, and a fraction (unbound) of 0.9. Values for inoculum and N_max were 6.5 log₁₀ CFU and 8.5 log₁₀ CFU, respectively (3; J. W. Mouton, A. A. T. M. M. Vinks, N. Punt, and W. A. Craig, presented at the 37th Interscience Conference on Antimicrobial Agents and Chemotherapy, Toronto, Canada, 1997, abstr. A22). The dosing regimens that resulted in an in silico static effect after 24 h were then determined for various dosing regimens, and the %fT_>MIC was determined using MicLab 2.33 (Medimatics, Maastricht, The Netherlands). For simulation of effects in humans, pharmacokinetic parameter estimates for healthy volunteers were used as reported previously (9): a V_c of 14 liters and a k_el of 0.46 h⁻¹.

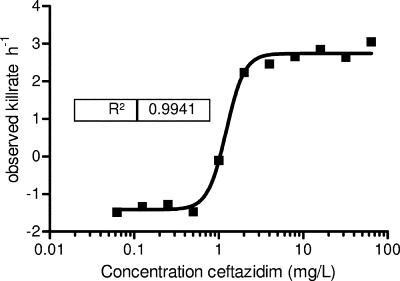
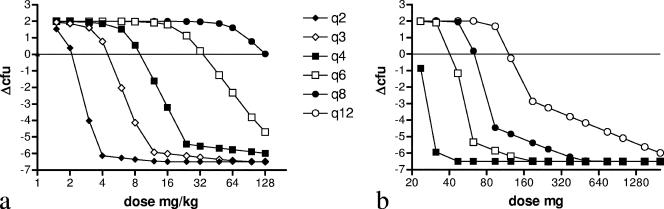
The MIC of ceftazidime was 1 mg/liter. The time-kill curves of ceftazidime followed a typical pattern, with maximum kill reached at around four times the MIC. This is more obvious from Fig. 1, showing kill rates of ceftazidime as a function of the concentration. The Hill equation fitted well to the data with an R² of 0.99. Table 1 shows the corresponding parameter estimates. The maximum KR obtained was 4.15 h⁻¹ after correcting for GR. Using the estimates in equation 1, the effect after 24 h of treatment was determined for various dosing regimens using simulated concentration-time curves based on mouse pharmacokinetics as inputs (Fig. 2a). The doses needed for an in silico static effect are summarized in Table 2 together with the corresponding %fT_>MIC values. The %fT_>MIC resulting in an in vivo static effect was between 35.7 and 38.1%.

FIG. 1.

Relationship between kill rates of P. aeruginosa ATCC 27853 and increasing concentrations of ceftazidime.

TABLE 1.

Parameter estimates of the ceftazidime concentration-effect relationship^a

In vitro pharmacokinetic-pharmacodynamic parameter	Value
	Estimate	95% CI
Growth rate (h−1)	−1.41	−1.65-−1.18
Observed maximum kill rate (h−1)	2.74	2.54-2.94
Corrected maximum kill rate (h−1)	4.15
Hill factor	3.96	2.25-5.57
EC50 (mg/liter)	1.22	1.08-1.39

^aEC₅₀, 50% effective concentration; CI, confidence interval.

FIG. 2.

Relationship between the dose and ΔCFU for different dosing frequencies after 24 h of treatment using mouse pharmacokinetics (a) and human pharmacokinetics (b). The intersections with the horizontal line (representing no net change in CFU after 24 h of exposure) correspond to the dosing regimens that result in an in vivo static effect.

TABLE 2.

Dosing regimens and corresponding %^fT_>MIC values based on mouse and human pharmacokinetics resulting in a net static effect after 24 h of simulating growth and kill kinetics^a

Regimen	Mouse		Human
	Dose (mg/kg of body wt)	%fT>MIC	Dose (mg)	%fT>MIC
q2	2.12	37.3	ND	ND
q3	4.60	38.1	ND	ND
q4	9.29	37.6	20.2	23.7
q6	35.6	36.5	38.9	36.3
q8	129.7	35.7	59.8	37.9
q12	−	−	121.0	37.7

^aq2, dose every 2 h; ND, not done; −, static dose could not be determined within the dosing range.

The same procedure was applied using pharmacokinetic parameter estimates observed for humans (Table 2 and Fig. 2b). The %fT_>MIC values for a static effect were in the same range as those observed for mice. A static effect during continuous infusion was observed at a concentration of 1.15 mg/liter, corresponding to a total daily dose of 200 mg. We also determined %fT_>MIC for a 2-log₁₀ drop. Corresponding values were between 45% and 50% for the dosing regimens as shown in Table 2.

In this study, we show that the concentration-effect relationship of ceftazidime in vitro predicts that 35 to 38% fT_>MIC is needed for an in vivo static effect in mice after 24 h of treatment independent of the dosing regimen.

While the MIC is measured at static concentrations, and the final effect observed can be ascribed to one specific value (usually in twofold dilutions), the effect of an antimicrobial is not an on-or-off phenomenon but rather follows a sigmoidal pattern that can be well described by the Hill function. Theoretically, an on-off phenomenon can be captured by the Hill equation only when the value of the Hill slope reaches infinity. Since the Hill slope in this study was estimated at around 4, it follows that concentrations above the MIC do contribute increasingly to the overall effect until the maximum effect is reached. The opposite is true for concentrations below the MIC. Since concentrations in vivo do fluctuate with intermittent dosing, the overall effect over time is the integral of these concentration fluctuations and the corresponding effects over time. Thus, the %fT_>MIC that results in a static effect is the net result of both growth and killing over time, and the value of the %fT_>MIC required for a static effect depends directly on the growth and kill kinetics.

Two important characteristics of in vitro time-kill curves that are often observed are the change in the kill rate after a number of hours of exposure and, for some drugs, regrowth. This has been taken into account by some models, for instance, by introducing an adaptation term (11, 16) or an alternative term to describe this phenomenon (7). While this is more obvious for some drugs than for others, the effects observed during the first few hours in the ceftazidime time-kill curves seem to well predict effects over a longer period of time. One of the explanations might be that the half-life in mice is relatively short and that exposure to adequate ceftazidime concentrations is therefore limited in time. As concentrations decline below a threshold value, bacteria will start to regrow. This has been observed, for instance, for ticarcillin (Mouton et al., presented at the 37th Interscience Conference on Antimicrobial Agents and Chemotherapy, Toronto, Canada, 1997, abstr. A22), ampicillin (18), and piperacillin (H. Derendorf, A. Kovar, T. Dalla Costa, A. Nolting, and K. H. Rand, presented at Pharmacokinetics and Pharmacodynamics in Animals, Reykjavik, Iceland, 1996). In effect, one could argue that by using the mouse model, the first part of the time-kill phenomenon, the relatively fast killing early on as opposed to slower killing at later time points, is entertained. However, this does not explain the similar effects observed at low and high dosing frequencies. In addition, the simulation of human pharmacokinetics, despite the difference in half-life, also resulted in approximately the same results as those obtained by using mouse pharmacokinetics.

We conclude that the concentration-effect relationship of ceftazidime as observed with in vitro time-kill curves well describes pharmacokinetic-pharmacodynamic relationships in vivo and reasonably well predicts the %fT_>MIC of 35 to 40% needed for a static effect as reported in the literature.