Abstract
Different combinations of genetic and environmental risk factors are known to contribute to the complex etiology of ischemic heart disease (IHD) in different subsets of individuals. We employed the Patient Rule-Induction Method (PRIM) to select the combination of risk factors and risk factor values that identified each of 16 mutually exclusive partitions of individuals having significantly different levels of risk of IHD. PRIM balances two competing objectives: (1) finding partitions where the risk of IHD is high and (2) maximizing the number of IHD cases explained by the partitions. A sequential PRIM analysis was applied to data on the incidence of IHD collected over 8 years for a sample of 5,455 unrelated individuals from the Copenhagen City Heart Study (CCHS) to assess the added value of variation in two candidate susceptibility genes beyond the traditional, lipid and body mass index risk factors for IHD. An independent sample of 362 unrelated individuals also from the city of Copenhagen was used to test the model obtained for each of the hypothesized partitions.
Keywords: IHD, genetics, PRIM, classification, epistasis
INTRODUCTION
Ischemic heart disease (IHD) is the leading cause of mortality and morbidity in westernized societies [Murray and Lopez, 1997]. The development of IHD is a direct consequence of interactions between the effects of many susceptibility genes and many environmental factors [Sing et al., 2003]. Because the combined number of interacting genes and environments is large, every incident case cannot have experienced the effects of the same combination of genetic variations and exposures to high risk environmental variations. In spite of this obvious consequence of a complex multi-factorial etiology, the common approach in medical practice is to classify and treat all individuals using one risk factor model created using information obtained from a pooled sample of cases. There is a need to identify subgroups of individuals at substantially increased risk of IHD that are each characterized by a particular combination of risk factors and their variations who may benefit from particular treatment regimes. To simplify the complexity, but still be able to generalize within well-characterized subgroups, we present here an application of the Patient Rule-Induction Method (PRIM) [Friedman and Fisher, 1999]. This statistical method balances two competing objectives: identification of partitions of individuals at substantially increased risk of IHD and maximization of the number of IHD cases explained by the partitions.
The PRIM was applied to model the cumulative incidence of IHD in a sample of 5,455 unrelated individuals from the Copenhagen City Heart Study (CCHS). A comprehensive set of risk factors established by prior population-based research studies with a documented role in the etiology of IHD were considered [Schnohr et al., 2002; Song et al., 2004; Wittrup et al., 1999b; Davignon et al., 1998; Reilly et al., 1991; Frikke-Schmidt et al., 2000a; Mahley et al., 1995]. The objective of the PRIM is to select variations in subsets of risk factors which identify a partition of individuals that has a statistically significant increased risk of disease. Iterative applications of the PRIM results in multiple, partition specific, predictive models. We applied the PRIM sequentially to determine if single nucleotide polymorphisms (SNPs) in two genes that impact the risk of IHD, apolipoprotein E (APOE) and lipoprotein lipase (LPL), add to the prediction of IHD beyond the traditional, lipid and body mass index (BMI) risk factors. The ability of the risk model obtained for each partition to predict IHD was evaluated in a sample of 362 unrelated individuals representative of the city of Copenhagen.
METHODS
PARTICIPANTS
The CCHS is a prospective longitudinal study of the general population of Copenhagen, Denmark described in Schnohr et al. [2001]. Individuals without prior IHD were recruited in 1976−1978, 1981−1983 and 1991−1994. During each recruitment period, individuals who were previously ascertained into the study were also re-evaluated. The PRIM prediction models were built using 5,455 participants who were ascertained in 1976−1978, were older than 45 years of age and did not have IHD at the third recruitment phase and were followed until December 31, 1999. A sample of 362 participants ascertained in 1981−1983, who were also older than 45 years of age and did not have IHD at the third recruitment phase and were followed until December 31, 1999, was used to evaluate the hypothesized risk models obtained. Informed consent was obtained from all participants. More than 99% were white and of Danish descent. The study was approved by a Danish ethics committee: Nos. 100.2039/91, Copenhagen and Frederiksberg committee.
VARIABLE DEFINITIONS
Information on diagnoses of IHD (World Health Organization; International Classification of Diseases, 8th edition: codes 410−414; 10th edition: codes I20-I25) was collected and verified through December 31, 1999 by reviewing all hospital admissions and diagnoses entered in the Danish National Hospital Discharge Register, all causes of death entered in the Danish National Register of Causes of Death and medical records from hospitals and general practitioners. The diagnosis of IHD included those with a myocardial infarction and/or characteristic symptoms of angina pectoris [Julian et al., 1997]. A diagnosis of myocardial infarction required the presence of at least two of the following criteria: characteristic chest pain, elevated cardiac enzymes and electrocardiographic changes indicative of myocardial infarction.
Smoking status, hypertension status, diabetes status, gender and age (at the third recruitment period) were denoted for the purposes of this study as traditional risk factors. Smoking, hypertension and diabetes have been shown to be the three most important predictors of IHD in both genders in this cohort [Schnohr et al., 2002]. These three risk factors were dichotomized and defined as ever-smokers, ever-diabetic and ever-hypertensive. If a participant smoked during the second or third recruitment period, (s)he was labeled as “ever-smoker.” The same rationale defined ever-diabetic and ever-hypertensive [Frikke-Schmidt et al., 2007]. Information about these three risk factors from the first recruitment period was discarded to ensure that the sample of participants used to build the PRIM models had a comparable amount of exposure for all predictors as the sample that was used to validate the models. Age was also dichotomized as greater than 65 and less than or equal to 65. Although the CCHS is a longitudinal cohort study that records incident cases of IHD, for the present study we consider the totality of cases at the end of the 8 years of follow up in a cross-sectional analysis to determine the added value of genetic variants for predicting the cumulative incidence of IHD.
Plasma levels of total cholesterol (CHOL), high-density lipoprotein cholesterol (HDL-C) and triglycerides (TRIG) and BMI were included in the PRIM analysis to evaluate their contribution to prediction of IHD beyond the traditional risk factors. CHOL and BMI were each categorized into three groups using 200 and 240 mg/dl and 25 and 30 kg/m2 as the cutpoints as suggested by Cleeman et al. [2001] and Donato et al. [1998], respectively. HDL-C and TRIG were dichotomized into low and high groups using 40 and 150 mg/dl as cutpoints, respectively, as suggested by Cleeman et al. [2001].
Genotype information was collected on five SNPs in the APOE gene and three SNPs in the LPL gene, denoted here as the genetic risk factors (see Fig. 1 in Frikke-Schmidt et al. [2007] for a feature map that gives the locations of these SNPs in the two genes). The APOE and LPL genes were selected because they encode proteins that are major components of human lipid metabolism [Mahley and Rall, 2001; Brunzell and Deeb, 2001] and because variants of these genes have been identified as statistically significant predictors of quantitative variation in lipid traits [Reilly et al., 1991; Frikke-Schmidt et al., 2000a; Mahley et al., 1995; Wittrup et al., 1997, 1999a, 2002] and inter-individual differences in IHD susceptibility [Song et al., 2004; Wittrup et al., 1999b; Frikke-Schmidt et al., 2000b] in population-based studies.
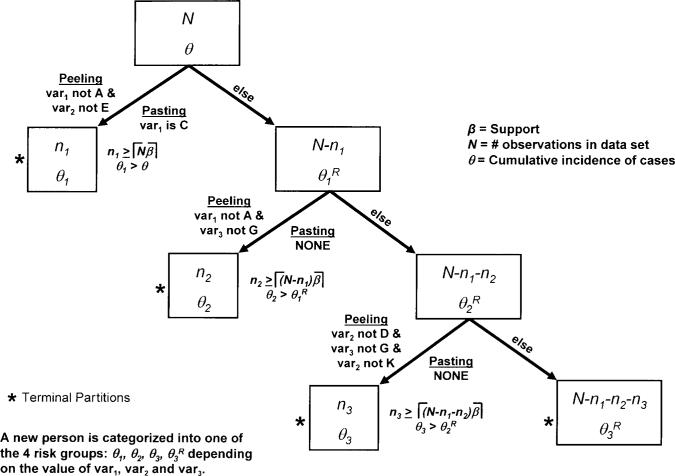
Fig. 1.
This illustration of the PRIM shows the peeling and pasting stages creating four partitions. The dataset contains N individuals, with a disease cumulative incidence of P. The first partition is defined by two peeling (‘var1 not A’ and ‘var2 not E’) and one pasting term (‘var1 is C’). The n1 individuals that are in this partition have a cumulative incidence of P1. After the first partition is produced, the remaining unassigned N–n1 individuals that were not placed in that partition are used to produce a second partition. The process of producing a new partition based on the unassigned individuals from the previous partition continues until all individuals are assigned to a partition. Sequential permutation testing is then used to determine how many of the produced partitions are statistically significant. The individuals that are not included in any of the statistically significant partitions are assigned to the remainder partition. In this illustration, only three partitions were statistically significant, leaving N–n1–n2–n3 individuals in the remainder partition.
STATISTICAL ANALYSES
PRIM.
The objective of a PRIM analysis is to select the subset of variables, and their values, that are the optimum predictors of the cumulative incidence of a disease in a subsample of individuals. Multiple mutually exclusive subsamples, denoted partitions, of the total sample may be produced. Each partition will include individuals with the same values for a subset of the predictor variables. The selected subset of predictor variables is expected to vary from partition to partition because of the heterogeneity of the etiological relationships between the outcome and the genetic and environmental agents of causation among individuals in a representative sample of the population at large.
Repeating the two stages of implementation of PRIM (peeling and pasting) creates the mutually exclusive partitions of individuals. Features of the peeling and pasting stages are illustrated in Figure 1. Peeling is an iterative process that creates a partition by excluding individuals with particular values of predictor variables, while pasting iteratively amends individuals to the partition, also based upon values of predictor variables, after the peeling stage has been completed. All possible potential values of each predictor variable are considered to find the optimum (typically defined as the largest cumulative incidence, θ) at each step of the peeling and pasting stages.
There are two ways that peeling and pasting stages can terminate: if the minimum support (β) is achieved or no term (defined by a predictor variable and its values) at a step achieves a threshold defined by the complexity (λ). The support for a partition is the number of individuals in that partition divided by number of unassigned individuals that could have potentially been in that partition. The minimum support is the proportion of unassigned individuals that must be in a partition. This parameter is selected via a grid search using a likelihood approach (see below). Complexity is the minimum increase in θ necessary to further refine a partition by incorporating another predictor and its values into the definition of the partition. Therefore, to produce a valid term at any of the peeling or pasting stages it must have enough individuals (≡ ⌈β × number of unassigned individuals⌉) and an increase in θ by at least λ.
In the illustration of PRIM presented in Figure 1, ‘var1 not A’ was the variable and its value, among all possible variables and values in the dataset, that identified a subset of individuals that resulted in a partition with the largest cumulative incidence of cases during the first peeling attempt such that there were enough individuals to satisfy β and θ increased by at least λ. Individuals having predictor term ‘var2 not E’ were added to the partition during the second peeling attempt that also satisfied the support and complexity criteria. However, no variable and value identified additional individuals that satisfied the support and complexity criteria during the third peeling attempt. Then the pasting process begins by examining all possible variables and values in the subset of observations excluded during the peeling process to determine if amending one combination to the current peeled partition will fulfill the complexity criterion. In the illustration given in Figure 1, individuals that were excluded during the peeling process having the value C for var1 were added back into the partition. No further pasting on the updated partition satisfied the complexity criterion and thus the first partition is finished.
After the first partition is produced, the remaining unassigned individuals (N–n1 in Fig. 1) that were not placed in that partition are considered for constructing a second partition. The process of producing a new partition based on the unassigned individuals from the previous partition continues until all individuals are assigned to a partition. Sequential permutation testing (see below) is then used to determine how many of the produced partitions have a statistically significant increase in cumulative incidence. The individuals that are not included in any of the statistically significant partitions are assigned to the remainder partition. Of the N individuals considered in the illustration presented in Figure 1, n1 were placed in partition 1 based on values of ‘var1’ and ‘var2’. The remaining N–n1 individuals are then used to build the second partition of n2 individuals. In this example, only three partitions were statistically significant, leaving N–n1–n2–n3 individuals in the remainder partition.
Determining the minimum support parameter.
Selection of the support parameter “involves both statistical and application domain dependent considerations” [Friedman and Fisher, 1999]. There is no standard, automated selection mechanism for reducing the inherent subjectivity in defining plausible “considerations.” A grid search of the support parameter space, ranging from 0.05 to 0.50 (incremented by 0.005), was employed to determine the optimal β. We only considered support parameters in this range to ensure that each partition consisted of at least 5%, but less than 50% of the unassigned individuals. The lower and upper bounds exist to ensure that a minimum percentage and at most half of individuals are determined to be high risk, respectively. For each of these potential support parameters, the PRIM was carried out and permutation testing (see below) was used to determine the number of significant partitions. To select a support parameter, the PRIM models for a set of significant partitions associated with a particular support parameter was compared to the null model via a likelihood ratio test (LRT) using logistic regression. The null model fit a logistic regression with the intercept as the only predictor, while the logistic regression for a support parameter used the partition class identifier from its corresponding PRIM model as a categorical predictor. The support parameter which resulted in the most significant LRT was chosen for use in the peeling and pasting stages when defining the optimal set of partitions. In other words, we chose the support parameter (and respective significant partitioning) that maximizes the explained deviance versus a model with no partitioning. Deviance is defined as the −2 times the log likelihood of a given model, computed using the predicted values and true response.
Permutation testing and error estimation.
Given the results of a PRIM analysis, sequential permutation testing was carried out to determine which of the partitions have a statistically significant larger cumulative incidence than expected by chance alone. Briefly, for each partition the available exchangeable observations are randomly shuffled and a PRIM model with only one partition is produced. The exchangeable observations for a partition are the set of observations from which the partition was created; therefore observations already assigned to a partition cannot be exchangeable for any subsequent partition. The same complexity and minimum support parameters that were used in the original analysis to obtain the observed cumulative incidence were used to obtain this partition. The cumulative incidence associated with the partition obtained when the observations are randomly shuffled represents a realization of the distribution of the cumulative incidence that is expected under the null distribution for the observed cumulative incidence. The reshuffling process is repeated k times to produce the null distribution of the observed cumulative incidence. If less than 5% of the k cumulative incidence values obtained via the permutation mechanism are greater than the observed cumulative incidence, the partition is declared to have a statistically significant increase in cumulative incidence.
Initially, we tested the first partition using the method outlined above (all available observations are considered exchangeable). In Figure 1, this corresponds to the total N observations. If the cumulative incidence of the first observed partition is declared significant, all of the individuals that are members of partition 1 are removed from the data set for testing the significance of the cumulative incidence associated with the second partition. This reduced data set (the N–n1 individuals not a member of partition 1 from Fig. 1) is then used to generate a null distribution to determine whether the cumulative incidence for the original second partition is statistically significant. Sequential testing is continued, excluding individuals in this fashion at each step, until a partition is declared not significant. The individuals from that partition and all subsequent partitions are included in a remainder partition.
Stepwise PRIM algorithm.
To test the added value of including additional variables in the model for predicting IHD, a stepwise PRIM analysis was employed. For the first step in the analysis, the traditional risk factors, smoking, hypertension, diabetes, gender and age, were used to build PRIM models. At the second step, each of the resultant partitions was split up into partitions using the PRIM and the lipid and BMI variables. The third step in the analysis used the genetic risk factors to determine their ability to define significant partitions within each of the partitions defined by the traditional, lipid and BMI risk factors in the first two stepwise applications of PRIM.
RESULTS
Summary statistics for data collected at the time of the third recruitment on the sample of 5,455 individuals who were enrolled during the first recruitment phase (1976−1978) of the CCHS and used to build the partitions is given in Table I. Five hundred nineteen (9.5%) developed IHD during the 8 year follow-up period from 1991−1994 through the end of 1999. To determine which predictors were associated with IHD, a χ2 test or t-test was used for categorical or continuous predictors, respectively. Participants that developed IHD were significantly older (5.1 years) and more often male. Those with IHD had a significant excess of smokers, diabetics and hypertensives. There was no evidence for a statistically significant association between IHD status and any of the eight genetic variations considered.
TABLE I.
Characteristics of participants in the Copenhagen City Heart Study recruited in 1976−1978 and followed until December 31, 1999
| Covariate | With IHD (n = 519) | Without IHD (n = 4,936) |
|---|---|---|
| Traditional risk factors | ||
| Age at exam 3 (yrs, ± SD) | 70.2 (8.8) | 65.1 (9.2)*** |
| Gender | ||
| Female | 233 (0.45) | 2,964 (0.60)*** |
| Male | 286 (0.55) | 1,972 (0.40) |
| Smoking | ||
| No | 187 (0.36) | 2,157 (0.44)*** |
| Yes | 332 (0.64) | 2,779 (0.56) |
| Diabetes mellitus | ||
| No | 466 (0.90) | 4,704 (0.95)*** |
| Yes | 53 (0.10) | 232 (0.05) |
| Hypertension | ||
| No | 77 (0.15) | 1,448 (0.29)*** |
| Yes | 442 (0.85) | 3,488 (0.71) |
| Lipids and BMI | ||
| Cholesterol | ||
| ≤200 | 71 (0.14) | 651 (0.13) |
| (200,240) | 164 (0.32) | 1,665 (0.34) |
| >240 | 284 (0.55) | 2,620 (0.53) |
| HDL —C | ||
| <40 | 90 (0.17) | 536 (0.11)*** |
| ≥40 | 429 (0.83) | 4,400 (0.89) |
| Triglycerides | ||
| <150 | 231 (0.45) | 2,706 (0.55)*** |
| ≥150 | 288 (0.55) | 2,230 (0.45) |
| BMI | ||
| ≤25 | 188 (0.36) | 2,179 (0.44)** |
| (25,30) | 225 (0.43) | 1,957 (0.40) |
| >30 | 106 (0.20) | 800 (0.16) |
| Genetic risk factors | ||
| APOE −491A>T (E560) | ||
| AA | 364 (0.70) | 3,526 (0.71) |
| AT | 144 (0.28) | 1,290 (0.26) |
| TT | 11 (0.02) | 120 (0.03) |
| APOE −427T>C (E624) | ||
| TT | 427 (0.82) | 3,946 (0.80) |
| TC | 87 (0.17) | 931 (0.19) |
| CC | 5 (0.01) | 59 (0.01) |
| APOE −219G>T (E832) | ||
| GG | 135 (0.26) | 1,404 (0.28) |
| GT | 274 (0.53) | 2,451 (0.50) |
| TT | 110 (0.21) | 1,081 (0.22) |
| APOE g.2059T>C (E3937) | ||
| TT | 364 (0.70) | 3,429 (0.69) |
| TC | 141 (0.27) | 1,375 (0.28) |
| CC | 14 (0.03) | 132 (0.03) |
| APOE g.2197C>T (E4075) | ||
| CC | 446 (0.86) | 4,151 (0.84) |
| CT | 68 (0.13) | 762 (0.15) |
| TT | 5 (0.01) | 23 (0.01) |
| LPL g.8756G>A (LPL9) | ||
| GG | 504 (0.97) | 4,803 (0.97) |
| GA | 15 (0.03) | 133 (0.03) |
| LPL g.16577A>G (LPL291) | ||
| AA | 489 (0.95) | 4,689 (0.95) |
| AG | 30 (0.05) | 245 (0.05) |
| GG | 2 (0.00) | |
| LPL g.22772C>G (LPL447) | ||
| CC | 424 (0.82) | 4,016 (0.81) |
| CG | 90 (0.17) | 868 (0.18) |
| GG | 5 (0.01) | 52 (0.01) |
All exonic sites in APOE and LPL are named according to human mutation nomenclature (Den Dunnen and Antonarakis, 2001). To correspond with well established literature names of promoter variants in APOE, nucleotide numbering is counted from transcriptional start site. The name in the parenthesises is shorthand notation used throughout the paper. The combination of the E3937 and E4075 SNPs represents the traditional three-allelic [ε2, ε3, ε4] APOE polymorphism.
Significant at 0.001 level of probability;
Significant at 0.01 level of probability.
For each of the PRIM models, the complexity parameter was set at zero and the support parameter was chosen from the results of the analyses presented in Figure 2 that were obtained in carrying out the algorithm described above. For each permutation test performed for every step in the analysis, the number of permuted samples, k, was 2,000. Utilizing a Dell High Performance Computing Cluster (62 nodes, 124 processors), the three step PRIM algorithm took 12 hours to complete. Figure 3 displays in a tree diagram the statistically significant partitions that resulted from the completion of the three steps of the analysis. Table II provides the description of the terms that defined each partition at each of the three steps.
Fig. 2.
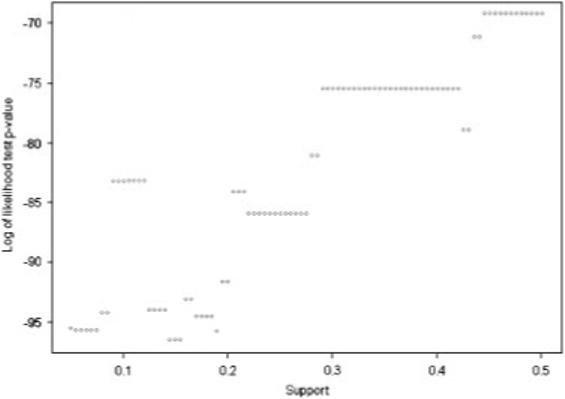
This plot is used to determine the support parameter used in the PRIM model of the variables in the first step (traditional risk factors). The support which achieves the smallest p-value is then used as the support parameter in the model for that step. This methodology is used to select the support parameter for each of the PRIM models constructed.
Fig. 3.
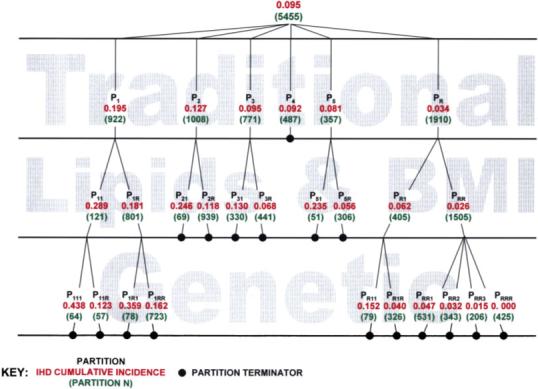
This is a tree-based graphical representation of the PRIM models used in this paper. Details on the variables and values used to define each partition are displayed in Table II. In this figure, the black text is the partition label; the red number below it is the cumulative incidence of IHD within that partition; and the green number in parenthesis below that is the sample size within that partition.
TABLE II.
Statistically significant partitions from 3 step PRIM analysis
| Partition label | Traditional IHD risk factor terms | Partition label | Lipids and BMI IHD risk factor terms | Partition label | Genetic IHD risk factor terms |
|---|---|---|---|---|---|
| P1 | >65 & male & hypertensive | P11 | HDL<40 & TRIG>150 & CHOL>200 | P111 | (E3937≠TC & E4075≠CT & E624≠TC & LPL291≠AG) or E560 = TT |
| P11R | not P111 | ||||
| P1R | not P11 | P1R1 | (E4075≠CT & E560≠AT & E624 = TC & LPL9≠GA) or E4075 = TT | ||
| P1RR | not P1R1 | ||||
| P2 | (>65 & female & smoker) or diabetic | P21 | HDL<40 & CHOL≠(200,240) | ||
| P2R | not P21 | ||||
| P3 | >65 & hypertensive & female & non-smoker & non-diabetic | P31 | (TRIG>150 & CHOL≠(200,240)) or CHOL<200 | ||
| P3R | not P31 | ||||
| P4 | <65 & male & smoker & hypertensive & nondiabetic | ||||
| P5 | Male & non-hypertensive & smoker & non-diabetic | P51 | (HDL<40 & CHOL<240) or BMI>30 | ||
| P5R | not P51 | ||||
| PR | Not P1-P5 | PR1 | BMI>25 & TRIG>150 & HDL>40 & CHOL>200 | PR11 | (E3937 = TC & E624≠TC & LPL291≠AG & LPL447≠CG) or E624 = CC |
| PR1R | not PR11 | ||||
| PRR | not PR1 | PRR1 | (E3937 = TT & E560≠AT & E624 = TT & LPL291≠AG) or LPL9 = GA | ||
| PRR2 | E3937≠TT & E560≠TT & E624≠CC & E832≠GG & LPL447 = CC | ||||
| PRR3 | E3937≠CC & E4075≠CT & E624 = TT & E832≠GG & LPL291≠AG & LPL447≠GG | ||||
| PRRR | not PRR1-PRR3 |
The resultant terms of the partitions from the 3 step analysis of the CCHS data are shown. The `partition label' columns correspond to those in Figure 3, with the respective terms listed in the column to the right. An `&' symbol represents an additional peeling term added to a partition, while an `or' represents a pasting term. The symbols `=', `>', `<', `≠' represent logical expression relating a predictor and its chosen values. For the remainder partitions, those with an `R' in the partition label, a `not' expression is used to illustrate that individuals in that partition are those not a member of the ones listed. The table should be read across, such that if an individual is in partition 111 if they also fulfill the requirements of partitions 1 and 11.
STEP 1 ANALYSES
The traditional risk factors were used to build a PRIM model on the entire data set of 5,455 individuals. Using the likelihood approach described above, 0.145 was chosen as the optimum support parameter (see Fig. 2). The second column in Table II displays the terms of the traditional risk factors that define each of the five statistically significant partitions. The cumulative incidence of IHD in these partitions ranged from 0.034 to 0.195 (Fig. 3). Eighty-eight percent of the cases placed into one of the five significant partitions. The first partition (hypertensive males, older than 65 years) had the largest cumulative incidence of 0.195, over twice the estimated cumulative incidence (0.095) for the population at large. The second partition (smoking females, older than 65 years or diabetic) had a cumulative incidence of 0.127 compared to 0.075 in the remaining sample after exclusion of individuals included in the first partition. The third partition (hypertensive, non-smoking and non-diabetic females, older than 65 years) had a cumulative incidence of 0.095 compared to 0.060 in the remaining sample after exclusion of the individuals included in the first and second partitions. The fourth partition (smoking, hypertensive and non-diabetic males, 65 years or younger) had a cumulative incidence of 0.092 compared to a cumulative incidence of 0.050 in the remaining sample after excluding those included in the first three partitions. The fifth partition (non-hypertensive, smoking and non-diabetic males) had a cumulative incidence of 0.081 compared to 0.041 in the remaining sample after excluding those in the first four partitions. The remainder partition had a cumulative incidence of 0.034 (Table II, Figure 3).
STEP 2 ANALYSES
A PRIM analysis was next performed on each of the six partitions (P1, P2, P3, P4, P5 and PR) produced by the analysis carried out in step 1 using the three lipid traits and BMI. Five of the six PRIM models (partitions P1, P2, P3, P5 and PR) produced further partitioning. These partitions are defined by the terms displayed in the fourth column of Table II. The selected support parameters for the sub-partitioning of partitions P1, P2, P3, P5 and PR were 0.130, 0.055, 0.350, 0.085 and 0.145, respectively. The cumulative incidences of the partitions defined by the second step of PRIM analyses ranged from 0.026 to 0.289. The terms used to partition the individuals from partition 1 were high TRIG, high CHOL and low HDL. The other partitions in this step were defined primarily by a variety of terms defined by the lipid variables.
STEP 3 ANALYSES
Next we used the genetic predictors to further partition each of the eleven partitions produced by the first two steps, P11, P1R, P21, P2R, P31, P3R, P4, P51, P5R, PR1 and PRR. Only 4 of the 11 step 2 partitions could be further partitioned using the genetics risk factors. The last column in Table II presents the terms that partitioned P11, P1R, PR1 and PRR using 0.455, 0.085, 0.180 and 0.325 as the selected support parameters, respectively. At least one term from each of the eight SNPs appeared in a minimum of one of these sub-partitions. The addition of the genetic risk factors identified a group of 425 individuals that had no observed IHD cases. The highest cumulative incidence observed after this third step in the analysis (0.438) resulted from a further partitioning of the P11 group, in part distinguished by the E3937 and E4075 SNPs that define the well-known ε2, ε3 and ε4 alleles of the APOE gene.
VALIDATION OF THE PARTITION MODELS
Assignment of risk to new individuals from the population of inference is done in a sequential fashion. That is, an individual is evaluated to determine whether they fall into the first partition of step 1 (i.e., hypertensive male, older than 65). If that individual is not a member of the first partition, (s)he is evaluated to determine whether (s)he belongs to the second partition established by the step 1 analyses (i.e., female smoker, older than 65 or diabetic). One continues in this manner for each individual until (s)he is assigned to a step 1 partition. The sequential nature of the assignment assures that each new individual is assigned to only one of the partitions at step 1. Then, given the step 1 partition assignments of all individuals, one considers assignment of each individual to a step 2 partition. Therefore, if a person was assigned any partition except P4 in step 1, a refined assignment including the step 2 predictors commences. Once the step 2 assignment has completed, one proceeds (if necessary) with step 3 assignments of all individuals to a terminal partition. Table III displays the predictions on the validation set of 362 individuals, enrolled into the CCHS during the second recruitment period. In spite of the limited size of this validation sample, which makes it difficult to definitively assess the PRIM models, the predicted number of individuals estimated to develop IHD is a close approximation of the actual number. Notable exceptions include partition PRRR which had an estimated risk of 0.000 (no cases of IHD in the sample used for model-building), but had two IHD cases in the validation sample. This discrepancy is most likely due to overfitting of the models to the model-building data set.
TABLE III.
Estimated IHD risk for participants entering CCHS during the 2nd recruitment period (1981−1983)
| Partition label | Estimated risk | Number of individuals | Estimated number of individuals developing IHD | Developed IHD (as of 31 DEC 1999) |
|---|---|---|---|---|
| P111 | 0.438 | 0 | 0 | 0 |
| P11R | 0.123 | 3 | 0 | 0 |
| P1R1 | 0.359 | 2 | 1 | 0 |
| P1RR | 0.162 | 44 | 7 | 7 |
| P21 | 0.246 | 8 | 2 | 4 |
| P2R | 0.118 | 51 | 6 | 9 |
| P31 | 0.130 | 4 | 1 | 1 |
| P3R | 0.068 | 16 | 1 | 0 |
| P4 | 0.092 | 45 | 4 | 6 |
| P51 | 0.235 | 9 | 2 | 0 |
| P5R | 0.056 | 38 | 2 | 2 |
| PR11 | 0.152 | 5 | 1 | 0 |
| PR1R | 0.040 | 33 | 1 | 1 |
| PRR1 | 0.047 | 46 | 2 | 3 |
| PRR2 | 0.032 | 17 | 1 | 1 |
| PRR3 | 0.015 | 9 | 0 | 0 |
| PRRR | 0.000 | 32 | 0 | 2 |
DISCUSSION
ANALYTICAL STRATEGIES
PRIM was introduced by Friedman and Fisher [1999] as an alternative to the greedy classification strategy implemented by the Classification and Regression Trees (CART) algorithm. PRIM mimics CART by applying simple Boolean rules to assign each individual to a partition of individuals with the same values of predictor variables. A direct comparison of the two methods is complicated by the differences in the parameters that define the rules for model fitting. Friedman and Fisher [1999] compared the two techniques by selecting optimal partitions from CART and finding PRIM partitions of approximately the same number and concluded that PRIM “exhibits performance superior to comparable procedures such as CART.” PRIM results in a lower deviance than CART for the same number of prediction classes for the data analyzed in our study. A tree grown until six prediction classes was reached for the CART analysis, resulting in a deviance of 3,239 compared to 3,222 from the PRIM analysis. PRIM should produce better predictive models than CART since it allows high risk individuals that were discarded at an earlier peeling operation to be pasted into a partition while permitting the user to control the “patience” or “greed” of the classification.
Our study is not the first to apply the PRIM to the analysis of medical data. However, it is the first application to the analysis of predictors of IHD. LeBlanc et al. [2002] developed a modified PRIM that was constrained to produce partition terms monotonically. That is, each produced partition term includes only one extreme of a continuously distributed or ordered categorical predictor variable. However, because their algorithm uses only continuous and ordered categorical variables as predictors, it excludes the consideration of genetic data since either an order or a numerical value would have to be assigned to a genotype class (both untenable, especially for the APOE genotype). Cole et al. [2003] used PRIM to detect genes that were differentially expressed while controlling the amount of false-negative errors. This method focused on the ratio of, and difference between, expressions of each gene in two conditions and did not include measures of SNP variation for the individuals under study. Yu et al. [2004] used the peeling and pasting procedures from PRIM as a part of the gene shaving method [Hastie et al., 2000] to identify haplotypes that are most likely to share a common ancestor.
Logistic regression is a standard analytical tool for testing the added value of the genetic effects for the prediction of IHD. To demonstrate the improvement gained by utilizing a PRIM analysis, a logistic regression analysis produced by following conventional methods was performed. Initially all nine of the non-genetic covariates introduced above and all of their possible pair-wise interactions were used as regressors in a logistic regression model for predicting IHD. The application of a backward elimination variable selection procedure resulted in the retention of the eight covariate effects and four pair-wise interactions between covariates presented in Table IV. Each of the eight SNPs under study were then tested to determine if it alone explained a statistically significant amount of variation beyond the covariates-only model. The results in Table V illustrate that none of the SNPs would have been deemed a significant predictor of IHD beyond the traditional risk factors. Our finding that the APOE gene does not improve the prediction of disease beyond traditional risk factors is supported by a recent study by Volcik et al. [2006]. While the logistic regression analysis establishes that the effect of each SNP may not be significant in the sample representative of the population at large, PRIM reveals that there are significant genotypic effects on risk of disease in particular sub-samples of such a sample. The key difference is that traditional analyses seek to develop a single prediction model for making inferences about genetic effects that are applicable to every individual in the population of inference under study, while the PRIM facilitates separate models of inferences about genetic effects that are appropriate for sub-populations of individuals.
TABLE IV.
ANOVA of significant main effects and interactions using logistic regression to predict IHD
| Covariate | df | χ2 statistic | p-value |
|---|---|---|---|
| BMI | 2 | 13.4 | 0.001 |
| Gender | 1 | 39.9 | 0.000 |
| Diabetes | 1 | 14.7 | 0.000 |
| Smoking | 1 | 9.3 | 0.002 |
| Hypertension | 1 | 42.3 | 0.000 |
| Cholesterol | 2 | 2.4 | 0.299 |
| Triglycerides | 1 | 5.1 | 0.024 |
| Age | 1 | 95.7 | 0.000 |
| BMI × Smoking | 2 | 8.1 | 0.017 |
| Gender × Cholesterol | 2 | 6.9 | 0.033 |
| Diabetes × Age | 1 | 6.9 | 0.008 |
| Smoking × Hypertension | 1 | 5.4 | 0.020 |
All marginal effects and their potential two-way interactions were tested.
TABLE V.
Tests of significance of SNP effects after inclusion of statistically significant traditional risk factors from Table IV
| SNP | df | χ2 statistic | p-value |
|---|---|---|---|
| LPL9 | 1 | 0.264 | 0.607 |
| LPL291 | 2 | 0.497 | 0.780 |
| LPL447 | 2 | 0.011 | 0.995 |
| E560 | 2 | 0.412 | 0.814 |
| E624 | 2 | 2.075 | 0.354 |
| E832 | 2 | 3.202 | 0.202 |
| E3937 | 2 | 0.172 | 0.918 |
| E4075 | 2 | 4.684 | 0.096 |
| ε2, ε3, ε4 | 5 | 5.247 | 0.386 |
The models produced in this analysis appear to predict well and were validated in a small independent sample from the CCHS. Validation of any model (or models) can only be produced using an independent sample from the same population of inference. Replication of these (or any) validated models built using observational human data is unachievable because it would require a replicate sample. Such a sample is impossible to obtain because it would require that the individuals in the new sample be drawn from a population of inference having the same relative allele and genotype frequencies and life histories of environmental exposures as the original population.
BIOLOGICAL-ETIOLOGICAL IMPLICATIONS
The literature is replete with studies which implicate high risk alterations of hundreds of the agents involved in the etiology of the onset, progression and severity of IHD [Lusis, 2006; Sing et al., 2003]. All cases of IHD cannot have experienced all of these high risk variations. The PRIM does not assume that every individual with disease has the same etiology, but addresses the question of which alterations in which risk factors are involved in predicting disease in which subset of individuals. In our study, PRIM partitioned the participants of the CCHS into 16 subsets of individuals with statistically significant (higher than expected by chance alone) risks. The acknowledged heterogeneity of the etiology of IHD is documented by the different combinations of predictors and predictor values that characterize these different partitions. As might be expected, when considering non-genetic risk factors only, older hypertensive males with low HDL and elevated total cholesterol and triglycerides have the greatest risk of IHD (cumulative incidence = 0.289, n = 121, steps 1 and 2, P11 in Fig. 3 and Table II). Adding information about the APOE and LPL genotypes increased the risk to 0.438 (n = 64, P111 in Fig. 3 and Table II) for a subset of this high risk group. Individuals in this subgroup are four times more likely to have IHD than individuals who are randomly selected from the population at large (cumulative incidence = 0.095).
Because of the involvement of the APOE and LPL gene products in regulating lipid metabolism, they are a priori assumed to likely have a significant impact on the prediction of IHD. However, the added value of measuring the eight single site APOE and LPL genotypic variations in the third stage of the stepwise PRIM analysis did not improve prediction in all partitions. This finding is consistent with our previous work [Reilly et al., 1991; Kardia et al., 1999; Lussier-Cacan et al., 2002; Zerba et al., 2000] which documented the context dependency of the APOE genotype effects on measures of lipid metabolism. It is also consistent with the argument that interactions between genetic and environmental agents, not their separate independent effects, are the primary causes of variability in traits that have a complex multifactorial etiology.
MEDICAL RELEVANCE
There is a long-standing controversy between those who advocate a rational, evidence based single risk factor model strategy for making recommendations that aims at improving health at the population level and those who face the everyday experience in medical practice that recognizes the uniqueness of patients who rarely fit into average risk groups defined from population studies. Genetic information is most often regarded to be of importance for evaluating the health of the population if it has an independent “causal” effect on a disease phenotype at the population level [Smith et al., 2006]. This assumption is seldom likely to be true as environmental context, indexed by variables such as age, gender, and body size, nearly always plays a role in determining the influence of genetic variation on measures of health that have a complex multifactorial etiology. As an alternative to population-based single model risk stratification schemes [Conroy et al., 2003; Anderson et al., 1990] and population-based marginal genetic effects [Smith et al., 2006], the PRIM makes possible a more personalized risk prediction strategy that incorporates both rare and common environmental and genetic risk factors, an objective that has been the goal of medical genetics in particular, and clinical practice in general.
In a time of limited health care resources, it is of greatest importance to identify the subsets of individuals with specific high risk combinations of environmental, biochemical and genetic markers that would benefit the most from intensified prevention and medical treatment. The common single model approach assumes that all cases of a disease having a complex multifactorial etiology in the reference population have a similar etiology [Conroy et al., 2003]. However, a large patient group will harbor extensive environmental and genetic heterogeneity [Sing et al., 2003] that is not likely to be captured with the application of a single statistical model derived from the average effects of risk factors. The models shown in Table II demonstrate that not all risk factors are predictors of IHD in all subsets of individuals. PRIM constructs models with subsets of predictor variables that are appropriate for subsets of individuals. The resultant partitions illustrate that the eight genetic variants under study contribute to the prediction of IHD only in particular subgroups of individuals defined by the traditional and established risk factors. In particular, individuals from the initial high risk (P1, cumulative incidence = 0.195) and low risk (PR, cumulative incidence = 0.034) partitions may be partitioned into ten subgroups with cumulative incidences ranging from 0.162 to 0.438 and 0.000−0.152, respectively. We suggest that the PRIM serves as a compromise between a single model of risk prediction for an average individual and individualized risk prediction models that presently are not quantifiable and result in unacceptable implementation costs for most health care systems. Furthermore, the stepwise application of PRIM that we present here mimics a physician's logic through the diagnostic process and can be easily converted into user friendly software applications.
Through the pasting process of PRIM, rare alleles or infrequent risk factors, such as diabetes in the CCHS, are included in the definition of the partitions, while other classification and regression techniques (including CART) do not have this capability. This feature is of high value in clinical practice because valid risk estimates for rare conditions in the general population are lacking. Only a few studies have been large enough to obtain odds or hazard ratio estimates for IHD for rare genetic variants [Nordestgaard et al., 1997; Tybærg-Hansen et al., 1998, 2005; Frikke-Schmidt et al., 2005; Cohen et al., 2006]. The SCORE project, which provides risk score algorithms for primary prevention [Conroy et al., 2003], does not include diabetes in the algorithm because it is infrequent, but instead assigns diabetes patients to higher risk age and gender groups.
Despite major influences on quantitative variation in lipid traits, and despite involvement in severe forms of dyslipidemia such as type III hyperlipoproteinemia [Mahley and Rall, 2001] and the chylomicronemia syndrome [Brunzell and Deeb, 2001], the marginal effects on IHD risk of genotypes defined by individual SNPs in APOE and LPL have been subtle [Song et al., 2004; Wittrup et al., 1999b]. Because these variations confer only minor marginal risk predictions at the population level compared to major traditional risk factors, these SNPs have not found their way into clinical practice. Our study suggests that an analytical strategy that acknowledges the genetic and environmental heterogeneity in the etiology of cardiovascular disease can identify subgroups of the population where genetic testing for the common variants in APOE and LPL could increase the ability to predict IHD markedly. Using such information could lead to a more efficient allocation of limited resources for diagnosis and treatment of IHD by targeting of intensified prevention and treatment towards those subsets with significantly higher risk, while not wasting precious resources on those subsets of individuals with significantly low IHD risk.
ACKNOWLEDGMENTS
We wish to thank Mette Refstrup, Pia T. Petersen, and Hanne Damm for expert technical assistance and Kenneth G. Weiss for his dedicated attention to the details of the data management and the two anonymous reviewers whose comments helped us to greatly improve the clarity of the manuscript.
Contract grant sponsors: Chief Physician Johan Boserup and Lise Boserup's Fund; The Danish Heart Foundation; The Danish Medical Research Council; Ingeborg and Leo Dannin's Grant; The Research Fund at Rigshospitalet; Copenhagen University Hospital, National Heart, Lung and Blood Institute; Contract grant number: HL072905; Contract grant sponsor: National Institute of General Medical Science grant; Contract grant number: GM065509.
REFERENCES
- Anderson KM, Odell PM, Wilson PWF, Kannel WB. Cardiovascular disease risk profiles. Am Heart J. 1990;121:293–298. doi: 10.1016/0002-8703(91)90861-b. [DOI] [PubMed] [Google Scholar]
- Brunzell JD, Deeb SS. Familial lipoprotein lipase deficiency, apoC-II deficiency, and hepatic lipase deficiency. In: Scriver CR, Beaudet AL, Sly S, Valle D, editors. The Metabolic and Molecular Bases of Inherited Disease. 8th edition McGraw-Hill; New York: 2001. pp. 2789–2816. [Google Scholar]
- Cleeman JI, Grundy SM, Becker D, Clark LT, Cooper RS, Denke MA, Howard WJ, Hunninghake DB, Illingworth DR, Luepker RV, McBride P, McKenney JM, Pasternak RC, Stone NJ, Van Horn L, Brewer HB, Ernst ND, Gordon D, Levy D, Rifkind B, Rossouw JE, Savage P, Haffner SM, Orioff DG, Proschan MA, Schwartz JS, Sempos CT, Shero ST, Murray EZ. Executive summary of the Third Report of the National Cholesterol Education Program (NCEP) expert panel on detection, evaluation, and treatment of high blood cholesterol in adults (Adult Treatment Panel III). Jama-J Am Med Assoc. 2001;285:2486–2497. doi: 10.1001/jama.285.19.2486. [DOI] [PubMed] [Google Scholar]
- Cohen JC, Boerwinkle E, Mosley TH, Jr, Hobbs HH. Sequence variations in PCSK9 low LDL and protection against coronary heart disease. New Engl J Med. 2006;12:1264–1272. doi: 10.1056/NEJMoa054013. [DOI] [PubMed] [Google Scholar]
- Cole SW, Galic Z, Zack JA. Controlling false-negative errors in microarray differential expression analysis: a PRIM approach. Bioinformatics. 2003;19:1808–1816. doi: 10.1093/bioinformatics/btg242. [DOI] [PubMed] [Google Scholar]
- Conroy RM, Pyörälä K, Fitzgerald AP, Sans S, Menotti A, De Backer G, De Bacquer D, Ducimetiere P, Jousilahti P, Keil U, Njølstad I, Oganov RG, Thomsen T, Tunstall-Pedoe H, Tverdal A, Wedel H, Whincup P, Wilhelmsen L, Graham IM. Estimation of ten-year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J. 2003;24:987–1003. doi: 10.1016/s0195-668x(03)00114-3. [DOI] [PubMed] [Google Scholar]
- Davignon J, Gregg RE, Sing CF. Apolipoprotein E polymorphism and atherosclerosis. Arteriosclerosis. 1998;8:1–21. doi: 10.1161/01.atv.8.1.1. [DOI] [PubMed] [Google Scholar]
- Den Dunnen JT, Antonarakis SE. Nomenclature for the description of human sequence variations. Hum Genet. 2001;109:121–124. doi: 10.1007/s004390100505. [DOI] [PubMed] [Google Scholar]
- Donato KA, Pi-Sunyer FX, Becker DM, Bouchard C, Carleton RA, Colditz GA, Dietz WH, Foreyt JP, Garrison RJ, Grundy SM, Hansen BC, Higgins M, Hill JO, Howard BV, Kuczmarski RJ, Kumanyika S, Legako RD, Prewitt TE, Rocchini AP, Snetselaar LG, Weintraub M, Williamson DF, Wilson GT, Brown CD, Ernst N, Hill DR, Horan MJ, Kiley JP, Obarzanck E, Hubbard VS, Schriger D, Chiquette E. Executive summary of the clinical guidelines on the identification, evaluation, and treatment of overweight and obesity in adults. Arch Intern Med. 1998;158:1855–1867. doi: 10.1001/archinte.158.17.1855. [DOI] [PubMed] [Google Scholar]
- Friedman JH, Fisher NI. Bump hunting in high-dimensional data. Stat Comput. 1999;9:123–143. [Google Scholar]
- Frikke-Schmidt R, Nordestgaard BG, Agerholm-Larsen B, Schnohr P, Tybjærg-Hansen A. Context dependent and invariant associations between lipids lipoproteins and apolipoproteins and apolipoprotein E genotype. J Lipid Res. 2000a;41:1812–1822. [PubMed] [Google Scholar]
- Frikke-Schmidt R, Tybjærg-Hansen A, Steffensen R, Jensen G, Nordestgaard BG. Apolipoprotein E genotype: epsilon32 women are protected while epsilon43 and epsilon44 men are susceptible to ischemic heart disease. The Copenhagen City Heart Study. J Am Coll Cardiol. 2000b;35:1192–1199. doi: 10.1016/s0735-1097(00)00520-9. [DOI] [PubMed] [Google Scholar]
- Frikke-Schmidt R, Nordestgaard BG, Schnohr P, Steffensen R, Tybjærg-Hansen A. Mutation in ABCA1 predicted risk of ischemic heart disease in the Copenhagen City Heart Study population. J Am Coll Cardiol. 2005;46:1516–1520. doi: 10.1016/j.jacc.2005.06.066. [DOI] [PubMed] [Google Scholar]
- Frikke-Schmidt R, Sing CF, Nordestgaard BG, Steffensen R, Tybjærg-Hansen A. Subsets of SNPs define rare genotype classes that predict ischemic heart disease. Hum Genet. 2007;120:865–877. doi: 10.1007/s00439-006-0233-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R, Eisen M, Ross D, Scherf U, Weinstein J, Alizadeh A, Staudt L, Botstein D, Brown P. ‘Gene shaving’ as a method for identifying distinct sets of genes with similar expression patterns. Genome Biol. 2000;1:00031–000321. doi: 10.1186/gb-2000-1-2-research0003. research. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Julian DG, Bertrand ME, Hjalmarson A, Fox K, Simoons ML, Ceremuzynski L, Maseri A, Meinertz T, Meyer J, Pyorala K. Management of stable angina pectoris—Recommendations of the Task Force of the European Society of Cardiology. Eur Heart J. 1997;18:394–413. doi: 10.1093/oxfordjournals.eurheartj.a015259. others. [DOI] [PubMed] [Google Scholar]
- Kardia SLR, Haviland MB, Ferrell RE, Sing CF. The relationship between risk factor levels and presence of coronary artery calcification is dependent on Apolipoprotein E genotype. Arterioscler Thromb Vasc Biol. 1999;19:427–435. doi: 10.1161/01.atv.19.2.427. [DOI] [PubMed] [Google Scholar]
- LeBlanc M, Jacobson J, Crowley J. Partitioning and peeling for constructing prognostic groups. Stat Methods Med Res. 2002;11:247–274. doi: 10.1191/0962280202sm286ra. [DOI] [PubMed] [Google Scholar]
- Lusis AJ. A thematic review series: systems biology approaches to metabolic and cardiovascular disorders. J Lipid Res. 2006;47:1887–1890. doi: 10.1194/jlr.E600004-JLR200. [DOI] [PubMed] [Google Scholar]
- Lussier-Cacan S, Bolduc A, Xhignesse M, Niyonsenga T, Sing CF. Impact of alcohol intake on measures of lipid metabolism depends on context defined by gender, body mass index, cigarette smoking, and Apolipoprotein E genotype. Arterioscler Thromb Vasc Biol. 2002;22:824–831. doi: 10.1161/01.atv.0000014589.22121.6c. [DOI] [PubMed] [Google Scholar]
- Mahley RW, Palaoglu KE, Atak Z, Dawsonpepin J, Langlois AM, Cheung V, Onat H, Fulks P, Mahley LL, Vakar F, Ozbayrakci S, Gokdemir O, Winkler W. Turkish Heart Study: lipids lipoproteins and apolipoproteins. J Lipid Res. 1995;36:839–859. [PubMed] [Google Scholar]
- Mahley RW, Rall SC. Type III Hyperlipoproteinemia Dysbetalipoproteinemia: the Role of Apolipoprotein E in Normal and Abnormal Lipoprotein Metabolism. In: Scriver CR, Beaudet AL, Sly S, Valle D, editors. The Metabolic and Molecular Bases of Inherited Disease. 8th edition McGraw-Hill; New York: 2001. pp. 2835–2862. [Google Scholar]
- Murray CJL, Lopez AD. Mortality by cause for eight regions of the world: Global Burden of Disease Study. Lancet. 1997;349:1269–1276. doi: 10.1016/S0140-6736(96)07493-4. [DOI] [PubMed] [Google Scholar]
- Nordestgaard BG, Abildgaard S, Wittrup HH, Steffensen R, Jensen G, Tybjærg-Hansen A. Heterozygous lipoprotein lipase deficiency: frequency in the general population effect on plasma lipid levels and risk of ischemic heart disease. Circulation. 1997;96:1737–1744. doi: 10.1161/01.cir.96.6.1737. [DOI] [PubMed] [Google Scholar]
- Reilly SL, Ferrell RE, Kottke BA, Kamboh MI, Sing CF. The gender-specific apolipoprotein E genotype influence on the distribution of lipids and apolipoproteins in the population of Rochester MN I Pleiotropic effects on means and variances. Am J Hum Genet. 1991;49:1155–1166. [PMC free article] [PubMed] [Google Scholar]
- Schnohr P, Jensen G, Lange P, Scharling H, Appleyard M. The Copenhagen City heart study—Introduction. Eur Heart J Suppl. 2001;3:H1–H83. [Google Scholar]
- Schnohr P, Jensen JS, Scharling H, Nordestgaard BG. Coronary heart disease risk factors ranked by importance for the individual and community. A 21 year follow-up of 12000 men and women from The Copenhagen City Heart Study. Eur Heart J. 2002;23:620–626. doi: 10.1053/euhj.2001.2842. [DOI] [PubMed] [Google Scholar]
- Sing CF, Stengard JH, Kardia SL. Genes Environment and Cardiovascular Disease. Arterioscler Thromb Vasc Biol. 2003;23:1190–1196. doi: 10.1161/01.ATV.0000075081.51227.86. [DOI] [PubMed] [Google Scholar]
- Smith GD, Gwinn M, Ebrahim S, Palmer LJ, Khoury MJ. Make it HuGE: human genome epidemiology reviews population health and the IJE. Int J Epidemiol. 2006;35:507–510. doi: 10.1093/ije/dyl071. [DOI] [PubMed] [Google Scholar]
- Song Y, Stampfer MJ, Liu S. Meta-Analysis: Apolipoprotein E Genotypes and Risk for Coronary Heart Disease. Ann Intern Med. 2004;141:137–147. doi: 10.7326/0003-4819-141-2-200407200-00013. [DOI] [PubMed] [Google Scholar]
- Tybjærg-Hansen A, Jensen HK, Benn M, Steffensen R, Jensen G, Nordestgaard BG. Phenotype of heterozygotes for low-density lipoprotein receptor mutations identified in different background populations. Arterioscler Thromb Vasc Biol. 2005;25:211–215. doi: 10.1161/01.ATV.0000149380.94984.f0. [DOI] [PubMed] [Google Scholar]
- Tybjærg-Hansen A, Steffensen R, Meinertz H, Schnohr P, Nordestgaard BG. Association of mutations in the apolipoprotein B gene with hypercholesterolemia and the risk of ischemic heart disease. New Eng J Med. 1998;338:1577–1584. doi: 10.1056/NEJM199805283382203. [DOI] [PubMed] [Google Scholar]
- Volcik KA, Barkley RA, Hutchinson RG, Mosley TH, Heiss G, Sharrett AR, Ballantyne CM, Boerwinkle E. Apolipoprotein E polymorphisms predict low density lipoprotein cholesterol levels and carotid artery wall thickness but not incident coronary heart disease in 12,491 ARIC study participants. Am J Epidemiol. 2006;164:342–348. doi: 10.1093/aje/kwj202. [DOI] [PubMed] [Google Scholar]
- Wittrup HH, Tybjærg-Hansen A, Abildgaard S, Steffensen R, Schnohr P, Nordestgaard BG. A common substitution (Asn291Ser) in lipoprotein lipase is associated with increased risk of ischemic heart disease. J Clin Invest. 1997;99:1606–1613. doi: 10.1172/JCI119323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wittrup HH, Tybjærg-Hansen A, Steffensen R, Deeb SS, Brunzell JD, Jensen G, Nordestgaard BG. Mutations in the lipoprotein lipase gene associated with ischemic heart disease in men. The Copenhagen City Heart Study. Arterioscler Thromb Vasc Biol. 1999a;19:1535–1540. doi: 10.1161/01.atv.19.6.1535. [DOI] [PubMed] [Google Scholar]
- Wittrup HH, Tybjærg-Hansen A, Nordestgaard BG. Lipoprotein Lipase Mutations Plasma Lipids and Lipoproteins and Risk of Ischemic Heart Disease: a meta-analysis. Circulation. 1999b;99:2901–2907. doi: 10.1161/01.cir.99.22.2901. [DOI] [PubMed] [Google Scholar]
- Wittrup HH, Nordestgaard BG, Steffensen R, Jensen G, Tybjærg-Hansen A. Effect of gender on phenotypic expression of the S447X mutation in LPL: the Copenhagen City Heart Study. Atherosclerosis. 2002;165:119–126. doi: 10.1016/s0021-9150(02)00183-1. [DOI] [PubMed] [Google Scholar]
- Yu K, Martin RB, Whittemore AS. Classifying disease chromosomes arising from multiple founders with application to fine-scale haplotype mapping. Genet Epidemiol. 2004;27:173–181. doi: 10.1002/gepi.20016. [DOI] [PubMed] [Google Scholar]
- Zerba KE, Ferrell RE, Sing CF. Complex adaptive systems and human health: the influence of common genotypes of the apolipoprotein E (ApoE) gene polymorphism and age on the relational order within a field of lipid metabolism traits. Hum Genet. 2000;107:466–475. doi: 10.1007/s004390000394. [DOI] [PubMed] [Google Scholar]