Detecting signals of drug–drug interactions in a spontaneous reports database

Abstract

Aims

The spontaneous reports database is widely used for detecting signals of ADRs. We have extended the methodology to include the detection of signals of ADRs that are associated with drug–drug interactions (DDI). In particular, we have investigated two different statistical assumptions for detecting signals of DDI.

Methods

Using the FDA's spontaneous reports database, we investigated two models, a multiplicative and an additive model, to detect signals of DDI. We applied the models to four known DDIs (methotrexate-diclofenac and bone marrow depression, simvastatin-ciclosporin and myopathy, ketoconazole-terfenadine and torsades de pointes, and cisapride-erythromycin and torsades de pointes) and to four drug-event combinations where there is currently no evidence of a DDI (fexofenadine-ketoconazole and torsades de pointes, methotrexade-rofecoxib and bone marrow depression, fluvastatin-ciclosporin and myopathy, and cisapride-azithromycine and torsade de pointes) and estimated the measure of interaction on the two scales.

Results

The additive model correctly identified all four known DDIs by giving a statistically significant (P< 0.05) positive measure of interaction. The multiplicative model identified the first two of the known DDIs as having a statistically significant or borderline significant (P< 0.1) positive measure of interaction term, gave a nonsignificant positive trend for the third interaction (P= 0.27), and a negative trend for the last interaction. Both models correctly identified the four known non interactions by estimating a negative measure of interaction.

Conclusions

The spontaneous reports database is a valuable resource for detecting signals of DDIs. In particular, the additive model is more sensitive in detecting such signals. The multiplicative model may further help qualify the strength of the signal detected by the additive model.

Introduction

Drug–drug interactions (DDI) occur when one drug influences the effects of another drug. This may subsequently cause a change in the pharmacodynamic or pharmacokinetic parameters which may lead to lack of efficacy or increased efficacy, or to an increase or a decrease in the number of reported adverse drug reactions (ADRs). Usually, DDIs are investigated before entry into the market by traditional clinical studies investigating possible variations of pharmacokinetics; in postmarketing, drug–drug interactions are reported to spontaneous reporting systems for ADRs. However,drug–drug interactions, as such, are relatively rarely reported and information about the pharmacokinetics of the drug in the patient experiencing an AE due to a drug interaction is usually lacking.

For signal detection regarding possible unexpected ADRs, various measures of disproportionality can be used, including proportional reporting ratios (PRRs) [1]. The basic principle of looking for disproportionality can be extended to the detection of DDIs.

The objective of this investigation was to assess the ability of statistical models to detect DDI signals in a postmarketing setting.

Methods

Data

We used the FDA's Adverse Events Reporting System (AERS), which is a computerized information database designed to support the FDA's postmarketing safety surveillance program for all approved drugs and therapeutic biological products. The database comprises adverse drug reaction reports sent by the manufacturers as required by regulation. Health care professionals and consumers send reports voluntarily through the MedWatch program.

The database consists of approximately 3 million reports and over 5 million events reported on drugs. The drugs of interest have been identified using generic and trade names.

We used a commercially available software package to access the database. The data were extracted in 2003 and 2004.

Definitions

A signal can be defined as an excess reporting of an adverse reaction for a drug, which reaches statistical significance, compared with all other drugs.

A signal for a DDI occurs when the risk of an adverse reaction related to the exposure to one drug varies with exposure to another drug.

Model

We applied both a multiplicative and an additive model to generate signals of DDI. The multiplicative model assumed the risk associated with a drug multiplies with the background risk, whilst the additive model assumed the risk associated with a drug adds to the background risk. To our knowledge, such a comparison of both the models, has not been studied before in the context of signal generation of DDIs.

Formulation of methodology

Let risk_(A,B) denote the risk (e.g. incidence rate, odds of developing the event, or percentage of subjects developing a particular event) of an adverse reaction associated with the two drugs A and B when given concomitantly. Similarly, let risk_(A,notB) denote the risk associated with drug A only, risk_(notA,B) the risk with drug B only and, risk_(notA,notB) the risk in the absence of both A and B.

Multiplicative model

When there is no interaction on the multiplicative scale, the relative risk associated with drug A is the same in both the absence and presence of exposure to drug B. Formally,

This equality implies:

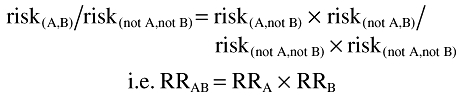where RR_A = risk_{(A,not B)}/risk_(notA,notB) is the relative risk associated with drug A in the absence of drug B and similarly for RR_B and RR_AB.

Under the assumption of no interaction, the relative risk associated with the drug combination is the same as the product of the relative risks associated with each drug in the absence of the other.

Thus if RR_AB/(RR_A × RR_B) is statistically different from 1, there is evidence of an interaction. In particular, whenever this measure is greater than 1, there is a positive interaction which is of interest from a safety perspective. In such a situation, the relative risk associated with two drugs administered in combination is greater than the product of the relative risks associated with each drug separately.

The formal statistical testing of the interaction term is achieved within the framework of log-linear regressions (e.g. logistic or Poisson regressions) [8]:

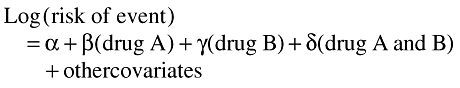Whenever, the coefficient δ is statistically significantly different from zero, there is evidence of an interaction. Values of δ greater than zero indicate a positive interaction, i.e. the risk of the event for the combination is greater than that predicted for the two drugs separately. Values of δ less than 0 indicate that the relative risk associated with the two drugs together is less than that predicted by the product of the relative risks for the two individual drugs. The exponential of δ, exp(δ), is the factor by which the relative risk associated with the combinations, A and B, exceeds that which is predicted by the product of A alone and B alone. We defined this term as the measure of interaction. When this measure of interaction is statistically significantly different (i.e. P < 0.05) from 1, there is evidence of an interaction. Whenever the term is significantly greater than 1, there is evidence of a positive interaction, that is, the relative risk for the combination is significantly greater than that predicted by the product of the relative risks for drug A alone and drug B alone.

Thus, values for exp(δ) statistically significantly greater than 1 indicate a positive measure of interaction in the multiplicative model.

Additive model

Under the additive assumption, no interaction is established when the excess risk associated with A in the absence of B is same as the excess risk associated with A in the presence of B:

This equality implies:

i.e. the excess risk associated with the combination is the same as the sum of the excess risks associated with each exposure in the absence of the other, where RD_AB = risk_(A,B) − risk_{(not A, not B)} is the excess risk associated with the two drugs in combination and similarly for RD_A and RD_B.

Thus, in the absence of an interaction under the additive assumption, the excess risk associated with the combination is the same as the sum of the excess risk associated with each drug separately.

When RD_AB > RD_A + RD_B (i.e. RD_AB − RD_A − RD_B >0) there is a potential interaction with an increased risk for the combination compared with that expected based on the individual drugs.

In modelling terminology, the following additive model can be applied:

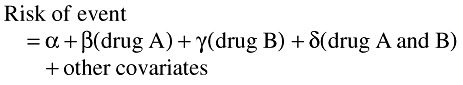Again, the measure of interaction is given by the coefficient δ, which is the amount by which the risk difference associated with the combination, A and B together, exceeds that which is predicated by the sum of A alone and B alone. Of interest are the statistical departures of δ from 0 and in particularly in values of δ greater than 0 which indicate positive interactions.

Thus values for δ statistically significantly greater than 0 indicate a positive measure of interaction in the additive model.

Proportional reporting

In a spontaneous reporting environment we only have events reported for a drug and not the total number of subjects exposed to the drug. Consequently, it is not possible to estimate the risk of an event associated with a drug. Instead, we defined the ‘proportional reporting’ of an event of interest on the drug. That is, out of the total number of events that are reported for the drug, we computed the proportion representing the event of interest. In modelling, proportional reporting is used to replace the direct measure of risk. Whilst proportional reporting may not always correlate with the true underlying risk of an adverse reaction, it is a well established measure for detecting signals of ADRs [1].

Application of the models

We applied both the additive and multiplicative models retrospectively to investigate four known DDIs and four drug-event combinations where there is currently no evidence of an interaction. We used the SAS procedure ‘proc genmod’ with the log-link function for the multiplicative model and the identity-link function for the additive model both under the assumption that the observed proportion follows a binomial distribution. We included, as covariates, the two drugs and their interaction term in the model. Table 1 summarizes the drug–drug interactions studied and Table 2 displays the corresponding data used for the analyses.

Table 1.

Examples of known and no known drug–drug interactions

Drug–Drug	Event	Mechanism of interaction
Known interaction
Methotrexate-diclofenac	Bone marrow depression	Inhibition of renal elimination of methotrexate
Simvastatin-ciclosporin	Myopathy	CYP450 inhibition
Ketoconazole-terfenadine	Torsade de pointes	CYP450 inhibition
Cisapride-erythromycin	Torsade de pointes	CYP450 inhibition
No known interaction
Fexofenadine-ketoconazole	Torsade de pointes	–
Methotrexate-rofecoxib	Bone marrow depression	–
Fluvastatin-ciclosporin	Myopathy	–
Cisapride-azithromycin	Torsade de pointes	–

Table 2.

Proportion of event of interests on all combinations of the two drugs

	No A, no B	A, no B	No A, B	A and B
Simvastatin(A)-ciclosporin(B) and MYP	2740/4869677	187/65940	113/45327	25/1342
Methotrexate(A)-diclofenac(B) and BMD	3732/4874109	282/63620	57/42612	27/1945
Ketoconazole(A)-terfenadine(B) and TdP	1497/4947013	12/11088	54/23683	7/502
Cisapride(A)-erythromycin(B) and TdP	1182/4900646	271/43497	101/37416	16/727
Methotrexate(A)-rofecoxib(B) and BMD	3767/4861514	310/63259	19/54795	2/2718
Fluvastatin(A)-ciclosporin(B) and MYP	2889/4925704	38/9913	137/46473	1/196
Cisapride(A)-azithromycin(B) and TdP	1518/5490501	293/44322	39/40140	2/776
Fexofenadine(A)-ketoconazole(B) and TdP	1540/4956019	11/14677	19/11544	0/46

BMD bone marrow depression; MYP myopathy; TdP Torsades de pointes.

Results

The measure of interaction on both multiplicative and additive scales for the eight drug–drug-event combinations investigated is summarized in Table 3. All four known DDIs were correctly identified by the additive model, since the measure of the interaction terms were statistically significantly greater than 0.

Table 3.

Summary of interactions

	Multiplicative model
	Measure of interaction		Additive model
	Measure of interaction δ	P-value	Measure of interaction δ	P-value
Known interaction
Simvastatin-ciclosporin and MYP	1.48	0.089	0.014	0.0002
Methotrexate-diclofenac and BMD	1.79	0.015	0.009	0.001
Ketoconazole-terfenadine and TdP	1.71	0.27	0.011	0.038
Cisapride-erythromycin and TdP	0.32	0.0001	0.013	0.014
No known interaction
Methotrexate-rofecoxib and BMD	0.34	0.14	−0.004	0.0001
Fluvastatin-ciclosporin and MYP	0.26	0.19	−0.002	0.83
Cisapride-azithromycin and TdP	0.11	0.002	−0.0047	0.01
Fexofenadine-ketoconazole and TdP	0	*	−0.002	0.0001

^*P value not estimated as one cell contains 0. BMD bone marrow depression; MYP myopathy; TdP Torsades de Pointes.

Under the multiplicative assumption, two of the four known interactions were identified as having the measure of interaction terms statistically (P< 0.05) or borderline (P< 0.1) significantly greater than 1. Furthermore, the model provided evidence of a trend towards a positive interaction for ketoconazole-tefenadine and torsade de pointes where the measure of interactions was 1.71 (P= 0.27). The multiplicative model, however, did not provide evidence of a positive interaction between cisapride-erythromycin and torsade de pointes.

All four examples of known non-DDIs were correctly predicted by the additive and multiplicative models, where the measure of interaction terms were either less than 1 (multiplicative model) or less then 0 (additive model), i.e., in concordance with current knowledge, the models provided no evidence of a positive interaction.

Discussion

A knowledge of drug–drug interactions is acquired during the life cycle of a drug starting with preclinical testing, through clinical development and postmarketing surveillance/experience. During the development cycle of a drug, the potential for drug–drug interactions cannot be exhaustively evaluated in phase 1 due to the limited number of drugs usually investigated at this stage. Furthermore, while published case reports provide useful general information, the case study approach still does not offer an adequate mechanistic understanding of potential clinical drug–drug interactions. As suggested in a recent publication [11], a population based approach can be used retrospectively to confirm known drug–drug interactions in a relevant patient population instead of healthy subjects and further characterize the anticipated interactions, although the outcome may be affected by, for example, limited sample size of patients on concomitant drug(s) of interest. However, the interaction profile of a drug may not be fully understood for several years after it is introduced onto the market. Studies looking at the frequency of interactions have reported incidences ranging from 4 to 20% [4, 5]. This wide range of results is mostly due to differences in the methodology of the studies (e.g. differences in study design, definition, source of the population). Consistent findings, however, indicate that populations at risk for drug interactions are likely to be those from primary health care and elderly patients [6, 7].

Drug–drug interactions, as such, are relatively rarely reported to spontaneous reporting systems for ADRs. Hence, we applied a method by which signals for drug–drug interactions can be detected using events in a spontaneous reporting system (the FDA-database). Multiplicative and additive models were fittedretrospectively to four known interactions and to four known non-DDI. For all known interactions, the additive model correctly provided statistical evidence of an increased reporting for the combination compared with that predicted for the two drugs separately. Thus, the additive model had 100% sensitivity in detecting signals of DDIs for the examples used. Similarly, the additive model correctly provided no evidence of increased reporting for the four drug associations not known to interact, thus suggesting 100% specificity. However, these results are based on only a small number of examples.

The multiplicative model provided evidence for two out of the four known interactions. For ketoconazole-terfenadine, whilst the interaction term showed a trend, it did not reach statistical significance (P= 0.27). This might have been due to the limited number of cases that were reported for the two drugs in combination using this model. Indeed, whilst over 10 000 events were reported for ketoconazole and over 20 000 for terfenadine, only about 500 events were reported for the combination. This, in turn, may reflect the cautious use of the two drugs together. For cisapride-erythromycin and torsade de pointes, the multiplicative model did not show a trend. The lack of evidence may again be due to the small number of events reported for the combination (about 700) reflecting good clinical practice. However, reporting proportions of torsades de pointes were 0.2 per 1000 reports (background drugs), 6.2 per 1000 (for cisapride), 2.7 per 1000 (for erythromycin) and 22.0 per 1000 (cisapride and erythromycin in combination) suggesting an absolute increase in the reporting of torsades de pointes with the combination. In order to have a multiplicative interaction, the reporting proportion of torsades would need to be in the order of 84 per 1000 reports on the combination. The multiplicative model correctly identified the four known non-DDIs.

Taking into account that the two models were applied to a limited number of DDIs, it appears that the additive model had better sensitivity for detecting signals for DDIs based on our data. This may be due to the lower threshold for the reporting rate to reach an interaction on the additive scale. However, due to the complex relationship between pharmacological and statistical interactions, it was thought important to apply both additive and multiplicative models for detecting signals. Indeed, positive signals with the multiplicative model would indicate a stronger signal as illustrated by the examples. Furthermore, it can be shown that when both drugs are positively associated with the event (or both drugs are negatively associated) then a positive interaction on the multiplicative scale will imply a positive interaction on the additive scale. Furthermore, algebraically it can also be shown that the only time there is a positive interaction on the multiplicative scale but not on the additive scale is when one drug is positively associated (say drug A) with the event, the other negatively (say drug B), and the risk of the two drugs together is less than that of drug A. Such scenarios, however, may be difficult to find in the context of drug therapy where the risk on the two drugs together is likely to be at least as high as that of the individual drugs. Thus from a signal detection perspective, a positive interaction on the multiplicative scale would also imply a positive interaction on the additive scale. The converse, however, is not always true as we have seen from the examples.

Whilst for drugs most commonly co-administered, interactions are detected by performing routine pharmacology studies, methodology based on spontaneous reports is the primary tool for detection of DDI for combination therapy less commonly administered. With the latter method, the additive model would be unlikely to trigger numerous signals based on the paucity of reports expected. However the additive model has a clear potential to identify a signal earlier than the multiplicative model. Such a technical signal would need further evaluation for understanding a possible association of an AE with a DDI and of their clinical relevance. It is also important to note that lack of a statistical interaction may not always mean lack of clinical relevance. Therefore, one should use these methods with some caution, particularly, when there is some prior clinical evidence of an interaction (e.g. from other drugs in the same class).

Whilst the possibility of report duplications cannot be ruled out, the purpose of assessing DDIs is to investigate the excess reporting of an event of interest on a combination of two drugs together which is beyond that predicted by each individual drug. It is unlikely that such a measure would bear any systematic bias due to duplication as it would apply to the denominator as well. Recently, however, a more sophisticated program has been developed, which will allow investigation of various duplication algorithms.

There have been two recent publications applying methodology for the retrospective detection of DDIs using a database for spontaneous adverse reactions [2, 3]. The method used a multiplicative model which demonstrated an interaction on both occasions. The first publication demonstrated a multiplicative interaction between oral contraceptives and itraconazole for the reporting of delayed withdrawal bleeding. The second paper demonstrated a multiplicative interaction between diuretics and NSAIDS for the reporting of decreased efficacy of diuretics. From the published data, we applied the additive model methodology and showed that it provided strong evidence of an interaction (P< 0.001). More recently, there has been interest in using empirical Bayesian methods for signal generation. The advantage is that the estimate of the risk of an association between a test drug and the reporting of an AE (e.g. the ratio of observed to expected number of events for a drug) and its corresponding statistical significance is combined into one estimate using Bayesian smoothing methods. These methods have been extended to investigate potential DDIs [9, 10]. The authors defined rules based on the smoothed estimates and their 90% confidence intervals to define an interaction. That is, the lower limit of the 90% CI of the estimate for the two drugs together must be greater than the upper limit of the 90% CI estimate for each of the two drugs. The method is formulated on the multiplicative assumption. It is not clear how these rules would be compatible with the classical definition of interaction which we have used to formulate our methodology.

Whilst the confidence intervals of the estimates can be easily calculated by hand or by a statistical program such as SAS, we decided to focus on the estimate and P values for proposing an objective threshold for detecting a DDI signal. It is difficult to interpret the confidence interval for such an estimate from spontaneous reports in the context of public health impact. Also the 95% CI may encourage researchers to define a less conservative threshold based on the lower limit of the interval thereby missing potential signals for important, but rare events. The 95% CI for an estimate which did not reach statistical significance would indicate that the risk of the signal is currently low.

We have developed our methodology using the same or a similar dataset to these authors. However, we have taken the methodology slightly further by considering the possibility of an additive interaction. Additive models have a clear advantage in that they help interpret a public health impact of adverse events. Indeed, it is possible that major interactions could be missed when data are only looked at in the multiplicative model. The importance of using the additive models for detecting signals of DDIs is further illustrated in the following example. Let us suppose the following risks (probabilities) are associated with drugs A and B regarding an adverse event:

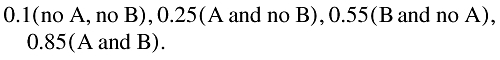It is clear that the risk for the combination is considerably higher than that for the individual drugs. For a commonly used drug, such a scenario could have a major public health impact. However, the measure of interaction on the multiplicative term is 0.62, suggesting no interaction (being less than 1). The measure of interaction on the additive scale is 0.15 which suggests a positive interaction (being greater than 0).

The population based approach suggests an alternative method for signal detection of DDIs using a prospectively designed population-based analysis as an add-on to phase 2 and phase 3 studies coupled with an organized, systemic approach to data collection [11]. This approach would fill in the gap between the traditional method used in phase 1 and our proposed signal detection method applied to spontaneous cases.

In conclusion, our proposed methodology provides a framework for the detection of DDIs in the setting of post marketing spontaneous reports. In particular, the additive assumption complements the existing methodology by providing a more sensitive approach. The multiplicative model may further help qualify the strength of the signal detected by the additive model. However, its sensitivity is limited by the number of events reported.