Loss of Stability: A New Look at the Physics of Cell Wall Behavior during Plant Cell Growth^,

Abstract

In this article we investigate aspects of turgor-driven plant cell growth within the framework of a model derived from the Eulerian concept of instability. In particular we explore the relationship between cell geometry and cell turgor pressure by extending loss of stability theory to encompass cylindrical cells. Beginning with an analysis of the three-dimensional stress and strain of a cylindrical pressure vessel, we demonstrate that loss of stability is the inevitable result of gradually increasing internal pressure in a cylindrical cell. The turgor pressure predictions based on this model differ from the more traditional viscoelastic or creep-based models in that they incorporate both cell geometry and wall mechanical properties in a single term. To confirm our predicted working turgor pressures, we obtained wall dimensions, elastic moduli, and turgor pressures of sequential internodal cells of intact Chara corallina plants by direct measurement. The results show that turgor pressure predictions based on loss of stability theory fall within the expected physiological range of turgor pressures for this plant. We also studied the effect of varying wall Poisson's ratio ν on extension growth in living cells, showing that while increasing elastic modulus has an understandably negative effect on wall expansion, increasing Poisson's ratio would be expected to accelerate wall expansion.

It is generally accepted that the fundamental behavior underlying all rapid plant growth is an irreversible stretching of primary cell walls due to mechanical loads generated by cell turgor pressure. Turgor pressure, the osmotically maintained hydrostatic pressure in living plant cells, and the mechanics of the cell wall itself, are undoubtedly among the most fundamental physical factors that dictate both cell growth and cell morphologies in plants (Zonia and Munnik, 2007). During plant cell growth, the cell wall system performs seemingly contradictory roles. On the one hand, it must be rigid enough to allow turgor pressure to build up, while on the other, it must be loosened in some way to permit cell enlargement during growth.

The physics underlying wall extension growth appears to be distinct from the biochemical events that constitute the broader background for all cell growth. While the study of biochemical precursors and cross-linkages emphasizes the importance of enzymatic activities such as the synthesis of wall components and the cleavage of hemicellulose tethers, etc., the biophysical approach focuses on the purely physical aspects of extension growth (e.g. wall stresses and strains, mechanical properties of the walls, and cell geometry). Obviously, an understanding of the physical principles underlying wall stress relaxation is essential to understanding the full spectrum of wall behaviors during growth. The biochemical approach to cell wall loosening has made notable advances in recent years (Cosgrove, 2006). However, our appreciation of the physical aspects of the process remains basically unchanged since the 1960s (Probine and Preston, 1962; Lockhart, 1965a, 1965b; Cleland, 1967; Ray et al., 1972).

In actively growing cells, because the walls are thin compared to the size of the cell, tensile stresses in the walls can be very high. Typical plant cell turgor pressures in the range of 0.3 to 1.0 MPa translate into between 10 and 100 MPa of tensile stress in the walls. In this regard, early students of the problem including Probine and Preston (1962), Lockhart (1965a), Cleland (1967), and also Ray et al. (1972) all recognized that cell enlargement begins with stress relaxation in the walls. They interpreted stress relaxation as a viscoelastic/creep-based process. Accordingly, most of the relevant experimental work on plant materials has been carried out under this viscoelastic/creep paradigm.

Studies based on viscoelastic/creep models, using Nitella or Chara internodal cells, have broadened our understanding of cell wall mechanical properties. For instance, creep-based uniaxial experiments have detailed the yield characteristics of plant cell walls and have demonstrated that the cell wall can be described as a viscoelastic/plastic material. These experiments also reveal the most important material property relating to wall elasticity, namely the Young's modulus of the cell wall. With experimental determination of Young's modulus the wall's structural and mechanical anisotropy can then be described in meaningful terms. Viscoelastic/creep-based experiments carried out in different media have also confirmed that the extensibility of cell walls is generally promoted by acid pH, which in turn has provided strong support for the acid growth theory. In fact, these experiments have provided a means of probing the complex of events leading to cell expansion.

Although the viscoelastic/creep model has been remarkably fruitful, difficulties have also been noticed by some researchers. For instance, although a reduction in turgor pressure of only 0.02 MPa can result in the immediate cessation of growth in living cells (Taiz, 1984), viscoelastic/creep-based models cannot predict a reasonable working turgor value for growing cells because viscoelastic/creep behavior can be shown to occur over a wide range of different load intensities in isolated cell wall materials (Preston, 1974; Dorrington, 1980).

We have proposed a new model of wall stress relaxation (Wei and Lintilhac, 2003; Wei et al., 2006) based on the assumption that any changes in cell turgor pressure, and in the resulting wall stresses, must occur gradually. The model is based on the theory of loss of stability. The notion was originally developed by the great mathematician Leonhard Euler to model the behavior of columns in compression, and then extended by physicists to treat tensile stress relaxation (Rzhanitsyn, 1955). The extension of the theory to tensile systems led to the recognition that the same thinking could be applied to any thin-walled pressure vessel. With a gradual increase in internal pressure the resulting stresses in the wall will gradually increase to a critical value, at which time loss of stability must occur, leading to stress relaxation in the wall (Panovko and Gubanova, 1965).

Turgor-driven growth of plant cells is a gradual process. In other words, in normal growing cells water transport and the resulting increases in turgor pressure are not subject to sudden, extreme excursions. This reality conforms to the fundamental prerequisite for loss of stability. It also requires that these loss of stability prerequisites can be met experimentally only under gradual ramp-loading conditions. In our uniaxial stretching experiments using isolated wall segments excised from growing Chara corallina cells we respected this requirement for a gradual ramp-loading regime. The results show that Chara cell wall materials respond to gradual ramp loading with a stress relaxation behavior that is entirely different from one based on a viscoelastic/creep mechanism (Wei et al., 2006). In particular, whereas a linear relationship between wall extension and log time is typical for creep-based experiments, it is not seen under ramp-loading conditions.

The work done in recent years in the lab of J.S. Boyer at the University of Delaware clearly shows the relationship between turgor pressure, cell wall materials, cytoplasmic input, and growth (Proseus and Boyer, 2005, 2006a, 2006b). In a quantitative comparison of isolated Chara wall tubes and living Chara cells (Proseus and Boyer, 2006a), Boyer's group found that at all turgor pressures and temperatures, the isolated wall tubes displayed turgor-driven growth indistinguishable in every respect from that of living cells, except that the rate decelerated over time in the isolated wall tubes while the living cells continued to grow rapidly. Boiling the isolated walls gave the same results, indicating that enzyme activity does not directly control wall extension in their experiments. These findings strongly suggest that wall extension growth is primarily a biophysical process, although ultimately dependant on enzymatic activity, and that under conditions where the enzymatic background can be subtracted the biophysical process still proceeds normally. They also found that in both living cells and in isolated wall tubes, any reduction in turgor pressure below a critical level terminated wall extension growth (Proseus and Boyer, 2006a). As mentioned earlier, this phenomenon is uniquely predicted by loss of stability theory (Wei and Lintilhac, 2003).

The first goal of this study is to present what one can infer from the loss of stability model about the relationship between turgor pressure of a growing cell and cell geometry. It has long been supposed that cell geometry and cell turgor are linked in growing cells. For instance, noting the reported discrepancy between multiaxial and uniaxial yield stress values in Nitella walls, Taiz (1984) proposed that geometrical considerations may be as important as wall mechanical properties in understanding the nature of cell turgor pressure. It has also been suggested that the multiaxially determined critical turgor pressure might be analogous to the point of dimensional instability in the balloon model of Hettiaratchi and O'Callaghan (1974; Taiz, 1984). The dimensional instability in the balloon model refers to the sudden increase in expansion rate of a balloon when the balloon's radius and the decreasing thickness of the membrane reach their critical values. The analogy breaks down, however, when one notes that the balloon is inflated by a compressible gas, so that instability can lead to aneurysm through the continued expansion of the gas, but plant cells are filled with an incompressible liquid, which means that barring additional water uptake the pressure immediately drops to zero once the cell wall expands. Also, unlike the membrane of a balloon, plant cell walls are continuously being thickened and strengthened so that under constant volume conditions the strength of the wall and the critical pressure value will continue to rise (Wei and Lintilhac, 2003), further obviating the possibility of aneurysm. This self-limiting control cycle limits cell volume growth during any single relaxation event and makes it unlikely that a sudden increase in the expansion rate will lead to catastrophic failure of the wall.

To explain cell wall behavior during growth, several other models including Green's movable yield-point theory (Green et al., 1971) and Cleland's two extension processes notion (Cleland, 1971) have been suggested. In general, these models involve the occurrence of viscoelastic-plastic extension in the walls and some empirical rules that account for specific behaviors. Dumais et al. (2006) have recently presented an anisotropic-viscoplastic model of plant cell morphogenesis by tip growth. To illustrate the role of turgor-induced wall stresses and the deposition of new wall materials in plant cell morphogenesis, they present three sets of equations whose solution demonstrates the importance of cell geometry, and of wall stresses and wall strains in the study of plant cell morphogenesis and growth. They also show that wall mechanical anisotropy is critical in the patterning of wall expansion growth.

The above models adequately explain several features of extension growth but they do not encompass any direct relationship between cell geometry and cell turgor pressure. We believe that loss of stability theory can address the issue of cell geometry while respecting the underlying facts of turgor pressure regulation. As we have shown in a spherical cell model, turgor pressure prediction from loss of stability theory includes both the cell's geometry and the wall's mechanical properties (Wei and Lintilhac, 2003). In this study we further develop the notion of loss of stability by rigorously extending the physics of loss of stability to free standing cylindrical cells. We also test the predictive strength of this approach by investigating the working turgor pressures of living Chara internodal cells of different ages.

The second goal of this study is to obtain a better understanding of the effects of basic material properties on wall extension growth. As we know, elastic modulus and Poisson's ratio are the two basic mechanical parameters that describe the elastic properties of materials satisfying Hooke's law. While the effect of wall elastic modulus on plant cell growth has been investigated in various ways, the effect of wall Poisson's ratio is still unstudied. Like any other elastic material, cell walls show typical two-dimensional stress-strain behavior, i.e. when cell wall material is under stress, strain is also induced in a direction normal to the direction of the stress. Poisson's ratio is the constant that reflects the proportionality between lateral contraction and longitudinal extension and directly reflects the compressibility of the material. We know from the familiar example of acid growth theory (Rayle and Cleland, 1992) that lowering wall elastic modulus promotes cell wall expansion growth, but we know little about the effect of wall compressibility and Poisson's ratio.

From the point of view of biophysics, the key controlling variables determining the characteristics of plant cell growth are water uptake and cell wall stress relaxation. While water uptake has been adequately explained by the theory of cell water relations, the physical mechanism of wall stress relaxation is still problematic. As pointed out by Burgert and Fratzl (2007), there has been very little theoretical coherence in our understanding of cell wall extensibility and wall stress relaxation. They note that “…cell wall extensibility has been often used in a rather imprecise way, describing elastic, viscoelastic, plastic and viscoplastic deformation properties” (quote from Burgert and Fratzl, 2007 [p. 198]). Our work is an attempt to codify what we now know in terms of strictly definable physical first principles.

RESULTS

Results of cell pressure probe measurements are shown in Table I. Turgor value is presented as mean ± sd (n = 6). Sequential internodal cells in the intact plant are numbered 1, 2, 3, 4, and 5 (cell 1 is the oldest and the most basal, cell 5 is the youngest and most apical). Direct comparisons show that older cells have higher turgor values than younger cells. Moreover, cell length is not a factor in the regulation of turgor value (in many cases cell 2 is longer than cell 1, yet its turgor value is still lower than that of cell 1).

Table I.

Cell radius R, wall thickness t, wall elastic modulus E, and measured cell turgor pressures P_turgor and the corresponding turgor predictions P_critical of sequential internodal cells of intact Chara plants (cell no. 1 being the oldest and most basal cell)

Data from direct measurements are expressed as mean value ± sd (n = 6). P_critical is turgor prediction from loss of stability theory, expressed as a range of pressures corresponding to a range of Poisson's ratios from 0.5 to 0 (see “Discussion”).

Cell Parameter	Cell No. 1	Cell No. 2	Cell No. 3	Cell No. 4	Cell No. 5
R (μm)	424 ± 33	435 ± 32	338 ± 26	291 ± 23	218 ± 18
t (μm)	1.01 ± 0.15	0.94 ± 0.16	0.74 ± 0.13	0.54 ± 0.07	0.33 ± 0.09
E (MPa)	361	338	289	240	213
Pturgor (Mpa; by probe)	0.51 ± 0.06	0.42 ± 0.05	0.34 ± 0.04	0.27 ± 0.04	0.19 ± 0.03
Pcritical (Mpa; prediction)	0.57–0.86	0.49–0.73	0.42–0.63	0.30–0.45	0.22–0.32

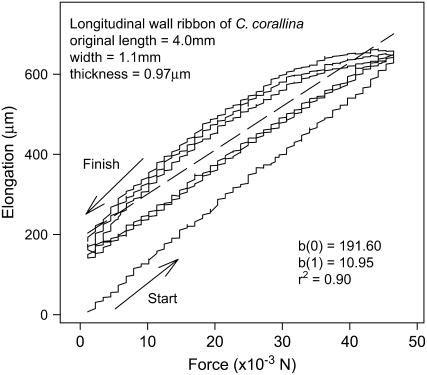
Figure 1 shows typical loading and unloading paths of a stretching experiment conducted on an excised wall ribbon. We excluded the first loading path for the calculation of the linear regression line (dashed line) because it differed significantly from all subsequent loading and unloading cycles. All wall ribbons were able to return to their original length when the peak force was ≤50 × 10⁻³ n, which demonstrates that the wall materials remained elastic throughout the experiment. The slope of the linear regression line, which allows us to calculate the elastic modulus, represents the elongation of the wall ribbon per 1 × 10⁻³ n change in load.

Figure 1.

Loading and unloading paths of a typical stretching experiment conducted on a wall ribbon obtained from a cell number 2. The r² and the slopes of the linear regression (dashed line), b(1), were calculated from data points in the loading and unloading cycles. Each loading and unloading cycle lasted about 10 min.

The calculated wall elastic moduli of each of the measured internodal cells are shown in Table I. These modulus values range from 213 to 361 MPa and agree with the results of previous studies (Wei and Lintilhac, 2003; Wei et al., 2006). In general, the walls of older cells had higher elastic moduli than those of younger cells.

Results of cell wall thickness and cell radius measurements for each cell are also shown in Table I. The critical pressure values are determined by substituting the cell dimensions and the computed elastic moduli into Equation 7. The resulting critical pressure values are listed in Table I and correspond to turgor predictions from loss of stability theory. They are expressed as a range of pressures representing the full range of possible Poisson's ratios from 0.5 to 0 (see “Discussion”).

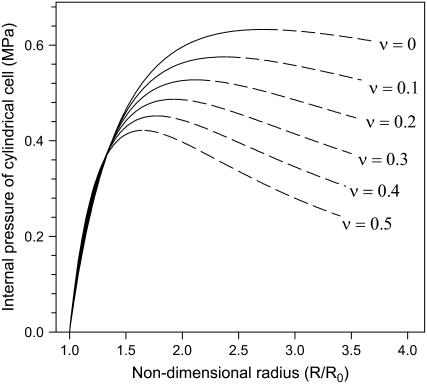
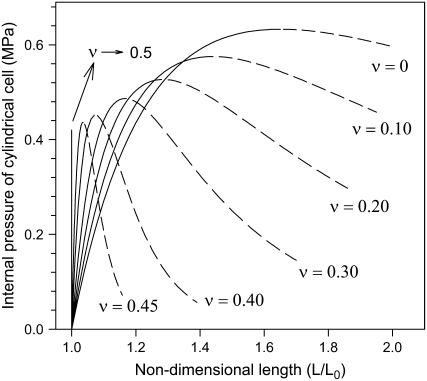
Figures 2 and 3 are graphic representations of Equations 5 and 6, respectively, after substituting the measured values for wall thickness, cell radius, and elastic modulus. They coincide with the general graphical presentation of loss of stability theory (Panovko and Gubanova, 1965; Wei and Lintilhac, 2003), i.e. each curve has a peak where the slope changes from positive to negative. Note that for any given Poisson's ratio value, the critical pressures for circumferential and longitudinal loss of stability are identical. For instance, for ν = 0.20, the peaks of the two curves are both positioned at P = 0.53 MPa.

Figure 2.

Relationship between turgor pressure and the nondimensional radius R/R₀, obtained by substituting measured values for wall thickness, cell radius, and elastic modulus of cell number 3 into Equation 5. After a monotonic increase in pressure, loss of stability (at the peak of the curve) occurs when the pressure reaches a critical value P_critical. All points on the rising portion of the curve (solid line) are stable states, while points on the falling portion (dashed line) are unstable states.

Figure 3.

Relationship between turgor pressure and the nondimensional length L/L₀, obtained by substituting measured values for wall thickness, cell radius, and elastic modulus of cell number 3 into Equation 6.

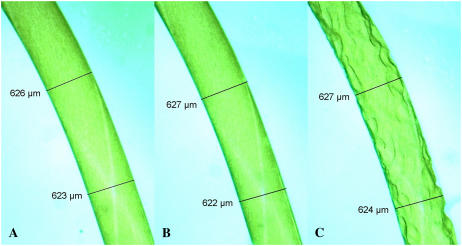
The three images comprising Figure 4 show a typical number 3 cell at different stages during plasmolysis: Figure 4A, fully turgid (immersed in the original growth medium); Figure 4B, less turgid (immersed in approximately 100 mm mannitol solution); Figure 4C, plasmolysis (immersed in approximately 200 mm mannitol solution). All plasmolysis experiments on Chara internodal cells show the same lack of cell shrinkage, which is to say, during mannitol-induced plasmolysis the measured diameter of living Chara cells does not decrease at all. This confirms our theoretical assertion that the cell radius measured after plasmolysis does not represent R₀, which should instead be calculated using the relevant equation.

Figure 4.

Photomicrographs of a cell number 3 during mannitol-induced plasmolysis. The dimensions of the cell remain constant as the cell turgor pressure decreases from the fully turgid state (A), to a less turgid (B), and finally to plasmolysis (zero turgor; C).

DISCUSSION

Loss of Stability in a Thin-Walled Cylindrical Pressure Vessel

In turgid plant cells, as in any pressure vessel, it can be shown that as pressure builds within the cell, tensile stresses in the wall increase, leading inevitably to loss of stability, unless some other mechanism intervenes. Panovko's work on the loss of stability of a thin-walled spherical shell has been reviewed by Wei and Lintilhac (2003). This early work outlined the material parameters of loss of stability in spherical pressure vessels. In extending this model from spherical to cylindrical geometries we are exposing previously unexplored applications of Panovko's original mathematical treatment and developing a predictive model that more nearly approximates conditions in axially extending plant cells. To emphasize the basic problems and pinpoint the onset of loss of stability we will present the mathematical treatment in somewhat simplified form.

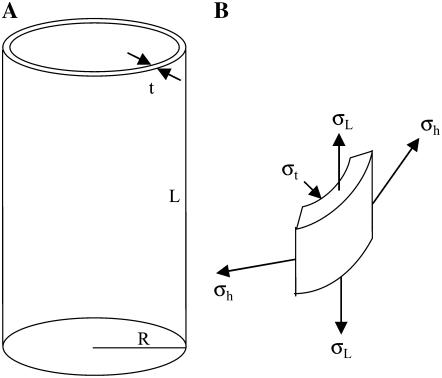
As shown in Figure 5, a long thin-walled cylindrical vessel with radius R and wall thickness t is subjected to an internal pressure P. Because of the axial symmetry of the structure, it is conventional to specify the wall stress by its three components: stress in the circumferential direction (termed hoop stress) σ_h, stress in the longitudinal direction σ_L, and stress in the radial direction (i.e. through the wall thickness) σ_t.

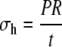(1)

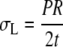(2)

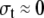(3)

Figure 5.

A, Hypothetical model for cylindrical plant cells. An elastic thin-walled cylindrical vessel with radius R, length L, and wall thickness t is subjected to an internal pressure P. Wall material is assumed to be mechanically isotropic. B, Stresses acting on an element of the shell wall. σ_h, σ_L, and σ_t are hoop stress, longitudinal stress, and radial stress, respectively.

Equations 1 and 2 illustrate the conventional truth that hoop stress must be twice the longitudinal stress; this is the basic feature of stress in any thin-walled cylindrical pressure vessel (Lockhart, 1965b). Equation 3 is based on the fact that radial stress through the wall thickness is very much smaller than the other two components, and can be set equal to zero.

Strains in the wall can similarly be expressed with three components: hoop strain ɛ_h, longitudinal strain ɛ_L, and strain through wall thickness ɛ_t. Because the strains in problems of loss of stability are large, they are often calculated in accordance with logarithmic deformation or true strain (Panovko and Gubanova, 1965),

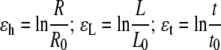(4)

where R₀, L₀, and t₀ are the initial radius, length, and wall thickness, respectively.

In a thin-walled cylindrical pressure vessel, Hooke's law relating stresses and strains in three dimensions can be conveniently expressed in matrix form (see Supplemental Appendix S1). Substituting Equations 1, 2, 3, and 4 into this matrix the internal pressure can be expressed as a function of the relative deformations in the circumferential and longitudinal directions (see Supplemental Appendix S1),

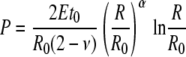(5)

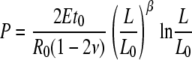(6)

where α and β are Poisson's ratio related factors and t₀, R₀, and L₀ are the initial wall thickness, the radius, and the length of the cell, respectively (see Supplemental Appendix S1).

We note that the exact numerical expressions of Equations 5 and 6 require the initial dimensions of the cell (t₀, R₀, and L₀), all of which can be obtained using Equations A3 and A5 (see Supplemental Appendix S1). To explicitly show the functional relationships of P versus R and P versus L we plot the equations by assigning the parameters with their physiological values. For instance, Figures 2 and 3 are plotted by substituting the measured values for wall thickness, cell radius, and elastic modulus of cell number 3 into Equations 5 and 6, respectively. Moreover, to reveal the relative deformations the horizontal axes have been expressed as ratios R to R₀ and L to L₀ (note this is justified because both R₀ and L₀ are constant). It is apparent that after a monotonic increase in pressure, the slope of each curve becomes zero when the pressure reaches a certain critical value P_critical. According to theory, this represents the instant when loss of stability occurs, initiating irreversible stress relaxation in the wall (Panovko and Gubanova, 1965).

Clearly, the relative deformations R/R₀ and L/L₀ denote the change in cell size during growth. Loss of stability theory suggests that cell turgor pressure under normal conditions is constantly hovering just under the critical pressure determined by cell geometry and wall elastic properties (Wei and Lintilhac, 2003). For this reason if we represent the ratio R/R₀ in Equation 5 by variable k, the solutions to the differential equations dP/dk = 0 will yield the critical R/R₀ at which loss of stability occurs. This critical R/R₀ turns out to be a function of Poisson's ratio only (Eq. A6 in Supplemental Appendix S1), which in turn enables estimation of R₀. For instance, for ν = 0.3 the critical R/R₀ is 1.92. The R₀ of the cell number 3 is then 338 μm/1.92, since the R of the cell is 338 μm. Similarly, the critical R/R₀ can also be used for estimation of initial thickness t₀ (Eq. A3 in Supplemental Appendix S1).

The expression for the critical pressure (i.e. the working turgor pressure for a growing cell) can therefore be obtained by substituting the critical R/R₀ back into Equation 6, giving:

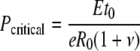(7)

where e is the base of natural logarithm.

Of course, the above procedure can also be applied to longitudinal terms, i.e. Equation 6. The critical pressure derived from Equation 6 turns out to be the same as that from Equation 5 (which is Eq. 7). This indicates that the mathematical outcomes of our model point to a rational conclusion—that the turgor pressure value that drives growth in girth is the same as that which drives growth in length, which is to say plant cells that are unconstrained by the pressures of surrounding tissues grow simultaneously in girth and in length (albeit not at the same rate). The graphical presentation of the equations, Figure 2, and Figure 3 also confirms that the P_critical of corresponding curves (i.e. the peaks) have the same values.

The Relationship between Cell Geometry and Cell Turgor Pressure

As mentioned above, the P_critical appearing in Equation 7 represents the working turgor pressure of growing cells. Therefore, the equation formalizes the relationship between the two elements: cell turgor pressure (P_critical) and cylindrical cell geometry (as represented by t₀ and R₀).

Despite the fact that the subscript 0 denotes the initial values for thickness and radius, t₀ and R₀ should not be mistaken for the wall thickness and cell radius of a very young cell. Rather, by the definition of logarithmic deformation (Eq. 4), t₀ and R₀ represent the hypothetical dimensions of a cell growing under conditions where the internal pressure is zero (clearly an impossibility). In the context of plant cell growth, therefore, the use of the terms t₀ and R₀ require some careful qualification. In traditional engineering usage they would simply represent the initial thickness and radius of a vessel wall before pressurization, but in unpressurized (plasmolyzed) plant cells we cannot assume that any measurement of thickness and/or radius represents an initial condition, because the cells have been continually pressurized since the last division and retain a permanent imprint of plastic deformation and continued wall relaxation, even after plasmolysis. The fact that cell diameter does not decrease with falling turgor values during plasmolysis (Fig. 4) confirms our assumption that the measured radius of the now flaccid cell cannot be taken as a valid determination of R₀.

The cylindrical solutions for loss of stability show that the true values of t₀ and R₀ are linked to the actual wall thickness t and cell radius R by Equations A3 and A6 (Supplemental Appendix S1). Thus Equation 7 does represent the relationship between cell geometry and cell turgor pressure. This relationship has been used to generate the predicted turgor pressures listed in Table I. Note that Equation 7 does not contain length terms (L, L₀), reflecting the fact that in long cylindrical cells turgor pressure is not related to the length of the cell. This has also been confirmed by pressure probe measurement (see “Results”).

It is significant that the relationship between cell geometry and cell turgor pressure as expressed in loss of stability theory is derived from physical first principles, and that the predicted turgor pressures fall within the expected physiological turgor range of the growing cells. This relationship shows that although the working turgor pressure of a growing plant cell can be shown to be a direct manifestation of the physical properties of its cell wall, it is also true that cell geometry plays a significant role in determining the effective value of P_critical, the turgor pressure value at which local wall material relaxes through instability.

Effect of Poisson's Ratio on Wall Extension Growth

In general, Poisson's ratio is known to be between 0 and 0.5 for all materials (Poisson's ratio = 0.5 is associated with incompressible materials such as rubber). It has been reported that the Poisson's ratio of onion (Allium cepa) epidermal peel (a multicellular structure with more or less turgid cells) is in the range of 0.18 to approximately 0.30 (Wei et al., 2001). However, we must accept that the Poisson's ratio of excised Chara cell wall material is really unknown. Therefore in this study we cover all the possibilities by systematically varying the Poisson's ratio from ν = 0 to ν = 0.5.

But while it follows that the effect of increasing elastic modulus on wall expansion must be negative (a stiffer wall stretches less), this study suggests that increasing Poisson's ratio has a positive effect on wall expansion growth. This can be seen in Figures 2 and 3, where an increase in the Poisson ratio of the wall lowers the value of critical pressure, thereby promoting cell wall expansion (low critical pressure means that wall stress relaxation happens at a lower turgor pressure, which implies that the cell needs to do less osmotic work to accomplish wall expansion).

This conclusion is confirmed by taking the total derivative of Equation 7:

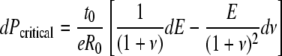(8)

This equation formalizes the combined effect of elastic modulus E and Poisson's ratio ν on the critical pressure. Note that the sign of the dE term is positive, yet the sign of the dv term is negative, indicating that the effects of varying E and ν on P_critical are opposite.

This study assumes a structurally isotropic wall with the cellulose distributed randomly in three dimensions, but plant cell walls are highly anisotropic (Baskin, 2005). For instance, it has long been known that plant cell walls have anisotropic elastic moduli (Probine and Preston, 1961). A recent study shows that in Chara cell walls the ratio of transverse to longitudinal moduli can range from 2.2 to 2.9 (Wei et al., 2006), but here we arbitrarily assign to the walls an isotropic elastic modulus value E that was transposed from originally longitudinal modulus measurements. A similar situation applies to Poisson's ratio. Early studies have shown that microfibrils in the walls of these giant algal cells are predominantly transverse (Probine and Barber, 1966), which suggests that the transverse Poisson's ratio may be very different from the longitudinal Poisson's ratio. Yet for simplicity in this study we assume that the Poisson's ratio of wall materials, ν, is constant throughout.

Furthermore, although the substitution of anisotropically specified wall parameters (such as Elastic Modulus and Poisson's ratio) into the stress and strain equations is possible, the analytical solutions to the equations are not available yet. As Panovko and Gubanova (1965) have pointed out, the key point lies in the demonstration that the validity of the concept of loss of stability does not depend on a particular assessment of Poisson's ratio. This can be seen in Figures 2 and 3, where all curves have the same pattern, i.e. after monotonic increase in strain they finally reach a point where the slope becomes zero. In other words, assignment of different Poisson's ratios and elastic moduli does affect the value of the critical pressure, but it does not eliminate loss of stability behavior.

Implications for Stress Relaxation in Plant Cell Walls

The theory of loss of stability diverges sharply from previous thinking on the underlying mechanics of stress relaxation in growing plant cell walls. The physical principles in which the theory is embedded are the general concepts of stress and strain. Once the geometry of the pressure vessel and the mechanical properties of the wall materials are in place then these general concepts and equations become specific. In this study Equations 1, 2, and 3 are the stress characteristics of any thin-walled cylindrical vessel. Equation 4 is employed because loss of stability always deals with large deformations, and we choose to follow Panovko's logarithmic method in describing the large strains. Equation A1 (see Supplemental Appendix S1) represents the stress-strain relationship of an ideal thin-walled cylindrical vessel in that it assumes isotropic behavior.

All of the above equations are static equations because they describe the steady-state relationship of stress and strain. But what if the internal pressure changes over time? For instance, in growing plant cells one can reasonably assume that the turgor pressure changes to some extent as the cell imports water and as new wall material is laid down. To make every moment in the process subject to a static analysis, the change in pressure has to be slow enough so that the changes in stress and strain are small, and that all of the equations remain valid. Experimentally, this feature has been demonstrated in uniaxial loading experiments in which slow ramp-loading conditions were used to meet the requirements for loss of stability (Wei et al., 2006). Under these conditions we have shown that once the load stopped ramping up, the change in strain also stopped immediately, indicating that ongoing relaxation in the tested materials could keep up with the slowly increasing stress intensities (Wei et al., 2006; Fig. 3, curve A). In other words, if changes in load (or pressure) are slow enough, every moment in the process can be regarded as a steady state.

In the case of cylindrical pressure vessels, just as in spherical ones, the occurrence of loss of stability is inextricably bound to the physics of the general stress-strain relationship, a fact that reaffirms our central tenet, which is that loss of stability is an inevitable result of the gradual loading process. After a monotonic increase in pressure, there comes a point where the slopes of the curves become zero. At this point, the stress cannot increase further and instability-induced stress relaxation follows.

Predicted versus Measured Turgor for Cylindrical Cells

P_critical is the highest possible pressure allowed by wall mechanics and system geometry. It is defined by the differential equations dP/dR = 0 and/or dP/dL = 0. This is particularly clear in the graphical interpretation of the definition where P_critical corresponds to the peak of the curve (Figs. 2 and 3). It is clear then that cell turgor pressure will never exceed P_critical, regardless of the cell's ability to uptake water. In growing cells, the driving force for water uptake (i.e. water potential gradient across the cell membrane) can only raise turgor pressure to the level of P_critical, at which point stress relaxation and cell wall expansion occur. For this reason we have suggested that the turgor pressure of actively growing cells should be constantly hovering near the critical value, P_critical (Wei and Lintilhac, 2003). In the case of maturing cells, on the other hand, the continued addition of secondary wall material and other encrusting substances such as lignin would raise P_critical to a level unattainable by turgor, thereby terminating growth.

All of the cells used in this study were actively growing cells. By measuring the working turgor pressure of each cell with the cell pressure probe and then dissecting the same cell to determine its wall thickness and its wall elastic modulus (for the calculation of P_critical), we can construct a direct comparison of observed turgor pressure and the turgor pressure predicted by loss of stability theory. Table I shows the measured turgor pressures (P_turgor) and the turgor predictions (P_critical) expressed as a range of pressures corresponding to a range of Poisson's ratios from 0 to 0.5.

Although the agreement between predicted and measured turgor values is good, the comparison between P_critical and measured turgor for each cell shows that P_critical is always somewhat higher than the measured turgor pressure. This discrepancy probably results from the localized nature of loss of stability in heterogeneous cell wall materials from living cells. Panovko pointed out that in cases where the wall thickness is uneven or has regions of variable modulus, loss of stability will happen preferentially at the site where it has the lowest P_critical value (Panovko and Gubanova, 1965). In this study, thickness measurements by microscopic interferometry can only give an overall regional thickness of the wall and cannot resolve local thin spots. This overall thickness measurement is then translated into an ideally cylindrical cell model of uniform thickness and modulus. Therefore, the calculated P_critical is always slightly higher than the working turgor pressure.

The link between turgor pressure and the critical pressure P_critical is central to our suggestion that loss of stability represents the mechanism underlying plant cell wall stress relaxation during normal turgor-driven growth. We have shown that stress relaxation in the wall during normal growth can take place only when cell turgor pressure rises to the critical pressure value. We can therefore predict two short-term behaviors. The first of these predictions is that any reduction in turgor pressure will cause growth to cease immediately and the second is that any reduction of wall elastic modulus, with its attendant reduction in the critical pressure value, will increase the cell's volume growth rate.

In fact, this relationship has also been noted in elongating oat (Avena sativa) coleoptiles treated either with mannitol to depress growth or with auxin to stimulate growth (Burgess, 1985). Burgess observed that if the bathing medium contained mannitol at a concentration just sufficient to lower cell turgor slightly without inducing plasmolysis, growth stopped, whereas when auxin was added to the medium resulting in a change in the elastic properties of the wall, the growth rate increased without any corresponding increase in turgor pressure. These experiments clearly support the link between turgor pressure and critical pressure P_critical that is anticipated by loss of stability theory.

Loss of stability emphasizes the physics of the wall relaxation process and as such it does not necessarily relate to our understanding of cell wall biochemistry. Although the terms wall loosening and stress relaxation have sometimes been used interchangeably to describe wall behavior during cell growth, they in fact refer to two different perspectives on the same phenomenon. Wall loosening refers to the unfastening of the wall matrix polymers, e.g. the scission of cross-links between cellulose microfibrils in the walls. This inevitably reflects a biochemical interpretation of wall behavior and implies changes in molecular size of wall matrix polysaccharides (Talbott and Ray, 1992a, 1992b). Stress relaxation, on the other hand, emphasizes the physical process that lowers the tension in the wall and therefore reflects a more biophysical interpretation of wall behavior.

The biochemical approach to cell wall loosening has made notable advances in the recent years. Cosgrove has recently reviewed the four wall loosening agents that directly or indirectly catalyze stress relaxation in plant cell walls (the primary wall and secondary wall loosening agents; Cosgrove, 2006). With regard to the study of the physical mechanism for wall stress relaxation, much work has been carried out through investigations on the stress-strain behavior of isolated cell wall materials in which mechanical testing is usually initiated with a sudden loading or a sudden displacement of the test materials. To reveal loss of stability behavior, however, wall stress relaxation experiments need to be conducted under gradual ramp-loading conditions.

CONCLUSION

Cylindrical loss of stability solutions provide the link between cell geometry and cell turgor pressure. As in the spherical cell model (Wei and Lintilhac, 2003), the cylindrical cell's geometry and wall mechanical properties merge into a single expression. The necessary condition—a gradual increase in pressure so that every moment in the process can be represented as a static state—is entirely in accordance with our common understanding of plant cell growth.

The critical pressure defined and predicted by the cylindrical loss of stability model basically agrees with the measured physiological turgor pressure of living Chara cells. Cell radius and wall thickness (but not cell length) are the key geometrical factors determining cell turgor pressure. Additionally, with regard to the elastic properties of wall materials, while an increase in elastic modulus inhibits cell wall expansion an increase in Poisson ratio promotes cell wall expansion.

The loss of stability model only addresses the physical constraints that govern stress relaxation in growing cell walls. It says nothing about the molecular characteristics of cell wall materials or the nature of the biochemical controls affecting growth. Clearly, considering the variety of cell shapes that can be found in real living plants this study provides a limited view of wall stress relaxation in cylindrical plant cells only. The principal barriers to a more complete understanding arise first from the fact that real plant cells are not ideal cylinders, second from the fact that plant cell walls are not mechanically isotropic, and last from the fact that plant cell walls are continuously changing in their biochemistry and structure during growth. However, we believe that it is possible to gain meaningful insight into the nature of wall stress relaxation and plant cell growth by using loss of stability theory as a basis for constructing predictive models.

MATERIALS AND METHODS

Plant Material and Growth Conditions

Cultures of Chara corallina were grown in a medium of 5% soil mixture in distilled water. Fast growing intact plants each consisting of five to six internodal cells were used for measurements (very young cells less than 3 mm in length were considered unusable). The most mature internode (i.e. the most basal one), labeled cell number 1 in this study, grew at a rate of about 5% increase in length per day. The youngest internodes (cell no. 5) grew at about 20% increase in length per day.

Measurement of Cell Turgor Pressure

The turgor pressures of internodal cells were measured directly using the cell pressure probe method (Steudle, 1993). Probing was carried out sequentially from the youngest to the oldest internodes while the whole intact plant was kept in water. Six intact plants were used for these turgor measurements.

To calculate turgor pressures predicted by loss of stability theory, cell radius was measured with an optical micrometer before probing the cell's turgor pressure.

Measurement of Wall Elastic Modulus

After probing, the cells were opened with a razor blade and the cytoplasm was removed with a hair loop. The walls were then cut into longitudinal ribbons for elastic modulus measurements. Cell wall thickness was measured by means of image duplicating interference microscopy according to Mach-Zender (Aus Jena, Peraval, see Preston, 1974). For the calculation of the optical path difference we assumed the refractive index of the wall materials to be 1.55 (Preston, 1974). The lengths and widths of the ribbons were measured with an optical micrometer.

To obtain the stress-strain relationships of the wall ribbons they were subjected to cyclic loading and unloading using a commercial version of a mechanical testing frame previously developed in this laboratory (Vitrodyne V-200, Liveco). This instrument incorporates a microprocessor-based feedback control system capable of operating either in strain-controlled or load-controlled mode. Details of this device have been described elsewhere (Wei et al., 2001). To automatically perform the loading and unloading experiment, the Vitrodyne was programmed to gradually increase the tensile load to a level (approximately 50 × 10⁻³ n), and then gradually reduce it to the initial value in about 1 × 10⁻³ n increments. The entire loading and unloading cycle was repeated two or three times to ensure that the system remained in the elastic range. During the experiments the tested wall ribbon was immersed in water.

Elastic modulus was calculated from the results of the loading and unloading experiment, which we plotted as wall elongation versus tensile force (Fig. 1). The slope of the regression line, ξ, was then used for the calculation of elastic modulus E:

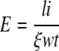where l, w, and t are the original length, width, and thickness of the wall ribbon, respectively; i is unit force.

Measurement of Dimension Variance during Plasmolysis

To distinguish between R₀ (the so-called initial radius) and R (cell radius at full turgor), dimensional changes were recorded as Chara internodes were bathed in a mannitol medium to reduce turgor pressure and induce plasmolysis. Cell radii were measured using an optical micrometer and repeatedly remeasured as 500 mm mannitol was slowly added until plasmolysis was observed (care was taken to ensure that the medium was well mixed).

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Appendix S1. Summary derivations of Equations 5 and 6.