Bone Geometry, Density and Strength Indices of the Distal Radius Reflect Loading via Childhood Gymnastic Activity

Abstract

The distal radius bears unique forces during gymnastic activity. Its relatively simple anatomy, minimal soft tissue envelope and varied composition make the distal radius ideal for evaluating the effects of loading on bone properties. For 56 premenarcheal gymnasts and non-gymnasts, ultradistal and 1/3 distal radius DXA scans measured bone mineral content (BMC), areal bone mineral density and projected area. Simplified geometric models were used to generate bone mineral apparent density (BMAD), geometric indices, strength indices and fall strength ratios. Ratios of regional BMC vs. total body fat free mass (FFM) were calculated. Separate Tanner I and II analyses of covariance adjusted bone parameters for age and height. Ratios were compared using maturity-matched analyses of variance. At the 1/3 region, periosteal width, BMC, cortical cross-sectional area, and section modulus were greater in gymnasts than non-gymnasts (p<0.05); 1/3 BMAD means were equivalent. Ultradistal BMAD, BMC and index for structural strength in axial compression were higher in gymnasts than non-gymnasts; ultradistal periosteal width was only larger in Tanner I gymnasts. Fall strength ratios and BMC/FFM ratios were greater in gymnasts (p<0.05). Geometric and volumetric responses to mechanical loading are site-specific during late childhood and early adolescence.

The distal radius bears unique forces during gymnastic activity, and fan beam magnification error is negligible at this site, making it ideal for DXA evaluation of associated bone properties. For 56 premenarcheal gymnasts and non-gymnasts, ultradistal and 1/3 distal radius DXA scans measured bone mineral content, areal bone mineral density and projected area. Simplified geometric models were used to generate bone mineral apparent density, geometric indices, strength indices and fall strength ratios. Ratios of regional bone mineral content vs. total body fat free mass were calculated. Separate Tanner I and II analyses of covariance adjusted bone parameters for age and height. Ratios were compared using maturity-matched analyses of variance. At the 1/3 region, periosteal width, bone mineral content, cortical cross-sectional area, and section modulus were greater in gymnasts than non-gymnasts (p<0.05); 1/3 bone mineral apparent densities were equivalent. Gymnasts’ ultradistal bone mineral apparent density, bone mineral content and index for structural strength in axial compression were higher; ultradistal periosteal width was only larger in Tanner I gymnasts. Fall strength ratios and bone mineral content vs. fat-free mass were greater in gymnasts (p<0.05). Gymnasts’ geometric and volumetric responses to mechanical loading are site-specific during late childhood and early adolescence.

INTRODUCTION

To date, most studies that evaluate the effect of mechanical loading on bone growth have focused on areal bone mineral density (aBMD) and bone mineral content (BMC), rather than on bone geometry. When considered, bone size is often used solely to adjust for the confounding effects of body size variation upon BMC or BMD, rather than as an outcome measure that varies as a function of physical activity. Few investigators have attempted to evaluate bone geometry in response to exercise; as a result, limited evidence has been provided for an effect of mechanical loading on bone architecture (1–7). Even fewer studies have demonstrated geometric adaptation to mechanical loading during growth (8–12).

Artistic gymnastics has been studied extensively as a model for the skeletal effects of impact loading. Because the unique weight-bearing function of the upper extremity in gymnastics is infrequently duplicated by other activity, the forearm is a particularly useful site for these evaluations. Within the forearm, the radius bears the brunt of impact forces, thereby providing a specific barometer of impact/weight-bearing activity experienced during gymnastics. In addition, the radius contains regions of bone that are predominantly cortical or predominantly trabecular, allowing for comparisons of bone tissue-specific responses. Compared to the more complex anatomy of the proximal femur or lumbar spine, the structure of the radius facilitates the use of a simplified model to derive geometric measures, bone mineral apparent density (BMAD), and indices of strength (13). Finally, in the distal forearm, there is negligible variation in soft tissue envelope dimensions; thus, variation in distance from the x-ray source and resultant fan-beam magnification error are both uniform and minimal (14).

Many studies have identified higher aBMD in gymnasts than non-gymnasts at the forearm and other weight-bearing sites (15–20); only one has explored the relative contributions of geometry and volumetric density (11). Previous analyses by our group demonstrated significantly higher areal BMD at the forearm in premenarcheal gymnasts relative to maturity-matched non-gymnasts; these differences persisted after adjustment for age, height and total body FFM (15). We hypothesized that variation in aBMD was due to both geometric and densitometric adaptations to impact loading, and that the ultradistal (metaphyseal, trabecular bone) and 1/3 (diaphyseal, cortical bone) regions of the radius would express these adaptations differently. The present study expands upon our prior work, reassessing scans from the established cohort in order to elucidate geometric, material, and strength properties of the ultradistal and 1/3 distal radius in premenarcheal gymnasts and non-gymnasts.

MATERIALS AND METHODS

Subjects represent a premenarcheal subset of 56 participants from an ongoing, longitudinal study of female artistic gymnasts and non-gymnasts (15). At enrollment, all participants (n=122) were aged 7–12 years and non-gymnasts were selected to match gymnasts for age and body size. Non-gymnasts were recruited from local grade schools, whereas gymnasts were recruited from local gymnastics clubs. Prior to study initiation, institutional review board approval was provided for the study design, and written informed consent was obtained from participants and their parents.

Participants were included in the present analyses if they reported self-assessed Tanner stage I (Tanner breast I and Tanner pubic I) or Tanner stage II (Tanner breast II and Tanner pubic II) at the time of an annual DXA scan. Non-Caucasian subjects were excluded from analyses, as there were insufficient numbers to account for racial variation. Gymnasts were included if they trained for at least 6 hours per week (hrs/wk) in the 2-year period prior to measurement, based upon a previous study (16). Following these criteria, 28 gymnasts and 28 non-gymnasts were evaluated.

All subjects attended semi-annual measurement sessions and completed questionnaires, assessing anthropometry, body composition, calcium intake and pubertal stage, as previously described (15). At these semi-annual sessions, weekly hours of organized physical activity (including gymnastics) were recorded by interview; for most gymnasts, gymnastics training was recorded in daily logs. Mean values for physical activity and calcium intake were calculated from records for the year prior to and including the focal DXA scan; these annual means were assessed as potential covariates of bone parameters. Pubertal stage and body size covariates were derived from assessments at the focal DXA session.

BONE MEASURES

Fan-beam DXA scans were performed on the distal third of the left forearm using a Hologic QDR 4500W scanner (Hologic Inc., Bedford, MA) and a standardized protocol; the coefficient of variation for the machine was 1%. Data were included for two regions of interest (ROI) in the distal radius: the ultradistal region, composed primarily of trabecular bone and the 1/3 region, composed primarily of cortical bone (see Figure 1). Hologic software (version 9.03D) was also used to calculate non-bone, fat free mass (FFM) and percentage of body mass as fat (%BF) from whole body scans. Forearm length (cm) was measured from the tip of the ulnar styloid to the tip of the olecranon with a ruler, by the DXA technician.

Figure 1. DXA Regions of Interest for the Distal Radius: Ultradistal, Mid-distal and 1/3.

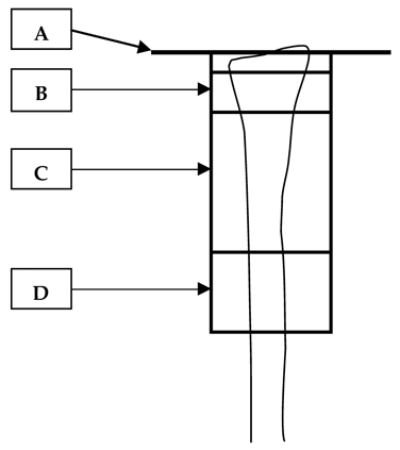
A= Reference line, drawn at the distal articular surface of the ulnar aspect of the radius.

B= Ultradistal ROI= 15.1 mm long (10.1–25.2 mm from the articular reference line).

C= Mid-distal ROI.

D= 1/3 ROI= 20.1–20.2 mm long, centered at 33% of measured ulna length.

Areal BMD (aBMD, g/cm²), projected area of the ROI (Area_ROI, cm²), length of the ROI (L_ROI, mm) and BMC of the ROI (g) were assessed for the ultradistal and 1/3 regions, separately. Ratio of regional BMC/total body FFM was calculated for each ROI to evaluate regional bone mineral accumulation (BMC_ROI) in relation to development of total body muscle (total body FFM) and mechanical loading applied during gymnastics. Mean ultradistal and 1/3 region periosteal widths (mm) were calculated by dividing Area_ROI by L_ROI, respectively. Results of analyses for mean periosteal width, Area_ROI, and periosteal cross-sectional area were similar; only periosteal width is reported.

GEOMETRIC MODELS

In order to derive measures of regional geometry and BMAD, models of simplified bone architecture were applied, as described below. Mathematical formulae are detailed in Table 1.

Table 1. Geometric and Bone Strength Formulae.

Estimate (units)	Description	Equation	Definitions
Ultradistal BMAD (g/cm3)	Bone Mineral Apparent Density, approximates total bone vBMD.	$\text{BMAD}=\frac{\text{BMC}\ast {\text{L}}_{\text{ROI}}}{\prod \ast {{\text{A}}_{\text{ROI}}}^2}$	BMC= bone mineral content; LROI= length of ROI= 15.1mm.
Ultradistal IBS (g2/cm4)	Index for Structural Strength in axial compression, incorporates geometry and total bone vBMD.	$\text{IBS}=\left({\text{BMAD}}^2\right)\ast {\text{A}}_{\text{C}}$ OR, by algebraic reduction, $\text{IBS}=\frac{1}{\prod }\ast {\text{aBMD}}^2$	Π =0.8, approximate relation of ultradistal bone width, depth and π; Ac= Π*W2(approximate ultradistal cross-sectional area); aBMD= areal BMD
1/3 BMAD (g/cm3)	Bone Mineral Apparent Density, modeled as a cylinder.	$\text{BMAD}=\frac{4·\text{BMC}·{\text{L}}_{\text{ROI}}}{\pi ·{{\text{A}}_{\text{ROI}}}^2}$	AROI= projected area of ROI; LROI= length of ROI; BMC= as above.
1/3 Z (mm3)	Section Modulus, index of bending strength.	$\text{Z}=\frac{\text{BMC}}{2\pi \rho }\left[\frac{\pi }{2}{\left(\frac{{\text{A}}_{\text{ROI}}}{{\text{L}}_{\text{ROI}}}\right)}^2-\frac{\text{BMC}}{\rho {\text{L}}_{\text{ROI}}}\right]$	ρ= 1.01 g/cm3 (uniform cortical vBMD);
1/3 CWT (mm)	Cortical Wall Thickness for a hollow cylinder of uniform cortical vBMD.	$\text{CWT}=\text{R}-\text{r}$ OR $\text{CWT}=\text{R}-{\left({\text{R}}^2-\left(\frac{\text{BMC}}{\pi \ast \rho \ast {\text{L}}_{\text{ROI}}}\right)\right)}^{1/2}$	$\text{periosteal\hspace{0.17em}radius}=\text{\hspace{0.17em}R}=\frac{1}{2}\ast \frac{{\text{A}}_{\text{ROI}}}{{\text{L}}_{\text{ROI}}}$ $\begin{array}{l}\text{endosteal\hspace{0.17em}radius}=\\ \text{r}={\left({\text{R}}^2-\left(\frac{\text{BMC}}{\pi \ast \rho \ast {\text{L}}_{\text{ROI}}}\right)\right)}^{1/2}\\ \rho =1.01\hspace{0.17em}\text{g}/{\text{cm}}^3\end{array}$
1/3 Cortical CSA (mm2)	Cross-Sectional Area of uniform cortical shell, resistance to load in axial compression.	$\text{CSA}=(\pi \ast \text{CWT})\ast (\text{W}-\text{CWT})$	CWT= cortical wall thickness; W= mean periosteal width, $\text{W}=\frac{{\text{A}}_{\text{ROI}}}{{\text{L}}_{\text{ROI}}}$
1/3 Intramedullary Diameter (mm)	Double the radius of the endosteal cavity.	Intramedullary Diameter= 2r $(2\text{r})=\text{W}-(2\ast \text{CWT})$	CWT= cortical wall thickness; r= radius of the endosteal cavity; W= mean periosteal width, $\text{W}=\frac{{\text{A}}_{\text{ROI}}}{{\text{L}}_{\text{ROI}}}$
Fall Strength Ratios	For 1/3 and ultradistal regions, indicative of strength under force of low trauma fall.	$1/3=\frac{Z}{Wt\times L_{\mathit{FOREARM}}}$ $\text{Ultradistal}=\frac{\mathit{IBS}}{Wt\times L_{\mathit{FOREARM}}}$	Z= 1/3 strength index; IBS= ultradistal strength index; Wt= total body mass; LFOREARM= ulna length (moment arm)

Ultradistal Region

In children, the ultradistal region is largely comprised of trabecular bone, with a cortical shell so thin that its depth cannot be measured accurately in vivo; therefore its assessment is simplified even in pQCT studies (21). As such, the ultradistal region was modeled as an elliptical cylinder of uniform volumetric density; “apparent” vBMD (BMAD) was calculated using the mean periosteal width and BMC of the ROI. To account for the elliptical geometry of the ultradistal radius, Sievänen et al determined that the coefficient Π approximates the general relationship between bone depth, mean periosteal width, and π (Π = 0.8); Π is used in computations of volume and/or cross-sectional area for this ROI (13). The index for structural strength in axial compressive loading, or IBS, was calculated to assess ultradistal bone strength (13). For a more detailed account, see Table 1.

1/3 region

In order to derive bone architecture and strength indices, the 1/3 region of the radial shaft was treated as a hollow cylinder, with all bone mineral distributed peripherally in a shell of uniform cortical thickness and vBMD. In accordance with the narrow range of chronological age and maturational variation in our sample, calculations employed a uniform cortical vBMD of 1.01 g/cm³; this value has been reported as a pQCT–measured mean cortical vBMD for Tanner II girls at the 65% region of the radial shaft (22). Furthermore, 1/3 cortical vBMD was assumed to be uniform across activity groups, based upon a pQCT study in which cortical vBMD did not differ between female competitive weightlifters and controls (3). Thus, our simplified model of the 1/3 radial shaft holds that: “periosteal width” is equal to “periosteal depth”; cortical vBMD is constant and equal to 1.01 g/cm³; thickness of the cortical shell is uniform; and all of the bone mineral mass is distributed within the cortical shell.

On this basis, we derived variables for the 1/3 region based upon the formulae of Sievänen et al (13). To assess the cortical shell, cortical wall thickness (CWT) and cortical compartment cross-sectional area were calculated. Intramedullary diameter was derived to assess cortical shell position, relative to the centroid. To assess bone strength in response to torsion and bending forces, we derived two related indices: section modulus (Z) and cross-sectional moment of inertia (CSMI), respectively. For a true cylinder, polar moment of inertia equals 2 × CSMI and indicates torsional strength (23). As results are similar, we report only section modulus. Calculations relied upon the equations of Sievänen et al and DXA-measured values for BMC, Area_ROI, L_ROI and calculated mean periosteal width (W) (See Table 1)(13).

Fall Strength Ratios

To assess bone strength relative to forces generated by a low trauma fall, we calculated a ratio of bone strength vs. the product of total body weight and a moment arm (weight × forearm length) (24–25). These ratios are described in the literature as “strength/weight ratios”, but we refer to them as “fall strength ratios”, to avoid confusion (24). Fall strength ratios were calculated using IBS for the ultradistal region and Z for the 1/3 region.

STATISTICAL ANALYSIS

The cohort was divided into subgroups based upon maturity level (Tanner I and Tanner II) and activity status (gymnasts and non-gymnasts). Comparisons were made between gymnasts and non-gymnasts within each maturity level. Analyses of variance (ANOVA) were used to test for significant differences between activity groups in age, body size and calcium intake, setting two-tailed alpha equal to 0.05. Site-specific, between-group differences in ratios of total body FFM/BMC and fall strength ratios were also assessed by ANOVA. For bone geometry, mass, density and strength variables, analyses of covariance (ANCOVA) were performed to adjust for age and height. Means, standard deviations, and significance levels (p-values) are reported for ANOVA comparisons of subject characteristics. For ANOVA and ANCOVA results, means, 95% confidence intervals and significance levels are reported.

Separate Pearson correlations for gymnasts and non-gymnasts assessed the association between dependent variables and age, body size, physical activity and calcium intake. For significant correlations between outcome variables and calcium intake or physical activity level, partial correlations were performed to adjust for the effects of age and height. Significant correlation coefficients and p-values are noted.

RESULTS

As previously reported in this cohort, gymnasts and non-gymnasts did not differ significantly in age, height, weight, FFM or calcium intake within either maturity group, although Tanner I non-gymnasts exhibited higher mean %BF than Tanner I gymnasts (Table 1)(15). Gymnastics participation (hrs/wk) was significantly higher in Tanner II than Tanner I gymnasts. Based upon exclusion criteria, all gymnasts had been participating in gymnastics for a minimum of two years at greater than 6 hrs/wk. Non-gymnasts performed a wide range of organized physical activities, at variable doses (hrs/week). All non-gymnasts with at least 5.0 hrs/wk of weight-bearing activity played basketball; many also participated in other activities, including soccer, lacrosse and dance.

Ultradistal Region

Tanner I gymnasts demonstrated significantly higher values than non-gymnasts for all bone outcomes, with differences persisting after ANCOVA adjustment for age and height (Table 2, Figure 2a). Similarly, Tanner II gymnasts exhibited higher means for all bone measures, although periosteal width did not achieve statistical significance (p<0.08). In addition, BMC/FFM and fall strength ratios were significantly higher among gymnasts than non-gymnasts (Figures 3a, 3b).

Table 2. Bone Parameters.

Bone parameters for the ultradistal and 1/3 distal radius are presented as raw means and means adjusted for age and height. Group means and 95% confidence intervals are listed separately for gymnasts and non-gymnasts for each Tanner stage. Plain text denotes raw values and ANOVA results; bold text denotes adjusted values and ANCOVA results. Italics denote derived variables.

	Tanner I		Tanner II
	Gymnasts (n= 12)	Non-Gymnasts (n= 10)	Gymnasts (n= 16)	Non-Gymnasts (n= 18)
Forearm Length (cm)	20.46 (19.72–21.20) 20.65 (20.18–21.11)	20.55 (19.74–21.36) 20.32 (19.82–20.83)	21.94 (21.38–22.49)* 22.17 (21.65–22.69)**	21.11 (20.59–21.64) 20.90 (20.42–21.39)
Ultradistal Radius
BMC (g)	0.90 (0.82–0.98)*** 0.91 (0.83–0.98)***	0.66 (0.57–0.75) 0.64 (0.56–0.73)	1.02 (0.95–1.10)*** 1.03 (0.97–1.09)***	0.84 (0.77–0.90) 0.83 (0.77–0.89)
Areal BMD (g/cm2)	0.365 (0.343–0.386)*** 0.367 (0.346–0.389)***	0.297 (0.273–0.320) 0.294 (0.270–0.318)	0.380 (0.363–0.396)*** 0.380 (0.363–0.397)***	0.320 (0.304–0.336) 0.320 (0.304–0.336)
Mean Periosteal Width (mm)	16.20 (15.43–16.96)* 16.33 (15.62–17.04)**	14.68 (13.84–15.52) 14.52 (13.74–15.30)	17.84 (17.06–18.63) 17.96 (17.25–18.66)	17.27 (16.53–18.01) 17.17 (16.51–17.83)
Bone Mineral Apparent Density (BMAD, g/cm3)	0.282 (0.267–0.298)* 0.282 (0.265–0.299)*	0.254 (0.236–0.271) 0.254 (0.235–0.272)	0.266 (0.254–0.279)*** 0.265 (0.251–0.279)**	0.233 (0.221–0.245) 0.234 (0.221–0.247)
Index of Structural Strength (IBS, g2/cm4)	0.168 (0.149–0.187)*** 0.170 (0.151–0.189)***	0.111 (0.091–0.132) 0.109 (0.088–0.129)	0.182 (0.167–0.196)*** 0.182 (0.167–0.197)***	0.129 (0.115–0.143) 0.129 (0.115–0.143)
1/3 Distal Radius
BMC (g)	1.09 (1.03–1.16)*** 1.10 (1.04–1.16)***	0.91 (0.84–0.98) 0.90 (0.83–0.96)	1.26 (1.18–1.34)** 1.27 (1.19–1.36)**	1.11 (1.03–1.18) 1.10 (1.02–1.17)
Areal BMD (g/cm2)	0.511 (0.487–0.535)* 0.516 (0.495–0.536)**	0.475 (0.449–0.501) 0.469 (0.447–0.492)	0.548 (0.526–0.569)* 0.551 (0.529–0.573)*	0.514 (0.494–0.535) 0.512 (0.491–0.532)
Mean Periosteal Width (mm)	10.62 (10.23–11.01)*** 10.62 (10.20–11.03)**	9.52 (9.09–9.94) 9.52 (9.07–9.98)	11.41 (10.92–11.90)* 11.44 (10.91–11.98)*	10.69 (10.23–11.15) 10.66 (10.16–11.16)
Bone Mineral Apparent Density (BMAD, g/cm3)	0.615 (0.577–0.654) 0.622 (0.586–0.658)	0.637 (0.594–0.679) 0.629 (0.589–0.668)	0.613 (0.579–0.647) 0.615 (0.578–0.653)	0.617 (0.585–0.649) 0.615 (0.580–0.650)
Section Modulus (Z, mm3)	99.76 (90.90–108.62)*** 100.17 (90.83–109.51)***	73.10 (63.39–82.80) 72.60 (62.34–82.86)	124.32(111.24–137.39)* 125.72 (112.02–139.43)*	102.44(90.12–114.77) 101.19(88.37–114.01)
Cortical Wall Thickness (mm)	1.99 (1.87–2.12) 2.02 (1.91–2.12)*	1.87 (1.73–2.00) 1.84 (1.72–1.95)	2.13 (2.02–2.24) 2.14 (2.03–2.26)	2.00 (1.90–2.11) 1.99 (1.88–2.10)
Cortical Cross-Sectional Area (mm2)	53.76 (50.66–56.86)*** 54.21 (51.25–57.17)***	44.70 (41.23–48.09) 44.16 (40.91–47.42)	61.97 (58.04–65.90)** 62.53 (58.54–66.51)**	54.45 (50.75–58.16) 53.96 (50.24–57.69)
Intramedullary Diameter (mm)	6.64 (6.13–7.14)* 6.58 (6.07–7.09)	5.79 (5.24–6.34) 5.85 (5.29–6.41)	7.15 (6.60–7.70) 7.16 (6.55–7.76)	6.69 (6.17–7.20) 6.68 (6.11–7.25)

BMD= bone mineral density; BMC= bone mineral content.

^*p<0.05,

^**p≤0.01,

^***p≤0.001, significantly higher mean for ANOVA and ANCOVA, respectively.

Figure 2.

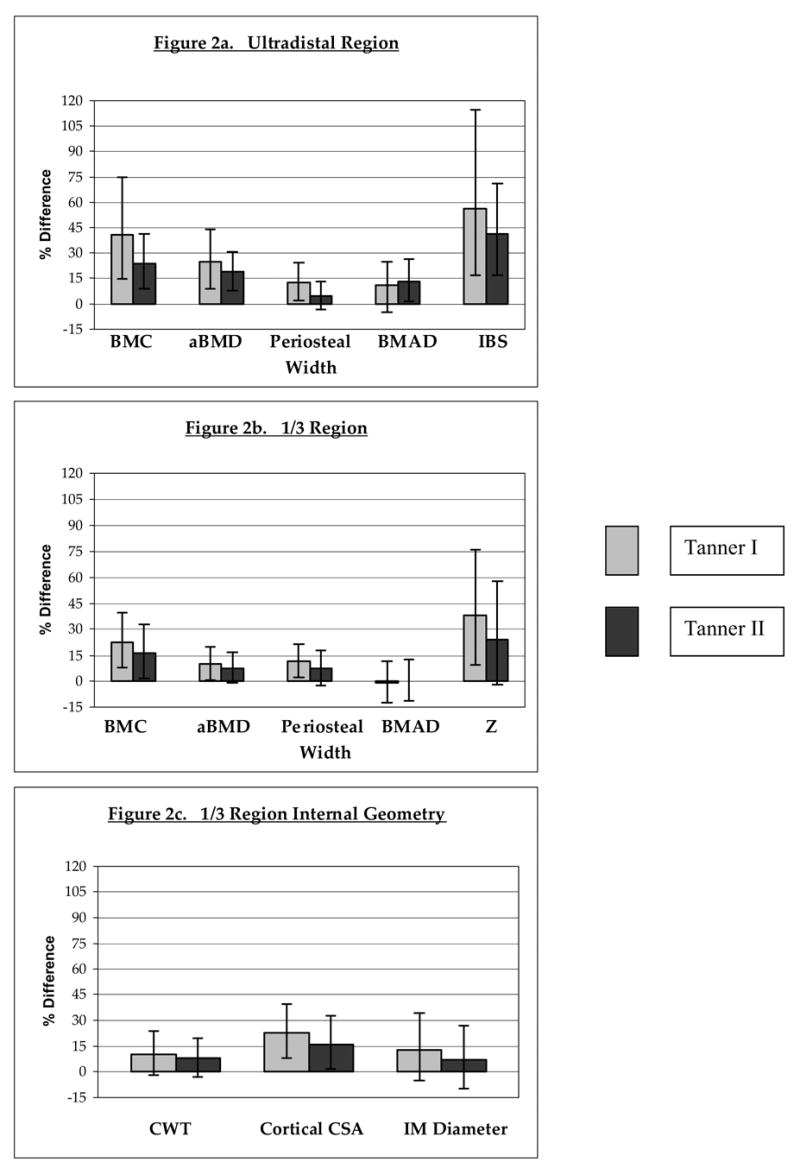
Percentage differences are depicted for bone parameters of gymnasts relative to non-gymnasts, divided by Tanner stage and bone site: a) ultradistal region; b) 1/3 region; c) 1/3 region internal bone geometry. Bars represent 95% confidence intervals.

BMC= bone mineral content; aBMD= areal bone mineral density; Periosteal Width= mean periosteal width; BMAD= bone mineral apparent density; IBS= index of bone strength in axial compression; Z= section modulus; CWT= cortical wall thickness; CSA= cross-sectional area; IM Diameter= intramedullary diameter.

For all percentage differences, p<0.05, except: Tanner II ultradistal mean periosteal width (p=0.076); 1/3 BMAD for both Tanner groups (p=NS); Tanner II 1/3 CWT (p=0.064); 1/3 IM diameter (Tanner I, p=0.06; Tanner II, p=NS).

Figure 3.

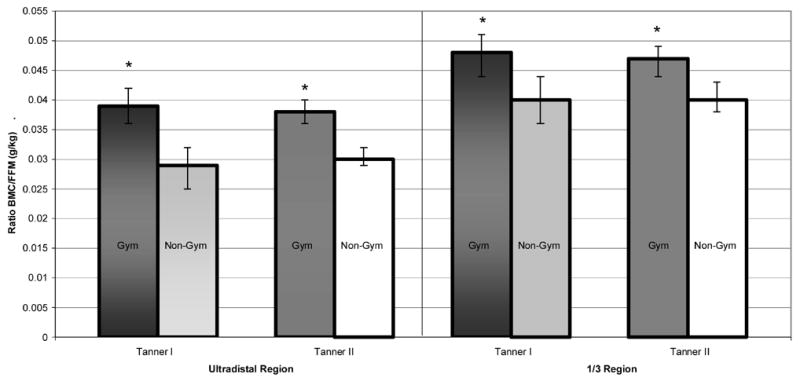
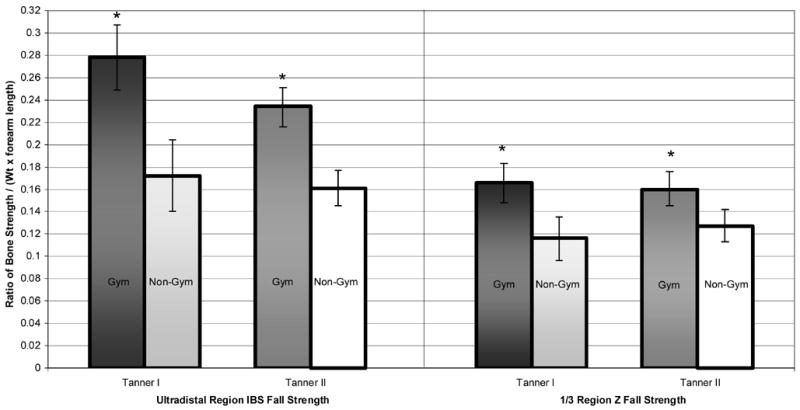
Ratios of BMC/FFM and fall strength are depicted as means with 95% confidence intervals for gymnasts (Gym) and non-gymnasts (Non-Gym), separated by Tanner stage and bone site: a) BMC/FFM; b) Z fall strength and IBS fall strength.

BMC= bone mineral content; FFM= DXA-measured fat-free mass;

Z Fall Strength = section modulus/(forearm length × weight);

IBS Fall Strength= index of structural strength in axial compression/(forearm length × weight);

* denotes Gym > Non-Gym, ANOVA p<0.05.

1/3 Region

After ANCOVA adjustment for age and height, Tanner I gymnasts demonstrated significantly higher adjusted means than non-gymnasts for all bone outcomes, except intramedullary width (p<0.07) and BMAD (Table 2; Figures 2b, 2c). Tanner II results were similar, except that differences in cortical wall thickness were not significant (p<0.07). For both maturity groups, BMC/FFM and bone fall strength ratios were significantly higher in gymnasts than non-gymnasts (Figures 3a, 3b). Means for BMC/FFM ratios were consistent within activity groups, across maturity levels.

CORRELATION RESULTS

FFM

At both sites, gymnast FFM was uncorrelated with BMAD (p>0.28). A strong trend of positive correlation was found between FFM and 1/3 intramedullary diameter in gymnasts (R=+0.37, p=0.055). All other bone measures and derived indices were positively correlated with FFM in gymnasts (R≥+0.38 to +0.76, p<0.05).

For non-gymnasts, correlation results were similar, with two exceptions: FFM was NEGATIVELY correlated with ultradistal BMAD (R=−0.45, p<0.02) and the positive correlation with cortical wall thickness did not achieve statistical significance (R=+0.35, p=0.06).

Height

Gymnasts demonstrated results for height correlations that were virtually identical in magnitude and direction to those for FFM, except that 1/3 intramedullary diameter was not correlated with height (p>0.30).

In non-gymnasts, height was a less potent correlate of bone variables than FFM; the only significant height correlates were: ultradistal mean periosteal width (R=+0.63, p=0.000), ultradistal BMC (R=+0.59, p=0.001), 1/3 aBMD (R=+0.44, p<0.05) and 1/3 CWT (R=+0.42, p<0.03). Strong trends were demonstrated for correlation of non-gymnasts’ height vs. ultradistal aBMD, ultradistal IBS, 1/3 BMC and 1/3 cortical cross-sectional area (all R>+0.36, p<0.11). At the ultradistal site, non-gymnast BMAD demonstrated a very strong trend toward an inverse relationship with height (R= −0.31, p=0.05).

Age

In general, age was the least potent correlate of bone outcome variables. For gymnasts, all bone variables were positively correlated with age (R=+0.45, p<0.02), except BMAD and intramedullary width. In contrast, for non-gymnasts, only ultradistal BMC and periosteal width were positively correlated with age (R>+0.50, p<0.01).

Physical Activity

Among the gymnasts, gymnastic activity (hrs/wk) was significantly, positively correlated with total forearm aBMD and all ultradistal measures except for BMAD. Gymnastics activity was significantly, positively correlated with all 1/3 measures, except for cortical wall thickness (R=+0.24, p<0.11), cortical compartment cross-sectional area (R=+0.36, p=0.06) and BMAD (no correlation). However, none of these correlations remained statistically significant after adjustment for age and height by partial correlation, although Z and periosteal width demonstrated strong trends (R=+0.39, p=0.05; R=+0.36, p<0.07).

In non-gymnasts, organized weight-bearing physical activity (hrs/wk) was not significantly correlated with any bone measure except for ultradistal BMAD (R= +0.44, p<0.02), for which height and FFM suggested inverse relationships. After adjustment for age and height, the partial correlation between physical activity and ultradistal BMAD remained statistically significant (R= +0.52, p< 0.01).

Diet

Calcium intake was not significantly correlated with any forearm measure, although a strong trend was demonstrated for negative correlation between ultradistal BMAD and calcium intake among non-gymnasts (R=−0.34, p<0.08). This relationship was not reflected by any correlation between calcium intake and ultradistal BMC, nor was there any correlation between calcium intake and any bone variable among gymnasts.

DISCUSSION

In this cohort of premenarcheal females, mechanical loading was associated with dramatic adaptations in bone strength indices. At the diaphysis, these adaptations were a function of larger bone geometry; volumetric apparent density was not elevated at this site. In contrast, at the metaphysis, greater bone strength in gymnasts was primarily a function of higher volumetric apparent density (BMAD); although for Tanner I gymnasts, larger geometry also contributed to ultradistal bone strength.

These site-specific adaptations may be attributable to differences in force application and bone composition at the 1/3 and ultradistal sites. At the diaphysis, cortical bone and bending forces predominate (3). Peripheral distribution of bone mass in an enlarged cortical shell provides the most efficient resistance to bending forces (3–4). Accordingly, gymnasts in the current study demonstrated greater 1/3 periosteal width and cortical cross-sectional area compared to non-gymnasts, indicating higher levels of periosteal apposition in response to mechanical loading. In contrast, at the primarily trabecular ultradistal site, bone is highly metabolically active and responsive to fluctuations in levels of circulating sex hormones. Wide, dense trabecular structure optimizes resistance to axial compressive forces that predominate at this location (3–4). Correspondingly, in the present study, gymnasts’ ultradistal bone strength is higher than non-gymnasts due to a combination of greater volumetric apparent density and bone width.

In gymnasts, elevated BMC levels indicate that mechanical loading enhances bone accrual via weight-bearing and impact loading. At both sites, adjusted BMC was augmented and the ratio of regional BMC/total body FFM was higher in gymnasts than in non-gymnasts. The magnitude of these differentials was dictated by bone site; gymnasts demonstrated advantages of 17.5 to 20% at the 1/3 region and 26.7 to 34.5% at the ultradistal region. The larger ultradistal differential suggests that adaptation to loading requires more bone mass at this metaphyseal site. This is not surprising, given that metaphyseal resistance to axial compression requires both high total bone density and CSA, whereas diaphyseal resistance to bending forces may be improved in a more efficient manner, through peripheral distribution of bone mass.

Observed differentials in BMD, BMC and geometry are amplified when considered in biomechanical terms; strength formulae multiply and exponentiate geometric and densitometric terms, exaggerating differences (see Table 1). In the current study, strength indices demonstrated 24–38% higher diaphyseal strength (Z) and 41–56% higher metaphyseal strength (IBS) in gymnasts than non-gymnasts. These gymnastics-related strength benefits are greater than the Z differential reported for sexual dimorphism in Tanner I children and similar to sexual dimorphism in Tanner II children (26).

Strength indices were calculated using DXA-measured BMC, and derived assessments of bone geometry and density. For example, at the ultradistal radius, IBS assesses bone strength using the square of BMAD and bone width, exponentially increasing the raw values. At the diaphysis, Z is related to the cubic function of bone width (in our case, derived from projected area) and amplifies width differences accordingly. Similarly, strength-strain index (SSI- the standard pQCT bone strength assessment) accentuates geometric differences by incorporating the vBMD of each pQCT voxel into the formula for Z (26). Between-group comparisons of SSI are analogous to comparisons of Z, if equivalent cortical vBMD is assumed; this simplification is supported by Ward et al (11), who did not identify significant differences in mean cortical vBMD between pre-pubertal gymnasts and non-gymnasts.

Fall strength indices were substantially higher in gymnasts than non-gymnasts at both sites. At the 1/3 region, activity group differentials were considerable (Tanner I gymnast advantage = 59.4%; Tanner II gymnast advantage = 34.3%), despite longer forearms in Tanner II gymnasts (forearm length is a factor in the ratio denominator). These advantages were even greater at the ultradistal region (Tanner I gymnast advantage= 45.3%, Tanner II gymnast advantage=61.6%). In this age range, at the ultradistal site, risk of low trauma fractures is high (24), and high fracture risk has been associated with “asynchrony” between linear growth velocity and bone mineral accrual (24). These fall strength index comparisons highlight the enhancement of bone strength attributable to loading, and support the theory that localized weight-bearing and/or impact activity may reduce risk of low trauma forearm fractures in this maturity range.

Previous investigators have provided evidence of a transient reduction in BMD related to high rates of linear growth during early puberty, suggesting asynchrony between linear growth and bone mass accumulation (28, 29). Specifically, a pronounced lag has been demonstrated for arm BMC peak velocity relative to height and total body FFM peak velocities (30). Thus, although FFM and height are typically strong predictors of BMD and BMC (due to parallel growth rates), the relationship uncouples during this phase of asynchrony. In the present analysis, non-gymnast ultradistal BMAD was negatively correlated with total body FFM, with a similar trend for height; this would be expected during a lag in BMC accrual. In contrast, gymnast ultradistal BMAD did not correlate negatively with height or FFM, suggesting that high levels of weight-bearing/impact activity may alleviate asynchrony between linear growth and bone mass accumulation at this site. Furthermore, non-gymnast ultradistal BMAD was positively correlated with hours per week of weight-bearing physical activity, corroborating the results of prior studies indicating that other weight-bearing activities may be associated with skeletal benefits (2, 6–7).

In a recent study, Ward et al used pQCT to assess the radius, comparing Tanner I gymnasts to non-gymnasts (aged 5.4–11.9 years) and analyzing males and females together (11). These comparisons yielded similar site-specific differences to those found in our Tanner I girls. In the radial diaphysis, total bone CSA and cortical CSA were higher in gymnasts than non-gymnasts for both studies, although percentage differences were of higher magnitude for our cohort. In our analyses, cortical wall thickness was elevated in female gymnasts compared to non-gymnasts, but Ward et al only found a significant differential in males. Finally, diaphyseal strength was greater for gymnasts than non-gymnasts in both studies. Our differential was four times greater than that reported by Ward et al (11), this may be due to examination of a different diaphyseal site (50% vs. 1/3).

At the ultradistal radius, Ward et al’s gymnasts exhibited higher total bone vBMD than non-gymnasts, similar to our own finding of higher apparent vBMD at this site. However, in contrast to our findings, Ward et al found no activity-related differences in total bone cross-sectional area at the ultradistal radius. Differences in the methodologies used to assess periosteal dimensions may explain the discordance between studies for metaphyseal comparisons. Our assessment of periosteal width is derived by dividing projected area by length of the ROI; this two-dimensional measure fails to account for variation in bone depth. As a result, if bone shape or aspect ratio (width vs. depth) differs substantially between subjects and/or systematically by activity group, then our bone width comparisons provide an incomplete assessment of bone geometry. In this case, failure to account for bone depth would yield different results from pQCT-measured total cross-sectional area, which assesses width, depth and shape.

In addition, our mean periosteal width reflects bone dimensions along the entire ROI, extending from approximately 5% to 12% of the ulna length (proximal to an ARTICULAR reference). In contrast, Ward et al used pQCT to measure cross-sectional area for a discrete 2 mm section of bone at 4% of the ulna length (proximal to a PHYSEAL reference). Our ultradistal ROI includes Ward et al’s pQCT site, but the majority of the ROI extends proximally from the pQCT site. Inclusion of proximal bone may account for the greater metaphyseal width demonstrated by gymnasts in our study, particularly if this proximal region is a more sensitive barometer of geometric change. This possibility is supported by findings from a study of female tennis players, where greater side-to-side percentage differences in bone area were demonstrated in the “mid-distal” region than at both ultradistal and 1/3 regions (5). The potentially hyper-responsive mid-distal region is contiguous with the proximal zone of our ultradistal ROI (see Figure 1).

Finally, Ward’s cohort included male subjects who were not equally represented in the two activity groups, over-representing males among non-gymnasts and females among gymnasts. This unbalanced inclusion of males may have reduced the magnitude and significance of all of Ward’s comparisons, as many of their analyses indicated smaller magnitudes for activity effects among males. Furthermore, other studies have reported sexual dimorphism in bone strength and other bone indices among pre-pubertal children (26, 27). Nevertheless, considering methodological differences, our results appear to complement and corroborate the pQCT findings of Ward et al.

Other studies have evaluated site-specific responses to loading, in the context of a racquet sports model. Several comparisons report side-to-side differences in the arms of adult players who began participation during childhood (1, 4, 5). Kontulainen et al used pQCT to assess the 50% humeral shaft site and the 4% distal radius site in women who began their sport at or before menarche (4). Greater side-to-side differences in BMC, total bone CSA, medullary cavity and cortical shell dimensions contributed to greater torsional Bone Strength Index at the humeral shaft for players compared to controls. In contrast, at the ultradistal radius, players exhibited a significant difference in total bone CSA between dominant and non-dominant arms, but this was not significantly greater than side-to-side differences observed in controls. Both BMC and trabecular density side-to-side percentage differences were significantly higher in players than controls at the ultradistal radius (4).

In a pQCT study of adult males, Haapasalo et al found greater total bone CSA in the dominant vs. non-dominant ultradistal radius, yet this difference was not significantly greater than the side-to-side percentage difference for controls (1). In contrast, BMC, total bone CSA, cortical CSA, and indices of bone strength all demonstrated greater side-to-side percentage differences for players vs. controls at the 30% radius and 50% humerus diaphyseal sites.

Ducher et al used DXA to evaluate side-to-side differences in aBMD and bone area, comparing tennis players and non-players (adult males and females). Percentage differences were greater for bone projected area than aBMD at the radial shaft (“mid-distal” and 1/3 regions), whereas aBMD differences were greater than bone projected area differences at the ultradistal region (5).

Although these studies of adult racquet sport participants do not directly compare players to controls, the side-to-side comparisons provide evidence of geometric response to loading at both diaphyseal and metaphyseal sites (1, 4, 5). Loading adaptations appear to emphasize geometry at the diaphysis and volumetric density at the metaphysis, as in our study.

In pre-pubertal female tennis players, Bass et al used MRI and DXA to assess side-to-side differences in humerus geometry and strength (12). At mid-shaft (50–60%) and distal (30–40%) humerus sites, significant side-to-side differences were demonstrated for total bone CSA and cortical compartment CSA. Intramedullary cavity CSA was significantly higher at the dominant mid-humerus, but not at the distal humerus for Tanner I girls. Significant side-to-side differences in polar moment of inertia (I_p, mm⁴) were identified for the 50% and 30–40% distal humeral shaft sites. These intrasubject comparisons at two diaphyseal humerus sites yielded lower percentage differences than our gymnast vs. non-gymnast analyses at the diaphyseal (1/3) radius; several factors may be responsible for this lower magnitude. First, loading adaptations were not evaluated at the same site. Bass et al assessed the humerus, whereas our work assessed the radius; these sites may exhibit different responses to loading. Second, it is likely that tennis and gymnastics apply loads at different magnitudes and in different directions. Finally, Bass et al’s side-to-side study design controls for inter-individual genetic variation, potentially obliterating interactions that may amplify responses to mechanical loading. Qualitatively, Bass et al’s findings are similar to ours, providing evidence that mechanical loading stimulates increased diaphyseal bone strength through enlarged total bone and cortical dimensions during growth.

Limitations

In general, fan beam DXA-derived measures of bone geometry, BMC and aBMD are subject to magnification error that varies by distance of the region of interest from the X-ray source (14). This error is particularly influential in comparisons involving different body sizes, where considerable variation in size of the soft-tissue envelope can result in large differences in distance of the ROI from the X-ray source. Because the distal forearm demonstrates negligible intra- and inter-subject variability in soft tissue envelope size, DXA-measured BMC, projected area and aBMD are reliable (14), providing accurate information for geometric and strength derivations.

Many of our analyses rely upon simplified geometric assumptions for derivations of bone geometry and strength indices (13). These bone assessments are based upon 2-dimensional measurements that do not account for bone depth out of the DXA plane or other variations in the 3-dimensional structure of the bone (31). Certainly, this methodology does not comprehensively assess complex bone architecture.

At the diaphysis, we relied upon a geometric model that assumes uniform peripheral distribution of bone to derive intramedullary and cortical compartment values from measured periosteal width and BMC. Our results yielded pronounced differences in cortical cross-sectional area for gymnasts compared to non-gymnasts, whereas intramedullary diameter differences were not demonstrated. These findings mirror the results of side-to-side comparisons in loaded vs. non-loaded arms of Tanner I, female tennis players; in this previously cited MRI study of the 30–40% distal humerus, significant differences were identified for cortical CSA and periosteal CSA, but not for intramedullary diameter (12). A similar pattern was reported by Ward et al for Tanner I gymnast vs. non-gymnast comparisons at the 50% radius (11). Concordance of our results with results from these 3-dimensional bone analyses supports the use of a simplified geometric model to interpret DXA data for the growing radius (11, 12). In addition, our derivations assume a uniform cortical vBMD of 1.01 g/cm³ for all gymnasts and non-gymnasts, supported by the results of Ward et al (11). Nonetheless, it should be noted that the validity of our results would be marred in the event of an activity-related cortical vBMD differential.

Thus, although the diaphysis is not truly a perfect hollow cylinder, use of Sievanen’s simplified model provides similar results to MRI and pQCT evaluations in this age group (11, 12). Future studies should directly assess the validity of this methodology, through analysis of contemporaneous DXA and pQCT scans in the context of physical activity, age and maturational variation; DXA-derivations and models should be compared to pQCT output for bone geometry, strength indices and compartmental vBMD.

Finally, gymnasts demonstrated elevated ultradistal BMAD, analogous to high total bone vBMD. Our DXA-derived methods cannot discern whether this higher apparent density is a function of increased trabecular volumetric density, increased cortical shell thickness, or a combination of the two. These properties must be specifically addressed using pQCT and/or micro-QCT to isolate the adaptation of cortical and trabecular structure to mechanical loading, accounting for male-female differences (32).

Conclusion

Bone response to mechanical loading is exhibited through site-specific variation in volumetric and geometric properties. Adaptation to weight-bearing/impact activity is dominated by elevated BMAD at the ultradistal radius and by larger bone geometry in the 1/3 region. Both ultradistal and 1/3 sites exhibit significant bone mass and strength benefits that are attributable to impact/weight-bearing stimulation in these premenarcheal girls. Thus, in this cohort, significant site-specific advantages in bone mass, strength and geometry underlie the areal BMD benefit associated with physical activity.