Abstract
This paper examines the relation between health, individual income, and relative deprivation. Three alternative measures of relative deprivation are described, Yitzhaik relative deprivation, Deaton relative deprivation, and log income difference relative deprivation, with attention to problems in measuring permanent disadvantage when the underlying income distribution is changing over time. We used data from the National Longitudinal Surveys of Youth, a US-based longitudinal survey, to examine the associations between disadvantage, measured cross-sectionally and aggregated over the life course, and intrauterine growth restriction (IUGR). We reject the hypotheses that any of the economic measures, whether permanent/contemporaneous or individual/relative, have different associations with IUGR in terms of sign and significance. There was some evidence that permanent economic disadvantage was associated with greater risk of IUGR than those on the corresponding contemporaneous measures. The fitted values from logistic regressions on each measure of disadvantage were compared with the two-way plots of the observed IUGR-income pattern. Deaton relative deprivation and log income difference tracked the observed probability of IUGR as a function of income more closely than the other two measures of relative deprivation. Finally, we examined the determinants of each measure of disadvantage. Observed characteristics in childhood and adulthood explained more of the variance in log income difference and Deaton relative deprivation than in the other two measures of disadvantage. They also explained more of the variance in permanent disadvantage than in the contemporaneous counterpart.
Keywords: Relative deprivation, Individual income, Intrauterine growth restriction (IUGR), USA
Introduction
There is wide agreement about the existence of an economic gradient in health (Marmot & Brunner, 2005; Marmot et al., 1991), but less agreement about how that economic gradient in health is related to relative economic status and income inequality. (Kawachi, Kennedy, & Wilkinson, 1999; Kawachi, Subramanian, & Almeida-Filho, 2002; Lynch et al., 2004; Marmot, 2006; Subramanian & Kawachi, 2004, 2006; Wilkinson & Pickett, 2006). Little systematic investigation has been conducted to explore the overlap between the effects on health of individual economic status, relative economic status, and income inequality. Comparisons across studies are complicated because empirical measures economic status are often chosen by data availability rather than well-developed theoretical linkages between the outcome of interest and the economic measure being employed (Braveman et al., 2005). Furthermore, there is increasing recognition that contemporaneous exposure to disadvantage may not have an immediate impact on health and that permanent measures over the life course may more strongly be related to health (Graham & Power, 2004; Kuh & Hardy, 2003; Mellor & Milyo, 2003; Reagan & Salsberry, 2005; Subramanian, Blakely, & Kawachi, 2003; Subramanian, Kawachi, & Kennedy, 2001). However, there is limited evidence about the contribution of permanent vs. contemporaneous disadvantage to the economic gradient in health. Finally, economic disadvantage is usually treated as exogenously determined, which obscures the determinants of disadvantage and limits the scope empirical evidence to guide policy interventions.
In this paper, we discuss the relation between individual income, relative deprivation, and income inequality. We describe alternative measures of relative deprivation, with attention to problems in measuring permanent disadvantage when the underlying income distribution is changing over time. We compare associations between measures of disadvantage and health of newborns, measured by intrauterine growth restriction (IUGR) in full-term infants. Because there is evidence that IUGR is tied to life course maternal factors (Lu & Halfon, 2003; Misra, Guyer, & Allston, 2003), we compare the effects of permanent and contemporaneous disadvantage on IUGR to test whether life course measures have larger effects than cross-sectional measures. (Doctor, O’Riordan, Kirchner, Shah, & Hack, 2001; Moore & Davies, 2005; Strauss & Dietz, 1998). We conclude with an examination of the life course correlates of disadvantage.
Theoretical considerations: individual income, relative deprivation, income inequality
Typically, health researchers control for access to material resources by including individual income, or a proxy for it, as a regressor in health outcome equations. Recognition that the marginal contribution of income to health declines with the level of income has led to the widely used specification of health as a function of the natural log of individual income. More recently, researchers have begun to explore the hypothesis that relative deprivation, measured as a function of income relative to one’s reference group, may be a more powerful predictor of health outcomes than individual income (Deaton, 2001; Eibner & Evans, 2005).
Relative deprivation was first formalized by Yitzhaki (1979), based on a concept suggested by Runciman (1966). Yitzhaki formulated the relative deprivation of individual i by computing the weighted sum of the difference between the income of individual i, xi, and the incomes of everyone in the reference groups with income above xi, where the weights are the fraction of the population with income at each level above xi. When dF(y) is the density function of the distribution of income, Yitzhaki’s formulation of relative deprivation (Yitzhaki relative deprivation) can be written as
Deaton suggested modifying the Yitzhaki measure by dividing it by mean reference group income. This normalization guarantees that Deaton relative deprivation is bounded between 0, for the individual with the highest income in the reference group, and 1, for the individual with the lowest income. Both measures are related to the Gini coefficient of aggregate income inequality. Yitzhaki relative deprivation has the property that total relative deprivation within a reference group equals mean reference group income times the Gini coefficient, i.e. ∫Yidf (y) = μG. Total Deaton relative deprivation equals the Gini coefficient.
Yitzhaki and Deaton relative deprivation are typically based on local reference groups stratified by geography, such as states or metropolitan statistical areas, and/or demographics such as education and race. The Deaton normalization is invariant to changes in price levels. When price levels vary across reference groups, one effect of the Deaton normalization is to control for local price level differences. The Yitzhaki relative deprivation measure can be modified to address these concerns by dividing by a regional price deflator. Hereafter, we refer to Yitzhaki relative deprivation as one that controls for local price level differences.
When the underlying income distribution is not changing, for example in a cross-section regression at a single point in time, the functional relations between individual income, Yitzhaki relative deprivation, Deaton relative deprivation and the Gini coefficient have two important implications for empirical estimates of the association between health and relative deprivation. In linear regression, the coefficient on Yitzhaki relative deprivation equals the coefficient on the Deaton relative deprivation multiplied by mean reference group income. This relation will not hold exactly in nonlinear regression. Second, if the distribution of income is approximately lognormal as has been argued for the United States, Germany and the United Kingdom (Clementi & Gallegati, 2005), it is not possible to identify separate effects of individual income, Yitzhaki or Deaton relative deprivation, and income inequality as measured by the Gini coefficient. The reason for the lack of identification is that the log normal distribution is a two parameter distribution defined entirely by its mean and standard deviation. There are only two degrees of freedom in the income distribution, so three independent parameters cannot be identified in a regression model.
Even if the distribution of income is not approximately log normal and identification of three separate effects is theoretically possible, researchers should be cautious about overfitting a model with measures of individual income, relative deprivation and income inequality. This can be seen clearly in the case of a linear regression of an individual health outcome on the natural log of individual income, ln yi, and Yitzhaki relative deprivation:
Integration over the entire income distribution and the zero mean random disturbance term yields the following equation for average health:
In this example, the effect of a small change in the Gini coefficient on average health is α2μ. If Deaton relative deprivation is used in place of the Yitzhaki relative deprivation, the effect of the Gini coefficient on average health of the reference group equals the coefficient on Deaton relative deprivation.
One can construct other measures of relative income that lack such a functional relation with the Gini coefficient. Whether or not this is a desirable property depends on the application. One candidate is the difference in the natural log of an individual’s income and the natural log of the incomes of reference group members who have higher income. A log difference measure of relative deprivation (log difference relative deprivation) can be formalized analogously to Yitzhaki relative deprivation by
There is no theoretical reason to prefer one measure of relative deprivation over another when the underlying distribution of income is not changing. All three share two basic similarities. All are convex functions of individual income, i.e., they decline with increases in individual income, holding constant the distribution of income, and the advantage of a fixed addition to income decreases as the level of income rises. Second, the three measures of relative deprivation all increase with increases in income inequality, holding constant the individual’s own income and mean reference group income (Rothschild & Stiglitz, 1970). In the case of a log normal distribution of income, an increase in income inequality is an increase in the variance of log income holding constant mean income. An increase in the dispersion of other distributions is formalized by a mean-preserving spread that places greater weight in the tails of the distribution without changing the mean. Another way to think about a mean-preserving spread in income is to consider its effect on the Lorenz curve. Atkinson (1970) showed that a mean-preserving spread in income causes the Lorenz curve to shift down, without crossing. Relative deprivation is increased for all people except those with income above the level affected by the mean-preserving spread.
The primary difference between the log difference relative deprivation and the Deaton or Yitzhaki relative deprivation for a given income distribution is best illustrated by a graph. Fig. 1 plots the log difference relative deprivation and the Deaton relative deprivation as a function of individual per capita income, holding constant the distribution of income. We generated per capital household income under the assumption that income had a log normal distribution, where the mean and standard deviation of log per capita income were calibrated from 2000 Census data. The x-axis represents the level of per capita income in thousands. They-axis represents log difference relative deprivation and Deaton relative deprivation. Log difference relative deprivation crosses Deaton relative deprivation at about the 95th percentile of income, as calculated from the 2000 Census. Log difference relative deprivation has a steeper slope and has greater curvature than Deaton relative deprivation. Thus the change in log difference relative deprivation associated with a given increase in income is substantially larger than the change in Deaton relative deprivation for most of the income distribution. (The 90th percentile in 2000 Census data was $33,000 per capita.) Furthermore, the difference between the effects of a given change in income on the two measures is larger at lower levels of income, holding constant the distribution of income.
Fig. 1.
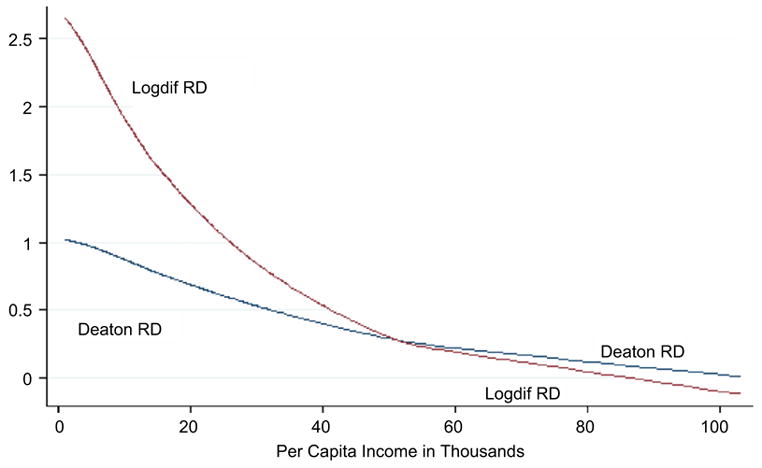
Plots of different measures of relative deprivation as a function of individual income, holding constant the distribution of income.
Comparisons across different measures of relative deprivation become more complex when measurements are taken over time and there are changes in both the mean and dispersion of the underlying income distribution. The empirical differences may be further complicated by changes over time in data collection procedures, especially with respect to top coding of income. An individual’s Yitzhaki relative deprivation and log difference relative deprivation are invariant with respect to changes in the income distribution that take place below his income, whereas Deaton relative deprivation is not invariant. In the case of a person with income at the 50th percentile, a 10% decrease in income of the first quartile will increase Deaton relative deprivation, because mean income declines, but leaves Yitzhaki relative deprivation and log difference relative deprivation unchanged, because the change occurred in the income distribution below the individual’s income.
Yitzhaki relative deprivation or log difference relative deprivation may be preferable to Deaton relative deprivation if theory suggests that health is not responsive to changes in the income distribution below the individual’s income, i.e. that people only make comparisons upwards. The log difference relative deprivation may be preferable to the other two if theory suggests that the effect of an increase in income has a substantially larger effect on relative deprivation at lower levels of income than at all but the highest levels of income, see Fig. 1.
Claims about associations between relative deprivation and health may not be robust to the formulation of relative deprivation when relative deprivation is measured over time and changes occur in both the mean and dispersion of the underlying income distribution. In English speaking countries, the decades since 1970 have seen large changes in income inequality as well as changes in mean income for different groups, who are often geographically concentrated. Gottschalk, Moffitt, Katz, and Dickens (1994) estimated that between one-third and one-half of the increase in earnings dispersion could be attributed to an increase in the dispersion of transitory income. Campbell, Lettau, Malkiel, and Xu (2001) found an increase in the volatility of individual stock prices relative to market volatility, which suggested that there has also been an increase in the dispersion of asset income over the last 30 years. These finding imply that contemporaneous income has become noisier as a proxy for permanent income in the US since 1970. Likewise, contemporaneous measures of relative deprivation have become noisier proxies for permanent ones. In considering the contribution of economic status to IUGR, permanent economic status may have a greater effect on health capital than contemporaneous measures, because formation of health capital is cumulative and contemporaneous measures are noisy proxies for permanent one.
We test for an association, not a causal relation, between disadvantage and IUGR. Understanding the underlying etiologies of poor birth outcomes remains a complex and important area of investigation (Basso, Wilcox, & Weinberg, 2006). The contributions of both maternal and paternal genotype (Lie, Wilcox, & Skjoerven, 2006; Reichman & Teitler, 2006; Selling, Carstensen, Finnstrom, & Sydsjo, 2006) as well as the socio-economic associations with IUGR are under intense study. Much of the recent work has focused on the association between IUGR with the maternal uterine environment (Fowden, Ward, Wooding, Forhead, & Constancia, 2006; Harding, 2001). For example, maternal preconceptional nutritional status and nutrition during pregnancy have been linked to the regulation of placental nutrient transport with implications for fetal growth (Bell & Ehrhardt, 2002; Fowden et al., 2006; Kramer, 1998; Kramer, Seguin, Lydon, & Goulet, 2000; Prada & Tsang, 1998; Sibley et al., 2005). Low prepregnancy weight status and small weight gain during pregnancy have been associated with low-income mothers (Kramer, 1998).
The effects of cigarette smoking during pregnancy has been extensively studied with fetal physiologic changes noted in response to maternal smoking during pregnancy (Pollack, Lantz, & Frohna, 2000). The mechanisms to explain these findings include a suppression of appetite caused by nicotine, a comprised uteroplacental vasculature induced by nicotine, and an increased exposure to carbon monoxide that decreases the fetal uploading of oxygen (Oncken, Hardardottir, & Smeltzer, 1998; Power & Jefferis, 2002). Smoking is known to occur more frequently in women of lower incomes, thus providing another channel through which SES is tied to IUGR (England, Kendrick, Gargiullo, Zahniser, & Hannon, 2001; Kramer et al., 2000; Lieberman, Gremy, Lang, & Cohen, 1994; Nordentoft et al., 1996; Okah, Cai, & Hoff, 2005).
Pregnancy-induced hypertension (Haelterman, Breart, Paris-Llado, Dramaix, & Tchobroutsky, 1997; Sibai, Dekker, & Kupferminc, 2005) and anemia have also been consistently associated with IUGR, both influenced by the economic status of the mother (Mahajan, Singh, Shah, Gupta, & Kochupillai, 2004; Prada & Tsang, 1998).
Any findings of an association between disadvantage and IUGR raise the question of what determines economic status. Individuals are not randomly assigned contemporaneous or permanent economic status. An association does not imply that there is a direct causal link between disadvantage and IUGR. As others have pointed out (Eibner & Evans, 2005; Kristenson, Eriksen, Sluiter, Starke, & Ursin, 2004), there may be an indirect pathway between health and economic status, in this case between IUGR and disadvantage that operates through maternal nutrition, smoking, pregnancy induced hypertension or maternal anemia.
Methods
Study population
We used data from the National Longitudinal Survey of Youth’s Child-Mother file (NLSYCM), a US-based longitudinal survey (Miller, 2004). The study sample was based on a nationally representative cross-section of women living in the US in 1978, born between 1957 and 1964, and over-samples of black and Hispanic women. The women were followed annually until 1994 and biennially thereafter. They report 3019 full-term, singleton, first births between 1979 and 1998. The final sample was 2676 women/infant dyads (89% of the original sample). We lost 118 observations because of missing data on birth weight. We also lost 222 observations because of missing data on disadvantage measures. The data are geocoded to the respondent’s metropolitan statistical area (MSA) of residence and their county of residence.
Data construction and measures
Dependent measure
The primary outcome of interest was IUGR in singleton, full-term infants born to first-time mothers. We limit the outcome to full-term infants, thus eliminating pre-term births, because pre-term births may have a different etiology (Kramer, Platt, Yang, McNamara, & Usher, 1999). A full-term infant was defined as an infant whose gestational age was reported as equal to or greater than 37 weeks. The identification and subsequent measure of an adverse birth outcome has been the subject of much discussion. For example, Wilcox (2001) has argued that the use of birth weight in population studies fails to account for other factors, e.g., gestational age. Even when gestational age is accounted for there are alternative measures for identifying small infants. Two such measures include the ponderal index, defined as birth weight (kg)/length (m)3) with percentiles developed by gestational weeks and small for gestational age (SGA), defined as birth weight below the tenth percentile, specific to gestational week (Zhang & Bowes, 1995). We use the Hoffman SGA criteria (Hoffman, Stark, Lundin, & Ashbrook, 1974) specific to gender. For example, an infant girl born at 40 weeks with a birth weight of less than 2919 g was classified as SGA. Birth weight, birth length and gestational age were reported by the mother beginning with the 1986 interview and biennially thereafter. The maximum reported gestational age was 42 weeks.
Economic measures of disadvantage
Log contemporaneous income
Maternal household income was obtained at each inter view and collected as a continuous measure with less than 2% of the sample incomes top coded. Total household income was top coded at $75,000 from 1979 to 1984 and $10 0,000 from 1985 to 1988. Beginning in 1989 the income of the top 2% was set to the average value of the income of the top 2%. Household income per capita was defined as total household income divided by the number of people in the household age 14 and above plus times the number of children under age 14. When household income was not available in the year of birth, we used household income from the previous interview. All income and relative deprivation measures were deflated to constant 1990 dollars in the Northeast with the annual regional price deflators reported by the Bureau of Labor Statistics. Per capita income was transformed by the natural logarithm to reflect concavity in the relation between income and IUGR.
Contemporaneous Yitzhaki relative deprivation
Data for reference group income were obtained from the 5% Public Use Micro samples (PUMS) of the 1980,1990 and 2000 decennial Censuses. Reference groups were defined by MSA of residence for urban respondents and counties groups, as defined by the Census, for rural respondents. About 2% of the highest income households were top-coded. In 1980, 1990 and 2000, the top-code was, respectively, $75,000, state median income above $400,000, and $999,998. In 1990 dollars, the top-code in 1980 was $119,000; in 2000, it was $759,000. Even absent any real changes in the distribution of income, relative deprivation would increase over time due to changes in top-coding procedures. The 1990 procedure of top-coding to the state median income of the top 2% is the best for purposes of calculating relative deprivation. To make relative deprivation more comparable a cross years, we used the 1990 conditional state median top code, appropriately deflated, and imputed this value when it exceeded the fixed top coding values in the 1980 and 2000 Census. This will mask real changes in the upper tail of the income distribution that occurred between 1980 and 2000, but it makes the relative deprivation values somewhat comparable across years.
Per capita income for each Census household in the NLSYCM respondent’s reference group was deflated by annual regional price deflators. Yitzhaki relative deprivation is the weighted sum of the difference between NLSYCM per capita income and the reference group per capita incomes exceeding it, divided by the weighted number of households in the reference group. Household weights reported in PUMS data indicated how many households each respondent household represented. We linearly interpolated relative deprivation for inter-Census years from calculations made using the two adjacent Census years. (For example, if a mother is observed in 1986 relative deprivation is .6 × reldep1980 + .4 × reldep1990, where the individual 1986 maternal income is used to compute relative deprivation using the 1980 Census and again using the 1990 Census.) Yitzhaki relative deprivation was divided by 1000, to facilitate presentation of the results.
Contemporaneous Deaton relative deprivation
It was calculated from the Yitzhaki measure, without division by 1000, divided by mean reference group income.
Contemporaneous Log difference relative deprivation
The calculation is similar to the Yitzhaki measure with the exception that NLSYCM per capita income and reference group income were replaced by their natural logarithms.
Log permanent income
The mother’s annual per capita income was calculated for all years when it was available from the beginning of the survey in 1979 until the year of birth of the child. Per capita annual income was deflated to 1990 dollars in the Northeast using annual regional price deflators published by the Bureau of Labor Statistics. Permanent income was the mean of deflated per capita income. The natural log of mean annual per capita income was the natural log of permanent income.
Permanent Yitzhaki relative deprivation
The annual contemporaneous Yitzhaki measure was calculated for each mother from 1979 until the year of birth of the child for all years in which per capita income was available. The Permanent Yitzhaki measure is the average of the annual values.
Permanent Deaton relative deprivation
The annual contemporaneous Deaton measure was calculated for each mother from 1979 until the year of the birth of the child from 1979 until the year of birth of the child for all years in which per capita income was available. The permanent Deaton measure is the average of the annual values.
Permanent log difference relative deprivation
The annual contemporaneous log difference measure was calculated for each mother from 1979 until the year of the birth of the child for all years in which annual per capita income was available. The permanent log difference measure is the average of the annual values.
Other covariates used in the analyses are defined in Table 1.
Table 1.
Description of sample (n = 2676)
| Variable | Mean (SD) or (%) |
|---|---|
| IUGR (defined as SGA) | 13% |
| Contemporaneous per capita income | $20,548 ($50,898) |
| ln contemporaneous income | 9.21 (1.42) |
| Contemporaneous Yitzhaki relative deprivation (divided by 1000) | 7.18 (4.48) |
| Contemporaneous Deaton relative deprivation | 0.46 (0.28) |
| Contemporaneous log difference relative deprivation | 0.70 (1.10) |
| Permanent income per capita | $12,987 ($16, 166) |
| ln permanent income | 9.12 (0.92) |
| Permanent Yitzhaki relative deprivation | 8.04 (3.44) |
| Permanent Deaton relative deprivation | 0.53 (0.21) |
| Permanent log difference relative deprivation | 0.81 (0.79) |
| White | 64% |
| Black | 21% |
| Hispanic | 15% |
| Drop out, maternal education <12 | 20% |
| High-school graduates, maternal education = 12 | 42% |
| Some college, 13 ≤ maternal education ≤ 15 | 21% |
| College, maternal education ≥ 16, | 17% |
| Mean marital status, average years married since leaving school and infant birth | 0.67 (0.32) |
| Father’s education—in years (grandfather of infant) | 10.98 (3.94) |
| Living with both parents at age 14 | 68% |
Data analysis
The analysis proceeded with a description of the sample. We estimated odds ratios using log is tic regression with IUGR as the outcome. The independent measures included indicators for race, Hispanic ethnicity, and education with the addition of one of the measures of economic disadvantage, both contemporaneous and permanent. We used state fixed effects to control for unobserved state differences in income inequality which may affect the generosity of the social safety net as well as state price level differences not otherwise captured by the annual regional price deflators.
As stated before, there is no theoretical reason to prefer one measure of disadvantage over another in an empirical application. But we have shown in Fig. 1 that the measures of disadvantage can have different empirical implications because of differences in their curvatures. To explore differences in the effect of alternative measures of permanent disadvantage on IUGR, we estimated the predicted probabilities of IUGR from the fitted values of each regression. We plotted the fitted values against permanent income and compared them to the observed relation between IUGR prevalence and permanent income.
To examine the observable determinants of disadvantage, we used ordinary least squares to regress each measure of disadvantage against traditional measures of socio-economic status including paternal education, family structure in adolescence, educational attainment, adult marital status, and race/ethnicity. We compare the fraction of total variance explained by these factors for each of the contemporaneous and permanent disadvantage measures.
Results
Table 1 presents the variables used in this analysis. Of the 2676 mothers, 64% were white, 21% were black, and 15% were Hispanic. The mean birth weight was 7.5 pounds (SD = 17 oz) or 3395 g and mean birth length was 20.24 in (SD = 1.42), with 13% of this sample meeting the threshold for IUGR. Twenty percent of mothers were high-school drop-outs; 42% had 12 years of education; 21% had some college; and 17% were college graduates. Mean marital status (fraction of years mother was married between leaving school and infant’s birth) was 67%. The mother’s own economic background measures showed that the mean number of years of education for her father was approximately 10 years and 68% of these women lived with both parents at age 14. Contemporaneous per capita income was higher than permanent per capita income, because income rises over the lifecycle. The standard deviation relative to mean of contemporaneous income was greater than that of permanent income. The same relation held between the contemporaneous and permanent measures of relative deprivation.
Table 2 presents the results of the state fixed effects logistic regression models with IUGR as the dependent variable and measures of economic status as the “risk”, controlling for race, ethnicity, and education status. The top half of the table displays the odds ratios and 95% confidence intervals using contemporaneous measures. Individual income and each of the three relative deprivation measures were significantly associated with IUGR. The bottom half of Table 2 displays the result using permanent measures of economic status. Again all four measures were significantly associated with IUGR. Results indicated that the effects on IUGR of permanent measures of economic status exceeded those of the respective contemporaneous measure.
Table 2.
Logistic odds ratios: dependent variable—IUG R; independent variable-measure of disadvantage a
| Measures of disadvantage | ||||
|---|---|---|---|---|
| Contemporaneous measures of disadvantage | ||||
| ln per capita income | 0.90 (0.83,0.97) | |||
| Deaton relative deprivation | 2.23 (1.39,3.58) | |||
| Yitzhaki relative deprivation | 1.06 (1.03,1.09) | |||
| Log difference relative deprivation | 1.14 (1.04,1.24) | |||
| Permanent measures of disadvantage | ||||
| ln per capita income | 0.84 (0.74,0.95) | |||
| Deaton relative deprivation | 3.63 (1.91,6.87) | |||
| Yitzhaki relative deprivation | 1.08 (1.04,1.13) | |||
| Log difference relative deprivation | 1.25 (1.09,1.42) | |||
State fixed effects regressions that include race/ethnicity and education covariates.
Each panel of Fig. 2 plots the fitted value of the logistic regression using a single measure of disadvantage against permanent per capita income compared with the observed probabilities of IUGR. Fig. 2a (log income) and Fig. 2b (Deaton relative deprivation) and show that the predicted probabilities using these measures closely track the observed empirical relation between IUGR and permanent per capita income. Fig. 2c (Yitzhaki relative deprivation) and Fig. 2d (Log difference relative deprivation) do not track the empirical distribution as well as Deaton relative deprivation and log income.
Fig. 2.
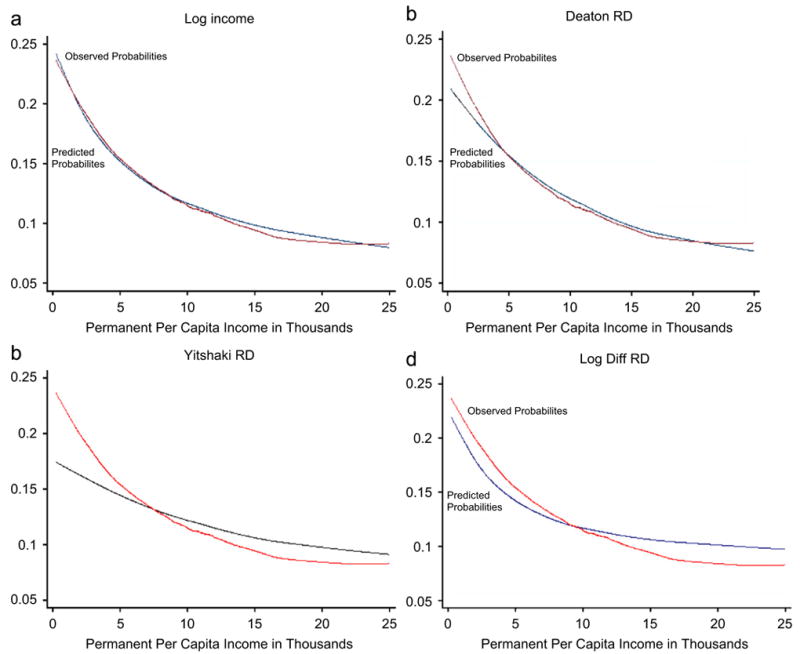
Comparison of the observed IUGR by income with predicted probabilities using alternative measures of permanent disadvantage.
Table 3 reports the results of OLS regressions examining the childhood and adult determinants of disadvantage. The coefficient estimates confirm that childhood and adult factors are statistically significant determinants of disadvantage. Childhood factors explained about half of the explained variance in the contemporaneous measures and about 2/3rds of the explained variance in the permanent measures. The R-squares on the permanent measures are at least as great as those on the contemporaneous measures. Observed characteristics explain 36% of the overall variance in the individualistic measure of disadvantage, i.e. log permanent income, and between 21% and 41% in the relative measures. The background characteristics explained 33% of the variance in permanent Yitzhaki relative deprivation, 41% of the variance in permanent Deaton relative deprivation, and 21% of the variance in permanent log difference relative deprivation.
Table 3.
State fixed effects OLS regressions of contemporaneous and permanent disadvantage (standard errors in parentheses) a
| Model 1 ln income | Model 2 Yitzhaki relative deprivation | Model 3 Deaton relative deprivation | Model 4 Log difference relative deprivation | |
|---|---|---|---|---|
| Contemporaneous measures | ||||
| Father’s education | 0.04 (0.01) | −0.07 (0.02) | −0.01 (0.001) | −0.02 (0.01) |
| Lived with both parents at 14 | 0.12 (0.05) | −0.83 (0.17) | −0.04 (0.01) | −0.10 (0.04) |
| Drop-out | −1.53 (0.08) | 4.90 (0.26) | 0.36 (0.02) | 0.77 (0.06) |
| High-school graduates | −0.93 (0.07) | 3.19 (0.21) | 0.22 (0.01) | 0.40 (0.05) |
| Some college | −0.59 (0.07) | 1.89 (0.24) | 0.13 (0.01) | 0.19 (0.06) |
| Mean marital status | −0.56 (0.08) | 3.07 (0.24) | 0.17 (0.01) | 0.50 (0.06) |
| Overall R–sq childhood factors only (1st two variables only) | 0.13 | 0.17 | 0.20 | 0.08 |
| Overall R–sq for reported regression with adult factors | 0.27 | 0.33 | 0.40 | 0.17 |
| Permanent measures | ||||
| Father’s education | 0.04 (0.04) | −0.10 (0.02) | −0.01 (0.001) | −0.03 (0.003) |
| Lived with both parents at 14 | 0.15 (0.03) | −1.00 (0.13) | −0.06 (0.01) | −0.17 (0.03) |
| Drop-out | −1.00 (0.05) | 2.11 (0.21) | 0.17 (0.01) | 0.43 (0.05) |
| High school graduates | −0.53 (0.04) | 1.03 (0.17) | 0.08 (0.01) | 0.15 (0.04) |
| Some college | −0.30 (0.05) | 0.29 (0.18) | 0.03 (0.01) | −0.0031 (0.04) |
| Mean marital status | −0.46 (0.05) | 3.03 (0.19) | 0.18 (0.01) | 0.44 (0.04) |
| Overall R–sq childhood factors only (1st two variables only) | 0.22 | 0.20 | 0.27 | 0.13 |
| Overall R-sq for reported regression with adult factors | 0.36 | 0.33 | 0.41 | 0.21 |
Race/ethnicity included in all models.
Discussion/conclusion
This paper considered the theoretical properties and empirical associations of four measures of disadvantage measured cross-sectionally and aggregated over the life course. The measures included three measures of relative deprivation, Yitzhaki, Deaton and log difference, and the natural log of individual income. We demonstrated that all measures of relative deprivation decline in income at an increasing rate, just as log income increases at a decreasing rate. IUGR was chosen as the dependent measure in the empirical application because economic disadvantage has consistently been associated with IUGR. Furthermore, because the etiology of IUGR is linked to the nutritional resources that the mother brings to the pregnancy, hypertension, and smoking history, measures of disadvantage based on access to resources over the life course may be more closely associated with IUGR than contemporaneous measures. Contemporaneous disadvantage is correlated with permanent disadvantage, but it is a noisy proxy for lifetime access to material resources. When comparing each contemporaneous measure with its permanent counterpart, we found that all were negatively associated with IUGR but that the permanent measures implied a greater level of risk. For example, the odds ratio for the Deaton relative deprivation measure was 2.23 (CI: 1.29, 3.58) and the permanent Deaton relative deprivation measure was 3.63 (CI: 1.91, 6.87).
We have noted that there is no theoretically correct measure of disadvantage. But empirically it is possible to compare the probability of IUGR predicted by each measure of disadvantage with two-way plots of the frequency of IUGR and individual income. Since each measure of disadvantage is a function of individual income, the predicted probabilities can be graphed along the same axes as the empirical frequencies. Fig. 2 is based on the smoothed empirical probability of IUGR as a nonparametric function of permanent per capita income. In each of the four panels, the predicted probabilities from logistic regression on one measure of permanent disadvantage are overlaid on the empirical probabilities. In order to facilitate comparisons, the predicted probabilities are shown as a function of permanent income rather than the transformed measures of deprivation.
Fig. 2a shows that the predictions of log permanent income for the relation between permanent per capita income and IUGR track the empirical probability very closely throughout the income distribution. Fig. 2b shows that permanent Deaton relative deprivation predicts the empirical probability except at levels of per capita income below $5,000. At the lowest levels of permanent Deaton relative deprivation under-predicts the true probability by 3 percentage points. Fig. 2c shows that permanent Yitzhaki relative deprivation under-predicts the probability of IUGR by up to 6 percentage points at per capita income below $7,000 and by about 3 percentage points at higher income levels. Fig. 2d shows that permanent log difference relative deprivation under-predicts IUGR by about 2 percentage points at per capita income below $9000 and by up to 3 percentage points at higher income levels.
Permanent Yitzhaki and logdif relative deprivation predict a much flatter relation between IUGR and permanent income than either the nonparametric empirical relation or those predicted by permanent Deaton relative deprivation and log permanent income. Thus Yitzhaki and log difference relative deprivation predict smaller benefits in terms of reduced IUGR from an increase in permanent income for an individual than the alternative two measures of permanent disadvantage. They also predict smaller benefits from revenue neutral income transfers from wealthy individuals to poor individuals.
Methodologically, one of the most important findings of the paper is that in the case of IUGR, log permanent individual income performs at least as well as relative measures. Calculation of relative deprivation is time and data intensive. If geographical reference groups are used, measuring relative deprivation requires researchers to have health outcome data with geographical identifiers so that data from larger, geographically representative data sets such as the IPUMS decennial Census can be merged. Computation of relative deprivation requires substantial programming; its implementation is computer intensive because of the need to create multiple relational data bases. Further study using different health outcomes and different data sets are required before a consensus can be reached about whether relative deprivation adds anything beyond that found using individual measures of deprivation.
We adopted a second approach to discriminate between measures of individual and relative deprivation by regression of disadvantage measures on family background and adult characteristics. We explained at least as much of the variance in each of the permanent measures than in their corresponding contemporaneous measure. This evidence suggests that contemporaneous measures of disadvantage, whether individual or relative, do not reflect the same variation in lifecycle disadvantage as the permanent measures. The exception is Deaton relative deprivation. Background characteristics explained 40% of the variance in both the contemporary and the permanent Deaton relative deprivation measures. Although permanent measures place greater demands on researchers, they probably capture access to resources available for health capital, which is the result of inputs at multiples points along the life course, more accurately than point in time measures of disadvantage.
Background characteristics explained more of the variation in log permanent income and permanent Deaton relative deprivation than in permanent Yitzhaki or reldep relative deprivation. Observed characteristics explained 40% of the variance in permanent Deaton relative deprivation, 33% of the variance in Yitzhaki relative deprivation, and 36% in log permanent income. But they explained only 21% of the variance in permanent log difference relative deprivation. This finding casts doubt on the use of log difference relative deprivation if researchers believe that disadvantage measures should be related to life course access to resources. Somewhat surprisingly indicators for race and ethnicity were not the driving factor behind variance in disadvantage. Race and ethnicity explained only 2–3% of the variation in disadvantage. The rest was explained by father’s education, having lived with both parents at age 14, education and adult marital status.
We performed a number of robustness tests: First, we re-ran the regressions with time fixed-effects. These were insignificant and did not affect the results. Second, we re-estimated the equations using a measure of permanent relative deprivation based on three observations per person, instead of unbalanced observation periods reported in the results section. Again the results were unchanged. Third, we also tested the robustness of our results with alternative definitions of IUGR, including low birth weight (below 2500 g) and the ponderal index (birthweight (kg)/length (m)3), identifying infants that were equal to or below the 10th percentile for their gestational age (defined in weeks) (Lubchenco, Hansman, & Boyd, 1966; Miller & Hassanein, 1971). Our results do not change based upon the definition of IUGR.
Our results present a cautionary tale about the relation between health, IUGR and measures of individual and relative deprivation. There is no right way to measure relative deprivation, only different ways to measure it. The different measures have different policy implications regarding the effect on IUGR of income transfers to the poor. Since variation in deprivation is related to intergenerational measures of education and marital stability, we need to recognize the indirect health benefits of policies to promote education and support marriage (Deaton, 2002). Collecting data on parental education and childhood family structure may be useful in explaining health outcomes. Further work needs to be done on nonlinearities in the effects of Yitzhaki and Deaton type relative deprivation measures. Other health outcomes need to be studied using multiple measures of relative deprivation. Future research should also explore different ways of aggregating a time series of contemporaneous relative deprivation to obtain a permanent measure. We used a simple average. Results may be sensitive to aggregation as well as the definition of relative deprivation (Deaton & Muelbauer, 1980).
Limitations
There are limitations of the study. The dependent measures were constructed based upon mother reported infant birth weight and length of gestation. We have not examined the question of how health behaviors, such as smoking during pregnancy, mediate the association between disadvantage and IUGR. This paper cannot rule out the possibility that the association between permanent disadvantage measures and IUGR is driven by omitted third factors. For example, we do not have data on maternal birth weight. Low maternal birth weight may lead to low adult socio-economic status (Currie & Moretti, 2005). Low maternal birth weight may affect the child’s birth weight through a genetic tendency towards low birth weight which appears (Selling et al., 2006), through the omission of a maternal birth weight variable, to be related to low socio-economic status. Other third factors could be at play if mothers who invest less in human capital also invest less in unobserved dimensions related to maintaining healthy pregnancies. We cannot rule out reverse causality between maternal health and permanent disadvantage (Meara, 2001). Thus all of the correlations between permanent disadvantage and IUGR should be interpreted as associations and not a causal relation.
Acknowledgments
This project was funded by NIH/NINR under R01 NR008512, Patricia Reagan, PI. We would like to thank Peihong Feng and Jirka Hana for excellent research assistance.
References
- Atkinson A. On the measurement of inequality. Journal of Economic Theory. 1970;2:244–263. [Google Scholar]
- Basso O, Wilcox AJ, Weinberg CR. Birth weight and mortality: Causality or confounding? American Journal of Epidemiology. 2006;164(4):303–311. doi: 10.1093/aje/kwj237. [DOI] [PubMed] [Google Scholar]
- Bell A, Ehrhardt R. Regulation of placental nutrient transport and implications for fetal growth. Nutrition Research Reviews. 2002;15:211–230. doi: 10.1079/NRR200239. [DOI] [PubMed] [Google Scholar]
- Braveman PA, Cubbin C, Egerter S, Chideya S, Marchi KS, Metzler M, et al. Socioeconomic status in health research: One size does not fit all. Journal of American Medical Association. 2005;294(22):2879–2888. doi: 10.1001/jama.294.22.2879. [DOI] [PubMed] [Google Scholar]
- Campbell JY, Lettau M, Malkiel BG, Xu Y. Have individual stocks become more volatile? An empirical exploration of idiosyncratic risk. The Journal of Finance. 2001;56(1):1–43. [Google Scholar]
- Clementi F, Gallegati M. Pareto’s Law of Income Distribution: Evidence for Germany, the United Kingdom, and the United States. Microeconomics. 2005 #0505006, EconWPA. [Google Scholar]
- Currie J, Moretti E. Short and long-run determinants of intergenerational transmission of birth weight. Cambridge, MA: National Bureau of Economic Research; 2005. Biology as destiny? [Google Scholar]
- Deaton A. Relative deprivation, inequality, and mortality. Research Program in Development Studies and Center for Health; Wellbeing Princeton University: 2001. pp. 1–45. [Google Scholar]
- Deaton A. Policy implications of the gradient of health and wealth. An economist asks, would redistributing income improve population health? Health Affairs (Millwood) 2002;21(2):13–30. doi: 10.1377/hlthaff.21.2.13. [DOI] [PubMed] [Google Scholar]
- Deaton A, Muelbauer J. Economics and consumer behavior. Cambridge: Cambridge University Press; 1980. [Google Scholar]
- Doctor BA, O’Riordan MA, Kirchner HL, Shah D, Hack M. Perinatal correlates and neonatal outcomes of small for gestational age infants born at term gestation. American Journal of Obstetrics and Gynecology. 2001;185(3):652–659. doi: 10.1067/mob.2001.116749. [DOI] [PubMed] [Google Scholar]
- Eibner C, Evans W. Relative deprivation, poor health habits and mortality. Journal of Human Resources. 2005;40(3):591–620. [Google Scholar]
- England LJ, Kendrick JS, Gargiullo PM, Zahniser SC, Hannon WH. Measures of maternal tobacco exposure and infant birth weight at term. American Journal of Epidemiology. 2001;153(10):954–960. doi: 10.1093/aje/153.10.954. [DOI] [PubMed] [Google Scholar]
- Fowden AL, Ward JW, Wooding FP, Forhead AJ, Constancia M. Programming placental nutrient transport capacity. Journal of Physiology. 2006;572(Pt 1):5–15. doi: 10.1113/jphysiol.2005.104141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottschalk P, Moffitt R, Katz L, Dickens W. The growth of earnings instability in the US labor markets. Brookings Papers on Economic Activity. 1994;94(2):217–272. [Google Scholar]
- Graham H, Power C. Childhood disadvantage and health inequalities: A framework for policy based on life course research. Child Care Health Development. 2004;30(6):671–678. doi: 10.1111/j.1365-2214.2004.00457.x. [DOI] [PubMed] [Google Scholar]
- Haelterman E, Breart G, Paris-Llado J, Dramaix M, Tchobroutsky C. Effect of uncomplicated chronic hypertension on the risk of small-for-gestational age birth. American Journal of Epidemiology. 1997;145(8):689–695. doi: 10.1093/aje/145.8.689. [DOI] [PubMed] [Google Scholar]
- Harding JE. The nutritional basis of the fetal origins of adult disease. International Journal of Epidemiology. 2001;30(1):15–23. doi: 10.1093/ije/30.1.15. [DOI] [PubMed] [Google Scholar]
- Hoffman HJ, Stark C, Lundin F, Ashbrook J. Analysis of birth weight, gestational age, and fetal viability, US Births, 1968. Obstetrical and Gynecological Survey. 1974;29(9):651–681. doi: 10.1097/00006254-197409000-00029. [DOI] [PubMed] [Google Scholar]
- Kawachi I, Kennedy BP, Wilkinson RC. Income inequality and health: Introduction. New York: The New Press; 1999. [Google Scholar]
- Kawachi I, Subramanian SV, Almeida-Filho N. A glossary for health inequalities. Journal of Epidemiology and Community Health. 2002;56(9):647–652. doi: 10.1136/jech.56.9.647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer MS. Socioeconomic determinants of intrauterine growth retardation. European Journal of Clinical Nutrition. 1998;52(Suppl 1):S29–S32. discussion S32–23. [PubMed] [Google Scholar]
- Kramer MS, Platt R, Yang H, McNamara H, Usher RH. Are all growth-restricted newborns created equal(ly)? Pediatrics. 1999;103(3):599–602. doi: 10.1542/peds.103.3.599. [DOI] [PubMed] [Google Scholar]
- Kramer MS, Seguin L, Lydon J, Goulet L. Socioeconomic disparities in pregnancy outcome: Why do the poor fare so poorly? Paediatric and Perinatal Epidemiology. 2000;14(3):194–210. doi: 10.1046/j.1365-3016.2000.00266.x. [DOI] [PubMed] [Google Scholar]
- Kristenson M, Eriksen HR, Sluiter JK, Starke D, Ursin H. Psychobiological mechanisms of socioeconomic differences in health. Social Science & Medicine. 2004;58(8):1511–1522. doi: 10.1016/S0277-9536(03)00353-8. [DOI] [PubMed] [Google Scholar]
- Kuh D, Hardy R. Women’s health in midlife: Findings from a British birth cohort study. Journal of British Menopause Society. 2003;9(2):55–60. doi: 10.1258/136218003100322206. [DOI] [PubMed] [Google Scholar]
- Lie RT, Wilcox AJ, Skjoerven R. Maternal and paternal influences on length of pregnancy. Obstetrics and Gynecology. 2006;107(4):880–885. doi: 10.1097/01.AOG.0000206797.52832.36. [DOI] [PubMed] [Google Scholar]
- Lieberman E, Gremy I, Lang JM, Cohen AP. Low birthweight at term and the timing of fetal exposure to maternal smoking. American Journal of Public Health. 1994;84(7):1127–1131. doi: 10.2105/ajph.84.7.1127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu MC, Halfon N. Racial and ethnic disparities in birth outcomes: A life-course perspective. Maternal and Child Health Journal. 2003;7(1):13–30. doi: 10.1023/a:1022537516969. [DOI] [PubMed] [Google Scholar]
- Lubchenco LO, Hansman C, Boyd E. Intrauterine growth in length and head circumference as estimated from live births at gestation al ages from 26 to 42 weeks. Pediatrics. 1966;37(3):403–408. [PubMed] [Google Scholar]
- Lynch J, Smith GD, Harper S, Hillemeier M, Ross N, Kaplan GA, et al. Is income inequality a determinant of population health? Part 1. A systematic review. Milbank Quarterly. 2004;82(1):5–99. doi: 10.1111/j.0887-378X.2004.00302.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahajan SD, Singh S, Shah P, Gupta N, Kochupillai N. Effect of maternal malnutrition and anemia on the endocrine regulation of fetal growth. Endocrine Research. 2004;30(2):189–203. doi: 10.1081/erc-200027380. [DOI] [PubMed] [Google Scholar]
- Marmot M, Brunner E. Cohort profile: The White-hall II study. International Journal of Epidemiology. 2005;34(2):251–256. doi: 10.1093/ije/dyh372. [DOI] [PubMed] [Google Scholar]
- Marmot MG. Status syndrome: A challenge to medicine. Journal of American Medical Association. 2006;295(11):1304–1307. doi: 10.1001/jama.295.11.1304. [DOI] [PubMed] [Google Scholar]
- Marmot MG, Smith GD, Stansfeld S, Patel C, North F, Head J, et al. Health inequalities among British civil servants: The Whitehall II study. Lancet. 1991;337(8754):1387–1393. doi: 10.1016/0140-6736(91)93068-k. [DOI] [PubMed] [Google Scholar]
- Meara E. Why is health related to socioeconomic status? The case of pregnancy and low birth weight. Cambridge, MA: National Bureau of Economic Research; 2001. [Google Scholar]
- Mellor JM, Milyo J. Is exposure to income inequality a public health concern? Lagged effects of income inequality on individual and population health. Health Services Research. 2003;38(1 Pt 1):137–151. doi: 10.1111/1475-6773.00109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller HC, Hassanein K. Diagnosis of impaired fetal growth in newborn infants. Pediatrics. 1971;48(4):511–522. [PubMed] [Google Scholar]
- Miller ST. A Guide to the 1979–2002 National Longitudinal Survey of Youths, 1979. Columbus, OH: Center for Human Resources Research; 2004. [Google Scholar]
- Misra DP, Guyer B, Allston A. Integrated perinatal health framework. A multiple determinants model with a life span approach. American Journal of Preventive Medicine. 2003;25(1):65–75. doi: 10.1016/s0749-3797(03)00090-4. [DOI] [PubMed] [Google Scholar]
- Moore VM, Davies MJ. Diet during pregnancy, neonatal outcomes and later health. Reproduction, Fertility and Development. 2005;17(3):341–348. doi: 10.1071/rd04094. [DOI] [PubMed] [Google Scholar]
- Nordentoft M, Lou HC, Hansen D, Nim J, Pryds O, Rubin P, et al. Intrauterine growth retardation and premature delivery: The influence of maternal smoking and psychosocial factors. American Journal of Public Health. 1996;86(3):347–354. doi: 10.2105/ajph.86.3.347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okah FA, Cai J, Hoff GL. Term-gestation low birth weight and health-compromising behaviors during pregnancy. Obstetrics and Gynecology. 2005;105(3):543–550. doi: 10.1097/01.AOG.0000148267.23099.b7. [DOI] [PubMed] [Google Scholar]
- Oncken C, Hardardottir H, Smeltzer J. Human studies of nicotine replacement during pregnancy. In: Benowitz N, editor. Nicotine safety and toxicity. Oxford: Oxford University Press; 1998. pp. 107–118. [Google Scholar]
- Pollack H, Lantz PM, Frohna JG. Maternal smoking and adverse birth outcomes among singletons and twins. American Journal of Public Health. 2000;90(3):395–400. doi: 10.2105/ajph.90.3.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power C, Jefferis BJ. Fetal environment and subsequent obesity: A study of maternal smoking. International Journal of Epidemiology. 2002;31(2):413–419. [PubMed] [Google Scholar]
- Prada J, Tsang R. Biological mechanisms of environmentally induced causes of IUGR. European Journal of Clinical Nutrition. 1998;52(S1):S21–S27. [PubMed] [Google Scholar]
- Reagan PB, Salsberry PJ. Race and ethnic differences in determinants of preterm birth in the USA: Broadening the social context. Social Science & Medicine. 2005;60(10):2217–2228. doi: 10.1016/j.socscimed.2004.10.010. [DOI] [PubMed] [Google Scholar]
- Reichman NE, Teitler JO. Paternal age as a risk factor for low birthweight. American Journal of Public Health. 2006;96(5):862–866. doi: 10.2105/AJPH.2005.066324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothschild M, Stiglitz J. Increasing risk I: A definition. Journal of Economic Theory. 1970;2(3):225–243. [Google Scholar]
- Runciman WG. Relative deprivation and social justice. London: Routledge and Kegan Paul; 1966. [Google Scholar]
- Selling KE, Carstensen J, Finnstrom O, Sydsjo G. Intergenerational effects of preterm birth and reduced intrauterine growth: A population-based study of Swedish mother-offspring pairs. Internationa Journal of Obstretrics and Gynaecology. 2006;113(4):430–440. doi: 10.1111/j.1471-0528.2006.00872.x. [DOI] [PubMed] [Google Scholar]
- Sibai B, Dekker G, Kupferminc M. Pre-eclampsia. Lancet. 2005;365(9461):785–799. doi: 10.1016/S0140-6736(05)17987-2. [DOI] [PubMed] [Google Scholar]
- Sibley CP, Turner MA, Cetin I, Ayuk P, Boyd CA, D’Souza SW, et al. Placental phenotypes of intrauterine growth. Pediatric Research. 2005;58(5):827–832. doi: 10.1203/01.PDR.0000181381.82856.23. [DOI] [PubMed] [Google Scholar]
- Strauss RS, Dietz WH. Growth and development of term children born with low birth weight: Effects of genetic and environmental factors. Journal of Pediatrics. 1998;133(1):67–72. doi: 10.1016/s0022-3476(98)70180-5. [DOI] [PubMed] [Google Scholar]
- Subramanian SV, Kawachi I, Kennedy BP. Does the state you live in make a difference ? Multilevel analysis of self-rated health in the US. Social Science & Medicine. 2001;53(1):9–19. doi: 10.1016/s0277-9536(00)00309-9. [DOI] [PubMed] [Google Scholar]
- Subramanian SV, Blakely T, Kawachi I. Income inequality as a public health concern: Where do we stand? Commentary on “Is exposure to income inequality a public health concern?”. Health Services Research. 2003;38(1 Pt 1):153–167. doi: 10.1111/1475-6773.00110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian SV, Kawachi I. Income inequality and health: What have we learned so far? Epidemiological Review. 2004;26(1):78–91. doi: 10.1093/epirev/mxh003. [DOI] [PubMed] [Google Scholar]
- Subramanian SV, Kawachi I. Whose health is affected by income inequality? A multilevel interaction analysis of contemporaneous and lagged effects of state income inequality on individual self-rated health in the United States. Health Place. 2006;12(2):141–156. doi: 10.1016/j.healthplace.2004.11.001. [DOI] [PubMed] [Google Scholar]
- Wilcox AJ. On the importance—and unimportance—of birth weight. International Journal of Epidemiology. 2001;30(6):1233–1241. doi: 10.1093/ije/30.6.1233. [DOI] [PubMed] [Google Scholar]
- Wilkinson RG, Pickett KE. Income inequality and population health: A review and explanation of the evidence. Social Science & Medicine. 2006;62(7):1768–1784. doi: 10.1016/j.socscimed.2005.08.036. [DOI] [PubMed] [Google Scholar]
- Yitzhaki S. Relative deprivation and the gini coefficient. The Quarterly Journal of Economics. 1979;93(2):321–324. [Google Scholar]
- Zhang J, Bowes W. Birth-weight-for-gestational-age patterns by race, sex, and parity in the United States population. Obstetrics and Gynecology. 1995;86(2):200–208. doi: 10.1016/0029-7844(95)00142-e. [DOI] [PubMed] [Google Scholar]


