Linking impulse response functions to reaction time: Rod and cone reaction time data and a computational model

Abstract

Reaction times for incremental and decremental stimuli were measured at five suprathreshold contrasts for six retinal illuminance levels where rods alone (0.002–0.2 Trolands), rods and cones (2–20 Trolands) or cones alone (200 Trolands) mediated detection. A 4-primary photostimulator allowed independent control of rod or cone excitations. This is the first report of reaction times to isolated rod or cone stimuli at mesopic light levels under the same adaptation conditions. The main findings are: 1) For rods, responses to decrements were faster than increments, but cone reaction times were closely similar. 2) At light levels where both systems were functional, rod reaction times were ~20 ms longer. The data were fitted with a computational model that incorporates rod and cone impulse response functions and a stimulus-dependent neural sensory component that triggers a motor response. Rod and cone impulse response functions were derived from published psychophysical two-pulse threshold data and temporal modulation transfer functions. The model fits were accomplished with a limited number of free parameters: two global parameters to estimate the irreducible minimum reaction time for each receptor type, and one local parameter for each reaction time versus contrast function. This is the first model to provide a neural basis for the variation in reaction time with retinal illuminance, stimulus contrast, stimulus polarity, and receptor class modulated.

Introduction

The reaction time to a visual stimulus represents the processing times of a cascade of neural elements beginning with the photoreceptors and culminating with the neural processes that initiate a motor response. Physiological recordings of rod and cone photoreceptor impulse response functions show a difference in the time to peak response on the order of 12–20 ms (Schneeweis & Schnapf, 1995; Verweij, Peterson, Dacey & Buck, 1999). There are also numerous psychophysical investigations of the temporal latency and reaction time characteristics of the rod system at scotopic light levels and the cone system at photopic light levels. Psychophysical studies show that cone reaction times are shorter than rod reaction times, however the estimated delays differ substantially among studies. Several studies reported rod-cone latency differences of 60–80 ms (Barbur, 1982; MacLeod, 1972; Sharpe, Stockman & MacLeod, 1989; van den Berg & Spekreijse, 1977) but for all of these, the stimulus conditions included higher cone stimulus contrast and/or greater cone light adaptation. Under conditions of comparable rod and cone light adaptation and stimulus contrast, using stimulus generation procedures like those of the present study, Sun, Pokorny & Smith (2001b) estimated the delay between rod and cone signals at mesopic light levels to be 8–20 ms, which is comparable to rod and cone photoreceptor impulse response function estimates from physiology.

The stimulus conditions for reaction time studies comparing rod and cone latencies included large differences in rod and cone light adaptation (Barbur, 1982; Mansfield, 1973; Pins & Bonnet, 1997). There are no comparisons at mesopic light levels where rods and cones are both active, due to the inability of conventional photostimulation techniques to produce stimuli that isolate rod or cone signal modulation. In this study we used a photostimulator with four primary lights that allowed independent control of the stimulation of the 4-receptor types in the human eye (Pokorny, Smithson & Quinlan, 2004; Sun, Pokorny & Smith, 2001a). Our first purpose was to compare the reaction time of rod and cone systems under scotopic and photopic light levels, as well as at mesopic light levels where both rods and cones are active.

Post-receptoral visual signals are conveyed through ON and OFF pathways, which provide excitatory responses to light increments and decrements, respectively (Schiller, 1992). Rod ON- and OFF-signals share the neural substrates of the cone pathway. The postreceptoral neurons conveying rod information have been ascribed to two primary pathways, one via ON rod bipolars, amacrine II cells, and ON and OFF cone bipolars, which is a high gain pathway hypothesized to mediate rod vision at low light levels. The second pathway transmits rod information via rod-cone gap junctions and ON and OFF cone bipolars, and is hypothesized to mediate rod vision at high scotopic and mesopic light levels (Reviewed byDaw, Jensen & Bunken, 1990; Sharpe & Stockman, 1999). Physiological investigations suggest that rod input is strong in the MC-pathway but weak or absent in the PC- and KC-pathways (Lee, Smith, Pokorny & Kremers, 1997). From psychophysical studies we assume that both rod and cone reaction times to luminance stimuli are mediated by the Magnocellular (MC) pathway. Supporting evidence comes from reaction times to cone-detected luminance stimuli (Nissen, Pokorny & Smith, 1979), and from identification of the inferred pathway mediating rod thresholds at mesopic light levels (Sun et al., 2001b). Results of latency studies of ON and OFF pathways are inconclusive. Some psychophysical studies suggested that the ON pathway was faster than the OFF pathway in the peripheral retina for both rod and cone systems (e.g.Bartlett, Sticht & Pease, 1968), while others have reached the opposite conclusion (Hansteen, 1971; Lewis, Dunlap & Matteson, 1972). Physiological recording from retinal Magnocellular ON and OFF cells demonstrated comparable time courses to rapid ON or OFF sawtooth stimuli at light levels where cones mediate the responses (Kremers, Lee, Pokorny & Smith, 1993). Our second purpose was to investigate response time to incremental or decremental stimuli that favor mediation by the rod and cone ON or OFF pathways at adaptation levels spanning the range from the scotopic to photopic vision.

Our study provides a rich reaction time data set that allows evaluation of a number of different modeling strategies. There is a long and diverse history on reaction time to visual stimuli and many models have been proposed (Luce, 1986). The most widely used empirical description of reaction time data is the Piéron function. Piéron (1914; 1952) proposed a power function to describe the relation between input (light intensity or contrast) and output (reaction time) in the human visual system that provides good fits to data (e.g.Mansfield, 1973; Plainis & Murray, 2000). The Piéron function is an empirical model without basis in underlying physiological mechanisms. Other modeling strategies for simple reaction times have focused primarily on the decision making process (Luce, 1986). These models do not take into account sensory processing. We developed a model with a sensory component that triggers the motor response. It employs impulse response functions appropriate for the modulated receptor class (rods or cones) and light level, and a motor trigger dependent on the integrated neural responses to the visual stimulus. While impulse response functions have been used in modeling reaction time data (Donner & Fagerholm, 2003; Smith, 1995; Wandell, Ahumada & Welsh, 1984), this is the first application to the modeling of reaction time variation with retinal illuminance, stimulus contrast, stimulus polarity, and receptor class modulated.

Part 1. Rod and Cone Reaction Times: Experiments and Data

Methods

Apparatus

We used a 2-channel Maxwellian view photostimulator, with 4 primaries for a central field and 4 primaries for a surround to control excitation of the rods and three cone types independently (Shapiro, Pokorny & Smith, 1996). A complete description of the design of the photostimulator was given by Pokorny et al. (2004) and examples of its implementation are detailed in Cao, Pokorny & Smith (2005)and Cao, Zele & Pokorny (2006). The primaries were derived from LED-interference filter combinations yielding dominant wavelengths of 459 nm (blue), 561 nm (greenish-yellow), 516 nm (green) and 658 nm (red). The radiances of the primaries were controlled by amplitude modulation of a 20 kHz carrier feeding into an eight-channel analog output Dolby soundcard (M-Audio-Revolution 7.1 PCI) with a 24 bits digital-to-analogue converter (DAC) operating at a sampling rate of 192 kHz. The output of the DAC was demodulated (Puts, Pokorny, Quinlan & Glennie, 2005) and sent to voltage-to-frequency converters that provided 1 µs pulses at frequencies up to 250 kHz to control the LEDs (Swanson, Ueno, Smith & Pokorny, 1987). Theoretically, the soundcard with demodulator has a precision of greater than 16 bits (Puts et al., 2005). Observer responses were recorded using a custom-made response device connected to the analog input channel of the M-Audio soundcard. Reaction time was signaled by the release of the button that interrupted a continuous 10 kHz sinusoidal signal and produced a steady voltage. The response button and soundcard combination produced less than 100 ms lag time; a value that would not materially affect measured reaction times. All stimuli were generated using custom engineered software driven by a Macintosh G5 computer.

Calibration Procedures

The photostimulator was calibrated using a two-step procedure. The first considered the physical light output of the instrument and the second involved observer calibrations to compensate for the difference in pre-receptoral filtering and receptoral spectral sensitivities between the observer and the CIE (1964) 10° Standard Observer.

Physical Calibration

The spectral output of each primary (LED-interference filter combination) was measured in 2 nm intervals with an Optronics OL754 spectroradiometer. The illuminance of each of the eight primaries was measured as a function of the digital voltage level with a PIN silicon photodiode and current amplifier connected to a precision digital scope meter (Fluke model 124). The digital voltage to illuminance relationship for each primary was fitted using a log transformed fourth-order polynomial from which a look-up-table was constructed.

The retinal illuminance of the center 561 nm primary set at its maximum output was measured with an EG&G model 550 photometer. The retinal illuminance of each remaining center primary was determined by the relative photopic illuminance calculated based on the spectral output of the primary and the 561 nm primary. The retinal illuminances of the surround primaries were determined by a center-surround matching procedure to establish the relative illuminance between center and surround primary pairs of the same wavelengths. During this procedure, the observer adjusted the irradiance of the surround primary to match the 50% level of the center primary.

Observer Calibration

The cone stimuli were specified in a relative cone Troland space (Smith & Pokorny, 1996) based on the 10° Standard Observer (Shapiro et al., 1996). We used an observer calibration procedure that compensated for pre-receptoral filtering differences between the observer and the Standard Observer (Pokorny et al., 2004; Sun et al., 2001a). At the same peripheral retinal location of the central field as for the experiments, the observer made a photopic color match between two successively presented displays, one containing a mixture of the 459 and 561 nm lights, the other a mixture of the 516 and 658 nm lights. The 561 nm primary served as the reference, and the observer made a match by varying three parameters; the luminance of the 459 nm light, the luminance ratio of the 516 and 658 nm lights, and the combined luminance of the 516 and 658 nm lights. By comparing the relative radiances of the four lights required by the individual with the theoretical values required by the 10° Standard Observer, we estimated the difference in sensitivity between the individual and the Standard Observer at each primary. This method assumes that an individual observer’s spectral sensitivities at the primary wavelengths do not differ significantly from linear transforms of the Standard Observer color matching functions. Pokorny et al. (2004) showed by calculation that the variation in spectral location of the L-cone spectral sensitivity associated with the common L-cone (A180) and (S180) polymorphism (Sharpe, Stockman, Knau & Jagle, 1998) results in error in receptor isolation of less than 2%. Thus, the calibration procedure can compensate for both individual prereceptoral differences and receptoral spectral sensitivity variation.

Stimuli

A 2° diameter stimulus field was embedded within a 13° annular surround (Fig. 1). A fixation point located the center at a 7.5° temporal eccentricity.

Figure 1.

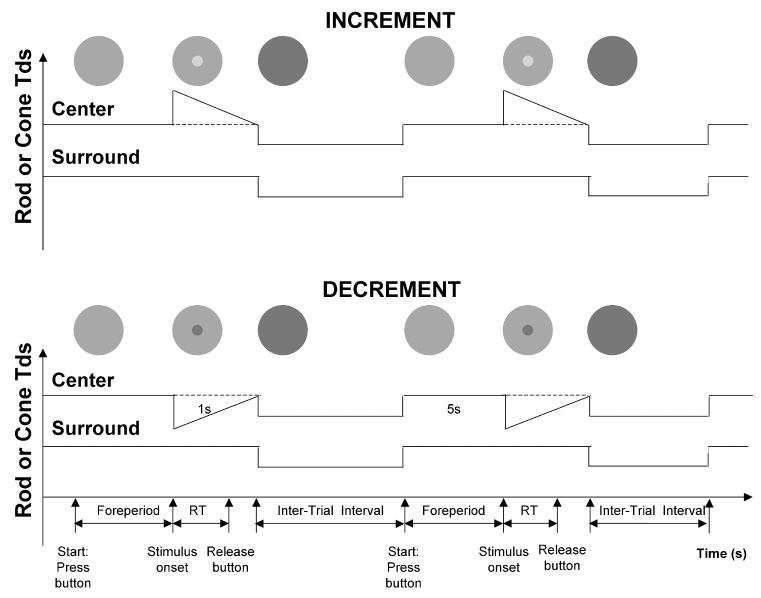
The schematic protocols of reaction time measurement for incremental and decremental stimuli. The observer first held a button. After a 5000 ms foreperiod, the rod or cone signal in the center (2° in diameter) was incremented (upper) or decremented (lower) in a 1-sec ramp waveform. The observer released the button as quickly as possible once a change in the center was detected. During the interstimulus interval, the retinal illuminance was reduced by 40% from the adaptation level to avoid Troxler’s effect.

For all conditions in this study, the cone chromaticities of the light in the center and surround were metameric to the equal-energy-spectrum (EES; L/(L+M) = 0.667, S/(L+M) = 1.0). During the reaction time measurements, the rod signal or cone luminance signal in the center was incremented or decremented using a Rapid-ON or Rapid-OFF ramp waveform of 1 sec duration (Fig. 1). The rationale for using the Rapid-ON or Rapid-OFF ramp waveform was to measure reaction times to the stimulus onset while minimizing adaptation to the incremental or decremental light stimuli. For the rod stimuli, the rod signal was varied while keeping the cone excitations constant. For the cone stimuli, the luminance was varied while maintaining a constant chromaticity (L/(L+M), S/(L+M)) and level of rod excitation.

The retinal illuminances spanned a 5 log unit range in 1 log unit steps from 0.002 to 200 photopic Td. At 0.002, 0.02 and 0.2 Td, no cone reaction time measurements could be determined; these light levels were below cone threshold. At 200 Td, rod reaction time was not assessed since the observers could not detect rod stimuli at the highest available contrast.

For each condition, five suprathreshold Weber contrast levels were tested. The incremental or decremental Weber contrasts (DI/I) ranged between 5% and 80% at 0.02-200 Td, with the range determined by the observer’s detection threshold contrast and the instrument gamut at the adaptation level. The rod response time at 0.002 Td was evaluated using a single primary (516 nm LED) to increase the instrument gamut, allowing rod increment contrasts up to 700%. At 0.002 Td, the incremental Weber contrasts were between 100% and 160% and the decremental Weber contrasts were between 45% and 85%. The 0.02 Td condition was replicated using the single-primary presentation. The data were no different from those obtained with 4-primary presentation, confirming the accuracy of the 4-primary rod signal presentation.

Procedure

The observer dark-adapted for 30 minutes prior to the beginning of data collection. Head position was maintained using a chin rest, and refractive correction (if required) was inserted on the instrument side of the 2 mm artificial pupil. In each session, a single condition (rod Rapid ON, rod Rapid OFF, cone Rapid ON, cone Rapid OFF) with one contrast and retinal illuminance was tested. The observer pressed the response button with the right thumb to initiate a 5000 ms foreperiod. The button press incremented the illuminance of the center and surround by 40% to minimize the Troxler effect (the fading of stationary objects in the peripheral visual field; Troxler, 1804). The stimulus followed the foreperiod. The observer was instructed to release the button as quickly as possible following the detection of a change in the central field. The reaction time was defined as the time between the onset of the stimulus and the release of the button. Fig. 1 includes a schematic representation of the experimental protocol.

We used a fixed rather than random foreperiod to maintain a constant adaptation level during each trial. The long duration foreperiod negated the possibility that the task became one of duration detection. Analysis of the preliminary data showed < 1% of the responses were anticipatory (RT <100 ms). If the fixed 5000 ms foreperiod were to become a duration detection task, reaction times would be independent of contrast and light level. The data show this is not the case.

The observers had extensive practice prior to formal data collection. Each session consisted of 30 trials with each condition repeated for 4–5 sessions. Each datum point represents a minimum of 120 repeats. Receptor class and retinal illuminance were randomized across sessions. The contrast sequence was randomized within sessions.

Trials with anticipatory (RT < 100 ms) or missed (RT ≥ 3000 ms) responses were discarded and the condition was repeated on the next trial. Reaction times greater than ± 2.5 standard deviations from the mean for a condition were deleted. Removing outliers using this method has higher or similar power to the method of calculating the median of the distribution instead of the mean (Ratcliff, 1993). Reported data are reaction time means and standard errors exclusive of outliers.

Observers

Two of the authors (DC and AJZ), both experienced psychophysical observers, participated in the experiments. Both are normal trichromats as assessed with the Neitz OT anomaloscope and Farnsworth-Munsell 100-hue test.

Results

Incremental and decremental rod and cone reaction times

The reaction times to rod and cone incremental and decremental stimuli for each contrast and retinal illumination are shown in Figure 2. In the figure, the left two columns show the reaction times to rod (circles) and cone (squares) stimuli for observer DC and the right two columns for observer AJZ. Each panel shows the reaction time (ms) as a function of Weber contrast for a single light level. Unfilled symbols represent reaction times to incremental stimuli and filled symbols indicate the reaction times to decremental stimuli. The top panel shows the data for 200 Td, the lower panels represent data collected at consecutive retinal illuminations that descend in 1 log unit steps over a 5 log unit range, to 0.002 Td (lowest panel).

Figure 2.

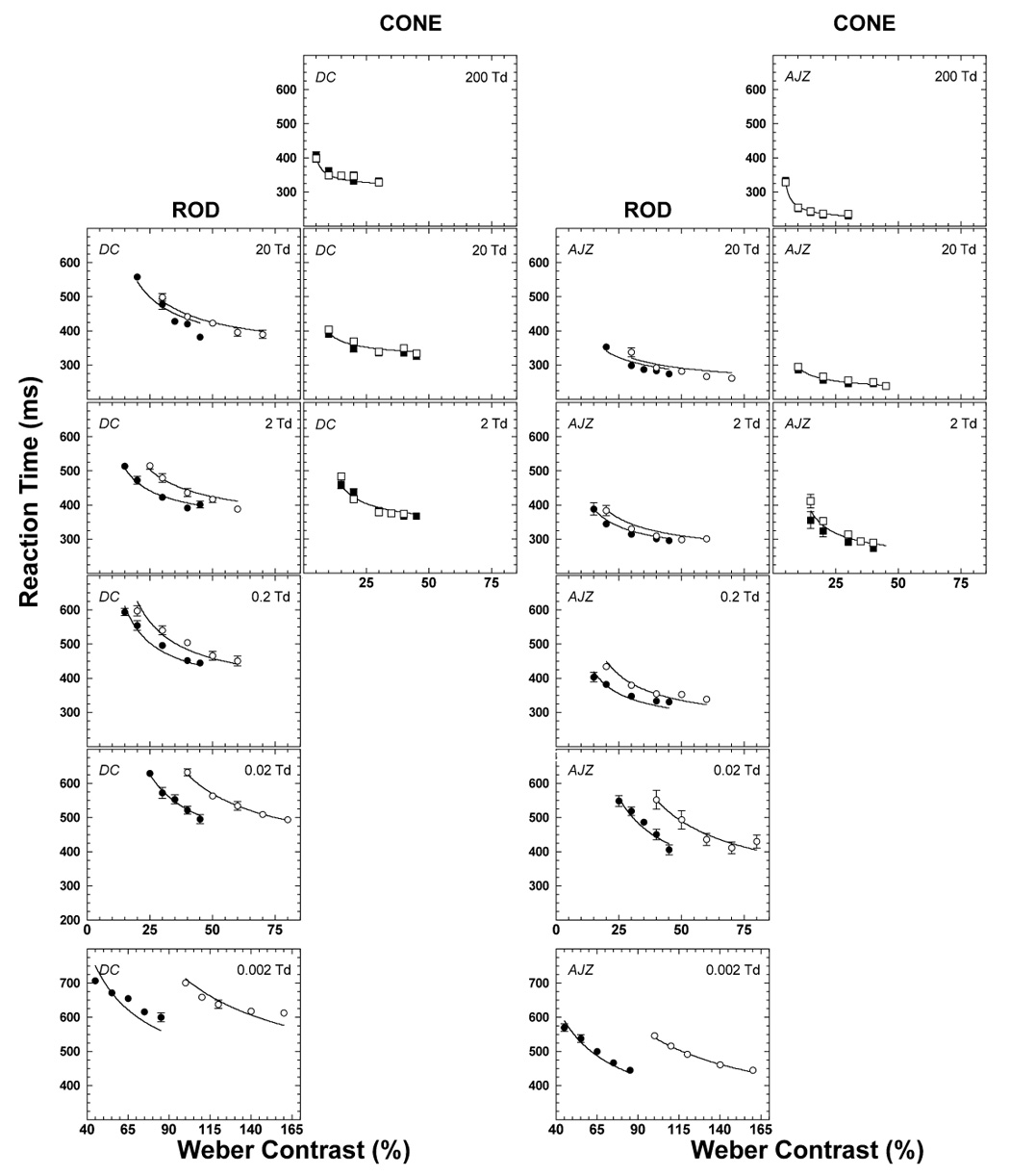
The measured reaction times with rod (circles) and cone (squares) stimuli for DC (the left two columns) and AJZ (the right two columns). Each panel shows the function of the reaction time with the increment (open symbols) or decrement (solid symbols) vs. contrast at the retinal illuminance level as labeled. The solid lines are fits of the model described in Part 2.

Overall, the pattern of reaction time data was very similar for both observers except for an absolute difference in reaction time between observers common to all conditions. Mean reaction times and associated variances (not shown) decreased with increasing contrast or retinal illuminance. For both rod and cone stimuli at all light levels, the coefficient of variation (ratio of the standard deviation to the mean) was largest (0.20–0.30) at the lowest contrast and reached asymptotic values of 0.10 at higher contrasts. These asymptotic coefficients of variation are comparable to the lowest values reported in reaction time studies of various design (Luce, 1986).

At 2 Td, rod and cone reaction times differed slightly: The difference in the asymptotic rod and cone reaction times was on average ~20 ms. At retinal illuminances ≥ 20 Td, cone RTs were shorter than rod RTs. For cone stimuli at 2, 20 and 200 Td, there were no differences between the reaction times to incremental and decremental stimuli at the same contrast level. For rod stimuli, however, reaction times to decrements were shorter than to increments of the same contrast at retinal illuminances ≤ 0.2 Td.

Figure 3 is a replot of the data in Figure 2 to allow comparison of reaction times for different light levels, receptor class and stimulus polarity. The left column shows data for observer DC and the right column for observer AJZ. Increments are shown in the upper panels, decrements in the lower panels. The rod data appear to group into two regions with similar reaction times. At retinal illuminances ≥ 0.2 Td, the difference in reaction time for the same contrast level was relatively small. At retinal illuminances ≤ 0.02 Td, reaction times were longer than those at the higher retinal illuminances. Cone reaction times decreased with increases in light level.

Figure 3.

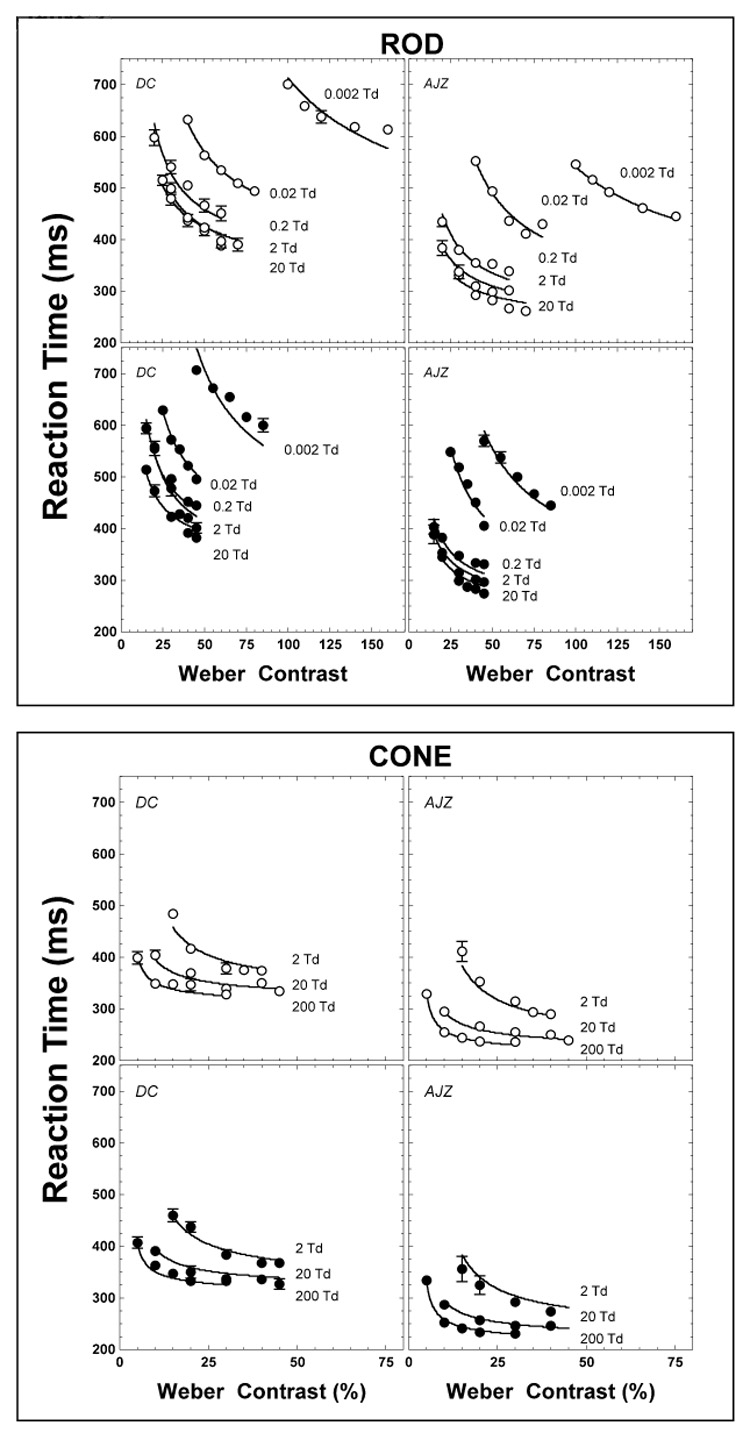
The measured reaction times with rod (circles) and cone (squares) stimuli replotted. Each panel shows the function of the reaction time with one condition (increment, open symbols, or decrement, solid symbols) at all light levels. The solid lines are fits of the model described in Part 2.

Part 2. Model

The model was developed to suggest a neural basis for the change in reaction time with retinal illuminance, stimulus contrast, stimulus polarity, and receptor class modulated. As such, it is deterministic in that it provides no mechanism to describe trial-to-trial variability in RT. For simple reaction times to a visual stimulus, the asymptotic variance of the response time is about 1000 ms (this study and others). There are a number of ways to model RT variability. One approach is to assume that the accumulation process is itself stochastic; that is, there is noisy stimulus information. Depending on how the process is conceived, this has typically led to a Poisson counter type (McGill, 1967) or diffusion/random walk (Luce, 1986; Ratcliff, 1978; Ratcliff, 1980) models. However, this is not the only way to do it. An alternative might be to postulate, as we do here, that information accumulation in the peripheral visual system is principally deterministic. With this approach, variation in RT might arise from a diversity of origins including sensitivity changes accompanying eye movements that occur at about the time of stimulus presentation and trial-to-trial variation in response criterion. Support for this perspective comes from single unit physiological studies. The responses of individual primate magnocellular ganglion cells on repeated presentations are highly stereotypical (Croner, Purpura & Kaplan, 1993; Sun, Ruttiger & Lee, 2004), with variability in the onset of firing to a moderate or high contrast stimulus on the order of 1–4 ms (Uzzell & Chichilnisky, 2004). Recordings from single primary visual cortex (V1) neurons in alert monkeys, gathered under conditions where eye position was relatively steady, are reported to be as reliable as the inputs from the retina and the thalamus (Gur & Snodderly, 2006). Variances were low for V1 cell responses recorded from layers, 2/3, 4A, 4B, 4C, 5 and 6. Measurements from V1 units made under more natural viewing conditions, where eye movements were not controlled, revealed higher response variance; higher by a factor of 6–10 (Gur, Beylin & Snodderly, 1997). Given the precision of magnocellular ganglion cell responses, a factor of 10 increase in variance would only account for a modest proportion of psychophysical RT variance. We infer that the principal source of reaction time distribution variance to suprathreshold stimuli is subsequent to the primary visual cortex.

The framework for the reaction time model is:

$$RT={RT}_0+f\left(R_S\right(t\left)\right)$$ (1)

where RT is the measured mean reaction time, RT₀ is the irreducible minimum reaction time, and R_S(t) is the stimulus-dependent neural response that triggers a motor response. RT₀ is primarily determined by the time of the motor response, initiated when the sensory component reaches a criterion value. The parameter RT₀ also incorporates fixed components such as synaptic delays and conduction times. Figure 4 shows the sequential processing stages in the model. In this model, an impulse response function appropriate for the light level and receptor class is convolved with the stimulus to yield a neural representation that triggers a motor response.

Figure 4.

The flow chart and schematic representation of the computational model for rod (left column) and cone (right column) reaction time. A) Rod and cone impulse response functions for the retinal illuminance levels. B) Incremental stimuli at five contrasts, at 0.02 Td for rods, and 20 Td for cones. C) Convolution of the stimuli with the impulse response functions. D) Integrated neural response used for reaction time determination, based on a time point at which the integrated difference just reaches a critical value (g).

We first established behavioral impulse response functions (IRFs) for rod and cone sensory signals that include post-receptoral processing (Fig 4A). The resultant IRFs are convolved with the stimulus (Fig 4B) to yield a neural sensory response R_S(t) (Fig 4C). Functions similar to R_S(t) have been used in models to relate threshold temporal contrast sensitivity functions to threshold pulse detection (Smith, Bowen & Pokorny, 1984; Swanson et al., 1987). Mean reaction times to suprathreshold stimuli are evaluated with an integration model that summates input from R_S(t) until a criterion value is reached. The criterion value initiates the motor response. The output of the integration model is shown in Fig 4D. We will describe each component in sequence.

Impulse response functions

The first component of the model is the IRF, which describes the visual system’s response to a light pulse with infinite height, infinitesimal width, and unit area (Watson, 1986). In a linear system, the response to any arbitrary stimulus input can be determined by convolving the IRF with the temporal waveform of the stimulus. Impulse response functions can characterize temporal responses at different levels in the visual system. We based the IRFs on psychophysical rather than retinal physiological data so that the IRFs included post-retinal temporal filtering (Lee, Pokorny, Smith, Martin & Valberg, 1990; Yeh, Lee & Kremers, 1995).

The IRF is predominantly monophasic for the rod system and biphasic for the cone system. The IRF is characterized by a gamma probability density function with time constant τ and number of stages n (Watson, 1986).

$$H(t,\tau ,n)=\frac{{(1/\tau )}^n}{(n-1)!}{t}^{n-1}{e}^{-t/\tau }$$ (2)

where H is the response amplitude, t is time. The IRF has unit area and the time to peak t_p is given by (n−1)τ.

For cones, an inhibitory component is added to reflect the biphasic nature of cone IRFs such that

$$A\left(t\right)=aH(t,{\tau }_1,n_1)-bH(t,{\tau }_2,n_2)$$ (3)

where A is the response amplitude, τ₁ is the time constant of the excitatory component, τ₂ is time constant of the inhibitory component, and a and b are the weights of the excitatory (with n₁ stages) and inhibitory (with n₂ stages) components. Note that the actual times to peak (t_p) and trough (t_t) of the cone IRFs depend on the values of τ₁, τ₂, a and b.

We derived parameters of the model rod and cone IRFs from published temporal contrast sensitivity functions (TCSFs) and two-pulse summation data gathered over a wide range of light levels. For the TCSFs, we determined IRFs using the method described by Stork and Falk (1987), with scaling and extrapolations at the low and high frequencies according to procedures described by Swanson et al. (1987). For two-pulse summation data, we estimated the IRFs using the exponentially damped, frequency modulated sinusoid model described by Burr and Morrone (1993) that has no minimum phase assumption. Data from published figures was extracted using GraphClick graph digitizer software (http://www.arizona-software.ch/applications/graphclick/en/).

There are several caveats concerning the methodology we used to derive IRFs from the published temporal modulation transfer functions. First, the impulse responses derived with the Stork and Falk (1987) method assume a minimum phase filter. There is uncertainty regarding the true impulse response shape because the minimum phase assumption is only one of a variety of solutions that can have identical temporal contrast sensitivity functions (Victor, 1989). Different assumptions could yield other impulse responses. The minimal phase assumption may cause a timing offset of the peak of the estimated IRFs relative to the “true” IRF. In terms of our model, if the timing offsets at each light assume a constant value, the irreducible minimum reaction time (RT₀) would be changed by a fixed factor. This would not affect the goodness of fit. Luminance IRFs derived from two-pulse data using a method that did not make the minimum phase assumption showed identical rising portions, but some amplitude differences at later times compared to those calculated assuming the minimum phase (Burr & Morrone, 1993). Shinimori & Werner (2003) found the derived impulse response functions were similar with or without minimum phase assumption. In our model the reaction time is largely dependent on the initial segment of the impulse response function. Thus any differences occurring later in the IRF would not affect the model fits. Second, there is the additional complexity in that the reconstruction of the IRFs can be altered by the low and high frequency extrapolation strategy, however Dagnelie (1987) reported that the Swanson et al method yielded results similar to those of the other possible procedures. A third issue concerns the propriety of using scaled IRFs derived from threshold contrast data to characterize IRFs at suprathreshold contrasts. Retinal magnocellular cells exhibit a compressive nonlinearity that is most apparent at high contrast levels (Kaplan & Shapley, 1986). The same contrast gain function can be demonstrated psychophysically in humans (Pokorny & Smith, 1997). Purpura, Kaplan and Shapley (1988) showed that MC contrast gain and the associated compressive nonlinearity decreased with decreasing light level. For the range of contrasts employed in the present experiment, the Purpura et al contrast gain functions show only minor deviations from linearity except for the highest contrast level condition at 200 Td. Since RT reached asymptotic levels for this stimulus condition it was not deemed warranted to introduce the added complexity of contrast gain into the model.

For rods we used TCSFs published by van den Berg and Spekreijse (1977), Hess and Nordby (1986), Nygaard and Frumkes (1985) and Smith (1973). The TCSFs reported in these studies are predominantly lowpass, with some slight low-frequency rolloff at the highest light levels. A summary of rod TCSF studies is given in Table 1. The results from three studies were not included. The first (Skottun, Nordby & Magnussen, 1981) was superseded by more comprehensive experiments on the same rod monochromatic observer (Hess & Nordby, 1986). The other two excluded studies employed large (≥6.2°) stimulus fields (Conner, 1982; Sharpe et al., 1989). These TCSFs are more bandpass than those of the studies included in Table 1. Stimulus fields containing significant low-frequency information can yield bandpass TCSFs at high scotopic and mesopic light levels (Smith, 1973).

Table 1.

A summary of rod and cone TCSFs and two-pulse summation studies.

Study	Receptor Type	Method	Adaptation Levela	Spatial Extent	Surround	Retinal Locus	Pulse Duration
Hess & Nordby, 1986	Rod	TCSF	0.003–130 ST	10×15° (0.3 cpd grating)	N/A	4–5°
Nygaard & Frumkes, 1985	Rod	TCSF	0.025–0.4 ST	2°	No	7°
Smith, 1973	Rod	TCSF	0.005–50 ST	7° (0.3 cpd grating)	N/A	7°
van den Berg & Spekreijse, 1977	Rod	TCSF	0.13 ST	5°	No	10°
de Lange, 1958	Cone	TCSF	4.3–430 PT	2°	Yes	Fovea
Keesey, 1970	Cone	TCSF	26–260 PT	1°	Yes	Fovea
Kelly, 1959	Cone	TCSF	1000 PT	2°	Yes	Fovea
Roufs, 1972	Cone	TCSF	2–525 PT	1°	No	Fovea
Swanson et al 1987	Cone	TCSF	0.9–900 PT	2°	No	Fovea
van der Gon/van der Tweel, 1961	Cone	TCSF	2–200 PT	0.37°	No	Fovea
van Nes et al, 1967	Cone	TCSF	0.85–850 PT	0.64 cpd grating	N/A	Fovea
Burr & Morrone, 1993	Cone	2 Pulse	163 PT	6.25° (1 cpd grating)	N/A	Fovea	8 ms
Herrick, 1972	Cone	2 Pulse	5.0–210 PT	1.1°	No	Fovea	5 ms
Ikeda, 1965	Cone	2 Pulse	61.2 & 328 PT	0.5°	Yes	Fovea	12.5ms
Meijer et al, 1978	Cone	2 Pulse	120 PT	1.6°	No	3.5°	10 ms
Roufs, 1973	Cone	2 Pulse	1–120 PT	1°	No	Fovea	2–3 ms
Shinomori & Werner, 2003	Cone	2 Pulse	49 PT	2.26° (Gaussian patch)	N/A	Fovea	1.2 ms
Uchikawa & Yoshizawa, 1993	Cone	2 Pulse	10 PT	1.5°	No	Fovea	10 ms
Uetsuki & Ikeda, 1970	Cone	2 Pulse	1–300 PT	0.5°	Yes	Fovea	10 ms

^aST: Scotopic Td PT: Photopic Td

We fitted a regression line to the t_p values determined from the IRFs derived from the published rod TCSFs (Fig. 5, left panel). From this we interpolated the t_p values from the regression line for the light levels used in our study. The time to peak (t_p) values (Eq. 2) are shown in Fig. 5 (left panel), plotted as a function of scotopic Td. The estimated rod t_p was 72, 62, 53, 44 and 34 ms at 0.002, 0.02, 0.2, 2 and 20 photopic Td, respectively. The left panel of Fig. 4A shows the calculated rod impulse response functions using Equation 2 with n = 7 and corresponding time constant τ, given by t_p/(n−1) and. The times to peak for the rod impulse response functions at different light levels are shown in Table 2.

Figure 5.

The parameters of the rod (t_p; left panel) and cone (t_p, t_t, and b; middle and right panels) impulse response functions derived from published TCSFs. The fitted regression lines (dashed lines) were used to estimate the timing parameters for the light levels in the study.

Table 2.

The values of parameters used for rod and cone impulse response functions.

	Parameter	Value
	tp	72 ms (0.002 Td)
		62 ms (0.02 Td)
ROD		53 ms (0.2 Td)
		44 ms (2 Td)
		34 ms (20 Td)
	n	7
	tp	48 ms (2 Td)
		39 ms (20 Td)
		30 ms (200 Td)
	tt	129 ms (2 Td)
		105 ms (20 Td)
		82 ms (200 Td)
CONE	a	1
	b	0.156 (2 Td)
		0.294 (20 Td)
		0.432 (200 Td)
	n1	7
	n2	7

For cones we used TCSF data from de Lange (1958), Kessey (1970), Kelly (1959), Roufs (1972), Swanson et al. (1987), van der Gon (data graphed in van der Tweel, 1961), and van Nes et al. (1967), and estimated the cone time to peak (t_p) and trough (t_t) using the same method as for the rod impulse response function. These are shown in Fig. 5 (middle and right panels). The results from Kelly’s (1961) parametric study were not included because the stimulus, a 68° edgeless field, yielded data that were more bandpass than TCSFs measured with smaller sharp-edged fields (Kelly, 1959). Also plotted in Fig. 5 are IRFs derived from two-pulse summation data (Burr & Morrone, 1993; Herrick, 1972; Ikeda, 1965; Ikeda & Boynton, 1965; Meijer, van der Wildt & van den Brink, 1978; Roufs, 1973; Shinomori & Werner, 2003; Uchikawa & Yoshizawa, 1993; Uetsuki & Ikeda, 1970). There is a small systematic difference between the cone time to peak (t_p) and trough (t_t) estimated from the TCSF data and the more direct estimates derived from the two-pulse summation data. An overview of the cone TCSF and two-pulse summation studies is given in Table 1.

The t_p and t_t values estimated from TCSFs and two pulse summation data are shown in Fig. 5 (middle panels) from which we estimated t_p and t_t for the light levels used in this study. The values of time to peak at 2, 20 and 200 Td are 48, 39 and 30 ms and the time to trough at 2, 20 and 200 Td are 129, 105 and 82 ms respectively. We set a in Eq. (3) to = 1.0 because the IRFs are normalized. The b values were determined according to the same methods as for the time constants, using only the values from TCSF data since the derived two-pulse IRFs were sometimes triphasic, producing deviant b values. The precise timings and amplitudes of the negative portion of the model IRFs are not critical since reaction time relies mainly on the early portion of IRFs. The estimated b values are 0.156, 0.294 and 0.432 at 2, 20 and 200 Td, respectively. The right panel of Fig. 4B shows the cone impulse response functions with these parameter values and n = 7. For both the rod and cone IRFs, an n = 7 was adopted for comparison with other behavioral estimates of the IRFs (e.g. Swanson et al). We further evaluated modeling strategies with values of n equal to 4 and 10. The total variance explained by the models between values of n equal to 4 and 10 varied less than 5% and the minimum reaction time derived from the model varied by no more than 10 ms. We also modeled the cone RT with parameters for cone IRFs estimated from TCSFs alone or the two-pulse summation data alone; the resulting total variance accounted for by altering the input parameters differed by less than 2.5%. The values of the parameters for cone impulse response functions derived from combined TCSF and two-pulse summation data are shown in Table 2. We found the values of τ₁ and τ₂ in Equation (3) such that the times to peak and trough were equivalent to the estimates in Table 2.

Neural-Sensory Process

A motor response is initiated when the integrated input passes a criterion level. The second component of the model involved establishing the criterion level for the motor trigger. To do this, we convolved the IRF (Fig. 4A) with each stimulus contrast and polarity at a given light level (Fig. 4B) to obtain a neural sensory response R_S(t) (Fig. 4C). The output of R_S(t) is integrated using a 200 ms rectangular moving window specified according to,

$$G_S(t_1)={\int }_{t_1}^{t_1+200}{R}_S(t)dt$$ (4)

where G represents the integrated neural response for a stimulus (S) with an increment or decrement relative to the background, and t₁ is the starting time point of the moving window. Parameter t₁ was incremented in 1 ms steps. The 200 ms rectangular integration window produces an equivalent model output as a function with a decay term. This is represented schematically in Fig. 4D.

The stimulus dependent component of reaction time f(R_S(t)) in Eq. (1) is determined by the time at which the integrated neural response reaches a critical value (g) set by the system, that is,

$$f(R_S(t))=G_S^{-1}(g),$$ (5)

where G_S⁻¹ represents the inverse function of G_S(t₁) in Eq. (4). This is represented schematically in the insert to Fig. 4D.

Model fitting

To fit the model, we assumed that, for a receptor type, the irreducible minimum reaction time RT₀ was the same for all conditions. For rod reaction times, the model had one free parameter for increments (g_i) and a second for decrements (g_d) at each light level. For cone reaction times, the incremental and decremental reaction times were closely similar, therefore one free parameter, (g), was estimated for both incremental and decremental conditions at each light level. The values of RT₀ and g were searched across all conditions to minimize the sum of square errors between the model output and the reaction time data. The parameter search was conducted in Matlab 7, using the Nelder-Mead simplex method (Lagarias, Reeds, M. H. Wright & Wright, 1998).

Fitting the computational model to the reaction time data

The solid lines in Fig. 2 and Fig. 3 are the model outputs with the fitted g-values shown in Fig. 6. The irreducible minimum reaction time RT₀ was 302 ms for rod stimuli and 279 ms for cone stimuli for observer DC, and 209 ms for rod stimuli and 185 ms for cone stimuli for observer AJZ. These values of RT₀ are in the range reported in the literature (Mansfield, 1973; Woodrow, 1915).

Figure 6.

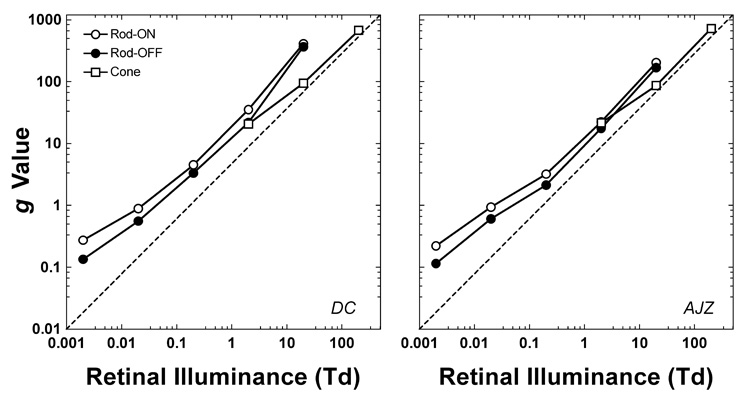
The fitted g values for DC and AJZ. For rod reaction time, the g-values are different between increment and decrement at each light level. For cone reaction time, the g-values are the same between increment and decrement at each light level.

Based on the amount of data variance accounted for by the model, the model accurately captures the major trends of the measured reaction times. The sole condition where the model fit was relatively poor was at 0.002 Td for observer DC. For the remaining conditions, the average variance explained by the model (R²) among all the RT-contrast functions was 0.90 (range 0.57–0.99) for observer DC and 0.89 (range 0.73–0.99) for observer AJZ. Best-fits of the empirical Piéron function to the individual RT-contrast functions (not shown), involved more free parameters and provided only modestly better fits; mean R²: 0.95 (range 0.87–0.99) for observer DC and 0.95 (0.85–0.99) for observer AJZ. In the experiment, we had 16 conditions (rod: 5 light levels at 2 polarities; cone: 3 light levels × 2 polarities). The Piéron function fits require 32 free parameters for each observer; our model has 15 free parameters: one global free parameter (RT₀) for each receptor class across all light levels and both stimulus polarities with 13 free parameters, 1 for each light level for cones and 2 for each light level for rods.

Discussion

4.1 Rod and cone reaction times

We measured simple reaction time to isolated rod and cone incremental and decremental stimuli at light levels where rods alone (0.002–0.2 Td), rods and cones (2–20 Td) and cones alone (200 Td) mediated vision. For each condition, reaction time decreased with increasing contrast or retinal illumination level. At 2 Td, asymptotic reaction times to rod and cone stimuli differed by about 15–20 ms, which is consistent with physiological (Schneeweis & Schnapf, 1995; Verweij et al., 1999) and psychophysical (Sun et al., 2001b) measurements under conditions of comparable rod and cone light adaptation.

4.2 Reaction times to increments and decrements

Our measurements indicated that there was no difference in reaction time to cone incremental and decremental stimuli, which is similar to Jaskowski (1984) and consistent with physiological data that show symmetrical responses of MC- ON and OFF cells to rapid ON or OFF sawtooth stimulus modulation (Kremers et al., 1993). However, there are literature reports that some, but not all observers, have lower cone decrement thresholds (reviewed by Bowen, Pokorny & Smith, 1989). At scotopic adaptation levels, sensitivity to decremental stimuli is reported to be greater than to incremental stimuli (Blackwell, 1946; Short, 1966).

Based on the Poisson nature of quantal absorption, Cohn (1974) hypothesized an asymmetry in detection threshold to increments and decrements due to a smaller variance in decrements than increments at dim light levels. We modeled quantal fluctuation for our rod stimuli using a Poisson random number generator. At each contrast and light level, we calculated the mean number of photons in the background and the incremental/decremental stimuli using the Equation provided in Kaiser & Boynton (1996). We generated 1000 hypothetical stimuli based upon the Poisson distributions for the mean number of photons in each condition. We then estimated the reaction time distributions for each condition using our model and calculated mean reaction times. We found that the model fits still required different g values for the incremental and decremental conditions, even at the lowest light level (0.002 Td) in our study. Therefore we conclude that quantal fluctuation can only partially account for the measured difference in the reaction times between rod increments and decrements. Additionally, a subsidiary experiment measured thresholds for increments and decrements. Incorporating these values, the model output showed that we still required separate g-values for the rod ON and OFF systems to obtain acceptable model fits to data. In other words, the measured difference in reaction time to rod increments and decrements cannot be fully accounted for by quantal fluctuation, or by a threshold difference for increments and decrements.

4.3 Computational model of rod and cone reaction times

The significance of the model we present is that it accounts for the measured rod and cone reaction time using impulse response functions derived from published psychophysical temporal modulation transfer functions and two-pulse summation data. We extended previous models by incorporating sensory components (rod and cone impulse response functions) into a reaction time model.

4.3.1. The irreducible minimum reaction time

In our model, the irreducible minimum reaction time (RT₀) is independent of stimulus polarity and light level for each receptor type. The difference in the fitted RT₀ for rod and cone stimuli was 15 ms for observer DC and 19 ms for observer AJZ. When we evaluated a common RT₀ for rod and cone stimuli, the fits were worse: the residual sum of squares was 11% higher for observer DC and 28% higher for observer AJZ.

Woodworth (1938) proposed using irreducible minimum reaction time to compare the temporal response speed of two different systems. This difference in rod and cone RT₀ may reflect the delay between rod and cone signals. The 15–19 ms difference in irreducible minimum rod and cone reaction times shows good concordance with the physiological (Schneeweis & Schnapf, 1995; Verweij et al., 1999) and psychophysical (Sun et al., 2001b) latency difference estimates.

4.3.2. What is the meaning of parameter g?

Rod and cone impulse response functions were derived from published temporal contrast modulation functions and two pulse summation data, and the amplitudes of the impulse response functions were arbitrary. We applied values of t_p and t_t to the equations for the rod and cone impulse response functions and set them to have a unit area (Fig. 4A). Consequently, the output from the convolution between the impulse response function and the stimulus had the same energy as the input. Therefore the g-value (Figure 6) is a scaling factor for the amplitude of the rod and cone impulse response functions at different retinal illuminances. The g-values were well-behaved, being monotonic functions of retinal illuminance for both rods and cones. The format of the g versus retinal illuminance function is the same as a threshold versus illuminance (TVI) function (the unit for g is Td.s). However the g-value function rises monotonically at lower light levels whereas the TVI function shows a linear segment where threshold is not dependent on background light level (Stiles, 1939; we confirmed the form of the TVI for our stimulus waveform and our observers). The linear region of the TVI function has been attributed to the presence of intrinsic noise in the visual system (Barlow, 1957). Threshold sensitivity and suprathreshold reaction time rely on different features of the underlying internal response generated by the visual stimulus (Zele, Cao & Pokorny, Submitted). A background raises thresholds only when the quantal absorptions from the background light exceed the intrinsic noise. The monotonic g-value function at lower light levels is likely a result of the suprathreshold RT stimuli having high signal/noise ratios compared to threshold level stimuli measured on the same backgrounds.

Psychophysical and electroretinographic studies suggest that there is a phase delay between the slow and fast rod pathways, which may result in flicker detection cancellation at a temporal frequency where the phase shift between pathways is 180° (Conner, 1982; Sharpe et al., 1989; Stockman, Sharpe, Ruther & Nordby, 1995; Stockman, Sharpe, Zrenner & Nordby, 1991; van den Berg & Spekreijse, 1977). For RT to an incremental or decremental stimulus, cancellation is not a major factor since the faster signal will be processed earlier than the slower signal. If interference substantially altered reaction times, the g-values in Figure 6 would deviate from the monotonic function.

For rod data at all the light levels, there were two different system gains, as suggested by two different slopes in the log g versus log Td plots (Fig. 6). At low light levels (0.002 – 0.02 Td), the slope was 0.65 for observer DC and 0.61 for observer AJZ; at high light levels (0.2 – 20 Td), the slope was 0.99 for observer DC and 0.92 for observer AJZ. This might reflect the different gains of the two rod pathways; i.e. the rod ON-bipolar, AII amacrine cell pathway and the rod-cone gap junction pathway, although there is insufficient data to confirm this idea. The rod ON and OFF systems had different g values at the same light levels (Fig. 6). The fitted g-values for the rod ON and OFF system incorporate the difference in the rod incremental and decremental stimuli due to quantal fluctuation (Cohn, 1974). The slope of the g-values for cone reaction time (2 – 200 Td) was similar to that for rod reaction time at low light levels (0.002 – 0.02 Td). Finally the rod and cone data had similar g values at 2 Td, indicating that the two systems have similar gains at this light level.

4.4. Summary

We measured reaction time to rod and cone incremental and decremental stimuli at different retinal illuminance levels. For each receptor type, reaction time decreased with an increase in the contrast and retinal illuminance level. Reaction time to rod decrements was shorter than that for rod increments at low light levels. For the same adaptation conditions, the difference in reaction time between rod and cone stimuli became larger at higher retinal illuminances. Our model, based on neural sensory responses successfully linked the rod and cone impulse response functions to the measured reaction times.