Cubic membranes: a legend beyond the Flatland* of cell membrane organization

Abstract

Cubic membranes represent highly curved, three-dimensional nanoperiodic structures that correspond to mathematically well defined triply periodic minimal surfaces. Although they have been observed in numerous cell types and under different conditions, particularly in stressed, diseased, or virally infected cells, knowledge about the formation and function of nonlamellar, cubic structures in biological systems is scarce, and research so far is restricted to the descriptive level. We show that the “organized smooth endoplasmic reticulum” (OSER; Snapp, E.L., R.S. Hegde, M. Francolini, F. Lombardo, S. Colombo, E. Pedrazzini, N. Borgese, and J. Lippincott-Schwartz. 2003. J. Cell Biol. 163:257–269), which is formed in response to elevated levels of specific membrane-resident proteins, is actually the two-dimensional representation of two subtypes of cubic membrane morphology. Controlled OSER induction may thus provide, for the first time, a valuable tool to study cubic membrane formation and function at the molecular level.

Introduction

Biological membranes are generally considered as rather flat bilayer sheets in the cell. The existence of nonlamellar structures of biological membranes, such as inverted hexagonal (H_II) or cubic (Q_II) phases, has long been a matter of dispute. The major experimental limitations of identifying 2D periodic hexagonal or 3D periodic cubic membrane morphologies in (living) cells are caused by the dimensions of these structures and by limited analysis tools at this size range in vivo. In vitro, complex lyotropic liquid crystalline phases, i.e., lamellar (L_α), H_II, or Q_II structures, are readily amenable to a range of experimental techniques, such as nuclear magnetic resonance, small-angle x-ray scattering, and differential scanning calorimetry. These techniques, however, are not feasible in whole cells because of limited resolution power and background noise. Thus, the experimental approach to uncover nonlamellar membrane structures in (fixed) cells is restricted to EM, leaving a wide range of interpretations for 3D structures between fact and artifact. Transmission EM (TEM) images are 2D projections of (ultra) thin, yet finitely thick (typically 70–90 nm), sections cut randomly through a 3D specimen. The comprehension of 3D structures based on 2D TEM projections is, thus, extremely difficult, particularly if the lattice size of the observed structure is in the same order of magnitude as the section thickness.

In recent years, tremendous progress has been made based on electron tomography (ET) that allows 3D reconstruction of sections that are up to 400 nm thick, with a resolution of ∼5 nm, i.e., approaching the molecular level (for review see Lucic et al., 2005). Specifically, cryo-ET from specimens in vitreous ice provides an excellent means to preserve cellular structure, which avoids artifacts found in conventional EM preparation techniques, and is also good for high-resolution analysis of membrane-bound organelles (Lucic et al. 2005; Hsieh et al., 2006). Despite the technological advantages of cryo-ET, most of the depictions of biological membranes that appeared in the literature during the past decades are derived from TEM of fixed and thin-sectioned cells and tissues. Dependent on the thickness and orientation of the ultrathin section, relative to the coordinates of an ordered 3D structure, various types of projection patterns are observed. Thus, for the past five decades, frequent misinterpretations of TEM micrographs of membrane-based cell ultrastructure were inescapable, particularly for the highly folded and interconnected cubic membrane morphologies.

Unusual membrane morphologies in biological systems

Extensive membrane proliferations leading to unusual and highly convoluted depictions in TEM have been observed in numerous cell types from all kingdoms of life and in virtually any membrane-bound cell organelles, especially smooth ER, plasma membrane, inner nuclear membrane, mitochondrial inner membrane, and chloroplast thylakoid membranes (Landh, 1996; Federovitch et al., 2005). Not surprisingly, the ER was found to be the most prominent target of morphological alterations because of its highly convoluted structure and central functions in membrane lipid synthesis, assembly, secretion of membrane and secretory proteins, ion homeostasis, and membrane quality control. Thus, these morphologies appear under numerous nicknames in the literature, such as “undulating membranes” (Schaff et al., 1976), “cotte de mailles” (Franke and Sheer, 1971), “membrane lattice” (Linder and Staehelin, 1980), “crystalloid membranes” (Yamamoto et al., 1996), “paracrystalline ER” (Wolf and Motzko, 1995), and “tubuloreticular structures” (Grimley and Schaff, 1976; Landh, 1995, 1996). The so-called “organized smooth ER” (OSER) that is formed in response to elevated levels of the membrane-resident protein cytochrome b(5) has recently been added to this list (Snapp et al., 2003).

Quite remarkably, the most prominent examples of ER expansion are related to lipid synthesis, viral infection, and drug detoxification. For example, cells of the adrenal cortex or Leydig cells of the testes, which synthesize large amounts of sterol, display dramatic proliferations of crystalloid ER (Sisson and Fahrenbach, 1967; Black, 1972). Several studies directly correlate overexpression of certain ER-resident proteins with 2D and 3D (cubic) periodic symmetry transition of the ER, implying a specific structure–function relationship of cubic membrane formation as a consequence of an altered protein or lipid inventory of the membrane. Overexpression of HMG-CoA reductase isozymes induces assembly of nuclear and cortical ER stacks with 2D symmetry, termed “karmellae,” in yeast (Wright et al., 1988; Profant et al., 2000). Overexpression of this enzyme in UT-1 (Chin et al., 1982) or CHO cells (Jingami et al., 1987; Roitelman et al., 1992) induces formation of crystalloid ER, which houses most of the HMG-CoA reductase protein (Anderson et al., 1983; Orci et al., 1984). The crystalloid ER membrane contains reduced levels of free cholesterol; sterol supplementation of these cells results in accelerated degradation of HMG-CoA reductase and the disappearance of the crystalloid ER (Orci et al., 1984). However, the enzymatic activity may not be the key factor in inducing ER structure alteration, as nonfunctional subdomains of ER-resident proteins also result in crystalloid ER formation. For instance, Yamamoto et al. (1996) reported that at least two regions of msALDH, but not the entire enzymatically active protein, may be required for the formation of the crystalloid ER in transfected COS-1 cells.

As a common theme, membrane rearrangements resulting in cubic morphologies may be a consequence of various cellular stresses, and may occur, e.g., as a response to hypoxia stress (Takei et al., 1994), drug treatment (Feldman et al., 1981), tumors (Schaff et al., 1976), or specifically, upon stimulation of B lymphocytes with lipopolysaccharide (Federovitch et al., 2005). Tubuloreticular structures are also formed in SARS-infected cells (Goldsmith et al., 2004) and, indeed, were subsequently identified to resemble cubic membrane architecture (Almsherqi et al., 2005). Tubuloreticular structures, therefore, have significant potential as ultrastructural markers in pathology (Ghadially, 1988).

Possibly the best-characterized cubic membrane transition was observed in the mitochondrial inner membranes of the free-living giant amoeba (Chaos carolinensis). In this organism, mitochondrial inner membranes undergo dramatic changes in 3D organization upon food depletion, providing a valuable model system with which to study induced membrane reorganization. Within 1 d of starvation, 70% of mitochondria undergo this morphological transition, which after 7 d of starvation is observed in virtually all mitochondria (Daniels and Breyer, 1968). Intriguingly, this process is fully reversible to wild-type morphology upon refeeding (Deng and Mieczkowski, 1998). Using ET, we have unequivocally demonstrated that inner mitochondrial membranes in C. carolinensis cells adopt cubic morphology. This starvation-triggered transition is accompanied by alterations in cellular oxidative stress response, which led us to speculate that cubic membrane formation may be related to oxidative stress (Deng et al., 2002).

Whether cubic membrane formation is solely a result of aberrant membrane protein and/or lipid interactions in infected or pathological states, or is a specific cellular response to these pathologies remains unclear. To some extent, regular 3D folding appears to be an intrinsic property of membranes that is enhanced under certain conditions; however, the specific mechanisms leading to cubic membrane formation are not known. Recently, Voeltz et al. (2006) discovered a novel class of proteins, termed reticulons, which are involved in shaping the highly curved tubular ER membrane. It is tempting to speculate that cubic membrane–inducing conditions may also interfere with reticulon function. However, the potential role of reticulons, or related proteins, in supporting or preventing the formation of karmellae, whorls, hexagonal, or cubic membrane structures remains to be determined.

Modeling cubic membranes

Nonlamellar arrangements of lipids in aqueous dispersions are well characterized in vitro and are of significant technological interest as biomimetics, matrices for membrane protein crystallization, and drug delivery systems (Barauskas et al., 2005). Among these nonlamellar lipid mesophases, cubic phases attract great attention because of their unique feature of 3D periodicity. These highly curved 3D periodic (n)-parallel membrane bilayers represent “infinite periodic minimal surfaces” (Hyde, 1996) that divide space into (n + 1) independent aqueous subcompartments. The type of surface symmetry may change, for instance, depending on the water content, giving rise to cubic structures with gyroid (Q_G), double diamond (Q_D), or primitive (Q_P) types of symmetry (Luzzati and Husson, 1962; Landh, 1995; de Kruijff, 1997; Hyde et al., 1997). Whereas infinite periodic minimal surfaces are extensively studied and applied in material sciences, structures in biological systems, such as cubic cell membranes, are obviously much less characterized and understood.

Identifying cubic membranes in cells

Two principal approaches are feasible to unequivocally determine cubic membranes in biological specimens based on EM. In EM tomography, a thicker sectioned specimen (up to 400 nm) is analyzed by intermediate voltage TEM at multiple tilted angles, yielding a large number of projections that are reconstructed by computational image analysis into a 3D representation of the object (Lucic et al., 2005). EM tomography has previously been successfully applied to determine cubic membrane transition of the inner mitochondrial membrane morphology in C. carolinensis upon starvation (Deng et al., 1999).

Alternatively, because cubic membrane morphologies adopt mathematically well defined 3D configurations (Fig. 1 a), images resulting from TEM of ultrathin sections can be matched to theoretical computer-generated projections; direct template correlative matching (DTC; Landh, 1995, 1996; Deng and Mieczkowski, 1998, Almsherqi et al., 2005) is a method based on pattern and symmetry recognition. With DTC, the electron density of the TEM image is correlated to a library of computer-generated 2D projection maps (cubic membrane simulation projection software; Deng and Mieczkowski, 1998; Fig. 1 b). These 2D projection catalogs represent cubic symmetries of gyroid G-, double diamond D-, and primitive P-surfaces, simulating various surface parameters, projection directions, and section thicknesses of a TEM specimen (Deng and Mieczkowski, 1998).

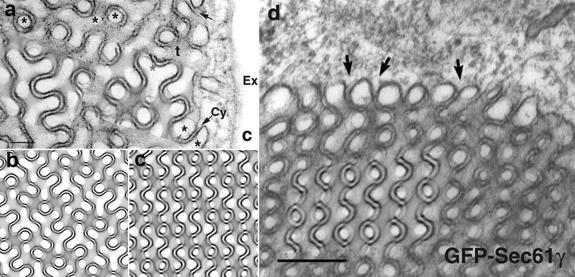
Figure 1.

Computer simulation of cubic membrane architecture. (a) A pair of 3D periodic cubic surfaces illustrates the structure and symmetry of the cubic regions of OSER membranes. Each surface shown represents the center of a membrane bilayer, indicating the close proximity of two bilayer membranes in that model. (b) Examples of computer-simulated 2D projections for the respective G- and D-type cubic surfaces, at different viewing angles. These simulated 2D projection maps form a library that is used to match the membrane patterns of interest, as observed by TEM.

Application of DTC to identify OSER as cubic membrane morphology

OSER was observed in COS-7 and CV-1 cells, having formed as a consequence of overexpression of cytochrome b(5) tagged with GFP (Snapp et al., 2003). OSER consists of a network of membranes that are arranged in a nonrandom order and display an equally spaced pattern with cubic symmetry. Comparison of the 2D TEM images with the “fingerprints” of the projection library suggested gyroid and double diamond cubic membrane configurations. Indeed, superimposition of computer-generated projections with subdomains of the TEM images match perfectly. Two examples of the image analysis are shown in Fig. 2. Subdomains of TEM micrographs correlate precisely with the computer-simulated 2D projection of a balanced double-membrane gyroid (G)-type (Fig. 2 a) and double diamond (D)-type (Fig. 2 d) of cubic morphology. The exact matching of the intricate, fine details of the projection map, such as the appearance of the dashed straight line, and of material density with the theoretical computer-generated projections (Fig. 2, b and c) can be taken as additional evidence of the cubic nature of OSER. Although OSER displays diverse patterns in the 2D TEM micrographs, they are all derived from exactly the same mathematically well defined 3D structures, but at varying sectional thicknesses and viewing directions. To further confirm the identity of the patterns beyond visual inspection, fast Fourier transform calculations were performed on the pattern of the membrane subdomain, in comparison to projections derived from the computer-generated library and the background of pattern-free membrane regions. The chosen domains typically showed reflection of at least the second order, and they support the identity of the image projections with the calculated data (unpublished data). These analyses strongly support the notion of the formation of a true cubic membrane morphology in CV-1 and COS-7 cells upon cytochrome b(5) overexpression. The controlled induction of OSER formation in an experimental system that is amenable to genetic manipulation may, indeed, open new perspectives for analyzing and understanding cubic membrane formation and its potential biological functions.

Figure 2.

Identification of cubic membrane morphologies in TEM micrographs. Two examples of the DTC method, applied to TEM images of OSER (adopted from Snapp et al., 2003). (a) The original TEM micrograph (Snapp et al., 2003 Fig. 2 c) matches perfectly to the theoretical superimposed projections of balanced (2-parallel surfaces) gyroid cubic membranes, as depicted in b. Asterisks indicate one of the multicontinuous, yet distinct, subvolumes of cubic membrane architecture. A double diamond projection (c) matches the TEM micrograph (d) adopted from Fig. 7 b of Snapp et al., (2003). The arrows in a and d indicate the continuity of one cubic membrane subvolume (between closely arranged bilayers) and the cytoplasm (Cy). Signature patterns of the theoretical projection are indistinguishable to the electron density pattern of the TEM micrographs. The simulated projections are generated from sections with a thickness of 1/4 of a unit cell, viewed along the direction [36, 30, 17] for gyroid (b) and [28, 16, 5] for double diamond-type (c). The unit cell is the smallest structural unit that possesses the symmetry and properties of cubic membranes. Bars: (a) 100 nm; (d) 160 nm.

The biological significance of cubic membrane formation

An important implication of Snapp et al. (2003) is related to the ease with which lamellar and bicontinuous cubic phases are interconverted. This conclusion is inferred from the fact that weakly dimerizing GFP and chimeric ER proteins with GFP on their cytoplasmic tails could induce OSER formation, but similar proteins with nondimerizing GFP tags could not. A previous work suggested that crystalloid ER biogenesis entailed a tight, zipperlike dimerization of the cytoplasmic domains of certain ER-resident proteins (Yamamoto et al., 1996). However, Snapp et al. (2003) found that OSER-inducing proteins can diffuse freely between OSER and the other ordinary lamellar ER, indicating that they may not be tightly bound in zipper structures. The low-affinity interaction between cytoplasmic domains of OSER-inducing proteins could explain phenomena such as (a) the heterogeneity of ER membrane structures observed, (b) the high rate of (reversible) lamellar cubic phase transition, and (c) the technical difficulties and limitations in isolating intact cubic membranes from biological samples for studies in vitro.

The weak molecular interaction that results in ER transformation could be attributed to the electrostatic interaction between the corresponding cytoplasmic domains of specific membrane-resident proteins (Masum et al., 2005). In vitro studies using monoolein membranes containing negatively charged dioleoylphosphatidic acid have shown that electrostatic interactions caused by surface charge of the membranes (Li et al., 2001), charged short peptides such as poly-l-lysine (Masum et al., 2005), and Ca²⁺ concentration (Awad et al., 2005) play an important role in phase transition between lamellar and cubic phases and in the stability of cubic phases. As electrostatic interactions in the membrane interface are altered either by the increase in surface charge density of the membrane or by the decrease in salt concentration, the lipid membrane phase may change from lamellar to cubic phase. Such cubic lipid phases may not only form to adapt altered membrane proteins or charge distribution, but may also provide the means to rapidly adjust cellular physiology to the changing environmental conditions, such as temperature. The “breathing” of cubic membranes, i.e., the changes in lattice size as demonstrated in vitro (de Campo et al., 2004), may represent an immediate biophysical response, which may allow for a rapid adaptation in water content and ion concentration/charge distribution in a given membrane compartment.

In conclusion, cubic membrane formation in biological systems, which are induced by lipid and protein alterations, drug intervention, or stress, is a widespread phenomenon that is only poorly understood. The apparent relation to pathological states will clearly spark more interest in investigating and understanding these intriguing membrane arrangements. However, novel techniques are required to address membrane transitions in living specimens and to understand the function of these membrane arrangements in the biological context.