Abstract
We introduce a non-parametric representation of transcription factor binding sites which can model arbitrary dependencies between positions. As two parameters are varied, this representation smoothly interpolates between the empirical distribution of binding sites and the standard position-specific scoring matrix (PSSM). In a test of generalization to unseen binding sites using 10-fold cross-validation on known binding sites for 95 TRANSFAC transcription factors, this representation outperforms PSSMs on between 65 and 89 of the 95 transcription factors, depending on the choice of the two adjustable parameters. We also discuss how the non- parametric representation may be incorporated into frameworks for finding binding sites given only a collection of unaligned promoter regions.
INTRODUCTION
The transcription of a gene is influenced by the binding of a protein, known as a transcription factor, to a short segment of DNA, known as a transcription factor binding site, in the regulatory region of the gene. Though the binding sites for a given transcription factor are generally composed of similar sequences of nucleotides, there can be considerable variability.
If the DNA of an organism has been sequenced, and if some binding sites for a given transcription factor are known, then one can try to locate additional binding sites computationally, by scanning the DNA for segments resembling the known binding sites. Stormo (1) surveyed approaches for doing this, focusing largely on a representation of binding sites known as a position-specific scoring matrix (PSSM), or a positional weight matrix (PWM). In a PSSM, each position of a binding site is modeled as making an independent contribution to the overall binding affinity of the site. Experimental evidence suggests that this assumption of independence is not always valid (see for example 2–4), but Benos et al. (5) argue that, ‘in most cases it provides a good approximation of the true nature of the specific protein–DNA interactions’.
Several representations that relax the assumption of independence have recently been shown to outperform PSSMs in certain tasks (6,7). But the first-order Markov model on Dirichlet priors used by Xing et al. (6) is limited in the dependencies it can model, and while the mixtures of trees and PSSMs described by Barash et al. can model arbitrary dependencies, they limited their tests to mixtures having two components, which cannot. [Barash et al. also briefly discuss using Bayesian networks, which can model arbitrary dependencies, but the figures in their supplementary web data (7; supplementary material A.2) suggest that the performance of Bayesian networks was inferior to that of trees, mixtures of trees and mixtures of two PSSMs. Note that the trees used by Barash et al. are just Bayesian networks in which each position is allowed to have at most one ‘parent’ position—this is similar to the model used by Agarwal and Bafna (8).]
Here we introduce a simple non-parametric representation of transcription factor binding sites, which can model arbitrary dependencies and that smoothly interpolates between a PSSM and the empirical distribution. Our goal in this work is to make better predictions about the locations of transcription factor binding sites. False-positive rates can be further reduced by combining model-based predictions with high-throughput experimental evidence (9). While the non-parametric model may not offer as much insight into the nature of the dependencies between positions as some other models, it has the virtue of being able to exploit such dependencies despite our incomplete understanding of their nature.
We tested the ability of our model to generalize using 10-fold cross-validation on binding sites for 95 TRANSFAC transcription factors, as in Barash et al. (7). Our model outperformed PSSMs on between 65 and 89 out of 95 transcription factors, depending on two adjustable parameters. In a similar test, the three models used by Barash et al. outperformed PSSMs on between 33 and 59 of the 95 transcription factors (7). Our non-parametric model is also applicable to other types of data, for example protein sequences.
MATERIALS AND METHODS
Position-specific scoring matrices
Let x1,…, xm denote the m known binding sites for a transcription factor F. We assume for now that each binding site xi = xi1 … xin ∈{A,C,G,T}n has the same width n, and that the binding sites have been aligned without gaps.
By a PSSM for F we shall mean a 4 × n matrix W, with rows indexed by nucleotides k∈{A,C,G,T} and columns indexed by positions j∈{1,…, n}, such that each entry W(k,j) is non-negative, and the four entries in each column sum to 1. The score associated with a DNA segment y = y1 … yn by the PSSM W is given by:
The entry W(k,j) can be interpreted as the marginal probability of nucleotide k appearing in position j in a randomly selected binding site for F. If we assume that the positions are independent, the score for y can be interpreted as the probability that a randomly selected binding site agrees with y in all n positions. [This explains our use of the notation Pr(y|W).]
Let mj(k) denote the number of sites xi for which nucleotide k appears in position j, i.e., mj(k) = #{i : xij = k}. We define the PSSM Wb to be the 4 × n matrix with:
Wb(k,j) = [mj(k) + bk]/(m + b).
Here the bk are pseudocounts—small sample-size regularizers, with an interpretation as Dirichlet priors in the Bayesian context (see for example 10). The total number of pseudocounts used is b = bA + bC + bG + bT. We shall call Wb the standard PSSM constructed from {x1,…, xm} using b pseudocounts.
Various choices for b appear in the literature, for example b = 0.01 (11), b = 1 (12), b = 2 (13), b = 4 (14), b = 5 (7) and b = √m (15). Some authors distribute the b pseudoucounts uniformly (i.e., set bA = bC = bG = bT = b/4), while others distribute them in proportion to the overall frequency of the nucleotides in the genome.
Mixtures of PSSMs
A mixture of the s PSSMs W1,…, Ws takes the form
for some αt ≥ 0 with
7). Note that mixtures of PSSMs can model probability distributions that single PSSMs cannot; for example the distribution in which Pr(AA) = Pr(CC) = 0.5 and the other 14 DNA segments of width 2 have probability 0. In fact, any distribution can be modeled as a mixture of PSSMs, though the number of components needed may be exponential in the site width n.
One way to construct a mixture of s PSSMs is to partition the set of m known binding sites into s subsets, G1,…, Gs, according to some criterion, and then to define PSSMt to be the standard PSSM for the binding sites in Gt with weight αt = #Gt/m. The total number of pseudocounts can be conserved for various choices of s and various weights αt by using αt b pseudocounts for component PSSMt.
The partition can also be into ‘soft’ clusters, where xi belongs to cluster Gt (with associated matrix PSSMt) with some probability pi,t. The Expectation Maximization (EM) algorithm (16) used in Barash et al. (7) proceeds by computing pi,t ∝ αt Pr(xi|PSSMt), then by recomputing the PSSM for each cluster based on the new estimates of its members. These two steps are repeated until convergence is reached. Although each iteration increases the likelihood of the training data, the EM algorithm is prone to getting stuck in local maxima; it also does not address the question of how many clusters to use.
A non-parametric model
Our approach can be viewed as a mixture of PSSMs in which each Gt is a singleton set consisting of the binding site xt; this gives a mixture of m PSSMs each with weight αt = 1/m. This is essentially a form of non-parametric density estimation (see for example 17)—we are placing a small lump of probability mass in the vicinity of each of the known binding sites. The shape of the lumps can be important, especially when the number of training cases, m, is small; using the standard PSSM Wb/m constructed from xt as the lump around xt gives a poor estimate of the density for small m, so we reshape the lumps as follows: let W0b denote the standard PSSM constructed from all m binding sites, using b pseudocounts, and let Wtb/m denote the standard PSSM constructed from just binding site xt using b/m pseudocounts. We take our lumps to be PSSMs that are linearly interpolated between W0b and Wtb/m. For β ∈[0,1], define Wtb,β to be βW0b + (1 – β)Wtb/m—note that this is an entry-wise weighted average of the matrices for W0b and Wtb/m (so is itself a PSSM), not a mixture of W0b and Wtb/m. We define our non-parametric model NONPARb,β to be a mixture of the m PSSMs Wtb,β, each with weight 1/m, so that:
Note that when β = 1, NONPAR is just the standard PSSM Wb constructed from {x1,…,xm} and when β = 0 it is a mixture of the Wtb/m. Setting β = 0 and b = 0 gives the empirical density.
Optimizing parameters globally and locally
The standard PSSM has one adjustable parameter, b, and NONPAR has two adjustable parameters, b and β. We can regard these parameters as either global (applying to all transcription factors) or local (applying to one transcription factor). Let Ω = {F1,…, Ft} denote a collection of transcription factors, and let B(Fi) denote a collection of binding sites for Fi. Let θ denote the vector of parameters we are trying to tune. Using a slightly modified version of maximum- likelihood estimation, we take our tuned parameters θ′ to be those for which:
Here MODELθi,x is the model (PSSM or NONPAR) built with parameters θ from all binding sites in B(Fj) aside from x, to control overfitting. The factor 1/width(x) normalizes for the variability of the widths of binding sites for different transcription factors. When tuning the parameters globally we set dj(i) = 1 for all i and j; when tuning the parameters locally for transcription factor Fj we set dj(j) = 100 and dj(i) = 1 for i ≠ j (this gives the binding sites for transcription factor Fj 100 times the weight of the binding sites for other factors, which act as regularizers; the choice of the weight 100 was ad hoc).
We confined b to take 10th-integer values and confined β to take 100th-integer values. In the case of PSSMs, we optimized b by evaluating the objective function for all 10th-integer values of b between 0 and 10. For NONPAR, we alternately clamped one parameter and set the other parameter to the best value in an 11-value window centered around its current value, and repeated these two steps until convergence was reached. While there is the possibility that this algorithm converges to a local rather than global maximum, in tests in which we exhaustively evaluated all 101 × 101 pairs of discretized values for b and β, we arrived at the same parameters as we did with the iterative algorithm. Thus, for the sake of efficiency we used the iterative algorithm in the experiments we describe below.
Remarks on parametric, non-parametric and semiparametric models
The distinction between parametric, non-parametric and semiparametric models, though perhaps more acute for densities on continuous spaces than on finite spaces (on which any function may be specified by a finite number of parameters), is nonetheless relevant for transcription factor binding sites.
A characteristic of parametric models is that the number of parameters does not increase when the number m of training cases increases, as is the case for PSSMs. For non-parametric models, the size of the model often grows linearly with m, as all the training cases are retained. This is true for our model NONPAR, although since there are only 4n distinct possible training sequences of width n, one could eventually arrest the growth of the model by accounting for the multiplicity of the training sequences that occur more than once. In some applications, retaining all the training cases is undesirable due to the increase in storage space and running time, but for our application it is not such a nuisance, since the number of known binding sites seldom exceeds 100. Mixture models are sometimes regarded as semiparametric, since the number of components in the mixture may increase as a sublinear function of m (see for example 17).
RESULTS
Test data
To facilitate comparison with the results in Barash et al. (7), we evaluated our method on the same set of aligned binding sites for 95 TRANSFAC (18) transcription factors that they used (7; supplementary material A.1). There were at least 20 binding sites for each of these 95 transcription factors. For 39 of these transcription factors, there is at least one missing value (denoted by a question mark) for at least one of the aligned binding sites.
We imputed the missing data as follows. (i) Some positions in the alignments consist mostly (sometimes entirely) of missing values. We trimmed the aligned sites so that they included only those positions in which at least half of the sites had non-missing values. (ii) We replaced any remaining missing value with the most frequently occurring nucleotide in that position for the other aligned binding sites. (For concreteness, the 15 ties were broken in favor of A over C over G over T—though this is arbitrary, it has little effect on the results.) Note that this is a maximum-likelihood completion of the data for the PSSM model. We used the same completion of the data when assessing both the PSSM and NONPAR models, so that when NONPAR outperformed PSSM it was not due to there being a better completion of the missing data in NONPAR than in PSSM. [It should be noted that due to the non-uniform way in which different genes have been investigated, the binding sites listed in TRANSFAC may not exactly be coextensive with the true binding sites of a transcription factor. Although high-throughput in vitro technologies for finding binding sites, such as SELEX (19), can avoid some of this discovery bias, in vitro binding affinities may differ from in vivo binding affinities (20).]
Average log-probability
As in Barash et al. (7), we first assessed our model by performing 10-fold cross-validation on known binding sites to measure the ability of the model to generalize to unseen binding sites. For each of the 95 TRANSFAC transcription factors F in our test set, the following procedure was used. (i) The m binding sites for F were randomly divided into 10 pools P1,…, P10 of equal size (±1). (ii) For i = 1,…, 10, models PSSMb and NONPARb,β were built from all the binding sites in the nine pools other than Pi. The parameters b and β were (optionally) tuned, using all of the binding sites for all of the 95 transcription factors, except for the binding sites in Pi. These models were used to compute log Pr(x|PSSMb) and log Pr(x|NONPARb,β) for each binding site x ∈ Pi. (iii) The average of the log-probabilities from step (ii), taken over all m binding sites, was computed for PSSM and also for NONPAR. (Note that the log-probability for each site x was computed using a model constructed from the nine pools that did not include x.) Two one-sided paired t-tests were performed on the collection of m paired differences log Pr(x|PSSM) – log Pr(x|NONPAR) of log-probabilities. As in Barash et al., we will say that a model is better than another for transcription factor F if its average log-probability is higher, and that it is significantly better if the corresponding paired t-test is significant at the 0.05 level. [The paired t-test is appropriate when the paired differences are normally distributed. In our tests, roughly half the transcription factors fail Lilliefors’ test for normality at the 0.05 level. We report P-values for one-tailed paired t-tests for ease of comparison with the results in Barash et al.; one sees the same general trends using the (non-parametric) sign-test for differences in medians, however.]
In the results reported in Barash et al., five pseudocounts were used for the PSSM models, distributed uniformly. In step (ii), we had the option of fixing or tuning the parameter b, and of tuning the parameter β either globally or locally. Tuning parameters locally usually gives better average log-probabilities, but tuning them globally provides ‘default’ parameters that work reasonably well for a range of transcription factors. (Since we left out some of the data each time we tuned the parameters globally, the resulting parameters varied slightly for different transcription factors or different folds of the cross-validation for a single transcription factor, but never by >0.1 for b or >0.01 for β; in what follows, we precede globally-tuned parameters with tildes to indicate this minor variability.) We distributed the pseudocounts for both PSSM and NONPAR uniformly in all our tests, following Barash et al. (7).
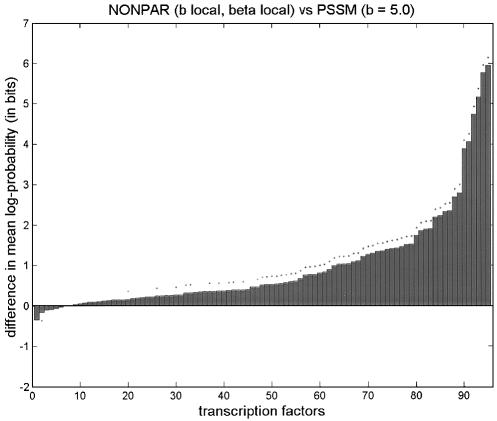
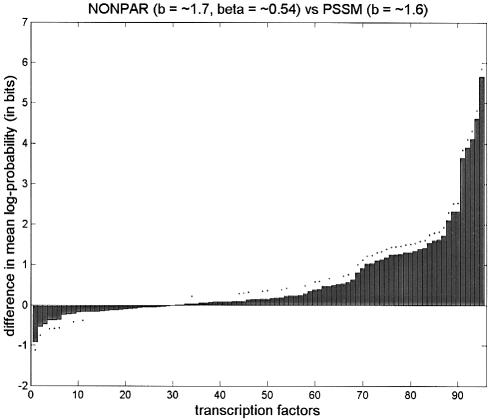
First we set b = 5 for PSSM, and tuned both b and β locally for NONPAR; NONPAR was better than PSSM for 89 of the 95 transcription factors (significantly better for 59, significantly worse for one). Next we set b = 5 for PSSM, and tuned both b and β globally for NONPAR. (The globally tuned value for b was ∼1.7, and for β it was ∼0.54.) NONPAR was better than PSSM for 84 of the 95 transcription factors (significantly better for 59, significantly worse for three).
These two comparisons were between versions of our model with tuned parameters and the same PSSM model with b = 5 used as a baseline for the comparisons in Barash et al. (7). As it may seem unfair to tune b for NONPAR but not for PSSM, we also did comparisons in which b was set to 5 in both models, and in which b was tuned either locally or globally in each model. The results of the comparisons are summarized in Table 1, with numbers of significant differences enclosed in parentheses. (As above, parameters preceded by tildes were tuned globally.)
Table 1. Comparison of NONPAR and PSSM for various parameters.
| NONPAR | PSSM | NONPAR | PSSM |
|---|---|---|---|
| b, β | b | better (sig) | better (sig) |
| local, local | 5.0 | 89 (59) | 6 (1) |
| ∼1.7, ∼0.54 | 5.0 | 84 (59) | 11 (3) |
| 5.0, local | 5.0 | 71 (45) | 24 (3) |
| 5.0, ∼0.48 | 5.0 | 67 (44) | 28 (7) |
| local, local | local | 68 (43) | 27 (3) |
| ∼1.7, ∼0.54 | ∼1.6 | 65 (41) | 30 (7) |
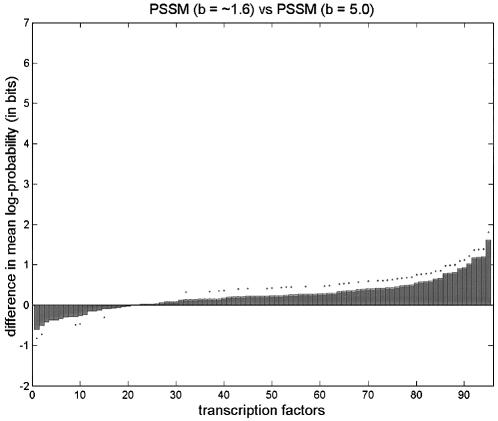
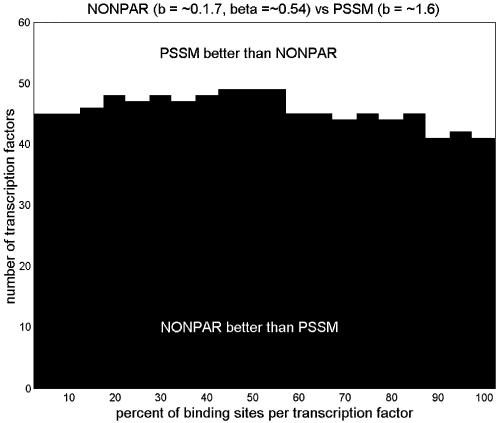
We also note that a PSSM with b tuned globally (to ∼1.6) was better than a PSSM with b = 5 for 75 of the 95 transcription factors (significantly better in 43 cases, significantly worse in five). But the differences in average log-probabilities were much less pronounced here than in the comparisons between PSSM and NONPAR, and NONPAR outperformed the tuned PSSM (Fig. 1).
Figure 1.
Comparison of average log-probabilities for PSSM and NONPAR for various choices of parameters b and β. Parameters preceded by tildes were tuned globally, and parameters called ‘local’ were tuned locally. Listed above each graph are two models. The vertical axis shows the average log-probability for the first model minus the average log-probability for the second model, for each of the 95 transcription factors. (Differences are sorted from smallest to largest.) A dot above a bar indicates that the difference in averages is significant at the 0.05 level using a one-tailed paired t-test. These graphs are in the same style as those by Barash et al. (7; supplementary material A.2), except that we also include dots below bars to indicate when the second method is significantly better than the first using the complementary one-tailed paired t-test.
We cannot compare our average log-probabilities directly to those in Barash et al. (7) because the precise numbers depend on how one randomly divides the transcription factors into 10 pools during cross-validation. But we can compare them indirectly, based on their performance relative to a PSSM with five pseudocounts. (One caveat is that Barash et al. used EM to get different completions of the missing data for different models, while we used a maximum-likelihood completion for PSSM when evaluating both PSSM and NONPAR.) In Barash et al., the tree network was better than PSSM for 33 of the 95 transcription factors (significantly better for 22), the mixture of two PSSMs was better than PSSM for 59 of the 95 transcription factors (significantly better for 33) and the mixture of two trees was better than PSSM for 57 of the 95 transcription factors (significantly better for 35) (7).
Barash et al. also note that at least one of the three dependency models is better than PSSM for 69 of the 95 transcription factors, with 14 ties and 12 losses (7). But this result is not comparable to the one-on-one comparisons, since they do not have a way of automatically selecting which of the three dependency models is most appropriate based only on the training data.
Scanning synthetic sequence
Let BIND denote a model, for example PSSM or NONPAR, for the probability distribution of the binding sites for some transcription factor. When scanning a collection of promoter regions for additional binding sites, those segments y for which Pr(y|BIND) is largest are not necessarily the best candidates. This is because some y are more likely than others to appear by chance in promoter regions, and because some promoter regions may be more likely a priori to harbor binding sites than others, based for example on microarray expression-levels (see for example 21) or ChIP localization data (see for example 22).
Combining high-throughput experimental evidence with model-based predictions of binding sites can help to reduce false-positive rates to acceptable levels (9). Having an accurate estimate of Pr(y|BIND) is valuable because probability theory provides a principled way of combining various sources of data. A common approach is to train an r-th-order Markov model, BG, on intergenic DNA, and to score sites on the basis of the odds Pr(y|BIND)/Pr(y|BG), or the posterior odds:
if a prior estimate Pr(BIND) of the probability that y is a binding site is available. [Here Pr(BG) = 1 – Pr(BIND).] One can then control the number of false-positives by choosing a cutoff on posterior odds and considering only candidate binding sites for which this threshold is exceeded. [In an r-th order Markov model BG, each nucleotide, given its r immediate predecessors, is conditionally independent of its other predecessors. Thus a 0th-order Markov model is just a specification of mono-nucleotide frequencies fA, fC, fG and fT. In this case the log of the odds for y = y1,…,yn is given by
with M(k,j) = log W(k,j) – log fk for the standard PSSM W; M is the (additive) weight matrix for the log-likelihood model in Heumann et al. (23).]
A less demanding task is just to scan for the sites with the highest posterior odds—here the exact probabilities are not important, only the rankings. Since PSSMs are essentially so-called ‘naive’ Bayes models (24), which can sometimes serve as good classifiers even when their probability estimates are inaccurate (25), we wanted to test whether the NONPAR model gave better rankings than PSSMs.
For this test we used a subset of the 95 transcription factors used above, consisting of those 60 that TRANSFAC associates with humans. We used a third-order Markov model trained on human promoter regions for BG (7), and generated a synthetic background sequence 2.5 million nucleotides long from this model. As above, we used 10-fold cross-validation on each transcription factor to compute Pr(y|BIND) for each known binding site y. We also computed the odds by dividing by Pr(y|BG) for each y. We then scanned the synthetic background sequence and counted the number of segments that had higher odds than y—this is the number of false-positives one would encounter in a list ranked by odds before getting to y, which we denote by FP(y). This is basically the same as embedding the known site into simulated background sequence as described in (6) and (7), except that it does not score those sites that overlap the embedded site. The rationale for embedding known sites in simulated background sequence instead of actual promoter regions is that the actual promoter regions may include additional binding sites not listed in TRANSFAC, making them less suitable as a negative control (6).
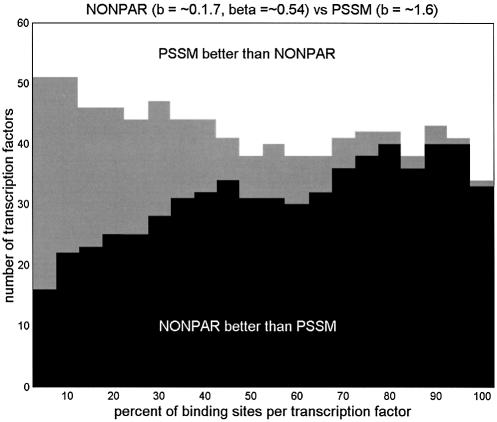
We computed FP(y) for each y using both PSSM and NONPAR as binding models. But averaging the number of false-positives over all binding sites for a given transcription factor does not always give a useful measure of performance, since these averages tend to be dominated by the single binding site with the most false-positives. We define FPt to be the average of the smallest t percent of the false-positive counts FP(y). To assess performance over a range of sensitivity levels, for each of the 60 transcription factors we computed FPt for both PSSM and NONPAR at each sensitivity level t = 5, 10, 15,…, 100. Then for each t we counted the number of transcription factors for which FPt for NONPAR was less than FPt for PSSM, the number for which FPt for PSSM was less than FPt for NONPAR, and the number for which they were equal. (Some of the ties might have been broken if we had scanned more than 2.5 million nucleotides.)
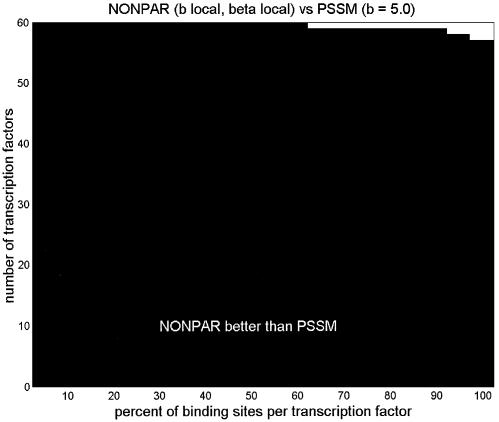
Figure 2 shows these counts as a function of t, for PSSM and NONPAR models both tuned globally. For every value of t, NONPAR beat PSSM more often than PSSM beat NONPAR. This was also true with parameters tuned locally for both models, and with b clamped to 5 for both models. To demonstrate that the average log-probability comparisons in the previous section were not dominated by a few outliers, we have also included in Figure 2 graphs showing the number of times NONPAR beats PSSM as a function of t, using the average of the smallest t percent of log-probabilities as the yardstick. (In these graphs we just consider the 60 human transcription factors.)
Figure 2.
(Top) The number of the 60 human transcription factors for which the average false-positive rate at t-percent sensitivity for NONPAR was lower than for PSSM (heights of black bars) and vice versa (heights of white bars). Heights of gray bars indicate the number of ties. (Middle) The number of the human 60 transcription factors for which the average log-probability at t-percent sensitivity for NONPAR was higher than for PSSM (heights of black bars) and vice-versa (heights of white bars). (Bottom) As in the middle graph, but with b = 5 pseudocounts used for PSSM, and with the parameters for NONPAR tuned locally. (In the upper two graphs, the parameters for PSSM and NONPAR were tuned globally.)
Finally, we did a test to assess the sensitivity and specificity one obtains by classifying a DNA segment y from a promoter region as a binding site whenever the posterior probability Pr(BIND|y) is >0.5. For this test we set the prior Pr(BIND) to be 30/(30000 × 500) = 1/500 000; this corresponds to a scenario in which there are ∼30 000 promoter regions, of average width ∼500, and a given transcription factor may bind to about 30 sites in total. In the course of the cross-validation described above, with parameters tuned globally for both PSSM and NONPAR, PSSM correctly classified 405 of the 2759 TRANSFAC binding sites as such, and on average misclassified fewer than one (0.34) of the 2.5 million synthetic background segments as binding sites; NONPAR correctly classified 450 of the 2759 TRANSFAC binding sites as such, and on average misclassified fewer than one (0.41) of the 2.5 million synthetic background segments as binding sites.
DISCUSSION
Tree networks (6,8) [and subclasses, di-nucleotide weight matrices (26,27) and first-order Markov models] offer a limited increase in expressiveness over PSSMs without too great an increase in the number of parameters that must be estimated. But for more expressive models such as higher-order Markov models or Bayesian networks, the paucity of training data makes it important to use sensible smoothing when estimating the parameters. We address this problem by using β to bias each component of NONPAR in the direction of a standard PSSM. For Bayesian networks and mixtures of PSSMs there is the additional problem that even if one has a criterion for model selection, it may be computationally unfeasible to find the best model relative to this criterion (7). Although NONPAR may be viewed as a mixture model, by building one component from each known binding site we side-step both the problem of getting stuck in local maxima with the EM algorithm, and the problem of choosing the number of components.
We have focused in this paper on the problem of finding additional binding sites for a transcription factor when a collection of aligned known binding sites is already available. Another important problem is to detect binding sites given only a collection of unaligned promoter regions for genes that are suspected of being co-regulated [see (1) for an overview]. Several algorithms for doing this, such as MEME (28), BioProspector (29) and AlignAce (12), use PSSMs to score different local alignments of the promoter regions when searching for binding sites. As was done with the models in Barash et al. (7), the model NONPAR can be swapped into a MEME-like framework in place of the PSSM. (Note that when using NONPAR to compute the score for a collection of aligned candidate binding sites, one should compute the score for each binding site using a NONPAR model built from just the other aligned sites.) In an EM-based framework such as MEME, using NONPAR would cause the running time to increase by a factor proportional to the number of candidate promoter regions being examined, since a model is built using a weighted average of all promoter regions. But by using a Gibbs-sampler based approach such as AlignAce, in which a model is built using only a small stochastic subset of these promoter regions at each step, the penalty in running time is less of a concern.
The model for binding sites described by Xing et al. (6) has an advantage over standard PSSMs, the models used by Barash et al. and NONPAR, in that it uses stronger prior biological knowledge about binding sites to avoid finding irrelevant conserved patterns in unaligned sequences. The basic idea is that in binding sites there can be positions that are strongly conserved and positions that are weakly conserved, and for most transcription factors the strongly conserved positions tend to occur in clusters rather than in isolation. Thus a first-order hidden Markov model with hidden states corresponding to strongly and weakly conserved positions, when trained on known transcription factors, will tend to prefer patterns having this characteristic clustering of strongly conserved positions over patterns in which the strongly conserved positions are interspersed randomly with weakly conserved positions.
Xing et al. use eight prototype Dirichlet-multinomial distributions, some strongly conserved and some weakly conserved, as their hidden states. Because their Markov model operates at the level of the Dirichlet priors for the multinomial distributions of nucleotides in each position and not on the multinomial distributions themselves, it can be used to produce a PSSM in which the number and distribution of pseudocounts in each position varies based on the estimates of the hidden states. We could in principle incorporate stronger biological prior knowledge into NONPAR by using this PSSM instead of the standard PSSM W0b when we form each mixture component Wtb,β = βW0b + (1 – β)Wtb/m. Finally, we note that we get similar results by taking Wtb,β = βW0b + (1 – β)Wt0, i.e., using no pseudocounts in the rightmost term, although in this case the optimal parameters change. A reason for using b/m is that then when β = 1, NONPAR reduces to a standard PSSM with b pseudocounts; and when β = 0, NONPAR reduces to mixture of m standard PSSMs each with b/m pseudocounts, for a total of b pseudocounts. Thus in some sense b can be interpreted as the number of pseudocounts used in NONPAR, regardless of which value of β is used to interpolate between these two extremes. [Note that the globally tuned value of b for PSSMs (∼1.6) is very nearly the same as the globally tuned value of b for NONPARs (∼1.7).] But if we use no pseudocounts in the rightmost terms, then in some sense the total number of pseudocounts is β·b. This variant of NONPAR has another interpretation, though: it is the mixture of m standard PSSMs, where the t-th PSSM is built from all the training sites {x1,…, xm} with d extra copies of xt thrown in. [Taking d = (m + b)(1 – β)/β gives the equivalence.]
This also suggests a generic strategy for getting arbitrary parametric probabilistic models to look more like empirical distributions, although for models that are not easily adapted to fractionally weighted data points one may need to take d to be an integer. This fits into the framework for designing ‘committees of models’ described by Christensen et al. (30). With d = 1, this gives what might be called an ‘inverse-jack knife’ approach, since it involves adding an extra copy of each data point in turn, rather than removing each data point in turn as with the usual jack-knife (31).
Acknowledgments
ACKNOWLEDGEMENTS
The authors would like to thank S. L. Wong and the anonymous referees for helpful suggestions. This research was sponsored in part by an institutional grant from the HHMI Biomedical Research Support Program for Medical Schools. O.D.K. was supported by an NRSA Fellowship from the NIH/NHGRI.
REFERENCES
- 1.Stormo G.D. (2000) DNA binding sites: representation and discovery. Bioinformatics, 16, 16–23. [DOI] [PubMed] [Google Scholar]
- 2.Man T.K. and Stormo,G.D. (2001) Non-independence of Mnt repressor-operator interaction determined by a new quantitative multiple fluorescence relative affinity (QuMFRA) assay. Nucleic Acids Res., 29, 2471–2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bulyk M.L., Johnson,P.L.F. and Church,G.M. (2002) Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors. Nucleic Acids Res., 30, 1255–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lee M.-L.T., Bulyk,M.L., Whitmore,G.A. and Church,G.M. (2003) A statistical model for investigating binding probabilities of DNA nucleotide sequences using microarrays. Biometrics, 58, 981–988. [DOI] [PubMed] [Google Scholar]
- 5.Benos P., Bulyk,M.L. and Stormo,G.D. (2002) Additivity in protein–DNA interactions: how good an approximation is it? Nucleic Acids Res., 30, 4442–4451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Xing E.P., Jordan,M.I., Karp,R.M. and Russell,S. (2002) A hierarchical bayesian markovian model for motifs in biopolymer sequences. In Becker,S., Thrun,S. and Obermayer,K. (eds), Advances in Neural Information Processing Systems 15. MIT Press, Cambridge, MA, in press. Available at http://www.cs.berkeley.edu/~epxing/ [Google Scholar]
- 7.Barash Y., Elidan,G., Friedman,N. and Kaplan,T. (2003) Modeling dependencies in protein-dna binding sites. In Vingron,M., Istrail,S., Pevzner,P. and Waterman,M. (eds), Proceedings of the Seventh Annual International Conference on Research in Computational Molecular Biology. ACM Press, New York, NY, in press. Available at http://www.cs.huji.ac.il/labs/compbio/TFBN/ [Google Scholar]
- 8.Agarwal P. and Bafna,V. (1998) Detecting non-adjoining correlations within signals in DNA. In Istrail,S., Pevzner,P. and Waterman,M. (eds), Second Annual Conference on Research in Computational Molecular Biology. The Association for Computing Machinery, New York, NY, pp. 2–7. [Google Scholar]
- 9.Liu X.S., Brutlag,D.L. and Liu,J.S. (2002) An algorithm for finding protein–DNA binding sites with applications to chromatin immunoprecipitation microarray experiments. Nat. Biotechnol., 20, 835–839. [DOI] [PubMed] [Google Scholar]
- 10.Durbin R., Eddy,S.R., Krogh,A. and Mitchison,G. (1998) Biological Sequence Analysis. Cambridge University Press, Cambridge, UK. [Google Scholar]
- 11.Chen Q.K., Hertz,J.Z. and Stormo,G.D. (1995) MATRIX SEARCH 1.0: a computer program that scans DNA sequences for transcriptional elements using a database of weight matrices. Comput. Appl. Biol. Sci., 11, 563–566. [DOI] [PubMed] [Google Scholar]
- 12.Hughes J.D., Estep,P.W., Tavazoie,S. and Church,G.M. (2000) Computational identification of cis-regulatory elements associated with functionally coherent groups of genes in Saccharomyces cerevisiae. J. Mol. Biol., 296, 1205–1214. [DOI] [PubMed] [Google Scholar]
- 13.Mironov A.A., Koonin,E.V., Roytberg,M.A. and Gelfand,M.S. (1999) Computer analysis of transcription regulatory patterns in completely sequenced bacterial genomes. Nucleic Acids Res., 27, 2981–2989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berg O.G. and von Hippel,P.H. (1987) Selection of DNA binding sites by regulatory proteins I: statistical-mechanical theory and application to operators and promoters. J. Mol. Biol., 193, 723–750. [DOI] [PubMed] [Google Scholar]
- 15.Lawrence C.E., Altschul,S.F., Boguski,M.S., Liu,J.S., Neuwald,A.F. and Wootton,J.C. (1993) Detecting subtle sequence signals: a Gibbs sampling strategy for multiple alignment. Science, 262, 208–214. [DOI] [PubMed] [Google Scholar]
- 16.Dempster A.P., Laird,N.M. and Rubin,D.B. (1977) Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B, 39, 1–38. [Google Scholar]
- 17.Bishop C.M. (1995) Neural Networks for Pattern Recognition. Oxford University Press, New York, NY. [Google Scholar]
- 18.Wingender E., Chen,X., Fricke,E., Geffers,R., Hehl,R., Liebich,I., Krull,M., Matys,V., Michael,H., Ohnhäuser,R., Prüß,M., Schacherer,F., Thiele,S. and Urbach,S. (2001) The TRANSFAC system on gene expression regulation. Nucleic Acids Res., 29, 281–283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tuerk C. and Gold,L. (1990) Systematic evolution of ligands by exponential enrichment: RNA ligands to bacteriophage T4 DNA polymerase. Science, 249, 505–510. [DOI] [PubMed] [Google Scholar]
- 20.Ponomarenko J.V., Orlova,G.V., Ponomarenko,M.P., Lavryushev,S.V., Frolov,A.S., Zybova,S.V. and Kolchanov,N.A. (2000) SELEX_DB: an activated database on selected randomized DNA/RNA sequences addressed to genomic sequence annotation. Nucleic Acids Res., 28, 205–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Spellman P.T., Sherlock,G., Iyer,V.R., Zhang,M., Anders,K., Eisen,M.B., Brown,P.O., Botstein,D. and Futcher,B. (1998) Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell, 9, 3273–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lee T.I., Rinaldi,N.J., Robert,F., Odom,D.T., Bar-Joseph,Z., Gerber,G.K., Hannett,N.M., Harbison,C.T., Thompson,C.M., Simon,I., Zeitlinger,J., Jennings,E.G., Murray,H.L., Gordon,D.B., Ren,B., Wyrick,J.J., Tagne,J.B., Volkert,T.L., Fraenkel,E., Gifford,D.K. and Young,R.A. (2002) Transcriptional regulatory networks in Saccharomyces cerevisiae. Science, 298, 799–804. [DOI] [PubMed] [Google Scholar]
- 23.Heumann J.M., Lapedes,A.S. and Stormo,G.D. (1994) Neural networks for determining protein specificity and multiple alignment of binding sites. In Altman,R., Brutlag,D., Karp,P., Lathrop,R. and Searls,D. (eds), Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. AAAI Press, Menlo Park, CA, pp. 188–194. [PubMed] [Google Scholar]
- 24.Duda R.O. and Hart,P.E. (1973) Pattern Classification and Scene Analysis. John Wiley and Sons, New York, NY. [Google Scholar]
- 25.Domingos P. and Pazzani,M. (1997) On the optimality of the simple Bayesian classifier under zero-one loss. Machine Learning, 29, 103–130. [Google Scholar]
- 26.Zhang M. and Marr,T. (1993) A weighted array method for splicing and signal analysis. Comput. Appl. Biol. Sci., 9, 499–509. [DOI] [PubMed] [Google Scholar]
- 27.Stormo G.D., Schneider,T.D. and Gold,L. (1986) Quantitative analysis of the relationship between nucleotide sequence and functional activity. Nucleic Acids Res., 14, 6661–6679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bailey T.L. and Elkan,C. (1994) Fitting a mixture model by expectation maximization to discover motifs in biopolymers. In Altman,R., Brutlag,D., Karp,P., Lathrop,R. and Searls,D. (eds), Proceedings of the Second International Conference on Intelligent Systems for Molecular Biology. AAAI Press, Menlo Park, CA, pp. 28–36. [PubMed] [Google Scholar]
- 29.Liu X., Brutlag,D.L. and Liu,J.S. (2001) BioProspector: discovering conserved DNA motifs in upstream regulatory regions of co-expressed genes. In Altman,R., Dunker,A., Hunter,L., Lauderdale,K. and Klein,T. (eds), Pacific Symposium on Biocomputing 2001. World Scientific Publishers, NJ, pp. 127–138. [PubMed] [Google Scholar]
- 30.Christensen S.W., Sinclair,I. and Reed,P.A.S. (2003) Designing committees of models through deliberate weighting of data points. J. Machine Learning Res., 4, 39–66. [Google Scholar]
- 31.Efron B. (1982) The Jackknife, the Bootstrap and Other Resampling Plans. SIAM, Philadelphia, PA.