Abstract
In the preparation of bioengineered reparative strategies for damaged or diseased tissues, the processes of biomaterial degradation and neotissue synthesis combine to affect the developing mechanical state of multiphase, composite engineered tissues. Here, cell-polymer constructs for engineered cartilage have been fabricated by seeding chondrocytes within three-dimensional scaffolds of biodegradable polymers. During culture, synthetic scaffolds degraded passively as the cells assembled an extracellular matrix (ECM) composed primarily of glycosaminoglycan and collagen. Biochemical and biomechanical assessment of the composite (cells, ECM, and polymer scaffold) were modeled at a unit-cell level to mathematically solve stress-strain relationships and thus construct elastic properties (n=4 samples per seven time points). This approach employed a composite spheres, micromechanical analysis to determine bulk moduli of: (1) the cellular-ECM inclusion within the supporting scaffold structure; and (2) the cellular inclusion within its ECM. Results indicate a dependence of constituent volume fractions with culture time (p<0.05). Overall mean bulk moduli were variably influenced by culture, as noted for the cell-ECM inclusion (Kc-m=29.7 kPa, p=0.1439), the cellular inclusion (Kc=5.5 kPa, p=0.0067), and its surrounding ECM (Km=373.9 kPa, p=0.0748), as well as the overall engineered construct (K=165.0 kPa, p=0.6899). This analytical technique provides a framework to describe the time-dependent contribution of cells, accumulating ECM, and a degrading scaffold affecting bioengineered construct mechanical properties.
Keywords: cartilage, tissue engineering, composite analysis, micro-mechanical model, bio-kinetics
1 Introduction
The prevalence of degenerative joint diseases such as osteoarthritis (OA) is substantial, affecting 20 million Americans, while the incidence is increasing with an aging population [1]. The clinical requirements for reparative therapies of damaged articular cartilage will also have to overcome its poor intrinsic healing capacity. Cell and scaffold composites form a tissue regeneration strategy which offers the potential to engineer functional cartilage and repair the articular surfaces.
In the design and application of engineered tissues, the processes of biomaterial degradation, and neotissue accumulation contribute to a time-dependent mechanical state of the resulting multiphase composite (a combination of multiple materials). Constructs used in engineered cartilage may consist of chondrocytes seeded on scaffolds of biodegradable polymers or using alternative techniques without the aid of synthetic materials [2].Inthe cell-polymer approach, synthetic scaffolds degrade passively in culture, as the cells assemble an extracellular matrix (ECM) composed primarily of glycosaminoglycan (GAG), and collagen [3]. Construct mechanics at first depend on the interaction between the cells and scaffold, and at intermediate times newly elaborated ECM also contributes. At late stages of construct maturation, the scaffold approaches complete resorption and the construct properties depend primarily on cell and ECM mechanics. The time-dependent changes in engineered cartilage composition thus complicate the prediction of construct mechanical properties. The predictive power of models that account for discrete contributions of construct constituents would be helpful in assessing experimental conditions that enhance neotissue maturation and the functional capacity of these constructs.
Bioengineered composite construction has been previously addressed in terms of stratifying tissue responses for osteochondral defect repair [4,5] characterizing cellular control of engineered cartilage heterogeneity [6,7], and assessing multiple constituents during development within the construct [8]. Recently, dynamic composite models formulated in a mechanistic approach have included a temporal component to predict constituent masses based on the initial culture preparation [3] and anabolic/catabolic influences [9,10]. These previous approaches justify coupling the bio-kinetics models with mechanical models to predict and/or assess functional outcomes of bioengineered composites.
As in many functional tissue engineering approaches, actually predicting the engineered construct's biomechanical characteristics based on the quantity and quality of its composite constituents has remained elusive. Mechanical bioreactors have provided fluid pressure and solid load transfer as a means to manipulate or control constituent dynamics toward improved construct functionality [11,12]. These techniques have statistically improved the mechanical properties of the resulting constructs, however individual constituent contributions to the dynamic composite have not been fully explored. During construct development, understanding the dynamic mechanical state of the cells, polymer scaffold, and ECM will clarify their relative influence on the mechanical properties at any point in time. Structure-function relationships have been described intimating microscale modeling as an appropriate next step to characterize the contributions of individual matrix components within construct mechanics [13,14]. Advanced cartilage microstructural [15] and growth [16] models have also provided insight toward understanding changes in soft tissue mechanics during maturation of native and engineered tissues. A composite mechanics approach can be used to highlight differences in synthesis and degradation when rates are often dependent upon the mechanical environment stimulus.
In order to understand the mechanisms associated with engineered tissue development, it is necessary to quantify the applied pressures and stress-strain state at the local level of cells, scaffold, and ECM. The objective of this study is to quantify the contribution of construct constituents (cells, ECM, scaffold) within the mechanical properties of developing engineered cartilage. It is assumed that the volume occupied by seeded chondrocytes is controlled and that the overall construct can be treated as a macroscopically homogenized material. A composite spheres inclusion model was formulated at the unit-cell level noting the spherical shape described in single-cell experimental approaches [17] and the physiologic relevance of naturally occurring, spherical tissue subunits known as chondrons [18]. The layering accumulation of pericellular and extracellular matrix supports a spherical construction of the composite [19]. Chondrocytes maintained in three-dimensional biomaterial scaffolds (hydrogels and fibrous meshes) also produced a localized spherical morphology and deposited newly synthesized matrix molecules radially, forming spherical pockets of new ECM per cell [20–23]. The composite spheres model is a reasonable approach to approximate this microenvironment.
The micromechanical, composite model evaluates the effective constituent mechanical properties through a mathematical derivation of the local stress and strain fields. As input, it incorporates constituent abundance via volume fractions and the overall construct mechanical properties, common specifications for engineered tissue design. ECM content is accounted for via matrix molecule accumulation. A tandem perspective is presented to determine both the cellular-ECM inclusion bulk modulus (Kc-m) within the supporting scaffold structure as well as the separate cellular (Kc) and ECM (Km) constituent bulk moduli. The mechanical model also adds to previously published kinetic models of matrix accumulation and scaffold degradation, providing a framework for predicting steady-state mechanical properties of engineered tissue constructs.
2 Methodology
2.1 Composite Spheres Models
2.1.1 Model 1—Cell-ECM Inclusion Within Scaffold
A composite sphere model is applied at the unit-cell perspective to represent the larger cylindrical construct volume mechanics (Fig. 1). The effective bulk modulus (K) for a spherical ECM-layered cell (r=a1) surrounded by a homogeneous scaffold matrix (r=b1), can be mathematically decomposed to quantify constituent contributions. If a cylindrical composite construct is subjected to a confined compression such that a transient hydrostatic stress is transmitted to an internal spherical element (where spherical coordinate, radial oriented stresses exist throughout equilibrium, σrr=σ0 at r=b1), an equivalent homogeneous material sphere is assumed subjected to the same stress. The boundary condition displacements are equated, between composite sphere and equivalent homogeneous sphere at the inclusion interface within the supporting material, to provide the same average dilatation within each [24]. Relationships between stress and strain during this scenario produce the solution for the effective bulk modulus incorporating the constituent moduli. For an isolated cell (the dilute solution), Eshelby's formula from elasticity theory [25] can be applied to formulate these relationships by calculating strain energies in heterogeneous (U) and identical homogenous (U0) systems
| (1) |
Internal surface (Si) integrations are then made involving specified applied stresses (σi) and the corresponding displacements (ui) where the superscript “0” identifies the homogeneous response. Spherical strain energy formulations provide the input for U0.Assuming the composite spheres interact (nondilute solution), the equilibrium equation to be satisfied (in spherical coordinates for tangential stress, σϕϕ =σθθ) provides the stress conditions
| (2) |
In terms of displacements (ui), Eq. (2) takes the form
| (3) |
The constants of integration from the solutions to these differential equations are determined from the boundary and continuity conditions. The local complementary energy, U=σ0/2K, provides an upper bound to extend the solution from a single composite sphere to the entire representative volume element thus solving for the effective bulk modulus. Finally, the nondilute solution (high concentration of interactive cells) gives the bulk modulus as [24]
| (4) |
Here the cell-ECM to scaffold volume fraction is defined as c1=(a1/b1)3 and indicates the relative amounts via a spherical-layer arrangement of the dynamic cell-ECM inclusion bulk modulus (Kc-m) within a scaffold of bulk (Ks) and shear (μs) structural or apparent moduli. During the experimental application here, the initial seeding of 2.5×106 cells (t=0) established the baseline average volume fraction of c1=0.256 (see the Volumetric Concentration section). As the construct “matures,” the cell-ECM inclusion begins to dominate the mechanics. Thus over time, the volume fraction approaches c1≈1, where radius-a1 increases due to ECM synthesis while radius-b1 decreases due to scaffold degradation. The bulk modulus of the construct theoretically becomes similar to native cartilage (at t=∞, K=Kc-m) with little or no lingering contributions from the original scaffolding material. Equation (4) can be reformulated to directly solve for Kc-m
| (5) |
Constituent volume fractions (c1) and elastic properties (K,Ks,μs) were measured from biochemical and biomechanical experiments, respectively, as a means to clarify the mechanical influence of the developing inclusion by defining its bulk modulus, Kc-m. Mechanical evaluation of disks without cultured cells and before degradation, provided the baseline scaffold property (E=4.1 kPa) from which Ks and μs were determined [26].
Fig. 1.
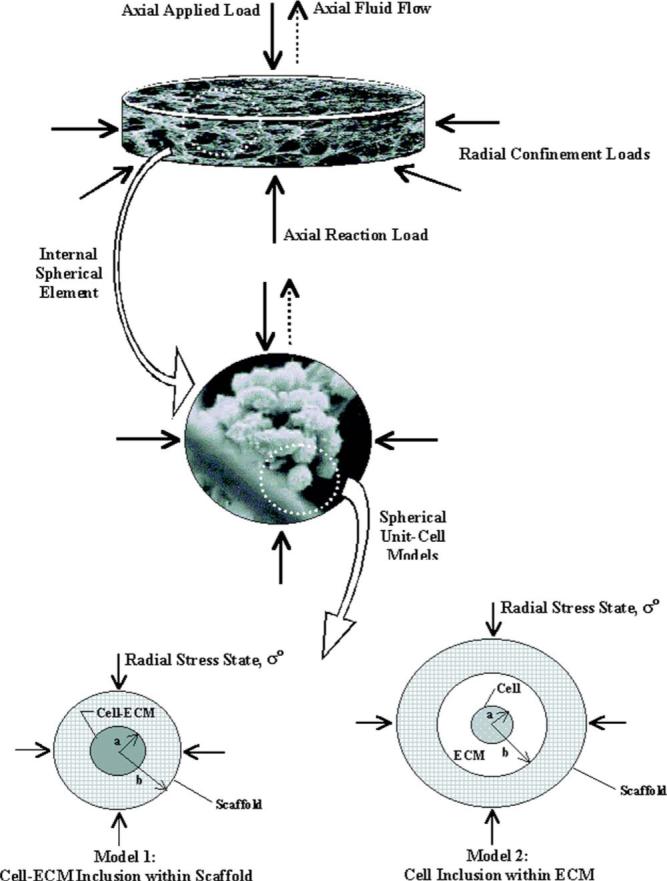
Hierarchical development of the mechanical composite sphere models. Here, scanning electron micrographs (SEMs) from a similar engineered cartilage design are shown as fill images [26] (courtesy of Mary Ann Liebert, Inc.). The applied and reaction loads at the construct scale (scaffold fibers at ×30 magnification) during confined compression are extended to a spherical element (cell, ECM, and scaffold constituents at ×1000 magnification). A single 10-μm-diameter chondrocyte becomes the centerpiece for the unitcell construction characterized by either a cell-ECM inclusion surrounded by a homogeneous scaffold (Model 1) or a three phase extension where the single cell inclusion is surrounded by synthesized ECM and supported within a homogeneous scaffold mesh (Model 2).All boundary and continuity conditions are reduced to the unit cell when defining the stress-strain relationship during the radial stress state (σ0). In Model 2, a far-field perspective with external boundaries sufficiently distant from the inclusion is assumed to dominate the effective construct properties (Ks=K).
2.1.2 Model 2—Cell Inclusion Within ECM
In a similar approach which separates the cellular and ECM components, the modulus of the homogeneous medium (comprised of the porous scaffold structure) is considered to be the effective bulk modulus of the construct (Ks=K). Here the spherical cell (r=a2) is surrounded by a layer of ECM (r=b2), within a more macroscopic view of the scaffold matrix, and then analyzed as a three phase model (Fig. 1). At early time points, the scaffold is subjected to deformation conditions at “large” distances from the cellular inclusion. This configuration is rendered equivalent to a completely homogeneous construct by requiring that they both store the same strain energy due to an identical average strain state as per elastic compatibility theory. Again, an application of Eshelby's formula to evaluate the strain energy stored during confined compression formulates a stress-strain relationship. The nondilute solution (high concentration of interactive cells) defines the effective bulk modulus as [24]
| (6) |
Here the cell to ECM volume fraction is c2=(a2/b2)3, characterizing the relative arrangement of the cellular inclusion bulk modulus (Kc) within the dynamic ECM and its bulk (Km) and shear (μm) moduli. As the construct develops over time (as t→∞), the volume fraction approaches the dilute solution where the ECM boundaries from each producing cell interact and the volume fraction becomes c2<<1 (radius-a2 remains fixed while radius-b2 increases), such that
| (7) |
The initial state, Eq. (6), can be reformulated to directly solve for Kc and Km, respectively
| (8) |
and
| (9) |
Again, volume fractions of constituents (c2) and construct elastic properties (K) were directly measured from biochemical and biomechanical experiments, respectively. In order to solve for the mechanical properties of both the cellular (Kc) and ECM (Km) constituent unknowns based on the imposed stress-strain state, a response surface methodology was applied [27] as a dual-parameter optimization.
For both models, isotropic relations provided input for the assumed properties as homogeneous media: μ=E/2(1+ν) and K=E/3(1−2ν). These relationships incorporated compressive elastic moduli (E) measured here and assumed Poisson ratios (ν) representing the range of measured values from tensile and compressive loading [28]. The effects of the assumed scaffold and composite construct Poisson ratios (ν=0.1–0.4 as typically reported for native and engineered cartilage) were also iteratively explored.
2.2 Construct Culture and Harvest
Twenty-eight cell-polymer constructs were prepared as previously described [11,3]. Briefly, bovine articular chondrocytes were harvested from the femoral condyles and tibial plateau of a single 2–3-month-old calf (Arena Brothers, Hopkinton, MA), within 6 h of slaughter. Cells were liberated via a 0.3% collagenase digestion overnight at 37°C on a horizontal shaker, counted, and stored in culture media (Ham's F-12, 10% heat-inactivated fetal bovine serum, 100 U/mL penicillin, 100 μg/mL streptomycin, 0.25 μg/mL amphotericin B, 50 μg/mL ascorbic acid) at 37°C for less than 48 h. Polymeric scaffolds were made from a nonwoven polyglycolic acid (PGA) fleece (Albany International Research, Mansfield, MA).A 12.7 mm punch was used to cut circular patches approximately 1 mm thick [11]. The patches were immersed in a 1% w/v poly-L-lactic acid (PLLA) solution in methylene chloride for 10 s and allowed to dry for at least 10 min. This process resulted in scaffolds with 27% PLLA to PGA by mass, at 97% porosity, and a mean dry mass of 18.15 mg. The scaffolds were then sterilized in ethanol for 30 min, allowed to dry in a desiccator for 24 h, and prewet in culture media at 37°C for 6 h prior to seeding. At seeding, the scaffolds were incubated with a suspension of 2.5×106 cells in 1.0 mL of culture media (described above) for 12 h at 37°C on a horizontal shaker. This seeding technique provided sufficient cellular attachment and dispersion throughout the scaffold pore volume as validated previously through cell counts [3,29] and histology [23]. Once seeded, the initial composite constructs (cells+scaffold) were transferred to 12-well plates for culture under standard incubation conditions in 3 mL of media, with media changes every 2–3 days.
Engineered cartilage constructs were then harvested at 2, 5, 8, 14, 35, 42, or 47 days (n=4 per time point) and thickness measurements taken (mean 0.87 mm±0.35 mm standard deviation). At each time point, a 6 mm sample was extracted with a biopsy punch along the center axis of each disk. The remaining piece was cut approximately in half with a scalpel (Fig. 2). The 6 mm sample was rinsed in phosphate buffered saline (PBS) and used for mechanical testing within 3 h of harvest. One remaining half was weighed, lyophilized, reweighed, and stored at −20°C until biochemical analysis, while the other half remained in culture for radiolabeling.
Fig. 2.
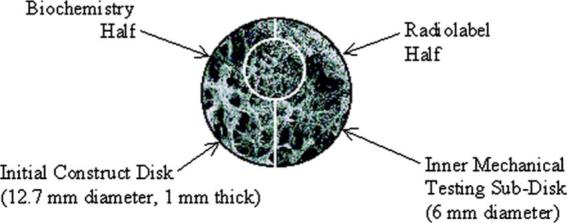
Division of engineered cartilage constructs at harvest. The initial 12.7-mm-diameter construct was divided into three parts: a 6-mm-diameter punch taken along a diametric axis, and two halves of the remaining piece. SEM fill image shown (×30 magnification).
2.3 Mechanical Testing
The 6 mm disks taken from each construct were tested in confined compression using a mechanical testing device (Dynastat, IMASS, Hingham, MA). Here a rigid, impermeable chamber contained the sample and prevented radial deformation during compressed loading by a rigid, permeable applicator directed along the longitudinal axis. This load state was considered to induce a transient pressurized environment due in part to proteoglycan osmotic pressures combined with a loading device limiting unidirectional fluid exudation (Fig. 1). Although a mean axial (A) to radial (R) pressure ratio of A/R=1.7 has been reported in a single cylindrically shaped cartilage explant over a range of compressive stresses [30], equal axial and radial stresses (A/R=1.0) were also indicated in that same study at stress-strain levels similar to that applied to the construct here. The stress state at equilibrium transmitted to the internal spherical-shaped, unit-cell element was expected to experience equal radial oriented stresses (spherical coordinates) which originated from the axial load and radial confinement applied to the overall cylindrical disk. Thus the radial-oriented, multiaxial loading state supports the appropriate application of the spherical governing equations and strain energy density formulations which established the modeled stress and strain relationships [31]. In application of this mechanical state, the disks were equilibrated in 0.15 M PBS at pH=7.4 and subjected to sequential deformation steps of 0.0245 mm (0.06 mm/s deformation rate) resulting in ∼3% strain increments up to 40% total strain. Load equilibrium was allowed over 100 s resulting in a mean stress relaxation time constant of the τ=21.7 s. High structural strains were necessary to illicit a load response (mean equilibrium compressive stress=−13.2 kPa) from the highly porous and relatively weak construct arrangement during culture. However, the cell-level displacement field was presumed to be continuous and single valued (no material overlap). After relaxation, the equilibrium stress at each static strain level was recorded. A linear regression of the equilibrium stress to applied strain was fit to determine the equilibrium confined compression modulus for the constructs. The 95% confidence interval of the correlation coefficients for all moduli regressions supported the linearity assumption (0.8619–0.9127).
2.4 Biochemical Assays and Volumetric Concentrations
Wet and dry masses of each sample were measured immediately after culture. Construct fragments reserved for biochemical mass analysis and volume fraction determination were digested in papain (0.125 mg/mL) overnight at 60°C. Sulfated GAG content was measured via the dimethylmethylene blue spectrophotometric method [32]. Collagen content was measured indirectly through a spectrophotometric assay for hydroxyproline [33] using a hydroxyproline to collagen ratio of 0.1 [34]. Cellular dry mass was estimated at 10−10 g/chondrocyte [35]. The initial dry mass of the scaffold alone (M0) was also measured and converted to degraded mass values over time (M) using the relationship
| (10) |
A scaffold-degradation time constant (τs=28.1 days, R2=0.90) was applied from previous results using similar polymer constructs [3,26]. All dry mass values for the ECM constituent (VECM=Vcollagen+VGAG), scaffold (Vscaffold), and cellular material (Vcell) were converted to composite subvolumes (Vi) using representative density values from the literature: ρcollagen=141 mg/cm3 [13]; ρGAG=80 mg/cm3 [36]; ρscaffold=4776 mg/cm3 [3]; ρcell=191 mg/cm3 (here). Density values were selected based on similarity with culture time, conditions, cell type, cell/tissue maturity, etc. The initial scaffold volumes determined from the mass conversion corroborated with the designed scaffold solid volume (3%) remaining in the biochemistry sample (0.00137 cm3, p>0.9999). Since direct cellular genetic content (DNA) was not measured, the cell population was assumed to remain constant throughout culture. This assumption was based on a one-sample t-test (p=0.0604) comparing the mean cultured cell population with the initial seeding of 2.5×106 cells from data produced by the same cell-polymer system [3].Although the samples were loaded in a hydrated state, molecular immobilized water mass and volume were not included in the volume fraction calculations since the confined compression platens allowed for partial fluid exudation during mechanical testing. Constituent volumes within the biomechanical samples (Vi) were averaged by cell count to produce per spherical unit-cell dimensions (radii ai and bi from Fig. 1) regardless of individual cell capacity or geometric uniformity. The averaged values were finally applied to the micromechanical, volume fraction parameter ci=(ai/bi)3, for i= Model 1 or 2.
Models describing the kinetics of ECM accumulation and scaffold degradation in engineered cartilage constructs were used to characterize the time-dependent changes in matrix molecule volume fractions [3]. This application was intended to demonstrate the utility of the previous dynamic models and parameterize the current results for direct comparison. The kinetics model was adapted to the “cell-ECM inclusion within scaffold” composite sphere description
| (11) |
as a predictive tool based on the construct initial condition (c0=0.256 cell to scaffold; no ECM), the steady-state condition (css=1.0 cell-ECM to scaffold), and a characteristic time constant (τ1) fit by nonlinear regression. In addition, the kinetics model was applied to the “cell inclusion within ECM” composite sphere analysis
| (12) |
based on the initial condition for this arrangement (c0=1.0 cell to ECM), the steady-state condition (css=0.15 cell to ECM), and another fit characteristic time constant (τ2).
2.5 Radiolabeling for Biosynthesis
At time of harvest, a half portion of each construct remained in the culture for evaluation of anabolic activity and ECM biosynthesis through the use of GAG radiolabeling. Each sample was incubated for 12 h in culture media supplemented with 20 μCi/mL 35S–SO4. After radio-labeling, 1.0 mL of labeling media was retained for scintillation counting. Construct portions were rinsed three times for 20 min in cold PBS with 0.8 mM sodium sulfate to remove unincorporated radiolabel. They were then weighed, lyophilized, reweighed, digested in papain, and stored at −20°C until scintillation counting. Counting occurred within a 1 h period (RackBeta 1211 Counter, Phamacia LKB Nuclear, Turku, Finland) and a biosynthesis rate was determined per each sample's dry mass.
2.6 Modeling and Statistical Analysis
Data analysis, variable manipulation, and statistical evaluation were completed using commercial software (microsoft excel 2000, Redmond WA; wolfram mathematica v4.1, Champaign, IL; and jmp v5.0.1, SAS Institute, Cary, NC, respectively). One- and two-factor analyses of variance (ANOVA) and regressions were applied. The statistical analyses tested the influence of culture time and constituent type on both the resulting volume fractions and bulk moduli. Statistical significance was considered at p<0.05 and Fischer's protected least significant difference (PLSD) post-hoc test was applied for pairwise analysis. Means, standard deviations (SD), and standard errors (SE) were determined for graphical purposes. Fitted properties were determined by minimizing the root mean square error as a percent of the model prediction (%rms).
3 Results
Constituent mechanical function was characterized throughout engineered tissue maturation by coupling a micromechanical model with a kinetic model. Many influential variables, including constituent volume fractions and culture time, were used to describe: (1) the cellular-ECM inclusion within the supporting scaffold structure; and (2) the cellular inclusion within its ECM. Overall, volume fraction descriptions of the cell-ECM inclusion (p<0.0001) and the cell inclusion (p<0.0001) models were statistically influenced by culture time (Fig. 3). Previous kinetic models accurately described temporal changes in construct composition. Time constants provide additional parameters describing the cell-ECM inclusion (τ1=13.3 days, %rms=10.12%, R2=0.94) and cell inclusion (τ2=5.5 days, %rms=20.95%, R2=0.92) volume fraction models. As a component of ECM development, GAG synthesis rates were culture time dependent (p<0.0001, Fig. 4(A)). Rates of proteoglycan synthesis was measured to test the hypothesis that biosynthesis is regulated by a negative-feedback accumulation mechanism, proposed earlier as the basis for the kinetic models [3]. Indeed, biosynthesis rates correlated well with the cell-ECM inclusion (R=0.70, p<0.0001) and the cell inclusion (R=−0.72, p<0.0001) volume fraction models (Fig. 4(B)).
Fig. 3.
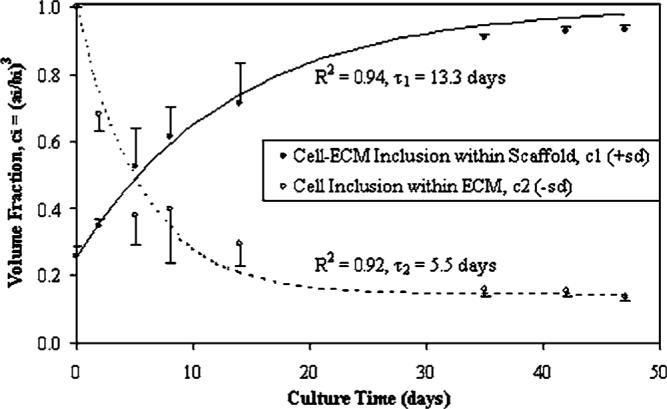
Development of engineered cartilage in culture as described by time-dependent volume fractions (p<0.0001) from the composite spheres models. Mean ± standard deviation (SD) values are shown for n=4 samples per culture time point. Curves represent the application of dynamic composition models [3] which predict ECM synthesis concomitant with scaffold degradation.
Fig. 4.
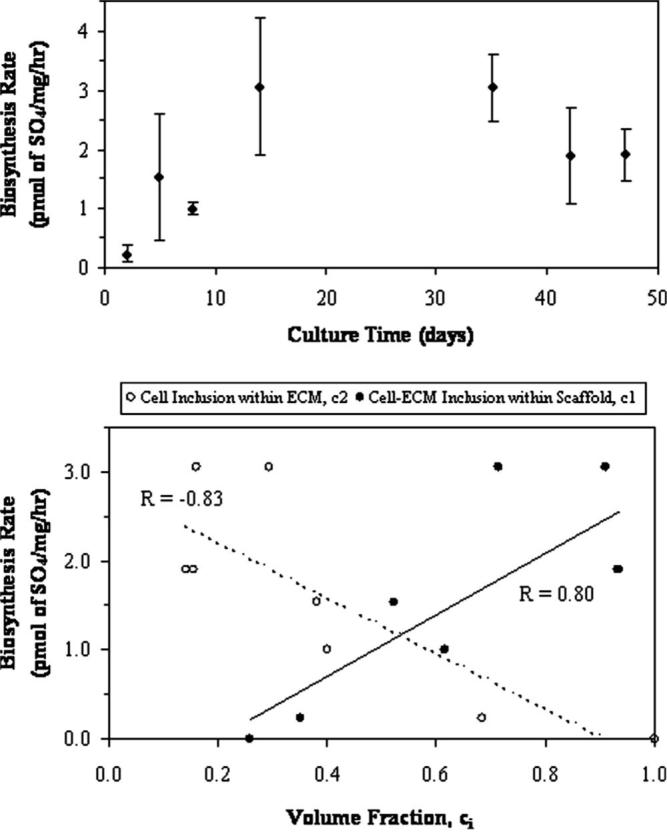
(A) Mean biosynthesis rates of GAG content (±SD) indicated a variability in production throughout culture time (p<0.0001). (B) The dependency of synthesis rate on ECM content is demonstrated in both composite sphere models. Here, ECM content as defined by two volume fraction approaches indicates direct or inverse proportional effects depending on how ECM is included in the model. Trendlines and correlation coefficients are shown as applied to mean values (error bars are indicated in (A)).
Overall, culture time minimally influenced bulk moduli when all constituents were examined together (p=0.2325). However, when each constituent was individually examined, the cell modulus (Kc) indicated the strongest influence by time (p=0.0067). The remaining constituent properties of ECM (Km, p=0.0748), cell-ECM (Kc-m, p=0.1439), and construct (K, p=0.6899) moduli demonstrated a weaker statistical influence due to high variability (Figs. 5 and 6). The effect of permutated Poisson ratios (ν=0.1 and 0.4) for the assumed construct and scaffold properties used in Eq. (5) also caused statistical variation in K and Kc-m values throughout the culture (Fig. 5(B)). The variability in cell (Kc) and ECM (Km) bulk moduli through culture time and due to assumed construct Poisson ratios (νconstruct=0.1 or 0.4) was also made apparent (Fig. 6). The effect of νconstruct, however, was a more consistent influence on moduli then when comparing time averages. Here, Km at νconstruct=0.4 was statistically greater than: Km at νconstruct=0.1 (p<0.0001), Kc at νconstruct=0.4 (p<0.0001), and Kc at νconstruct=0.1 (p<0.0001). Also, Km at νconstruct=0.1 was statistically greater than: Kc at νconstruct=0.4 (p=0.0163) and Kc at νconstruct=0.1 (p=0.0133). Finally, a two-factor analysis examining composite constituents while accounting for culture time indicated Km to be statistically larger than K (p=0.0002), Kc-m (p<0.0001), and Kc (p<0.0001) when νconstruct=νscaffold=0.4.
Fig. 5.
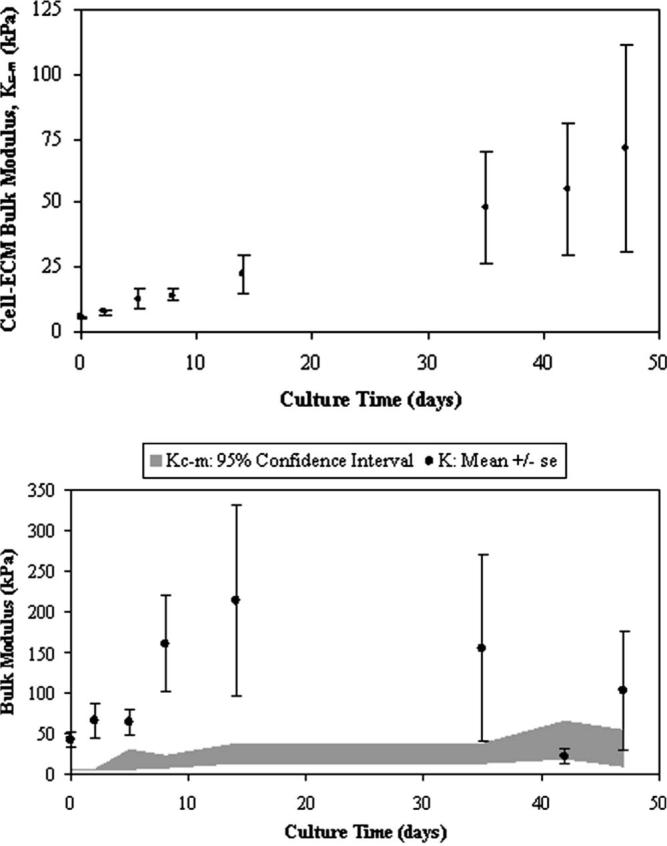
(A) Time-dependent bulk modulus values (p=0.1439) of the cell-ECM inclusion as determined from the composite spheres model (Eq. (5)) where the assumed Poisson ratios are νconstruct=0.4 and νscaffold=0.4. Mean ± standard error (SE) values are shown for n=4 samples per culture time point. (B) Construct modulus (K) including the variability due to the influence of νconstruct=0.1 or 0.4 (mean ± SE). There is a 95% confidence interval of the cell-ECM bulk modulus (Kc-m) due to iterative variations in νconstruct=0.1 or 0.4 and νscaffold=0.1 or 0.4 as indicated by the gray bar, smoothed through time.
Fig. 6.
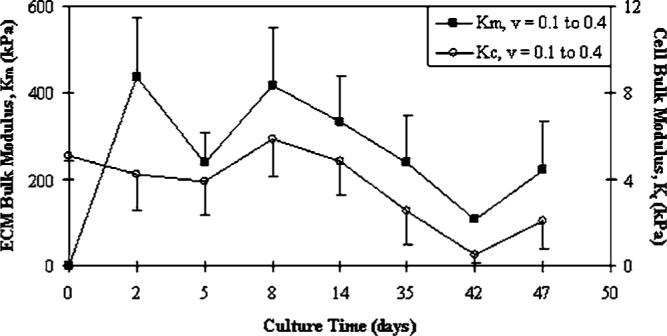
Variation of cell (p=0.0067) and ECM (p=0.0748) constituent bulk moduli over time. Comparison of Poisson ratio variability (νconstruct=0.1 or 0.4) on cell and ECM bulk moduli as calculated from Eqs. (8) and (9)(mean values, Km+SE and Kc−SE). The ECM modulus is statistically greater than the cell modulus at all analyzed values of νconstruct (p<0.05). Note, Km=0 at t=0 indicates that ECM was not present at cell seeding.
4 Discussion
Regenerative therapies offer great potential in the repair of damaged or diseased, load-bearing tissues. Maturing engineered cartilage is a complex composite of time-dependent composition and mechanical properties where the biochemical and mechanical characteristics of the resulting implant material are critical to its function. Cultured chondrocytes, de novo synthesized ECM, and a degrading polymer scaffold were modeled at a micromechanical, unit-cell level to determine their individual effect on the overall construct elastic properties. This approach employed a composite sphere, stress-strain analysis to describe the mechanical contributions of: (1) the cellular-ECM inclusion within the supporting scaffold structure; and (2) the cellular inclusion within its ECM. The composite sphere analyses were coupled with kinetic models of engineered cartilage matrix accumulation and scaffold degradation to describe time-dependent changes in construct mechanical properties. This mathematical framework facilitated a means to explore structure-function relationships and culture-time influences on construct mechanical properties.
Here the composite analysis utilized biochemical and biomechanical experiments as input to the parametric approach. The time-dependent nature of the developing construct was examined via culture time influences and dynamic models. Volume fractions calculated from constituent concentrations and masses were effective metrics of composition. The time-dependent maturation of these constructs was similar to earlier work using an analogous experimental arrangement [11,3,26]. In addition, a model based on a previously posed negative-feedback mechanism regulating ECM biosynthesis was supported by the data. The resulting elastic properties of the cell-ECM composite were positively influenced by culture time albeit with much variability.
Separate cell and ECM constituent elastic properties were also highly variable and dependent upon underlying assumptions and input parameters. Moduli were determined over time, even indicating a cellular “softening” response (Fig. 6). This phenomenon may suggest a covariant relationship where the cellular properties are altered once a sufficiently stiff pericellular matrix has accumulated. In comparison, the mechanical properties available from the literature were typically direct measurements of individual chondroctyes and/or ECM samples, derived from native tissue rather than engineered, often made under unidirectional loading, and at single time points. Values of Kc=0.83 kPa, Km=208.3 kPa, μm=227.3 kPa, and νm=0.1 have bee reported from experiments directly characterizing native cartilage cells [37,38] and ECM [39], respectively. Individual cell mechanics applications often include micropipette aspiration utilizing incompressible linear elastic continuum theory [40] or viscoelastic solid models [41]. Additionally, cytoindentation techniques apply unidirectional loads via an atomic force microscope [42] or similar cantilever [43]. When modeled as a linear solid half-space, cartilage cell (Kc=1.2 kPa, μc=0.12 kPa) and ECM (Km=330 kPa, μm=430 kPa) properties have been reported [41] similar to the present composite cell and ECM values. Recent work applying unconfined compression to individual chondrocytes also described similar cellular moduli (Ec=1.48 to 2.58 kPa, depending on the continuum model)[44]. Likely reasons that constituent moduli resulting from more uniaxial testing would differ from those presented here are the hydrostatic compression load state model and the layered-sphere boundary conditions would tend to stiffen the stress-strain environment. Reports of cells and neotissue compressed within seeded gels, Ec=3.2 kPa [45] and Ec=2.7 kPa [42], may provide a closer composition and stress-strain environment to that presently analyzed. In general, the results support a composite mechanics approach in that characterizations at the unit-cell level can be derived based on measurements at the larger effective level.
This composite arrangement has been previously applied in a computational framework to native cartilage mechanics [46,47]. These earlier works mathematically explored the contributions of variations in tissue constituents to overall tissue mechanics. The two-phase composite arrangements specifically examined the effect of proliferating populations of chondrocytes as alterations in the concentration of cellular inclusions within a homogenous medium of ECM. Nonlinear decreases in normalized Poisson ratio and nonlinear increases in normalized elastic modulus were computationally shown due to increasing cell concentration over a range of 0–30% [47]. Thus the dependence of the mechanical properties of cartilage on the cell-inclusion volume fraction parameter was demonstrated. The seeding density influence on cartilage elaboration and mechanical properties has also been measured in engineered constructs [48]. In the present work, constituent volume fractions were also influential, although dynamic concentrations were driven by the combined, competing effects of ECM accumulation and scaffold degradation rather than proliferating cells. This analytical approach provided an opportunity to explore dynamic constituent properties in situ without subjecting isolated individual components to nonphysiologic manipulation [17] or applying purely mathematical techniques which reduce elastic theory to discrete numerical solutions [49].As a caveat, the composite modeling technique determines aggregate properties. The results do not incorporate specific structural/spatial effects, geometric discontinuities due to shape, or biological discontinuities such as cell “clustering” within explants, especially at early culture time points where a dilute suspension of cellular inclusions may be prevalent.
Many parametric assumptions were referenced from the literature and applied to the analysis including cell and matrix properties, constituent densities, degradation time constants, and mechanistic models. A quantification of property variance due to typical isotropic Poisson ratio assumptions was made and presented in Figs. 5(B) and 6. The challenge in quantifying actual native or engineered cartilage Poisson ratios has led to a range of acceptable values dependent on material assumptions [50]. If the tissue is assumed to be isotropic or transversely isotropic and a positive applied stress produces a positive strain to yield positive work, then the Poisson ratios are restricted by the equations
| (13) |
However, if the tissue is orthotropic in nature, and the elastic and shear moduli are positive by definition, then the determinant of the stiffness matrix must also be positive [51]. This leads to the anisotropic restriction of
| (14) |
for νij where i, j= ratio of strain in x, y, and z axes where νij may be greater than 0.5. Recently, advanced experimental techniques have characterized directional-dependent Poisson ratios in the transition from tension to compression during uniaxial loading [52], in the separation of flexural and membrane stresses during bending [28,53], and from contact mechanics during indentation [54]. As explored here and elsewhere [49], the implications of empirical and theoretically derived Poisson ratios can influence the accuracy of native and engineered tissue models.
The biokinetic model components dependent upon mechanistic degradation and synthesis processes were supportive of earlier experiments from which they were developed [11,3,26]. However, the effect of a constant versus increasing chondrocyte population assumption was influential. As noted earlier, a comparison of the mean cultured cell population with a similarly applied initial seeding density (p=0.0604) supported the constancy assumption [3], especially for the shorter culture period here. In an engineered cartilage study using a polyglycolic acid fiber-only scaffold and a dynamic bioreactor culture system, cell populations fully attached to the scaffolds and were noted to increase fourfold over a similar period based on percent wet weight [55]. Using an assumed positive cell growth rate based on a larger initial seeding density [26], larger volume fractions (ci) were indeed calculated in comparison. A mean difference of Δc1=cconstant−cincrease=−0.033 (%Δc1=−5.9%) for the “cell-ECM inclusion within scaffold” model was statistical (p<0.0001). This effect was concomitant with a mean difference of Δc2=cconstant−cincrease=−0.149 (%Δc2=−76.7%) for the “cell inclusion within ECM” model (p<0.0001). Unfortunately, actual cell populations throughout the culture time were not measured to rectify this issue. Another possible error included the translation of the measured biochemical mass values to volume fractions, which were dependentupon the constituent density assumptions. Here, representative density values from near-similar culture/cell/tissue environments were used. These represent typical values as reported in the literature when describing cartilage constituent densities [13,36]. A more accurate and validating scenario would have utilized density values directly determined from the same engineered cartilage constructs. An alternative analysis could examine the contributions of hydrodynamic radii in the calculation of ECM and polymeric molecular volume fractions. This technique would incorporate trapped or “immobilized” water volume associated with the molecular network during functional loading. This molecular hydrodynamic state has been characterized for cartilage ECM via individual and grouped GAG “rods” [56]. Unfortunately, this approach would have incorporated a molecular resolution not consistent with either the presented tissue-level biochemical or biomechanical analyses applied to the engineered cartilage samples. Also, the immobilized water effect was assumed to be minimal since the constituent concentrations (ci) were ratio parameters calculated from unit-cell radial dimensions rather than a metric of absolute volumes. Any substantial trapped water volume included in the ratio of cell, ECM, or scaffold materials was thought to be equivalent and effectively cancelled out.
Limitations in the experimental design included the effect of small sample sizes per culture time group. Earlier power studies indicated sufficient statistical strength in determining biochemical time dependencies [3]. However, the effect of compounding variances from both biochemical and biomechanical measurements could have been minimized with the transition from small sample to larger sample statistics [27]. Another potential design limitation includes the use of the PLLA-PGA fibrous scaffold as a modeled homogeneous material. An alternative substrate such as a hydrogel may provide better scaffold to cell load transmission within the imposed stress-strain environment. Although large structural strains were applied to the constructs (up to 40%), compatibility within small displacement elasticity theory was presumed to be maintained at the cell, scaffold, and ECM levels [57]. Overall, the assumptions were required to make progress toward satisfying the modeling objectives and overcoming stepwise limitations. Attempts will be made to validate this approach throughout the hierarchical framework using alternative scaffold materials and refined parametric control as well as direct mechanical measurements of cell properties using optical tweezing and particle image velocimetry [58].
This cell-based composite model provides a unique perspective for interpreting the mechanical development of engineered cartilage. Due to the spherical nature of chondrocytes and the layering accumulation of pericellular and extracellular matrix surrounded by a host biomaterial, a composite model based on spherical construction remains a useful approach, despite the variations shown here. It is expected that this analytical tool will support cell-based reparative strategies that overcome the limited healing capacity of diseased or damaged cartilage by providing a technique to characterize cell-level properties from tissue-level or cell population measurements.
Acknowledgment
The authors recognize the technical assistance of Dr. Amit Roy. Funding for this project was provided by the Center for Tissue Engineering, University of Massachusetts Medical School, and NIH Grant No. DE014288 from the National Institute for Dental and Craniofacial Research to SSK and Kohles Bioengineering.
References
- 1.Praemer A, Furner D, Rice DP. Musculoskeletal Conditions in the United States. American Academy of Orthopaedic Surgeons; Rosemont, IL: 1999. [Google Scholar]
- 2.Masuda K, Sah RL, Hejna MJ, Thonar EJ. “A Novel Two-Step Method for the Formation of Tissue-Engineered Cartilage by Mature Bovine Chondrocytes: The Alginate-Recovered-Chondrocyte (Arc) Method,”. J. Orthop. Res. 2003;21(1):139–148. doi: 10.1016/S0736-0266(02)00109-2. [DOI] [PubMed] [Google Scholar]
- 3.Wilson CG, Bonassar LJ, Kohles SS. “Modeling the Dynamic Composition of Engineered Cartilage,”. Arch. Biochem. Biophys. 2002;408(2):246–254. doi: 10.1016/s0003-9861(02)00562-3. [DOI] [PubMed] [Google Scholar]
- 4.Schaefer D, Martin I, Jundt G, Seidel J, Heberer M, Grodzinsky A, Bergin I, Vunjak-Novakovic G, Freed LE. “Tissue-Engineered Composites for the Repair of Large Osteochondral Defects,”. Arthritis Rheum. 2002;46(9):2524–2534. doi: 10.1002/art.10493. [DOI] [PubMed] [Google Scholar]
- 5.Hung CT, Lima EG, Mauck RL, Taki E, LeRoux MA, Lu HH, Stark RG, Guo XE, Ateshian GA. “Anatomically Shaped Osteochondral Constructs for Articular Cartilage Repair,”. J. Biomech. 2003;36(12):1853–1864. doi: 10.1016/s0021-9290(03)00213-6. [DOI] [PubMed] [Google Scholar]
- 6.Klein TJ, Schumacher BL, Schmidt TA, Li KW, Voegtline MS, Masuda K, Thonar EJ, Sah RL. “Tissue Engineering of Stratified Articular Cartilage From Chondrocyte Subpopulations,”. Osteoarthritis Cartilage. 2003;11(8):595–602. doi: 10.1016/s1063-4584(03)00090-6. [DOI] [PubMed] [Google Scholar]
- 7.Waldman SD, Grynpas MD, Pilliar RM, Kandel RA. “The Use of Specific Chondrocyte Populations to Modulate the Properties of Tissue-Engineered Cartilage,”. J. Orthop. Res. 2003;21(1):132–138. doi: 10.1016/S0736-0266(02)00105-5. [DOI] [PubMed] [Google Scholar]
- 8.Davisson T, Sah RL, Ratcliffe A. “Perfusion Increases Cell Content and Matrix Synthesis in Chondrocyte Three-Dimensional Cultures,”. Tissue Eng. 2002;8(5):807–816. doi: 10.1089/10763270260424169. [DOI] [PubMed] [Google Scholar]
- 9.Saha AK, Mazumdar J, Kohles SS. “Prediction of Growth Factor Effects on Engineered Cartilage Composition Using Deterministic and Stochastic Modeling,”. Ann. Biomed. Eng. 2004;32(6):871–879. doi: 10.1023/b:abme.0000030262.82626.9c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Saha AK, Mazumdar J, Kohles SS. “Dynamic Matrix Composition in Engineered Cartilage With Stochastic Supplementation of Growth Factors,”. Australas. Phys. Eng. Sci. Med. 2005;28(2):97–104. doi: 10.1007/bf03178699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pazzano D, Mercier KA, Moran JM, Fong SS, DiBiasio DD, Rulfs JX, Kohles SS, Bonassar LJ. “Comparison of Chondrogensis in Static and Perfused Bioreactor Culture,”. Biotechnol. Prog. 2000;16:893–896. doi: 10.1021/bp000082v. [DOI] [PubMed] [Google Scholar]
- 12.Hung CT, Mauck RL, Wang CC-B, Lima EG, Ateshian GA. “A Paradigm for Functional Tissue Engineering of Articular Cartilage via Applied Physiologic Deformational Loading,”. Ann. Biomed. Eng. 2004;32(1):35–49. doi: 10.1023/b:abme.0000007789.99565.42. [DOI] [PubMed] [Google Scholar]
- 13.Williamson AK, Chen AC, Sah RL. “Compressive Properties and Function-Composition Relationships of Developing Bovine Articular Cartilage,”. J. Orthop. Res. 2001;19(6):1113–1121. doi: 10.1016/S0736-0266(01)00052-3. [DOI] [PubMed] [Google Scholar]
- 14.Williamson AK, Masuda K, Thonar EJ, Sah RL. “Growth of Immature Articular Cartilage In Vitro: Correlated Variation in Tensile Biomechanical and Collagen Network Properties,”. Tissue Eng. 2003;9(4):625–634. doi: 10.1089/107632703768247322. [DOI] [PubMed] [Google Scholar]
- 15.Guilak F, Mow VC. “The Mechanical Environment of the Chondrocyte: A Biphasic Finite Element Model of Cell-Matrix Interactions in Articular Cartilage,”. J. Biomech. 2000;33(12):1663–1673. [PubMed] [Google Scholar]
- 16.Klisch SM, Chen SS, Sah RL, Hoger A. “A Growth Mixture Theory for Cartilage with Application to Growth-Related Experiments on Cartilage Explants,”. J. Biomech. Eng. 2003;125(2):169–179. doi: 10.1115/1.1560144. [DOI] [PubMed] [Google Scholar]
- 17.Shieh AC, Athanasiou KA. “Principles of Cell Mechanics for Cartilage Tissue Engineering,”. Ann. Biomed. Eng. 2003;31(1):1–11. doi: 10.1114/1.1535415. [DOI] [PubMed] [Google Scholar]
- 18.Poole CA, Flint MH, Beaumont BW. “Chondrons in Cartilage: Ultrastructural Analysis of the Pericellular Microenvironment in Adult Human Articular Cartilages,”. J. Orthop. Res. 1987;5(4):509–522. doi: 10.1002/jor.1100050406. [DOI] [PubMed] [Google Scholar]
- 19.Poole AC. “Articular Cartilage Chondrons: From, Function, and Failure,”. J. Anat. 1997;191:1–13. doi: 10.1046/j.1469-7580.1997.19110001.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Benya PD, Shaffer JD. “Dedifferentiated Chondrocytes Reex-press the Differentiated Collagen Phenotype When Cultured in Agarose Gels,”. Cell. 1982;30(1):215–224. doi: 10.1016/0092-8674(82)90027-7. [DOI] [PubMed] [Google Scholar]
- 21.Chang J, Poole CA. “Sequestration of Type VI Collagen in the Pericellular Microenvironment of Adult Chrondrocytes Cultured in Agarose,”. Osteoarthritis Cartilage. 1996;4(4):275–285. doi: 10.1016/s1063-4584(05)80105-0. [DOI] [PubMed] [Google Scholar]
- 22.Quinn TM, Schmid P, Hunziker EB, Grodzinsky AJ. “Proteoglycan Deposition Around Chondrocytes in Agarose Culture: Construction of a Physical and Biological Interface for Mechanotransduction in Cartilage,”. Biorheology. 2002;39(1–2):27–37. [PubMed] [Google Scholar]
- 23.Rotter N, Bonassar LJ, Tobias G, Lebl M, Roy AK, Vacanti CA. “Age Dependence of Biochemical and Biomechanical Properties of Tissue-Engineered Human Septal Cartilage,”. Biomaterials. 2002;23(15):3087–3094. doi: 10.1016/s0142-9612(02)00031-5. [DOI] [PubMed] [Google Scholar]
- 24.Christensen RM. Mechanics of Composite Materials. Krieger; Malabar, FL: 1991. pp. 31–72. [Google Scholar]
- 25.Eshelby JD. “The Continuum Theory of Lattice Defects,”. In: Seitz F, Turnbull D, editors. Progress in Solid State Physics. Vol. 3. Academic; New York, NY: 1956. p. 79. [Google Scholar]
- 26.Moran JM, Pazzano D, Bonassar LJ. “Characterization of Polylactic Acid-Polyglycolic Acid Composites for Cartilage Tissue Engineering,”. Tissue Eng. 2003;9(1):63–70. doi: 10.1089/107632703762687546. [DOI] [PubMed] [Google Scholar]
- 27.Montgomery DC. Design and Analysis of Experiments. 5th ed. Wiley; New York, NY: 2001. [Google Scholar]
- 28.Roy R, Kohles SS, Zaporojan V, Peretti GM, Randolph MA, Xu J, Bonassar LJ. “Analysis of Bending Behavior of Native and Engineered Auricular and Costal Cartilage,”. J. Biomed. Mater. Res. 2004;68A(4):597–602. doi: 10.1002/jbm.a.10068. [DOI] [PubMed] [Google Scholar]
- 29.Rotter N, Bonassar LJ, Tobias G, Lebl M, Roy AK, Vacanti CA. “Age Dependence of Cellular Properties of Human Septal Cartilage: Implications for Tissue Engineering,”. Arch. Otolaryngol. Head Neck Surg. 2001;127(10):1248–1252. doi: 10.1001/archotol.127.10.1248. [DOI] [PubMed] [Google Scholar]
- 30.Khalsa PS, Eisenberg SR. “Compressive Behavior of Articular Cartilage is Not Completely Explained by Proteoglycan Osmotic Pressure,”. J. Biomech. 1997;30(6):589–594. doi: 10.1016/s0021-9290(97)84508-3. [DOI] [PubMed] [Google Scholar]
- 31.Kohles SS, Wilson CG, Bonassar LJ. “A Composite Spheres Analysis of Engineered Cartilage Mechanics.”; Proceedings of the SEM Annual Conference and Exposition on Experimental and Applied Mechanics; Portland, OR. Jun 7–9, 2005. Paper, No. 71. [Google Scholar]
- 32.Farndale RW, Buttle DJ, Barrett AJ. “Improved Quantitation and Discrimination of Sulphated Glycosaminoglycans by Use of Dimethylmethylene Blue,”. Biochim. Biophys. Acta. 1986;883:173–177. doi: 10.1016/0304-4165(86)90306-5. [DOI] [PubMed] [Google Scholar]
- 33.Woessner JF. “The Determination of Hydroxyproline in Tissue and Protein Samples Containing Small Portions of this Imino Acid,”. Arch. Biochem. Biophys. 1961;93:440–447. doi: 10.1016/0003-9861(61)90291-0. [DOI] [PubMed] [Google Scholar]
- 34.Hollander AP, Heathfield TF, Webber C, Iwata Y, Bourne R, Rorabeck C, Poole AR. “Increased Damage to Type II Collagen in Osteoarthritic Articular Cartilage Detected by a New Immunoassay,”. J. Clin. Invest. 1994;93(4):1722–1732. doi: 10.1172/JCI117156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Freed LE, Vunjak-Novakovic G, Biron RJ, Eagles DB, Lesnoy DC, Barlow SK, Langer R. “Biodegradable Polymer Scaffolds for Tissue Engineering,”. Biotechnology. 1994;12(7):689–693. doi: 10.1038/nbt0794-689. [DOI] [PubMed] [Google Scholar]
- 36.DiMicco MA, Sah RL. “Dependence of Cartilage Matrix Composition on Biosynthesis, Diffusion, and Reaction,”. Transp. Porous Media. 2003;50:57–73. [Google Scholar]
- 37.Jones WR, Ting-Beall HP, Lee GM, Kelley SS, Hochmuth RM, Guilak F. “Alterations in the Young's Modulus and Volumetric Properties of Chondrocytes Isolated From Normal and Osteoarthritic Human Cartilage,”. J. Biomech. 1999;32(2):119–127. doi: 10.1016/s0021-9290(98)00166-3. [DOI] [PubMed] [Google Scholar]
- 38.Shin D, Athanasiou K. “Cytoindentation for Obtaining Cell Biomechanical Properties,”. J. Orthop. Res. 1999;17(6):880–890. doi: 10.1002/jor.1100170613. [DOI] [PubMed] [Google Scholar]
- 39.Athanasiou KA, Rosenwasser MP, Buckwalter JA, Malinin TI, Mow VC. “Interspecies Comparisons of In Situ Intrinsic Mechanical Properties of Distal Femoral Cartilage,”. J. Orthop. Res. 1991;9(3):330–340. doi: 10.1002/jor.1100090304. [DOI] [PubMed] [Google Scholar]
- 40.Haider MA, Guilak F. “An Axisymmetric Boundary Integral Model for Assessing Elastic Cell Properties in the Micropipette Aspiration Contact Problem,”. J. Biomech. Eng. 2002;124(5):586–595. doi: 10.1115/1.1504444. [DOI] [PubMed] [Google Scholar]
- 41.Trickey WR, Lee GM, Guilak F. “Viscoelastic Properties of Chondrocytes From Normal and Osteoarthritic Human Cartilage,”. J. Orthop. Res. 2000;18(6):891–898. doi: 10.1002/jor.1100180607. [DOI] [PubMed] [Google Scholar]
- 42.Bader DL, Ohashi T, Knight MM, Lee DA, Sato M. “Deformation Properties of Articular Chondrocytes: A Critique of Three Separate Techniques,”. Biorheology. 2002;39(1–2):69–78. [PubMed] [Google Scholar]
- 43.Koay EJ, Shieh AC, Athanasiou KA. “Creep Indentation of Single Cells,”. J. Biomech. Eng. 2003;125(3):334–341. doi: 10.1115/1.1572517. [DOI] [PubMed] [Google Scholar]
- 44.Leipzig ND, Athanasiou KA. “Unconfined Creep Compression of Chondrocytes,”. J. Biomech. 2005;38(1):77–85. doi: 10.1016/j.jbiomech.2004.03.013. [DOI] [PubMed] [Google Scholar]
- 45.Knight MM, van de Breevaart Bravenboer J, Lee DA, van Osch GJ, Weinans H, Bader DL. “Cell and Nucleus Deformation in Compressed Chondrocyte-Alginate Constructs: Temporal Changes and Calculation of Cell Modulus,”. Biochim. Biophys. Acta. 2002;1570(1):1–8. doi: 10.1016/s0304-4165(02)00144-7. [DOI] [PubMed] [Google Scholar]
- 46.Wu JZ, Herzog W, Epstein M. “Modelling of Location- and Time-Dependent Deformation of Chrondrocytes During Cartilage Loading,”. J. Biomech. 1999;32(6):563–572. doi: 10.1016/s0021-9290(99)00034-2. [DOI] [PubMed] [Google Scholar]
- 47.Federico S, Herzog W, Wu JZ, La Rosa G. “A Method to Estimate the Elastic Properties of the Extracellular Matrix of Articular Cartilage,”. J. Biomech. 2004;37(3):401–404. doi: 10.1016/s0021-9290(03)00280-x. [DOI] [PubMed] [Google Scholar]
- 48.Mauck RL, Seyhan SL, Ateshian GA, Hung CT. “Influence of Seeding Density and Dynamic Deformational Loading on the Developing Structure/Function Relationships of Chondrocyte-Seeded Agarose Hydrogels,”. Ann. Biomed. Eng. 2002;30(8):1046–1056. doi: 10.1114/1.1512676. [DOI] [PubMed] [Google Scholar]
- 49.Michalek AJ, Iatridis JC. “A Numerical Study to Determine Pericellular Matrix Modulus and Evaluate Its Effects on the Micromechanical Environment of Chondrocytes,”. J. Biomech. 2007;40(6):1405–1409. doi: 10.1016/j.jbiomech.2006.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kiviranta P, Rieppo J, Korhonen RK, Julkunen P, Toyras J, Jurvelin JS. “Collagen Network Primarily Controls Poisson's Ratio of Bovine Articular Cartilage in Compression,”. J. Orthop. Res. 2006;24(4):690–699. doi: 10.1002/jor.20107. [DOI] [PubMed] [Google Scholar]
- 51.Jones RM. Mechanics of Composite Materials. 2nd ed. Taylor & Francis; Philadelphia, PA: 1999. pp. 55–186. [Google Scholar]
- 52.Chahine NO, Wang CC, Hung CT, Ateshian GA. “Anisotropic Strain-Dependent Material Properties of Bovine Articular Cartilage in the Transitional Range From Tension to Compression,”. J. Biomech. 2004;37(8):1251–1261. doi: 10.1016/j.jbiomech.2003.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kohles SS. “Response Surface Analysis of Flexural and Membrane Stresses to Characterize Flexible Biologic Materials,”; Proceedings American Society of Biomechanics, 28th Annual Meeting; Portland, OR. Sep 8–11, 2004. p. 116. [Google Scholar]
- 54.Jin H, Lewis JL. “Determination of Poisson's Ratio of Articular Cartilage by Indentation Using Different-Sized Indenters,”. J. Biomech. Eng. 2004;126(2):138–145. doi: 10.1115/1.1688772. [DOI] [PubMed] [Google Scholar]
- 55.Vunjak-Novakovic G, Obradovic B, Martin I, Bursac PM, Langer R, Freed LE. “Dynamic Cell Seeding of Polymer Scaffolds for Cartilage Tissue Engineering,”. Biotechnol. Prog. 1998;14(2):193–202. doi: 10.1021/bp970120j. [DOI] [PubMed] [Google Scholar]
- 56.Quinn TM, Dierickx P, Grodzinsky AJ. “Glycosaminoglycan Network Geometry May Contribute to Anisotropic Hydraulic Permeability in Cartilage Under Compression,”. J. Biomech. 2001;34(11):1483–1490. doi: 10.1016/s0021-9290(01)00103-8. [DOI] [PubMed] [Google Scholar]
- 57.Cook RD, Young WC. Advanced Mechanics of Materials. Macmillan; New York, NY: 1985. pp. 49–88. [Google Scholar]
- 58.Tretheway DC, Kohles SS. “Instrument Development: An Integrated Optical Tweezer/micro-PIV System to Investigate Cell Biomechanics,”. National Science Foundation, Bioengineering & Environmental Systems Division, Major Research Instrumentation Program; Portland, OR: 2006. Progress Rep. No. BES-0521637. [Google Scholar]


