Response Properties of Neighboring Neurons in the Auditory Midbrain for Pure-Tone Stimulation: A Tetrode Study

Abstract

The complex anatomical structure of the central nucleus of the inferior colliculus (ICC), the principal auditory nucleus in the midbrain, may provide the basis for functional organization of auditory information. To investigate this organization, we used tetrodes to record from neighboring neurons in the ICC of anesthetized cats and studied the similarity and difference among the responses of these neurons to pure-tone stimuli using widely used physiological characterizations. Consistent with the tonotopic arrangement of neurons in the ICC and reports of a threshold map, we found a high degree of correlation in the best frequencies (BFs) of neighboring neurons, which were mostly <3 kHz in our sample, and the pure-tone thresholds among neighboring neurons. However, width of frequency tuning, shapes of the frequency response areas, and temporal discharge patterns showed little or no correlation among neighboring neurons. Because the BF and threshold are measured at levels near the threshold and the characteristic frequency (CF), neighboring neurons may receive similar primary inputs tuned to their CF; however, at higher levels, additional inputs from other frequency channels may be recruited, introducing greater variability in the responses. There was also no correlation among neighboring neurons' sensitivity to interaural time differences (ITD) measured with binaural beats. However, the characteristic phases (CPs) of neighboring neurons revealed a significant correlation. Because the CP is related to the neural mechanisms generating the ITD sensitivity, this result is consistent with segregation of inputs to the ICC from the lateral and medial superior olives.

Introduction

The inferior colliculus (IC), the main auditory nucleus in the mammalian midbrain, occupies a central role in the ascending auditory pathway because it is the first nucleus that receives virtually all neural information originating in the auditory nerves of both ears (Adams 1979; Brunso-Bechtold et al. 1981). The central nucleus of the inferior colliculus (ICC), which receives the majority of the ascending inputs, is arranged in parallel sheets or laminae defined by the parallel arrangement of the primary cell dendrites and the incoming axons. The primary cell type, the disc-shaped cell, by far the most common cell type in the central nucleus, has planar dendritic fields that align to create parallel sheets (Oliver and Morest 1984). Incoming axons run parallel to these sheets. The input from lower nuclei tend to form distinct projection bands that partly interleave and partly overlap with axon bands from other nuclei (Henkel and Spangler 1983; Oliver et al. 1997; Shneiderman and Henkel 1987).

Many questions about the relationship between single-unit–response properties and the complex laminar structure of the IC remain unanswered. The strongest evidence of a functional arrangement is a tonotopic map that is orthogonal to the anatomical laminae (Merzenich and Reid 1974). Because the laminae correspond to isofrequency planes, a number of studies have investigated the existence of maps for response properties other than best frequency within a lamina (Ehret 1997; Ehret et al. 2005; Schreiner and Langner 1988, 1997; Stiebler 1986). If multiple maps are superimposed on each lamina in the ICC, we could hypothesize two possible effects. If all maps are aligned with each other, neighboring neurons would be expected to have similar response properties; however, if each map has its own distinct orientation, a more complex structure would be expected. Further features of the organization in the IC may arise from the neurons' intrinsic membrane properties. ICC disc-shaped cells differ greatly in their composition and distribution of ionic membrane channels, particularly K⁺ channels (Peruzzi et al. 2000; Sivaramakrishnan and Oliver 2001). This variation in membrane properties can give rise to different processing of incoming information, even for cells that have similar synaptic inputs. It is not known whether cells having similar membrane channel properties cluster together in distinct regions or whether they are widely distributed throughout the ICC.

Studies of response maps and physiological organization have typically relied on traditional, serial recording of single units and histological reconstruction of electrode tracks to identify spatial organization of physiological responses. However, recording from more than one neuron in a localized region of space using single-unit, single-electrode recording is extremely challenging (Syka et al. 1981). The tetrode recording technique (Wilson and McNaughton 1993) offers the opportunity to record simultaneously from neurons that are spatially close together. Tetrodes, closely spaced, four-channel electrodes, record multiunit spiking activity from neurons in the vicinity of the recording site. Spatial sampling from the four channels facilitates reconstruction of the single-unit spike trains that contribute to the multiunit recording because the relationships among the action potential waveforms observed across the four channels differ for neurons at different locations in space. Tetrode recordings are beginning to be applied to studies of the auditory system (Otazu and Zador 2004; von der Behrens et al. 2007).

To gain understanding of the relationship between anatomical organization and physiological properties in the ICC, we used tetrodes to record simultaneously from neighboring neurons in the cat IC and compared the response properties of these neurons for pure-tone stimuli using physiological characterizations applied widely in studies of the auditory system. If ICC cells are spatially organized by a given physiological property, we would expect to see a high degree of similarity among neighboring neurons in that particular property. We find that some properties such as best frequency and threshold tend to be similar in neighboring neurons, whereas other properties are not. A preliminary report of this work was previously presented (Seshagiri and Delgutte 2004).

Methods

Animal preparation

All experimental procedures were in accordance with National Institutes of Health regulations and approved by the animal care committee of the Massachusetts Eye and Ear Infirmary. The data presented here were collected from the inferior colliculi of 13 adult cats. The methods for preparation of the animals were similar to those described by Lane and Delgutte (2005). Briefly, healthy adult cats received an initial intraperitoneal injection of diallyl barbituric acid in urethane (75 mg/kg); additional doses were administered as necessary to maintain deep levels of anesthesia. A tracheal canula was inserted to provide a clear passageway for respiration. A rectal thermometer was used to monitor body temperature, which was maintained at 37.2°C. Heart rate, respiration rate, and exhalation pCO₂ were also monitored.

Surgically, both pinnae were partially dissected away and the ear canals cut to allow insertion of closed acoustic assemblies. To prevent buildup of static pressure in the middle ear, we drilled a small hole in each bulla and affixed a 30-cm plastic tube. In 10 of the 13 experiments, the posterior surface of the IC was exposed by a posterior-fossa craniotomy and aspiration of the overlying cerebellum. In the remaining three experiments, the dorsal surface of the IC was exposed by a craniotomy anterior to the tentorium and aspiration of the underlying occipital cortex; part of the bony tentorium was removed to allow better visualization of the IC.

The animal was placed in a double-walled, electrically shielded, soundproof chamber. To assess the status of the cochlea and auditory brain stem, we measured the click-evoked auditory brain stem response (ABR) between vertex screw and a tooth bar by averaging 500 responses to a 100-μs click stimulus (10/s). We measured the response to clicks delivered binaurally as well as monaurally to each ear. This was repeated for a series of levels from −70 to −40 dB re 1V(∼30- to 60-dB SPL peak amplitude) in 5-dB steps. We measured the ABR level series immediately before and after the brain aspiration, and the measurement was also repeated periodically during the experiment to check for changes in threshold. In all experiments, the ABR thresholds never changed by >5 dB, which was considered acceptable.

Data acquisition and stimulus delivery

All recordings from the IC were made with tetrodes constructed as described by Gray et al. (1995). Briefly, four 12-μm, Teflon-insulated nichrome wires (Kanthal Palm Coast) were wound together and the insulation was melted to bind the four wires together. At one end, the wires were cut at an angle to create a beveled tip. The resulting electrode contains four recording sites spaced about 20 μm apart. The recording sites were gold plated to lower the impedance at 1 kHz to within 400–800 kΩ. Tetrodes were mounted on a remote-controlled, hydraulic microdrive (Kopf 650). In the 10 experiments with the posterior-fossa opening, we oriented the tetrodes nearly horizontal in a parasagittal plane parallel to the isofrequency laminae of the ICC (Merzenich and Reid 1974). In the remaining three experiments with dorsal exposure of the IC, we oriented electrodes in a nearly dorso-ventral direction and advanced the electrode along the tonotopic axis of the ICC. Because we were interested in characterizing sensitivity to interaural time differences (ITDs), we typically positioned our electrode in low-frequency regions of the ICC. Agar was used to fill the cranial cavity and reduce brain stem pulsation as needed.

All acoustic stimuli were digitally generated (16 bits, 100 kHz) and then converted to analog signals (NIDAC 6052e; National Instruments). Custom-built programmable attenuators set the stimulus level at each ear with 0.1-dB resolution. The attenuated signals were delivered to closed acoustic assemblies inserted into the cut ends of the ear canals. The assemblies contained an electrodynamic speaker (Realistic 40–1377; Radio Shack, Ft. Worth, TX) and a calibrated probe-tube microphone (Larson Davis 3250). To ensure a flat frequency response at the tympanic membrane, we measured the sound pressure at the tympanic membrane as a function of frequency and then used the calibration to set the sound pressure level.

Experimental procedure

During the experiment, we visually monitored the waveforms of all four tetrode channels on an oscilloscope. One of the four channels was selected for the presence of actions potentials and fed into a trigger device and event timer that recorded the times of each threshold crossing with 1-μs resolution.

We used a 500-ms, 60-dB SPL frozen broadband noise burst as a search stimulus and advanced the tetrode until we observed spikes. Once spikes were encountered, we selected the channel with the largest spikes to feed into the event timer and measured a frequency-tuning curve based on the multiunit activity using an automated tracking procedure (Kiang and Moxon 1974). If the tuning curve exhibited sharp frequency tuning, we assumed the tetrode was in the central nucleus.

In the first four experiments, we studied response properties at each site with little feedback on the number and degree of isolation of single units contained in the tetrode recording. For the last nine experiments, we implemented an on-line preliminary spike-sorting algorithm to improve feedback on the quality of recording. For these experiments, we first recorded the neural response to a frozen broadband noise stimulus, applied our spike detection and sorting algorithm to the recording (see the appendix), and observed the clustering of spike waveforms. If the recording contained at least two well-isolated single units, we studied the site in more detail; otherwise, we continued advancing the electrode.

Throughout recording from a single site in the later experiments, we occasionally repeated the broadband noise measurement and checked the clustering of spike waveforms to ensure stability of the recording. If a cluster disappeared or a new cluster appeared, we either ceased recording from that location or discarded previous measurements and started a new set of measurements.

Once we identified a stable recording site with at least two well-isolated clusters, we first measured responses as a function of frequency and level. Because we reconstruct our single-unit response off-line from multiunit recordings, we use the threshold and characteristic frequency (CF) of the multiunit tuning curve to help identify appropriate ranges of level and frequency for measuring responses. Typically, we measured frequency–response curves both near threshold (within 15 dB SPL of the multiunit threshold at CF) and at a moderate to high sound level (20–30 dB above the lower level). We also measured the rate–level function for pure tones at the multiunit CF. Stimuli were typically delivered monaurally to the contralateral ear, although ipsilateral or binaural stimulation was also used if this produced markedly higher firing rates.

For characterizing frequency tuning, we used either 150- or 200-ms tone bursts followed by either a 150- or 300-ms silent interval between stimuli, respectively. Responses were typically measured as a function of frequency in 0.25-octave steps over a 4-octave range centered at the multiunit CF. For measuring responses as a function of level, we used 250-ms tone bursts followed by a 250-ms silent interval. Responses were measured as a function of level in 5-dB steps over a range of ≥60 dB, starting from a level 5–10 dB below the multiunit threshold. The stimuli were presented 50 times each at each frequency or level.

If the electrode was in a low-frequency (<2-kHz) region of the ICC, we also measured the binaural beat response (Yin and Kuwada 1983). In early experiments, we measured the beat response only at the multiunit CF. In later experiments, we measured the beat response at four to five frequencies spanning the range over which we observed beat sensitivity in the multiunit response from one tetrode channel. Binaural beat stimuli had a 2-Hz beat frequency, with the ipsilateral ear higher in frequency. Whenever possible, the beat stimuli were presented continuously over 75 s (150 cycles of the beat period). For sites that exhibited significant adaptation to the continuous beat, we presented a 1.5-s beat stimulus followed by a 500-ms silent interval between stimulus presentations. This stimulus, containing three beat periods, was presented 50 times to obtain data from a total of 150 beat cycles.

Data analysis

Single-unit reconstruction

Methods for tetrode recording, processing, and single-unit spike train reconstruction are described in detail in the appendix. Briefly, at each recording site, we sampled the signals from all four tetrode channels at 20 kHz and stored them to disk. Off-line, the signals were digitally band-pass filtered (300–3,000 Hz); 60-Hz noise was removed from the recording by computing the period average of the signal over a period of 1/60 s and then subtracting the periodic waveform constructed from repeating the period-averaged waveform. We applied the spike detection algorithm described in theappendix to identify the times of all putative neural events. For every neural event, a 0.75-ms sample of the waveforms from each channel was collected. Using the collected waveforms from each channel, we sorted the data based on the principal component weights for each channel. Events generated from an individual neuron cluster together in principal component space and define the spike times for each single unit in our recording.

Characterization of response properties

Best frequencies and bandwidths were estimated from average rate responses measured as a function of frequency. The rate was averaged over a window from the onset of the stimulus to 25 ms after the stimulus ended. To improve the precision of these estimates, we applied a cubic spline interpolation to the rate–frequency curve to increase the frequency sampling by a factor of 10. Using the interpolated curve, the best frequency (BF) was defined as the frequency that elicits the maximum spike rate (Kiang 1984). In a few cases where the single-unit response was primarily inhibitory, we defined the BF as the frequency that elicits the minimum spike rate.

To characterize the width of tuning, we measured the bandwidth of the rate–frequency curve at a rate halfway between the maximum rate and the spontaneous rate. We call this metric the “50% bandwidth.” We used the average spike rate during the silent intervals between stimuli across all frequencies as a measure of spontaneous rate.

Pure-tone thresholds were obtained from average rate responses measured as a function of level for tones at the multiunit CF. We increased the level resolution by a factor of 10 by applying a cubic spline interpolation to the rate–level curves. To determine the threshold, we first computed the mean and SD of the spontaneous rate across every stimulus presentation and level. The threshold was then defined as the level at which the rate just exceeds the mean spontaneous rate plus 2 SDs. In cases when the spontaneous rate was zero, the threshold was defined as the lowest level that produced at least five spikes across all 50 stimulus presentations of the 250-ms stimulus (0.4 spike/s).

For binaural beat responses, we characterized the mean interaural response phase by using a vector-averaging approach (Goldberg and Brown 1969). We converted the spike times to phase angles relative to the binaural beat period and computed a vector average across all spikes to obtain the mean interaural phase difference (IPD). In the cases when the binaural beat stimuli were presented in 1.5-s bursts to avoid adaptation, we discarded the first beat period of each stimulus presentation in computing the mean IPD to avoid bias from the sharp onset transient.

For sites in which the binaural beat responses were measured at several frequencies, we investigated how the best IPD depends on frequency for each single unit and estimated the characteristic delay (CD) and the characteristic phase (CP) (Yin and Kuwada 1983). Briefly, we fit a weighted regression line to the mean phase as a function of frequency for each unit. Only data points for which the distribution of response phases was significantly different from uniform [P < 0.001, Rayleigh test of uniformity (Fisher 1993)] were included in the fit. The slope of the regression line gives the CD and the intercept gives the CP. We then checked the linearity of the data points using the test described by Yin and Kuwada (1983) with a criterion of P < 0.005. Units with nonlinear frequency-phase relationships were discarded from further analysis of CP and CD.

Results

We present data recorded from 44 sites in 13 cats from which we isolated 145 single units. On average, we recorded 3.7 units per site with a maximum yield of 7 units from a single site. Our goal was to compare response properties of pairs of neighboring neurons, and we have a total of 193 such pairs (e.g., a site with four units [A, B, C, D] gives six pairs: [A, B], [A, C], [A, D], [B, C], [B, D], and [C, D]). We investigated the similarities and differences between members of each pair in best frequency, width of frequency tuning, pure-tone threshold, shape of frequency response areas, temporal discharge patterns, and ITD sensitivity.

Effective recording radius of the tetrode

The neurons that contribute to extracellular recordings such as those obtained using tetrodes likely lie within some maximum radius around the electrode tip. This radius is defined by the electrode properties as well as the extracellular currents at the site of generation and the rate of decay of the electric potential in the tissue. Because tetrodes record the action potential from a neuron at four different locations, we can estimate the rate of decay of action potential amplitudes extracellularly to obtain an estimate of the effective recording radius of the tetrodes. Estimating this radius helps us to interpret our results, particularly in relation to the widths of the fibrodendritic laminae.

We followed a method used by Gray et al. (1995) in the primary visual cortex to estimate the effective distance over which a tetrode effectively records single units. Specifically, we assume that current decays exponentially with distance and define the effective recording radius as the distance at which the amplitude of the extracellular action potential falls to 10% of its amplitude at the generator site. To estimate the rate of decay, we observe that the average amplitude decay of all our recorded action potentials across any pair of electrodes is a factor of 0.74 (σ = 0.18). However, these action potentials come from unknown spatial locations relative to the recording electrodes. Therefore to estimate the path length over which this decay occurs—that is, the difference in path length from the neuron to any pair of recording sites from the tetrode—we assume that the neurons are distributed uniformly and average over all possible neuron locations to get an estimate of the average path length difference. For a 20-μm spacing between tetrode tips assumed to form a square, the average path length difference is 12.5 μm. Therefore assuming an average decay factor of 0.74 over an average distance of 12.5 μm, and assuming that the decay is exponential, we find that the distance over which spike amplitude decays by 90% would be almost 100 μm. Because the spike-to-background noise ratio rarely exceeds 10:1 in our recording, we take this value as the effective recording radius of our tetrodes.

Best frequency

Many reports of frequency tuning in the auditory system measure tuning curves, which are isorate contours in the frequency-versus-level plane. The characteristic frequency (CF) is defined as the frequency where the tuning curve has the lowest level (Kiang 1984). Tuning curves are typically measured by a tracking procedure that requires feedback about the average firing rate at each level and frequency (Kiang and Moxon 1974). Because we did not have access to the separated responses of each single unit during the experiment, we could not measure isorate responses with an efficient tracking procedure. Instead, we measured the responses as a function of frequency at a fixed level. From these rate–frequency curves, we measured the best frequency (BF), i.e., the frequency that elicits the maximum rate response at a given level (Kiang 1984). This measure depends on the level at which the rate–frequency curve is measured. If the level is near the pure-tone threshold of a unit, the BF should be very close to the unit's CF. We typically measured the BF at 5–10 dB above the threshold at the multiunit CF, which was obtained from a multiunit isorate tuning curve.

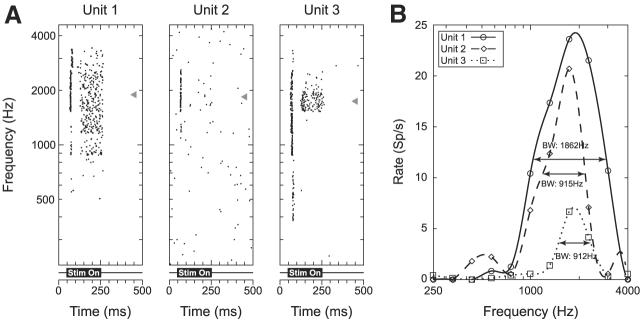
Figure 1A shows dot raster plots as a function of frequency for three units recorded simultaneously from the same site. These three units exhibit similar best frequencies (triangles), even though their temporal discharge patterns differ significantly. The BFs are 1,892, 1,840, and 1,741 Hz, spanning a range of about 0.12 octave.

Fig. 1.

Responses to pure tones as a function of frequency for 3 simultaneously recorded single units. A: dot raster display for each of the 3 units in response to pure-tone stimuli (25 dB SPL). Stimulus is on from 50 to 250 ms as indicated below each raster plot. Gray triangles indicate the best frequencies (BFs) for each unit (1,892, 1,840, and 1,741 Hz, respectively). B: rate–frequency curves corresponding to the dot raster displays from A. Horizontal lines indicate the half-bandwidths for each unit (1,862, 915, and 912 Hz, respectively).

From our sample of 193 neighboring pairs, we discarded 33 pairs from 11 sites because the rate–frequency curves were measured at levels >15 dB above the multiunit threshold. For the remaining 160 pairs from 33 sites, Fig. 2 shows a scatterplot of the BF of one unit against the BF of the other unit in the pair. Because we specifically targeted regions of the ICC tuned to low frequencies, the majority of the units have BF values <3 kHz. In general, the BFs of neighboring neurons are similar. The median difference between BFs is 0.16 octave, and 69% (111/160) of the pairs have BFs within 0.25 octave of each other, which corresponds to the typical frequency spacing used in our measurements. Nine pairs from five sites showed a BF difference >0.5 octave and only five pairs from two sites showed a BF difference >1 octave. The correlation between BFs of neighboring pairs is high (R² = 0.795). If we consider only the sites with BF values <5 kHz, which accounts for most of the data, R² drops to 0.627, which is still highly significant (P < 0.001).

Fig. 2.

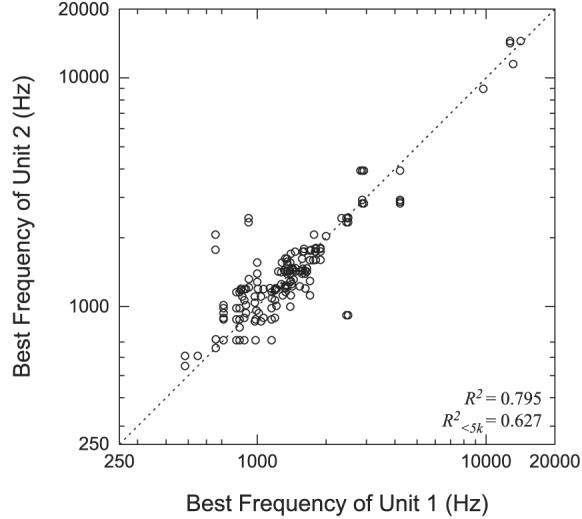
Comparison of BFs between neighboring neurons. Each point represents the BF of the first unit vs. the BF of the second unit for every neighboring neuron pair. There is no significance to which unit is labeled 1 and which is labeled 2. Dotted line indicates identity.

Width of frequency tuning and shape of frequency response area

To quantify the width of tuning, we measured the 50% bandwidth of the rate–frequency curves. The 50% bandwidth is the width of the curve measured halfway between the maximum rate and the spontaneous rate. Figure 1B shows the rate–frequency curves for the three units whose dot raster responses are shown in Fig. 1A. For each curve, the horizontal line indicates the rate at which the 50% bandwidth was measured. The bandwidths (1,862, 912, and 915 Hz) are more variable than the BFs.

Figure 3 shows a scatterplot comparing the 50% bandwidths between each of the 160 neighboring pairs used for the BF comparison. The 50% bandwidth was typically measured at 5–10 dB above the multiunit threshold. The 50% bandwidths show only a weak correlation (R² = 0.12) among neighboring neuron pairs, but this correlation is nevertheless highly significant (P < 0.0001). The median bandwidth difference between neighboring pairs is 0.24 octave with 25% of the pairs showing a bandwidth difference >0.5 octave.

Fig. 3.

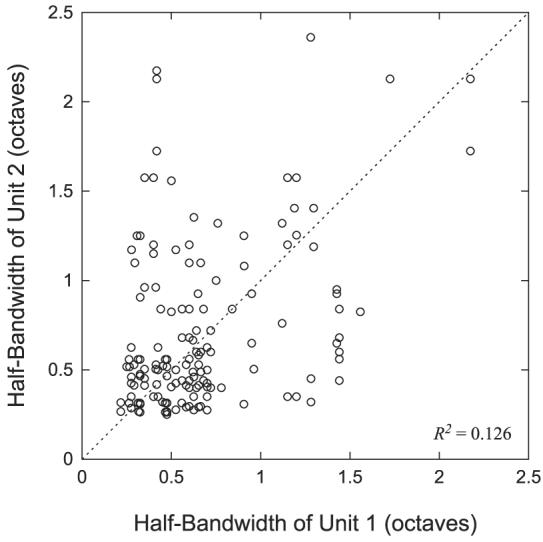
Comparison of half-bandwidths of neighboring neuron pairs. Each point represents the half-bandwidth of the first unit vs. the half-bandwidth of the second unit for each neighboring neuron pair. There is no significance to which unit is chosen as unit 1 or unit 2.

We also looked at characterizations of the frequency response areas and the similarities of response types among neighboring neurons. Several schemes for classifying frequency response areas of IC neurons have been proposed (Egorova et al. 2001; Hernandez et al. 2005; Ramachandran et al. 1999). Here, we focus on the classification scheme defined by Ramachandran et al. (1999) because it is based on data from the cat, whereas the other schemes are for rats and mice, which hear poorly at low frequencies where most of our neuron BFs are located. Using a decerebrate preparation, Ramachandran defined three response map shapes: Type V, Type I, and Type O based on patterns of excitation and inhibition. Due to the influence of anesthesia in our experiments, we do not typically see spontaneous activity, so assessing inhibitory effects can be difficult. However, we were able to approximate the classification scheme of Ramachandran et al. (1999) by examining both rate–level functions and changes in bandwidth with stimulus intensity for our units.

Ramachandran et al. (1999) defined Type V units as primarily excitatory, with a pronounced widening of bandwidth at higher levels. In contrast, the tuning of Type I units remains relatively narrow due to inhibitory sidebands. Type O units have a closed response area, i.e., a region of excitation limited to a narrow range of frequencies and levels. To approximate this scheme, we first classified as Type O any unit whose rate–level function was nonmonotonic and dropped to a rate <1/3 of the maximum at high levels. For the remaining neurons, we looked at the change in bandwidth from a lower level (5–10 dB re threshold) to a level 20–30 dB higher, as well as the absolute bandwidth at the higher level. We classified as Type V any neuron whose bandwidth more than doubled from the lower to the higher intensity and whose bandwidth at the higher level exceeded 2 octaves. We classified as Type I any neuron whose bandwidth did not double from the lower to the higher level and whose bandwidth at the higher level was <2 octaves. We used the category Other to place all units whose behavior did not fall into any of these categories. Figure 4 shows the frequency response area curves for three units recorded from the same site with a BF ≈ 1,500 Hz. The three responses were classified as type V, type I, and type O, showing that responses of all three types can be found at the same site.

Fig. 4.

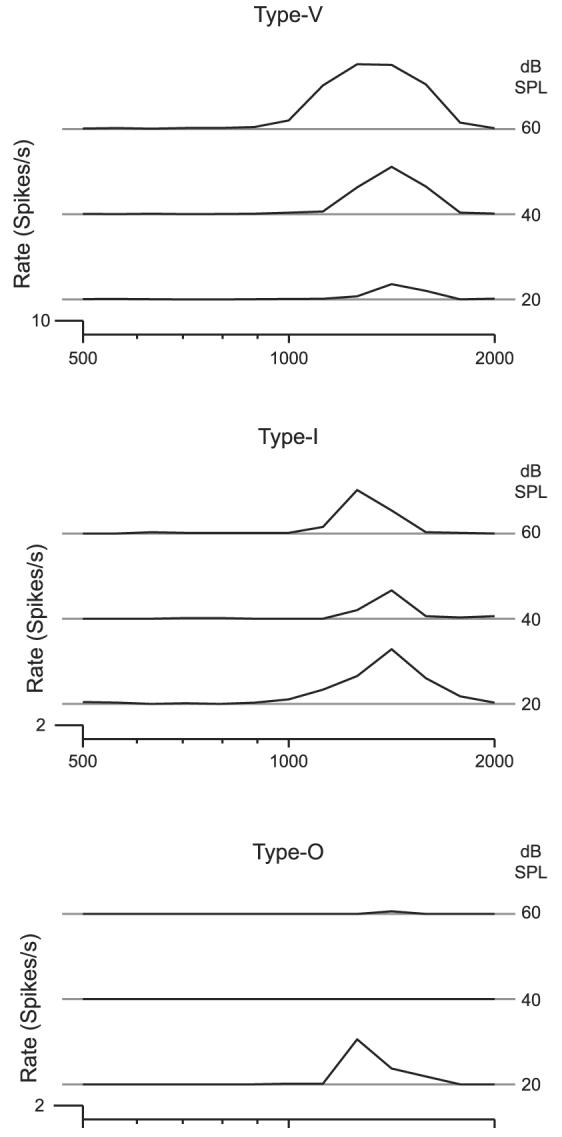
Frequency response areas for 3 units recorded from the same recording site. Type V: these units are characterized by a broadening of the bandwidth at higher sound levels. Type I: these units are characterized by little or no change in the bandwidth with increasing sound levels. Type O: these units are characterized by a decrease in spike rate at BF at higher sound levels.

Among 75 single units for which rate–frequency curves were measured for at least two levels: 16 (21%) were classified as Type V; 43 (57%) as Type I; 12 (16%) as Type O; and 4 (5%) as Other. From these 75 units, we had 95 neighboring neuron pairs. Response area types for these pairs were distributed as shown in Table 1. To assess whether the observed distribution is consistent with the hypothesis that these unit classes are randomly distributed across recording sites, we created 50,000 data sets by randomly assigning unit types at each site based on their relative proportions among single units and then computing the distribution of unit class pairs for each random assignment. From the 50,000 trials, we computed the 95% confidence intervals for each entry in Table 1 under the null hypothesis. We found that all 10 entries fall within the 95% confidence bounds, indicating that we cannot reject the hypothesis that these response area types are randomly distributed across recording sites.

Table 1.

Frequency of pairwise combinations of frequency–response map types among neighboring neuron pairs

	Type V	Type I	Type O	Other
Type V	7
Type I	19	34
Type O	2	21	4
Other	2	5	1	0

Threshold

We characterized the effects of stimulus level on the response to a pure tone near the best frequency. Figure 5A shows dot raster plots as a function of level for four units simultaneously recorded at the same site. For these four units, the thresholds are similar, but the dependence of rate on level differs among the units. The latter is more easily seen in Fig. 5B, which shows the rate–level curves for the four neighboring units. Because the rates differed widely among the units, the rate–level curves have been normalized to their maximum. Units 1 and 2 have a nonmonotonic behavior; that is, the rate peaks at a particular level above which the rate decreases; in contrast, the rate of Unit 3 continues to increase with increasing level after reaching a plateau at intermediate levels. Unit 4 shows only slight nonmonotonicity. The fact that monotonic and nonmonotonic units are found at the same site is consistent with the lack of a tendency for Type O units, which are strongly nonmomotonic, to segregate from Type V and Type I units, which are more monotonic.

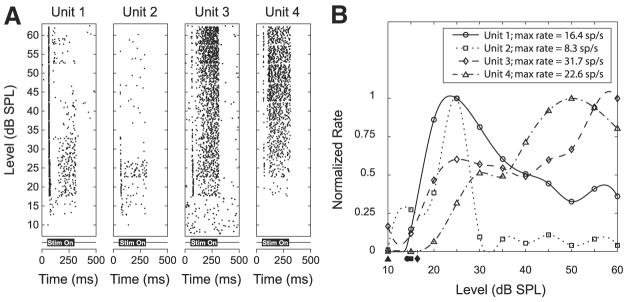
Fig. 5.

Responses to pure tones as a function of stimulus level for 4 simultaneously recorded single units. A: dot raster displays for each of the 4 units in response to a pure tone (1 kHz) of varying level. Stimulus is on from 50 to 300 ms as indicated below each raster plot. B: rate–level curves corresponding to the dot rasters in A. All the curves have been normalized to a maximum rate of 1. Filled symbols below the x-axis indicate the thresholds for each unit. Range of thresholds is <10 dB. These 4 units exhibit a mix of nonmonotonic and monotonic rate–level dependencies.

The filled symbols on the horizontal axis in Fig. 5B indicate the thresholds for each of the four single units. The thresholds span a range of <10 dB. Overall, we measured rate–level curves for 121 neighboring neuron pairs from 26 sites. Of these 121 pairs, threshold could not be determined for 13 pairs from two sites because these units responded at the lowest level tested. Figure 6 shows a scatterplot of the thresholds for the 108 remaining pairs. The dashed lines define the boundaries outside of which the pairs differ in threshold by >10 dB. Only two pairs differ by >10 dB and neither pair exceeds a difference of 11 dB. R² = 0.90, indicating a very strong relationship between pure-tone thresholds of neighboring neuron pairs.

Fig. 6.

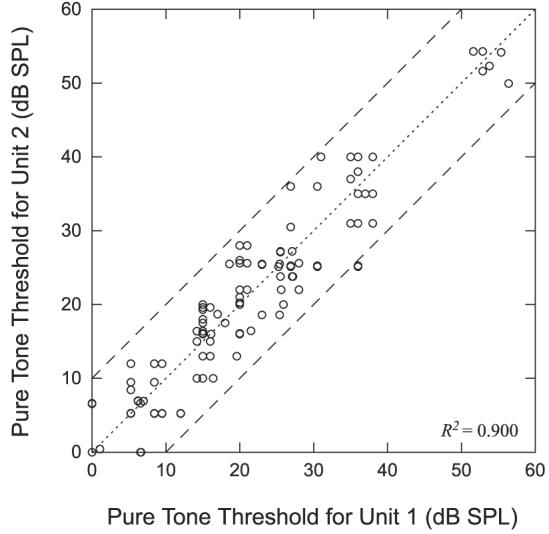
Comparison of pure-tone thresholds at the BF for neighboring neuron pairs. Dashed lines indicate threshold differences of ±10 dB. There is no significance to which unit is labeled unit 1 or unit 2.

Temporal discharge patterns

Temporal discharge patterns in response to pure-tone stimulation at CF provide an important characterization of single-unit responses throughout the auditory system. The dot raster displays in Fig. 1A suggest that neighboring units in IC can have very different discharge patterns. To quantify these observations, we classified temporal discharge patterns based on a scheme introduced for the ICC by LeBeau et al. (1996). This classification scheme includes six different peristimulus time histogram (PSTH) types: chopper, pauser, onset, on-sustained, on-chopper, and sustained.

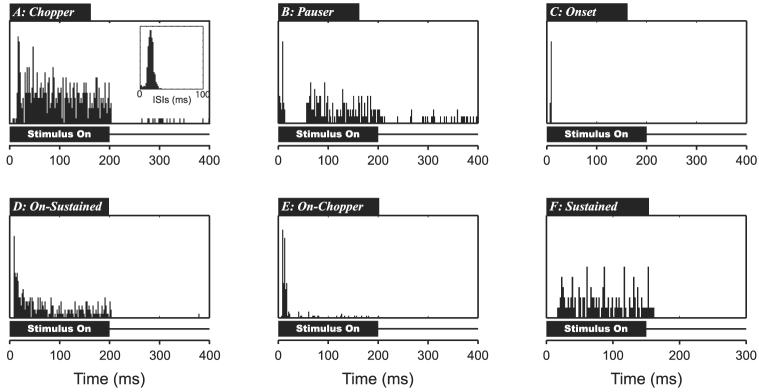
Figure 7 illustrates examples of each PSTH type. Chopper responses (Fig. 7A) have a sustained firing throughout the stimulus duration with regular intervals between successive action potentials, which sometimes result in multiples peaks in the early part of the PSTH. The first-order interspike interval (ISI) histogram (Fig. 7A, inset) shows a clear peak at the preferred chopping period (26.8 ms). To quantitatively define chopper units, we adopted a measure used by Young et al. (1988) in the cochlear nucleus based on the coefficient of variation (CV), which is the ratio of the SD of the interval distribution to the mean of the distribution. We designated any unit whose ISI distribution has a CV <0.35 as a chopper. Pauser responses (Fig. 7B) exhibit a large onset peak with a significant reduction or cessation of activity for ≤25 ms after the onset, followed by resumption of sustained firing. Onset units (Fig. 7C) exhibit a large peak of no longer than 30 ms after the stimulus onset with little or no activity after the onset response. On-sustained responses (Fig. 7D) exhibit a large onset peak followed by sustained firing. On-sustained units, similar to primary-like units in the cochlear nucleus, are distinguished from pausers by the lack of a gap after the onset and from choppers in that they have irregular ISIs. On-chopper responses (Fig. 7E) have a large onset response of no more than 30 ms with little or no activity observed in the rest of the stimulus duration. The on-chopper, however, differs from the onset response because it exhibits two or more distinct peaks within the onset response. Finally, sustained units (Fig. 7F) respond throughout the duration of the stimulus without any obvious onset component. Temporal discharge patterns that did not fall into any of these categories were labeled as “other.”

Fig. 7.

Examples of different poststimulus time histogram (PSTH) types in response to 200-ms pure tones. A: Chopper, firing with multiple peaks and/or low CV. B: Pauser, characterized by large onset peak followed by period of little or no activity then sustained firing. C: Onset, large onset peak followed by little or no activity. D: On-Sustained, large onset peak that settles into sustained firing. E: On-Chopper, large onset peak with little or no sustained activity; onset response has ≥2 peaks. F: Sustained, no significant onset peak but sustained activity throughout stimulus.

In some instances, the PSTH changed with level, although the majority of our single units exhibited a relatively stable PSTH across a wide range of levels once level was sufficiently above threshold. Among 130 single units for which we measured pure-tone responses at multiple levels, 28 (22%) units showed changes in PSTH type with level. Of these 28 units, over half (16) exhibited a transition from an onset response at lower levels to a different PSTH type at higher levels, with most of these (13/16) transitioning from onset to pauser. For the purpose of characterizing the responses with a single descriptor, we used the PSTH measured at about 25–35 dB above threshold, which was the most stable. Using this criterion, Table 2 shows the distribution of response types for the 130 single units from 36 sites for which we have characterized temporal discharge patterns. The most common response type was pauser (55/130, 42%) followed by onset (41/130, 32%).

Table 2.

Incidence of different temporal discharge patterns in the ICC as seen by LeBeau et al. (1996) and from our recordings

PSTH Type	LeBeau et al. (1996)	Current Study
Pauser	23% (16/70)	42% (55/130)
Onset	21% (15/70)	32% (41/130)
On-Sustained	20% (14/70)	8% (10/130)
Sustained	19% (13/70)	8% (11/130)
Chopper	9% (6/70)	6% (8/130)
Other	6% (4/70)	3% (4/130)
On-Chopper	3% (2/70)	1% (1/130)

Table 3 shows the frequencies of all pairwise combinations of response types between neighboring pairs. Given the prevalence of pauser and onset patterns, it is not surprising that the most common pairs are Pauser–Pauser, Onset–Onset, and Pauser–Onset. To determine whether the paired combinations differed from the expected distribution for randomly distributed unit types across recording sites, we followed a procedure similar to the one we used for response area comparisons. Keeping the number of units from each site as observed in the data, we randomly assigned a PSTH type to each unit based on the proportions of PSTH types we observed. Repeating this process 10,000 times, we obtained distributions for each entry in Table 3 and computed confidence intervals. We found that all entries except three fall within the 95% confidence interval. The three pairwise combinations with frequencies that exceed the 95% confidence interval are Onset–On-Sustained, On-Sustained–On-Sustained, and On-Sustained–Sustained. Because all three elements contain On-Sustained units, this may suggest a slight tendency for On-Sustained units to be locally segregated. Despite this exception, overall, the temporal discharge patterns appear to be randomly distributed across recording sites.

Table 3.

Frequency of pairwise combinations of temporal discharge patterns among neighboring neuron pairs

	Onset	Chopper	Onset-Chopper	Pauser	Onset-Sustained	Sustained	Other
Onset	24
Chopper	5	0
Onset-Chopper	1	1	0
Pauser	51	10	4	31
Onset-Sustained	1	3	0	8	6
Sustained	9	3	0	9	9	3
Other	4	0	0	2	0	0	1

Sensitivity to interaural time differences

Many single-unit studies of the inferior colliculus have characterized binaural interactions, particularly sensitivity to interaural time differences (ITDs), which are the most important sound localization cues for sounds containing low-frequency energy (Palmer and Kuwada 2005). Here, we consider whether ITD sensitivity is similar among neighboring neurons.

The top four panels in Fig. 8 show dot rasters in response to binaural beats at the CF for four simultaneously recorded neurons. The horizontal axis corresponds to 1.5 s of the recording and contains three cycles of the 2-Hz binaural beat. The period histogram for each unit, locked to the 500-ms beat period, is shown below each raster plot. All four units respond preferentially to a limited range of interaural phase differences (IPDs). However, the mean response IPDs (triangles) for these units differ greatly. For these four units, the mean IPDs are 0.10, −0.22, −0.03, and 0.12.

Fig. 8.

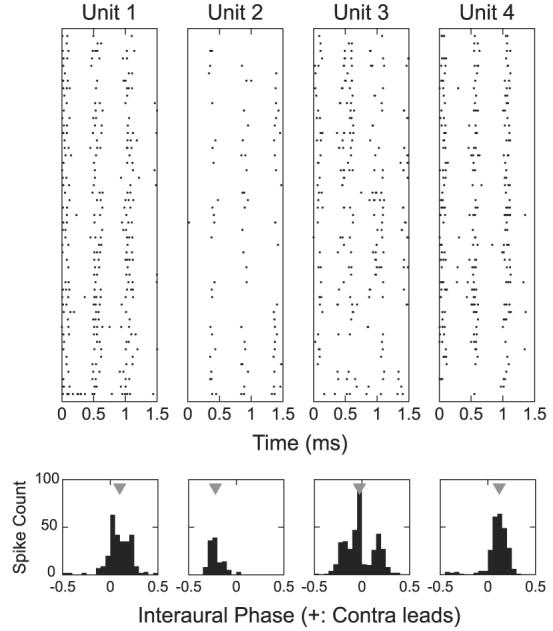
Interaural phase difference (IPD) sensitivity of neighboring neurons. Top: dot rasters for 4 simultaneously recorded neighboring neurons in response to a binaural beat stimulus at the BF (915 Hz, 50 dB SPL). Beat period is 500 ms. Bottom: period histograms computed over the beat period for each of the 4 units. Gray triangles indicate the mean interaural phase.

We recorded the responses to binaural beats at the multiunit CF at 27 sites in seven cats, yielding a total of 93 single units and 130 neighboring pairs. For every single-unit response to binaural beats, the Rayleigh test of uniformity (Fisher 1993) was used to determine whether the period histogram may arise from a uniform distribution, which would indicate no beat sensitivity. The null hypothesis of uniformity was rejected for P < 0.001. With this test, we find that 9 of 93 single units from 6 of the 27 recording sites are not beat sensitive. All six sites also contained at least one beat-sensitive unit. Therefore >20% of the sites in our sample contained at least one unit that was beat sensitive and one unit that was not.

For the 107 neighboring pairs of beat-sensitive neurons, we calculated the mean interaural phase of response (Yin and Kuwada 1983). Figure 9 shows a scatterplot of mean IPDs for each neighboring pair. We have adjusted the mean IPD of some of the units by adding or subtracting one cycle to minimize the difference between the phases for each pair. The dotted line indicates identity, whereas dashed lines indicate the boundaries beyond which mean IPDs differ by >1/4 cycle. Among these 107 pairs, 29 (27%) have mean IPDs that differ by >1/4 cycle. The correlation coefficient for these data is 0.585, which may appear significant at first sight. However, because phase is a circular variable, the interpretation of a linear correlation coefficient is tricky. To test whether the correlation is statistically significant, we randomly generated sets of 107 pairs of data points independently where the IPD values were drawn with replacement from our set of observed IPDs. As with our data, all pairs with differences >1/2 cycle were adjusted by adding or subtracting one cycle to minimize the difference between the phases for each pair, and then we computed the correlation coefficient. We repeated this for 50,000 randomly generated data sets to obtain confidence limits for the correlation coefficient under the null hypothesis of no correlation between neighboring pairs. We find that the 95% confidence interval (0.35, 0.62) for the correlation coefficient under the null hypothesis contains the observed correlation (0.585), indicating that the best IPD appears to be randomly distributed across recording sites.

Fig. 9.

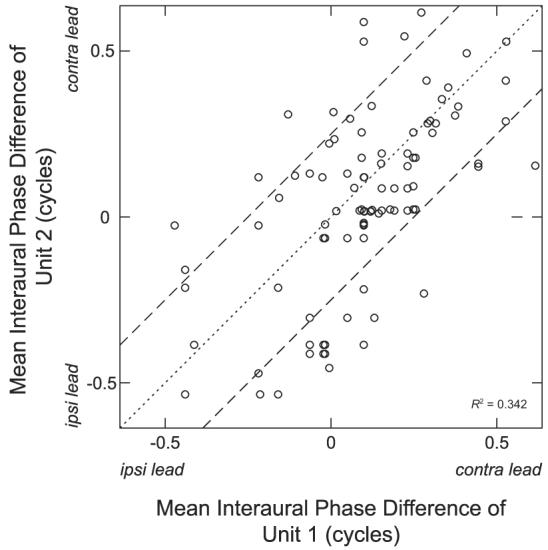
Comparison of mean IPDs for neighboring neuron pairs. There is no significance to which unit is chosen as unit 1 or unit 2. All IPDs were measured using binaural beats near the multiunit characteristic frequency (CF). Dotted line indicates identity. Dashed lines indicate IPD difference of 0.25 cycle.

For 19 single units at six sites, we were able to measure the binaural beat response for at least five frequencies around the best frequency. From these measurements, we estimated the characteristic delay (CD) and characteristic phase (CP) by fitting a weighted regression line to plots of mean response IPD as a function of frequency and testing for the linearity of regression (Yin and Kuwada 1983). Figure 10 shows phase as a function of frequency with weighted regression lines for four units (which are not from the same site). The first two (Fig. 10, A and B) pass the linearity test, whereas the last two (Fig. 10, C and D) do not and were not used for estimating CD and CP. After applying the linearity test, four of the six sites show a mix of units with linear and nonlinear phase–frequency relationships, and five of the six sites contain at least two units with linear phase–frequency relationships. From these five sites, we have 14 units and 17 neighboring pairs where both units exhibit a linear phase–frequency relationship. Figure 11, A and B shows scatterplots for CD and CP respectively for these 17 pairs. Error bars indicate 95% confidence intervals of the parameter estimates from the linear regression. The CD shows little sign of any correlation between neighboring neurons (ρ = −0.19, P = 0.43). On the other hand, the characteristic phase relationship between neighboring neuron pairs appears quite strong with a correlation coefficient of 0.84. Applying the same correlation test for circular variables used for the best-IPD comparison, we find that the 95% confidence interval for the correlation coefficient if the CPs were randomly distributed would be [0.41, 0.76], so the observed correlation (0.84) is significant at the 0.05 level.

Fig. 10.

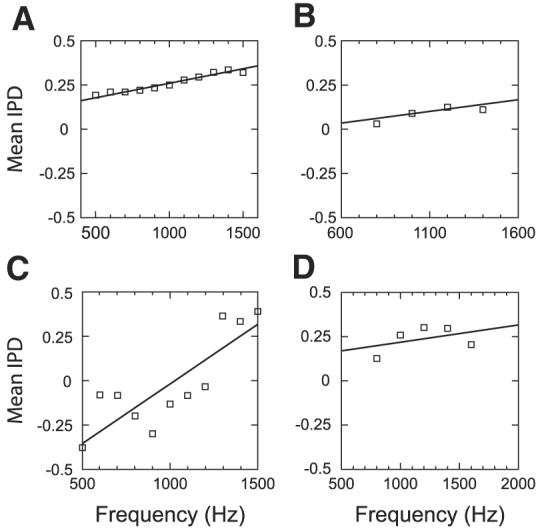
Weighted regression lines fit to plots of mean response IPD against binaural-beat frequency for 4 single units (not from the same site). Phase–frequency relationships in A and B pass the linearity test, whereas those in C and D do not.

Fig. 11.

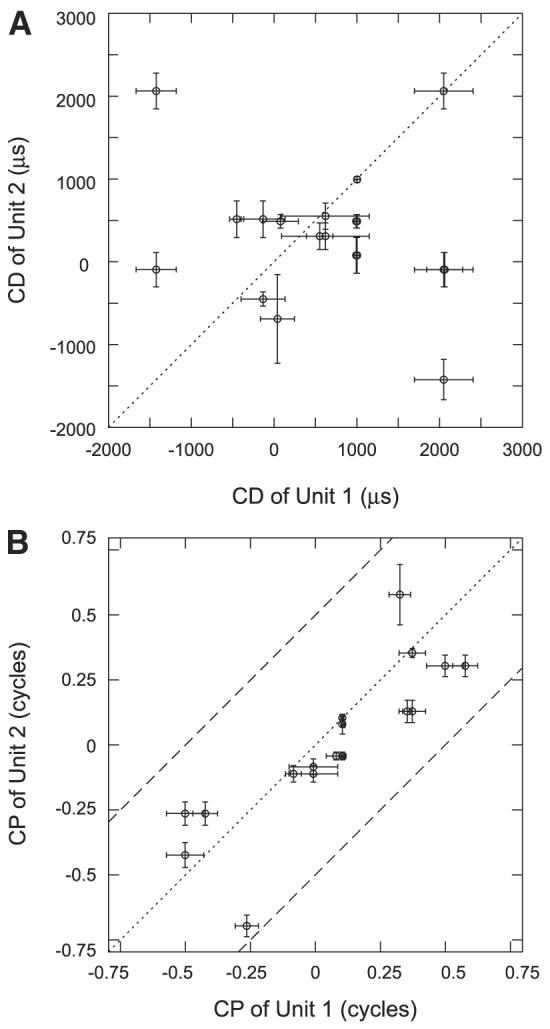
Comparisons of characteristic delay (CD, A) and characteristic phase (CP, B) between neighboring neurons. There is no significance as to which unit is labeled 1 or 2. Error bars show SEs of the estimates of CP and CD.

Effect of BF differences on other characterizations

Given our focus on similarities and differences among response properties of neighboring neurons, a natural question is whether greater spatial separation leads to greater differences in response properties. Earlier, we estimated the effective recording radius of our tetrodes to be about 100 μm. Because thicknesses of the laminae in the ICC lie between 70 and 150 μm (Malmierca et al. 2005; Oliver and Morest 1984; Rockel and Jones 1973), it is likely that our tetrodes can sometimes simultaneously record from neurons located in adjacent laminae. Because the laminae correspond to isofrequency planes, we examined whether differences in response properties between neuron pairs are affected by BF differences between the neuron pairs.

Using the tonotopic mapping data of Merzenich and Reid (1974), we estimated the rate of variation of BF with depth in the 1-kHz region of the ICC to be about 2.4 octaves/mm. Based on this estimate, we divided our neuron pairs into three groups. The first group contains those unit pairs whose BF difference is <0.17 octave; this corresponds to the 70-μm lower limit of the laminar width and contains those units that clearly lie within a single lamina. The second group contains those pairs whose BF differences lie between 0.17 and 0.36 octave; these BF differences correspond to distances between 70 and 150 μm, so we are uncertain whether the units belong to the same lamina. The last group consists of pairs whose BF differences are >0.36 octave; these differences correspond to distances of >150 μm, which is outside the estimated width of laminae in the ICC. We compared differences in response properties between these three groups of unit pairs.

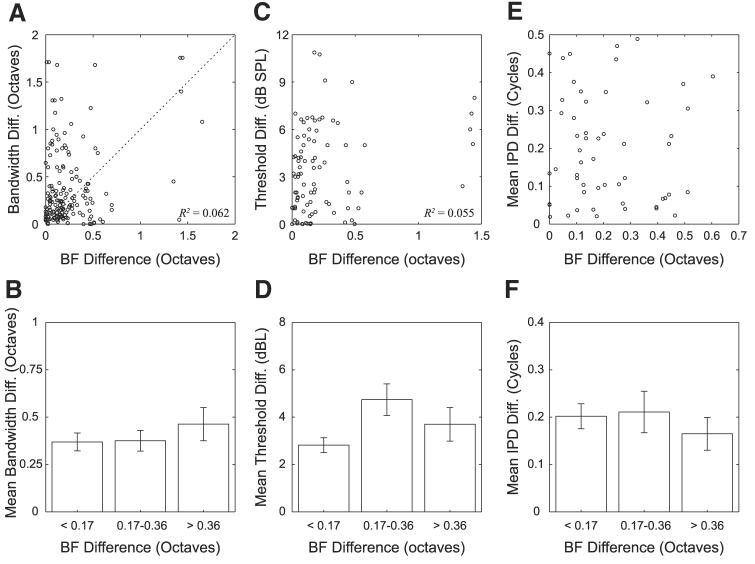
The top panels of Fig. 12 show scatterplots comparing the difference in BFs (expressed in octaves) with differences in both bandwidths (Fig. 12A) and pure-tone thresholds (Fig. 12C). Qualitatively, these figures show very little dependence on BF differences. The bottom panels show the means and SDs of bandwidth differences (Fig. 12B) and threshold differences (Fig. 12D) for each of the three groups of pairs divided by BF difference. The differences in mean values between the three groups are small compared with the error bars. This is confirmed by a one-way ANOVA, which showed no significant effect of the BF difference group on bandwidth differences [F(2,163) = 0.64, P = 0.53]. A separate ANOVA showed no significant effect of the BF difference group on threshold differences [F(2,84) = 4.22, P = 0.02].

Fig. 12.

Comparison of BF differences between neighboring neuron pairs with differences in other response properties. Top: scatterplots comparing BF differences with differences in bandwidths (A), thresholds (C), and mean response IPDs (E). Bottom: mean and SE of each variable on top for 3 groups of pairs defined on basis of BF difference.

To investigate whether units with small BF differences are more likely to have similar frequency response area types, we tabulated the number of neighboring neuron pairs with the same and different frequency response area types for each of the three BF difference groups. Table 4 shows the distribution. We used a χ²-test to determine whether the observed distribution is consistent with the null hypothesis that the proportions of similar frequency response area types are uncorrelated with BF differences. The χ²-test shows no significant effect of BF differences on differences in frequency response area types [χ²(5) = 0, P = 1.00].

Table 4.

Difference in frequency–response area (FRA) types between neighboring neuron pairs broken down into three groups defined by BF differences

	FRA Type
BF Difference	Same	Different	Number of Pairs
<0.17	20	31	51
0.17–0.36	9	14	23
>0.36	9	14	23

We also examined whether larger BF differences might be correlated with differences in types of temporal discharge patterns. Table 5 shows the differences in temporal discharge patterns for the three BF difference groups. We used a χ²-test to determine whether the observed distribution of temporal pattern differences is consistent with the null hypothesis that these differences are uncorrelated with BF differences. The χ²-test shows no significant effect of BF differences on differences in temporal discharge patterns [χ²(3) = 1.617, P = 0.53].

Table 5.

Difference in temporal discharge patterns between neighboring neuron pairs broken down into three groups defined by BF differences

	PSTH
BF Difference	Same	Different	Number of Pairs
<0.17	35	38	73
0.17–0.36	17	22	39
>0.36	11	22	33

Last, we considered the effect of BF differences on differences in ITD sensitivity. Figure 12E shows a scatterplot of differences in mean response IPD against BF differences. Qualitatively, we see very little correlation. This is confirmed by an ANOVA, which reveals no effect of BF difference groups on IPD differences [F(2,52) = 0.44, P = 0.65].

In short, we found no evidence that larger differences in BF between units in a pair correlate with a larger differences in any other response property.

Discussion

We used tetrodes to simultaneously record from neighboring ICC neurons and to compare pure-tone response characteristics of neighboring neuron pairs. Across the different response characteristics that we have investigated, we found varying degrees of similarity and difference between the pairs. Some of these results are consistent with previous studies and expectations about arrangements and response maps in the ICC; however, others suggest a complexity of organization not previously reported.

Best frequency

In general, neighboring neuron pairs have similar best frequencies, consistent with the tonotopic organization of the ICC (Merzenich and Reid 1974; Roth et al. 1978). Nevertheless, a few pairs (9/160) showed relatively large BF differences (>0.5 octave).

Some of the variance in the BFs at each recording site might be explained by the sensitivity of the BF estimate to stimulus level. We have tried to keep our rate–frequency measurements as close to the pure-tone threshold as possible; however, in some cases, BFs may have been measured at levels as high as 15 dB above threshold. Under these conditions, two units that have nearly identical CFs (as determined from an isorate tuning curve) might have slightly different BFs when one of the rate–frequency curves is measured at 10–15 dB above threshold. Neighboring neurons do not have identical pure-tone thresholds, so the rate–frequency curves are measured at different levels with respect to threshold for these units. To estimate the effect of small threshold differences among neighboring units on our BF calculations, we computed the change in BF with level for 53 units for which we had measured rate–frequency curves at more than one level. The mean rate of change of BF with level for these units was 0.013 octave/dB (range: 0–0.08 octave/dB). The mean threshold difference we observe between neighboring neuron pairs is 3 dB. Therefore we expect threshold differences to introduce an average BF difference of 0.04 octave. This is substantially less than the average BF difference (0.16 octave) between neighboring neuron pairs, suggesting that the variation in BF with level may account for some, but not all, of the observed BF differences between neighboring units.

Based on the decay of spike amplitude across tetrode recording contacts, we have estimated the effective recording radius of our tetrodes to be about 100 μm. The width of the fibrodendritic laminae in the ICC is about 70–150 μm (Malmierca et al. 2005; Oliver and Morest 1984; Rockel and Jones 1973). Therefore from a single site we may record responses from neurons in adjacent laminae and, using the estimated rate of frequency change with distance of about 2.4 octaves/mm, we would expect to see units with BF differences >0.36 octave.

Schreiner and Langner (1997) argued that, rather than being gradual, the tonotopic organization of the ICC is actually layered. They observed sudden jumps in BF of about 0.2–0.3 octave in penetrations along the tonotopic axis of the cat IC, which they interpret as resulting from the crossing of a boundary between adjacent laminae. Furthermore, they found a slow gradient of BF within each lamina, orthogonal to the main tonotopic axis. If such a layered frequency organization holds, we would expect to see a bimodal distribution of BF differences among neighboring neuron pairs depending on whether the two neurons are in the same lamina (BF difference <0.2 octave) or in adjacent laminae (BF difference >0.3 octave). Our results (Fig. 12) show no evidence for such a bimodal distribution. It is possible that the BF of the multiunit activity studied by Schreiner and Langner (1997) does not reflect the variability in the BFs of the underlying single units, or that the layered tonotopic organization is not as pronounced in the low-BF region, which we studied, than in the 3- to 5-kHz region where Schreiner and Langner (1997) show most of their data. Random errors in our BF measurements may also have smeared the bimodal distribution.

Width of frequency tuning and response area types

We found a weak, but significant, correlation between the 50% bandwidths of neighboring neurons. In contrast, using serial recordings from single units and multiunits, Schreiner and Langner (1988) reported the existence of a map of Q₁₀ in the cat ICC orthogonal to the tonotopic axis. Differences between the two studies may result in part from the use of Q₁₀versus 50% bandwidth as a measure of tuning. Q₁₀ is the ratio of the CF to the width of the isorate tuning curve measured 10 dB above the threshold at CF. Because we typically measure 50% bandwidth from rate–frequency curves within 10 dB of threshold, we may reasonably expect the 50% bandwidth to show a strong inverse correlation with Q₁₀, so that small differences in 50% bandwidths between neighboring pairs correspond to small differences in Q₁₀. Another difference may be that data from Schreiner and Langner (1988) come from higher-frequency regions of the ICC (3–12 kHz) than our data. The largest bandwidths we observe are about 2.5 octaves, with over 70% of the bandwidths being <1 octave. By contrast, Schreiner and Langner (1988) reported values as large as 8 octaves. Schreiner and Langner (1988) used multiunit data that they estimate come from two to five different units. The multiunit responses are likely to exhibit larger bandwidths than those of the single-unit responses. To address this issue, we looked at the 50% bandwidths of the unsorted multiunit responses from our tetrode recordings. The largest bandwidth was 4 octaves and almost all the bandwidths were <3 octaves, which is still considerably more narrowly tuned than the 8 octaves reported by Schreiner and Langner (1988). It is possible that we sampled only a limited region within each lamina, or that bandwidths are organized differently at low frequencies compared with high frequencies.

We also used width of tuning (and monotonicity of rate–level curves) to characterize the frequency response maps of neurons according to the classification scheme defined for the IC by Ramachandran et al. (1999). Over half of our neurons (57%) were classified as Type I, with Type V and Type O each accounting for less than a quarter of the population. These proportions are broadly similar to those reported by Ramachandran and May (2002) for units with BFs <3 kHz (22% Type V; 48% Type I; 30% Type O). Ramachandran et al. (1999) showed that the proportions of Type I and Type O units increase with BF, whereas the proportion of Type V decreases, so it is important to make cross-study comparisons for similar BF ranges.

It has been suggested that these different unit types may represent a functional segregation of ascending inputs from different brain stem auditory nuclei to the ICC (Chase and Young 2005; Davis 2002; Ramachandran and May 2002; Ramachandran et al. 1999). If so, we would expect a tendency for neighboring neurons to have the same type of frequency response map because there is considerable anatomical evidence that projections from different brain stem nuclei are at least partially segregated in ICC (Henkel and Spangler 1983; Oliver et al. 1997; Shneiderman and Henkel 1987). Contrary to this prediction, analysis of the distribution of response maps among neighboring unit pairs revealed no significant deviation from a random distribution across recording sites, suggesting a complex organization and mixing of these different functional response patterns within local regions. One caveat is that our data are from anesthetized animals, whereas the classification scheme of Ramachandran et al. (1999) was proposed for data obtained from decerebrate cats. This difference is important because unit classification in anesthetized preparations can be ambiguous due to the lack of spontaneous activity. Specifically, Ramachandran et al. (1999) partly define both Type O and Type I response areas by inhibitory effects observed in a reduction of firing rate below spontaneous activity. Additionally, the response area type of a given neuron might change when anesthesia is introduced as occurs in the dorsal cochlear nucleus (Evans and Nelson 1973). It is nevertheless somewhat reassuring that the proportions of the three response area types in our single units are similar to those observed by Ramachandran and May (2002).

The similarity in the proportion of Type O units between our study and that of Ramachandran and May (2002) may appear to conflict with the hypothesis put forth by Ramachandran et al. (1999) that Type O units receive predominant inputs from Type IV units in the dorsal cochlear nucleus (DCN) because Type IV units are rarely found under barbiturate anesthesia (Evans and Nelson 1973; Rhode and Kettner 1987). To test this hypothesis, Davis (2002) recorded from Type O neurons in IC both before and after injecting lidocaine to disable spike conduction in the dorsal acoustic stria (DAS), which carries the projections from DCN to IC. A majority of the Type O units showed greatly reduced responsiveness after lidocaine injections in DAS, consistent with the hypothesis, but a minority actually showed increased responses. It is possible that our tetrodes have a bias toward recording from this minority of Type O units, which do not seem to receive predominant inputs from DCN and may be created anew in the IC. It is also possible that Type IV units in DCN are less likely to be eliminated by our anesthesia, which is a mixture of Dial (a barbiturate) and urethane, than by pure barbiturates. Urethane has a mechanism of action different from that of barbiturates (Hara and Harris 2002). Finally, it is possible that our criteria for defining Type O units are more inclusive than those used by Ramachandran et al. (1999), although it is hard to see how our example unit in Fig. 4 could be classified as anything but a Type O. This possibility is hard to evaluate because Ramachandran et al. (1999) did not describe their classification scheme in a way that could be implemented algorithmically.

Thresholds at BF

We found that the pure-tone thresholds of neighboring unit pairs are highly correlated, with virtually all the pairs showing thresholds within 10 dB of each other. This result is consistent with the report of a threshold map in the mouse ICC (Stiebler 1986). The small differences in thresholds between neighboring unit pairs may be due in part to measurement errors. We determined threshold based on a change in average firing rate from spontaneous activity. In a few cases, the temporal discharge patterns showed visually noticeable deviation from spontaneous activity at levels below rate threshold. More significantly, the rate–level curves were measured at the CF of the multiunit activity for all units at a given site rather than at the exact CF of each single unit. Given that BF differences of as much as 0.25 octave are not uncommon among neighboring pairs, our threshold estimates could differ appreciably even if the thresholds at CF are identical. Despite these caveats, the correlation between thresholds of neighboring units was extremely high.

Temporal discharge patterns

One of the clearest differences we observed among neighboring neurons in the ICC was in the temporal discharge patterns. Onset and pauser units dominated our sample and, accordingly, the most common pairings between neighboring pairs were onset–onset, onset–pauser, and pauser–pauser. Our overall distribution of temporal discharge patterns is compared in Table 1 with the distribution seen by LeBeau et al. (1996) in the guinea pig IC. The rank orders of proportions of each discharge pattern are similar, although we encounter more pauser and onset units. This may arise from species differences, differences in regions sampled because we focused on low-frequency units, or differences in the cells sampled by the different electrodes used.

The contingency table of discharge pattern pairings (Table 3) showed no major deviation from the hypothesis that the discharge patterns are randomly distributed across recording sites. The temporal discharge patterns of IC neurons could largely replicate the temporal patterns of their predominant ascending inputs from the brain stem, or they could also reflect processing occurring at the level of the IC itself. Despite the common morphology of the disc-shaped principal cells, studies in slice preparations reveal the existence of multiple physiological classes of neurons defined by membrane channel properties, particularly K⁺ channels (Peruzzi et al. 2000; Sivaramakrishnan and Oliver 2001). The temporal discharge patterns in response to acoustic stimulation may reflect a combination of the membrane properties seen in the slice preparation as well as the patterns from the synaptic inputs (Sivaramakrishnan and Oliver 2001). If the different temporal discharge patterns arise primarily from differences in membrane properties, then our results would suggest that the different cell classes defined by membrane properties are randomly distributed within the IC. Such a result would be in sharp contrast to the cochlear nucleus, where morphology and physiological response types are closely related, and cells of the same type tend to be grouped together, with some regions containing almost pure populations of certain cell types (Rhode and Greenberg 1992).

Sensitivity to interaural time difference

ITD sensitivity in the IC is thought to be largely inherited from the sensitivity of inputs from binaural nuclei in the superior olive, principally the medial and lateral superior olives (MSO and LSO) (Ingham and McAlpine 2005). Therefore comparing ITD sensitivity for neighboring pairs gives information about the organization of these inputs.

Even though we targeted low-frequency, ITD-sensitive regions of the IC, 22% of the recording sites contained at least one single unit that was not beat sensitive. Specifically, we had a total of nine nonbeat-sensitive single units and 20 pairs containing one beat-sensitive unit and one nonbeat-sensitive unit. This suggests that, although there are regions that predominantly contain IPD sensitive units, it is not a hard rule that all cells in a particular region must be IPD sensitive. This additionally suggests that inputs from MSO may be interspersed with inputs from other sources that are not ITD sensitive, consistent with anatomical studies (Oliver 1987).

We found that mean response IPDs are not strongly correlated between neighboring neurons when stimulated with binaural beat stimuli at CF (Fig. 9). This lack of correlation in mean IPDs is consistent with the lack of any discernable correlation in the characteristic delays seen in the pairs for which we are able to measure binaural beat responses at several frequencies (Fig. 10A). The lack of a statistically significant correlation in CD may partly reflect the small sample size. However, we observed neighboring pairs with CDs separated by as much as 3.5 ms. The apparently random organization of CDs and best IPDs in IC is consistent with the failure to find a point-to-point mapping along the rostrocaudal dimension in projections from MSO to the ipsilateral IC (Oliver et al. 2003).

Although the best IPD and CD show no relationship between neighboring pairs, we did observe a significant relationship in characteristic phase (CP) (Fig. 10B). The CP is often interpreted as reflecting the mechanism of binaural processing. Specifically, CPs near 0 or 1 reflect peak-type ITD sensitivity, which is believed to arise through coincidence detectors that receive excitatory input from both ears as in the MSO (Goldberg and Brown 1969; Yin and Chan 1990); conversely, CPs near 0.5 reflect trough-type ITD sensitivity, which likely arises from neurons that receive an excitatory input from one ear and an inhibitory input from the other ear as in the LSO (Batra et al. 1997; Joris and Yin 1995). Neurons that have CPs between 0 and 0.5 may receive convergent inputs from both MSO and LSO (McAlpine et al. 1998; Yin and Kuwada 1983), or the ITD sensitivity derived from their excitatory inputs may be modified by inhibitory inputs tuned to a different ITD (Cai et al. 1998). If this interpretation of the CP is correct, the tendency of neighboring neurons to have similar CPs suggests that inputs from MSO and contralateral LSO may remain largely segregated in IC, consistent with anatomical studies (Loftus et al. 2004).

In measuring the CD and CP, we discarded units that did not have a linear phase–frequency relationship. Overall, among 19 single units at six sites (24 pairs) for which we measured responses to binaural beats at multiple frequencies, six units (7 pairs) failed to pass the linearity criterion. This result is consistent with previous reports that nearly half of ITD-sensitive units in the IC exhibit a nonlinear IPD–frequency relationship (Kuwada et al. 1987; McAlpine et al. 1998; Yin and Kuwada 1983). More significantly, the units that have a linear phase–frequency relationship do not seem to be spatially segregated from those with more complex behavior.

McAlpine et al. (1998) suggested that units with nonlinear phase–frequency relationships may result from convergence of inputs tuned to different frequencies and having different CDs. By using a second tone to suppress the response to a putative input, they were able to linearize some phase–frequency responses, although some units still exhibited a complex phase–frequency relationship with a suppressor tone. If this interpretation is correct, our results suggest that these multiple inputs do not influence all units in a specific region; we see evidence of complex phase–frequency relations alongside units with linear phase–frequency relationships.

Differences in response with spatial separation

Based on estimates of the effective recording distance of our tetrodes in IC, we have argued that it is likely that we occasionally recorded from units located in different laminae. Because units in different laminae would likely have different BFs (Schreiner and Langner 1997), we investigated whether large differences in BF, and therefore large differences in spatial separation, may reflect greater differences in response properties of neuron pairs. We found no statistically significant effect of BF difference on differences in bandwidth, threshold, response area type, temporal discharge pattern, or ITD sensitivity. In other words, the large differences in response properties we observed are as likely to exist between neurons from the same lamina as well as between neurons from adjacent laminae.

Summary

In conclusion, the most highly correlated properties among neighboring neurons were the best frequency and pure-tone threshold at BF. Bandwidths, frequency response area types, temporal discharge patterns, and ITD tuning showed much greater differences among neighboring neurons. The former involve measurements at low stimulus levels near the neurons' characteristic frequency; the latter requires measurements either away from the CF or at higher levels. One possible explanation for this dichotomy is that neighboring neurons receive similar primary inputs tuned to their common CF; however, at higher levels, additional inputs from other frequency channels may be recruited that could introduce greater variability in the responses.

This simple model of inputs to ICC cells is supported by recent studies. Snyder and Sinex (2002) studied changes in multiunit frequency tuning in the IC in response to focal lesions of the cochlea. They hypothesized that, if neurons tuned a particular frequency in the IC receive inputs that are only similarly tuned, then lesioning these frequencies in the cochlea should destroy frequency tuning of individual neurons in that frequency region of the IC. Instead, they found that focal lesions in the cochlea affect the tuning of individual neurons across a wide region along the tonotopic axis of the IC, and that the effects on the tuning curves of individual neurons are limited to a restricted band around the frequency affected by the cochlear lesion. These results suggest that IC neurons receive inputs tuned to a wide range of frequencies, each making a specific contribution to the overall tuning observed in the IC.

Malmierca et al. (2005) support this hypothesis with anatomical results on the organization of axonal projections from the cochlear nucleus in the IC. They observe both endings with large synaptic boutons and inputs with smaller boutons. The larger boutons are narrowly focused, suggesting that these may be the primary inputs defining the CF of the IC neurons; however, the smaller boutons, which are not as well focused and span a wider range than the lamina defined by the larger boutons, may contribute off-frequency inputs to neighboring laminae.

We have characterized response properties of neighboring neurons to pure-tone stimuli. We found that the responses can differ sharply at moderate to high sound levels and at frequencies away from the CF, suggesting a complex organization of inputs. Because most sounds encountered in daily tasks such as sound localization and identification are well above threshold, neighboring neurons may respond quite differently from each other during these tasks. It remains to be seen how neighboring neurons with seemingly different pure-tone response properties would respond to more complex stimuli during the performance of specific detection and processing tasks. The tetrode technique is well suited to chronic implantation (Wilson and McNaughton 1993) and could well prove helpful in such investigations.

APPENDIX

Here we describe our methods for reconstructing single-unit spike trains from tetrode recordings. Because the four recording sites of tetrodes are closely spaced (∼20 μm), action potentials originating from neurons in the vicinity of the tetrode tip typically appear on all four tetrode channels. However, because of spatial variation among the four tip locations relative to a neuron's location, the action potentials from a given neuron may have quite different amplitudes between any two tetrode channels. The low-impedance recording sites record multiunit responses, and we reconstruct the spike trains of individual neurons contributing to the multiunit responses by grouping neural events by the relationships of the action potential waveforms across the four tetrode channels. This reconstruction consists of two stages: spike detection and spike classification or “sorting.”

Spike detection

Once the tetrode recordings have been filtered, sampled at 20 kHz, and stored as described in methods, the first task is to identify the times of all candidate action potentials. For this purpose, we apply an amplitude threshold in the four-dimensional (4D) space defined by the tetrode signals. Assuming the background noise is a 4D stationary Gaussian random process, we estimate the covariance matrix for the noise and identify all points whose Mahalanobis distance r (Duda et al. 2001) exceeds a threshold of r = 4 as candidate action potentials.

Spike classification

Once we have identified a set of candidate neural events, we extract 15 samples (0.75 ms) of the waveform from each channel centered around every event time. Therefore given N events, we have four sets of N waveforms where each waveform is 15 samples long. To identify which events originate from the same neuron, we look at the four waveforms associated with each neural event and group events having similar waveform relationships across channels. We use principal component analysis to facilitate the comparison of waveforms shapes (Abeles and Goldstein 1977).

For each of the four sets of waveforms, we compute the principal components for the entire data set and the principal component weights associated with each of the waveforms. To find groups of similar events, we look at the 4D space defined by the first principal component weights in each channel. In this space, we expect events with similar waveform relationships to cluster together. To select these clusters, we look at the six two-dimensional (2D) projections of the 4D space. Figure A1 shows principal component clustering from one 2D projection; three distinct clusters are visible. From each of these projections, we manually select every distinct cluster. Taking the intersection of these clusters across all six projections gives us a final set of clusters. Figure A2 shows the six 2D projections for the same recording as in Fig. A1. The large cluster located near the origin in Fig. A1 clearly splits into two distinct clusters in the projection shown in Fig. A2, (bottom right).

Fig. A1.

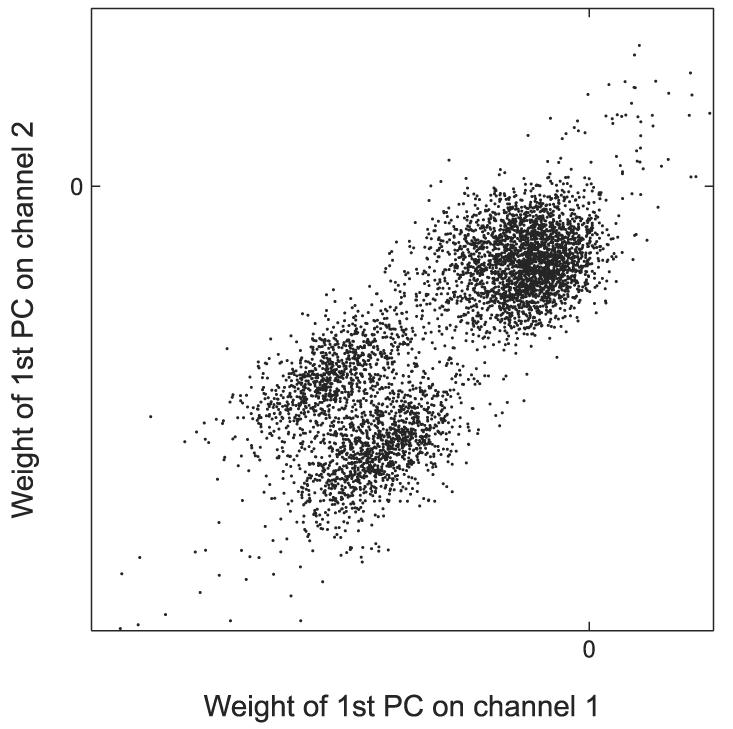
Clustering in one 2-dimensional (2D) projection of the 4-dimensional (4D) space of principal component weights. This projection reveals 3 clusters.

Fig. A2.

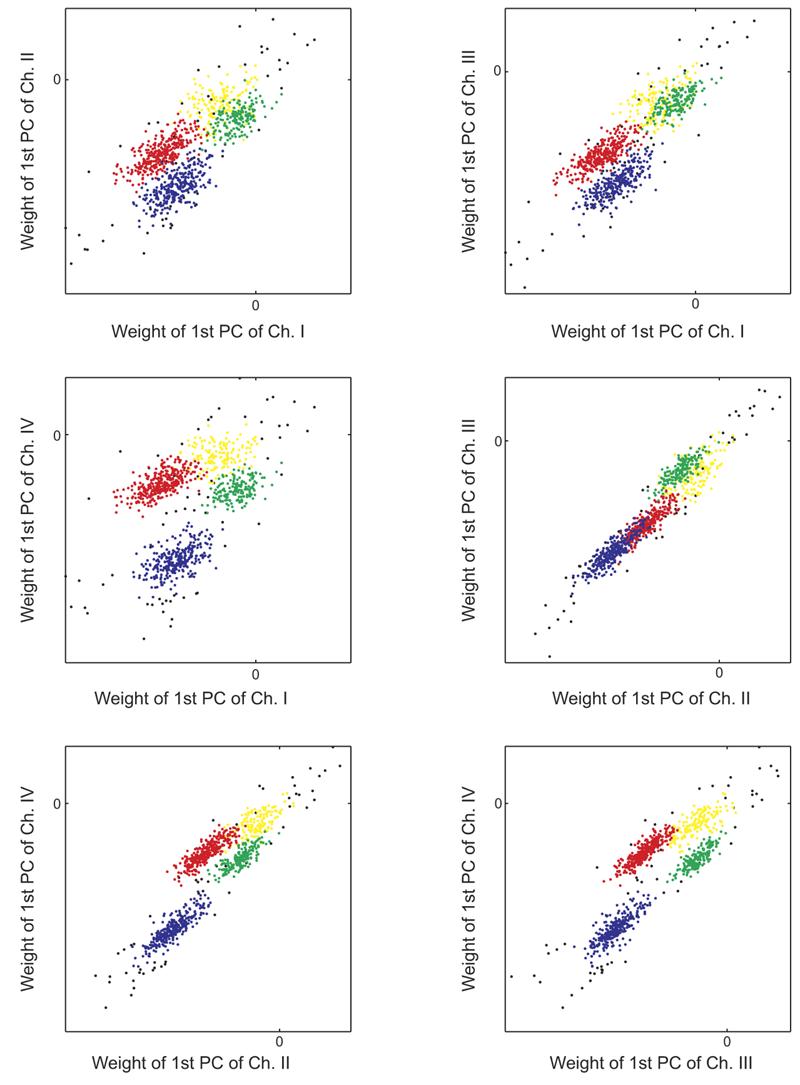
Each panel shows one 2D projection of the 4D principal component space. Clusters in blue, red, and green are well separated and presumably reflect the activity of distinct single units. Fourth cluster in yellow likely consists of false detections and low signal-to-noise ratio spikes. Black dots show outlying events that are unclassified.

To complete the spike classification, we compute the mean and covariance matrix of each hand-selected cluster in 4D space and assign each event to the closest cluster based on the Mahalanobis distance. We discard all outlying events whose Mahalanobis distance from any cluster is >4.5. On average, the proportion of such unsorted events was 6.4%, with a maximum of 11%. In addition, we also routinely discard the cluster centered nearest to the origin of the 4D space. This cluster typically contains false detections and action potentials too small to be reliably classified. Figure A2 shows an example of the sorted data in the six 2D projections, with each cluster being coded by a different color. The unsorted events are shown in black, whereas the discarded cluster near the origin is shown in yellow.

Last, we apply two different tests to make sure each cluster represents a single-unit spike train. First, we examine all the waveforms from a single channel superimposed on each other to make sure that all the spikes are similar. If there are visually different spikes, we discard the cluster. We repeat this for all four tetrode channels. Second, we analyze the ISIs to make sure we do not have spikes occurring within the refractory period, which would indicate that more than one unit is present. We discard any cluster for which >2% of the ISIs are <1 ms.