Is strong hydrogen bonding in the transition state enough to account for the observed rate acceleration in a mutant of papain?

Abstract

Nitriles are good inhibitors for the cysteine protease papain. However, a single amino acid mutation (Gln-19 → Glu-19) in the active site makes the mutant enzyme a good catalyst for nitrile hydrolysis. A theoretical approach was used to examine the differential transition state stabilization in the papain mutant relative to the wild-type enzyme. Based on this study, we concluded that strong hydrogen bonding in the transition state is responsible for the observed rate enhancement of 4 × 10⁵.

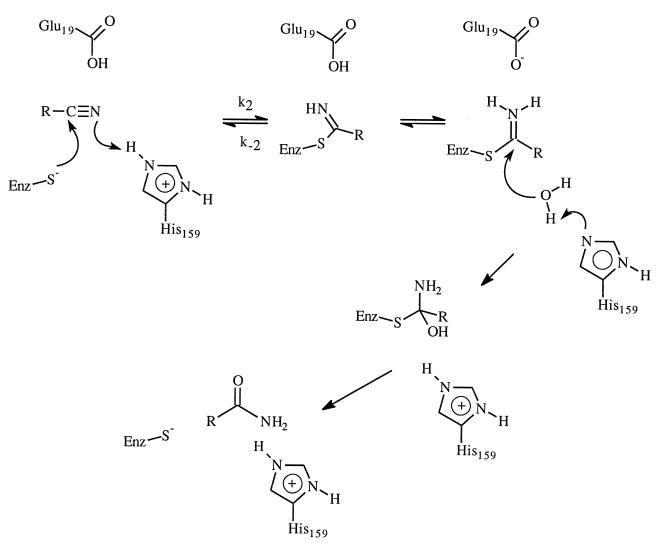
One of the promises of protein engineering is the ability to create proteins with new or modified properties (1). In the past, progress has been made in areas such as altering substrate specificity, improving thermostability, and enhancing stability and function of enzymes in nonaqueous environments (2–4). However, given our current understanding of the structure–function relationships of enzymes, conversion of enzyme functionality to a different task has not been very successful except perhaps in the generation of catalysts from catalytic antibodies (5) and new catalysts from several enzymes (1, 6, 7). One such exception is the Gln-19 → Glu-19 mutant of the cysteine protease papain reported by Menard and coworkers (7). They were able to engineer a peptide nitrile hydratase activity into the cysteine protease papain by a single mutation of an active site residue (Gln-19 → Glu-19). The k_cat for nitrile hydratase activity of the mutant enzyme at pH 5 is at least 4 × 10⁵ times the k_cat of the wild-type enzyme. This represents a remarkable example of the potential of rational enzyme redesign. Nitriles are generally resistant to hydrolysis except under drastic conditions. Although nitriles are important organic compounds, their use in synthetic transformation is limited by the drastic conditions required for hydrolysis. Enzyme-catalyzed transformations of nitriles are very attractive due to the mild conditions under which transformation reactions can be performed (8–10). Thus, it would be highly desirable to have enzymatic hydrolysis of nitrile functional groups without affecting other functional groups such as ester and acetal. The ability to engineer nitrile hydratase activity into existing enzyme is, therefore, remarkable and has great biotechnological implications. The great rate enhancement observed for the papain mutant was attributed to the ability of Glu-19 to assist acid-catalyzed hydrolysis by providing a proton (Scheme SI) (7).

Scheme I.

Papain belongs to cysteine peptidase family of enzymes; it catalyses the hydrolysis of peptide, amide, ester, and thiol ester (11). The catalytic mechanism was elucidated based on many experimental studies (11–16). The hydrolysis reaction involves the formation and breakdown of an acyl–enzyme intermediate. Like serine proteases, stabilizing the oxyanion tetrahedral intermediate by the enzyme is critical for the catalytic efficiency. The amide hydrogen of Cys-25 and the side chain amide hydrogen of Gln-19 forms two hydrogen bonds with the oxyanion of the tetrahedral intermediate in both the acylation and deacylation steps. Peptide aldehydes and nitriles are good reversible inhibitors for papain (15) and are believed to be good transition state analog owning to the formation of covalent adducts by the thiolate attack on aldehydes and nitriles. In the latter cases, a covalent thioimidate is formed; however, the enzyme is incapable of efficiently hydrolyzing this adduct and breakdown of the adduct to nitrile is favored. The above-mentioned success of engineering nitrile hydratase activity into papain further demonstrated the advance of current understanding of cysteine peptidases.

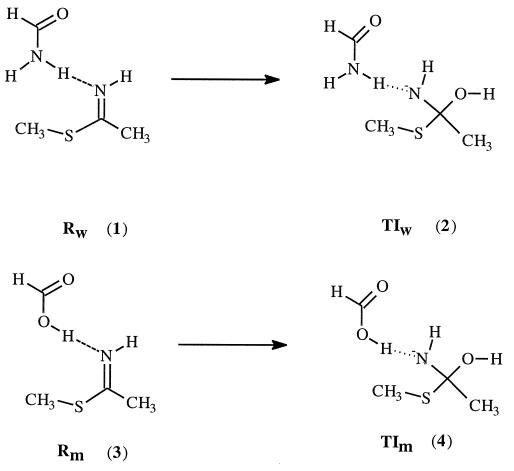
Our interest in this enzyme revolves around the question whether the strong hydrogen bonding in the transition state is enough to account for this observed large rate enhancement. To address this question, we used a quantum chemistry approach. Since the mutation introduced is a very small mutation (changing from NH₂ to OH), the structural perturbation caused by this mutation would be rather small, and the structures of the mutant enzyme and the wild-type enzyme are expected to be very similar. We examined the hydrogen bonding in the reactants (the enzyme–substrate complex) and the tetrahedral intermediate by using appropriate active site model compounds. As demonstrated before, the tetrahedral intermediate is a reasonable approximation to model the transition state of protease and lipase (16–18). Scheme SII depicts the model compounds used. Geometry optimizations were carried out at the HF/6–31+G* level of theory using the gaussian 94 program (19). Energy of each species was then calculated using the B3LYP/6–311++G** method (20, 21). To investigate the effect of dielectric medium on the calculated results, we also performed further calculations in the presence of a reaction field using the self-consistent isodensity polarized continuum model (SCI–PCM) approach (22–24) as implemented in the gaussian 94 program. The dielectric constant used was 4.

Scheme II.

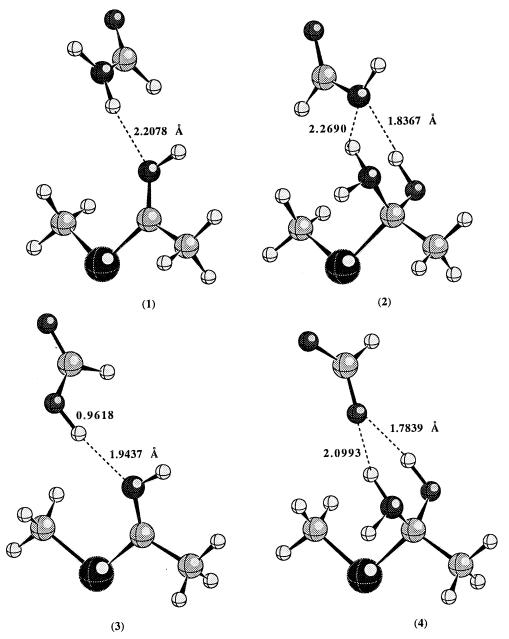
Fig. 1 displays the optimized geometry of each complex involved at the HF/6–31+G* level of theory. In the reactant, the thioimidate remains neutral; proton transfer from acid to thioimidate does not take place. However, in the tetrahedral intermediate, the negative charge is on the nitrogen, which has a much higher pK_a than either the carboxylic acid of Glu-19 or the side chain amide hydrogen of Gln-19; proton transfer occurs spontaneously. In the tetrahedral intermediates, there are two hydrogen bonds present. The lone pairs of electrons on the nitrogen and oxygen atoms of the tetrahedral intermediates are in such an orientation to facilitate the breaking of the C—S bond.

Figure 1.

The calculated geometries of hydrogen bonded complexes (1–4) at the HF/6–31+G* level of theory.

Other factors being equal, the hydrogen bonding contribution to the rate enhancement for Gln-19 → Glu-19 mutation is approximated by the difference (ΔE_4-2 − ΔE_3-1) in the calculated energy difference between 4 and 2 (ΔE_4-2) and between 3 and 1 (ΔE_3-1). The calculated differential hydrogen bonding stabilization of the transition state relative to the reactant between mutant papain and the wild-type enzyme is about 8.5 kcal/mol at the B3LYP/6–311++G** level of theory. The experimental differential transition state stabilization that corresponds to the 4 × 10⁵ rate enhancement is about 7.6 kcal/mol. To check what effect the protein environment might have on the calculated value, ab initio self-consistent reaction field calculations were performed. When the calculations were repeated in the presence of a reaction field with dielectric constant of 4, the calculated differential hydrogen bonding stabilization becomes even larger (about 13.0 kcal/mol). We realize that the experimental value corresponds to free energy difference, while the calculated value is potential energy difference. However, the entropy contribution to the free energy difference is probably negligible since the structural perturbation caused by Gln-19 → Glu-19 mutation is expected to be very small. Thus, the comparison between the experimental and calculated values is reasonable. Clearly the hydrogen bonding is strong enough to account for the observed rate enhancement. Recent studies on model compounds also suggest that differential hydrogen bonding could contribute significantly to the catalytic efficiency of enzymes (25).

We noticed the continuing debate regarding the role of strong, short hydrogen bonds in enzyme catalysis (26–28). Normally, there are unusual isotopic fractionation factors, ¹H-NMR shift, and IR frequencies associated with a short strong hydrogen bond. The existence of short strong hydrogen bonds in gas phase and solid state has been well documented (29). However, the existence of these hydrogen bonds in enzyme active sites has not been firmly established and is still a subject of continuing debate. The issue in debate is whether these hydrogen bonds can explain the enzyme catalysis. Generally it is difficult to determine the strength of an individual hydrogen bond in enzyme catalysis. Often, geometrical and/or spectroscopic criteria are used to claim the existence of these hydrogen bonds. However, as argued by Guthrie (28), is there any relation between the strength of the hydrogen bond and these unusual properties? This is still an unanswered question. Model compounds are generally used to probe the strength of hydrogen bonds in nonaqueous environment. Conflicting conclusions are often obtained. Earlier studies suggested that hydrogen bonds are not strong enough to explain the enzyme catalysis (28). However, a recent report seems to suggest that it is possible (25). As indicated above, an alternative approach is to examine the differential hydrogen bonding strength during enzyme catalysis using either experimental (such as site-directed mutagenesis) or theoretical techniques.

In summary, it is clear, based on our theoretical calculations, that the observed rate enhancement for hydrolysis of peptide nitrile by a papain mutant can be accounted for by the strong hydrogen bonding in the transition state.