Quantitative evaluation of linear and nonlinear methods characterizing interdependencies between brain signals

Abstract

Brain functional connectivity can be characterized by the temporal evolution of correlation between signals recorded from spatially-distributed regions. It is aimed at explaining how different brain areas interact within networks involved during normal (as in cognitive tasks) or pathological (as in epilepsy) situations. Numerous techniques were introduced for assessing this connectivity. Recently, some efforts were made to compare methods performances but mainly qualitatively and for a special application. In this paper, we go further and propose a comprehensive comparison of different classes of methods (linear and nonlinear regressions, phase synchronization (PS), and generalized synchronization (GS)) based on various simulation models. For this purpose, quantitative criteria are used: in addition to mean square error (MSE) under null hypothesis (independence between two signals) and mean variance (MV) computed over all values of coupling degree in each model, we introduce a new criterion for comparing performances. Results show that the performances of the compared methods are highly depending on the hypothesis regarding the underlying model for the generation of the signals. Moreover, none of them outperforms the others in all cases and the performance hierarchy is model-dependent.

I. Introduction

Brain functional connectivity is defined as the way different brain areas interact within networks involved during normal (as in cognitive tasks) or pathological (as in epilepsy) activity. It can be characterized by the temporal evolution of the cross-correlation (in a wide sense) between signals recorded from spatially-distributed regions. During the past decades, numerous techniques have been introduced for measuring this correlation. In the early fifties, the first developed methods [1] were based on the cross-correlation function and its counterpart in the frequency domain, i.e., the coherence function [2, 3] just after fast Fourier transform (FFT) algorithms were introduced [4]. Some other methods based on a similar concept but using time-varying linear models to estimate the cross-correlation were introduced later and were used to characterize the relationship between brain oscillations in the time and/or frequency domain [5, 6].

As aforementioned methods are mostly linear, recently a considerable number of studies have been dedicated to the development of nonlinear methods [7], mostly because of the nonlinear nature of mechanisms at the origin of EEG signals. A family of methods based on mutual information [8] or on nonlinear regression [9, 10] was first introduced in the EEG field. Another family is currently developing, based on works related to the study of nonlinear dynamical systems and chaos [11, 12]. The latter family can be divided into two groups: (i) phase synchronization (PS) methods [13, 14] which first estimate the instantaneous phase of each signal and then compute a quantity based on co-variation of extracted phases to determine the degree of relationship; (ii) generalized synchronization (GS) methods [15, 16] which also consist of two steps, in the first one, state space trajectories are reconstructed from scalar time series signals and in the second one, an index of similarity is computed to quantify the similarity between these trajectories.

Given the number and the variety of methods introduced for characterizing brain signal interactions and considering the diversity of situations in which these methods are applied, there is a need for identifying objectively, among available methods, those which offer the best performances.

Recently, some efforts have been made for comparing methods but mainly qualitatively [17, 18] and for particular applications [19, 20].

In this paper, we go further and propose a comprehensive comparison of the aforementioned classes of methods (linear and nonlinear regression, phase synchronization, and generalized synchronization) based on various simulation models (linearly correlated noises, nonlinear coupled oscillators and coupled neuronal population models) in which a coupling parameter can be tuned. Methods are compared according to quantitative criteria: (i) the mean square error (MSE) under null hypothesis (independence between the two analyzed signals); (ii) the mean variance (MV) computed over all values of the coupling parameter in each model; (iii) in addition to two preceding criteria, we proposed a new criterion related to the method sensitivity.

The paper is organized as follows: Section II introduces simulation models and briefly reviews some of the methods widely used in the field of EEG to estimate the degree of relationship between two signals. Results are presented in Section III and discussed in Section IV.

II. Methods

A. MODELS

In this section general features of models considered in this study are introduced. Each of them is a more or less simplified version of a general finite dimensional state-space model with three inputs and two outputs. This general model denoted by $M_{X,Y}^C$ is decomposed in two sub-systems S₁ and S₂ as illustrated in Fig. 1. To describe state evolution (on discrete time or on continuous time) of the global system two finite dimensional marginal state vectors, respectively denoted X and Y, must be introduced. In an EEG measurement perspective, X and Y macroscopically represent dynamical states of two functionally interdependent neuronal subpopulations, respectively. Each subsystem is specified by a state evolution equation:

FIG. 1.

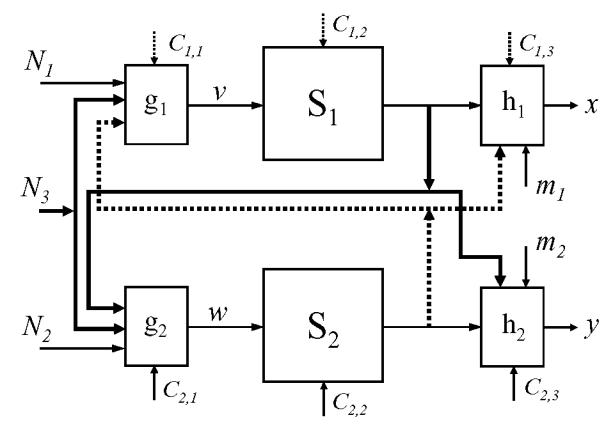
General finite dimensional state-space model (composed of two coupled sub-systems S₁ and S₂) with three inputs N1, N2, N3 and two outputs x, y. Models considered in this study correspond to simplified versions of this model. See text for details.

$$\{\begin{array}{l}X(t+\tau )=F_{\tau }^C(X(t);v(\theta ),t\le \theta \le t+\tau ),\hspace{0.17em}X(t)\in {\mathbb{R}}^m\hfill \\ Y(t+\tau )=G_{\tau }^C(Y(t);w(\theta ),t\le \theta \le t+\tau ),\hspace{0.17em}Y(t)\in {\mathbb{R}}^n\hfill \end{array}$$

where matrix C = (C_i,j) is a matrix of positive numbers interpreted in the sequel as a coupling parameter which weights the effect of “non-autonomous” terms ν and w respectively on states X and Y (Fig. 1).

The inputs N₁, N₂, and N₃ are mutually independent, zero-memory, zero-mean and unit-variance stochastic processes (white noises) which can be interpreted, in a physiological perspective, as influences from distant neural populations. Input N₃ corresponds to a possible shared afference. The scalar outputs x and y, in the same perspective, correspond to two EEG channels. If it exists, the dynamical ‘coupling’ between states X and Y is represented through a functional dependence of ν on Y and on the shared input N₃ and through the dependence of w on X and N3:

$$\{\begin{array}{l}v(t)=g_1(C_{1,1},N_1(t),N_3(t),Y(t))\hfill \\ w(t)=g_2(C_{2,1},N_2(t),N_3(t),X(t))\hfill \end{array}.$$

The models for the two output scalar signals are:

$$\{\begin{array}{l}x(t)=h_1(X(t),Y(t),m_1(t))\hfill \\ y(t)=h_2(X(t),Y(t),m_2(t))\hfill \end{array}$$

g₁, g₂, h₁ and h₂ are deterministic functions. The measurement noises, if present, are modeled by two independent random processes m₁(t) and m₂(t).

If ν does not depend on Y(.) and w does not depend on X(.) and if furthermore N₃ = 0, then the two subsystems S₁ and S₂ are disconnected. In this case and when inputs N₁ and N₂ are present, outputs x and y are statically independent if h₁ (resp. h₂) is not a function of Y (resp. X). Then equations become x(t) = h₁ (X (t)) and y(t) = h₂ (Y (t)), in absence of measurement noise.

The dashed lines in Fig. 1 correspond to the influences of S₂ on the signal x. These influences are not considered in the present study (neither a feedback influence of X on Y nor a forward influence of Y on x) except for one model (the model denoted by M₁ here after). This consideration corresponds to a causal influence directed from S₁ to S₂ and clearly does not address the most general bidirectional situation which is beyond the scope of this paper. Consequently, matrix C is the parameter which tunes the dependence of y on X. When C is null no dependence exists. Dependence between the two systems is expected to increase with C coefficients. Depending on model type, for large values of these coefficients and when N₂=0 and m₂=0, output y becomes a deterministic function of state X and of N₃.

In order to comprehensively simulate a wide range of coupled temporal dynamics we used various mathematical models as well as a physiologically-relevant computational model of EEG simulation from coupled neuronal populations. Motivations for the choice of these kinds of relationship models in the context of brain activity are discussed in a previous work [21].

Degenerated model M₁ is derived by setting C_1,1 = C_2,1 = c and by letting the other matrix coefficient equal to zero with x = X = ν and y = Y = w. This model generates two broadband signals (x, y) from the mixing of the two independent white noises (N₁, N₂) with the common noise (N₃):

$$\begin{array}{l}x=(1-c)N_1+c{N}_3\\ y=(1-c)N_2+c{N}_3\end{array}$$

where 0 ≤ c ≤ 1 is the coupling degree; for c = 0 the signals are independent and for c = 1 they are identical.

In model M₂, the general description above reduces to: ν = N₁, w = N₂, x = h₁ (X), C_2,3 = c, and y = h₂ (X,Y,c). The other coefficients of the matrix C are all equal to zero. In practice, four low-pass filtered white noises (NF₁, NF₂, NF₃, and NF₄) are combined in two ways to generate two narrowband signals around a frequency f₀. Generated signals share either a phase relationship (PR) or an amplitude relationship (AR), only:

$$\begin{array}{l}PR:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\{\begin{array}{l}x=A_{1}cos(2\pi f_{0}t+{\phi }_1)\hfill \\ y=A_{2}cos(2\pi f_{0}t+c{\phi }_1+(1-c){\phi }_2)\hfill \end{array}\\ AR:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\{\begin{array}{l}x=A_{1}cos(2\pi f_{0}t+{\phi }_1)\hfill \\ y=(c{A}_1+(1-c)A_2)cos(2\pi f_{0}t+{\phi }_2)\hfill \end{array}\end{array}$$

where $A_1=\sqrt{{NF}_1^2+{NF}_2^2},\hspace{0.17em}{A}_2=\sqrt{{NF}_3^2+{NF}_4^2},\hspace{0.17em}{\phi }_1=arctan\left(\frac{{NF}_2}{{NF}_1}\right),\hspace{0.17em}{\phi }_2=arctan\left(\frac{{NF}_4}{{NF}_3}\right)$, and 0 ≤ c ≤ 1. For c = 0, the two generated signals have independent phase and amplitude and for c = 1, they have identical phase or amplitude.

We also evaluated interdependence measures on coupled temporal dynamics obtained from two models of coupled nonlinear oscillators, namely the Rössler [22] and Hénon [23] deterministic systems. In model M₃, where two Rössler systems [24] are coupled, the driver system is

$$\begin{array}{l}\frac{{dx}_1}{dt}=-{\omega }_x{x}_2-x_3\\ \frac{{dx}_2}{dt}={\omega }_x{x}_1+0.15x_2\\ \frac{{dx}_3}{dt}=0.2+x_3(x_1-10)\end{array}$$

and the response system is

$$\begin{array}{l}\frac{{dy}_1}{dt}=-{\omega }_y{y}_2-y_3+c(x_1-y_1)\\ \frac{{dy}_2}{dt}={\omega }_y{y}_1+0.15y_2\\ \frac{{dy}_3}{dt}=0.2+y_3(y_1-10)\end{array}$$

here ω_x = 0.95, ω_y = 1.05, and c is the coupling degree. For this model, C_2,1 = c (other C_i,j are equal to zero), ν = N₁ = N₂ = N₃ = 0, w = g₂ (X, c) and the outputs are linear forms of the state vectors: x = h₁(X) = HX and y = h₂(Y) = HY.

In model M₄, we used two Hénon maps to simulate a unidirectional coupled system. The Hénon map [25] is a nonlinear deterministic system which is discrete by construction. Here, the driver system is

$$x[n+1]=1.4-x^2[n]+b_{x}x[n-1]$$

and the response system is

$$y[n+1]=1.4-(cx[n]y[n]+(1-c)y^2[n])+b_{y}y[n-1]$$

where c is a coupling degree and b_x = 0.3; to create different situations, once b_y is set to 0.3 to have two identical systems (M_4a) and once b_y is set to 0.1 to have two non-identical systems (M_4b).

For each of these two cases (identical or different systems), we added some measurement noise to verify the robustness of estimators against changes in signal-to-noise ratio (S/N), here we evaluated the noise-free case (S/N=inf.) and S/N=2. S/N was computed as the ratio of standard deviation (Std) of the signal over the Std of the noise. In this case, this model matches the general description figure with C_2,1 = c, ν = N₁ = N₂ = N₃ = 0, w = g₂(X, c), x = h₁(X) = HX + m₁, and y = h₂ (Y) = HY + m_2.

Finally, to further match dynamics encountered in real EEG signals, especially in epilepsy, we considered a physiologically-relevant computational model of EEG generation from a pair of coupled populations of neurons [26]. Each population contains two subpopulations of neurons that mutually interact via excitatory or inhibitory feedback: main pyramidal cells and local interneurons. The influence from neighboring is modeled by an excitatory input p(t) (i.e., here N₁ or N₂) that globally represents the average density of afferent action potentials (Gaussian noise). Since pyramidal cells are excitatory neurons that project their axons to other areas of the brain, the model accounts for this organization by using the average pulse density of action potentials from the main cells of a first population as an excitatory input to a second population of neurons. A connection from a given population i to a population j is characterized by parameter K^ij which represents the degree of coupling associated with this connection. Other parameters include excitatory and inhibitory gains in feedback loops as well as average number of synaptic contacts between subpopulations. Appropriate setting of parameters K^ij allows for building systems where neuronal populations can be unidirectionally and/or bidirectionally coupled. In model M5, we considered the case of two populations of neurons unidirectionally coupled (K¹² = c is varied and K²¹ stays equal to 0). This model was used to generate two kinds of signal: background (M₅(BKG)) and spiking (M₅(SPK)) EEG activity. For both cases, normalized coupling parameter was varied from 0 (independent situation) to 1 value under which temporal dynamics of signals stay unchanged. Following the general description of the simulation model we have, C_2,1 = c, ν = N₁, w = g₂ (X, c, N₂) = N₂ + cHX, N₃ = 0, x = h₁ (X) = HX and y = h₂ (Y) = HY. Here, HX and HY are linear forms of the state vectors

B. Interdependence measures and coupled systems

In experimental context, the classical approach to evaluate a functional coupling between two systems S₁ and S₂ is a two steps procedure. The first step consists in building an indicator of relationship between state vectors X and Y. The second step focuses on the estimation of the indicator as a function of the two outputs x and y observed over a sliding window of fixed length. The window length is set so that the observed signals are locally stationary. A naïve approach is to reduce this functional coupling to the value of parameter C in a given model $M_{X,Y}^C$, and hence to restrict the characterization to an estimation of this parameter. Indeed a value of C is not a definitive answer to the problem. The link, in a given model, between this value and the joint dynamical activity of coupled systems is generally not simple to establish theoretically. However, in some particular cases it can be derived analytically (see appendix A). Even in the case where we have an exact mathematical model $M_{X,Y}^C$ allowing to accurately simulate the joint evolution of state vectors X and Y, it can be hard to closely analyze the functional relationship between them. The difficulty is that a general definition of a functional relationship index $r(M_{X,Y}^C)$ from X to Y, which should be taken as an “absolute reference”, does not exist (a particular definition will generally capture only some cross-dynamical features). Furthermore a theoretical definition is not sufficient. It is also necessary to make a measurement from output signals x and y, i.e., to build an estimator r̂(x, y) of $r(M_{X,Y}^C)$. In a model identification approach a natural estimator should be $\widehat{r}(x,y)=r\left(M_{X,Y}^{\widehat{C}(x,y)}\right)$ where Ĉ (x, y) is an estimation of C in model $M_{X,Y}^C$. This model based approach is beyond the scope of this paper. Our concern here is essentially to compare various coupling functionals R (x, y) defined directly on a pair of scalar observation signals without explicit reference to an underlying model. In this study, compared functionals and corresponding estimators R̂ (x, y) are those widely used in the literature (see section II.C). These measures can be considered as descriptive methods.

C. Evaluated interdependence measures

We investigated the most widely used methods for characterizing stationary interactions between systems. These may be divided into three categories: (i) linear and nonlinear regression: Pearson correlation coefficient (R²), coherence function (CF) and nonlinear regression (h²); (ii) phase synchronization: Hilbert phase entropy (HE), Hilbert mean phase coherence (HR), wavelet phase entropy (WE) and wavelet mean phase coherence (WR); (iii) generalized synchronization: three similarity indexes (S, H, N) and synchronization likelihood (SL).

Here we review succinctly their definitions.

i) For two time series x (t) and y (t), Pearson correlation coefficient is defined in the time domain as follows [27]

$$R^2=\underset{\tau }{max}\frac{{cov}^2(x(t),y(t+\tau ))}{var(x(t))·var(y(t+\tau ))}$$

where var, cov, and τ denote respectively variance, covariance, and time shift between the two time series.

The magnitude-squared coherence function (CF) can be formulated as [28]:

$${\mid {\rho }_{xy}(f)\mid }^2=\frac{{\mid S_{xy}(f)\mid }^2}{S_{xx}(f)·S_{yy}(f)}$$

where S_xx (f) and S_yy (f) are respectively the power spectral densities of x(t) and y(t), and S_xy (f) is their cross-spectral density. It is the counterpart of R² in the frequency domain and can be interpreted as the squared modulus of a frequency-dependent complex correlation coefficient. Among nonlinear regression analysis methods, we chose a method introduced in the field of EEG analysis by Lopes da Silva and colleagues [29] and more recently evaluated in a model of coupled neuronal populations [30]. Based on the fitting of a nonlinear curve by piece-wise linear approximation [31], this method provides a nonlinear correlation coefficient referred to as h²:

$$h_{xy}^2=\underset{\tau }{max}\left(1-\frac{var(y(t+\tau )/x(t))}{var(y(t+\tau ))}\right)$$

where

$$var(y(t+\tau )/x(t))\triangleq \underset{g}{argmin}\left(E{[y(t+\tau )-g(x(t))]}^2\right)$$

where g (·) is a function which approximates the statistical relationship from x (t) to y (t).

ii) Phase synchronization estimation consists of two steps [13]. The first step is the instantaneous phase extraction of each signal and the second step is the quantification of the degree of synchronization via an appropriate index. Phase extraction can be done by different techniques. Two of them are used in this work: the Hilbert transform and the wavelet transform. Using the Hilbert transform, analytical signal associated to a real time series x (t) is derived:

$$Z_x(t)=x(t)+i\text{H}[x(\text{t})]=A_x^H(t)e^{i{\phi }_x^H(t)},$$

where H, ${\phi }_x^H$, and $A_x^H(t)$ are respectively the Hilbert transform, the phase, and the amplitude of x (t). Complex continuous wavelet transform can also be used to estimate the phase of signal [32]:

$$W_x(t)=(\psi \ast x)(t)=\int \psi (t^{\prime })x(t-t^{\prime })d{t}^{\prime }=A_x^W(t)·e^{i{\phi }_x^W(t)},$$

where ψ, ${\phi }_x^W$ and $A_x^W(t)$ are respectively a wavelet function (e.g., Morlet used here), the phase, and the amplitude of x (t). Once phase extraction is performed on the two signals under analysis, several synchronization indexes can be used to quantify phase relationship. In this study, we explored two of them both based on the shape of the probability density function (pdf) of the modulo 2π phase difference (φ = (φ_x − φ_y) mod 2π). The first index is stemmed from Shannon entropy and defined as follows [33]:

$$\rho =\frac{H_{max}-H}{H_{max}},H=-\sum _{i=1}^M{p}_{i}ln{p}_i,$$

where M is the number of bins used to obtain the pdf, p_i. is the probability of finding the phase difference φ within the i-th bin, and H_max is given by ln M. The second index which named mean phase coherence corresponds to $\mid \mathbb{E}[e^{i\phi }]\mid$ and is estimated in [34] by:

$$R=\mid \frac{1}{N}\sum _{t=0}^{N-1}{e}^{i\phi (t)}\mid$$

where N is the length of time series. Combining two ways of phase extraction and two indices for quantification of phase relationship, we obtain four different measures of interdependencies: Hilbert entropy (HE), Hilbert mean phase coherence (HR), wavelet entropy (WE), and wavelet mean phase coherence (WR).

iii) Generalized synchronization is also a two step procedure. First, a state space trajectory is reconstructed from each scalar time series using a time delay embedding method [35]. This technique makes it possible to investigate the interaction between two nonlinear dynamical systems without any knowledge about governing equations. First, for each discrete time n a delay vector corresponding to a point in the state space reconstructed from x is defined as:

$$X_n=\left(x_n,x_{n+\tau },\dots ,x_{n+(m-1)\tau }\right),n=1,\dots ,N$$

where m is the embedding dimension and τ denotes time lag. The state space of y is reconstructed in the same way. Second, synchronization is determined via a suitable measure. Four measures, all based on conditional neighborhood, are presented in this study. The principle is to quantify the proximity, in the second state space, of the points whose temporal indices are corresponding to a neighboring points in the first state space. Three of these measures S, H, and N [15], which are also sensitive to the direction of interaction, originate from this principle and use an Euclidean distance:

$$\begin{array}{c}{S}^{(k)}(X\mid Y)=\frac{1}{N}\sum _{n=1}^N\frac{R_n^{(k)}(X)}{R_n^{(k)}(X\mid Y)},\\ H^{(k)}(X\mid Y)=\frac{1}{N}\sum _{n=1}^{N}log\frac{R_n^{(N-1)}(X)}{R_n^{(k)}(X\mid Y)},\\ N^{(k)}(X\mid Y)=\frac{1}{N}\sum _{n=1}^N\frac{R_n^{(N-1)}(X)-R_n^{(k)}(X\mid Y)}{R_n^{(N-1)}(X)},\end{array}$$

where $R_n^{(k)}(X)$ is computed as

$$R_n^{(k)}(X)=\frac{1}{k}\sum _{j=1}^k{\mid X_n-X_{r_{n,j}}\mid }^2$$

and $R_n^{(k)}(X\mid Y)$ is

$$R_n^{(k)}(X\mid Y)=\frac{1}{k}\sum _{j=1}^k{\mid X_n-X_{s_{n,j}}\mid }^2$$

where |·| is the Euclidean distance; r_n,j, j = 1,…,k and s_n,j, j = 1,…,k respectively stand for the time indices of the k nearest neighbors of X_n and Y_n.

The fourth measure, referred to as the synchronization likelihood (SL) [16], is a measure of multivariate synchronization. Here we only focus on the bivariate case. The estimated probability that embedded vectors X_n are closer to each other than a distance ε is

$$P_{x,n}^{\epsilon }=\frac{1}{2(w_2-w_1)}\sum _{\begin{array}{c}j=1\\ w_1<\mid n-j\mid <w_2\end{array}}^N\theta (\epsilon -\mid X_n-X_j\mid )$$

where θ stands for Heaviside step function, w₁ is the Theiler correction and w₂ determines the length of sliding window. Letting $P_{x,n}^{\epsilon }=P_{y,n}^{\epsilon }=P_{\mathit{ref}}$ be a small arbitrary probability, the above equation for X_n and its analogous for Y_n, gives the critical distances ε_x,n and ε_y,n from which we can determine if simultaneously X_n is close to X_j and Y_n is close to Y_j, i.e., H_n,j =2 in the equation below

$$H_{n,j}=\theta ({\epsilon }_{x,n}-\mid X_n-X_j\mid )+\theta ({\epsilon }_{y,n}-\mid Y_n-Y_j\mid )$$

Synchronization likelihood at time n can be obtained by averaging over all values of j

$$S_n=\frac{1}{2P_{\mathit{ref}}(w_2-w_1)}\sum _{\begin{array}{c}j=1\\ w_1<\mid n-j\mid <w_2\end{array}}^N(H_{n,j}-1)$$

All aforementioned measures but H, are normalized between 0 and 1; the value of 0 means that the two signals are completely independent. On the opposite, the value of 1 means that the two signals are completely synchronized.

D. Comparison criteria

For all models and all values of the degree of coupling parameter, long time-series were generated in order to address some statistical properties of the computed quantities: (i) the mean square error (MSE) under null hypothesis (i.e., independence between two signals), which could be interpreted as a quadratic bias, defined by $E\left\{{\left({\widehat{\theta }}_0-{\theta }_0\right)}^2\right\}$ where E is the mathematical expectation, θ₀ = 0 and θ̂₀ is the estimation of θ₀; (ii) the mean variance (MV) computed over all values c_i, i = 1,2,…,I of the degree of coupling and defined as $\frac{1}{I}\sum _{i=1}^{I}E\left\{{\left({\widehat{\theta }}_i-E\left({\widehat{\theta }}_i\right)\right)}^2\right\}$ where I is number of coupling degree points and θ̂_i is the estimated relationship for the coupling degree c_i; (iii) in addition to two above criteria, we introduced the median of local relative sensitivity (MLRS) as a comparison criterion, it given by:

$$\mathit{MLRS}=\mathit{Median}(S_i/{\overline{\sigma }}_i),\hspace{0.17em}{S}_i=\frac{{\widehat{\theta }}_{i+1}-{\widehat{\theta }}_i}{c_{i+1}-c_i},\hspace{0.17em}{\overline{\sigma }}_i=\sqrt{\frac{{\widehat{\sigma }}_i^2+{\widehat{\sigma }}_{i+1}^2}{2}}$$

where S_i, is the increase rate of the estimated relationship and σ̄_i is the square root of the average of estimated variances associated to two adjacent values of the coupling degree. This quantity is a reflection of the sensitivity of a method with respect to the change in the coupling degree. We have also retained the median of the distribution of local relative sensitivity instead of its mean because the fluctuation in its estimation may make this distribution very skewed. Contrary to MSE and MV, higher MLRS values indicate better performances.

For all models and all values of the degree of coupling, Monte Carlo simulations were conducted to compare interdependence measures provided by methods described in section II.C. For τ parameter used in GS methods, first the mutual information as a function of positive time lag is plotted and then as described in [36] time lag τ was chosen as the abscissa value corresponding to the first minimum this curve. The embedded dimension m, in these kinds of methods, was determined from the Cao method [37]. Appendix B provides details about implementation of methods

III. Results

Mean value and variance for each coupling degree are shown in Figures 2 to 7 for all methods except H that does not provide normalized quantity. For model M₁ (Fig. 2), all quantities but N reach the value of 1 for c = 1. R² and h² methods behave very similarly because the relationship in M₁ is completely linear.

FIG. 2.

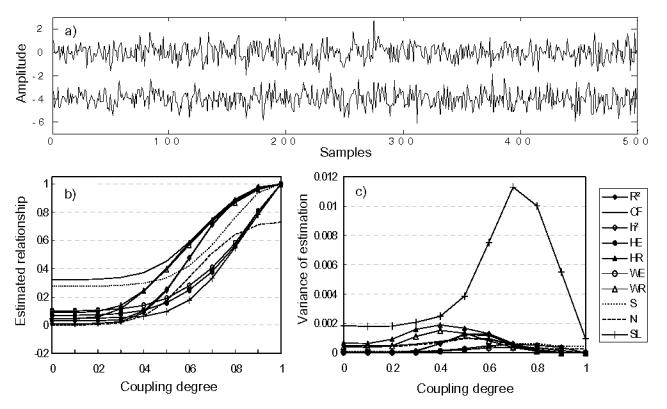
Results obtained in model M₁ (stochastic broadband signals), using Monte-Carlo simulation for Pearson correlation coefficient (R²), coherence function (CF), nonlinear regression (h²), Hilbert phase entropy (HE), Hilbert mean phase coherence (HR), wavelet phase entropy (WE) and wavelet mean phase coherence (WR), three similarity indexes (S, H, N) and synchronization likelihood (SL). (a) Simulated signals generated by model M₁, (b) estimated relationships and (c) variances of estimation.

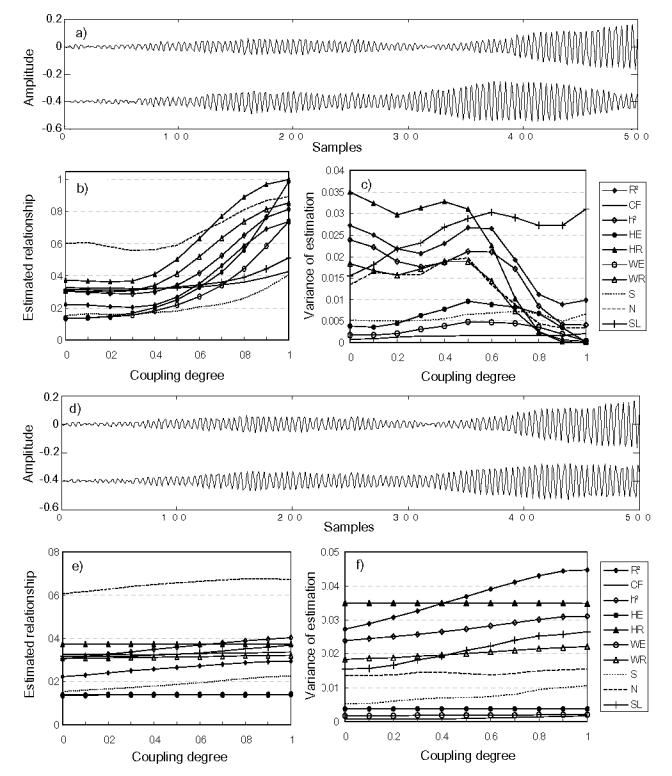
FIG. 7.

Results obtained for model M₅ (neuronal population model), (a) Simulated signals by model M₅(BKG), (b) Estimated relationship, and (c) variances of estimation, for the background activity, (d)–(f) Results for the spiking activity case.

Regarding phase synchronization measures, we observed similar method behavior as curves were found to be very close to one another. For signals generated with model M₁, SL was also found to have the maximum variance among all measures particularly for the high values of the coupling parameter, as depicted in Fig. 2 (c). This result was not expected because the variance generally falls for the high relationship degree. Finally, we also observed in M₁ that S and CF have non-negligible MSE under null hypothesis compared to other measures.

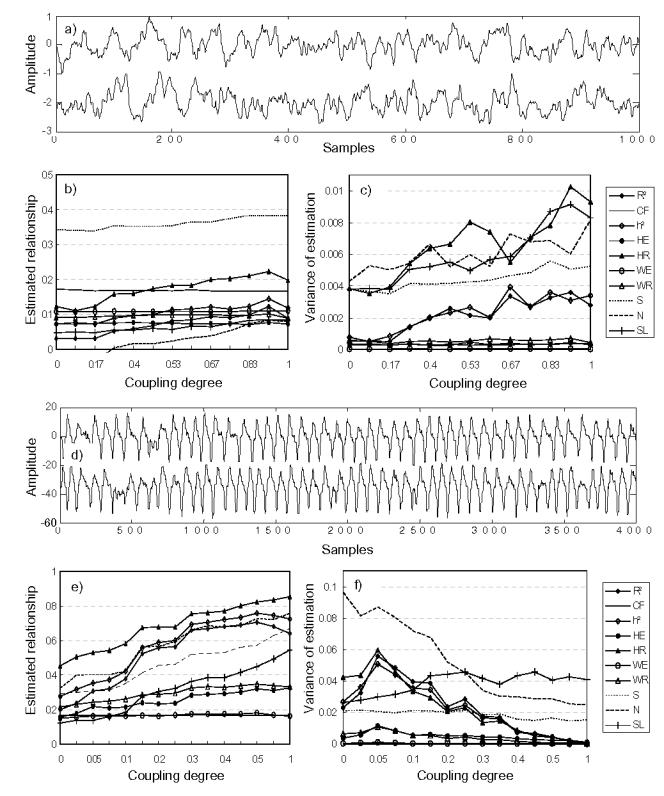
Results obtained in model M₂ are shown in Fig. 3. For phase relationship only (PR) (Fig. 3 (a)–(c)), we observed that PS methods exhibit higher performances than other methods as expected. Similarly, R² and h² methods gave rather good results. On the opposite, GS methods and coherence had lower performances. In the case of amplitude relationship only (AR) (Fig. 3 (d)–(f)), PS methods did not present any sensitivity to changes in the degree of relationship as expected from their definitions. GS, R², and h² methods provided quantities which slightly increase with increasing degree of coupling. Finally, despite what is commonly thought, CF showed only slight sensitivity to amplitude co-variation.

FIG. 3.

Results obtained in model M₂ (stochastic narrowband signals), (a) Simulated signals generated by model M₂ (PR), (b) estimated relationships, and (c) variances of estimation, for the phase relationship (PR) case, (d)–(f) Results for the amplitude relationship (AR) case.

In this study, nonlinear deterministic systems (models M₃ and M₄) were used only for comparing the performances of relationship estimators. Their properties were not investigated into details here as they have already been analyzed in many previous studies [38]. For the two coupled Rössler systems (Fig. 4), we found that SL method had both the least MSE under the null hypothesis and the best sensitivity with respect to change in the coupling degree. However, its variance stayed high compared to other methods. Qualitatively, PS methods performed better in this case. A striking result was also obtained in this case: several methods (R², h² and WE) provided quantities which first increased and then decreased for increasing low values of the coupling parameter (0<c<0.14).

FIG. 4.

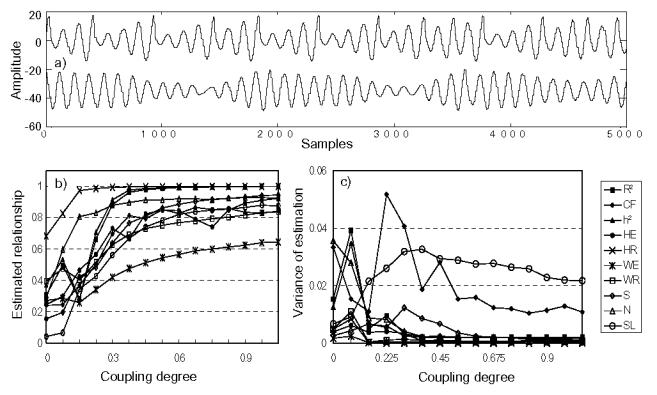
Results obtained by model M₃ (Rössler coupled systems), (a) Simulated signals, (b) estimated relationship and (c) variances of estimation.

For coupled identical Hénon systems (M_4a), N performed better than other methods (Fig. 5). For non-identical Hénon systems (M_4b), GS methods still exhibited best performances (Fig. 6). Although MSE and MV were found to be reduced with addition of measurement noise for all methods, it is worth to mention that regression methods are generally more robust against noise than other approaches, especially for non-identical coupled systems.

FIG. 5.

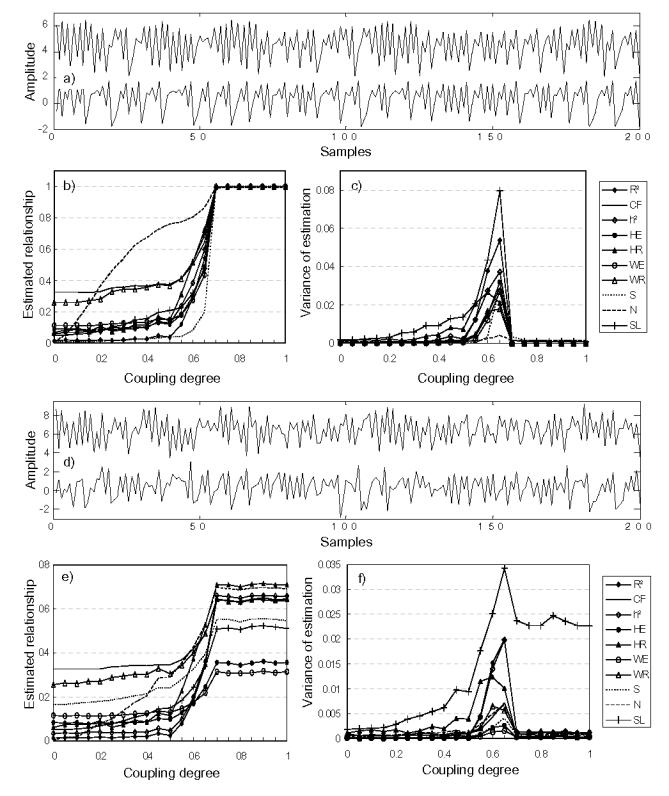
Results obtained for model M_4a (identical Hénon coupled systems), (a) Simulated signals generated by model M_4a(S/N=inf., the noise-free case), (b) estimated relationship, and (c) variances of estimation, for the noise-free case, (d)–(f) Results for the S/N(signal-to-noise ratio)=2 case.

FIG. 6.

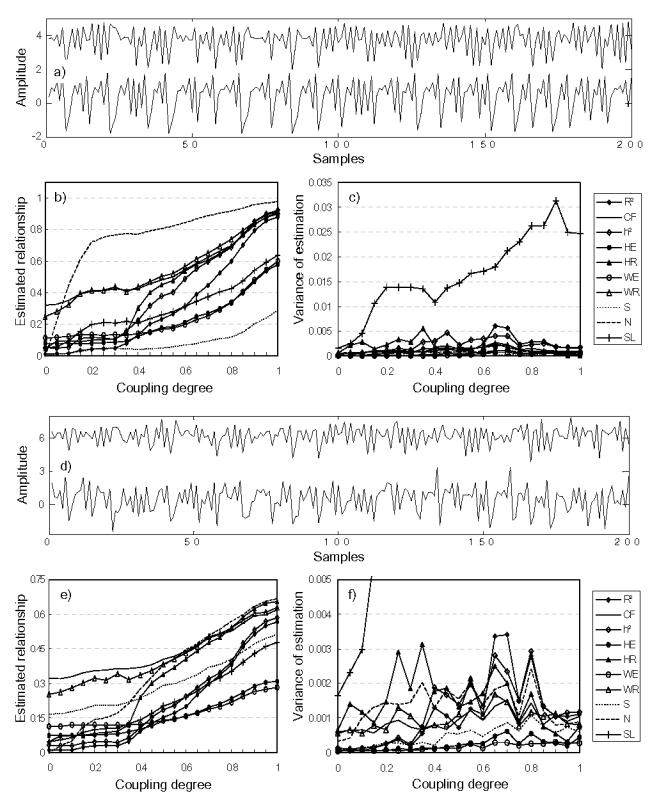
Results obtained for model M_4b (non-identical Hénon coupled systems), (a) Simulated signals generated by model M_4b(S/N=inf., the noise-free case), (b) estimated relationship, and (c) variances of estimation, for the noise-free case, (d)–(f) Results for the S/N(signal-to-noise ratio)=2 case.

For the neuronal population model (model M₅), signals were generated to reproduce normal background EEG activity (M₅(BKG)) or spiking activity (M₅(SPK)) as observed during epileptic seizures. Properties of these signals are very close to those reported in a previous attempt for comparing relationship estimators [17]. In our study, the relationship between the two modeled populations of neurons was unidirectional. As shown in [18] in the case of background activity using surrogate data techniques, the relationship between signals in this model are mainly linear. Thus we expected all methods to exhibit similar behavior in this case. Results showed that increasing the degree of coupling between neuronal populations did not lead to significant increase of computed quantities, as shown in Fig. 7 (a)–(c). In this situation CF and all the PS methods but HR do not detect any relationship; other methods detect a weak relationship. For spiking activity, results for all methods are reported in Fig. 7 (d)–(f). As an interesting result, we observed that WE and CF were almost blind to the established relation. Similarly, HE and WR only displayed small increase with increasing of degree of coupling but their variance was low. R², h², S and HR methods exhibited good sensitivity. However, MSE under null hypothesis was found to be high for HR.

Results presented in Figures 1 to 6 are summarized in tables I to III which respectively give the MSE under null hypothesis, the MV and the MRLS for all methods and simulation models (see appendix C for confidence intervals). For each studied situation, the best method is highlighted with gray color. Methods that were found to be insensitive with respect to changes in the coupling degree are denoted by symbol “*”. From these tables, we deduced that for model M₁, R² is the most appropriate estimator based on defined criteria. For model M₂, in the case of phase relationship, PS methods (especially WE) perform better than other methods. In the case of amplitude relationship, there is no consensus for the choice of a best method as all methods are more sensitive to the phase of signals than to their envelope. For the coupled Rössler systems (M₃), PS methods are more suitable. For Hénon coupled systems, S and N methods had higher performances, on average but R² was found to be more robust in the presence of added noise. For the neuronal population model, in the background activity situation, R² and h² methods detected the presence of a relationship and performed better than other methods; this tendency was also confirmed in the spiking activity situation. However, it was difficult to determine the overall best method in this second case since criteria did not lead to consensual results.

TABLE I.

MSE Values and standard deviations (see Appendix C for computation) for studied methods and models. “*” denotes methods that are nearly insensitive to changes in the coupling degree and for which this criterion is not applicable.

	M1	M2	M3	M4a (S/N=inf)	M4a (S/N=2)	M4b (S/N=inf)	M4b (S/N=2)	M5(SPK)	M5(BKG)
R2	0.12 ±0.004	76.42 ±4.55	109.55±2.55	0.28 ±0.01	0.22 ±0.01	0.26 ±0.03	0.22 ±0.02	63.17 ±3.08	1.54 ±0.09
CF	104.48 ±0.33	108.22 ±0.41	91.14 ±5.61	107.14 ±0.32	107.83 ±0.41	102.53 ±0.08	104.17 ±0.37	*	*
h2	1.10 ±0.01	117.45 ±3.78	151.14±2.38	3.43 ±0.04	1.33 ±0.01	2.73 ±0.02	1.12 ±0.02	103.79±3.25	5.99 ±0.13
HE	4.98 ±0.02	23.11 ±0.61	63.82 ±0.38	8.09 ±0.03	6.87 ±0.03	6.00 ±0.01	5.69 ±0.02	28.75 ±0.49	*
HR	3.00 ±0.11	175.56±5.52	473.07±2.23	6.26 ±0.21	4.99 ±0.13	2.74 ±0.06	3.04 ±0.10	249.31±5.28	18.99 ±0.61
WE	10.54 ±0.02	20.48 ±0.32	76.47 ±0.55	13.01 ±0.04	13.27 ±0.05	12.98 ±0.01	12.76 ±0.03	*	*
WR	8.78 ±0.1	113.65±2.97	161.50 ±1.36	68.97 ±0.32	65.79 ±0.35	62.26 ±0.05	64.22 ±0.28	53.39 ±0.88	*
S	75.51 ±0.1	28.45 ±0.82	26.59 ±0.48	0.03 ±0.0001	27.47 ±0.06	0.03 ±0.0002	27.41 ±0.07	107.53 ±2.51	120.04 ±0.104
H	0.44 ±0.28	2228.14 ±34.87	441.99 ±14.04	1.86 ±0.18	0.50 ±0.09	1.04±0.22	0.39 ±0.21	651.21±45.65	4.21 ±11.60
N	0.41 ±0.35	378.44 ±3.50	116.76±5.77	0.63±0.34	0.30±0.27	0.55 ±0.32	0.33 ±0.26	201.46 ±15.30	4.90 ±1.87
SL	4.28 ±0.33	115.25±2.58	8.50 ±2.19	4.18 ±0.33	4.47 ±0.25	3.83 ±0.23	3.74 ±0.30	41.32 ±5.58	6.16±0.88

TABLE III.

MRLS Values. “*” denotes methods that are nearly insensitive to changes in the coupling degree and for which this criterion is not applicable.

	M1	M2(PR)	M2(AR)	M3	(S/N=inf)	(S/N=2)	(S/N=inf)	M4b (S/N=2)	M5(SPK)	M5(BKG)
R2	57.6	3.94	0.41	1.38	6.99	2.93	21.31	16.85	1.3	1.2
CF	56.4	1.30	*	2.20	5.68	1.94	17.17	9.41	*	*
h2	35.6	4.06	0.36	0.98	6.91	0.56	20.62	16.42	1.8	1.1
HE	40.9	6.58	*	15.5	7.16	3.98	20.54	15.58	1.2	*
HR	42.5	6.5	*	8.87	6.79	4.77	21.45	15.38	1.2	0.7
WE	47.0	6.69	*	13.8	11.18	5.07	19.20	11.75	*	*
WR	46.6	6.76	*	8.83	10.27	4.68	20.05	14.80	1.2	*
S	31.1	2.23	0.84	6.91	19.40	10.26	31.51	18.03	0.9	0.05
H	30.3	2.84	0.77	3.53	25.07	15.28	24.56	16.59	0.7	0.9
N	29.0	3.02	0.60	3.46	25.42	15.70	12.32	17.04	0.4	0.9
SL	8.32	0.772	0.41	3.52	2.41	2.61	4.90	3.84	1.3	0.007

In order to globally compare the three groups of methods, we averaged results obtained in each simulation model for each criterion. Results are synthesized in Fig. 8. For model M₁, regression methods perform better than others as the MV is the lowest while the MRLS is the highest. For model M₂ (in the case of PR), it is evident that PS methods are the most appropriate. For model M₂ (in the case of AR), there is no consensus for the best method. For model M₃, PS methods outperform others although they are characterized by higher MSE values. For model M₄ (considering the four situations), GS methods have the lowest MSE and PS methods have the lowest MV. As far as the MRLS is concerned, these two groups of methods perform equally. Finally, for the neuronal population model M₅, regression methods outperform others in the case of normal background EEG activity. For spiking epileptic-like activity, these methods, in addition to PS methods have also higher performances than GS methods.

FIG. 8.

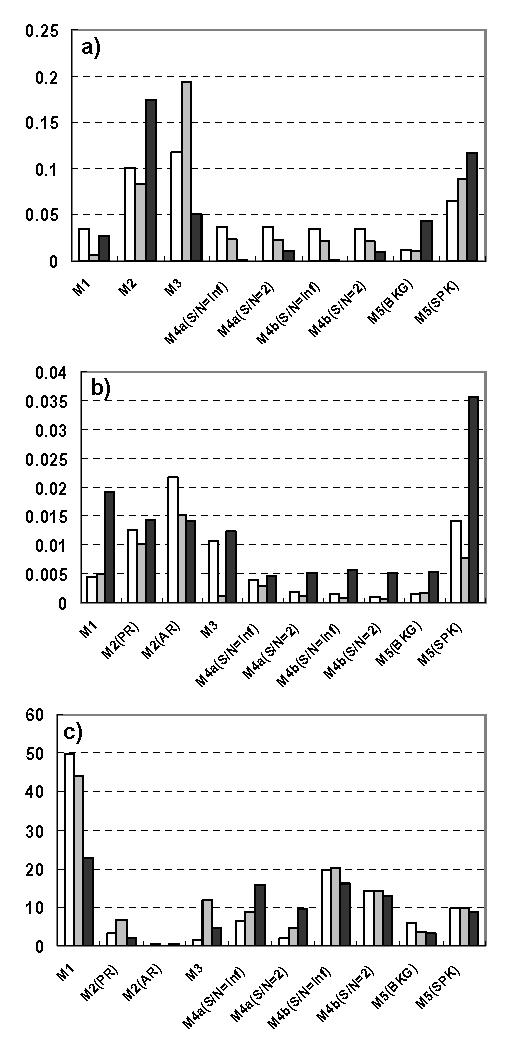
Mean values of (a) MSB, (b) MV, and (c) MRLS for the three categories of methods (white: regression methods, grey: PS methods, and black: GS methods). Note that, inversely to MSB and MV, higher MLRS values indicate better performances.

IV. Discussion and conclusions

Numerous methods have been introduced to tackle the difficult problem of characterizing the statistical relationship between EEG signals without any a priori knowledge about the nature of this relationship. This question is of great interest for understanding brain functioning in normal or abnormal conditions. Therefore, these methods play a key role as they are supposed to give important information regarding brain connectivity from electrophysiological recordings. In this work, we compared the performances of various estimators for quantifying statistical coupling between signals and characterizing interactions between brain structures. We analyzed, quantitatively and as comprehensively as possible, various kinds of estimators using different models of relationship for representing the wide range of signal dynamics encountered in brain recordings. In this regard, our study differs from that of Schiff et al. [39] who evaluated one method to characterize dynamical interdependence (based on mutual nonlinear prediction) on both simulated (coupled identical and non identical chaotic systems as those used here) and real (activity of motoneurons within a spinal cord motoneuron pool) data. It also differs from other evaluation studies which mainly focused on qualitative comparisons [17, 18] and for particular applications [19,20].

In the particular field of EEG analysis, the model of coupled neuronal populations is of particular relevance since it generates realistic EEG dynamics. In this model, for background activity (that can be considered as a broadband random signal), we found that coherence and phase synchrony methods (except HR) were not sensitive to the increase of the coupling parameter whereas regression methods (linear and nonlinear) exhibited better sensitivity. This result may be explained by the fact that the interdependence between simulated signals is not entirely determined by a phase relationship. This point is crucial since it illustrates the fact that the choice of the method used to characterize the relationship between signals is critical and may lead to possible misleading interpretation of EEG data.

In addition, as background activity can be recorded in epileptic patients during interictal periods, our results also relate to those recently published by Morman et al. [19] in the context of seizure prediction. For thirty different measures obtained from univariate and bivariate approaches, authors evaluated their ability to distinguish between the interictal period and the pre-seizure period (sensitivity and specificity of all measures were compared using receiver-operating-characteristics). In both types of approach (and consequently for bivariate methods similar to those implemented in the present study) they also found that linear methods performed equally good or even better than nonlinear methods.

Moreover, we did not report results about the capacity of some measures to characterize the direction of coupling in some models (in particular in asymmetrically coupled oscillators or neuronal populations). This issue which is beyond the scope of the present study has already been addressed in other reports. For instance, Quian Quiroga et al. [40] quantitatively tested two interdependence measures on coupled nonlinear models (similar to those used here) for their ability to determine if one the systems drives the other.

To sum up, the main findings of this study are the following: (i) some of the compared methods are insensitive to particular signal coupling; (ii) results are very dependent on signal properties (broad band versus narrow band); (iii) generally speaking, there is no universal method to deal with signal coupling, i.e., none of the studied methods performed better than the other ones in all studied situations; (iv) as R² and h² methods showed to be sensitive to all relationship models with average or good performances in all situations.

This latter point led us to conclude that it is reasonable to apply R² and h² methods as a first attempt to characterize the functional coupling in studied systems in absence of a priori information about its nature. In addition, in the case where such information is available, this study can help to choose the appropriate method among those studied here.

TABLE II.

MV Values and standard deviations. “*” denotes methods that are nearly insensitive to changes in the coupling degree and for which this criterion is not applicable.

	M1	M2(PR)	M2(AR)	M3	M4a (S/N=inf)	M4a (S/N=2)	M4b (S/N=inf)	M4b (S/N=2)	M5(SPK)	M5(BKG)
R2	3.6±0.4	200.1±3.4	366.6±5.6	65.5 ±0.6	51.7±1.9	23.9 ±0.4	17.4±0.1	10.9±0.2	215.8±2.5	21.2±0.3
CF	5.0 ±0.5	14.4 ±0.6	*	199.4 ±1.3	26.6±1.2	13.1±0.4	11.6±0.1	9.2 ±0.3	*	*
h2	3.7 ±0.4	161.0 ±2.9	274.8 ±4.0	60.4 ±0.6	42.0±1.4	23.3 ±0.4	21.5±0.1	11.8±0.3	205.0±2.4	22.6±0.3
HE	2.4 ±0.3	57.2 ±1.3	*	19.0±0.3	25.5±1.0	4.2±0.1	4.2±0.03	2.3 ±0.1	45.3 ±0.5	*
HR	8.8 ±0.6	206.7 ±3.9	*	10.1±0.3	49.6±1.4	28.0 ±0.4	17.9±0.1	14.8 ±0.3	217.5 ±2.8	65.5±0.8
WE	1.5±0.3	29.4 ±0.8	*	6.3 ±0.1	20.1±0.9	3.3±0.1	3.1±0.03	1.7±0.1	*	*
WR	6.0±0.4	118.6±2.3	*	17.6 ±0.3	23.2±1.1	14.6 ±0.4	11.4±0.1	10.1±0.3	38.4 ±0.5	*
S	2.8 ±0.5	58.1 ±1.0	74.6 ±1.1	48.8 ±0.5	20.8±1.0	6.6±0.2	1.2±0.01	4.7±0.2	183.7 ±2.0	44.1±0.9
H	9.8 ±0.9	2066.6 ±40.9	2441.3 ±42.0	3408.4 ±19.3	701.4±29.2	54.9 ±1.4	182.4 ±2.0	46.4 ±1.2	2942.3 ±25.8	70.6±15.3
N	5.0 ±0.5	120.5 ±3.1	142.3±3.5	68.4 ±0.7	12.5±0.8	1.36±0.4	8.4±0.1	13.4 ±0.3	501.1 ±5.1	60.1±5.7
SL	44.8 ±1.5	253.4 ±3.8	209.1 ±3.1	253.5 ±1.4	104.2±2.7	138.2 ±1.2	163.5 ±0.6	139.2 ±1.3	383.8±3.5	59.2±1.0

APPENDIX A: MATHEMATICAL EXPRESSION OF THREE COUPLING FUNCTIONALS

In the ideal case, analytical expression of R(x,y) as a function of coupling parameter values is required to compute MSE. Generally, this analytical expression can not obtained except for the special cases that are developed hereafter for model M₁ (R²) and model M₂ (PR).

Since the noises used in model M₁ are independent zero mean and unit variance white noises, we can compute theoretical value for R² as follows:

$$cov(x_1(t),x_2(t+\tau ))=E[x_1(t)·x_2(t+\tau )]=\{\begin{array}{ll}0\hfill & if\hspace{0.17em}\tau \ne 0\hfill \\ c^2\hfill & if\hspace{0.17em}\tau =0\hfill \end{array}$$

and

$$var(x_1(t))=var(x_2(t+\tau ))=E[x_1^2(t)]=E[x_2^2(t+\tau )]={(1-c)}^2+c^2$$

Substitution of theses two equations in R² definition leads to:

$$R^2(c)=\frac{c^4}{{\left({(1-c)}^2+c^2\right)}^2}$$

For model M₂(PR), theoretical value could be derived for the phase synchronization methods; the phase difference in this model is

$$\mathrm{\Delta }\phi =(c{\phi }_1+(1-c){\phi }_2-{\phi }_1)mod(2\pi )=(c-1){\phi }_1+(1-c){\phi }_{2}mod(2\pi )$$

As φ₁ and φ₂ are independent and uniformly distributed on [−π, π], the mean phase coherence can be derived as follows:

$$\begin{array}{c}E(e^{i\mathrm{\Delta }\phi })=E(e^{i\left[[(c-1){\phi }_1+(1-c){\phi }_2]mod2\pi \right]})=E(e^{i[(c-1){\phi }_1+(1-c){\phi }_2]})=E(e^{i(c-1){\phi }_1})E(e^{i(1-c){\phi }_2})\\ E(e^{i\alpha \phi })=\frac{1}{2\pi }{\int }_0^{2\pi }{e}^{i\alpha u}du=\frac{1}{2\pi }\frac{1}{i\alpha }(e^{i2\pi \alpha }-1)=e^{i\pi \alpha u}\frac{sin\pi \alpha }{\pi \alpha }\\ E(e^{i(c-1){\phi }_1})E(e^{i(1-c){\phi }_2})=e^{i\pi (c-1)u}\frac{sin\pi (c-1)}{\pi (c-1)}{e}^{i\pi (1-c)u}\frac{sin\pi (1-c)}{\pi (1-c)}={\left[\frac{sin\pi (1-c)}{\pi (1-c)}\right]}^2\end{array}$$

For other synchronization indexes based on Shannon entropy, theoretical value can also be derived. As the probability distributions of φ₁ and φ₂ are uniform on [−π,π], those of (c − 1)φ₁ and (1 − c)φ₂ are also uniform on the interval [−π(1 − c), π(1 − c)]. Therefore the probability density of the sum X = (c − 1)φ₁ + (1 − c)φ₂ is the convolution product of the probability densities of (c − 1)φ₁ and (1 − c)φ₂ :

$$p(x)=\{\begin{array}{l}\frac{1}{2\pi (1-c)}\left(1-\mid \frac{x}{2\pi (1-c)}\mid \right),if-2\pi (1-c)\le x\le 2\pi (1-c)\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{otherwise}\end{array}$$

Defining the phase difference modulo 2π, Δφ = Xmod2π, considering the parity of p(.) and denoting h(x) = p(x)1_ℝ⁺, the continuous probability distribution of Δφ can be written as p_Δ(x) = h(x) + h(2π − x). After partitioning [0,2π] in M intervals of length $\delta =\frac{2\pi }{M}$ we consider the associated discrete probability distribution $p_k={\int }_{k\delta }^{(k+1)\delta }{p}_{\mathrm{\Delta }}(x)dx$, k = 0,..., M − 1 and its normalized entropy $\rho =\frac{H_{max}-H}{H_{max}}$ where $H=-\sum _{i=1}^M{p}_{i}ln{p}_i$ is the standard entropy. For large M we have:

$$\begin{array}{l}H=-{\sum }_0^{M-1}P([k\delta ,(k+1)\delta ]){log}_{2}P([k\delta ,(k+1)\delta ])\\ \simeq -{\sum }_0^{M-1}{p}_{\mathrm{\Delta }}(k\delta )\delta {log}_2(p_{\mathrm{\Delta }}(k\delta )\delta )=\\ =-{\sum }_0^{M-1}{p}_{\mathrm{\Delta }}(k\delta )\delta {log}_2(p_{\mathrm{\Delta }}(k\delta ))-{log}_2(\delta ){\sum }_0^{M-1}{p}_{\mathrm{\Delta }}(k\delta )\delta \\ \simeq -{\sum }_0^{M-1}{p}_{\mathrm{\Delta }}(k\delta )\delta {log}_2(p_{\mathrm{\Delta }}(k\delta ))-{log}_2(\delta )\\ \simeq -{\int }_0^{2\pi }{p}_{\mathrm{\Delta }}(x){log}_2(p_{\mathrm{\Delta }}(x))dx-{log}_2(\delta )\\ H_{max}\simeq -{\int }_0^{2\pi }\frac{1}{2\pi }{log}_2(\frac{1}{2\pi })dx-{log}_2\left(\frac{2\pi }{M}\right)={log}_2(2\pi )-{log}_2(2\pi )+{log}_2(M)\\ \Rightarrow H_{max}={log}_2(M)\end{array}$$

APPENDIX B: IMPLEMENTATION DETAILS

To consider the non-stationary nature of EEG signals, especially in the epileptic situation, measures were estimated over a sliding window on long duration signals (20000 samples). Window length was equal to 512 samples corresponding to 2 sec of our real EEG data sampled at 256 Hz. Sliding step was set to 10 samples. These parameters were empirically chosen with respect to a compromise between the quality of estimates (the longer the window, the better) and the dynamics of changes in the relationship (when changes are abrupt, a short window is preferred).

Implementation details for all methods are sum up as follows:

For R² and h², the time shift (in samples) between two signals was allowed to vary in the range of −10 ≤ τ ≤ 10. The periodogram method (FFT blocks of 256 samples) was used to estimate the power spectra and cross-spectrum of analyzed signals. The magnitude-squared coherence (CF) was computed from these estimates and averaged over the whole frequency band. For the phase synchronization methods (HR, HE), the Hilbert transform was implemented using the FFT: the analytical signal is obtained from the inverse FFT performed on the signal spectrum S restricted to positive frequencies (i.e., by setting S(f) = 0 for f < 0). Signals were not prefiltered before application of the Hilbert transform. For the wavelet transform, we implemented a continuous wavelet method (so-called ‘Morlet wavelet’). Measures (WR, WE) built from the wavelet transform were obtained from averaging over frequency sub-bands. For the generalized synchronization methods (S, N, H, SL), state space reconstruction parameters details (i.e., time lag τ and embedding dimension d) for all models are summarized in Table IV. In addition, for these methods, the Theiler correction was chosen equal to time lag τ to prevent the information redundancy in used data.

TABLE IV.

State space reconstruction parameters used in computing the interdependencies by generalized synchronization methods

	M1	M2 (PR, AR)	M3	M4(a,b) (S/N=inf)	M4(a,b) (S/N=2)	M5(SPK)	M5(BKG)
τ	1	1	32	1	1	20	20
d	10	10	4	5	10	10	10

APPENDIX C: CONFIDENCE INTERVALS ON MEASURED VALUES

Given c_i value, we assume that the estimations $T_k^i={\widehat{R}}_L\left(x_k^i,y_k^i\right)$, k = 1,..., N are random variables that obey the same probability distribution as the random variable $a_i^2{\sum }_1^{K_i}{u}_k^2=a_i^2{\chi }_{K_i}^2$ where a_i is a scaling parameter and where the u_k are K_i mutually independent and identically distributed (index i stipulate the dependence on parameter c_i) Gaussian random variables, with zero mean and unit variance. The ${\chi }_{K_i}^2$ term corresponds to a χ² law with K_i degrees of freedom. Indeed, the χ² approximation was found to approximate histograms computed from simulated $T_k^i$ better than Gaussian distribution.

Classical derivations from Gaussian moments properties give the following relationship:

$E(T_k^i)=K_i{a}_i^2$ and $\mathit{VAR}(T_k^i)=2K_i{a}_i^4$. Hence, the two parameters $a_i^2$ and K_i can be estimated by application of the moments estimation method which leads to formulas ${\widehat{a}}_i^2=\frac{S_i}{2{\widehat{\theta }}_i}$ and ${\widehat{K}}_i=\frac{{\widehat{\theta }}_i^2}{2S_i}$ where $S_i=\frac{1}{N-1}\sum _{k=1}^N{(T_k^i-{\widehat{\theta }}_i)}^2$ is the unbiased estimated variance of $T_k^i$ and ${\widehat{\theta }}_i=\frac{1}{N}\sum _{k=1}^N{T}_k^i$ its estimated mean.

Considering furthermore the random variables $S_i=\frac{1}{N-1}\sum _{k=1}^N{(T_k^i-{\widehat{\theta }}_i)}^2,\hspace{0.17em}S=\frac{1}{M}\sum _{i=0}^{M-1}{S}_i$, and $M{Q}_0=\frac{1}{N}\sum _{k=1}^N{(T_k^0)}^2$, the problem is to quantify roughly their statistical dispersions. Although the pdf of $T_k^i$ are not Gaussian, those of θ̂_i, S_i, and MQ_i can reasonably be modeled as Gaussian (central limit effect). Consequently, approximations of corresponding standard deviations allow characterization of dispersions.

• Variance of θ̂_i

$$\mathit{VAR}({\widehat{\theta }}_i)=\frac{1}{N}\sum _{k=1}^N\mathit{VAR}(T_k^i)\simeq \frac{S_i}{N}$$

• Variances of S_i, and S

$$\begin{array}{c}\mathit{VAR}(S_i)=\frac{1}{{(N-1)}^2}{\sum }_{k=1}^N\mathit{VAR}({(T_k^i-{\widehat{\theta }}_i)}^2)\simeq \frac{1}{{(N-1)}^2}{\sum }_{k=1}^N\mathit{VAR}({(T_k^i)}^2)\\ \mathit{VAR}(S)=\mathit{VAR}(\frac{1}{M}{\sum }_{i=0}^{M-1}{S}_i)=\frac{1}{M^2}{\sum }_{i=0}^{M-1}\mathit{VAR}(S_i)\end{array}$$

• Variance of MQ₀

$$\mathit{VAR}(M{Q}_0)=\mathit{VAR}(\frac{1}{N}{\sum }_{k=1}^N{(T_k^0)}^2)=\frac{1}{N}{\sum }_{k=1}^N\mathit{VAR}({(T_k^0)}^2)$$

Finally, the variance $\mathit{VAR}({(T_k^i)}^2)=E({(T_k^i)}^4)-{(E({(T_k^i)}^2))}^2$ is computed as follows.

Let ${\mu }_m^{\prime }=E(T^m)$ and μ_m = E((T − E(T))^m) be moments of order m in the case where the mean of random variable T is zero and none zero, respectively.

As $T_k^i$ is assumed to be a ${\chi }_K^2$ random variable, we can write (Stuart et al. [41]) that μ₂ = 2K_i, μ₃ = 8K_i, and μ₄ = 12K_i (K_i + 4). From formulas (Stuart et al. [41], page 542) ${\mu }_2^{\prime }={\mu }^2+{\mu }_1^{\prime 2},\hspace{0.17em}{\mu }_4^{\prime }={\mu }_4+4{\mu }_3{\mu }_1^{\prime }+6{\mu }_2{\mu }_1^{\prime 2}+{\mu }_1^{\prime 4}$, we get the results:

$${\mu }_2^{\prime }=2K_i+K_i^2,$$

$${\mu }_4^{\prime }=48K_i+44K_i^2+12K_i^3+K_i^4$$

which lead to

$$\mathit{VAR}(T^2)={\mu }_4^{\prime }-{\mu }_2^{\prime 2}=48K_i+40K_i^2+16K_i^3$$

and finally to

$$\mathit{VAR}({(T_k^i)}^2)=a^8(48K_i+40K_i^2+16K_i^3)\simeq {({\widehat{a}}^2)}^4(48\widehat{K}+40{\widehat{K}}_i^2+16{\widehat{K}}_i^3)$$