Mechanics of Single Cells: Rheology, Time Dependence, and Fluctuations

Abstract

The results of mechanical measurements on single cultured epithelial cells using both magnetic twisting cytometry (MTC) and laser tracking microrheology (LTM) are described. Our unique approach uses laser deflection for high-performance tracking of cell-adhered magnetic beads either in response to an oscillatory magnetic torque (MTC) or due to random Brownian or ATP-dependent forces (LTM). This approach is well suited for accurately determining the rheology of single cells, the study of temporal and cell-to-cell variations in the MTC signal amplitude, and assessing the statistical character of the tracers' random motion in detail. The temporal variation of the MTC rocking amplitude is surprisingly large and manifests as a frequency-independent multiplicative factor having a 1/f spectrum in living cells, which disappears upon ATP depletion. In the epithelial cells we study, random bead position fluctuations are Gaussian to the limits of detection both in the Brownian and ATP-dependent cases, unlike earlier studies on other cell types.

INTRODUCTION

It has become increasingly clear that cells are mechanically sophisticated, integrating mechanosensory inputs about their surroundings and using them during motility as well as differentiation and proliferation decisions (1–3). In parallel with this growing awareness, a number of methods have been developed for studying cells' mechanical properties, such as their shear modulus (4–9) and their intrinsic fluctuations (10,11) due to Brownian motion, cell trafficking, and remodeling. Cells' frequency-dependent shear modulus, or rheology, is typically inferred either from deformation in response to an applied force or torque (4–7) (active microrheology) or from the Brownian motion of embedded or attached tracer particles (8,9) (passive microrheology). Although the results of the many different methods can give wildly different estimates of cells' overall mechanical stiffness, they consistently indicate that cells are predominantly elastic at low frequencies having a shear modulus with a power-law form, G*(ω) ∼ ω^β, with small exponents β < 0.25.

Recently, we have shown (9) that many of the published cell rheology data correspond to one of two master curves, which we argued are associated with two spatially separate intracellular compartments, one deep in the cell interior and the other closer to the outer membrane. Earlier studies have also found evidence for a compartmented response (8,12,13). Not surprisingly, methods based on small external probes generally report the outer compartment response. Of these, one of the most widely used is magnetic twisting cytometry (MTC), based on rocking an external, integrin-adhered magnetic bead using an oscillatory magnetic field as sketched in Fig 1. Although the results of MTC correlate well with intracellular measurements in some cases (9), the specific rheological contributions, if any, of cell substructures such as focal adhesions and stress fiber networks (14) remain undetermined.

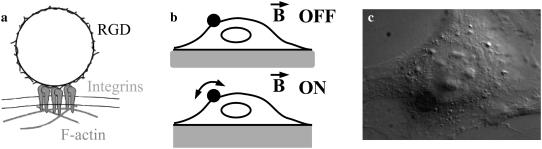
FIGURE 1.

Principles of the experiment. (a) The probe consists of a magnetic particle coated with an RGD peptide specifically recognized by integrin transmembrane proteins, which physically connect the bead to the intracellular cytoskeleton. (b) Two types of experiments can be performed: passive experiments with the magnetic field off in which the fluctuating motion of the bead is tracked; or active experiments in which the magnetic field is on and the bead displacement in response to the oscillating torque applied to the cytoskeleton is measured. (c) Differential interference contrast micrograph of a cell with a bead attached on its top. The microscope is focused on the cell nucleus and the bead, pointed to by a dashed circle, thus appears out of focus.

In this article, we describe a unique instrument and experimental approach that combines MTC with a laser deflection method for high-speed and precision particle tracking. At a given magnetic torque, different magnetic particles show a broad distribution of rocking amplitudes, displaying both large cell-to-cell variations and time dependence. Other implementations of MTC compensate for these variations by ensemble averaging—either over whole dishes via magnetometry measurements (13,15) or by pooling cell-scale video microscopy data (7). Here, we instead rock the bead at two different frequencies simultaneously, allowing us to more precisely determine the frequency dependence and temporal variations of the rocking amplitude in single beads and cells.

The rheology inferred from single-cell MTC is rigorously in agreement with the corresponding ensemble average, indicating that the observed power-law behavior is not due to, nor significantly affected by, the averaging process. The same instrument is well suited to the study of the adhered beads' passive random motion (8), termed laser tracking microrheology (LTM). As we noted in an earlier publication (9), for many beads LTM and MTC report different rheology, suggesting that bead rocking and bead translation can probe the cytoskeleton at different depths and thus report the response of different networks. Here we analyze the statistical properties of the random bead translations during a brief time interval (or lag time). In contrast to other reports (11) and some expectations for glassy materials (16), we find that bead translations are Gaussian at all lag times.

The temporal fluctuations of the MTC signal provide insights into the bead cell contact. When a bead is rocked simultaneously at two frequencies, the variations in rocking amplitude at both frequencies are found to be highly correlated and directly proportional. That is, the mechanism responsible for the variations gives rise to a frequency-independent, multiplicative random function of time, whose temporal correlations are described by a 1/f power spectrum in living cells. When cells are ATP depleted, the mean rocking amplitude does not change significantly, but the temporal variations become much smaller. In general, changes in cells' actual stiffness (e.g., due to contractile agonists or filament depolymerization) are coupled to changes in the frequency dependence of cells' rheology (7). In contrast, the bead cell contact area or adhesion strength are usually considered to contribute a frequency-independent prefactor to the rocking amplitude. As a result, although actual cell stiffness fluctuations cannot be ruled out as an explanation for the rocking amplitude variations, they are more likely due to ATP-dependent remodeling processes at the bead/cell interface.

MATERIALS AND METHODS

Cell culture and ATP depletion

TC7 African green monkey kidney epithelial cells (gift of D. E. Discher) were primarily used in this study, but representative measurements on NIH-3T3 fibroblasts and F9 carcinoma cells (ATCC) show similar results. Following standard protocols, cells were cultured in plastic culture flasks using Dulbeco's modified Eagle's medium (DMEM; Invitrogen, Carlsbad, CA) supplemented with 10% bovine calf serum (Hyclone, Logan, UT) and antibiotic cocktail (50 mg/ml gentamicin (Sigma-Aldrich, St. Louis, MO) and penicillin-streptomycin (75 I.U./ml and 75 μg/ml) solution (ATCC)) at 37°C and 5% CO₂. For viewing, cells were transferred to petri dishes with collagen I coated glass coverslip (BD BioCoat; BD Biosciences, San Jose, CA) bottoms. All cell types were incubated overnight before experiments. For ATP-depletion experiments, cells were incubated with serum-free medium for at least 2 h before incubation with the ATP depletion medium: DMEM with added (final concentration) 50 mM 2-D-deoxyglucose and 0.05% NaN₃ (Alfa Aesar, Ward Hill, MA). Immunofluorescence has been used to characterize the structure of the cytoskeleton for both control cells and ATP-depleted cells as described previously (17). Magnetic beads bearing an arginine-glycine-aspartate (RGD) peptide are attached before ATP depletion.

Microscopy and cell incubation

Cells were imaged with an inverted microscope (DM-IRB, Leica, Deerfield, IL) using a 100×, numerical aperture (NA) = 1.4, oil immersion objective, mounted on a 3′ × 6′ pneumatic vibration isolation table (65–753, TMC, Peabody, MA). To enable the use of an oil immersion condenser, a custom top dish was constructed which supports an upper coverslip submerged in the medium ∼0.5 mm above the bottom coverslip. During data collection the condenser and objective are heated to 37°C and the atmosphere above the medium reservoir maintained at 5% CO₂ with a continuous humidified gas stream (Fig. 2 b). Cell viability for up to 8 h on the microscope was confirmed under these conditions.

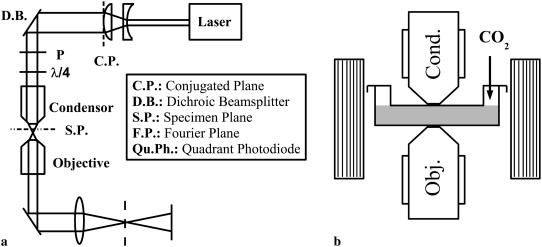
FIGURE 2.

(a) An ultralow noise laser is mounted onto the microscope stage to illuminate the bead. A polarizer and a λ/4 wave plate combination are used as an optical isolator before a telescope which increases the beam size to 2 mm. A dichroic beamsplitter is used to align the beam with the microscope optical axis. The dark-field image is then formed on a quadrant photodiode by placing a beamstop in the Fourier plane of the third lens (dashed line). (b) The magnetic field is generated by two rectangular Helmholtz coils mounted on the microscope stage and placed on each side of the dish. A stream of 5% CO₂ humidified air maintains a constant pH. The high NA objective and condenser are heated by a metallic ring, thus warming the sample by simple contact.

Magnetic bead preparation and attachment

We use a protocol described by Wang et al. (15): 0.25 mg of 4.5 μm ferromagnetic beads (Spherotech, Libertyville, IL) are washed once in 1% bovine serum albumin to avoid sticking of the beads to the tube walls and three times in a carbonate buffer (pH = 9.2) before incubation with a 50 μg/ml RGD peptide (AC-G(dR)GDSPASSKG₄S(dR)-NH₂; Integra Life Sciences, Plainsboro, NJ) solution in 1 ml carbonate buffer, overnight at 4°C. Beads were then washed several times in first phosphate-buffered saline and finally in DMEM before incubation with cells. Cells were first incubated in a serum-free medium for 45 min. Beads were allowed to adhere to cells for 30 min, after which unadhered or weakly adhered beads were removed by gentle washing. Control measurements without added RGD peptide show negligible binding, confirming specific binding, presumably to the cells' α₅β₁ integrin receptors and thus to the intracellular cytoskeleton (15). Moreover, the number of adhered beads increased with both increasing peptide concentration or incubation time during bead preparation. All measurements on non-ATP-depleted cells are performed within 3 h of initial bead/cell contact, and after 8 h a significant fraction of beads are phagocytosed.

Laser deflection bead tracking system

Our laser deflection particle tracking system consists of three parts: 1), an illumination system that launches a Gaussian laser beam into our microscope's oil immersion condenser lens (which in turn focuses it onto the magnetic bead), 2), an imaging system that magnifies and spatially filters the same laser beam after it emerges from the microscope's side camera port and directs it onto a quadrant photodiode, and 3), an amplifier, filter, and digitizer to record the photodiodes' analog signals. The optical arrangement is sketched in Fig. 2 a.

To minimize sensitivity to vibration, the laser illumination system is miniaturized and all components mounted in a rigid 30 mm cage assembly (Thor Labs, Newton, NJ), which in turn is attached robustly to the microscope's body casting. The illumination beam is provided by a 5 mW, red emitting (λ = 638 nm) collimated circularized laser diode module (31-0144-000, Coherent, Auburn, CA). Unlike other laser diode modules that use temperature control for stability, this compact unit achieves ultralow intensity noise and mode-hop-free performance by virtue of an internal high-frequency (>1 GHz) modulation sweeping the diode over several adjacent longitudinal modes. The beam diameter is first doubled to 2 mm using a Galilean beam expander having a plano-concave lens (f₁ = −15 mm) and a plano-convex lens (f₂ = 30 mm) and then sent into the microscope condenser by reflection off a 45° dichroic beamsplitter (Chroma Technologies, Rockingham, VT), which transmits light from the built-in halogen illuminator (enabling rapid changeover to conventional phase-contrast visualization of the bead/cell).

The beam expander is focused such that a diffraction-limited beam waist is formed at a plane conjugate to the microscope illuminator's field diaphragm, ensuring that the beam will be collimated in the specimen plane. This degree of beam expansion causes the Gaussian illumination spot in the specimen plane to be ∼10 μm in diameter, illuminating our 4.5-μm diameter bead with an almost uniform plane wave. The illuminating beam is aligned with the condenser's optical axis using the two rotational degrees of freedom on the dichroic and body translating the entire laser/expander/dichroic cage assembly in the two horizontal directions to provide the other two degrees of freedom. An optical isolator consisting of a polarizer and a λ/4 wave plate reduces possible contributions from back reflections into the diode and is rotated to modulate illumination power.

After passing through the microscope's condenser, specimen, and objective, a lens (f₃ = 75 mm) placed in the optical path relays the image located just outside the side camera port to a quadrant photodiode while providing an additional magnification of 4.5×, ensuring that the 2 mm diameter bead image occupies ∼2/3 of the quadrant photodiode diameter. Conventional laser deflection systems place the photodiode at a conjugate back aperture to detect the angular deflection of the light transmitted through the bead. In contrast, we place the detector in an image plane, which allows us to track the “shadow” of our ∼50% opacity magnetite-loaded beads. This achieves a highly reproducible and easy to calibrate tracking sensitivity (i.e., volts per nanometer of deflection). To improve the signal/noise performance and vibration rejection, we invert the contrast of the bead shadow using a Fourier filter at the L₃ Fourier plane. The Fourier mask consists of a thin (100 μm) opaque fiber blocking the (transformed) illumination beam, effectively converting the system to a dark-field imaging system. The quadrant photodiode is mounted on an XY mount to allow both fine centering of the bead image onto the quadrant and the calibration of tracking sensitivity.

We use a commercial quandrant photodiode circuit as a low-noise preamplifier (OSI Optoelectronics, Newbury Park, CA). The right to left (RL) and top to bottom (TB) output current are filtered through a single pole, low-pass filter (RC = 10 μs) and further amplified to match the ±5 V input range of our a multichannel high-speed digitizer (763507-02, National Instruments, Austin, TX) mounted in a standard PC computer. The system optical magnification and analog gain are set so the range of linear response of voltage to displacement (∼±0.5 μm) spans the entire digitizer input voltage range (±5 V). Together with the “position” signals, the total photocurrent is recorded for use in computing the voltage to displacement calibration. Ultimately, the tracking precision of this system is limited to ∼0.2 nm at a 100 kHz bandwidth by photon statistics (shot noise) in the detected laser light. Although precision or bandwidth could be improved by a higher illumination power, we limited the power absorbed by our opaque beads to <1/3 mW to minimize heating effects (computed to be ∼1°C/mW). Moreover, at this laser power the optical forces on the bead may be safely neglected.

Bead polarization and rocking field

After the beads are attached to cells, they are magnetized vertically (perpendicular to the dish bottom) using a ∼1000 Gauss vertical magnetic field lasting ∼200 μs. This field pulse is generated off microscope by the discharge of a large capacitor through a coil and high-current rectifier. Once on the microscope, beads are selected visually to confirm that they are attached to the apical surface of the cell with a finite contact area, not to a thin process such as the lamellipodium, and that they have not been internalized. A small subset of beads shows very large rocking amplitudes in response to even weak magnetic fields, suggesting that they are weakly bound; these are excluded.

Beads are rocked with an oscillatory horizontal magnetic field generated by two symmetrically located rectangular coils ∼4 cm from the field of view, sized to allow a petri dish to fit within them (Fig. 2 b). The use of a horizontal rocking magnetic field rather than a vertical field (as used in literature reports) reduces the maximum strength of the resulting magnetic field to ∼10 Gauss (peak to zero, thermally limited). The horizontal field, however, significantly reduces the frequency-dependent amplitude and phase shifts caused by eddy currents in the conducting body of the microscope objective and condenser. A custom-built precision voltage to current amplifier converts signals from a function generator to a maximum current of 100 mA, with a compliance voltage sufficient to drive the coils' reactive impedance up to 1000 Hz. Measurements using a small pickup coil at the sample location and a precision analog integrator show no detectable shift in amplitude or phase over the entire frequency range used from 0.1 to 1000 Hz.

In the literature (7,18), the absolute value of the bead torque is computed by calibrating the bead's magnetic moment, enabling the estimation of the absolute cell stiffness if the bead-cytoskeleton contact geometry is known and assumed to be mechanically homogeneous. In our study, we do not try to estimate the magnitude of the magnetic torque, the cells' absolute stiffness, or the validity of the assumptions required to make such a calculation, being concerned instead with relative changes in stiffness versus frequency and time. However, both the magnetic moment of our commercially available beads and the applied torque are likely at least several times smaller than those used in other studies (7).

Data logging and analysis

The digitizer simultaneously digitizes five signals at 50 kHz: the RL and TB differential quadrant output photocurrents, the total photodiode current, and the two sinusoidal references used to drive the rocking magnetic field. The calibration factor necessary to convert the RL and TB signals to micron displacements is obtained by starting with a motionless bead centered on the diode and by measuring the lateral displacement of the quadrant photodiode necessary to create a variation of 8 V in the RL signal. This quadrant displacement is then simply related to the corresponding bead displacement using the optical magnification (450×).

During MTC (active) experiments, a two-channel LabView digital lock-in is used to compute, in real time, the amplitude and phase of the rocking displacement at ω and 3ω for both driving frequencies. The lock-in allows the user to select a low-pass filter type and its time constant; we used a simple boxcar convolution filter of the heterodyned displacement signal. The times varying amplitude and phase at both frequencies are logged to disk at 10 Hz. The second harmonic signal is monitored to check for linear response. Specifically, we expect the amplitude of the second harmonic signal (3ω) to be no larger than 1% of that of the fundamental (ω), which was the case for all measurements reported here. We study the temporal variations of the rocking amplitude by computing the Fourier power spectral density of the varying amplitude signal. The low-pass filter used in our digital lock-in introduces a sinc²(ω) modulation to the computed spectra; we divide out its contribution before repartitioning the spectrum logarithmically to smooth it.

During LTM (passive, rocking field off) experiments, the five signals are logged to disk at 50 kHz. Offline, the RL and TB signals are converted to displacement and used to compute the time-averaged mean-square displacement (MSD) of the bead. To maximize the range of timescales probed, we typically record two files, one at 50 kHz sampling rate for 30 s and the other at 500 Hz sampling rate for 10 min.

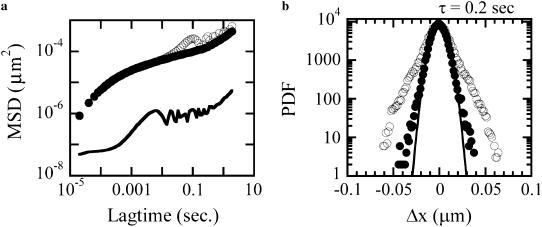
The contributions from noise and vibration may be characterized by tracking an immobilized bead, as shown in Fig. 3 a. At the shortest lag times, the MSD has a roughly constant value of 6 × 10⁻⁸ μm², corresponding to the shot-noise-limited tracking precision of 0.2 nm in one dimension. At longer lag times the effects of vibrations dominate; from a few milliseconds to a second, their root mean-squared amplitude is typically ∼1 nm but varies from day to day. Although most tracer MSDs were above this noise and vibration floor, in cases where there was a vibration contribution to the MSD, it could be removed using narrow-band notch filters (Fig. 3 a). Typically, filters removing 1–3 narrowband (<1 Hz) signals in the 5–200 Hz range are adequate. This filtering is also important for examining the probability distribution function (PDF) for bead displacements; vibration can cause the distribution at some lag times to be artificially non-Gaussian (Fig. 3 b). As in the literature (11,16), the degree of non-Gaussianity can be assessed by the use of a non-Gaussian parameter, 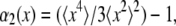where 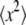and 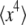are the second and fourth moments of the probability distribution of random, zero-mean variables x.

FIGURE 3.

(a) MSD versus lagtime τ for respectively unfiltered (○) and filtered (•) fluctuations of the bead position and for a bead stuck onto the coverslips (line), which gives the noise level on the determination of the position. (b) PDF of bead displacements at the lag time τ = 0.2 s from a trajectory before digital filtering (○) and after filtering (•) with a band-reject filter at f = 5 Hz.

Mean-square displacements are computed from the (optionally filtered) trajectory and converted to complex moduli using a modified version (19) of the method described in Mason (20). Briefly, we employ a generalized Stokes-Einstein relation (GSER):

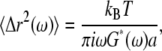(1)

where k_B is the Boltzmann's constant, T is the absolute temperature, a is the sphere radius, and 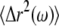is the unilateral Fourier transform of the three-dimensional MSD (20). Although our approximate numerical method minimizes the effects of truncation errors, we do not report rheology computed within a half decade of our extremal frequency limits. Since Eq. 1 was derived for an embedded spherical particle rather than one adhered with a finite contact area, the inferred shear moduli are likely systematically underestimated but should have the correct frequency dependence. As with the MTC analysis, our focus here is on the frequency dependence of the rheology, rather than absolute stiffness values.

RESULTS AND DISCUSSION

Two-frequency MTC findings

The rocking amplitude of externally adhered beads in response to a fixed amplitude and frequency sinusoidal torque shows large temporal variations (Fig. 4 a). These are presumably due to time-dependent changes in the cytoskeletal segment being probed (remodeling), changes in the bead-cell contact area, or both. Unlike anecdotal reports by other researchers, we searched for and did not find a systematic trend in the time dependence, e.g., a systematically stiffening or softening of the inferred response. For this reason, we will assume that the time dependence is due to spontaneous changes in the cell, rather than a specific response to our very small amplitude (<1% strain) deformation.

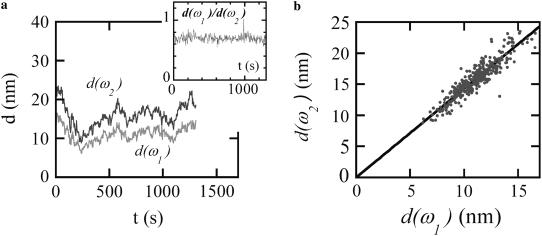
FIGURE 4.

(a) Time-dependent variations of the rocking amplitudes d(ω₁) and d(ω₂) measured simultaneously at two different frequencies in response to a double sinusoidal driving torque: ω₁ = 1.3 Hz, ω₂ = 63 Hz with constant amplitudes Γ(ω₁) and Γ(ω₂). The rocking amplitudes are determined from a digital lock-in having a bandwidth of 0.1 Hz. Inset: Variations of the ratio d(ω₁)/d(ω₂). (b) The two rocking amplitudes are strongly correlated and appear to be proportional.

In general, the bead rocking amplitude at a given frequency d(ω) is expected to satisfy |G(ω)| = A Γ(ω)/d(ω), where |G(ω)| is the magnitude of the dynamic shear modulus at ω, the rocking frequency, Γ(ω) is the amplitude of the applied magnetic torque, and A is a geometrical constant depending on the cell/bead contact area, which is generally considered to be frequency independent (18). For this reason, if the frequency dependence of the inferred |G(ω)| changed with time, it would provide evidence for changes to the physical shear modulus, whereas if the frequency dependence was time invariant, the variations in rocking amplitude could just as well be explained by changes to the bead-cell contact geometry. In practice, the time-dependent variations in the rocking amplitudes measured simultaneously at two different frequencies, d(ω₁) and d(ω₂), are strongly correlated (Fig. 4 b). Moreover, the varying amplitudes are strictly proportional, implying that the frequency dependence of the inferred shear modulus (but not necessarily its overall amplitude) is time invariant.

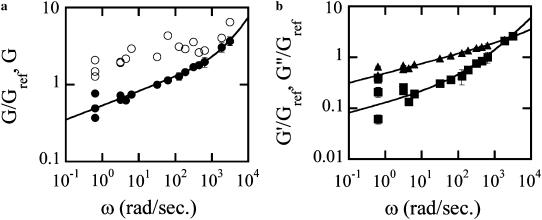
To compute the frequency-dependent shear modulus using an active experiment, the rocking frequency must be varied over a wide range. When rocking at a single frequency, temporal variations in the rocking amplitude cause stiffness estimates made at different times to vary wildly, contributing a large amount of variance to the inferred rheology as illustrated in Fig. 5 a. We can essentially eliminate this problem by using one of the lock-in channels for a fixed frequency reference while sweeping the other channel over a wide range. Since the time-dependent variations were shown to be proportional at all frequencies, we can plot the ratio G/G_ref of the swept frequency to the reference frequency to render a clearer picture of the shear modulus' frequency dependence (Fig. 5 a).

FIGURE 5.

(a) Elastic complex modulus as a function of frequency as measured by applying an oscillating torque for, respectively, unnormalized (○) and normalized (•) modulus. (b) Real and imaginary part of the complex modulus: G′and G″ the elastic and loss modulii obtained using G/G_ref and the phase shift between the applied torque and the deformation. Lines are best fits using Eq. 1. Reference frequency ω_ref = 30 rad/s.

The normalized, G/G_ref frequency dependence is much smoother and can be fit with

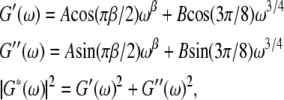(2)

with β typically in the range 0.1–0.3, as previously described (17) and in agreement with population-averaged measurements of Fabry et al. (7). Using the phase shift measured for the sweeping frequency, we can directly obtain the real and imaginary part of the complex modulus: G′(ω) = G/G_ref cos(φ), G″(ω) = G/G_ref sin(φ), as plotted in Fig. 5 b. The weak power-law in ω^β is related to the stress relaxation in the network as a whole. Although its origin is still unknown, such a form implies there is no characteristic time in the system but rather a broad distribution of relaxation times. The ω^3/4 power-law dominates the high-frequency behavior and has been associated (21) with similar behavior in semiflexible polymers due to transverse filament fluctuations. It remains unclear whether the stiffness at low and high frequencies is due to the same physical structure.

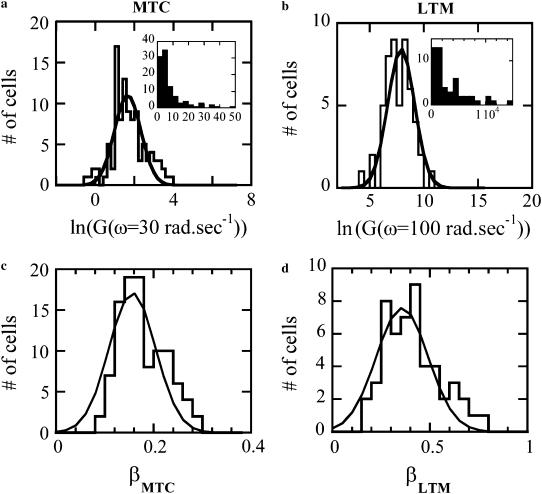
Rather than determining the frequency-dependent rheology by sweeping the frequency, the rheology exponent β can be inferred from the phase shift between the torque and the rocking displacement. At frequencies where the frequency dependence can be approximated by a single power-law, the phase shift φ and exponent β are proportional: 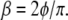To study the cell-to-cell variation in apparent cell stiffness and rheology exponent, we measured the rocking amplitude and phase shift at a fixed frequency, ω = 30 rad/s for N = 103 cells. The amplitude histogram is in agreement with a lognormal distribution as shown in Fig. 6 a (that is, a histogram of the logarithms of the amplitudes is well fit by a Gaussian). In the inset, the linear amplitude histogram is reported for comparison. It remains unclear to what extent the broad variance of amplitudes is the result of actual cell-to-cell variations in stiffness or differences in bead cell contacts. Two-point microrheology measurements of cells show much smaller variance (9). This latter method reports the deep cellular interior rather than the cortical region probed by MTC. In Fig. 6 c, the statistical distribution of power-law exponents is shown, together with the best fit Gaussian with a mean value β = 0.16 and standard deviation σ = 0.05. This standard deviation is likely due in part to instrumental noise and in part to actual cell-to-cell variations; the standard deviation from fitting frequency sweep measurements is ∼0.03, whereas phase measurements averaged over 30 min yield a standard deviation of ∼0.02.

FIGURE 6.

Distribution of, respectively, the amplitude logarithm (a and b) and exponents (c and d) measured with active experiments (a and c), N = 103 and the passive fluctuations (b and d). N = 52. Distributions are fit by a Gaussian. Insets of a and b are the corresponding histograms of modulus amplitude.

Although the weak power-law rheology we observe is broadly consistent with that seen in nearly all other cell rheology studies, it should be noted that the specific rheology exponent we observe (β = 0.16) and its sensitivity to pharmacological interventions differ significantly from published results (7). Indeed, it has been shown that the results of MTC experiments are highly sensitive to bead preparation and chemistry (22). This is consistent with the idea that MTC beads can be coupled to one or more intracellular structures (e.g., actin cortex, stress fibers, intermediate filaments), each of which may have their own distinct rheological response. Because of this sensitivity to bead preparation, ligand type, and surface density, however, it is not clear to what extent our MTC findings are generalizable. As we reported in a previous publication (9), the close correspondence of our MTC findings with published intracellular results (8) combined with our bead-labeling controls (see Materials and Methods) suggest that our MTC approach consistently reports intracellular rheology in the cortical region. A major difference between findings is that our results appear largely insensitive to myosin inhibition (17), whereas other MTC measurements are strongly affected by contractile agonists or myosin perturbation (23). A simple explanation for this discrepancy would be that our tracers do not recruit contractile stress fibers to the contact region (consistent with immunostaining results, not shown, and literature results using similar bead labeling (13)), whereas other particle preparations do (24). These differences in stress fiber recruitment may be due to RGD density or particle surface texture; clearly more experiments are needed.

Spectral analysis of rocking amplitude variations

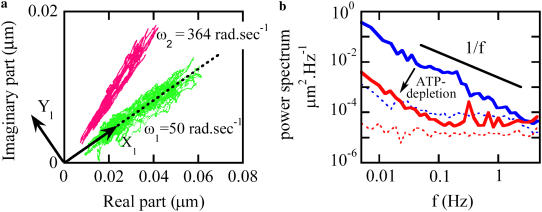
To study the timescales associated with the rocking amplitude time dependence, we computed their power spectral densities. Fig. 7 a shows the time-dependent complex rocking amplitude at two different frequencies on the complex plane. The time dependence leads to large changes in the radial (amplitude) direction, with comparatively small changes in polar angle (phase). (This finding is mathematically related but not equivalent to the finding above that the time variation at different frequencies is highly correlated.) Typical power spectra computed from the time-dependent amplitude of the rocking motion for control and ATP-depleted cells are displayed in Fig. 7 b. In normal cells, the amplitude variations have a slightly steeper than 1/f functional form over the observable range, 0.01 < f < 2 Hz. The mechanism responsible for this time dependence is clearly ATP dependent, dropping by two orders of magnitude when ATP (and other nucleotides) are chemically depleted by ∼95–98%. In that case, the spectra drops below our estimated detection limit (∼10⁻⁴ μm²/Hz) at higher frequencies, leading to a crossover there to a nearly white noise form. Very similar results are found at different rocking frequencies, which is expected given the correlation of time dependence measured at different rocking frequencies.

FIGURE 7.

(a) Plot of complex MTC rocking displacement signals at two frequencies, 50 rad/s (green) and 364 rad/s (pink). Time variation in the rocking amplitude is much greater than in the rocking phase. X₁ and Y₁ show transformed coordinates aligned and orthogonal to the mean phase of the rocking signal. (b) Power spectra of the MTC rocking amplitude (X₁) variations for a TC7 control cell (blue) and an ATP-depleted TC7 cell (red) for 50 rad/s driving. The line indicates a 1/f slope. Corresponding power spectra computed from the orthogonal signals (Y₁) provide in situ estimates for instrumental noise floors (dashed curves). Similar results were replicated for a few cells in both cases.

In general, the rocking amplitude reported by our lock-in instrument contains background contributions from random translational motions of the probe particle (which are larger than our instrument's random measurement error). Because the cell-specific random motion (to be analyzed below) itself varies from cell to cell, the background spectrum from this noise needs to be separately estimated in situ for each tracer. Since the random motion is not synchronous with the rocking frequency, its contribution is phase angle independent. For this reason, we estimate the background contribution by computing the power spectrum of the signal, which is orthogonal (90° out of phase) with the mean-phase angle (see Fig. 7 a). The weak frequency dependence of the computed background for control cells can be interpreted as weak evidence for either small time dependence of the rocking phase angle or nonstationarity of the tracer's random motion versus time. Comparable analyses, for example power spectra of the time-dependent amplitude ratio, yield similar results.

The near 1/f spectrum is indicative of a continuous, nearly uniform distribution of correlation times, rather than a single correlation time. Indeed, attempts to directly compute a temporal correlation function yielded unsatisfying results (not shown) that depended systematically on the duration of the amplitude trajectory analyzed. Although the rocking amplitudes varied by a large amount during our 30 min experiments, this variance was still smaller than that observed among an ensemble of cells. In other words, the rocking data are not statistically ergodic even on the longest timescales we considered. Noise with a 1/f power spectrum is ubiquitous in systems containing a number of strongly coupled interacting elements that either fail to reach equilibrium (or ergodicity) or do so only very slowly. Numerous examples occur in financial markets, ecological systems (population dynamics), biological systems (heart rhythms), as well as physical examples including percolation and aggregation.

The very commonness of such noise, however, means that its identification provides little clue as to the mechanism behind it. The fact that the time dependence appears to be proportional at all frequencies, however, is just what would be expected for a mechanism based on temporal changes to the coupling between the bead and the cytoskeleton. For this reason, we conjecture that ATP-dependent remodeling of the integrin contacts between the cell and the bead, integrin clustering, or connections from the integrins to the cytoskeleton are responsible for the time dependence. An alternative hypothesis would be if the shear modulus of the cyctoskeletal compartment sensed by MTC itself varied significantly in stiffness but not in its frequency dependence. For example, studies of reconstituted actin suggest that internal network stiffness (e.g., from myosin activity) can control the low-frequency shear modulus (25,26). This explanation for our findings, however, is difficult to support given our earlier finding (17) that our MTC results are invariant under myosin II inhibition (blebbistatin) and have altered frequency dependence under F-actin disruption (latrunculin A).

Laser tracking microrheology findings

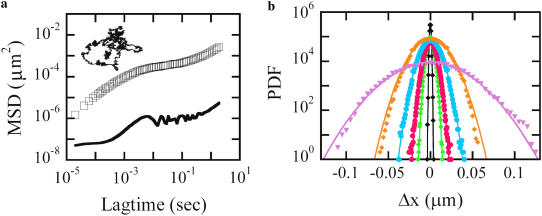
For the passive (LTM) experiment, the magnetic field is turned off and the adhered bead's small random motions are followed. The bead trajectory is inferred from the differential photodiode signals and converted to time-averaged physical mean-squared displacement (MSD); typical results for a bead integrin attached to a control cell, based on a 20 min trajectory, is shown in Fig. 8 a. In normal cells, the MSD cross over to a superdiffusive behavior starting around 0.1 s. This crossover moves to longer lag times when cells are ATP depleted, as we have reported previously. As the random motions at these longer lag times are non-Brownian in nature, the fluctuation-dissipation theorem does not hold.

FIGURE 8.

(a) Typical MSD and trajectory (inset) of a bead attached to the apical surface of a control TC7 cell (open symbols). Typical noise-induced MSD of an immobilized tracer is included for comparison (solid symbols). (b) The corresponding PDF of the random displacements at lag times τ(s) = 2 × 10⁻⁵ (black), 3.4 × 10⁻⁴ (green), 1.4 × 10⁻³ (pink), 2.4 × 10⁻² (blue), 0.1 (orange), and 0.5 (purple). Lines are best fits with a Gaussian distribution.

To examine the statistical character of the random bead displacements, one can compute the probability density function for the displacements during a given lag time interval. In control cells, we find such probability density functions to be Gaussian, as shown in Fig. 8 b, at all accessible lag times, 20 μs < τ < 0.5 s, including both those where the motion is predominantly Brownian and those where it is ATP dependent. Specifically, we find a negligibly small non-Gaussian parameter (see Materials and Methods), α₂(Δx(τ)) < 0.1, for all τ. This is consistent with the fact that no large discrete steps are observed in the trajectory (Fig. 8 a, inset). Our findings, however, are contrary to comparable published studies performed on smooth muscle cells (11), which reported a large non-Gaussianity under control conditions, with a peak parameter α₂(Δx(τ = 0.2 s)) = 0.7. The authors associated those non-Gaussian displacements with the qualitatively similar motion (termed dynamical heterogeneity) observed in colloidal glass models (16).

Although that study's observation of non-Gaussian displacement was taken as support for the applicability of the soft glassy rheology (SGR) model to cells, our contrary observation certainly does not disprove SGR. Dynamical heterogeneity occurs on length scales associated with microscopic rearrangement events. Probes that are significantly larger than that scale will see the combined action of many small non-Gaussian displacement events which will tend to regress to a Gaussian distribution. Thus, although observing Gaussian displacements is plausibly consistent with SGR, we are forced to the conclusion that either the dynamical heterogeneity in smooth muscle cells has a significantly larger length scale than in epithelial cells (both studies use similar size probe beads) or that the non-Gaussian motion observed by Bursac et al. (11) was not related to dynamical heterogeneity. As smooth muscle cells are contractile, a simple explanation would be that the large bead excursions observed are related to cell-scale contractile activity.

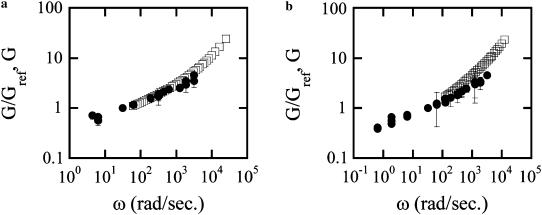
Before computing the rheology from LTM data using the GSER, the MSDs are truncated to remove the long lag time, non-Brownian data. In Fig. 9, we present two typical complex elastic modulus frequency dependences obtained on two different cells. MTC and LTM measurements performed on the same cells and beads allow the results to be compared. Because the absolute shear moduli computed by both methods are not directly comparable, the curves are rescaled vertically to match at a single frequency and their frequency dependences compared. As described previously (9), only in ∼15% of the data is a satisfactory agreement obtained (Fig. 9 a), whereas in other cases (Fig. 9 b), the frequency dependence reported by the two methods is significantly different. On the basis of the latter data agreeing with intracellular rheology measurements (9), we have argued that this is indicative of LTM being able to probe deeper, mechanically distinct intracellular structures than MTC.

FIGURE 9.

Complex elastic modulus as a function of frequency, obtained by actively rocking the bead (MTC, circles) and by measuring the bead Brownian fluctuations (LTM, squares) on the same cell. (a) and (b) correspond to results obtained for two different cells. Note: LTM curves are rescaled vertically to correspond to the MTC value at ω = 30 rad/s to compare the functional form (slope) of the curves at frequencies where they overlap.

Statistical distributions of the amplitude and exponent for MSDs are reported in Fig. 6, b and d, and are in agreement with other reports (4). They have been measured by power-law fitting the MSDs on a decade centered around ω = 100 rad/s, for which the effects of both the non-Brownian regime and the crossover to a β power-law is minimal. As in the active experiments, the amplitude is lognormally distributed: Fig. 6 b reports the log-amplitude, fitted by a normal distribution, and the inset shows the same distribution on a linear scale. The LTM exponents are more broadly distributed than in the MTC case and have a higher mean value. This is presumably due to LTM reporting either the same structure as MTC or alternatively the deeper interior, which has a systematically higher rheology exponent (9).

CONCLUSION

This study uses a dual frequency MTC technique combined with laser deflection tracking to determine the precise frequency dependence of cells' rheology and probe the time dependence of the MTC rocking signal. The frequency dependence measured for single cells shows remarkably little cell-to-cell variation and corresponds closely to ensemble-averaged results. No spontaneous time-dependent changes to cells' frequency-dependent response were reliably detected; the dramatic time dependence of the rocking amplitude manifests as a frequency-independent multiplicative factor at all observable frequencies. This finding is most readily explained by the remodeling of the geometric structure of the magnetic bead's interface with the cytoskeleton. A spectral analysis of the rocking time dependence shows a broad distribution of characteristic times for this remodeling, having a 1/f form. This frequency dependence, which was found to be ATP dependent, is more likely reflective of the dynamics of integrin clustering or the phagocytic signaling pathway than anything to do with the cytoskeleton.

Moreover, the use of laser deflection tracking allows us to examine the tracers' spontaneous random motions on a wide range of timescales at high spatial resolution. Here we examined the statistical character of the random motion in detail. In contrast to earlier published reports, the motions have a purely Gaussian character at all timescales in both normal and ATP-depleted epithelial cells. The rheology computed from the tracers' random motion (LTM) does not correspond to that from MTC for the majority of tracers, indicating that the rocking and translational motion of the same magnetic bead typically probe different intracellular structures. The instrument and analytical approach we have used here should be well suited to future studies dissecting the intracellular contributors (e.g., cortical or deeper networks, cell membrane, adhesion complex, stress fibers, etc.) to the MTC method.