Hybrid Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulations of HIV-1 Integrase/Inhibitor Complexes

Abstract

Human immunodeficiency virus (HIV)-1 integrase (IN) is an attractive target for development of acquired immunodeficiency syndrome chemotherapy. In this study, conventional and coupled quantum mechanical and molecular mechanical (QM/MM) molecular dynamics (MD) simulations of HIV-1 IN complexed with 5CITEP (IN-5CITEP) were carried out. In addition to differences in the bound position of 5CITEP, significant differences at the two levels of theory were observed in the metal coordination geometry and the areas involving residues 116–119 and 140–166. In the conventional MD simulation, the coordination of Mg²⁺ was found to be a near-perfect octahedral geometry whereas a distorted octahedral complex was observed in QM/MM. All of the above reasons lead to a different pattern of protein-ligand salt link formation that was not observed in the classical MD simulation. Furthermore to provide a theoretical understanding of inhibition mechanisms of 5CITEP and its derivative (DKA), hybrid QM/MM MD simulations of the two complexes (IN-5CITEP and IN-DKA) have been performed. The results reveal that areas involving residues 60–68, 116–119, and 140–149 were substantially different among the two systems. The two systems show similar pattern of metal coordination geometry, i.e., a distorted octahedron. In IN-DKA, both OD1 and OD2 of Asp-64 coordinate the Mg²⁺ in a monodentate fashion whereas only OD1 is chelated to the metal as observed in IN-5CITEP. The high potency of DKA as compared to 5CITEP is supported by a strong salt link formed between its carboxylate moiety and the ammonium group of Lys-159. Detailed comparisons between HIV-1 IN complexed with DKA and with 5CITEP provide information about ligand structure effects on protein-ligand interactions in particular with the Lys-159. This is useful for the design of new selective HIV-1 IN inhibitors.

INTRODUCTION

Acquired immunodeficiency syndrome (AIDS), caused by human immunodeficiency virus (HIV), is an epidemic worldwide disease. Combinations of drugs targeting reverse transcriptase (RT) and protease (PR) enzymes, known as the highly active antiretroviral therapy (HAART), is currently used for the treatment of HIV-1 infection. However, the limitation of RT and PR inhibitors in terms of their side effects and drug resistance leads to an effort to develop new drugs to be a third component of HAART. Thus, HIV-1 integrase (IN) has become an attractive target for AIDS therapy. There is no known similar enzyme in human, therefore, specific inhibitors of HIV-1 IN are expected to have minimal side effects as compared to other antiviral agents.

HIV-1 IN is a 32-kDa enzyme comprising three functional domains, N-terminal (residues 1–50), catalytic core (residues 50–212), and C-terminal (residues 212–288). The catalytic residues, Asp-64, Asp-116, and Glu-152, are in the catalytic core domain coordinating one or two divalent metal ions. Divalent metal ions, such as Mg²⁺ or Mn²⁺, are required for the catalytic activity of IN. Although two metal ions have been proposed to be present in the IN active site, as seen in avian sarcoma virus (ASV) IN (1) a single metal is present in the resolved x-ray structures of HIV-1 IN (2,3). Moreover, the second metal has been proposed to present in the HIV-1 IN active site once it binds with the substrate (4,5).

HIV-1 IN functions by catalyzing the insertion of viral DNA, synthesized by the HIV-1 RT from viral RNA, into the host chromosome using a two-step mechanism. In the first step, named 3′-processing, IN removes a dinucleotide from each 3′-end of the viral DNA. In the next process, named strand transfer, IN joins the previously processed recessed 3′-ends to 5′-positions on opposite strands of the target DNA, across a five-basepair stretch. The final step, which may not involve IN, is the cleavage of the dinucleotide overhangs and ligation. Subsites for 3′-processing and strand transfer have been proposed (6) based on the hypothesis that the 3′-processing step occurs in the active site area in the vicinity of Mg²⁺ since the divalent cation is critical for the 3′-processing activity. The 3′-processing cavity is formed by residues Asp-64, Cys-65, Thr-66, His-67, Glu-92, Asn-120, Phe-121, Asp-116, and Mg²⁺ ion whereas an area made by residues Gln-62, Ile-141, Pro-142, Tyr-143, Gln-148, Ile-151, Glu-152, Lys-156, Asn-155, and Lys-159 represents the strand transfer cavity.

During the last few years, a large number of compounds have been reported to inhibit HIV-1 IN (7–11). Among the several classes, the diketo acid is one of the most widely developed since this group of compounds shows high potency and high selectivity. In this study, special attention is paid to the two diketo acid derivatives, 5CITEP and DKA (Fig. 1). The general structure of 5CITEP is very similar to that of DKA, except that the tetrazole ring is replaced by a carboxylic acid group in DKA. Nevertheless these two compounds differ in inhibition activity. In the presence of Mg²⁺, DKA is about 16-fold and 50-fold more active than 5CITEP for 3′-processing and strand transfer reactions, respectively (5). In addition, the inhibitory activities of these two compounds are metal dependent (4,5).

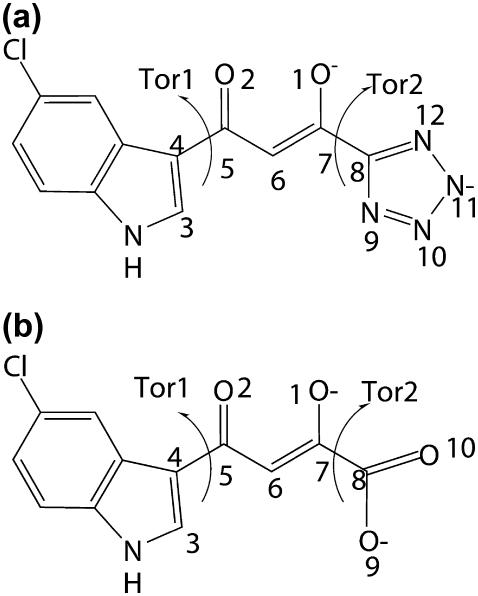
FIGURE 1.

Chemical structure and atomic definition of (a) 5CITEP and (b) DKA.

Several computational methodologies, including molecular docking (6,10,12–15) and pharmacophore modeling (16–19) have been employed to elucidate the binding mode of diketo acid compounds. Many of them reveal that the mechanism of the inhibition of this class of compound is due to the chelation of the keto-enol group by the divalent metal ion. Furthermore, although the x-ray structure of the complex between HIV-1 IN and 5CITEP is available (20) its mechanism of action is not yet fully understood. In the cocrystal complex, 5CITEP is located in the center of the active site, lying between Asp-64, Asp-116, and Glu-152. The keto-enol motif of 5CITEP forms a hydrogen-bond with Glu-152 whereas all four nitrogen atoms in the tetrazole ring form hydrogen-bonds with Asn-155, Thr-66, Lys-159, and Lys-156. The indole ring of the ligand is pointed toward Gln-148. However, this bound conformation of 5CITEP in the cocrystal structure is possibly not in the bioactive form because of the crystal packing effects that arise from the close contact between both subunits A of the dimeric form of HIV-1 IN. Furthermore, two 5CITEP molecules hydrogen-bond with one another as they bind to two active sites. This is supported by several docking calculations (5,21,22) of 5CITEP into the HIV-1 IN catalytic core domain showing that the bound conformation of 5CITEP in the cocrystal structure could not be reproduced.

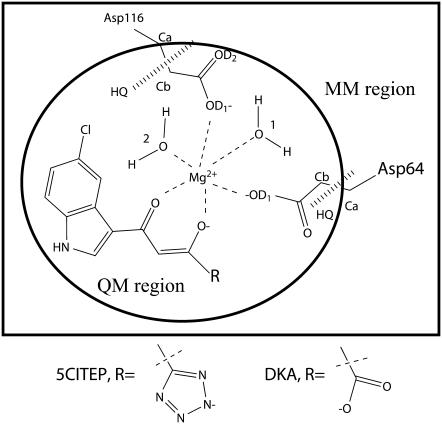
Because the mechanism of action of the diketo acid compound probably involves the metal ion, metal-binding models of diketo acid derivatives and diketo-like compounds have been recently proposed (4,23–26) suggesting that the Mg²⁺ is chelated by ligands via their keto-enol or carboxylic acid moieties. In our previous work (N. Nunthaboot, S. Pianwanit, V. Parasuk, J. O. Ebalunode, J. M. Briggs, and S. Kokpol, unpublished data), we also have proposed models of metal-ligand binding based on the assumption that: i), ligands (5CITEP and DKA) are in their dianionic form based on the experimental studied by Maurin and co-workers (27); ii), only one Mg²⁺ is modeled in the active site since the DNA substrates are not included in our structures; and iii), the keto-enolate group of the ligand directly forms a coordination complex with Mg²⁺. A schematic representation of the ligand binding to the HIV-1 IN active site is illustrated in Fig. 2. Since 5CITEP and DKA are positioned in the 3′-processing cavity where the Mg²⁺ is located, the proposed models of ligand binding should represent their inhibition mechanisms at the 3′-processing step that requires divalent metal ion. Our proposed metal-ligand models are the initial structures used in this study.

FIGURE 2.

Schematic drawing of proposed metal-ligand binding of HIV-1 IN-inhibitor complexes. QM regions used in QM/MM calculation are encircled. HQ refers to hydrogen link atom HQ type, which is added between the α-carbon and β-carbon of both Asp-64 and Asp-116.

Although molecular dynamics (MD) simulations of either HIV-1 IN complexed with inhibitor or the free enzyme have been carried out (28–33) to the best of our knowledge, this is the first time combined quantum mechanical/molecular mechanical (QM/MM) simulations have been reported for an HIV-1 IN-inhibitor complex. In addition, ligand orientations as well as protein-ligand interaction modes are different from those used in the classical MD simulations. In the QM/MM concept, the system is partitioned into a QM region and a classical MM region (34). An interesting species (such as ligand or protein active site), the QM region, is treated quantum mechanically whereas the rest of the system (surrounding amino acids and solvent), the MM region, is described by classical molecular mechanics. Ideally, the QM region should be treated by ab initio (35) or density functional theory (36), however the computational cost of such a high level of QM is prohibitively expensive, especially when applied to significant portions of an enzyme's active site. In this study, a semiempirical approach (34) was used for the QM region.

The main aim of this study was to investigate structural and dynamical properties of HIV-1 IN complexed with ligands. Hybrid QM/MM simulations of the HIV-1 IN complexed with DKA (IN-DKA) or with 5CITEP (IN-5CITEP) were carried out. An effort has been made to explain the difference in inhibitory potency of the two compounds. Moreover, to provide a point of comparison with conventional MD, we also performed a classical MD simulation of IN-5CITEP and the results obtained from the two levels of theory (MM and QM/MM) were compared. A detailed analysis suggests that a hybrid QM/MM is most appropriate for the complexes used in this work.

METHODOLOGY

System preparation and conventional MD simulation

Initial structures of the two systems of HIV-1 IN-inhibitor complexes were taken from our preliminary work (N. Nunthaboot, S. Pianwanit, V. Parasuk, J. O. Ebalunode, J. M. Briggs, and S. Kokpol, unpublished data). In the first system, IN-5CITEP, HIV-1 IN is in complex with 5CITEP and in the second system, IN-DKA, the protein is in complex with DKA. We give a brief summary of the important details of the starting structures. In both systems, Mg²⁺ is octahedrally coordinated with the OD1 atoms of residues Asp-64, Aps-116, O atoms of water molecules (water No. 1 and water No. 2) and O atoms belonging to the keto-enolate moiety of the ligands whose dianionic form was used (Fig. 2). No unusual amino acid ionization states were identified through application of the ionization state prediction methodology in the UHBD program (37) (i.e., Lys and Arg = +1, Asp and Glu = −1, His = 0).

In each system, the complex was solvated with a 28-Å radius sphere of TIP3P water centered on the Mg²⁺ ion in the active site. Overlapping water molecules whose oxygen atoms were closer than 2.8 Å to any other heavy atom were removed. Subsequently, the added water molecules were energy minimized using the two series of 300 steps of steepest descent (SD) following by two series of 500 steps of adopted basis Newton Raphson (ABNR) to relieve steric clashes within the system. The solvent sphere was equilibrated (at 300 K) for 25 ps with protein and ligand fixed. These solvation procedures (sphere addition, water deletion, and equilibration) were repeated several times to avoid solvent cavities. As a result, the IN-5CITEP system contained 2406 solute atoms (protein, Mg²⁺, 5CITEP, two “catalytic” water molecules) and 7371 water atoms, whereas for the IN-DKA system, the numbers of solute (protein, Mg²⁺, DKA, two catalytic water molecules) and solvent atoms were 2404 and 7365, respectively.

In each case, the enzyme-inhibitor complex was energetically minimized using the two series of 300 steps SD and 1000 steps ABNR. The system was further slowly heated from 10 to 300 K in three 10-ps intervals, 10–100 K, 100–200 K, and 200–300 K. Afterward, the complex was equilibrated for 300 ps and the resulting structure was consequently used as the starting configuration for QM/MM MD simulation. For the conventional MD simulation, the system was further equilibrated with stochastic boundary conditions (38) over 1000 ps and the production run was collected from 400 to 1000 ps.

All calculations were conducted using the CHARMM suite of programs, version 29b2 (39). For classical MD simulation, CHARMM parameters for both ligands were constructed by analogy with similar molecular structure in the all-atom CHARMM27 parameter set. The torsional energies for the C5-C6 and C7-C8 bonds (see Fig. 1) were slightly increased to keep the O1 and O2 atoms coplanar with the C4, C5, C7, and C8 atoms. Atomic net charges were obtained by the restricted electrostatic potential fitted charges at the HF/6-31G (d). More details of ligand setup are provided in Supplementary Material. A stochastic boundary molecular dynamics (38) simulation was employed. The 28-Å sphere was subdivided into the reaction zone (0–22 Å) treated by Newtonian dynamics and a buffer zone (22–26 Å) treated by Langevin dynamics. Protein atoms within the buffer region were harmonically restrained to their minimized positions. Friction coefficients of 250/ps and of 62/ps (40) were used for nonhydrogen protein atom and water oxygen atoms, respectively. Amino acid residues that were more than 26 Å away from the center of the sphere were restrained during the calculations. To prevent escape of water molecules, a deformable boundary potential (41,42) at 28 Å was employed. The SHAKE (43) algorithm was employed to constrain all bond containing hydrogen atoms. The time step was 1 fs. A nonbonded cutoff with an atom switching function in the region from 8 to 13 Å was used to smoothly scale down the interaction to zero at 13 Å.

QM/MM setup

The QM region contains the acetate side chains of Asp-64 and of Asp-116, two “catalytic” water molecules, an Mg²⁺ ion, and the ligand totaling 47 and 45 atoms, including two H-link atoms, in the IN-5CITEP and IN-DKA systems, respectively (Fig. 2). To ensure that the MM charges were treated consistently in the Hamiltonian for the QM atoms, all QM atoms were defined as a single group. The hydrogen link atoms, HQ type (44), were added between the Cα and the Cβ of aspartic acids to saturate the QM and MM boundary. The overall charge in the QM region was −2e for both systems. The QM atoms were described by the semiempirical PM3 method (45–47) whereas the other atoms were treated by a classical CHARMM22 force field (48). QM/MM energy minimization (250 steps of SD followed by 750 steps of ABNR) was performed for each system. Afterward, the QM/MM MD simulation was conducted using the same conditions as the classical MM simulation and was run for 1200 ps, with the final 600 ps taken as the production data.

RESULTS AND DISCUSSION

In this section, comparison of the results between MM and QM/MM calculations of the IN-5CITEP system was made to elucidate the differences between the two levels of theories. Then, the results of the QM/MM simulations between the IN-DKA and IN-5CITEP complexes were analyzed and discussed to describe their structural and dynamical properties.

Comparison of IN-5CITEP using MM and QM/MM force fields

Structural dynamics of the HIV-1 IN

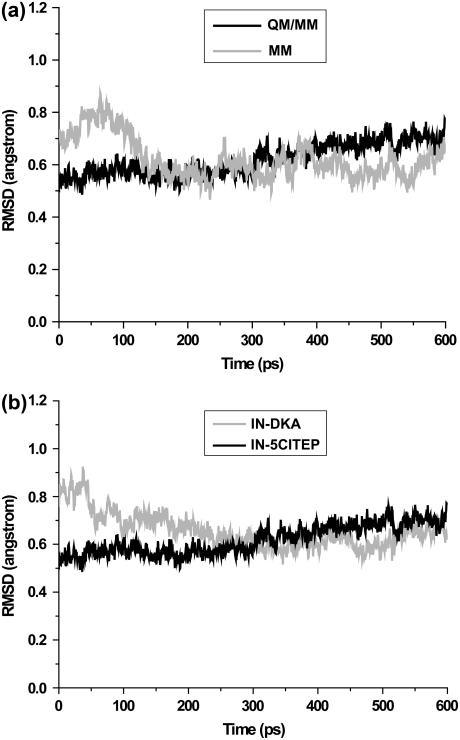
To compare the use of MM and QM/MM parameters, MD simulations of IN-5CITEP based on classical and QM/MM parameters were examined. Trajectory analyses were carried out on the production runs, i.e., 400–1000 ps and 600–1200 ps for the conventional MD and hybrid QM/MM MD simulations, respectively. To assess the stability of the MM and QM/MM trajectories, the root mean square deviations (RMSD) for all heavy atoms were plotted versus simulation time. Fig. 3 a shows RMSD with respect to the average structures of the two simulations. It can be clearly seen that both simulations produced stable trajectories as indicated by their small RMSDs (∼0.6 Å). The small RMSD fluctuation of the two trajectories during the course of dynamics runs confirms they were reasonably stable systems.

FIGURE 3.

Root-mean-square deviations of all heavy atoms with respect to the average structure versus simulation time. Panel a compares heavy atom RMSDs of IN-5CITEP obtained from conventional MD and QM/MM MD simulations. Panel b compares heavy atom RMSDs between IN-DKA and IN-5CITEP taken from a hybrid QM/MM MD simulations.

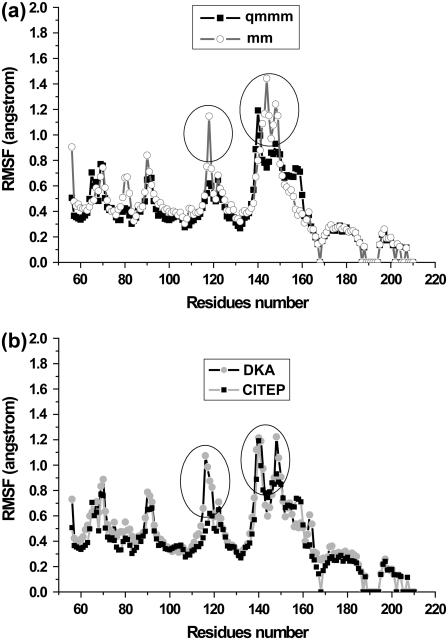
To find out which part of protein shows high flexibility, the root mean square fluctuation (RMSF) of backbone atoms for each residue during the MD simulations was monitored, as depicted in Fig. 4 a. The MM results revealed that the largest fluctuations of the protein are seen in the two areas corresponding to residues 116–119 and residues 140–149. Meanwhile, the QM/MM calculation showed that only the loop region 140–149 was found to be flexible whereas residues 116–119 were quite rigid throughout the simulation.

FIGURE 4.

Average root-mean-square fluctuation (RMSF) of protein backbone atoms as a function of residue number. Panel a compares the RMSF of protein structure of IN-5CITEP complex taken from the classical and hybrid QM/MM MD simulations. Panel b compares the RMSF of protein backbones of IN-DKA and IN-5CITEP complexes obtained from QM/MM MD simulations.

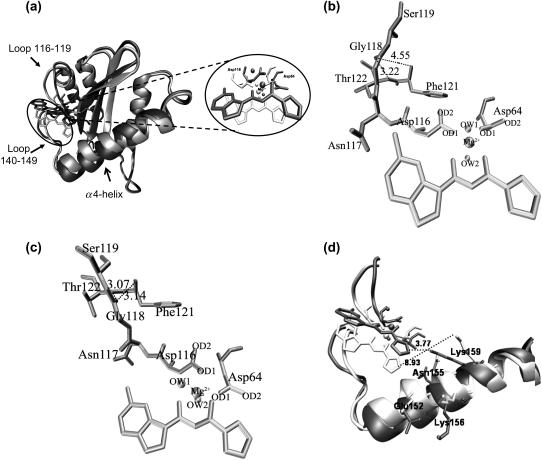
The superimposition of the average structures of the protein taken from the two simulations is illustrated in Fig. 5 a. The RMSD of all heavy atoms in the protein between the two simulations is 1.36 Å. As can be clearly seen, two significant differences in protein structure between the two levels of theory are the conformations in the area involving residues 116–119 and residues 140–149. The RMSD (all heavy atoms) of amino acid residues 116–119 and 140–149 of the average structures between MM and QM/MM simulations are 1.24 and 1.77 Å, respectively. The conformation of Asp-64 using MM parameters was somewhat similar to that of using QM/MM whereas Asp-116 adopted a different orientation in the two levels of calculations. Due to the adjustment of Mg²⁺ and 5CITEP to the new equilibrated state of the system, Asp-116 adopted its conformation to preserve the interaction with this catalytic metal ion. This leads to the conformational difference of the region containing residues 116–119. In this area, we note that Gly-118 exhibited the highest fluctuation. In the conventional MM simulation, this loop adopted a conformation away from residues Phe-121 and Thr-122, making it difficult for Gly-118 to form hydrogen-bonds with the above-mentioned two amino acids (Fig. 5 b). An analysis of hydrogen-bonding shows that hydrogen-bonds occur through 20% of the simulation between Gly-118 and Phe-121, and 30% of the time between Gly-118 and Thr-122. On the contrary, in the QM/MM MD simulation, Gly-118 is located close to Phe-121 and Thr-122. The carbonyl oxygen of Gly-118 is positioned between the NH atoms of Phe-121 and Thr-122, thus, it is easier for Gly-118 to establish such hydrogen-bonds (Fig. 5 c). These hydrogen-bonds are almost always present during the dynamics simulation, indicated by 83% and 97% of an occurrence of hydrogen-bond between Gly-118 and Phe-121 and between Gly-118 and Thr-122, respectively. Apparently, the rigidity of Gly-118 observed in QM/MM is due to hydrogen-bond between its carbonyl oxygen and the NH belonging to Phe-121 and Thr-122.

FIGURE 5.

(a) Superimposition of the protein conformation of the average structure obtained from conventional MD (light gray) and taken from a combined QM/MM MD calculation (dark gray). Residues Asp-64, Asp-116, and inhibitors are shown as stick models whereas Mg²⁺ ion and the catalytic water molecules are displayed in balls. Panels b and c display hydrogen-bonds between amino acids located in 116–119 obtained from conventional and QM/MM MD simulations of IN-5CITEP complex, respectively. (d) Stereo view of the catalytic loop region (residues 140–149) and the α4-helix. Selected residues and inhibitors are displayed in stick models. The distances between ligand and Lys-159 are shown in dotted lines. The figures were generated using VMD (54).

We now turn our attention to the loop involving residues 140–149. The large flexibility of this loop is not surprising since it is located at the surface of the protein and is flanked by Gly residues. Moreover, the observed high mobility of this loop is in agreement with the previous MD simulations of HIV-1 IN and with crystal structures (i.e., this loop is typically not resolved) (20,28,30). It is worth mentioning that although loop 140–149 is very flexible, it does not undergo the same conformational changes in the two simulations (Fig. 5 d). The MM results show larger fluctuations of this loop than that observed in the QM/MM calculation. The pink and blue ribbons represent the MM and QM/MM results, respectively, with key residues rendered as stick models. As can be seen, the different conformation of this particular flexible loop resulted in a variation of the conformation of the α4-helix of the region consisting of residues 148–166. Amino acids located in this α4-helix take on very different conformations, which leads to different interactions between the ligand and the protein, especially in salt-bridge interactions, as discussed in the next section.

Mg²⁺ coordination and inhibitor binding mode

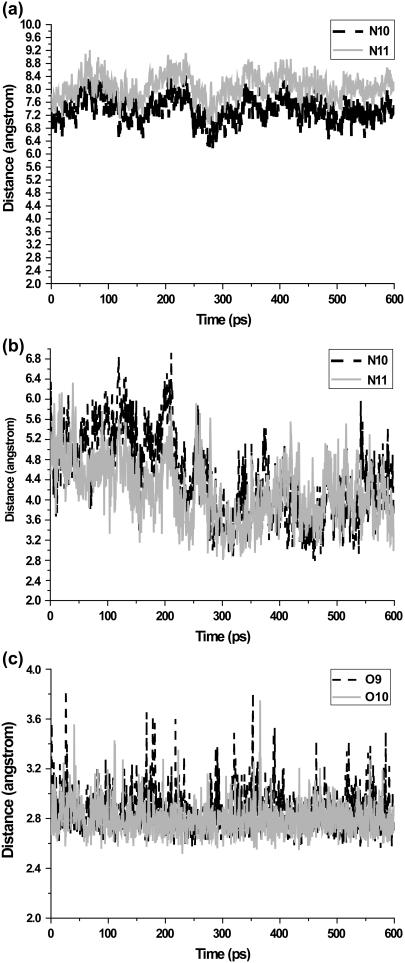
One significant difference observed between the two levels of theory is the coordinating distances between Mg²⁺ and its chelated oxygen atoms. The key distances between the catalytic metal ion and the coordinated oxygen atoms were plotted as a function of simulation time, as illustrated in Fig. 6. For the classical MD simulation, the Mg²⁺ was octahedrally coordinated by the two aspartate residues (Asp-64 and Asp-116) via their OD1 atoms, the oxygen atoms (O1 and O2) of the keto-enolate moiety of 5CITEP, and the two oxygen atoms of the catalytic water molecules (OW1 of water No. 1 and OW2 of water No. 2). The chelate distances between Mg²⁺ and the aforementioned oxygen atoms fluctuate in the range of 1.8–2.0 Å (Fig. 6 a), which are close to a perfect octahedral geometry. However, in the QM/MM simulation, the Mg²⁺ formed a distorted octahedral complex with the surrounding oxygen atoms. The distances between Mg²⁺ and four oxygen atoms (O1, O2 of 5CITEP, OD1–Asp-116, and OW2) are ∼1.8 Å whereas the other two (Mg²⁺–OD1–Asp-64 and Mg²⁺–OW1) are ∼2.5 Å, as depicted in Fig. 6 b. The different coordination geometry of Mg²⁺ produced by MM and QM/MM leads to different conformations of Asp-116 and induces a different conformation of loop 116–119, as mentioned earlier.

FIGURE 6.

Time evolution of the interatomic distances between Mg²⁺ and its coordinating atoms obtained from (a) conventional MD of IN-5CITEP, (b) QM/MM of IN-5CITEP, and (c) QM/MM of IN-DKA.

We next turn to an analysis of inhibitor binding mode. Both MM and QM/MM results showed that 5CITEP occupied the active site region of HIV-1 IN, although with a somewhat different position. Generally, 5CITEP shared common features of binding in which the keto-enolate motif directly interacted with the Mg²⁺ ion with the tetrazolate ring pointed toward the region involving residues Asn-155, Lys-156, and Lys-159 (Fig. 5 d). The salt bridge between the ligand and the enzyme was monitored during the course of the MD trajectory. Surprisingly, no salt link was observed between the protein and 5CITEP in the classical MD simulation. This is because Lys-159 is located far from 5CITEP (∼6.8–9 Å; Fig. 7 a), hence, the tetrazolate motif of the ligand is not able to form a salt bridge with this particular residue. On the other hand, in the QM/MM trajectory, the ligand adopted an orientation allowing it to make this type of interaction with Lys-159. This is supported by a plot of distance versus simulation time between the tetrazolate anion and the ammonium group of Lys-159, as demonstrated in Fig. 7 b.

FIGURE 7.

Plots of the salt link distances between the negatively charged group of ligand and the ammonium group of Lys-59. The distance between tetrazolate ring of 5CITEP and the ammonium nitrogen of Lys-159 taken from the conventional MD is shown in panel a, whereas that from QM/MM is given in panel b. Panel c shows the distance between carboxylate oxygens of DKA and the terminal ammonium nitrogen of Lys-159.

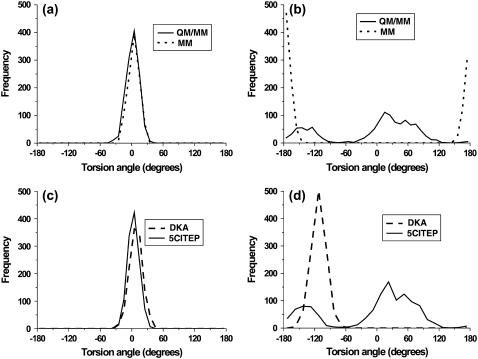
To further examine the mobility of 5CITEP, a detailed discussion is focused on the conformational changes of torsional angles Tor1 (C3-C4-C5-C6) and Tor2 (C6-C7-C8-N9) (defined in Fig. 1). Remarkable differences were observed for the angle Tor2 whereas no significant difference was found for the angle Tor1 (Fig. 8, a and b). For angle Tor1, both the MM and QM/MM simulations show only one sharp peak at ∼0° suggesting the single preferential conformation of the indole ring of 5CITEP. During the simulation period, the indole ring of the ligand always maintains a coplanar conformation relative to the keto-enolate motif. Additionally, the MM results indicated again a single preferential conformation of the tetrazolate ring of 5CITEP, as evidenced by the angle Tor2 at ∼±180°. On the other hand, the QM/MM MD simulation produced two favorable conformations of the tetrazolate ring. The first conformation corresponds to Tor2 at from about −180 to −100° and another one corresponds to 0–90°. The broader and higher peak of Tor2 at 0–90° indicated higher mobility and higher probability of finding this conformation. The observation of double peaks in QM/MM might be due the smaller repulsion between the negatively charged group of 5CITEP and the surrounding amino acids such as Glu-152 (tetrazolate–Glu-152, ∼9.0 Å). It is apparent that atomic charges are better distributed in QM/MM, so it shows the smaller repulsion. In contrast, MM has more localized charges, hence, the repulsion between the tetrazolate anion and neighboring amino residues (tetrazolate–Glu-152, ∼4.5 Å) is stronger. The planar orientation presumably has the lowest repulsion. The tetrazolate ring therefore remains at this position for the whole period of simulation. This leads to the finding of a single sharp peak of Tor2 in the classical MD simulation.

FIGURE 8.

Comparison of the distributions of torsional angles (a) Tor1 and (b) Tor2 of 5CITEP using MM and QM/MM. Comparison of the distributions of torsional angles (c) Tor1 and (d) Tor2 of both DKA and 5CITEP taken from QM/MM MD simulation.

It is obvious that conventional and coupled QM/MM MD simulations reveal somewhat different structural and dynamical behaviors for the HIV-1 IN-5CITEP complex. It has been reported that mixed QM/MM approaches exhibited advantages over classical force fields (49,50). QM/MM yields the results much closer to experimental data than those of MM force fields. Thus a combined QM/MM has been selected to study HIV-1 IN-ligand complexes that will be discussed in depth below.

Comparison of QM/MM results between IN-DKA and IN-5CITEP

Stability of MD trajectories

The stability of the MD trajectories of the two systems was evaluated by plotting of RMSD values to their average structures (Fig. 3 b). The mean RMSD value of both systems exhibits convergence to ∼0.6 Å. The steady and small magnitude of RMSD fluctuation suggests that the overall structure of the protein remained stable over the course of the MD simulations. Therefore, our MD trajectories should provide a suitable basis for more detailed analyses.

Residue fluctuation

For each system, a detailed analysis of RMSF of protein backbone atoms for each residue is illustrated in Fig. 4 b. The remarkable differences between IN-DKA and IN-5CITEP were again observed in residues 116–119, which are located in the 3′-processing cavity, and the loop residues 140–149. In the former loop, Asp-116 and Asn-117 of the IN-DKA complex undergo large amplitude movement during the trajectories, whereas this motion is small in the IN-5CITEP complex. Regarding loop residues 140–149, although it was found to be very flexible in the two systems, this catalytic loop region exhibited different conformational changes in the two complexes. The IN-DKA complex exhibited a greater fluctuation of residue Gln-148 compared to that in the IN-5CITEP system.

Structural difference between IN-DKA and IN-5CITEP

The superimposition of the average structure between IN-DKA and IN-5CITEP is given in Fig. 9. The RMSD of heavy atoms in the protein between the two complexes is 1.34 Å suggesting a significant difference of the protein structure. As can be seen in Fig. 9, three apparent differences in the HIV-1 IN structure between the IN-DKA and IN-5CITEP complexes are noticeable around regions formed by residues 60–68, 116–119, and 140–149. In the IN-DKA complex, the side chains of both Asp-64 and Asp-116 are almost perpendicular to the plane defined by the keto-enolate motif of DKA whereas these two residues are mostly horizontal to the plane of the ligand in IN-5CITEP. The adapted side chain of Asp-64 in IN-DKA allows its OD1 and OD2 atoms to coordinate the divalent metal ion (see Fig. 6 c). Unlike IN-DKA, in IN-5CITEP, only the OD1 atom of Asp-64 chelates with the Mg²⁺ ion (see Fig. 6 b). The conformational difference of the Asp-64 side chain in the two complexes affects the length of the β1-sheet, which consists of seven residues (60–66) in IN-DKA and nine residues (60–68) in IN-5CITEP.

FIGURE 9.

(a) Superimposition of average structure obtained from QM/MM MD simulations between IN-DKA (cyan) and IN-5CITEP (ice blue). Binding modes of DKA (b) and 5CITEP (c) in the HIV-1 IN active site. Mg²⁺ ion is displayed as a green ball. The coordinating distances between Mg²⁺ and its chelating atoms are represented in dotted lines. The figures were generated using VMD (54).

In addition, Asp-116 in the IN-DKA complex adapted its side-chain conformation to allow a hydrogen-bonding network to form between their OD1 and OD2 atoms and OW2 of water No. 2. In contrast, in the IN-5CITEP complex only the OD1 of Asp-116 was hydrogen-bonded to OW2. Thus, the HIV-1 IN-DKA complex was stabilized by a larger number of hydrogen-bonds with water than those in the IN-5CITEP system. Furthermore, the conformational difference of Asp-116 results in conformational changes in residues 117–119 in the IN-DKA complex.

The final substantial difference was detected in the catalytic loop region involving residues 140–149. In fact, this loop is very flexible in nature (residues 140 and 149 are glycines) and different crystal structures of HIV-1 IN exhibit various conformations of this particular loop, and in many cases, absence of coordinates as it as too flexible. The heavy atom RMSD value of amino acids 140–149 between the average structure of IN-DKA and IN-5CITEP was 3.08 Å indicating a large difference of the catalytic loop between the two complexes, especially Gln-148 (RMSD = 0.71 Å). It has been hypothesized that Gln-148 is involved in the position of viral DNA binding before strand transfer into host DNA (51), thus the behavior of this residue might be crucial for DNA binding. For IN-5CITEP, the rigidity of Gln-148 occurs because the O of Gln-148 is capable of forming a hydrogen-bond with the NH of Gln-146 (20%) and with the NH of Glu-152 (80%) more than that found in IN-DKA (O (Gln-148)–NH (Glu-152) = 70%). This hydrogen-bond formation was also observed in the previously reported conventional MD simulations (28). One remarkable observation between the two complexes is the length of the α4-helix residues, which probably arose from the conformational change of Gln-148. This helix in IN-DKA spans residues 149–166, which is one residue shorter than that in IN-5CITEP (residues 148–166). In the x-ray structure (1QS4) as well as in the wild-type model of the conventional MD simulation (28) of the x-ray complex structure of HIV-1 IN-5CITEP, this helix involves residues 150–166 and 149–165, respectively. Moreover, the instability of this helical behavior was also observed in the conventional MD simulation of the apo HIV-1 IN catalytic core domain containing one Mg²⁺ (33).

Inhibitor binding mode/structural features of the inhibitor

It is clear from Fig. 9 a that both DKA and 5CITEP occupied nearly the same region in the active site of HIV-1 IN and they showed a similar pattern of inhibitor binding orientation. For each system, the keto-enolate moiety of the ligand chelated the Mg²⁺ ion whereas the chloroindole ring was located close to residues Thr-115, Asn-117, and Gly-118. An electrostatic interaction was also observed between the chlorine atom in the indole ring and the amide group of Asn-117. The NH of the indole ring of the two ligands is exposed to solvent and does not make contact with any residue. Furthermore, the carboxylate group of DKA was pointed toward Lys-159 whereas 5CITEP oriented its tetrazolate anion toward this residue. The salt bridges were observed between the ammonium group of Lys-159 and the carboxylate (DKA) or the tetrazolate ring (5CITEP), which will be discussed in the “Salt-bridge analysis” section.

To further investigate the structural changes of ligands, the torsional angles Tor1 (C3-C4-C5-C6) and Tor2 (C6-C7-C8-O9, C6-C7-C8-N9), denoted in Fig. 1, of DKA and 5CITEP were statistically analyzed as a population frequency (Fig. 8). The Tor1 distribution peaks of the DKA and 5CITEP mostly overlap whereas the Tor2 angles do not. Both DKA and 5CITEP produced a single preferential coplanar conformation of indole ring, as evidenced by the only one peak for Tor1 at ∼0° (Fig. 8 c). For the torsional angle Tor2, a single preferential conformation of the carboxylate moiety of DKA was represented by a single sharp peak at ∼−120° (Fig. 8 d). This sharp and pronounced peak implied a low flexibility of the carboxylate functional group in a narrow range. Meanwhile, 5CITEP yielded two preferential conformations of the tetrazole ring, as mentioned in the “Mg²⁺ coordination and inhibitor binding mode” section, i.e., two broad peaks at Tor2 = from −180 to −100° and at Tor2 = 0–90°. At Tor2 = from −180 to −100°, the N10 of the tetrazole ring was close to Lys-159 whereas at Tor2 = 0–60°, the N11 was close to the same residue. This suggests that the tetrazolate ring of 5CITEP might alternate between two conformations in the binding pocket and also supports the finding that either N10 or N11 of 5CITEP can make a salt link with Lys-159. The higher peak at Tor2 = 0–90° indicates a higher probability of finding the N11 in a salt bridge with Lys-159 as compared to N10. According to the observations above, it is worth noting that the rigidity of Tor2 in DKA is probably due to the existence of a stronger salt bridge to Lys-159 for the entire simulation. In contrast, the tetrazolate moiety of 5CITEP formed a weaker salt link with Lys-159.

Mg²⁺ coordination

To explore the dynamical properties of the divalent cation and its coordination state, the interatomic distances between Mg²⁺ and the chelating oxygen atoms are plotted as a function of simulation time (Fig. 6, b and c). For IN-DKA, there are seven oxygen atoms (OD1-Asp-64, OD2-Asp-64, OD1-Asp-116, OW1, OW2, O1, and O2 of DKA) whose distances are able to coordinate with the metal ion. The distances between Mg²⁺ and OD1-Asp-64, OW2, O1, and O2 were observed at ∼1.8 Å whereas the other three (Mg²⁺–OD2–Asp-64, Mg²⁺–OD1–Asp-116, and Mg²⁺–OW1) were found to be 2.5 Å (Fig. 6 c). These coordination distances were stable along the whole trajectory. It appears that the Mg²⁺ bound tightly with the OD1-Asp-64, OW2, O1, and O2 of DKA, as indicated by their shorter distances (1.8 Å). The Mg²⁺ forms a distorted octahedral complex in which the carboxylate group of Asp-64 is twisted toward the catalytic metal ion, allowing both OD1 and OD2 to chelate the Mg²⁺ in a monodentate configuration (Fig. 9 b).

For IN-5CITEP, Mg²⁺ yields a somewhat similar pattern of Mg²⁺ coordination state as found in IN-DKA. As mentioned above (section MM), Mg²⁺ is chelated by six oxygen atoms (O1-Asp-64, OD1-Asp-116, OW1, OW2, O1, and O2 of 5CITEP). In IN-5CITEP, Asp-64 uses only its OD1 atom to chelate the Mg²⁺ (Mg²⁺–OD2–Asp-64 = 4.5 Å) whereas both OD1 and OD2 were seen to coordinate the divalent cation in IN-DKA. The coordination distances were 1.8 Å (Mg²⁺–OD1–Asp-116, Mg²⁺–OW2, Mg²⁺–O1, and Mg²⁺–O2) and ∼2.5 Å (Mg²⁺–OD1–Asp-64 and Mg²⁺–OW1) (Fig. 6 b). In this system, the Mg²⁺ is tightly bound with the OD1 atom of Asp-116 rather than OD1 of Asp-64 (found in IN-DKA). This distorted octahedral geometry of Mg²⁺ coordination (Fig. 9 c) persists for the entire course of the simulation.

It is worth noting that besides its catalytic role, the Mg²⁺ also plays a structural role. In the HIV-1 IN active site, two Asp residues (Asp-64 and Asp-116) and the keto-enolate motif of the inhibitor are close to each other and form a carboxylate cluster, thereby generating an excess of negative charge in the binding pocket. The positive charge of Mg²⁺ is necessary to stabilize the carboxylate cluster by diminishing the electrostatic repulsion between these oxygen atoms.

Salt-bridge analysis

Ionic interactions play a critical role in biological systems, therefore, a detailed analysis of salt-bridge formation between HIV-1 IN and ligands was carried out for the dynamics trajectories. The distances between the negatively charged group (carboxylate or tetrazolate) of ligand and the ammonium group of Lys-159 as a function of simulation time were plotted in Fig. 7. In IN-DKA, the average distances between the negatively charged group of the ligand (O9 and O10) and the ammonium nitrogen (NZ) of Lys-159 is ∼2.8 ± 0.17 Å (Fig. 7 c) implying that this strong salt-bridge finding was observed throughout the simulation period. In contrast, there is a weaker ionic interaction between the tetrazolate ring of 5CITEP and the Lys-159 during the first 200 ps of the simulation (Fig. 7 b). Within this period, the average distances between the tetrazolate ring and Lys-159 (NZ) are longer than ∼4 Å (N10–NZ = 5.21 ± 0.57 and N11–NZ = 4.59 ± 0.52). For the remainder of the simulation, the tetrazolate ring of 5CITEP moved closer to Lys-59 (N10–NZ = 4.07 ± 0.69 and N11–NZ = 3.97 ± 0.57), thus, the ionic interaction becomes stronger as compared to that found in the early stage of the production phase. It should be mentioned that although an ionic interaction between 5CITEP and Lys-159 can occur, it is weaker than those observed in the IN-DKA complex.

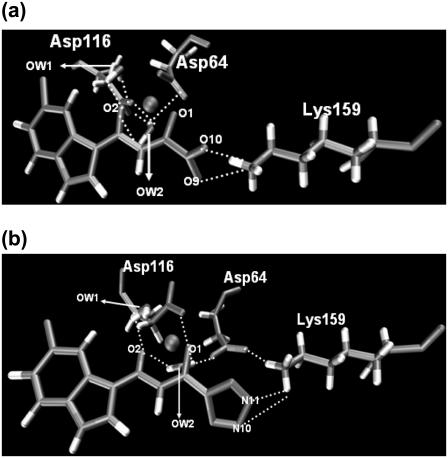
To clearly demonstrate the dynamic nature of the salt links between HIV-1 IN and the two inhibitors, snapshots were taken from trajectories of IN-DKA and IN-5CITEP complexes and are given in Fig. 10. In both complexes, only residue Lys-159 was found to form a salt link with ligands. In IN-DKA, the ammonium group of Lys-159 interacts with the carboxylate moiety of DKA (Fig. 10 a) whereas that of the residue interacts with the tetrazolate ring as found in IN-5CITEP (Fig. 10 b). A hydrogen-bond was observed between bulk water and the NH of indole ring of inhibitors in the two systems. In addition, the ligand also formed hydrogen-bonds with the bridging water in the active site of HIV-1 IN, as discussed in the next section. It is worth mentioning that the strong salt link between Asp-64 and Lys-159 was detected in the IN-5CITEP complex (Fig. 10 b). Meanwhile, the salt link between these two amino acids was not observed in the IN-DKA complex because of the long distance (longer than 6.5 Å) between these two residues.

FIGURE 10.

Snapshots of the active site of HIV-1 IN-DKA complex (a) and HIV-1 IN-5CITEP complex (b). Hydrogen-bonds and salt bridges are indicated by dotted lines. All distances are in angstroms. The figures were generated using VMD (54).

According to the existence of a strong salt link between DKA and HIV-1 IN throughout the simulation, ionic interaction seems to be a major reason why DKA is a more potent inhibitor than 5CITEP.

Role of water molecules

It is well known that water molecules are important in biological systems, including in catalysis and in mediating ligand binding. The x-ray structure of the HIV-1 IN-5CITEP complex (20) revealed that four interfacial water molecules were located close to Asp-64, Asp-116, and 5CITEP. These water molecules as well as the side-chain oxygen atoms of both aspartic residues were found to octahedrally coordinate the Mg²⁺ ion. The importance of these water molecules in HIV-1 IN is uncertain. Based on an MD simulation study (29) of the x-ray structure of the HIV-1 IN-5CITEP complex, it was shown that water molecules present in the active site may be crucial for bridging between the NH of indole ring of ligand and carbonyl oxygen of Asp-64 and OD of Asn-155, through hydrogen-bonding interactions.

In this study, our attention was focused on the two “catalytic” water molecules (water No. 1 and water No. 2) coordinated to the Mg²⁺. The positions of both water molecules were taken from the x-ray cocrystal structure of HIV-1 IN/5CITEP (1QS4) i.e., water No. 226 and water No. 443. To study the role of these water molecules, the hydrogen-bond bridges between these water molecules and protein as well as ligand were examined along the MD trajectories. The two systems exhibited a somewhat similar pattern of bridging water molecules between Asp-64, Asp-116, and the keto-enolate motif of the ligands (Fig. 10). These coordinated water molecules did not significantly move and did not exchange with the bulk water. The hydrogen-bond bridges formed by water molecules between the ligand and aspartic acids can therefore stabilize the binding between inhibitors and HIV-1 IN. It should be pointed out that a number of hydrogen-bonds between the bridging water molecules and the protein, as well as the ligand in IN-DKA, were larger that those seen in the IN-5CITEP complex. In IN-DKA, both OD1 and OD2 atoms of Asp-64 and Asp-116 were involved in a hydrogen-bond network with waters whereas only the OD1 atoms of these two residues were hydrogen-bonded to the bridging water in IN-5CITEP. Besides the bridging between protein and ligand, these two water molecules sometimes mediated hydrogen-bond bridges between Asp-64 and Asp-116.

Residue contributions

To elucidate the role of individual MM residues in stabilizing or destabilizing the QM subsystem, an amino acid decomposition analysis (52,53) was carried out as described below. The QM/MM interaction energy, which consisted of electrostatic and van der Waals terms, of each frame was computed. Afterward, each MM residue was removed, one by one, and the QM/MM interaction was recalculated. The contribution of each individual amino acid is defined in terms of the energy difference resulting from the residue deletion. Although, the average contributions were examined from a set of 120 snapshots (at every 5 ps from 600 to 1200 ps), the results should qualitatively estimate which amino acids significantly stabilize (positive) or destabilize (negative) the QM subsystem.

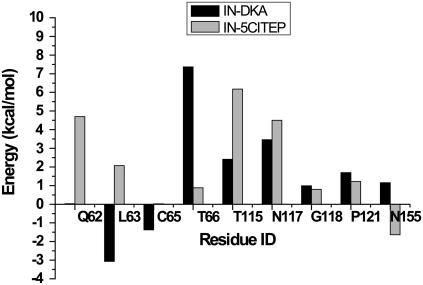
Fig. 11 shows the contributions of each MM residue in stabilizing or destabilizing the QM part of the IN-DKA and IN-5CITEP complexes. The standard deviations of each residue contribution are given in Table 1. It should be pointed out that the contributions of the stabilizing amino acids are much more important than those of the destabilizing ones. For both complexes, among all residues, Lys-159 exhibited the greatest contribution in stabilizing the QM subsystem, as indicated by its high interaction energy (∼180 kcal/mol for both systems). This stabilizing effect is mainly due to a strong ionic interaction between the QM part and Lys-159, i.e., the negatively charged group of ligand (carboxylate or tetrazolate) and the positively charged of ammonium group of Lys-159. The remarkable differences between the two complexes are the roles of Gln-62 and Leu-63. Gln-62 neither stabilizes nor destabilizes the QM part in IN-DKA complex, however, in IN-5CITEP, it plays a stabilizing role. Moreover, Leu-63 provides a major destabilizing effect on the IN-DKA complex whereas it yields a stabilizing effect on the IN-5CITEP complex. This arises from the differential ability for forming hydrogen-bonds between the O of Leu-63 and the NH of Asp-116 between the two complexes. Furthermore, the QM part of IN-DKA is stabilized by Thr-66 with a higher magnitude than that observed in IN-5CITEP. Residues Thr-115, Asn-117, and Phe-121 play a critical role in stabilizing the QM subsystem in both complexes. The roles of Cys-65, Gly-118, and Asn-155 in terms of stabilizing or destabilizing are unclear due to the high values of their standard deviations.

FIGURE 11.

Amino acid decomposition analysis showing contributions of each individual MM amino acid to the QM subsystem. Stabilizing and destabilizing interactions are represented as positive and negative energy values, respectively. Only residues exhibiting an energy >1 kcal/mol are shown.

TABLE 1.

Standard deviation (SD) of amino acid decomposition analysis

Amino acid	SD (kcal/mol)
	IN-DKA	IN-5CITEP
Gln-62	0.82	0.87
Leu-63	1.70	0.98
Cys-65	2.30	2.41
Thr-66	2.38	2.09
Thr-115	1.42	0.85
Asn-117	1.97	1.24
Gly-118	1.13	0.94
Phe-121	0.33	0.51
Asn-155	2.40	1.14
Lys-159	4.70	5.92

CONCLUSION

There are two important aspects of the analysis of our results. The first one is the comparison of the results obtained from conventional and mixed QM/MM MD simulations of IN-5CITEP to determine whether classical MD is sufficient and suitable for the studied systems. Another aspect is how IN-DKA and IN-5CITEP complexes differed in the QM/MM simulations. Our results are consistent with the higher potency of DKA as compared to 5CITEP.

Comparison of HIV-1 IN structures taken from classical and QM/MM simulations reveals two notable differences around residues 116–119 and 140–149. In the conventional MD, residues 116–119 show high mobility, however, this loop was quite rigid in the QM/MM simulation. This is probably because in conventional MD, Gly-118 occasionally forms a hydrogen-bond with Phe-121 and Thr-122 whereas in the QM/MM study, it is always involved in a hydrogen-bond. Moreover, differences in the dynamics of loop residues 140–149 lead to substantially different orientations of key amino acids, particularly Lys-159 in the α4-helix between the two calculations. Another significant difference between the two levels of calculation is the coordination geometry of Mg²⁺ which is found to be octahedral and distorted octahedral for the MM and QM/MM simulations, respectively. In addition, the bound positions of 5CITEP in the classical and QM/MM MD simulations are quite different. In the MM study, the ligand is positioned far from Lys-159, thus, it cannot form a salt link with this residue. On the contrary, a salt bridge between this amino acid and 5CITEP was detected in the QM/MM study.

In addition, detailed structural analyses of the HIV-1 IN complexed with either DKA or 5CITEP indicate that the protein and inhibitor in the two complexes display a different dynamical behavior. Substantial structural differences were found at: i), residues 60–68; ii), residues 116–119; and iii), residues 140–149 (a flexible loop). The IN-DKA complex exhibits a shorter β1-sheet (60–66) than in the IN-5CITEP complex (residues 60–68). Furthermore, loop residues 116–119 in IN-DKA is much more curved than that seen in IN-5CITEP. Moreover, the side chains of Asp-64 and Asp-116 in the two systems are significantly different resulting in a somewhat different pattern of the distorted octahedral geometry of Mg²⁺ between IN-DKA and IN-5CITEP systems. In the IN-DKA complex, Asp-64 oriented its OD1 and OD2 atoms to chelate the Mg²⁺ in a monodentate configuration whereas only the OD1 is used to coordinate the divalent metal ion in the IN-5CITEP complex. Moreover, both OD1 and OD2 belonging to Asp-116 in IN-DKA are involved in water-mediated hydrogen-bonding whereas only the OD1 of IN-5CITEP can form a hydrogen-bond with a bridging water molecule.

The bound position of DKA and 5CITEP is somewhat similar. The keto-enolate moiety directly interacts with the Mg²⁺ whereas the carboxylate (for DKA) or tetrazolate (for 5CITEP) is oriented toward residue Lys-159. Moreover, the keto-enolate motif of both DKA and 5CITEP is indirectly hydrogen-bonded to Asp-64 and Asp-116 via bridging water molecules. An analysis of the conformational dynamics of the ligand reveals that the DKA conformation is quite rigid across the MD simulation whereas the 5CITEP conformation exhibits high mobility. Furthermore, a strong salt link between DKA and HIV-1 IN existed for the entire course of the simulation whereas that between 5CITEP and Lys-159 was weaker. This means that ionic interactions were stronger in the IN-DKA complex as compared with the IN-5CITEP system. This supports experimentally observed the higher potency of DKA as compared to 5CITEP. Amino acid energy decomposition is also in support of the important role of Lys-159 in the mechanism of action. In general, our study provides insights into the detailed mechanism of action of DKA and 5CITEP and suggests why DKA is a more potent inhibitor, when compared with 5CITEP, against HIV-1 IN.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.