Eavesdropping on the Social Lives of Ca²⁺ Sparks

Abstract

Ca²⁺ sparks arise from the stochastic opening of spatially discrete clusters of ryanodine receptors called a Ca²⁺ release unit (CRU). If the RyR clusters were not spatially separated, then Ca²⁺ released from one RyR would immediately diffuse to its neighbor and lead to uncontrolled, runaway Ca²⁺ release throughout the cell. While physical separation provides some isolation from neighbors, CRUs are not incommunicado. When inter-neighbor interactions become large enough, Ca²⁺ waves spontaneously emerge. A more circumscribed interaction shows up in high-speed two-dimensional confocal images as jumping Ca²⁺ sparks that seem to be sequentially activated along the Z-line and across Z-lines. However, since Ca²⁺ sparks are stochastic events how can we tell whether two sparks occurring close together in space and time are causally related or appeared simply by coincidence? Here we develop a mathematical method to disentangle cause and coincidence in a statistical sense. From our analysis we derive three fundamental properties of Ca²⁺ spark generation: 1), the “intrinsic” spark frequency, the spark frequency one would observe if the CRUs were incommunicado; 2), the coupling strength, which measures how strongly one CRU affects another; and 3), the range over which the communication occurs. These parameters allow us to measure the effect RyR regulators have on the intrinsic activity of CRUs and on the coupling between them.

INTRODUCTION

The physical separation of Ca²⁺ release units (CRUs) as discrete clusters of ryanodine receptors is essential for local control of excitation-contraction coupling in striated muscle (1). If the CRUs were not separated then Ca²⁺ released from an RyR would be immediately communicated to its neighbor and trigger regenerative Ca²⁺ release throughout the cell. The discreteness of CRUs is manifest in Ca²⁺ sparks (2–5), the highly localized release of Ca²⁺ from the sarcoplasmic reticulum (SR). The distance between the CRUs in the plane of the Z-line in mammalian cardiomyocytes has been estimated to be ∼0.3–0.4 μm based on electron microscopy (6); between ∼0.65 and ∼1 μm (7,8) based on confocal measurements of fluorescently labeled RyR antibody; and ∼0.8 μm (in rat, (9)) or ∼2 μm (in cat, (10)) based on distances between spark or activation sites on Ca²⁺ waves. The longitudinal spacing of CRUs coincides with the Z-line separation and is ∼2 μm (7,11).

These separation distances are evidently sufficient to provide a degree of isolation between CRUs that prevents runaway Ca²⁺ release but not to the degree that the CRUs are incommunicado. Under certain conditions, communication between CRUs via Ca²⁺ diffusion can result in Ca²⁺ waves (12–14). More subtly, Parker et al. (9) found more circumscribed communication in which one spark triggers one or two other sparks within ∼15 ms of each other. These triggered sparks were only observed with the transverse confocal line scans (i.e., directed perpendicular to the cardiomyocytes long axis) and not with longitudinal line scans. This observation is explained by the closer transverse spacing of CRUs (∼0.5 −1 μm) in the plane of the Z-line than between Z-lines (∼2 μm). Similarly, Brum et al. (15), using rapid two-dimensional scanning, found sequential activation of sparks parallel to the Z-line in frog skeletal muscles.

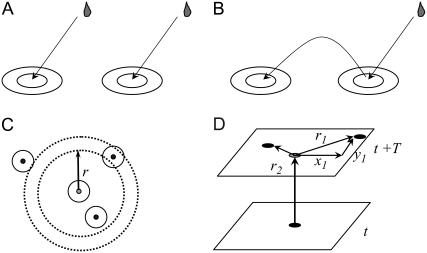
Images collected on rapid scanning two-dimensional confocal microscopes that survey a large area (∼2000 μm²) of the cell often show large number of sparks that appear like raindrops on a pond. One's attention is often drawn to sparks that seem to be coupled because they occur closely in space and time, giving the impression that sparks are jumping (Fig. 2). It is important to assess the magnitude of coupling between sparks because if a sufficient number in a small region occur in a short time period they can coalesce into Ca²⁺ waves (12,14), which could trigger an abnormal action potential and possibly arrhythmias (16–19). However, just as it is impossible to say whether two sets of ripples on a pond were caused by two raindrops (Fig. 3 A) or whether one set was caused by the splash from one raindrop (Fig. 3 B), when only the ripples are observable, we cannot determine for any particular pair of sparks whether they are causally or coincidentally related.

FIGURE 2.

Jumping sparks. Shown are sequential confocal images taken at 12.5 ms intervals (time flows left to right). Vertical bar on the right equals 1 μm. See text for additional details.

FIGURE 3.

The raindrop analogy. Ripples on a pond can arise in two ways, either by separate raindrops (A) or from splashes (B). In the former case, the two ripples are coincidental, in the latter, the ripples are causally related. (C) Geometry for computing the number of ripples (solid circles) around the central ripple (shaded circle) as a function of distance from the center. The dotted lines define the annulus whose inner radius is r and outer radius is r +Δr. (D) Schematically shows how distances between central spark and neighbors are computed. Each plane is a confocal image. Solid circles mark the position of the central spark first occurring at time t and the neighboring sparks first occurring at t+T. Position of the central spark on the t+T image is marked by the shaded circle. The value r is the Euclidean distance between the central spark and its neighbors.

In this article, we develop a method to disentangle cause and coincidence in the origin of sparks in a statistical sense. We will show how to derive from the probability distribution of distances between sparks, three fundamental properties of spark generation: 1), the intrinsic spark frequency, the spark frequency one would observe if the CRUs were incommunicado; 2), the coupling strength; and 3), the coupling space constant. These parameters quantify the intrinsic properties of CRUs and communication between themselves. These parameters allow us to measure the effect that RyR regulators have on the intrinsic activity of CRUs and on the coupling between them.

METHODS

Cell isolation

Male Sprague-Dawley rats (Harlan, Indianapolis, IN) were anesthetized with isoflurane supplemented with O₂. After suppression of reflexes, the hearts were removed via midline thoracotomy and a standard enzymatic technique was used to isolate the ventricular cells as described previously (20). All animals and procedures were handled strictly in accordance to the National Institutes of Health guidelines and our Institutional Animal Care and Use Committee approved protocols. Chemicals and reagents were purchased from Sigma-Aldrich (St. Louis, MO) if not specified otherwise.

Indicator loading

The cells were loaded with Fluo-4 (Molecular Probes-Invitrogen, Carlsbad, CA) in Tyrode (Ty) solution containing (in mM): 145 NaCl, 4 KCl, 1 CaCl₂, 0.33 NaH₂PO₄, 1 MgCl₂, 10 HEPES, 10 glucose (pH 7.3, adjusted with NaOH), and 2.5 μM fluo-4 acetylmethyl ester (Molecular Probes-Invitrogen) at room temperature for 45 min. Di-8-ANEPPS (Molecular Probes-Invitrogen), 15 μM, was added to the above solution in the last 15 min of the loading period to label the sarcolemma and t-tubules. The cells were studied within 2 h after loading.

Preconditioning train

To achieve a uniform SR Ca²⁺ load, cells in Ty were field-stimulated (1 Hz) for 2 min, allowing ample time for the cell contraction to reach a steady state. Confocal image acquisition started 10 s after stopping field stimulation.

Confocal microscopy

Experiments were carried out on the Zeiss 5 Live confocal microscope (Carl Zeiss, Jena, Germany) equipped with a 100 × 1.4 numerical aperture Plan-Apo oil objective (Zeiss). The indicators were excited with a 488 nm laser and the emitted light was passed through a 520 nm longpass filter. Images were scanned bidirectionally at 80 Hz. The zoom factor was set to 1, which produces an x-y pixel size of 0.12 μm × 0.12 μm.

Spark detection and determination of spark frequency

Sparks were detected using the approach described in Bányász et al. (21). Because we need the spark coordinates in relationship to the Z-lines, the image of the cell is manually rotated so that the longitudinal axis of the cell is aligned horizontally. Alignment accuracy was improved by lining up the di-8 ANEPPS labeled t-tubules with vertical gridlines superimposed on the cell image.

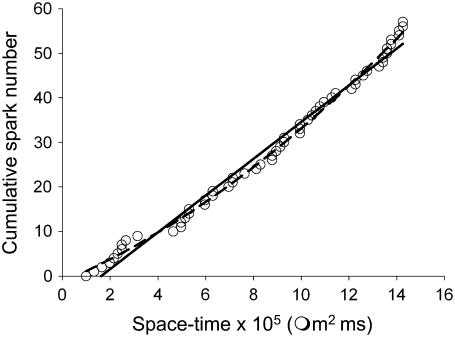
The Ca²⁺ spark frequency, γ_total, for a cell was determined from the slope of the cumulative spark number (CSN) plotted against the product of time and cell area (21). The reason for the subscript total in γ_total is explained later. A linear CSN plot means that the spark frequency is constant. Only those cells in which the spark frequency was constant were used in the analysis. (See the discussion after Eq. 17 to see why we only use cells with constant spark frequency.) The CSN plot sometimes has a quadratic or other nonlinear shape, which means that the spark frequency is not constant. We need a way to objectively and automatically determine whether the CSN plot is linear. We used two tests to determine whether the CSN plot is linear or quadratic. First, we used an ANOVA to test whether the sum of squared deviations between the linear and quadratic fitted curves and the data were significantly different at a probability level of α = 0.01. If the probability (from the F distribution) was >α, then the CSN was considered to be linear. However, even when the probability was <α (meaning the linear and quadratic plots were statistically distinguishable), the difference might not be meaningful. Fig. 1 shows such an example. The open circles are the measured CSN, the solid line is the linear fit, and the dashed curve is the quadratic fit. The two fits are statistically distinguishable but the difference does not appear meaningful. To understand why this occurs we first note that the number of degrees of freedom (df) used in the ANOVA is N_sparks-2 and N_sparks-3 for the linear and quadratic curves, respectively, and N_sparks is the number of sparks. Since N_sparks is typically 50 or more, df is almost the same for both functions. Therefore, if the CSN plot deviates even slightly from linearity, the null hypothesis (the CSN is linear) is almost always rejected because the quadratic fit produces a smaller sum of squared deviations.

FIGURE 1.

How γ_total is determined. The number of sparks (cumulative spark number, CSN) is plotted against the product of the time the spark occurred (time/frame × frame number) and the area of the cell. The CSN is fit to both a line and a quadratic. Although the quadratic fit is statistically better, the curvature is negligible in the data range so this CSN is considered to be linear. The solid line is the best linear fit.

The intuitive notion of a meaningful difference is captured in the magnitude of the curvature (the coefficient of the quadratic term, c₂). Let the linear fit be given by y = a₁ + b₁x and the quadratic fit be y = a₂ + b₂x + c₂x². To measure the relative contributions of the linear and quadratic terms we compare 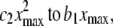where x_max is the maximum space-time value. If the ratio 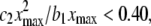then we say that the difference is not meaningful and we say that the CSN plot is linear. For the data in Fig. 1, this ratio is 0.395, just below the cut-off so the CSN is considered to be linear. This particular set of data was chosen to show the worst-case data that would be used in our subsequent analysis. The spark frequency equals the slope of the CSN plot, b₁.

Definition of neighbors

Let the coordinates of a spark occurring at position (x, y) at time t be given by (x, y, t). We say that spark S is in the neighborhood of the central spark S₀, if d_Xmin ≤ |x−x₀| ≤ d_Xmax, d_Ymin|y−y₀| ≤ d_Ymax, and 0 < |t−t₀| ≤ d_T, where (x₀,y₀,t₀) are the coordinates of S₀. The reason for using nonzero lower bounds, d_Xmin = 0.7 μm and d_Ymin = 0.3 μm, is to preclude counting S₀ as being its own neighbor. This could occur if the rise of the spark continues over successive frames although this is unlikely since the time per frame is 12.5 ms and the spark rise-time is ∼5 ms. A false neighbor could also be generated if there was a small shift in the center of mass of S₀ in successive frames; the nonzero lower bounds reduce the number of these kinds of false-positive neighbors. We chose d_Xmax = d_Ymax = 15 μm. This distance might seem far outside the realm of what a neighborhood should be but, as we will explain later, the determination of γ depends on measuring very distant neighbors. The reason for not choosing d_Xmax ≫ 15 μm is to keep the size of the entire neighborhood around the width of the cell. By setting d_T = 15 ms, we limit neighboring sparks only to those occurring one frame after S₀.

Probability density estimation using kernel methods

We will need to estimate the probability density function (pdf), f(r), of the distribution of distances from the central spark. The histogram is the most familiar method of obtaining the pdf. The histogram is, however, sensitive to the bin width and the location of the bin boundaries. Kernel methods for estimating the probability density (22) do not have bin boundaries and are less sensitive than the histogram to changes in bandwidth (w, the analog of bin width).

The quantity f(r) is constructed as follows. For each unique distance r_i we define the function

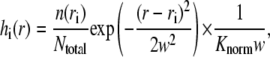(1)

where n(r_i) is the number of sparks that are at a distance r_i from the central spark and N_total is the total number of sparks. The factor 1/(K_normw),

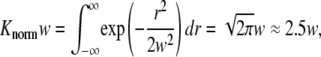(2)

normalizes h_i(x) so that its integral equals n(r_i)/N_total. The pdf is

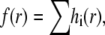(3)

where the index runs over all unique distances. Note, by construction, the integral of f(r) over all r equals unity.

Simulating Ca²⁺ sparks

We simulated sparks using a two-dimensional lattice with a CRU on each lattice point. CRUs were separated along the x and y axes by l_x and l_y, respectively, and the lattice dimension was 40 μm on each side. We used a very high CRU packing density, 100/μm² (l_x = l_y = 0.1 μm) or 50/μm² (l_x = 0.2 μm, l_y = 0.1 μm), which are 200- or 100-times higher than in real cells, simply to get a lot of sparks in a short time. Each CRU has an intrinsic firing rate of γ. If a CRU at lattice point i, j fires at time k, then it changes the firing probability rate of the neighboring CRUs at time k+T to φ given in Eq. 6. The value r is the Euclidean distance between CRU i, j and the CRU of interest. The influence of CRU i, j does not extend beyond time k+T. The intrinsic frequency γ, coupling strength A, and the coupling space constant ρ are input parameters to the program. To determine whether a CRU will fire at k+T, φT is computed (with T = 1) and a random number from a uniform distribution is generated. The CRU fires only if this number is <φT.

RESULTS

Jumping Ca²⁺ sparks

An example of jumping sparks is shown in the successive confocal images (time flowing from left to right) of Fig. 2. The horizontal axis lies parallel to the cell's longitudinal axis (the x axis) and the vertical axis is parallel to the transverse axis (y axis). A spark appears in the second frame; the arrow tip points to the center of the spark. In the third frame another spark appears to the left and above the original spark; the arrow tip still points to the center of the original spark. Subsequent images show sequential activation of sparks along the transverse axis. The horizontal bars at the left edge mark the vertical positions of the centers of the sparks. When viewed in rapid succession, this sequential activation of sparks gives one the illusion that a spark is jumping from site to site.

Separating cause from coincidence

One would be hard pressed not to believe there was some causal relationship between the Ca²⁺ release sites to give rise to the jumping sparks in the example above. However, in any stochastic system there are bound to be events that occur close together in space and time simply by coincidence while other closely juxtaposed events may be causally related.

To develop our method for disentangling cause from coincidence, we will proceed as follows. First, we consider an analogy between raindrops on a pond and sparks. This simple physical model is very helpful for identifying the essential features of the problem. Second, we derive the expression, f*(r), that gives the distribution of sparks as a function of distance from the central spark using a model that ignores the contributions of noncentral sparks. We will find that the predictions based on this too simple model do not completely agree with our simulation results. Nevertheless, the simplicity of this model makes it easier to introduce the key concepts. Next, we expand the model to include the contributions from the noncentral sparks and we will see that this necessitates adding a small correction term to the formulas derived from the simpler model. Finally, we apply the method to determine the intrinsic frequency, the coupling strength, and the coupling space constant to real data obtained from rat ventricular myocytes.

The raindrop analogy

Fig. 3 shows how two ripples on a pond can be formed by either two separate raindrops (Fig. 3 A) or by one raindrop and a splash (Fig. 3 B). In the case of Fig. 3 A, the two ripples occur by coincidence; there is no causal relationship between the two raindrops. In Fig. 3 B, however, the two ripples are causally related; the ripple on the left is caused by a splash from the raindrop that caused the ripple on the right. If only ripples are visible (not the raindrops or splashes), how can we assess the frequency that a splash from a raindrop causes another ripple? Imagine a snapshot of the ripples on the pond and focus your attention on the center of one ripple, the central ripple—the circle with the shaded center in Fig. 3 C. Let n(r) be the number of centers of ripples (solid circles) within an annulus of radius r and thickness Δr. Since a splash from the central ripple is unlikely to travel far, the number of ripple centers in a very large radius annulus should be proportional to the product of the area of the annulus, 2π r Δr, and the frequency of the raindrops (raindrops/time/area), γ,

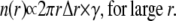(4)

Close to the central ripple, raindrops and splashes would create ripples so n(r) is

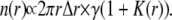(5)

K(r), the coupling kernel, describes the number of splashes at a distance r per raindrop. We would expect that K(r) decreases monotonically to zero so Eq. 5 merges smoothly to Eq. 4.

The value γ is the intrinsic frequency; it is the frequency of the raindrops and it is also the frequency of ripples that would be observed if no splashing occurred. According to Eq. 4, n(r) is a linear function for large r and its slope is proportional to γ. This is a remarkable result, as it tells us that we can determine the frequency of raindrops simply by measuring the spatial distribution of ripples. Later we will show that this is almost but not completely correct.

A simple, incomplete, but conceptually useful model of Ca²⁺ spark coupling

Our method for determining the magnitude of Ca²⁺ spark coupling and the intrinsic spark frequency follows by simply substituting sparks for ripples. Fig. 3 D shows schematically how the n(r) is determined from two-dimensional confocal images. The solid circle on the lower rectangle is the position of the central spark that occurs on the confocal image at time t. The upper rectangle is the confocal image at time t + T. (At a typical 80 Hz scan rate, T = 12.5 ms.) The shaded circle on this rectangle is the position of the central spark, which may or may not be present in the image. The solid circles are sparks that first make their appearance at t + T. The Euclidean distances, r, between the central spark and the other sparks at t + T are computed. The quantity n(r) is the number of sparks that are at a distance between r and r + Δr from the central spark. This procedure is repeated for each spark. In other words, each spark is treated as a central spark.

The coupling kernel

Let γ be the intrinsic spark frequency; its units are number of sparks/time per CRU. This is the spark frequency you would measure if one spark did not influence the probability of another spark occurring. Experimentally, this influence could be reduced by loading the cell with a Ca²⁺ buffer such as EGTA to reduce the diffusion of Ca²⁺ from a release site to a neighboring CRU. This influence is also nil far from the central spark. When a spark occurs, Ca²⁺ diffuses to neighboring CRUs and increases their probability of firing so we expect the spark frequency near the central spark would increase above the intrinsic frequency to γ(1 + K(r)). A Ca²⁺ spark has a roughly Gaussian profile (9,23,24) and we found that the spark is spatially symmetric (21). We, therefore, provisionally choose the coupling kernel to be a spatially symmetric Gaussian and define the spatially dependent spark frequency, φ(r), to be

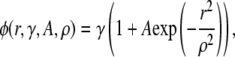(6)

where A is coupling magnitude and ρ is the coupling space constant. The challenge is to determine γ, A, and ρ from the spatial distribution of sparks, n(r).

The quantity φ(r) is the probability of a spark occurring per unit time. Therefore, the probability that a CRU at a distance r from the central spark will fire within T is given by

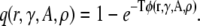(7)

(This is simply the complement of the waiting time distribution; see Izu et al. (25).) The number of sparks expected in an annulus around the central spark within time T equals the product of the number of CRUs in the annulus and the probability of firing,

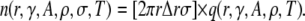(8)

The first set of factors is the annulus area times the CRU density (CRU/area), σ. In all cases we have encountered the following inequality holds:

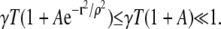(9)

Under this condition Eq. 7 simplifies to 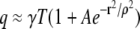and Eq. 8 has the same form as Eq. 5. For brevity we will often write n(r) in place of n(r,γ, A,ρ,σ,T).

The quantity n(r) is the number of sparks at a distance r from a single central spark. Let N(r) be the aggregate number of sparks at distance r from all central sparks. (Recall that each spark is used as a central spark.) Then N(r) is

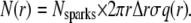(10)

Instead of working with N(r), it is more convenient to work with its density f(r) defined by

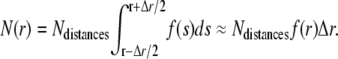(11)

Rearrangement of Eqs. 10 and 11 gives

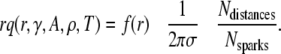(12)

The first term on the right is the probability density of the distance distribution between central and noncentral sparks, the second term is a cell structure factor as it involves the CRU density, and the last term is a ratio of extensive quantities that depend on the size of the data set. For 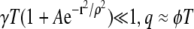and Eq. 12 simplifies to

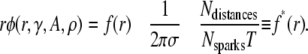(13)

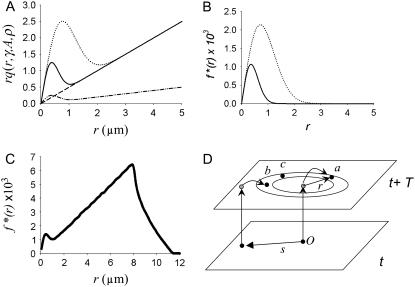
The r q(r,γ,A,ρ,T) curves, shown in Fig. 4 A for different combinations of γ, A, and ρ, have two distinctive features. First, they become linear for large r. This happens because, far from the influence of the central spark, the number of sparks in each annulus depends primarily on the product of the intrinsic spark frequency and the area of the annulus, which scales linearly with r. This linear behavior is analogous to Eq. 4 of the raindrop problem, where ripples caused by splashing are unlikely far from the central ripple, and so the number of ripples depends only on the intrinsic raindrop frequency. Differentiating Eq. 12 shows that the slope of r q(r,γ, A, ρ, T) converges to 1− e^−γT for large r. Since T is known, it follows that γ can be determined from the slope of the scaled density of distances given in Eq. 12. Under conditions where Eq. 9 holds, the slope of f*(r) is simply γ . In Fig. 4 A, γ was set to 3 × 10⁻⁴ for three curves drawn with solid, dashed, and dotted lines. Note that they all converge to the same slope at large r. The curve drawn with dashed-dotted lines was generated using γ = 1 × 10⁻⁴ and has a correspondingly shallower slope than the others.

FIGURE 4.

Distribution of neighbor distances from the central spark. (A) Plot of rq(r,γ, A, ρ). (Dashed line, γ = 5 × 10⁻⁴, A = 0, ρ = 0.5; solid curve, same as before except A = 10; dotted curve, same except ρ = 1.0. Dot-dash curve, γ = 1 × 10⁻⁴, A = 10, ρ = 0.5.) (B) Difference curve, rq(r,γ, A, ρ)− rq(r,γ, 0, ρ). Line style corresponds to panel A. (C) Normalized distance distribution f*(r) for simulated data. (D) Schematic of a more complete model showing how a noncentral spark at 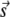contributes to sparks (labeled b) in the annulus. Colors of circles (solid and shaded) have the same meaning as in Fig. 3 D. Spark c occurred spontaneously and spark a was triggered by the central spark at the origin O.

The second distinctive feature of f*(r) is the hump at r ≈ 0. This hump represents the increased number of sparks that are triggered close to the central spark. The height and breadth of this hump depends on the coupling magnitude and the coupling space constant. Setting A = 0 means coupling is absent and f*(r) is a straight line (dashed line). The difference between the curves is shown in Fig. 4 B for A = 10, ρ = 0.5 (solid curve) and A = 0. The integral of this difference over r is the excess number of sparks expected due to spark coupling in the region 0 < r < R in the time between t and t +T, ɛ(R,A),

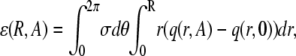(14)

where the dependence on the other parameters have been dropped for brevity. When the integration is carried over all R, the excess is

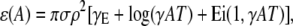(15)

where γ_E ≈ 0.5772 is Euler's number and Ei is the exponential integral (26). (The appearance of the expression in the brackets is astonishing. It is closely related to the famous relationship between the logarithm and the harmonic series, 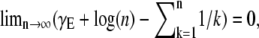which has played an important role in the development of the Riemann hypothesis (27).) As the coupling magnitude goes to zero, the term in the brackets goes to zero so the excess ɛ also goes to zero, as we would expect.

The slope of f*(r) at r = 0 is γ (1 + A) so the value of A is obtained from the slope of f*(r) at the origin. We obtain ρ from the position of the peak of the hump of the f*(r) curve, r_peak, by

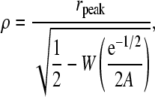(16)

where W is the Lambert W(x) function that solves We^W = x (28). The important point of this part of the analysis is that γ, A, and ρ are obtained from the density distribution of distances from the central spark.

Testing the predicted values of γ, A, and ρ against simulated data

Sparks were simulated as described in the Methods with known input values of γ, A, and ρ. Fig. 4 C shows f*(r) for the simulated sparks when the input values were γ = 5 × 10⁻⁴, A = 10, and ρ = 0.5 μm. As with the theoretical curves in Fig. 4 A, this measured f*(r) curve has a hump near r = 0 and becomes linear at large r. Unlike the theoretical curve, this f*(r) curve declines to zero beyond ∼8 μm. This decline is an artifact of the finite neighborhood size. The linear portion (from ∼2 to 8 μm) is sufficient to determine γ.

According to our analysis above, the slope of the linear portion of f*(r) should be equal to the intrinsic spark frequency γ = 5 × 10⁻⁴. The measured slope is 8.14 × 10⁻⁴ (see first row of Table 1, entry γ_fstar). Clearly, something must be missing from this simple model.

TABLE 1.

Comparison of input, measured, and estimated coupling parameter values

#	γinput	γtotal	γfstar	γcalculated	Ainput	Acalculated	ρinput	ρcalculated
1	5.0	8.14	8.14	4.82	10	10.00	0.5	0.51
2	4.0	5.76	5.70	3.93	10	9.32	0.5	0.53
3	3.0	3.86	3.90	3.18	10	8.38	0.5	0.46
4	2.0	2.35	2.35	2.04	10	8.56	0.5	0.48
5	1.0	1.09	1.16	1.00	10	9.75	0.5	0.53
6	1.0	1.05	1.13	1.00	5	5.00	0.5	0.53
7	1.0	1.14	1.21	0.95	5	6.13	1.0	0.94
8	5.0	6.18	6.18	5.18	10	7.93	0.5	0.47
9	3.0	3.38	3.39	3.17	10	7.93	0.5	0.47
10	5.0	8.03	8.06	4.72	10	10.25	0.5, 1.0	0.73
11	3.0	3.87	3.87	3.06	10	8.70	0.5, 1.0	0.68

The values γ_input, A_input, and ρ_input are the values input into the simulation program. The subscript calculated indicates the parameter values calculated from analysis. The value γ_total is the spark frequency is obtained from the slope of the best fit line to the cumulative spark number. The quantity γ_fstar is the spark frequency obtained from the linear part of f*(r), i.e., large r. All values of γ are multiplied by 10⁴. In simulations 1–7 the CRUs were symmetrically spaced with l_x = l_y = 0.1 μm; in simulations 8–11, the CRUs were asymmetrically distributed with l_x = 0.2 μm and l_y = 0.1 μm. In simulations 8 and 9, the coupling kernel was symmetric (ρ_x= ρ_y = ρ); in 10 and 11, ρ_x = 1.0 μm and ρ_y = 0.5 μm.

A more complete model of spark coupling

We erred in the derivation for the expression of n(r) by not accounting for sparks at time t +T that were triggered by noncentral sparks at time t. Fig. 4 D is a more accurate depiction of the origins of sparks. Let the central spark occur at the origin O on the image frame at time t and let a noncentral be at position vector 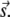The shaded circles at t+T mark the positions occupied by these sparks at t. The solid circles are new sparks that just appeared at t + T. The three sparks in the annulus could have been triggered by the central spark (a), by the noncentral spark (b), or might have arisen spontaneously without influence of either earlier sparks (c). The error in our simple model was to treat all sparks at t + T to be either of types a or c. To handle the more complex case that includes sparks of type b, let us first suppose that there are sparks at time t at position vector 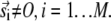Each of these sparks will trigger ɛ(γ,A,ρ,T,σ) excess sparks at t + T. The total number of excess sparks equals ɛ(γ,A,ρ,T,σ) × M. We are not interested, however, in the total number of excess sparks but rather the number of sparks in the annulus between r and r + Δr. The number of sparks triggered at t + T is

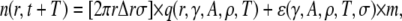(17)

where the first term is identical to Eq. 8 and m is the number of the 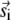sparks that have contributed to sparks in the annulus. In general, this m is unknown because the distribution of the 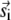vectors is unknown. Recall, however, that q(r,γ,A,ρ,T) − q(r,γ,A = 0,ρ,T) is sharply peaked at r ≈ 0. Therefore, for the m sparks to trigger sparks in the annulus, those m sparks must be close to the annulus itself, which allows us to make the approximation m = n (r,t). Substituting n(r,t) for m in Eq. 17 gives the time evolution equation for n(r,t) (see Fig. 5 D, inset and text below). Under steady-state conditions, n(r,t + T) = n(r,t) ≡ n(r), so the distribution of sparks about the central spark at the origin is

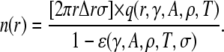(18)

Comparing Eqs. 8 and 18 we see that by not counting the contributions of the noncentral sparks, we underestimate the number of sparks in the annulus by a factor of 1−ɛ. We note that ɛ → 0 as A → 0, so Eq. 18 converges to Eq. 8.

FIGURE 5.

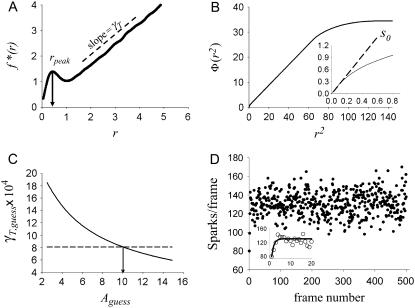
Recovering the spark coupling parameters. (A) Data in Fig. 4 C truncated beyond r = 6 μm. The value γ_T is found from the slope of the linear part of f*(r) and the arrow points to r_peak where the f*(r) curve has zero slope. The integral of f*(r), Φ, shown in B, is plotted against r². Because Φ is less subject to noise it is used for finding the slope at r = 0, shown in the inset. The Padé approximant ar²/(1+br²) is fit to Φ for r ≈ 0 and the slope s₀ is calculated from the approximant. Panel C shows how A is found from the intersection of the computed γ_T (solid curve) and the value of γ_T measured in panel A (dashed line). The intersection occurs at 10.00, exactly equal to the value of A used in the simulations. The number of sparks occurring on the simulation lattice at each time step is shown in D. The mean number of sparks/frame is 130.7. The inset shows the early time evolution of the number of sparks. The solid line is the theoretical evolution curve given by Eq. 20.

It is important to understand the range of r over which Eq. 18 is valid. In Eq. 17 each of the addends are on the order of r, denoted O(r). For r ≈ 0, however, the addends are of different orders. The first addend, [2πrΔrρ] × q(r, γ, A, ρ, T), is O(r). The second addend is O(r²) since m must be proportional to the number of CRUs in the circle around the origin, m = O(r²). Therefore, near the origin, Eq. 17 is not valid n, and n(r) given by Eq. 8 must be used instead.

Reanalysis of the simulation data

Substituting Eq. 18 in place of 2πrΔrσq(r) in Eq. 10 leads to the modified version of Eq. 12:

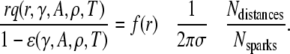(19)

We used Eq. 19 to reanalyze the data in Fig. 4 C for large r. Unlike in the simple model, where the slope of f*(r) at large r depended only on γ, in this more complex model the linear part of f*(r) depends on γ, A, and ρ. The following procedure is used to solve for these parameters.

1. The slope of the linear part of f*(r) is measured; call this γ_fstar and in this case, γ_fstar = 8.139 × 10⁻⁴ (Fig. 5 A).

2. Measure the location of the peak of the hump of f*(r), r_peak (Fig. 5 A).

3. Plot the integral of f*(r), Φ(r²) against r² (Fig. 5 B). We use the integral for data analysis because it is smoother than f*(r). Measure the slope of Φ(r²) at r = 0; call it s₀ (Fig. 5 B, inset). These three measured values—γ_fstar, r_peak, and s₀—will allow us to uniquely determine γ, A, and ρ.

4. Let A_guess be the guessed value of A.

5. Compute γ_guess according to γ_guess = 2s₀/(1 + A_guess).

6. Compute ρ_guess using A_guess in Eq. 16.

7. Compute ɛ by substituting A_guess, γ_guess, and ρ_guess in Eq. 15.

8. Compute γ_T,guess = γ_guess/(1−ɛ).

9. Increment A_guess and return to Step 4.

The function γ_fstar,guess (A_guess) is shown as the solid curve in Fig. 5 C. The correct value of coupling magnitude, A, is the solution to γ_fstar,guess (A) = γ_fstar. This equation can be solved graphically as shown in Fig. 5 C. The dashed horizontal line is at the level of γ_fstar. This line intersects the γ_fstar,guess curve at A. For the simulated data, this value of A turns out to be 10.0, identical to the input value used in the simulation. Based on this value of A, ρ is found to be 0.507 (using Eq. 16), very close to the input value of 0.50. The measured slope of Φ(r²) at r = 0 is s₀ = 2.70 × 10⁻³, so the calculated value of γ is γ = 2s₀/(1 + A) = 4.92 × 10⁻⁴, which is also close to the input value of 5.00 × 10⁻⁴. We see that the intrinsic frequency is accurately recovered when the contributions from the noncentral sparks are accounted for.

We can gain more insight into the meaning of γ_fstar by obtaining the spark frequency in a more traditional way. Fig. 5 D shows the number of sparks on each image frame; the mean number is 130.8 sparks/frame. As described in Bányász et al. (21), we determine the total spark frequency, γ_total, by first plotting the cumulative spark number (CSN) as a function of time then fitting a line to the data as was done in Fig. 1. To obtain γ_total, we divide the slope of the fitted line (130.7 sparks/frame) by the frame area (40 × 40 μm²), by the time per frame (T = 1 ms), and by the CRU density (σ = 100 CRU/μm²), which gives γ_total = 8.14 × 10⁻⁴. This value agrees exactly with γ_fstar measured from the slope of the linear part of f*(r). We call this the total frequency because it includes all sparks without regard to whether the sparks arose independently or due to coupling.

The equality of γ_fstar and γ_total shows that γ_fstar measures the total spark frequency. Results for this and other simulations using different values of γ, A, and ρ are shown in entries 1–7 in Table 1. In all cases we see that γ_total ≈ γ_fstar. Note that the total frequency can be considerably higher than the intrinsic frequency (63% higher for the first case), although the difference gets smaller as the intrinsic frequency decreases (see Eq. 22). This table shows that using the procedure described above, we are able to recover the intrinsic frequency, the coupling magnitude, and the coupling distance with reasonable accuracy.

The dynamical relationship between the intrinsic and total spark frequencies

We can get a better understanding of the relationship between the intrinsic and total frequency by seeing how the spark frequency evolves as shown in the inset of Fig. 5 D. The evolution equation for the total number of sparks is (see Eq. 17)

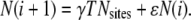(20)

For γ = 5 × 10⁻⁴, A = 10, and ρ = 0.5, the excess sparks ɛ = 0.39. The solid line is the graph of the evolution equation (Eq. 20). To see how the numbers of sparks evolve, we start with zero sparks on frame 0. There are 400² CRUs each with an intrinsic firing frequency of 5 × 10⁻⁴/ms. Within T = 1 ms we then expect to see 400² × (5 × 10⁻⁴/ms) × 1 ms = 80 sparks. There just so happens to be 80 sparks on frame i = 1. Starting the random number generator with a different seed value would produce slightly different numbers of sparks.

Each of the 80 sparks on frame i = 1 will trigger, on average, 0.39 additional sparks on frame i = 2 for a total of 80 × 0.39 = 31 sparks. These will be added to the ∼80 sparks that would intrinsically occur. We expect, therefore, 80 + 31 = 111 sparks on frame 2; we observe 99. On frame 3, we expect to see 0.39 × 111 + 80 = 123 sparks; we observe 120. We see that N(i) rapidly evolves to the steady-state value of 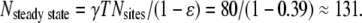As noted above, the measured mean number of sparks/frame is 130.8. From this value we calculate the total spark frequency of 8.14 × 10⁻⁴ /ms as was done above.

Therefore, we can say that the total spark frequency γ_fstar is the steady-state spark frequency that evolves due to spark coupling when the intrinsic frequency is γ, the coupling magnitude is A, and the coupling distance is ρ.

Effect of asymmetric CRU distribution and anisotropic Ca²⁺ diffusion

The simulations up to now used a distribution of CRUs that was symmetric along the x and y axes. However, as we noted in the Introduction, the distance between CRUs within the plane of the Z-line is ∼0.5–1 μm, whereas the Z-lines are spaced ∼2 μm apart. Based on our immunolabeling studies we estimate the mean nearest-neighbor distance between CRUs in the plane of the Z-line is 1 μm (7). We therefore carried out simulations in which the CRU separation distances along the x and y axes had a 2:1 ratio. As before, we used a high packing density (σ = 50/μm², l_x = 0.2 μm, l_y = 0.1 μm) to generate many sparks in a reasonable time. The results of these simulations are given in entries 8–11 in Table 1.

Simulations 1 and 8 differ only in the lattice structure. The values γ, A, and ρ are the same, yet γ_total is larger for simulation 1. This is reasonable because the CRUs are closer together along the x axis in simulation 1 than in simulation 8, thereby increasing the probability that one CRU will trigger another. The intrinsic frequency is accurately recovered. The calculated coupling magnitude is 20% lower than the input value (7.93 vs. 10), reflecting the smaller interaction between CRUs along the x axis than along the y axis.

We found that Ca²⁺ sparks in ventricular myocytes have a circular shape, suggesting that Ca²⁺ diffusion is isotropic (21). Parker et al. (9), however, determined that Ca²⁺ diffuses anisotropically based on the different spark profiles obtained when the confocal line scan is directed longitudinally (x axis) or transversely (y axis). We studied how such a diffusional anisotropy would affect the calculated values of γ, A, and ρ by using an asymmetric coupling kernel in our spark simulations. We used ρ_x = 1 μm and ρ_y = 0.5 μm as our inputs to reflect the 2:1 diffusional anisotropy measured by Parker et al. The results are given in entries 10 and 11. We again see that γ_total is considerably larger than γ and that the analysis can recover the intrinsic frequency and coupling magnitude reasonably accurately. Because the analysis of the distribution of distances is based on a symmetric kernel (see Eq. 6), the calculated ρ (0.73 and 0.68 μm) is, as expected, between ρ_x and ρ_y.

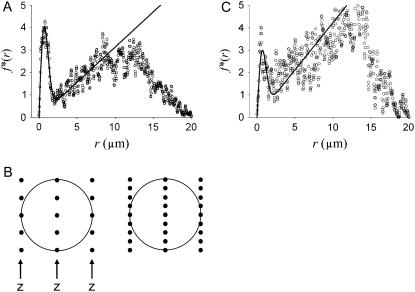
Spark coupling in rat ventricular myocytes

Ca²⁺ sparks were detected in ventricular myocytes using the spark detection algorithm and statistical sieve described in Bányász et al. (21). We used only cells that had a constant spark frequency for two reasons. The first and obvious reason is that unless the spark frequency is constant there is no sensible spark frequency. The second and subtler reason is because the analysis presented above used the assumption that the spark numbers had reached a steady state (see the discussion pertaining to Eq. 17). For each cell we measured the distances between the central spark and its neighbors as described in the Methods.

Fig. 6 A shows the distribution of distances from central sparks. The sparks were measured in 63 cells in standard Ty obtained from four rats. The f*(r) curve has the characteristic M-shape similar to that from the simulated spark data in Fig. 4 C. As before, we determined A by solving γ_T,guess (A) = γ_T. In this case, we measured γ_T = 2.86 × 10⁻⁵/ms/μm² and we got A = 45.9. Based on this value of A, we calculate γ = 2.78 × 10⁻⁵ and ρ = 1.01 μm. Using these values, the peak value of rφ(r, γ_T, A, ρ) (see Eq. 13) overshoots the f*(r) curve by ∼40%. This is not surprising since these parameter values are obtained from just three pieces of data: the slopes of f*(r) at r = 0 and at the linear section, and the position of r_peak.

FIGURE 6.

(A) Distribution of neighbor distances of rat ventricular myocytes in standard Ty. (B) Lattices used to estimate waiting time before at least one CRU (solid circles) within a 2 μm radius (large circle) of the central spark. Z-lines, labeled z, are 2 μm apart. For the lattice on the left, the CRU spacing within the plane of the Z-line is 1 μm and 0.5 μm for the lattice on the right. (C) Distribution of neighbor distances of rat ventricular myocytes in low Na Ty.

A more accurate way of determining γ_T, A, and ρ is to fit rφ(r, γ_T, A, ρ) to f*(r). Fitting is usually more robust since it uses all of the data points of f*(r). The initial guesses of γ_T, A, and ρ that the fitting program (ProFit 6.0.6, Quansoft.com, Uetikon am See, Switzerland) needs are the values determined from the three-point analysis above. The results of the fitting are γ_T = 3.14 × 10⁻⁵/ms/μm², A = 29.75, and ρ = 0.97 μm. Based on these values the intrinsic frequency is γ = 3.08 × 10⁻⁵/ms/μm². The solid curve in Fig. 6 A is the graph of rφ using the fitting parameter values.

Spark rate in the absence and presence of coupling

Consider a particular CRU, its intrinsic firing rate is 3.08 × 10⁻⁵/μm²/ms × 2 μm²/CRU = 6.16 × 10⁻⁵ /ms/CRU. In the absence of previous sparks or equivalently, the absence of coupling, the probability that this CRU will fire and be observed as a spark sometime in the next T = 12.5 ms (the time between confocal image frames in our experiments) is found by setting A = 0 in Eq. 7, q(r, 6.16 × 10⁻⁵, 0, 0.97, 12.5) = 7.697 × 10⁻⁴ ≈ 7.700 × 10⁻⁴ = γ T. This means that if spark coupling were zero, then on average this particular CRU will fire once in 1/7.7 × 10⁻⁴ = 1299 image frames. Note that the value of r is irrelevant, since A = 0.

Instead, now suppose that a spark, S₀, fires at t = 0 and that our CRU is 1 μm away from it. The firing of S₀ increases the firing rate of our CRU more than 10-fold from 6.16 × 10⁻⁵/ms/CRU to 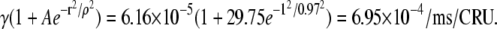The probability that this CRU will fire within the next T = 12.5 ms is q(1.0, 6.16 × 10⁻⁵, 29.75, 0.97, 12.5) = 8.65 × 10⁻³. We see that spark S₀ increases the probability of this CRU firing 11-fold so, on average, this CRU will fire once every 1/8.65 × 10⁻³ = 115 frames instead of every 1299 frames.

E pluribus unum

We have just calculated the change in the firing frequency of one particular CRU when there is a nearby spark. However, we are not concerned whether one particular CRU fires but rather, out of the many CRUs in the neighborhood of the spark, whether at least one fires. Because the coupling distance is ρ ≈ 1 μm, the spark's influence beyond ∼2 μm is nil. This is a convenient distance as this is the typical sarcomere length in the resting cardiac cell. The frequency that a CRU is triggered to fire by the neighboring spark depends on the local packing density of the CRUs. Based on our previous work (7), we use σ = 0.5/μm² as the average packing density. However, there is considerable variation in the transverse packing density (7–9) so let us calculate the spark frequency for two possible packing densities shown in Fig. 6 B. In Fig. 6 B, the transverse spacing of the CRUs is 1 μm and the longitudinal spacing of the Z-lines (marked by z) is 2 μm; this gives a packing density of 0.5/μm². The circle encloses those CRUs that are within 2 μm of the central spark. The probability that at least one of these CRUs will fire within 12.5 ms, 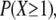is equal to 1− (probability that none fire)

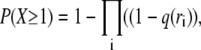(21)

where the products are taken over all CRUs in the circle. In the case where the transverse spacing is 1 μm, P(X ≥ 1) = 0.0214 so on average, the central spark needs to fire 1/0.0214 ≈ 47 times before seeing at least one CRU in its 2 μm neighborhood fire. When the CRU transverse spacing is 0.5 μm, 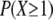increases to 0.0621 because there are more CRUs in the neighborhood and because those CRUs that are 0.5 μm away have a higher firing frequency. In this case, the central spark needs to fire only ≈16 times before at least one neighboring CRU fires.

By contrast, if coupling were absent then the central spark will fire 217 times (transverse CRU spacing =1 μm) or 130 times (transverse CRU = 0.5 μm) on average before at least one CRU in the 2 μm neighborhood would fire.

What is the intrinsic frequency?

In our simulations, we calculated the intrinsic frequency γ from the total frequency γ_total, which matched very well to the unique γ value that was input into the simulation. Interpreting the calculated intrinsic frequency is more complex for real cells because each myocyte has a different total frequency. The mean spark frequency based on γ_total is 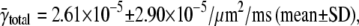the median is 1.54 × 10⁻⁵/μm²/ms, and the maximum frequency is 1.34 × 10⁻⁴/μm²/ms. The distribution of spark frequencies is very skewed to the left with most cells having low spark frequencies but a few cells having high frequencies (see Fig. 4 of (21)). The calculated intrinsic frequency of 3.08 × 10⁻⁵/μm²/ms is larger than the mean of γ_total. The difference between γ (or γ_total) and 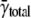depends on how the contribution of each cell's spark frequency is weighted. In calculating 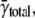each cell's contribution was equally weighted regardless of how many sparks were present. By contrast, because γ_total derives from the number of distances between sparks, those cells that have a large number of sparks (generally those with high spark frequencies) contribute more heavily to γ_total. Neither 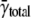nor γ_total is inherently “better”; they are simply different ways of representing the data.

Spark coupling in myocytes bathed in low Na⁺ Ty

To test whether our method could detect changes in spark coupling under different experimental conditions, we measured sparks in myocytes bathed in the Ty in which the Na⁺ concentration had been reduced from 145 to 115 mM and n-methyl d-glucamine added (30 mM) to maintain the same osmolarity. Lowering bath Na⁺ causes an increase in the cytosolic Ca²⁺ concentration by increasing the reverse-mode Na⁺-Ca²⁺ exchange rate, which should increase the spark frequency. As before, we limited our analyses to cells that had constant spark frequency.

As expected, the spark frequency was higher in the low Na⁺ Ty. The 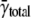was 3.73 × 10⁻⁵ ± 3.40 × 10⁻⁵/μm²/ms; the median frequency was 2.74 × 10⁻⁵/μm²/ms (compared to 1.54 × 10⁻⁵), and the maximum frequency was 1.68 × 10⁻⁴/μm²/ms (compared to 1.34 × 10⁻⁴). The spark frequency distribution was highly skewed as in standard Ty.

Fig. 6 C shows the distribution of distances and the solid curve is rφ(r,γ_T,A,ρ), with the best-fit parameters γ_total = 4.24 × 10⁻⁵/μm²/ms, A = 15.31, and ρ = 0.97 μm. Based on these parameters, the intrinsic frequency is γ = 4.19 × 10⁻⁵/μm²/ms. We see that the higher spark frequency in low Na⁺ Ty is reflected in the larger value of γ_total and γ compared to that in the standard Ty. The coupling space constant is the same in both solutions. The coupling strength in low Na⁺ Ty, however, is only half that in standard Ty. One possibility that might account for this difference is a difference in the spark amplitudes, which is a measure of the amount of Ca²⁺ released. The mean spark amplitude (defined in (21)) is larger in standard Ty than in low Na⁺ Ty (0.136 vs. 0.117, p < 10⁻⁴, t-test), possibly due to the reduced SR Ca²⁺ load that we detected using caffeine release experiments (Y. Chen-Izu and T. Bányász, unpublished results). A complication in interpreting these results is that the lower spark amplitude, combined with a higher resting fluorescence level, could reduce the number of sparks that are detected, causing underestimation of both γ and A from their true values.

The magnitude of spark coupling depends on the sensitivity of CRUs to changes in the ambient cytosolic Ca²⁺ concentration ((Ca²⁺)_i). Treatment with low Na⁺ Ty increases baseline (Ca²⁺)_i so any increase in (Ca²⁺)_i due to CRU firing would likely lead to a greater number of neighbors firing than if the baseline (Ca²⁺)_i were lower. However, the probability of firing is also strongly dependent on the SR Ca²⁺ load (29,30) so changes in coupling reflect the competing influences of higher (Ca²⁺)_i and lower SR Ca²⁺ load. In the case of low Na⁺ Ty, our analysis suggests that the lower SR Ca²⁺ load dominates.

DISCUSSION

The Ca²⁺ spark frequency is exquisitely sensitive to the SR Ca²⁺ content (29,30), the cytosolic Ca²⁺ concentration (31), phosphorylation of ryanodine receptors (32,33), among a host of other factors (34). Accordingly, the spark frequency can be used to gauge the nanoscopic environment of the RyR clusters and their regulation in a manner analogous to the open probability of single ion channels. The analogy between analysis of Ca²⁺ sparks and single ion channels would be complete if Ca²⁺ sparks occurred independently. However, Parker et al. (9) and Brum et al. (15) have clearly demonstrated that not all sparks occur independently as the firing of one spark can increase the probability of nearby spark occurring.

In this article, we solve the problem of decomposing the spark frequency into 1), the part that reflects the intrinsic firing frequency of the CRUs; and 2), the part that reflects the coupling between CRUs. The intrinsic firing frequency is denoted γ and the degree of coupling between CRUs is characterized by the coupling strength A and the coupling space constant ρ. We have shown how these parameters are determined from the distribution of distances between sparks.

Sparks greatly increase firing frequency of neighboring CRUs

The spark coupling parameters for cells in standard Ty are A ≈ 30, γ = 6.16 × 10⁻⁵/ms, and ρ ≈ 1 μm. This means that the occurrence of a spark S₀ will increase the firing frequency of a CRU that is 1 μm away (1 + 30e⁻¹) = 12-fold (see Eq. 6) to 7.4 × 10⁻⁴/ms. If the CRU was only 0.5 μm away, the firing frequency would increase (1 + 30e^−0.25) = 24-fold. On the other hand, a spark occurring on one Z-line has little influence on a CRU on the adjacent Z-line that is 2 μm away. In this case, the firing frequency increases only (1 + 30e⁻⁴) = 1.6-fold. This result is consistent with Parker et al.'s observed absence of coordinated firing of sparks separated by 2 μm (9).

The 12- or 24-fold increase in firing frequency is surprisingly large. This indicates that CRUs on the same Z-line strongly influence each other's firing. Despite the large increase in firing frequency, it is still quite rare to see coupled sparks because the intrinsic firing rate is small. This is analogous to increasing the number of white marbles 10-fold from 10 to a 100 in an urn of 10,000 black marbles. Although the frequency of randomly choosing a white marble is 10-fold higher, the probability of getting a white marble is still very low. This explains why the total frequency γ_total is only slightly higher than the intrinsic frequency (3.14 × 10⁻⁵ vs. 3.08 × 10⁻⁵/μm²/ms) despite a coupling strength of 30. Our results are similar to those of Brum et al. (15), who found that treatment of skeletal muscle with 1 mM caffeine greatly increased the number of neighboring sparks but these still constituted only 1–2% of all sparks.

Synergistic effect of high spark frequency on Ca²⁺ wave initiation

We previously showed that when CRUs in a small neighborhood fire synchronously, the firing probability of adjacent CRUs increases greatly due to superadditivity of sparks (25). Since the probability of multiple sparks occurring close together in space and time increases with spark frequency, it is clear why Ca²⁺ waves are more likely to occur when the spark frequency is high. It is worth dissecting the relationship between spark frequency and Ca²⁺ wave frequency, in light of the difference between the total and intrinsic spark frequencies.

The ratio of the total to the intrinsic spark frequency is 1/(1−ɛ) (this follows from the steady-state form of Eq. 20). In the physiological range of γ, we can represent ɛ using the first-order term of the Taylor series expansion of Eq. 15, 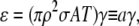giving

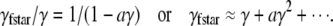(22)

For the parameters obtained from cells bathed in Ty, a = 538.4 ms μm². When the coupling strength is zero, a = 0. (Fitting entries 2–5 of Table 1 to the first two terms of Eq. 22 confirms the accuracy of the predicted relationship between γ_fstar and γ . In this case the coefficient of γ is 0.91 ± 0.03 and the coefficient of γ² is 1301 ± 93.)

Equation 22 has the important meaning that higher intrinsic frequencies begat even higher total frequencies; this is the content of the quadratic and higher order terms in the Taylor expansion. The quadratic (and higher order) term represents the spark-induced sparks. The higher the intrinsic frequency, the more prominent are the spark-induced sparks' contribution to the total spark frequency. For example, at low to moderate spark frequencies, ∼3 × 10⁻⁵/μm²/ms, only ∼1–2% of sparks would be triggered by neighboring sparks. At high spark frequencies of ∼1.5 × 10⁻⁴/μm²/ms, ∼9% of the sparks would arise due to coupling.

The rate of wave initiation depends on the number of sparks that occur in a small neighborhood in a short time span (25). This number reflects the total spark frequency. It follows then that the rate of wave initiation increases linearly with γ for small γ. But as Eq. 22 shows, the spark-induced spark rate increases with γ². Therefore, a high spark frequency acts synergistically on the rate of wave initiation.

Examination of the underlying assumptions of the method

We chose the coupling kernel to be a Gaussian function because the Ca²⁺ distribution underlying a spark (35,36) and the spark itself (9,24) are approximately Gaussian. When the CRU currents are large then the Ca²⁺ distribution will have a flat-topped (platykurtic) shape and the coupling kernel would be better represented by a Gaussian-like function exp(−rⁿ/ρⁿ). A nice property that these Gaussian-like functions share is that the coupling strength A can be evaluated from the slope of f*(r) at r = 0 without knowledge of ρ. This decoupling of A and ρ simplifies their determination from f*(r). Because of the good fit between φ(r)r and f*(r) using the standard Gaussian function (n = 2), we did not attempt to try to use different values of n.

The simulation lattices were two-dimensional and modeled infinitely thin confocal optical slices. Real confocal images record sparks at the focal plane and the projections of sparks off the focal plane. The distance between a central spark and one occurring off the focal plane would be underestimated (see Fig. 3 of (7)). This leads to an overestimation of the number of sparks occurring at small distances and, hence, to an overestimation of the coupling strength A. We do not know the magnitude of this overestimation. The magnitude will scale with the axial resolution of the confocal microscope. However, the large variation in the CRU distances in the plane of the Z-line (7–9) might overwhelm errors incurred by the underestimation of distances to out-of-focus sparks.

Our analysis is based on the assumption that the spark frequency is constant (see the discussion before Eq. 18). Therefore, we cannot apply the analysis to quantify spark coupling at the verge of Ca²⁺ wave initiation when the spark frequency is rapidly increasing. However, the method described here can still be used to determine how multiple sparks affect the probability of firing of a neighboring CRU. Our previous work showed that the probability grows faster than a linear function of the number of sparks (Fig. 3 of (25)). The way we can apply the method is to sort through the spark data and find those sparks pairs that are close together and occur simultaneously (on the same image frame). Then, spark distance distribution from these central pairs can be constructed and γ, A, and ρ can be determined as described above. The number of such pairs is expected to be low so large numbers of sparks will be needed to obtain these parameters.

SUMMARY

The control of cardiac excitation-contraction coupling crucially depends on the spatial separation of the CRUs. Their physical separation insulates but do not isolate the CRUs from each other. The method we have developed in this article allows us to quantify the communication between CRUs and thereby eavesdrop on the social lives of Ca²⁺ sparks.