High-Resolution Structure of a Na⁺/H⁺ Antiporter Dimer Obtained by Pulsed Electron Paramagnetic Resonance Distance Measurements

Abstract

Transient or partial formation of complexes between biomacromolecules is a general mechanism used to control cellular functions. Several of these complexes escape structure determination by crystallographic means. We developed a new approach for determining the structure of protein dimers in the native environment (e.g., in the membrane) with high resolution in cases where the structure of the two monomers is known. The approach is based on measurements of distance distributions between spin labels in the range between 2 and 6 nanometers by a pulsed electron paramagnetic resonance technique and explicit modeling of spin label conformations. By applying this method to the membrane protein homodimer of the Na⁺/H⁺ antiporter NhaA of Escherichia coli, the structure of the presumably physiological dimer was determined. It reveals two points of contact between the two monomers, with one of them confirming results of earlier cross-linking experiments.

INTRODUCTION

Many processes in living cells depend on the transient or partial formation of complexes between biomacromolecules. These processes include signal transduction via protein cascades, regulation of gene expression, and the control of individual activities of transporters and enzymes. The structure of such complexes may be difficult to elucidate by crystallographic techniques, as packing interactions in the crystal compete with the weak interactions holding together a complex that is in equilibrium with its components. The Na⁺/H⁺ antiporter NhaA of Escherichia coli (1) is a case in point. This antiporter is involved in the regulation of intracellular pH, cellular Na⁺ content, and cell volume—functions shared with many other Na⁺/H⁺ antiporters of microorganisms, plants, and animals. Although regulation of the Na⁺ content is based on the level of expression of nhaA, the pH response occurs on the protein level. NhaA is downregulated below pH 6.5 and exhibits an activity increase by a factor of 1000 upon shift to alkaline pH with maximum activity at pH 8.5. Dimer formation of NhaA was observed in a low-resolution structure obtained by cryoelectron microscopy (cryo-EM) on two-dimensional (2D) crystals (2,3), and functional complementation of mutants that are lethal at high pH and Na⁺ concentration suggests that the antiporter functions as a dimer (4).

This suggestion is also supported by cross-linking experiments. Reversible incomplete pH-dependent dimerization was observed in the pH range between 5.8 and 8.0 by pulsed electron paramagnetic resonance (EPR) distance measurements between spin-labeled mutants of NhaA reconstituted into liposomes (5). Yet, a recently obtained highly resolved x-ray structure displays nonphysiological association of the molecules in three-dimensional (3D) crystals (6), even though the monomer structure appears to be in good agreement with the structure observed in the dimers in 2D crystals (7). The crystal structure provides substantial insight into the possible locations of the ion translocation site and of the pH sensor. It suggests that long-range interactions in the protein are required to transmit the signal from this pH sensor to the translocation site. However, the detailed structural changes during ion transport, and in particular the possible role of dimerization, remain unknown. In this context, we report here on a novel approach of protein-protein interaction analysis and its application to the determination of the structure of the presumably physiological NhaA dimer in its downregulated state.

Assuming that the structure of the two NhaA monomers is nearly unchanged in the dimer with respect to the crystal structure (Protein Data Bank identifier 1ZCD), only the relative arrangement of the two molecules has to be determined to obtain a structure of the dimer. This corresponds to solving the problem of docking two biomacromolecules based on long-range distance constraints. To discuss interactions in the interface between the two moieties, this arrangement needs to be known with atomistic resolution. Our approach to this type of problem relies on site-directed spin labeling (SDSL) (8) combined with measurements of label-to-label distances (9) and restraint-driven rigid body transformations (10). By applying a pulsed electron-electron double-resonance technique (11,12), we obtain distance constraints in the range between 20 and 60 Å. As this range matches the dimensions of biomacromolecules, a relatively small number of distance constraints provides a unique structure. Compared to a recently introduced approach that also combined x-ray data and pulsed EPR distance measurements for reconstruction of the chemotaxis receptor-kinase assembly (13), our method for the first time, to our knowledge, utilizes information on the distribution of distances (14) to match a modeled conformational distribution of the spin labels (15–17).

By this technique we overcome the intrinsic imprecision of SDSL EPR caused by its reliance on labels with a size of ∼1 nm and obtain a resolution of the dimer model that is limited only by the resolution of the x-ray structure of the monomer. As EPR does not require any long-range order in the packing, this approach allows us to determine the structure of a membrane protein dimer in liposomes, i.e., in an environment that is closer to the physiological environment than a protein crystal or 2D crystal. Furthermore, external parameters such as the pH value can be controlled. Similar techniques should be applicable to heterodimers of both soluble and membrane proteins or to complexes of proteins with RNA or DNA. Therefore, we first discuss the general approach for structure elucidation of a complex of two macromolecules, while pointing out simplifications that could be made for the symmetric homodimer of NhaA. Then we describe the obtained structure of the NhaA dimer, and, finally, we discuss its functional implications.

MATERIALS AND METHODS

Preparation and labeling of NhaA

The generation of nhaA alleles encoding single Cys NhaA molecules used in this study has already been described (4,18). For overexpression, the resulting single Cys NhaA encoding plasmids were transformed into E. coli TA-16. TA-16 is nhaA⁺nhaB⁺lacIQ and otherwise isogenic to TA-15 (19). Cells were grown aerobically in Luria-Bertani medium (20) containing 100 μg/ml ampicillin and 50 μg/ml kanamycin at 37°C to an A_{420 nm} of 1.0. After induction with 0.5 mM isopropyl-thio-β-D-galactoside and further growth for 3 h, membranes were prepared as described (21) using a cell disruptor (IUL Instruments, Königswinter, Germany). NhaA was solubilized and purified by Ni-nitrilotriacetic acid affinity chromatography as described (22). Labeling the single Cys NhaA with (1-oxyl-2,2,5,5-tetramethylpyrroline-3-methyl)-methanethiosulfonate (MTSSL, Toronto Research Chemicals, Toronto, Canada) was performed on the column.

For this purpose, 1 mM MTSSL in buffer W (20 mM Tris-HCl, pH 7.5, 500 mM NaCl, 5 mM imidazole, 10% glycerol (v/v), 0.1% β-D-dodecylmaltoside (w/v)) was applied to the column and incubated at 4°C for 3 h. Unbound label was removed by washing the column with buffer W, and labeled protein was eluted with 300 mM imidazole in buffer W. After elution the protein was reconstituted under nonreducing conditions into liposomes composed of E. coli lipids (Avanti Polar Lipids, Alabaster, AL; 67% phosphatidylethanolamine, 23.2% phosphatidylglycerol, and 9.8% cardiolipin) at a lipid/protein ratio of 20:1 (w/w) as described (21). Finally, the proteoliposomes were washed twice with 50 mM KPi, pH 7.5, and resuspended in 10 mM KPi, pH 5.8, 100 mM KCl, and 5 mM MgCL-2 to yield a NhaA concentration of 50–100 μM. Proteoliposomes were frozen and stored in liquid nitrogen until use.

EPR measurements

Four-pulse double electron-electron resonance (DEER) measurements were performed at a Bruker Elexsys 580 spectrometer (Bruker Biospin, Karlsruhe, Germany) equipped with a 3 mm split-ring resonator under conditions of strong overcoupling (Q » 100) at a temperature of 50 K. Before insertion into the probe head, the samples were shock-frozen in liquid nitrogen to avoid crystallization of water. The four-pulse DEER sequence (π/2)_ν1 − τ₁ − (π)_ν1 − t′ − (π)_ν2 − τ₁ + τ₂ − t′ − (π)_ν1 − τ₂ − echo was used (12). The π/2 and π pulses at the observer frequency ν₁ had equal pulse lengths of 32 ns to ensure equal excitation bandwidths, whereas the π pulse at the pump frequency ν₂ had a length of 12 ns to maximize modulation depth while still keeping the two excitation bands separate. These conditions maximize sensitivity of the experiment (23). The long interpulse delay was τ₂ = 2000 ns except for mutants E-82R1, S-87R1, and N-177R1, where it was 2300 ns, and A-118R1, where it was 2500 ns. An initial value of t′ = 80 ns and an increment Δt′ = 8 ns were used to acquire the time trace. To suppress proton modulation, data were added for eight equidistant values of τ₁ between 200 and 256 ns. A phase cycle +x/−x was applied to the first pulse and the two signals were subtracted. The pump frequency ν₂ (typically 9.33 GHz) was set to the center of the resonator mode and to coincide with the global maximum of the nitroxide spectrum. The observer frequency ν₁ was set to the local maximum at the low-field edge of the spectrum (ν₁ − ν₂ = 65 MHz). Accumulation times for the data sets varied between 8 and 14 h. Data were analyzed for dipolar evolution times t = t′ − τ₁ ≥ 0.

Estimates of mean distances

The home-written program DeerAnalysis2006 (24) was used for processing the primary experimental data V(t). To account for suppression of short distances due to low modulation depth (24,25), the background for a 2D distribution of the spin-labeled objects was computed from a distance distribution that is defined as P_B(r) ≡ 0 for r < 1.5 nm and otherwise as P_B(r) = 2c₂r, where c₂ is the area density of singly spin-labeled objects. The background factor B(t) was determined with an optimized fit range (24), and the baseline-corrected form factor F(t) = [V(t) − B(t)]/B(t) was computed. The distance distribution P(r) for the spin labels within the same dimer was then estimated by Tikhonov regularization (26), using the L curve as a criterion for selecting the optimum regularization parameter (27,28). The mean distance of the distance distribution was computed, disregarding any minor peaks that were well separated from the major peak.

Grid search for determination of the initial structure

A grid of angle values θ and φ and of translation parameters x and y was set up. For each parameter set (θ_k, φ_k, x_k, y_k), mean distances 〈r_i〉_M0 for the model are computed, where index k runs over all grid points and index i runs over the selected labels (A-202R1: i = 1, K-221R1: i = 2, H-225R1: i = 3, and E-241R1: i = 4). The initial structure corresponds to the parameter set, for which the root mean-square deviation (r.m.s.d.)

(1)

is minimum. We find θ₀ = 45°, φ₀ = 320°, x₀ = −40 Å, and y₀= 20 Å.

Structure refinement by direct fit to the primary experimental data

Nelder-Mead simplex minimization of the r.m.s.d. between simulated and experimental four-pulse DEER data was used for structure refinement. Simulation of four-pulse DEER data involved the following steps. For a given parameter set (θ, φ, x, y), the theoretical distance distribution P_T,i(r) between N-O midpoints for all nine labels was computed as described above. This distance distribution was then converted to a theoretical form factor F_T,i(t) by applying subroutine pcf2deer of the DeerAnalysis2006 package (24). The theoretical four-pulse DEER data are computed as

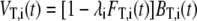(2)

where the theoretical background factor B_T,i(t) is computed with subroutine pcf2deer from a distance distribution P_B,i(r), which is identical zero for r < 15 Å and given by P_B,i(r) = c_2,i r for r ≥ 15 Å. The modulation depth λ_i and the concentration parameter c_2,i are determined by minimizing the r.m.s.d. between V_T,i(t) and the primary experimental data V_i(t) for this label, i.e., by a fit within a fit procedure. The figure of merit of the model is the sum of these minimum r.m.s.d. values for all nine labels, depending on (θ, φ, x, y). Minimization with respect to these four parameters provides the geometric parameters for the final structure.

Estimate of the resolution of the structure

The final structure was systematically tested with respect to the influence of the number of constraints and of the experimental noise on backbone atom positions. To this end the 36 possible combinations of seven out of the nine existing DEER data sets were used, and the noise level in each individual DEER data set was estimated from the difference between experimental and simulated data for the final structure obtained with all nine data sets. For each of the 36 combinations the whole procedure of structure determination was repeated four times. In each trial the noise level of the DEER traces was doubled with respect to the original data by adding different pseudorandom artificial noise. This procedure gave a family of 144 approximate structures of the dimer. Each of these structures was superimposed onto the final structure from refinement with all nine constraints using the Magic Fit function of DeepView (29), and the backbone r.m.s.d. of each structure from the final structure was computed using DeepView scripting language. The total r.m.s.d. of the whole structure family from the final structure was 0.6 Å, which compares to a 3.45 Å resolution of the crystal structure used in deriving the dimer structure.

Superposition of the EPR and cryoelectron microscopy structures

A 2D electron density map of a single dimer was cut out from Fig. 4 of Williams (3) and was converted to a smooth grayscale picture using Corel PhotoPaint to ensure better visibility. Utmost care was taken not to suppress or enhance any features of the original density map as published in Williams (3). Both in the cryo-EM and in the EPR structure, the membrane normal is known. Superposition thus involves the fitting of only one unknown parameter, an angle θ_EM corresponding to an Euler rotation about the C₂ symmetry axis of the dimer. This angle was fitted by visual inspection of the superposition picture.

FIGURE 4.

EPR structure of the dimer of the Na⁺/H⁺ antiporter NhaA of E. coli. (a) Overview of the whole structure. (b) Contacts between the two-stranded antiparallel β-sheets (residues 39–60). (c) Contacts between helices VII and IX. Highlighted residues are proposed to be directly involved in intermolecular interactions. Created with DeepView (29).

RESULTS AND DISCUSSION

Structure determination and refinement

In the first stages of structure determination, we treat the two component molecules as rigid bodies with structures known from previous crystallographic or NMR studies. The relative arrangement of two rigid bodies is fully described by six parameters: the three Euler angles accounting for the rotational degrees of freedom and the three components of a translation vector. A unique structure can thus be obtained by measuring six distances between the components. In practice, the actual number of distance constraints should exceed the number of free parameters at least by a factor of two. This allows us to test whether the components can indeed be treated as rigid bodies and to estimate the uncertainty of the obtained structure. Such a number of distance constraints can be obtained for proteins by current SDSL and pulsed EPR methodology (30). In the case of a symmetric homodimer, as assumed for NhaA, C₂ symmetry reduces the number of parameters to four (Fig. 1). Two angles, θ and φ, determine the orientation of the symmetry axis in the frame of the monomer coordinates.

FIGURE 1.

Overview schematic for the general EPR structure determination approach for protein dimers. Steps labeled with an asterisk require an existing structure of the monomers, e.g., from previous x-ray or NMR work.

The coordinates of the second molecule are then generated from the coordinates of the first molecule by a rotation about the C₂ axis (z axis) by 180°, taking the origin of the frame as the geometric center of the protein, and by a subsequent translation by a vector (x, y, 0). The translation is within the membrane plane. We decided to determine the four structural parameters θ, φ, x, and y based on nine distance measurements by the four-pulse DEER sequence (12), using single cystein mutants E-82R1, S-87R1, A-118R1, N-177R1, A-202R1, K-221R1, H-225R1, E-241R1, and V-254R1 labeled with the methanethiosulfonate spin label (MTSSL) (R-1 corresponds to MTSSL-labeled cystein). As a basis for the structure determination, we first converted all DEER data sets to distance distributions by Tikhonov regularization (26) with the optimum regularization parameter determined from the L curve (27,28) and computed mean distances. Previously, mean distances have been found to be stable parameters of broad distance distributions, which are not much affected by the ill-posedness of the data conversion from time to distance domain (31). This first step of data analysis is illustrated in Fig. 2 for the mutant K-221R1, and the mean distances are given in Table 1.

FIGURE 2.

Estimate of the mean distance on the example of spin label K-221R1. (A) Normalized primary experimental data (solid line) and fit by a homogeneous background distribution in a plane for r > 1.5 nm (dotted line, fit range right from the vertical dashed line). Left from the dashed line the fit is extrapolated and is invalid for t < 0. (B) Normalized form factor (solid line) and best fit by Tikhonov regularization with optimized regularization parameter (dotted line). (C) L curve of Tikhonov regularization. The solid circle denotes the selected corner of the L curve, corresponding to a regularization parameter α = 10. (D) Distance distribution obtained by Tikhonov regularization. The mean value of the distance for the peak between the two vertical dashed lines, 〈r〉_T = 2.83 nm, was used in the first stage of structure determination.

TABLE 1.

Mean distances between spin labels in the NhaA dimer (in angstroms)

Mutant	E-82R1	S-87R1	A-118R1	N-177R1	A-202R1	K-221R1	H-225R1	E-241R1	V-254R1
〈r〉T (Å)	44.8	47.3	45.8	48.4	34.1	28.3	44.5	25.7	18.9
〈r〉M (Å)	50.3	53.6	81.8	54.7	36.0	28.6	46.1	27.5	16.2

The value obtained by Tikhonov regularization is 〈r〉_T, and the value corresponding to the final structural model is 〈r〉_M. Values that were used in the first stage of structure determination are marked by bold typeface.

To obtain a first set of geometrical parameters (θ, φ, x, y) without making any further assumptions on the structure, the full parameter space should be searched. We performed a grid search as described in the Materials and Methods section for the range of θ from 0° to 90° and of φ from 0° to 355°, both in steps of 5°. For the translation parameters x and y we tested a range from −100 to 100 Å in steps of 5 Å. These ranges ensured that all relative arrangements were included for which the two molecules can actually be in contact with each other. During the grid search we fitted the mean distances between the spin labels in the structural model to mean experimental distances. The mean experimental distances were obtained by model-free analysis of the label-to-label distance distribution (14,15,24). For the modeling of the conformational distribution, we used a library of 62 rotamers of MTSSL attached to a cystein residue and considered restrictions due to clashes with neighboring protein side groups or with the backbone by a Lennard-Jones potential parameterized as in the optimized potential for liquid simulations force field (32). The label site was identified with the midpoint of the N-O bond of the spin label. In the grid search we used the minimum number of four distance constraints. That way we could select residues with a mean distance in the range where it can be determined most precisely by pulsed EPR (20–45 Å). For NhaA, these are residues A-202R1, K-221R1, H-225R1, and V-241R1. The initial parameter set obtained by the grid search is θ₀ = 45°, φ₀ = 320°, x₀ = −40 Å, and y₀ = 20 Å.

In the first refinement step we fitted the parameter set by minimizing the r.m.s.d. between the primary experimental DEER time traces and simulated DEER time traces. This fitting procedure utilizes the full information on the distance distribution contained in the primary DEER data while avoiding the ill-posed problem of explicitly converting the time-domain data to a distance distribution. The simulated DEER time traces are based on the modeled distance distribution between the label sites, considering all 62 rotamers in each moiety with their appropriate weighting factors derived from the Lennard-Jones potential. A 2D background function was used in the DEER simulations to account for contributions from neighboring dimers (5). In this refinement step all nine distance constraints were used. The best-fit parameter set is θ₀ = 42.7°, φ₀ = 324.0°, x₀ = −39.7 Å, and y₀ = 20.1 Å.

The change compared to the values previously found in the grid search with only four of the nine constraints is relatively small. This suggests a good internal consistency of the experimental data and thus validity of the hypothesis that the two monomers move as rigid bodies. The quality of the final fit is illustrated in Fig. 3. The modulation depth λ_i ranges between 0.09 and 0.23 for most residues, probably reflecting differences in labeling efficiency. We may not exclude that the extent of dimer formation also varies somewhat for the different labeling sites. Exceptionally low modulation depths are observed for mutants E-82R1 (λ = 0.02) and V-254R1 (λ = 0.04). In the latter case, the low modulation depth is probably due to suppression effects for distances shorter than 1.8 nm (24,25). The background density ranges between 0.043 and 0.102, with the lowest value again corresponding to mutant E-82R1. The relatively narrow range for the background density suggests that separation into background and form factor works well.

FIGURE 3.

Fits of primary experimental DEER data (black lines) by simulated data (red lines) corresponding to the final structure of the NhaA dimer and a distribution of spin label conformations modeled by a rotamer library.

Although the fit quality is generally good, significant deviations of the fits (red lines) from the experimental data (black lines) are observed for the two cases with the most nicely resolved oscillations, A-202R1 and K-221R1. This indicates limitations in the precision of the modeling of the conformational distributions by our rotamer approach, which may be due to our neglect of any interactions of the label with the protein except for van der Waals interactions. The modeled distance distributions appear to be somewhat broader than the true distributions. More sophisticated modeling of the label conformations by molecular dynamics simulations (15,33) could be integrated into our approach. It was recently demonstrated that such modeling significantly improves agreement with experimental spin-to-spin distances compared to simply interpreting them as C^β-C^β distances (15).

This raises the question of how imperfections of the conformational modeling and noise in the experimental data influence the precision of the four geometrical parameters and thus the resolution of the structure. We checked this by examining a family of structures that was obtained by considering only seven out of the nine constraints. Structures that result from using any combination of seven constraints in both the initial grid search and first refinement have the same or a larger final r.m.s.d. compared to our best-fit structure. To estimate the reliability of the final coordinates, we repeated refinement four times for any of the 36 combinations of seven out of nine constraints while doubling the noise amplitude of the experimental data by adding pseudorandom numbers. Using only seven of the nine constraints ensured that errors in modeling the label conformations and in the assumption of rigid-body behavior of the components contribute to the scatter in the coordinates. The backbone r.m.s.d. of the resulting set of 144 structures with respect to the best-fit structure is only 0.6 Å, which suggests that the quality of the final structure is limited by the resolution of 3.45 Å of the crystal structure of the monomer rather than by the SDSL EPR docking fit.

This resolution is significantly better than the one achieved in an earlier EPR docking approach that was based on continuous wave EPR-derived distance constraints (10). The main improvements are the use of longer-range and higher precision distance constraints from a pulsed EPR method and utilization of information on the whole distribution of distances rather than of only a single number for the site-to-site distances. These two features also distinguish our approach from protein-protein docking approaches based on NMR shift data or other “ambiguous interaction restraints” (34). Due to the requirement for spin labels our approach is more invasive compared to NMR titration. However, if labeling sites are carefully selected and are reexamined after solving the structure, any influence of the labels on protein-protein complex formation can be excluded.

The structure obtained at this point exhibits contacts between the two component molecules in three parts of the sequence, from residues 39 to 60 (β-sheets), from 202 to 211 (helix VII), and from 253 to 259 (helix IX). There exist no strong clashes between side group atoms and no clashes at all between backbone atoms of the two monomers. Nevertheless, it has to be realized that the side chains of the contact-forming residues are unlikely to be oriented in the same way as in the crystal structure of the monomer. As we do not have experimental information on side-chain orientation, we optimized the interface by repeated energy minimization using the GROMOS96 force field (35) as implemented in DeepView (29). The converged structure after 10 minimizations (Fig. 4 a) is the final structure discussed in the following.

Contacts in the NhaA dimer

Contacts between the two monomers in the dimer were analyzed with the CSU software (36). The main intermolecular contact is mediated by the two-stranded antiparallel β-sheets, which are probably held together by four hydrogen bonds formed between residues Q-47 and R-49 and backbone groups of the respective other β-sheet (Fig. 4 b) and by a number of hydrophobic contacts. Residue Q-47 is also involved in stabilizing the nonphysiological dimer observed in 3D crystals (7). Contact between helices VII and IX (Fig. 4 c) is restricted to a few residues and most likely involves a hydrogen bond between R-204 und V-254 as well as hydrophobic contacts of R-204 and L-210 with W-258. In general the interface is not densely packed, which indicates a relatively weak binding between the moieties, in agreement with the pH dependence of dimer formation (5) and the dissociation of the physiological dimer during 3D crystallization. Location of residue V-254 in the interface was suggested before by a cross-linking study (4). Indeed, we find a distance of 8.1 Å between the S atoms of the corresponding cysteins. This is in good agreement with the finding that the rigid cross-linking agent p-phenylenedimaleimide, which can cross-link only residues that are at least 10 Å apart, causes a change in the pH profile of NhaA activation (3). In contrast, the flexible cross-linking agent 1,6-bismaleimidohexane does not cause such a change. Location of residue V-254 in the interface may also explain the low modulation depth, i.e., lower propensity for dimer formation observed in our earlier work when mutating this residue (5).

Contacts between the two monomers are restricted to one of the two bundles of six helices, the interfacial domain (blue line in Fig. 5). According to previous work, this interfacial domain contains the pH sensor of NhaA around residues 241–252 (6). The other bundle of six helices contains the putative ion translocation path and thus forms the translocation domain (red line in Fig. 5). Although the two domains appear distinct, there are interdomain contacts. Helix I (residues 12–30) in the interfacial domain interacts with helix XII (357–382) near the periplasmic side and with helix IVc near the cytoplasmic side (6).

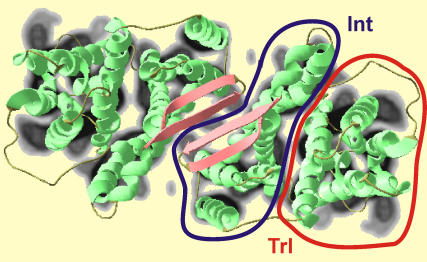
FIGURE 5.

Comparison between the EPR structure and the electron density projection to the membrane plane obtained by cryo-EM on 2D crystals (2,3). The interfacial domain Int and the ion translocation domain Trl involved in Na⁺ and H⁺ transport are indicated by the blue and red lines, respectively.

Comparison with the low-resolution structure

Although no information from the cryo-EM structure in 2D crystals (2,3) was used, there is a rather good agreement between this structure and our EPR structure, in particular in the interfacial domain (Fig. 5). This is not a trivial result, as the present EPR study is performed on NhaA dimers in liposomes rather than in 2D crystals where packing effects might have influenced the structure of the weakly bound dimer. Indeed our finding contrasts with a fit of the high-resolution monomer 3D crystal structure to the electron density obtained by cryo-EM, which predicted that the two-stranded antiparallel β-sheets would collide and should thus be displaced by ∼6 Å out of the membrane plane and by ∼6 Å toward the molecule center (6). However, such a structure would imply shorter distances for residues A-202R1 and K-221R1 than we observe. As the DEER data for these two residues are of high quality, we can exclude this arrangement of the two moieties at least in liposomes. The disagreement may arise from the attempt to perfectly superimpose not only the interfacial domain but also the ion translocation domain Trl, which appears to be slightly displaced in our structure with respect to the cryo-EM data.

The displacement of the translocation domain relative to the interfacial domain could be a packing artifact of either the high-resolution monomer structure or the cryo-EM structure. In the former case, the artifact would transmit to the EPR structure of the dimer, as we assumed rigid body motion of the two domains as a whole. Such a displacement in the 3D crystals may be induced by crystal contacts that stabilize the nonphysiological dimer, which are observed for residues D-354, E-356, and N-359 in the translocation domain. This domain includes helices III (residues 95–116), IV (121–143), and V (150–175) and the helices X, XI, and XII with their intervening loops comprising residues 290 to the C-terminus. Among the residues selected for mutation and distance measurements only, A-118 is situated within this domain. Because of the long-distance between sites A-118R1 in the two moieties of ∼82 Å, our DEER data may not be sensitive to a displacement of this residue by up to 10 Å. A displacement of the translocation domain in liposomes compared to the crystal structure of the monomer would thus be consistent with our data, but we cannot exclude that the difference is rather between liposomes and 2D crystals.

Functional implications of the EPR structure

For residues H-225R1 and V-254R1 (5) as well as A-118R1 and N-177R1, we tested for pH dependence of the distance distribution by performing measurements at pH 5.8, 7.0, and 8.0. Quite unexpectedly, in none of these cases were any significant changes detected. Only the depth of the DEER modulation, which corresponds to the extent of dimer formation, varies with pH (5). This indicates that the structure of the interfacial domain, i.e., of the antiparallel β-sheets and helices I–III and VI–IX, is conserved during pH changes. Also the interface between these domains appears to be conserved although propensity for dimer formation varies slightly.

Due to the scarcity of labeled residues in the translocation domain and the large separation between the two translocation domains in the dimer, we cannot exclude that this domain moves with respect to the interfacial domain on changing pH. In fact, with the pH sensor being located around residues 241–252 (6) and Na⁺/H⁺ transport probably involving relative movement of helices IVc (residues 121–131) and XIp (residues 340–350) (5), a change in the relative arrangement of the two domains might be the most likely explanation for transmittance of the signal from the pH sensor to the translocation pathway. The putative pH sensor is located near the contact region between helices VII and IX in the dimer. Mutation of V-254, which forms a hydrogen bond with R-204 across the interface, was found to change the pH dependence of activity (37). Note also that the interface between the two monomers is lined by a number of polar residues (Fig. 6). Among them K-204 has a predicted pK_a value of 7.1 in a membrane environment (38). Protonation/deprotonation of this residue may influence contacts between the monomers.

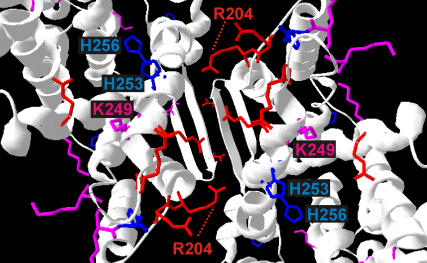
FIGURE 6.

Distribution of arginine (red), lysine (purple), and histidine (blue) residues near the interface. Figure created with DeepView (29).

Signal transmittance between the translocation and interfacial domains is also required to rationalize functional complementation between the conditional lethal mutants. For instance, in the mutant H-225R, antiporter activity increases between pH 6 and 7 but is shut off again at pH > 7, so that the mutant is lethal at pH 8.5 and high Na⁺ concentration (4). Likewise, mutant G-338S is lethal, but for a different reason: in this mutant antiporter activity persists at pH below 7 so that at high Na⁺ concentration pH in the cell becomes too low (4). If both mutants are coexpressed, the cells survive under the conditions that kill them if only one of the mutants is present. Such functional complementation between remote sites is only feasible if ion translocation is a process that involves a cooperative, but asymmetric motion of both moieties of the dimer.

This raises the questions of how local structural changes in the two domains of a monomer are coupled and how structural changes are transmitted between the monomers in the dimer. Remarkable in this respect is the particularly high number of potentially positively charged residues (R-303, R-304, H-243, R-245, K-249, R-250, H-253, H-256), which are at or close to the cytoplasmic contact site of the monomers (Fig. 6). Taking into account that the predicted pK_a values for R-204, H-253, and H-256 (38) allow protonation/deprotonation events in the range between pH 5–7.5, it can be envisaged that pH directly influences contacts between the monomers. This idea is in agreement with the previous finding that pH influences the monomer-dimer equilibrium of NhaA (5).

Among the residues that can be protonated/deprotonated in the transition region, R-204 may play a pivotal role in this process since it appears to form a hydrogen bond across the interface with the carbonyl group of V-254 in the other monomer. V-254 in turn is in hydrophobic contact with R-250 in its own moiety. These interactions may also ensure contact between large clusters of residues strongly interacting within a monomer across the interface. These clusters were identified by a recent continuum electrostatics analysis of the monomer and involve E-78, R-81, E-82, E-252, H-253, and H-256 belonging to the pH sensor and D-133, R-203, H-243, K-249, and R-250 (22). The clusters provide a coupling between the putative ion translocation domain and the interfacial domain, as residue D-133 is located in the narrow passage of the translocation channel (6).

Residue H-225, which is spatially close to the pH sensor cluster, mediates contact between the interfacial domain, in which it is located, and residues A-172 and Y-175 in the translocation domain of the same moiety. Replacement of the histidine by arginine in the conditional lethal mutant H-225R may modify or destroy this contact, which needs to exist in one of the two moieties to ensure activity. A further contact between the translocation and interfacial domain in the same moiety is provided by residues 135–143 in helix IVc, which is in the cytoplasmic part of the putative ion translocation channel with residues 12–19 in helix I. Likewise some residues in the range between 64 and 72 in helix II have contact with residues in the range between 341 and 350 in helix XIp, which is in the periplasmic part of the ion translocation channel. Interestingly, helix IVc and helix XIp were suggested to be the moving parts in pH regulation of NhaA activity (6).

Based on the EPR structure of the dimer, one may now speculate that the proposed movement of helix IVc during activation is related to a movement of the cytoplasmic end of helix I toward the interface, whereas the proposed movement of helix XIp is related to a movement of the periplasmic end of helix II toward the interface. Activation would thus correspond to a clockwise rotation of the interface or, keeping the interfacial domains fixed, to an anticlockwise rotation of the two translocation domains with respect to the interface (seen from the periplasmic side). The displacement of the translocation domain seen in the EPR structure compared to the cryo-EM structure roughly corresponds to such an anticlockwise rotation, although it has to be said that the wild-type is still inactive at the pH of 5.8 where most of the EPR distance measurements were performed and that the reasons for the displacement are currently unknown. Clearly, structural information at pH above 6.5 is required to prove or refute the hypothesis and to obtain further insight into the cooperative motion of the two moieties of the dimer that appears to be the basis of ion translocation.

In conclusion, it is demonstrated that SDSL combined with pulsed EPR measurements of distances in the range between 20 and 60 Å and modeling of the conformational distribution of the spin label side groups provides a new approach for elucidating structures of dimers or complexes of biomacromolecules with essentially the same resolution that can be obtained for the structures of the constituents. The method does not provide experimental information on a possible repacking of side chains in the interface. In contrast to most established techniques, this approach is applicable even if interactions between the molecules are rather weak and complex or dimer formation is thus incomplete. It does not require crystallization; so that structures of membrane protein complexes can be determined in liposomes where external parameters such as pH can be varied.