Molecular Basis of the Apparent Near Ideality of Urea Solutions

Abstract

Activity coefficients of urea solutions are calculated to explore the mechanism of its solution properties, which form the basis for its well-known use as a strong protein denaturant. We perform free energy simulations of urea solutions in different urea concentrations using two urea models (OPLS and KBFF models) to calculate and decompose the activity coefficients. For the case of urea, we clarify the concept of the ideal solution in different concentration scales and standard states and its effect on our subsequent analysis. The analytical form of activity coefficients depends on the concentration units and standard states. For both models studied, urea displays a weak concentration dependence for excess chemical potential. However, for the OPLS force-field model, this results from contributions that are independent of concentration to the van der Waals and electrostatic components whereas for the KBFF model those components are nontrivial but oppose each other. The strong ideality of urea solutions in some concentration scales (incidentally implying a lack of water perturbation) is discussed in terms of recent data and ideas on the mechanism of urea denaturation of proteins.

INTRODUCTION

Molecules in cells function in a highly crowded, concentrated, nonideal solution environment. Therefore, the usual treatments that make use of concepts from the ideal, infinite dilution solution limit are quantitatively inadequate for many biological problems. Urea is an interesting case. It has a strong concentration-dependent effect on the folding/denaturing transition for proteins in solution. This might appear to be due to nonideality in solution. In fact, in some concentration scales it shows substantial deviations from ideality. Yet, in the molar scale, it appears almost ideal. Much literature has been devoted to how urea must change water's structure to make its solution such a powerful denaturant (1). Theoretical work from this lab and experiments from others question the water structure change hypothesis (2,3).

The effect of osmolytes and a multicomponent environment in general is to change the chemical potentials of the components, most notably that of the macromolecular solutes. Such changes result in differences in stability for conformations and oligomerization versus simple aqueous solutions. The effects can be quite significant for biological systems where common use is made of urea, proline, sucrose, glycerol, etc. (4,5). To consider these effects we must consider the system's free energy (or activity) in general.

The Gibbs free energy change, dG, is

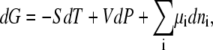(1)

where S is the entropy, T is absolute temperature, P is pressure, n_i is the number of the i^th species and μ_i its chemical potential. The systems in which we are interested, for the most part, in this work are isothermal-isobaric systems. In a multicomponent mixture, the thermodynamic condition of the system is expected to be strongly affected by the chemical potentials. However, interpretation and even measurement of chemical potential or activity is confounded by standard state and even the concentration scale used.

It is convenient to start from the understanding of ideal solution properties to understand real systems. Ideal solutions are a convenient if occasionally misleading approximation to real solutions, much as an ideal gas is an approximation to real gases. There are two well-known ideal solutions. One is the symmetric ideal solution and the other is a dilute ideal solution (6). Isotopic and some isomeric mixtures are typical examples which are often very close to a symmetric ideal solution. However, most pure electrolytes and osmolytes are in the solid state for the range of temperature and pressure in which we are interested. It is notoriously difficult to determine the relative activity of the solid state with respect to the pure liquid experimentally. In such cases, the infinitely dilute state can often be used as the standard state, and one then considers the deviation from the dilute ideal solution.

No real solution is an ideal solution exactly. Adding solutes to liquid water generally causes, to a greater or lesser extent, colligative effects such as vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure changes. These properties depend only on the number of solute molecules in the case of a dilute ideal solution. They are relatively independent of chemical properties of solutes for dilute solutions. They generally depend on species and concentrations of solutes in real solutions.

The existing solution theories which use the infinitely dilute state as the standard state most often explain solution behavior only in a very dilute solution. There is no complete, analytic theory which can explain experimental data at concentrations of >1.0 mol/L. In development of such theory, Rösgen et al. were recently very successful in fitting partition function ratios as parameters to experimental data in an activity series with analysis based on a derivation arising from a semi-grand canonical ensemble (7,8). Here, using urea solutions as a case of interest, we would like to address whether the fitted parameters are true representations of the ratios of low order partition functions or just effective coefficients, i.e., direct representations or renormalized. We discuss the dependence on the urea model parameters as well in Results and Discussion.

It is generally cumbersome to obtain experimental solvation free energy (excess chemical potential) in most electrolytes and osmolytes. One reason is that relative activity coefficients depend nontrivially on the concentration scale used. Another reason is because the vapor pressure at room temperature is often too small to measure accurately. Smith et al. (9) estimated the solvation free energy of urea computationally. However, their estimation is based on some assumptions. Because there is no experimental data on the vapor pressure of urea at room temperature (urea is essentially nonvolatile), they estimated from an extrapolated value of the vapor pressure at high temperatures. It is difficult to validate these estimations because existing experimental data on urea vapor pressure is inconsistent, and with questionable accuracy (10,11). The validity of the extrapolation method to low temperatures is similarly unclear. Urea solutions show a striking apparent dependence on how we view them in terms of standard state and concentration scale. They are close to a dilute ideal solution in the molarity scale, but not for other scales such as the mole fraction or molality, nor for a symmetric ideal solution (9) as we show below. We also show that it is possible to understand the near ideality of urea solutions that occurs with certain scales and reference systems by molecular simulation with appropriate theoretical analysis.

There is no direct experimental solvation free energy (excess chemical potential) data for urea solutions. Thus, it is difficult a priori to judge the applicability of the various force fields for urea from the solvation free energy value calculated using simulations. Experimental aqueous solvation free energy data exists only for a few solutes such as some small alkanes, alcohols, and amides, because such solutes are volatile at room temperature. Instead, for urea we have only the experimental activity coefficient data (12–14). Experimental activity coefficients are obtained from osmotic coefficient data on urea with knowledge of the osmotic pressure of water via the Gibbs-Duhem relation.

In principle, for any force field, the activity coefficient of urea can be obtained through calculation of the chemical potential at different concentrations, although that requires high precision to compare with experiment. In this article, we examine how and why the activity coefficient changes in different concentrations of urea solutions. We use free energy calculations with sampling from molecular dynamics simulations with two different all-atom force fields to generate hypotheses about the mechanism to explain the activity at the molecular level. We hope to clarify the origin of the behavior of urea in aqueous solution as a prelude to considering its profound effect on proteins.

Calculating the chemical potential with sufficient precision to obtain activity coefficient changes is still a challenging computational problem. It is necessary to calculate the chemical potential quite precisely to estimate the change in an activity coefficient by simulations. Here we combine and contrast the thermodynamic integration method, perturbation method, and Bennett's acceptance ratio method for our activity coefficient calculations. We compare simulation results with experimental data over a wide range of urea concentrations.

In the next section, we review the theoretical framework of ideal and nonideal solutions as well as the often confused concentration dependence. The calculational methods to obtain sufficiently precise chemical potentials are also explained. Readers familiar with the connections of Raoult's and Henry's laws to the modern theories of solution may skip Ideal Solutions. In Methods, the models and details of the simulation are presented. In Results and Discussion, in the context of both the models, the data are given. Conclusions is devoted to our remarks about what our results imply about the mechanism of action of urea on proteins.

THEORY

For our subsequent analysis, we must separate and quantify the effects of standard state from concentration-scale dependence of the chemical potential or activity coefficients. We start with a discussion of ideality which has more than one definition in the literature. This will be important to relate molecular level correlations to the various measures of nonideality.

Ideal solutions

We first review the theoretical definitions of an ideal solution to set our work in context. The reader familiar with this area and interested in the case of urea solutions may skip to Methods. The concept of an ideal solution was first developed by Raoult historically (15). Raoult found that the vapor pressure of a component over a liquid solution at equilibrium is proportional to the mole fraction of the component in solution,

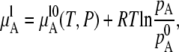(2)

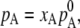(3)

where 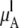is chemical potential of the substance A in the mixture solution, 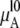is chemical potential of A in pure A, p_A is the partial vapor pressure of A in the mixed solution, and 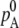is the vapor pressure of pure A.

Here, the ideal solution is defined as the solution which satisfies the following relation for mole fractions 0 ≤ x_A ≤ 1:

(4)

In this definition, it is not necessary to assume that vapor is an ideal gas. This type of ideal solution has been called a symmetric ideal solution (6). In Eq. 4 the second term, right side, is always ≤0.0, and it implies that the chemical potential in a mixture is always smaller than that in the pure liquid. Note that symmetric ideal solutions are defined at constant temperature and pressure.

The Gibb's free energy difference per molecule or chemical potential, Δμ, when an ideal solution is made from n_A of substance A and n_B of substance B becomes

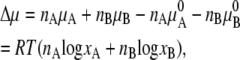(5)

with change in enthalpy, ΔH, and entropy, ΔS,

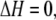(6)

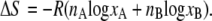(7)

Thus, there is no enthalpy change (no heat of mixing) (Eq. 6). Equation 7 is the entropy of mixing in an ideal gas. Therefore the difference in chemical potential between the system of n_A moles of pure A and the mixture system of solution of n_A moles of A and n_B moles of B is

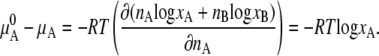(8)

This makes clear that the second term on the right-hand side of Eq. 4 is the contribution from the entropy of mixing.

What are necessary and sufficient conditions for such ideal solutions? By differentiating Eq. 4 by x_A we have

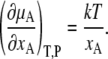(9)

On the other hand, we know from Kirkwood-Buff theory (16),

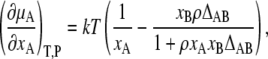(10)

where ρ is the number density, ρ = ρ_A + ρ_B = 〈N_A〉 /V + 〈N_B〉 /V, and

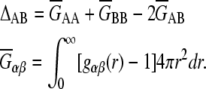(11)

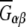is called the Kirkwood-Buff integral which requires the radial pair distribution, g_αβ(r), as a function of distance, r, between molecular species α and β.

Therefore, the necessary and sufficient condition is that there are no excesses or deficits of one molecule around another versus a simple random distribution on average or that

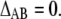(12)

In many solutions, the vapor pressure of solvent of very dilute solute solutions obeys

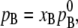(13)

where, from now on, we consider A as solute and B as solvent. This is the empirical law for infinitely dilute solutions at constant T. Thus, in particular, pure solvent is an ideal solution. When the solvent obeys Raoult's law in dilute solutions, the solute follows

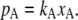(14)

Here, p_A is vapor pressure of solute and k_A is a constant which depends on the species of the solute. This relation is derived straightforwardly by integrating the Gibbs-Duhem relation. This is called Henry's law (17). In this case, the chemical potential of solute becomes

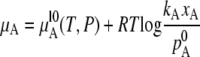(15)

at x_A ∼ 0 (we assume that the gas phase is an ideal gas or very dilute). Henry's law can be derived differently as follows. When the mole fraction of solute approaches 0, its vapor pressure also approaches 0, and so

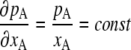(16)

is another statement of Henry's law. Therefore, the existence of this proportionality relation does not depend on the species of the solutes or the number of components of the solution. The proportionality constant k_A contains the actual dependence on the substance. Similarly, we obtain the following relations by using different units such as molality, m, or molarity, ρ, instead of mole fraction, respectively,

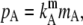(17)

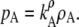(18)

The vapor pressure of the solute in an infinitely dilute solution is proportional to mole fraction, molality, or number density. Here, we showed the proportional relations to vapor pressure, but one can derive similar relations for activity.

The validity of the concentration dependence of Henry's law depends on the species of the substances involved, but is often a good approximation at low concentration where we do not expect significant associations or influences among the solute molecules. If Henry's law is satisfied at high concentration, the chemical potential is the same as that of the infinitely dilute solution, that is, a dilute ideal solution.

If the chemical difference between solute and solvent is very small and the solution is a symmetric ideal solution, Henry's law is then satisfied as long as we use mole fraction or molarity scales. In other words, if it is a symmetric ideal solution with similar molecular volumes, it is also a dilute ideal solution in mole fraction scale and molarity scale. The dilute ideal solution in the molality scale is exceptional and it is not a symmetric ideal solution even if it is a dilute ideal solution as explained later.

The regular solution defined by Hildebrand is the solution which satisfies the following (18):

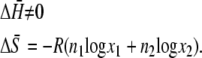(19)

This differs subtly from Raoult's definitions in Eqs. 6 and 7 by the allowed change in ΔH. This is consistent with the assumption that there are no specific interactions such as associations between molecules so that the distribution and orientation of molecules are completely random. Therefore, a urea solution is not expected to be regular because it has specific strong interactions and local orientational preferences via hydrogen bonds. In regular solutions, thermal fluctuations are assumed to be strong enough to overcome the specific or orienting interactions between different molecules and cause random mixing. If the difference between two molecules is large and random mixing does not occur, solubility is generally small in this case and it becomes a very dilute solution. As a result, there will be little direct interactions between solute molecules.

Concentration scale dependence of nonideality

We now discuss general solutions which deviate from ideal solutions and the dependence of measured changes in activity on concentration scales. We may write

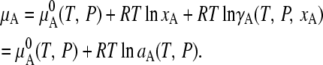(20)

Here, a_A is relative activity and γ_A is the activity coefficient. The value 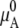is the chemical potential of pure A, so γ_A = 1 when x_A = 1. Various nonideal effects are all included in γ_A in this expression. Note that a_A is deemed “relative” because we used a standard state. If we consider μ_A without choosing a standard state,

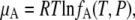(21)

where f_A is the absolute activity.

As above, a natural choice of the standard state is a pure solute solution. However, most pure salts and many osmolytes are solid and not liquid in the range of temperature and pressure in which we are usually interested (∼1 atm, ∼298 K). In this case, 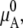which is the chemical potential of the pure liquid, is not measurable experimentally. Another natural choice of the standard state is the infinitely dilute solution. Therefore, in many cases we take infinite dilution as the standard state for osmolytes.

The fact that relative activity is thus defined in various, disparate ways causes confusion in the literature. Only when the relative activity with respect to the pure liquid can be evaluated experimentally is it the custom to take pure liquid as the standard state. We often take the infinite dilute solution as the standard state because it can be referred to easily experimentally.

The activity coefficient at mole fraction x when the standard state is infinitely dilute may be introduced in the following way:

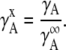(22)

Here, 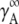is the activity coefficient of the infinite dilute solution. Using 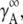Eq. 20 becomes

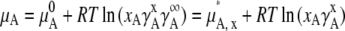(23)

using the infinite dilution standard state. Thus, we define the sum of the chemical potential of pure A and the contribution from the infinitely dilute standard state as

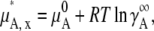(24)

which can be referenced experimentally.

We next consider the consequences of concentration scale change from mole fraction to molality [mol/kg]. Molality can be expressed

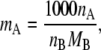(25)

where M_B is the mass [g/mol] of the solvent B, and n_A and n_B are the mole numbers of the substances A and B in the system. The relation between mole fraction and molality is simply

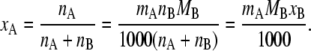(26)

Substituting Eq. 26 in the first equation of Eq. 23, we have

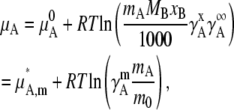(27)

where m₀ = 1 [mol/kg] was introduced to make the content of the ln dimensionless and

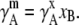(28)

With this we define

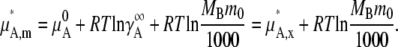(29)

Equations 28 and 29 are the activity coefficient and chemical potential in the infinite dilution standard state with the molality scale, respectively.

Similarly for molar concentration units referenced to infinite dilution,

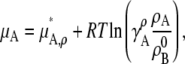(30)

where 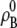[mol/L] is the number density of the pure solvent B and again makes the argument of the 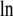dimensionless and makes the activity coefficient in the infinitely dilute solution 1.0 (see Eq. 31 below). The activity coefficient and standard state chemical potential in the molarity scale are

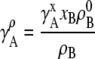(31)

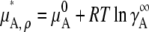(32)

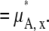(33)

The well-known relation between the molality and the molarity activity coefficients for a given temperature and density can be obtained similarly:

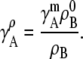(34)

Alternatively, one could just use the analytic transformation between the concentration scales, which does not require knowledge of the density at the relevant temperature previously derived, to good accuracy (7).

The chemical potential of solute A in ideal dilute solutions (x_A ∼ 0, x_B ∼ 1) are thus expressed in any of the following ways,

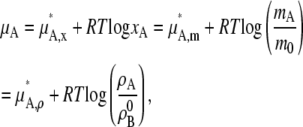(35)

and the chemical potentials in terms of activities, and activity coefficients for general nonideal, dilute solutions are

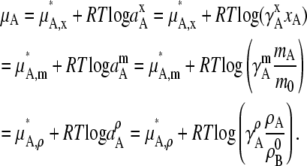(36)

The molality and mole fraction of solutions do not depend on temperature, but molarity does depend on temperature because the volume and thus, density, changes with respect to temperature. Given this and the volume-versus-mass issue, the apparent nonideality of a given solution is qualitatively very different if we choose different concentration scales except in the limit of infinitely dilute solutions where γ becomes 1.0 in every scale.

Reference state forms of chemical potential

In this section, we formally explore the consequences of interpreting the chemical potential changes for different reference systems in various concentration units. The object here is to phrase the relevant relations in terms of quantities readily computable from simulation or liquid state theory. Besides the numbers of molecules of each species, we will require the average volume, 〈V〉 and the excess chemical potential.

We perform our simulations found in Results and Discussion in the isobaric-isothermal or NPT ensemble for the calculations of the excess chemical potential. Equation 59 could be used to calculate chemical potential but refers to a different ensemble. In general, one could simply Legendre-transform the results. However, because the correlation between volume and energy in Eq. 59 is small in urea solutions (the correlation coefficient magnitudes in our simulations were ∼0.15), we can reliably, approximately transform Eq. 59 to

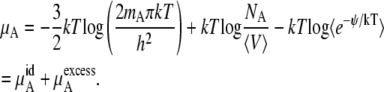(37)

Here, the ensemble average is taken over 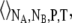and

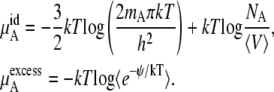(38)

Urea solutions at room temperature and pressure are dense liquids and urea is too large for a successful implementation of the particle insertion method for 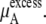We evaluated three other methods below, thermodynamic integration, perturbation theory, and the Bennett-Pande acceptance ratio method, for an estimation of 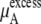of Eq. 37. This term is often interchangeably referred to as either the excess chemical potential or the solvation free energy. The detailed conditions of our simulations are described later in Methods.

Given the breakdown of μ_A in Eq. 37, we now write the chemical potential form in terms of quantities readily available from simulation in the mole fraction, molality scale, and molarity scale below:

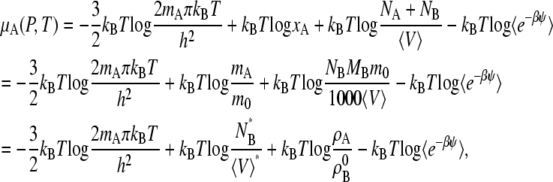(39)

where the terms with * are the values at the infinitely dilute state.

Let us first consider infinite dilution as the standard state. Consider the deviation from the dilute ideal solution. In the mole-fraction scale standard state, the chemical potential and activity coefficient become

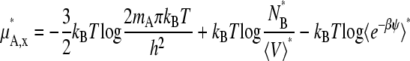(40)

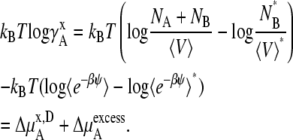(41)

In the molality scale, we thus have

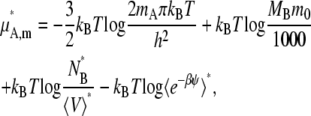(42)

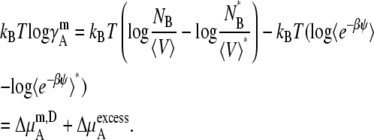(43)

We see that the relationship between activity coefficients in the mole fraction and molality case is the same as shown in Eq. 28. Namely, Eqs. 41 and 43 are consistent with Eq. 28 as they should be.

In the case of the molarity scale, however, we have

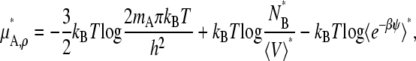(44)

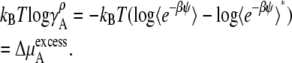(45)

These equations (Eqs. 41, 43, and 45), in terms of readily computable quantities, show how the meaning of nonideal solutions change when the concentration scale changes. The activity coefficient in the molarity scale measures only the excess free energy difference (solvation free energy difference). As is well known but often underappreciated, the apparent deviation from ideality for dilute solutions strongly depends on the scale.

We next consider the nonideal deviation for a symmetric ideal solution reference. Pure solute is the standard state in this case. However, symmetric ideal solutions are usually defined with the mole fraction scale (Eq. 4), not with molality or molarity. Therefore, the standard state and activity coefficient may be written as

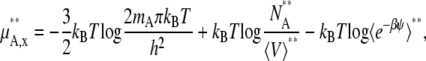(46)

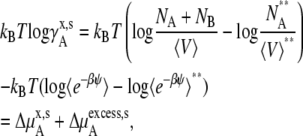(47)

where the terms with ** are the values for a pure solute state. There are two ways to make the activity coefficient 1.0:

• Case 1:

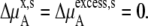
• Case 2:

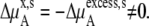
In a mixture of very similar molecules, case 1 is approximately achieved. This is the familiar example of a symmetric ideal solution. Case 1 also makes Δ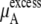 in Eq. 41 and Δ 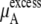in Eq. 45 0.0. Therefore, if it is a symmetric ideal solution and the number of total molecules in the system per volume is constant (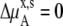), it is also a dilute ideal solution in mole fraction scale and molarity scale. However, 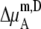in Eq. 43 is not 0.0 because the number of solvent molecules changes, so symmetric ideal solutions are not dilute ideal solutions in the molality scale.

We may also take the pure solute as the standard state in molality scale and molarity scale. This choice, however, does not measure the deviation from symmetric ideal solutions because symmetric ideal solutions are usually defined by the mole fraction scale. In the molality scale, the standard state and activity coefficient may be defined as

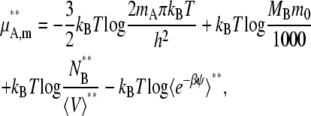(48)

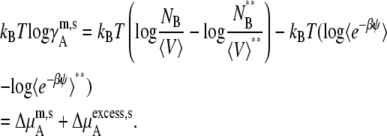(49)

Without any solvent molecules, we have a numerical problem. In Eqs. 48 and 49 the standard state in pure solute effectively causes

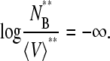(50)

Therefore, it is not reasonable or convenient to take the pure solute state as the standard state in the molality scale.

For the molarity scale, the standard state and activity coefficient would be

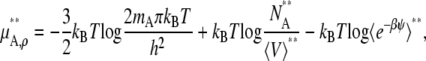(51)

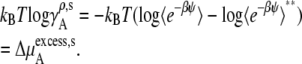(52)

Clearly, standard state and concentration scale choices change the meaning of the activity coefficient in a qualitative and quantifiable way.

Excess chemical potential calculation by simulation

We next require an accurate way to calculate the change in excess free energies or chemical potentials in solution for adding a solute. To explore mechanism and to control for force field, two variants are used below, well-known OPLS (19) and the newer KBFF by Smith and co-workers (20). We demonstrate the efficiency and precision characteristics for three methods of calculation. We present a brief review of the methods here first for coherence. Considerably more detailed technical reviews exist in the recent literature (21).

Thermodynamic integration method

The well-known thermodynamic integration method calculates the free energy difference between the state i and the state j by

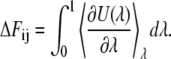(53)

Here, we assumed the potential energy function U(λ) is written as a function of a coupling parameter, λ, and λ = 0 and λ = 1 correspond to the state i and the state j, respectively. We can define many different functional dependencies on λ corresponding to different integration paths. The simple linear ramp is

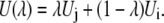(54)

We consider the beginning and final system to correspond to N particle system and N + 1 particle system, respectively. There is a well-known pole at the origin for the Lennard-Jones interaction with respect to λ. To avoid numerical instability, a nonlinear function is sometimes used to alleviate large absolute values at a small λ. The following soft-core potential function was developed to avoid singularity in van der Waals (vdW) interactions, to calculate the free energy difference precisely (22,23):

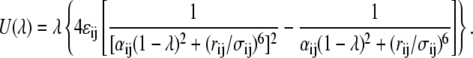(55)

We adopted this soft-core potential in our calculations.

Perturbation method

In so-called thermodynamic perturbation methods we derive without any approximations:

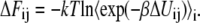(56)

This equation means that we can obtain the free energy differences between the state i and the state j by calculating the ensemble average of exponential of the potential energy difference at the state i ensemble. This method is only useful when the state j may be conveniently sampled from state i. To avoid difficulty one typically divides the region into many subregions:

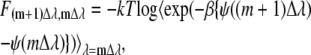(57)

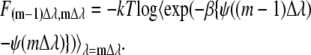(58)

This method of small windows or steps is exacerbated if the energy barrier in or between subregions is large. A different approach to a solution is to use nonphysical sampling such as embedding the problem in a higher dimensional space or using generalized ensemble methods. We found we could use Eq. 57 or 58 because our urea solution was not so complicated.

Widom test particle insertion method

For completeness we mention the Widom insertion method which has uses both conceptual and practical (21,24). The basic equation of Widom method (24) can be derived like Eq. 56 in the NPT ensemble,

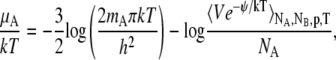(59)

where we show the equation in the case of a monoatomic. In the NVT ensemble we have

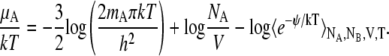(60)

In this method we insert a particle randomly in the system and calculate the potential energy with which the inserted particle interacts. This method works very well in low density systems, but fails in dense liquids and solids especially when the inserted molecule is large. Therefore the precision of calculation is often not sufficient, especially in calculating activity coefficients, with this method.

In the case of polyatomic molecules, the chemical potential becomes the following one instead of Eq. 59,

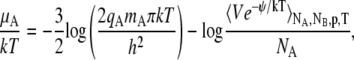(61)

where q represents the rotational, vibrational, electronic, and nuclear partition function terms. We assume that these terms can be separated from the configuration integral without concern about whether they are expressed classically or quantum-mechanically. This assumption breaks down when strong intramolecular interaction changes the counting of degree of freedom. In this article we set q = 1 (Eq. 59).

Bennett-Pande ratio method

The Bennett method (25) for optimizing sampling was originally implemented to accelerate convergence of Monte Carlo methods. More recently Pande and co-workers (26) used this principle to achieve optimal sampling in a variant of the familiar thermodynamic perturbation theory method. The input data to calculate the free energy is the same essentially. The difference with perturbation methods is the numerical precision. Bennett's method minimizes statistical error. The two basic equations are

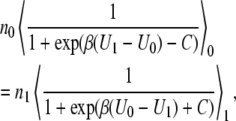(62)

where

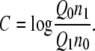(63)

Here, n₀ and n₁ are the sample numbers in the ensembles at the state 0 and the state 1, respectively. In practice, we plot both sides of Eq. 62 as a function of C, and solve for the C which satisfies this equation. We then have

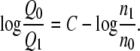(64)

If we collect the same number of samples (n₀ = n₁), we can calculate the free energy difference:

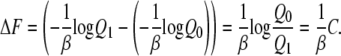(65)

This method uses the same input data as perturbation method (U₁–U₀), but recent studies show that it is often the best way to obtain free energy differences (26–28).

METHODS

We wish to understand the mechanism by which a model might reproduce experiment. As a control and illustration, we evaluated two different urea models, namely OPLS (19) and KBFF (20) and examine the dependence of the activity coefficients on the force-field parameters. We show the parameters of these two models in Table 1. The geometry of the urea models is the same. We adopted TIP3P model for water and the minor consequences have been noted previously (2).

TABLE 1.

Force-field parameters for the OPLS model (19) and KBFF model (20)

	Mass	Charge	ɛ(kJ/mol)	σ(nm)
OPLS
O	15.999	−0.390	0.87864	0.296
C	12.011	0.142	0.43932	0.375
N1	14.007	−0.542	0.71128	0.325
H11	1.008	0.333	0.00000	0.000
H12	1.008	0.333	0.00000	0.000
N2	14.007	−0.542	0.71128	0.325
H21	1.008	0.333	0.00000	0.000
H22	1.008	0.333	0.00000	0.000
KBFF
O	15.999	−0.675	0.56000	0.310
C	12.011	0.921	0.41700	0.377
N1	14.007	−0.693	0.50000	0.311
H11	1.008	0.285	0.08800	0.158
H12	1.008	0.285	0.08800	0.158
N2	14.007	−0.693	0.50000	0.311
H21	1.008	0.285	0.08800	0.158
H22	1.008	0.285	0.08800	0.158

KBFF urea model was developed to reproduce the experimental activity data. In Weerasinghe and Smith (29), they determined a charge distribution for urea atoms by using Kirkwood-Buff integrals obtained from simulations. Kirkwood-Buff relations yield the derivative forms of activity coefficients. It is necessary to integrate them subsequently by, for instance, assuming the experimentally suggested functional form. However, Kirkwood-Buff G factors converge very slowly and it is difficult to obtain precise values from simulation.

The OPLS parameters have been used extensively in the literature to model and simulate a variety of systems. The OPLS model was fit to several liquid state properties including heats of solvation among others (19).

By using two different models we hope to get an idea of the force-field dependence in the implied mechanism. In this article, for these potentials, we calculate the chemical potential directly from the simulations by the methods described in Theory and thereby obtain the relative activity coefficients to compare directly with experiment. Thus, we test multiple methods over a range of concentrations in hopes of obtaining sufficient precision to evaluate the accuracy of the models for this purpose. In future work we will consider three component solutions which include a polypeptide.

We prepared urea aqueous solutions at seven different concentrations for the OPLS and KBFF models from dilute solution to the pure urea. We first estimated the molecular volume for one urea roughly to obtain the expected concentrations. It was approximately two and half times the volume of one water. For the pure solute solution state, since urea is a solid at room temperature, a pure urea sample was equilibrated at a higher temperature and super-cooled to 298 K.

To prepare our solutions we took an equilibrated water box and the urea box, and randomly removed the required urea and water molecules from each of these boxes in turn to achieve the required numbers for the desired solution concentrations. Rather than the standard replacement, we put these two boxes in contact with the normal periodic boundary conditions at the large volume equivalent to the two pure liquids. Next the volumes were shrunk to the target value to mix the urea and water. Thus, we prepared the systems by deciding the number of urea and water molecules and shrinking to a given volume. We performed a minimization for 500 steps and mixed for 100 ps of NVT simulation for each concentration. Temperature was controlled by Nosé method to 298 K (30). In this process it was found that the mixing occurred not only spontaneously but in fact quite rapidly, on the order of the time to shrink the box. We next performed 300 ps NPT equilibrations at 298 K and 1 atm using the Nosé-Anderson method for the temperature and pressure control (30,31). The final system sizes are close to 34 Å × 34 Å × 34 Å in each case.

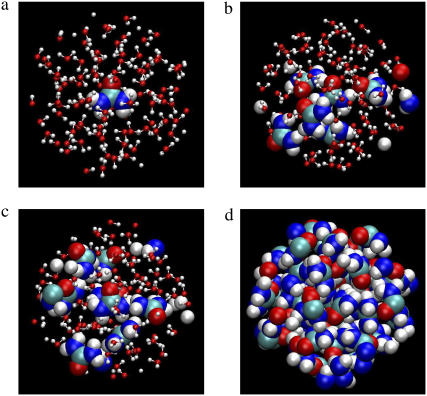
We thus obtained the initial configurations of urea solutions at seven different concentrations for two different urea models. The number of total systems considered is 14 (7 concentrations × 2 urea model). All the systems in our simulations are listed in Table 2. We show typical snapshots of configurations of KBFF urea solutions in Fig. 1, which qualitatively confirms the good mixing.

TABLE 2.

Symbols are N_u, number of urea molecules, and N_w, number of water molecules

	Nu	Nw	Mole fraction	Molality	Molarity	Volume	Density
OPLS	1	1305	0.0007657	0.04253	0.04288	38.73	1.011
	47	1188	0.03806	2.196	2.029	38.47	1.046
	95	1077	0.08106	4.896	4.089	38.58	1.081
	142	955	0.1294	8.254	6.152	38.32	1.115
	189	838	0.1840	12.52	8.209	38.23	1.149
	248	661	0.2728	20.83	11.04	37.31	1.193
	530	0	1.0	—	22.65	38.85	1.361
KBFF	1	1305	0.0007657	0.04253	0.04286	38.75	1.010
	47	1188	0.03806	2.196	2.013	38.78	1.037
	95	1077	0.08106	4.896	4.027	39.17	1.064
	142	955	0.1294	8.254	6.031	39.10	1.093
	189	838	0.1840	12.52	7.993	39.27	1.118
	248	661	0.2728	20.83	10.70	38.50	1.156
	530	0	1.0	—	22.41	39.27	1.346

The units of molality, molarity, volume, and density are (mol/kg), (mol/L), (nm³), and (g/cm³) respectively.

FIGURE 1.

Typical snapshots of KBFF urea solutions. The figures correspond to the systems of mole fraction 0.0007657 (a), 0.08106 (b), 0.1840 (c), and 1.0 (d), respectively. Only atoms within the sphere with 9.0 Å radius in the center of the specific one urea molecule are drawn. Urea molecules are drawn as space-filling and water molecules are ball-and-stick. VMD was used for this figure.

Because all systems have very similar box size, we used the same cutoff length 15 Å for vdW interactions, which was >4σ. We used a link-cell Ewald method for electrostatic interactions (32). In the studies undertaken here it may be quite important to estimate the electrostatic interactions accurately to correctly distinguish among the potential energy models. Free energy calculation is known to be very sensitive to the method used for electrostatic energy calculation (33).

We calculated the chemical potentials by Eq. 37 inserting one urea molecule. The term for 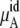of Eq. 38 was calculated using the temperature and average volumes. 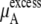of Eq. 38 was calculated by three different methods. Those are the thermodynamic integration method, perturbation method, and Bennett acceptance ratio method. In calculating 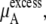we divided the potential energy of the inserted urea molecule into the vdW and electrostatic terms for subsequent analysis.

In the case of vdW interactions, a soft-core potential (Eq. 55) was used. The range for λ was divided into 50 subregions (= 51 points). We thus calculated 51 λ-points of the integrand of Eq. 53 for the thermodynamic integration method and for the perturbation method using Eqs. 57 and 58. The same sampling data as used for the perturbation method was used for the Bennett method after Pande. In the case of the electrostatic interaction contributions, we used Eq. 54 and divided λ into 25 subregions (= 26 points). By performing the repulsive core first, there is no remaining singularity, so it is not necessary to use soft-core potential for electrostatic interactions.

In the case of thermodynamic integration method, plotting the integrand of Eq. 53 at the calculated λ-points and integrating numerically we obtain the excess chemical potential. In the case of the perturbation and Bennett methods, we used Eqs. 57, 58, and 62, respectively. Summing up the subdivisional free energy difference at the calculated λ-points produces the excess chemical potential. The input data to Eq. 62 is U_j–U_i and this is the same as the perturbation method case. As we show in the section below, these three different methods give us almost the same values if the sampling yields enough precision as expected. We show some example figures of the free energy calculation paths below.

RESULTS AND DISCUSSION

Chemical potential calculations

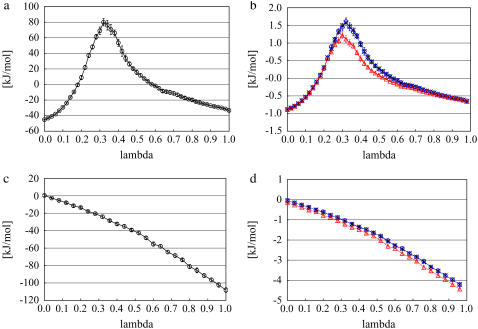
We now consider the results of the calculations of μ^excess as well as μ as a function of concentration and standard state. Fig. 2 a shows the integration path in the case of the most dilute KBFF solution. The error bar of each point was estimated by dividing the data into 10 blocks and calculating the standard deviation of the average values. The error bars were largest in the region of most curvature. That region demands more sampling for precise estimations. The points between 0.26 < λ < 0.60 in Fig. 2 a were calculated from 1-ns simulations, and other points were from 160-ps simulations. Integrating this path from 0 to 1 gives the free energy difference of the vdW transfer from vacuum to solution. Fig. 2 c is the corresponding figure for the electrostatic part. Summing up the integrated values of Fig. 2, a and c, becomes the total free energy difference (the excess chemical potential).

FIGURE 2.

The excess chemical potential integrand components in the case of the most dilute KBFF urea solution. (a) Integration path for the calculation of vdW terms of excess chemical potential by thermodynamic integration method. Integrating this path about lambda becomes the total vdW excess chemical potential. (b) The 51 λ-points for the calculation of vdW terms of excess chemical potential by Bennett acceptance ratio method (black asterisk) and perturbation method (+, estimation Eq. 57, blue circle; –, estimation Eq. 58, red triangle). Adding the differences of 51 points becomes the total vdW excess chemical potential. Asterisk and circle overlap very well. (c) Similar to panel a for electrostatic terms. (d) Similar to panel b for electrostatic terms.

Fig. 2, b and d, show the calculated values of the λ-points at the most dilute solution for the perturbation method and Bennett method using the KBFF model. We see that Bennett estimation points almost overlap perturbation ones. Summing the values yields the total free energy difference.

Based on the experimental trends we expected the deviations from ideality to be difficult to obtain with sufficient precision to evaluate the difference between models. Thus we tested the precision and convergence of the three different free energy techniques. We confirmed that the free energy values calculated by these three different methods gave similar values for each system. For example, in the system of Fig. 2 the obtained values by thermodynamic integration method, perturbation method, and Bennett method are respectively 2.147, 2.113, and 2.138 kJ/mol for the vdW part, and −46.411, −46.393, and −46.398 kJ/mol for the electrostatic part, respectively. Testing of convergence in model systems showed that the Bennett method as implemented by Pande and co-workers (26) gave the least errors for a given amount of sampling (data not shown). Given that and the sub kJ/mol precision of all the methods, we used the estimations by the Bennett method in the following analysis for all the other systems.

Table 3 shows the chemical potentials and their components obtained from our simulations. Because μ_A of OPLS is more negative than that of KBFF at the same concentration, OPLS urea dissolves in aqueous model solutions using the TIP3P water model better than KBFF urea.

TABLE 3.

Chemical potential and its components for OPLS and KBFF model urea solutions using Eq. 37

Mole fraction		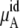		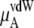	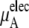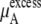μA
OPLS
0.0007657	−41.31	0.87	−56.00	−55.13	−96.44
0.03806	−31.76	0.66	−56.40	−55.74	−87.49
0.08106	−30.02	0.33	−56.19	−55.86	−85.88
0.1294	−29.01	0.49	−56.56	−56.07	−85.08
0.1840	−28.29	0.040	−56.63	−56.59	−84.88
0.2728	−27.56	−0.63	−57.11	−57.73	−85.29
1.00	−25.78	−1.29	−56.43	−57.72	−83.50
KBFF
0.0007657	−41.31	2.14	−46.40	−44.26	−85.57
0.03806	−31.78	1.29	−45.57	−44.29	−76.06
0.08106	−30.06	0.38	−44.79	−44.41	−74.46
0.1294	−29.06	−0.27	−44.22	−44.49	−73.54
0.1840	−28.36	−1.16	−43.12	−44.28	−72.64
0.2728	−27.64	−2.44	−41.83	−44.28	−71.91
1.00	−25.80	−4.82	−37.40	−43.23	−69.03

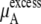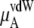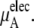
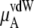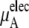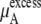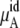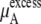The quantity consists of two terms, the vdW part and the electrostatic part plus becomes in Eq. 37. The quantity plus becomes the chemical potential μ_A. The units of chemical potential are (kJ/mol).

The ideal part of the chemical potential does not depend as strongly on the interaction model (see, for instance, Eq. 38). In fact only small differences in volume or density are model-dependent. The deBroglie wavelength term is clearly common for OPLS and KBFF solutions. 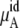increases as the concentration increases because the number of urea molecules per volume increases (see Eqs. 37 and 38). Thus, the entropy at higher urea concentration (mole fraction) is smaller than in the lower one, as it should be.

We see that 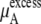of KBFF solutions, the excess chemical potential, is almost constant except for the pure urea system. This requires a remarkable cancellation to obtain the same excess solvation free energy at different urea concentration for the KBFF force field. On the other hand, for the OPLS force field, 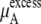decreases as the concentration increases. For such a force field, we see that the total chemical potential change and the excess part move in different directions. Interpreting only the excess solvation part of the free energy, as is often done in simple modeling, would indicate that urea dissolves in higher urea concentration solutions more favorably.

In Table 3 we examine the potential components of 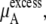that is, 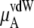and 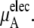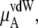the vdW part of the excess chemical potential, shows a decreasing trend as the concentration increases for both models. However, this tendency does not imply that, in urea solutions, cavity formation is more favorable than in pure water, as we have the attractive part contributions to consider. Ikeguchi et al. (34) calculated the free energy profile using a Lennard-Jones potential by changing σ at constant ε and clearly showed that the larger the excluded volume is made, the less soluble in aqueous urea the solute is than in pure water. Therefore this decreasing trend of the vdW part with increasing concentrations is caused not because urea solutions necessarily prefer just the cavity formation more than pure water in high urea concentrations, but because they prefer vdW interactions with the inserted urea more.

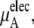the electrostatic term, is remarkably independent of concentration for the OPLS model with noisy variations on the order of tenths of a kJ/mol. On the other hand, the KBFF model shows a smooth 5 kJ/mol change over the concentration range studied here. We interpret that as a growth in unfavorable electrostatic interactions in KBFF solutions as the urea concentration gets higher. KBFF has substantially larger atomic charges than OPLS or other common models. This charge contribution is opposed by almost equal and opposite favorable vdW interaction contributions. This results in an excess chemical potential 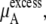which becomes quite flat with respect to concentration for the KBFF model solutions. In contrast, the OPLS 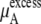decreases monotonically as the concentration is increasing.

The total chemical potential, μ_A, increases (becomes less negative) as the concentration increases for both solutions partially because of the entropic effect, which is included in 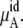Given the size of the terms we find the influence on μ_A from 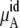is stronger than that from 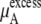for urea solutions.

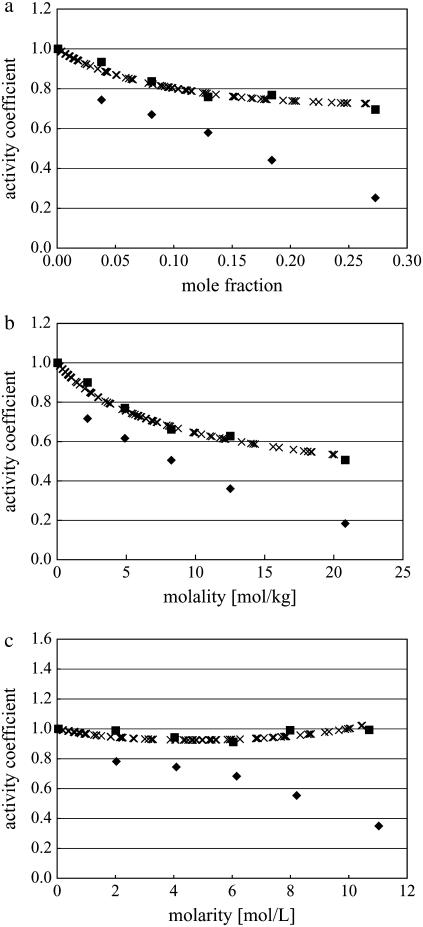
Fig. 3 shows the activity coefficients in different concentration scales: mole fraction scale (Fig. 3 a), molality scale (Fig. 3 b), and molarity scale (Fig. 3 c). For these plots we took the standard state as the most dilute system in our simulations, approximating infinite dilution in the traditional computational way. The original experimental data (12–14) was in the molality scale, and it was necessary to transform the data to obtain the experimental activity coefficients in the different scales. We transformed the concentration scale by using experimental density data (35) from the molality scale (Fig. 3 b) to mole fraction (Fig. 3 a) and molarity scales (Fig. 3 c) by using Eq. 28 and Eq. 34. Note that we did not use any experimental data for our simulated activity coefficients. We first see that the variation in activity coefficients is striking with respect to the different concentration scales. The values in the three different scales coincide with each other only in very low concentration solutions as expected.

FIGURE 3.

Activity coefficients in various scales. (a) Activity coefficients in the mole fraction scale. (b) Activity coefficients in the molality scale. (c) Activity coefficients in the molarity scale. Solid square marks are for KBFF urea solution by our simulations. Solid diamond marks are for OPLS urea solution by our simulations. Multiple marks are for experimental values (12–14,35).

We see in Fig. 3 that activity coefficients of the KBFF model fit the experimental ones very well, as expected, since that was the basis on which the force field was parameterized. On the other hand, the OPLS are systematically smaller than experiment. That model was not fit to the activities. Our high precision method to calculate activity coefficients showed that the KBFF model in fact reproduces the experimental data even better than the authors expected in Weerasinghe and Smith (20). Because Kirkwood-Buff G factors are the functions which converge very slowly both in time and length, a direct chemical potential calculation by a thermodynamic method like Pande's Bennett method gives more easily controlled precision.

Consider the origin of the difference of activity coefficients. Fig. 3 a shows the activity coefficients in the mole fraction scale. The simulation data was calculated by Eq. 41. A urea molecule is some 2.5 times larger than a water molecule, so 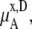which is a function of the number of solute and solvent molecules per volume, decreases as the concentration of urea increases. This contributes in the well-known classic manner to make the activity coefficients smaller as the concentration increases. If the volume of the solute is smaller than that of solvent, the effect becomes the opposite. However, in most aqueous solutions, water is smaller than the solute so this term contributes to make the activity coefficients smaller.

Fig. 3 b displays our results in the molality scale. It was calculated by Eq. 43. The quantity 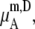which is a function of the number of solvent molecules per volume, always decreases as the concentration of solute increases. It also contributes to make the activity coefficients smaller as the concentration increases.

Fig. 3 c shows that KBFF model solutions are remarkably close to an ideal solution in the molarity scale. The activity coefficients in this scale are based on Eq. 45. Therefore the ideality in molarity scale is based on the characteristic that the excess chemical potential (solvation free energy) is nearly the same at different concentrations (see Table 3). On the other hand, the activity coefficients of OPLS urea solutions decrease as the concentration increases. This is because the solvation free energy of OPLS urea solutions decreases as the concentration increases (see Table 3). We again note that the activity coefficient in the molarity scale most clearly reflects the excess chemical potential or the excess solvation free energy.

We compare the results in Table 4. Of course 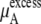for a given model is common. The tables clearly show the influence of concentration scale in 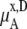and 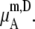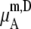is always smaller than 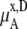in the same system from the definitions (see Eqs. 41 and 43), as a result the activity coefficients in the molality scale are always smaller than those in mole fraction scale.

TABLE 4.

Activity coefficients in different scales

x		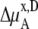	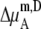Δ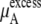
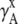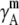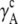OPLS
0.0007657	0.000	0.000	0.000	1.000	1.000	1.000
0.03806	−0.122	−0.216	−0.610	0.744	0.717	0.782
0.08106	−0.259	−0.466	−0.731	0.671	0.617	0.745
0.1294	−0.406	−0.748	−0.944	0.580	0.505	0.683
0.1840	−0.563	−1.065	−1.462	0.442	0.361	0.554
0.2728	−0.805	−1.593	−2.604	0.253	0.184	0.350
1.00	−2.242	—	−2.592	0.142	—	0.351
KBFF
0.0007657	0.000	0.000	0.000	1.000	1.000	1.000
0.03806	−0.141	−0.235	−0.027	0.934	0.900	0.989
0.08106	−0.295	−0.503	−0.146	0.837	0.770	0.943
0.1294	−0.455	−0.796	−0.228	0.759	0.661	0.912
0.1840	−0.629	−1.131	−0.025	0.768	0.627	0.990
0.2728	−0.882	−1.669	−0.017	0.696	0.506	0.993
1.00	−2.268	—	1.033	0.608	—	1.517

See Eqs. 41, 43, and 45 for the definitions of and Δ The values x, m, and c stand for mole fraction, molality, and molarity, respectively.

The activity coefficient is often considered as the coefficient of the concentration in various contexts including the chemical potential expression. In this use, the supposition is that regardless of concentration scale, if the activity coefficient of the substance is doubled the same chemical potential is obtained by half the amount of the substance. However, this use of the concepts is confusing because of the strong dependency of activity coefficient on the scale as we have seen. The classic definition is useful only for very dilute solutions, in which every scale gives essentially the same value. The supposition is not valid for high solute concentrations such as in living cells. Strictly speaking, activity is not an effective concentration as pointed out previously (7).

We suggest that it is appropriate to use the chemical potential itself to avoid confusion in theoretical studies. The chemical potential does not depend on which scale we use. One difficulty is that what we most often obtain from experiments are activity coefficients in molality scale. It is necessary to have the reference state value to recover chemical potential, which is unfortunately essentially inaccessible experimentally.

Our simulation results show the KBFF urea model (20) well reproduces the experimental data. Other simple, nonpolarizable models could reproduce the experimental activity coefficient data but it is not obvious what other forms such a model might take. The reason that the KBFF urea model reproduces the experimental activity coefficients is because the excess chemical potential is almost the same at different concentrations. This is caused by a cancellation of the vdW part with the electrostatic part as the concentration increases. On the other hand, in the OPLS urea model, vdW contribution decreases slightly but the electrostatic part does not tend to increase as the concentration increases, and this contributes to a smaller activity coefficient. Note that, if one could design force-field parameters such that the vdW part increases while the electrostatic part appropriately decreases, an ideal solution in the molarity scale would result.

The KBFF urea model was developed by integrating inverse Kirkwood-Buff theory. As KB theory address only the derivative forms, additional information is necessary to obtain the absolute values. Thus only the derivative of the activity coefficient is expressed by Kirkwood-Buff G integrals. It is necessary to assume the appropriate excess Gibbs free energy form to obtain the activity coefficient. We cannot know the absolute activity itself only from Kirkwood-Buff theory. The excess chemical potential cannot be obtained experimentally in most osmolytes and electrolytes because the vapor pressure at room temperature is too low to measure accurately.

Our simulation results show that the excess solvation free energy of KBFF model is roughly 10.0 kJ/mol higher than that of OPLS model (see Table 3). On the other hand, a 1–2 kJ/mol difference from the chemical potential in the standard state (the most dilute system) produces the difference of activity coefficients (see Table 4).

This implies that the large difference of the solvation free energy regulates a small difference for the activity coefficients. The KBFF model reproduces the experimental activity coefficient data, but the validity of solvation free energy is unknown. There is no experimental solvation free energy data for urea, so it is presently difficult to judge which urea model does better for the excess solvation. Weerasinghe and Smith (20) is the first attempt to make a thermodynamically accurate force field based on Kirkwood-Buff theory. Not every molecular or macroscopic property is given by any one approximate, mean-field force field and OPLS has many properties not including activity which better reproduce experiment (19) than KBFF.

Parameter comparison

We next consider the solution theory for analyzing experimental activity coefficients which was recently developed in the literature (7,8). There an analytic activity coefficient form was derived using only the first few terms of a semi-grand canonical ensemble. The fits to the experimental data for urea (and other compounds) of activity coefficient data were essentially quantitative from dilute solution to saturation (see (8) for the details). The question of physical interpretation of the parameters cannot be answered uniquely without establishing whether the fitting coefficients relate directly to ratios of low order configurational integrals or include the effects of higher order term effectively.

To briefly review the procedure we define the number of waters N_w, the chemical potential of the solute μ, the pressure P, and the temperature T, which are constant in the Hill nonvolatile-solute semi-grand canonical ensemble. The average number of solute molecules in the system is then generally written as

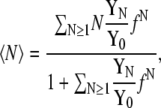(66)

where the isothermal-isobaric partition function with N solutes is

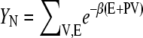(67)

and the absolute activity is

(68)

In the case of the infinite dilute solution, Eq. 66 becomes

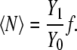(69)

Thus the chemical potential in the infinite dilute state is

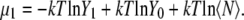(70)

This term can be extracted readily from the results of the previous section for urea.

When the solution has finite concentration, additional terms are necessary. If we assume that fY₁/Y₀ is small, Eq. 66 can be approximated with the first two terms as

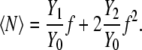(71)

The activity coefficient in molality scale, m, becomes

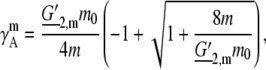(72)

where for a thermodynamic hydration number, N_w, and the molar weight of water, M_w, we define

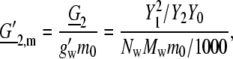(73)

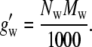(74)

The quantity m₀ = 1 [mol/kg] was introduced to make the term dimensionless. In this case the activity coefficient, Eq. 72, may be fitted to the experimental data by one parameter G′_2,m = 23.5. Because the value of g′_w (= effective gram molecular weight of water × Avogadro's number) is unknown, it is difficult to compare this parameter with our simulation results directly. Note that the experimental data is fit with one parameter to a few percent up to the solubility limit.

In the case that fY₁/Y₀ is not small it must be included in the denominator and Eq. 66 is approximated as

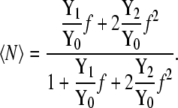(75)

In this case, the activity coefficient in the molality scale becomes

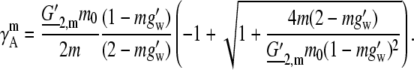(76)

This function must be fit to the experimental data using two parameters, and the combinations G′_2,m and g′_w were chosen. The obtained values of G′_2,m and g′_w are ∼20.98 and 0.003060, respectively, imply G₂ is 0.06420 and the number of water molecules, N_w, obtained is 0.1698 from Eq. 74. N_w can be interpreted as the limiting thermodynamic solvation number of urea for the truncated series Eq. 66 extrapolated from the solubility limit. Clearly the value 0.1698 is unreasonably small when viewed from a molecular perspective.

We can remold this into a form compatible with our current analysis. Substituting g′_w value into Eq. 73 and taking a natural log, we obtain

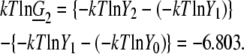(77)

Let us consider whether this value obtained from the parametric method is consistent compared with our simulated chemical potentials. The chemical potential in the infinite dilute solution was Eq. 70, and thus the chemical potential for the double molecule system can be expressed as

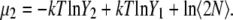(78)

On the other hand, our simulation data in Table 3 shows that the excess term of the chemical potential 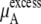is essentially constant at low concentrations. For example, the difference in chemical potential of the ∼2 M and ∼4 M systems is ∼1.6 kJ/mol for both OPLS and KBFF models. This difference is mainly caused not by the excess chemical terms but by the second term of 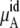in Eq. 38. Namely, the doubling of concentration causes a difference of kT ln 2 ∼ 1.7. This property will be also true at two lower concentrations such as 0.01 M and 0.02 M because of the nearly constant excess term 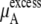obtained from the simulations at low concentrations (see Table 3). Therefore, our simulations suggest that

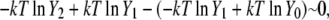(79)

which is consistent with near ideality in the molar scale but different from the two-parameter fitting result of −6.803 kJ/mol.

Our simulation data combined with the one parameter fitting result gives a more reasonable solvation number N_w = 1:23.5 × 1000/18.05 = 2.36 (note that the proportion of urea and water is 1:2.665 in the solubility limit). Therefore the small improvement of the fitting by using two parameters instead of one parameter is due to the effective inclusion of higher order term effects. The balance in the fitted terms truncated at second order gives the apparently physically unreasonable hydration number.

We can consider the dependence on the concentration scale used in fitting the experiments. When we use the experimental data and fitting function in mole fraction scale instead of molality scale, the results become the same as in molality scale, that is to say, we again obtain N_w = 0.1698. However, above we obtained a different value in the case of the molarity scale. This is a consequence of the volume terms that are included for the activities for molality and mole fraction (Eqs. 41 and 43) versus its absence in the molarity scale, Eq. 45. The activity coefficient in molarity scale is

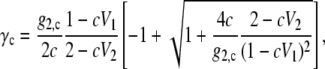(80)

where g_2,c = G₂/V₀, V₀ is the volume occupied by water in the absence of the solute, and V₁ and V₂ are the apparent volumes occupied by what might be thought of as a grouping of one or two solute molecules at a suitable concentration in solution. Under the assumption of a second order truncation, V₂ was set to the volume in the solid state (7). The values g_2,c and V₁ obtained from the fitting to the experimental activity coefficient in the molarity scale were 20.83 [mol/L] and 0.05254 [L/mol], respectively. By setting V₀ as the volume of pure water at 298 K, we obtained G₂ = 0.3764, which differs from the fitted result in molality scale G₂ = 0.06420. While this may reflect the affect of implicitly including higher order terms by truncation, we also note that the assumed constants V_i are not in both fits. The validity of the assumption that G′_2,m and g′_w (N_w) are constant at different concentrations is also unclear.

We can arrive at a similar conclusion about the magnitude of Eq. 77 by considering the following argument based on the volume expansion. In previous work (7) we have shown that V₂ is well approximated by the partial molar volume of the solute in the crystal. Then the Y₂ term corresponds to the neat system containing 100% urea. Note that since we assume rapid convergence of the series, slightly varying V₂ can correspond to any situation between 50% urea and 100% urea. We then obtain kTlnG₂ 1 kJ/mol, the difference between mu_ex in the N = 1 urea system and the pure urea system. Either argument gives a similar answer, kT lnG₂ = 0 – 1 kJ/mol, which differs from the fitted Eq. 77.

Nevertheless, the low order expansion method clearly fits a variety of solute experimental data very well. We can interpret why the parametric method succeeded as follows. The experimentally estimated partition functions of most osmolytes have simple shapes with respect to f. Thus, we rarely need go beyond the second-order term approximation in the fit. Based on our analysis above, we expect that more terms must be taken into account for some solutions. Therefore, it seems that the successful fitting with Eq. 76 was made possible not because high order terms in Eq. 66 can always be neglected and approximated by Eq. 76 but because the effect of the high order terms was included in an effective or renormalized way in the low order fitted coefficients. Further research is necessary to understand the physical meaning of the parameters from such data fits.

CONCLUSIONS

In this article, we considered the mechanism by which urea achieves its ideality in the molar scale. The activity coefficient changes quantitatively and qualitatively when using different concentration scales and standard states. The most useful and often used scale for the experiment is molality scale because it is easy to measure weight experimentally. The mole fraction scale is often preferred theoretically because Raoult's law was originally developed on the basis of mole fraction. The molarity scale is often used and has also been recommended on theoretical grounds (36). In very dilute solutions these three scales give us nearly the same activity coefficient. In older classic studies, solutions were usually implicitly considered to be dilute enough to ignore the dependency on different scales. However, in concentrated systems such as living cells, solutions often become dense, and the concentration-scale dependence of the activity coefficients becomes critical to the interpretation of thermodynamic data.

The concept of an ideal solution derives historically from two different points of view given by the symmetric ideal solution and the dilute ideal solution. This difference can be considered to be a difference in both the standard states and scales employed. If the solution is a symmetric ideal solution and the number of the total molecules per volume is constant at different concentrations, it is also a dilute ideal solution in mole fraction scale and molarity scale. The molality scale activity coefficient is exceptional and it cannot be represented as a symmetric ideal solution.

In addition to the difference of the scales and standard states, the origin of nonideality or what makes the activity coefficient differ from unity, obviously depends on the chemistry of the system. To understand the nature of urea-water solutions, we performed free energy simulations of urea solutions for a pair of popular molecular models for different concentrations to examine the origin of the thermodynamic behavior at the molecular level. In a very dilute solution (<0.05 mol/L), the activity coefficients in every scale were almost the same, but when the urea concentration increased the differences became apparent.

The KBFF urea model reproduced the experimental activity coefficient data very well because the excess chemical potentials are almost constant in different urea concentrations. This was due to the compensation between a decrease of the vdW part and an increase of electrostatic part as concentration increased. The activity coefficients of OPLS urea solutions were generally smaller than the experimental data reflecting a different compensation.

The activity coefficient is a very sensitive measure for solution properties and requires very precise chemical potential difference calculations. Performing free energy simulations with a satisfactory precision is still a challenging problem, especially in multicomponent systems. The urea and water system is a rather simple system, which does not have local minimum states deep enough to thwart convergence, but still required considerable computational effort for sampling. To obtain a sufficiently accurate chemical potential computationally for more complicated systems such as three-component systems or protein systems, more efficient sampling methods will be necessary.

For a large number of proteins, urea induces cooperative transitions of proteins from the native state (N) to denatured ensembles (D). The transitions that exhibit reversible two-state behavior make possible the determination of the free energy change for protein denaturation (37,38). The method of determination, known as the linear extrapolation model (LEM), is based on the known linear dependence of the denaturation free energy change on the molar concentration of urea

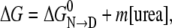(81)

where the parameters m and 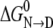are the slope and intercept of an experimentally determined plot of ΔG versus [urea](37). Both parameters provide key thermodynamic descriptions of the transition, with 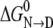giving the free energy change of conversion in the absence of denaturant and m measuring the efficacy of urea in transforming N to D.

The LEM, used extensively in the protein folding field, is empirical, and it has long been known that ΔG is a linear function with respect to the molar urea concentration only; molal or mole fraction concentration scales do not give valid m and 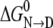parameters. Given that urea behaves as an ideal solution only with respect to the molar scale, the results in Fig. 3 c provides a clear rationale for the success of the LEM empirical relationship and not with other concentration scales.

Other factors, as well, are important in the success of the LEM. Urea exhibits a favorable interaction with the native and denatured states, with a larger number of interaction sites occurring with the denatured states in comparison with native. The favorable interaction is quite modest with urea out-competing water by a very small margin for sites of interaction (39). By analogy to a binding plot, the urea site-interaction is in the first-order portion of the curve, even at high urea concentration. The success of the LEM is attributable to important roles played by both the ideal behavior of urea on the molar scale and the weak first-order interaction of urea with protein. The basic thermodynamics of urea solutions presented here provides the foundation for investigating the interaction of urea with peptides and larger proteins. Our future work will address these issues.