Abstract
We have reinvestigated the conformation of NAD+ bound to dogfish lactate dehydrogenase (LDH) by using an NMR experiment that allows one to exploit nuclear Overhauser effects to determine internuclear distances between pairs of protons, without perturbation of spin-diffusion effects from other protons belonging either to the cofactor or to the binding pocket of the enzyme. The analysis indicates that the structure of bound NAD+ is in accord with the conformation determined in the solid state by x-ray diffraction for the adenosine moiety, but deviates significantly from that of the nicotinamide. The NMR data indicate conformational averaging about the glycosidic bond of the nicotinamide nucleotide. In view of the strict stereospecificity of catalysis by LDH and the conformational averaging of bound NAD+ that we infer from solution-state NMR, we suggest that LDH binds the cofactor in both syn and anti conformations, but that binding interactions in the syn conformation are not catalytically productive.
In systems that can be crystalized, the conformation of substrates and cofactors bound to high molecular weight enzymes can be derived from x-ray diffraction studies. In cases where the exchange between the bound and free forms is fast, information from diffraction can be supplemented by solution-state one- or two-dimensional exchange transferred nuclear Overhauser effect spectroscopy (ET–NOESY) (1, 2). The transferred NOE method uses excess substrate or cofactor, so that the resonance lineshapes resemble those of the substrate or cofactor in free solution, whereas cross-relaxation or NOEs are predominantly determined by internuclear distances within the substrate or cofactor in the bound form. In applications to systems such as the cofactor NAD+ in rapid exchange with dogfish lactate dehydrogenase (LDH) (3–5), it is usually assumed that ET–NOESY data can be interpreted on the assumption that, at least for short mixing times, spin-diffusion effects can be ignored. Spin diffusion occurs when the magnetization migrates through a set of nuclei in several consecutive steps, and can, in principle, be taken into account by the relaxation matrix method (6–12) provided all pathways can be measured. In this paper, it will be shown that spin-diffusion effects occur in the LDH⋅NAD+ complex that involve not only protons belonging to the cofactor, but also protons belonging to the binding pocket of the enzyme. Such indirect processes cannot be analyzed properly by full relaxation matrix methods, because it is impossible to identify all protons in the enzyme pocket and their dipolar coupling partners. Nevertheless, these indirect relaxation pathways can be largely eliminated by an NMR experiment where spin diffusion is quenched (13–17). Other methods for suppressing spin diffusion (7, 18–23), or accounting for it in other ways (24, ∥) have been proposed. There are analogies between the approach discussed here with the situation that arises if all protons belonging to the binding pocket were replaced by deuterium, although there are some fundamental differences between the two approaches that will be discussed. The structural information derived from the cross-relaxation rates of nicotinamide proton pairs deviates from the structure obtained from x-ray crystallography. With the quenching of spin diffusion, the data strongly support conformational averaging about the glycosidic bond.
Theory.
Cross-relaxation leads to a migration of longitudinal magnetization Mz(τm), which can be described by solving a set of differential equations that can be traced back to Solomon (25–27):
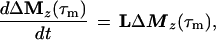 |
1 |
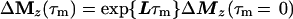 |
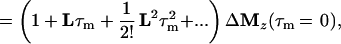 |
2 |
where τm is the mixing time of the ET–NOESY experiment, ΔMz(τm) is a vector representing the deviations from equilibrium Mz(τm)– Mzeq of the longitudinal magnetization components of N spins, and L = −R + K is comprised of the relaxation matrix R (with diagonal elements ρii and off-diagonal elements σij, which are proportional to rij−6) and the exchange matrix K. In simple cases, the expansion of Eq. 2 can be truncated to the term linear in τm for short mixing times, so that the structural information contained in the elements σij of L can be retrieved by linear regression using the initial rate approximation. However, for systems such as the complex LDH⋅NAD+ where the molecular mass is on the order of 140 kDa and the correlation time at least 60 ns, the quadratic term proportional to L2 τm2 is important even for short mixing times (11, 28, 29). The spin-diffusion effects described by quadratic and higher order terms can lead to a blurring of the information about internuclear distances even for relatively short mixing times.
Molecular System.
LDH catalyzes the reduction of pyruvate by NADH to form lactate and NAD+. The transfer of a proton and two electrons (formally a hydride) from the nicotinamide ring of NADH to pyruvate happens with a nearly ideal stereospecificity (the error rate is estimated to be < 10−9) (30). The catalytic step mediated by LDH is essential in the glycolysis part of the Cori cycle taking place in active skeletal muscles and erythrocytes. Because knowledge of the conformation of cofactors and substrates bound to enzymes is essential for understanding their function, and because the binding site for NAD+ is similar in a variety of dehydrogenases such as skeletal muscle LDH, alcohol dehydrogenase, glyceraldehyde-3-phosphate dehydrogenase, and malate dehydrogenase, it is of interest to determine reliable geometric information about enzyme-cofactor complexes in solution. The NAD+ binding region as determined by x-ray crystallography is made up of four α helices and six strands of parallel β sheets known as the Rossmann fold or dinucleotide binding domain. NAD+ is bound in an extended conformation. The adenosine moiety in NAD+ binds to a hydrophobic crevice, and the nicotinamide ring binds with the reactive side in a polar environment, whereas the other side of the nicotinamide ring faces hydrophobic residues.
MATERIALS AND METHODS
Purification of Dogfish LDH.
LDH was purified from frozen muscle tissue of the Atlantic spiny dogfish, Squalus acanthias, using procedures described elsewhere (31, 32). The enzyme then was dialyzed against 99.9% D2O containing 50 mM phosphate, pH 7.0. The final concentration of enzyme was adjusted to 17.5 mg/ml by adding dialysis buffer. Aliquots containing the appropriate concentration of NAD+ cofactor (5 mM) were frozen by dropwize addition to liquid nitrogen. The frozen pellets were lyophilized for 24 h under vacuum produced by a mechanical pump. The samples were stored under dry nitrogen at −20°C. The samples were rehydrated by addition of 700 μl of 99.99% D2O to a final concentration of [LDH] ≈ 0.5 mM and [NAD+] ≈ 5 mM.
NMR Spectroscopy.
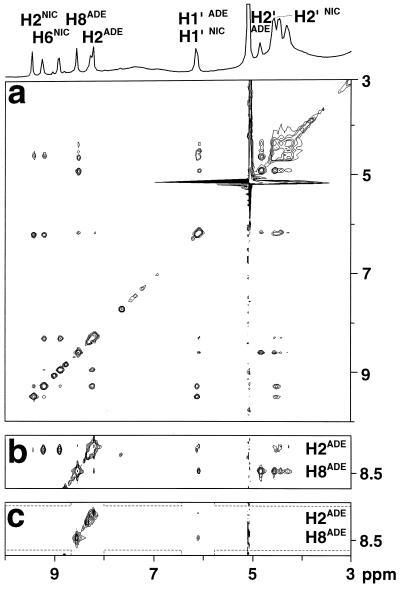
The conventional NOESY experiment (33, 34) is modified (Fig. 1a) by inserting a doubly selective radio-frequency pulse in the middle of the mixing time τm to obtain the so-called QUIET-NOESY sequence (quenching of undesirable indirect external trouble in NOESY) (13, 17). This allows one to invert two spectral regions selected to include the chemical shifts of a “source” and a “target” proton, which are chosen because their distance (i.e. their mutual cross-relaxation rate) is of strategic importance to resolve a conformational ambiguity. An inversion pulse with the envelope of a Q3 Gaussian cascade and a duration of 12 ms can be made doubly selective by placing the carrier frequency midway between the two chemical shifts and by modulating the amplitude with a function cos ωat, where ωa is equal to half the difference between the chemical shifts (13, 17). During the first half of the mixing time, the magnetization of the source spin migrates not only to the target spin, but also to other protons in the vicinity, including “indirect” protons Hi that belong to the binding pocket of the enzyme. The doubly selective inversion pulse changes the sign of the longitudinal magnetization components of both the source and target spins, so that their mutual Overhauser effect continues to build up during the second half of the mixing time. However, barring accidental degeneracy, the other (indirect) spins are not inverted by the doubly selective inversion pulse, and the flow of magnetization from the source to the indirect Hi spin in the first half of the mixing time is reversed in the second half. Likewise, the flow from Hi to the target spin is largely canceled. The net effect is that, to a good approximation, only direct cross-relaxation between the source and target spins will give rise to a cross-peak in ET–NOESY, and that contributions due to indirect Hi protons will be suppressed, provided the latter’s magnetization components are not accidentally inverted by the doubly selective pulse. The effect bears some similarities, but is not identical, to what can be obtained by replacing all protons belonging to the binding pocket by deuterium nuclei‖. In this case, one would not only expect to suppress the cross-relaxation rates σij between cofactor protons and enzyme deuterons, but also to reduce the diagonal elements ρii that describe the longitudinal self-relaxation of the cofactor protons in the Solomon equations (see Eq. 1). The attenuation of self-relaxation represents an additional benefit of deuteration that cannot be obtained by simple manipulations of the magnetization. All experiments reported here were carried out on a Bruker DMX 300 system at 8°C. Build-up plots were recorded for 0 < τm < 300 ms. Complementary ET-NOESY experiments were carried out with a Varian Unity Plus 720 MHz spectrometer but are not shown here.
Figure 1.
(a) Pulse sequence used for the QUIET–ET–NOESY experiment where spin-diffusion pathways are quenched by doubly selective inversion of selected source and target protons. (b) One-dimensional spectrum of the LDH⋅NAD+ complex in D2O, with [LDH] ≈ 0.5 mM, [NAD+] ≈ 5 mM, recorded at 8°C on a Bruker DMX 300 spectrometer, showing sharp resonances due to the cofactor and broad resonances due to the enzyme.
Data Processing.
The data were processed using Bruker xwinnmr 1.1 software. Two-dimensional spectra were acquired with 12-ppm windows in both dimensions, 512 t1-increments with 2,048 points each were recorded with 16 scans and a relaxation interval of 1 s. No zero-filling was used and window functions with π/2-shifted sine-bell in ω1 and exponential multiplication in ω2 with a line broadening of 2 Hz were applied before two-dimensional Fourier transformation. Baseline correction using a second-order polynomial function was applied to all spectra in both dimensions. Peak intensities were determined using the xwinnmr 1.1 integration module and used as input for a fitting program written in matlab (35) to carry out a linear regression with least-square fitting of cross-peak intensities (normalized by the corresponding diagonal peak intensities) as a function of the mixing time in the interval 0 < τm < 100 ms. Usually, it is not possible to derive accurate cross-relaxation rates from ET–NOESY data without using a full relaxation matrix analysis which takes into consideration the whole network of participating spins. In the LDH⋅NAD+ complex this represents a particularly daunting problem due to the lack of information about the indirect protons belonging to the binding pocket and their dipolar couplings with the cofactor. In QUIET–ET–NOESY, however, spin diffusion is largely suppressed, so that this cumbersome approach is not necessary because the two spins of interest behave almost as an isolated two-spin system (36). We used the initial rate approximation (27, 37) for mixing times up to 100 ms.
X-Ray Distances.
To identify protons belonging to the binding pocket that could mediate spin diffusion, we used the x-ray coordinates of a ternary complex of dogfish LDH with NADH and oxamate determined from diffraction data at 2.1 Å resolution (J. P. Griffith and M. G. Rossmann, Protein Data Bank file 1ldm). Oxamate was excluded, and the positions of the protons were determined based on geometry and optimal hydrogen bonding using the program charmm (38). The energy of the resulting structure was minimized to remove poor nonbonded interactions using parameters described previously (39), and 60 steps of the steepest descent algorithm with main-chain atoms harmonically constrained, followed by 100 steps of the conjugate gradient algorithm without constraints. All protons within a radius of 4.5 Å around the relevant NAD+ protons were identified and taken into account in the following discussion.
RESULTS
The one-dimensional NMR spectrum shown in Fig. 1b of LDH and NAD+ in excess with respect to LDH exhibits very broad lines from the enzyme, and some relatively sharp resonances resulting from the averaging of the signals of the free and bound forms of the cofactor. The conventional two-dimensional ET–NOESY spectrum in Fig. 2a shows cross-peaks between cofactor resonances that primarily reflect cross-relaxation processes in the bound form because those in the free form are negligible.
Figure 2.
(a) Conventional two-dimensional ET–NOESY of the LDH⋅NAD+ complex, recorded with a mixing time τm = 150 ms. Relevant NAD+ protons are labeled with ADE for adenosine and NIC for nicotinamide. (b) Strip from the ET-NOESY spectrum of a shown with lower contours. (c) Corresponding strip from a QUIET–ET–NOESY spectrum recorded under identical conditions. Doubly selective inversion was achieved by applying a 12-ms cosine-modulated Gaussian cascade Q3 in the middle of the mixing time to invert two frequency bands (represented by dashed lines), each of ≈1.1 ppm width, centered around 6.07 ppm (to invert H1′ADE of the adenosine) and 8.36 ppm (to invert both adenosine protons H2ADE at 8.13 ppm and H8ADE at 8.47 ppm). No water suppression methods were used.
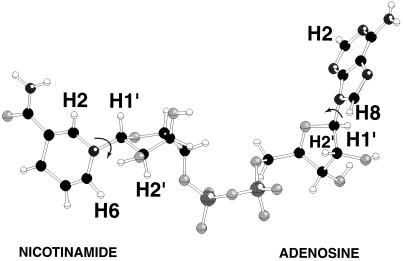
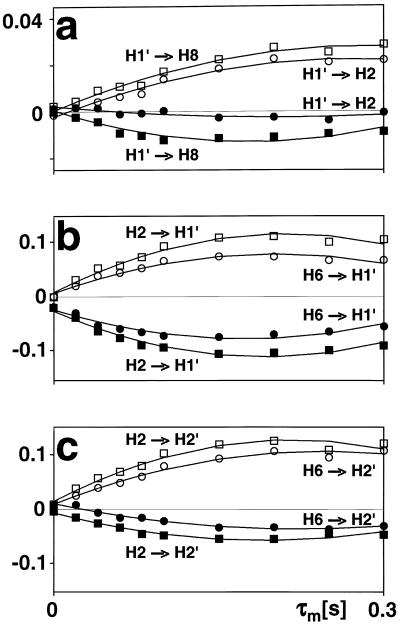
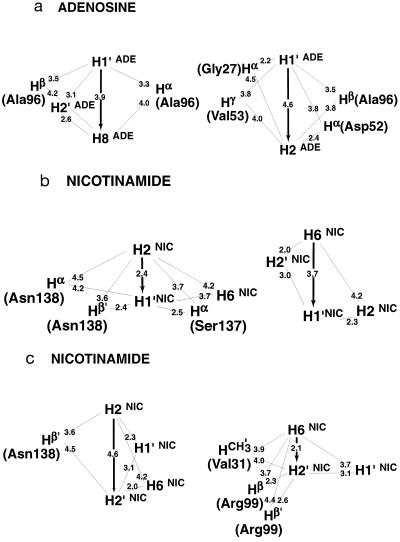
A direct two-spin interpretation of ET–NOESY intensities (Fig. 2 a and b) would indicate that, in the bound form, the aromatic H2ADE and H8ADE protons of the adenosine are at similar distances from the H1′ADE proton of the adenosine, an unreasonable conclusion given the structural constraints of adenosine nucleoside. The energy-minimized structure derived from x-ray diffraction (J. P. Griffith and M. G. Rossmann, Protein Data Bank file 1ldm) indicates an extended conformation of the cofactor within the binding pocket, as shown in Fig. 3, with distances of 4.6 Å (H2ADE–H1′ADE) and 3.9 Å (H8ADE–H1′ADE). The problem inherent to conventional NOE studies stems from the possibility that the magnetization is not transmitted directly from H2ADE (or H8ADE) to H1′ADE, but first from H2ADE (or H8ADE) to one or several unknown protons Hi that belong to the binding site of LDH, and from there to the H1′ADE proton of the adenosine. To resolve the ambiguity, we measured cross-peak intensities as a function of mixing time using the method discussed above that effectively restricts cross-relaxation to a pair of spins. In the case of the LDH⋅NAD+ complex, the H1′ADE proton was taken to be the source spin, and the H2ADE and H8ADE protons were both target spins (Figs. 2c and 4a). The two telltale cross-peaks at ω2 = 6.07 ppm (H1′ADE) show a different behavior when spin diffusion is quenched: the peak correlating H2ADE and H1′ADE is strongly attenuated in the modified experiment, thus indicating that the corresponding peak in conventional ET–NOESY (Fig. 2b) must be due primarily to spin diffusion. Thus, the cross-relaxation rate between H2ADE and H1′ADE tends to be overestimated in ET–NOESY, so that the distance between these protons will be underestimated. For cross-relaxation between H1′ADE and H2ADE, there are several protons belonging to the LDH binding pocket that may be involved in the flow of magnetization. The energy-minimized proton coordinates derived from diffraction data indicate that the protons Hα(Gly27), Hα(Asp52), and the methyl protons of Val53 and Ala96 all should lie in the proximity of H2ADE and H1′ADE of the adenosine moiety (Fig. 5a). Although their identity can be inferred from the x-ray structure, the protons belonging to the binding pocket of a large enzyme cannot be probed by magnetic resonance because of their line widths, and therefore cannot be taken into account in a full relaxation matrix analysis. Nonetheless, their contributions to spin diffusion are suppressed in the QUIET–ET–NOESY experiment of Fig. 2c, because their chemical shifts do not lie within one of the inverted regions. In contrast to H2ADE, the intensity of the cross-peak between H8ADE and H1′ADE is hardly attenuated when spin diffusion is suppressed (Fig. 4a), which indicates a direct NOE between these two spins. In the bound form, the adenosine H8ADE or H1′ADE proton are far (>3.9 Å) from any other proton except the adenosine H2′ADE.
Figure 3.
Structure of NAD+ in the binding pocket of LDH as derived from x-ray diffraction, obtained from Protein Data Bank file No. 1ldm.
Figure 4.
Build-up curves obtained by recording spectra at different mixing times. Conventional ET–NOESY amplitudes, which are positive, are represented by open circles and squares, while QUIET–ET–NOESY amplitudes, which are negative because of the inversion in the middle of the mixing time, are represented by filled symbols. The cross-peak amplitudes were normalized with respect to the diagonal peaks. The initial slopes were determined by linear fitting, and polynomials were used only for graphical purposes. (a) Cross-relaxation from adenosine ribose H1′ADE to adenosine H8ADE (squares) and from H1′ADE to adenosine H2ADE (circles). The latter build-up is strongly attenuated when spin diffusion is suppressed. (b) Cross-relaxation from nicotinamide H2NIC to ribose H1′NIC (squares) and from H6NIC to H1′NIC (circles). (c) Cross-relaxation from nicotinamide H2NIC to ribose H2′NIC (squares) and from H6NIC to H2′NIC (circles).
Figure 5.
Representation of the x-ray distances between spins that are relevant to the cases studied in Fig. 4 a–c. All distances are drawn to scale.
The orientation of the nicotinamide ring with respect to the neighboring ribose is relevant to the understanding of LDH catalytic activity. In this case, the aromatic nicotinamide proton H2NIC (or H6NIC) can be chosen as the source spin and the H1′NIC (or H2′NIC) ribose proton as the target. For the cross-relaxation processes H2NIC → H1′NIC and H6NIC → H1′NIC, the suppression of spin diffusion by QUIET–ET–NOESY has little effect (Fig. 4b), indicating that these two cross-peak intensities are primarily due to direct Overhauser effects. However, the build-up between H6NIC and H1′NIC is too rapid for protons that should be separated by 3.7 Å if the x-ray structure is relevant, whereas that between H2NIC and H1′NIC is too weak for a distance of 2.4 Å. In contrast to the NOEs observed on H1′NIC, cross-relaxation between H2′NIC and either H2NIC or H6NIC is attenuated when diffusion is quenched in the QUIET–ET–NOESY experiment (Fig. 4c), thus hinting at the existence of protons that are close enough to mediate spin diffusion. The x-ray structure suggests that H1′NIC, H6NIC, and Hβ′(Asn138) might be responsible for spin diffusion in the case H2NIC → H2′NIC (Fig. 5c). The magnetization transfer H6NIC → H2′NIC is also significantly attenuated by quenching spin diffusion, although this cannot be explained by the x-ray structure because a distance between H6NIC and H2′NIC of only 2.1 Å is so short that spin diffusion is unlikely to interfere. In addition, the NOE between H6NIC and H2′NIC is smaller than that between H2NIC and H2′NIC. A possible resolution to the enigmatic relaxation behavior of the nicotinamide nucleotide is presented in Discussion.
Further experiments were developed to attempt the identification of protons belonging to the binding pocket that could be responsible for spin diffusion. In principle, contributions to ET–NOESY cross-peaks involving aliphatic protons of the enzyme can be suppressed in an experiment using a band-selective pulse instead of the doubly selective pulse of Fig. 1a. In this context, “aliphatic” stands for all protons with resonances below 4 ppm, which can be inverted in the middle of the mixing time by a band-selective inversion pulse applied at −0.3 ppm with a bandwidth of about 2,400 Hz (8 ppm at 300 MHz). This can be achieved by using a Q3 pulse (13, 40–42) with a duration of 2 ms, which should be reasonably effective even if the T2s of the LDH protons are very short. In this experiment (data not shown), the peak intensities remained the same as in conventional ET–NOESY. We therefore may conclude tentatively that the protons of the LDH binding pocket that mediate spin diffusion between NAD+ protons do not resonate below 4 ppm. This excludes a participation of the Hγ(Val53) and Hβ(Ala96) protons in the cross-relaxation between H1′ADE and H2ADE in the adenosine moiety (Fig. 5a), although the x-ray distances would seem to make these protons possible candidates. It is possible that Hγ(Val53) and Hβ(Ala96) do not participate actively because they cross-relax rapidly with other spins within the enzyme. Similarly, Hγ(Val31), Hβ′(Arg99) and Hβ′(Asn138) can be excluded from playing a role in spin diffusion. These conclusions appear to be compatible with the x-ray structure. On the other hand, the negative outcome of the experiment with band-selective inversion of all aliphatic protons does not allow one to exclude Hα(Gly27) and Hα(Asp52), which are likely to resonate above 4 ppm, from playing a role in spin diffusion between H1′ADE and H2ADE (Fig. 5a). In general, the band-selective inversion experiment does not allow one to exclude any backbone Hα, any aromatic protons, or, if the studies are carried out in light water, any amide protons.
By extracting cross-relaxation rates from the initial slope of the cross-peak intensities as a function of the mixing time for experiments where spin-diffusion is quenched (filled symbols in Fig. 4), assuming negligible contributions from free NAD+, and assuming that the local correlation times are the same for the two internuclear vectors, we can estimate the ratio of the distances according to:
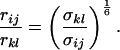 |
3 |
The observed averaged σkl values should be almost equal to the true cross-relaxation rates in the bound form scaled by the molar fraction of bound form (2, 11). The scaling factor cancels in the ratio of Eq. 3, so that this ratio appears to be a good approximation in all examples discussed, because we are concerned with interactions between a ribose proton and an aromatic proton.
DISCUSSION
The effects of spin diffusion are evident when comparing intensities in conventional ET–NOESY and QUIET–ET–NOESY. Examination of Fig. 4 shows that the initial slopes of the NOE build-up curves are significantly smaller in QUIET–ET–NOESY in 3 of 6 cases (adenosine H1′ADE–H2ADE; nicotinamide H2′NIC–H2NIC, and H2′NIC–H6NIC). That the intensities in conventional ET–NOESY are boosted by spin diffusion must be attributed to the presence of one or several “indirect” protons that are closer to the “directly” involved protons than the latter are to each other. In systems undergoing exchange, the enhancement by an indirect proton is significantly greater if the latter belongs to the enzyme than if it belongs to the cofactor, assuming a similar spatial arrangement (11). Thus, an indirect NOE enhancement via intermolecular relaxation pathways is more effective than via intramolecular pathways within the cofactor when the latter can shuttle back and forth between free and bound states. Magnetization that migrates to an “indirect” proton belonging to the cofactor tends to dissipate during the time spent in the free state, where cross-relaxation is negligible, but longitudinal relaxation still effective. Note that in Fig. 4, the initial slopes in QUIET–ET–NOESY never appear to be greater than those in ET–NOESY. Indeed, for cases where interactions to many neighboring spins act as a “relaxation sink” and therefore attenuate direct NOEs, the results of QUIET–ET-NOESY would be expected to be similar to those of conventional ET–NOESY, because inversion pulses do not alter the self-relaxation rates.
Adenosine Base-Ribose Interactions.
For the proton pairs of the adenosine base, the differences between QUIET–ET–NOESY and conventional ET–NOESY can be readily interpreted with reference to the crystallographic structure of an LDH complex. For the adenosine proton pair H1′ADE–H8ADE, both experiments give comparable initial slopes, indicating negligible contributions from spin diffusion. This proton pair is separated by as much as 3.9 Å in the x-ray structure, but there are no LDH protons that are close enough to both H1′ADE and H8ADE (i.e. < 3.9 Å) to enhance their NOE intensity. The possibility of two-step transfer processes within the cofactor is suggested by the presence of two cross-peaks in conventional ET–NOESY (Fig. 2a) that correlate H1′ADE and H8ADE with H2′ADE. However, intramolecular cross-relaxation is less efficient, and spin diffusion mediated by the H2′ADE proton is weak, given the outcome of the QUIET–ET–NOESY experiment. On the other hand, a significant spin-diffusion contribution is observed for the adenosine pair H1′ADE–H2ADE (Fig. 4a). In the crystal structure of an LDH complex, Hα(Gly27), Hα(Asp52) and the methyl protons of Val53 and Ala96 are nearer to both H1′ADE and H2ADE than the direct distance of 4.6 Å between them (Fig. 5a). The negative result of the band-selective inversion experiment allows one to exclude the methyl protons and indicates that Hα(Gly27) and Hα(Asp52) must be primarily responsible for the indirect contributions to the cross-peak between H1′ADE and H2ADE. The QUIET–ET–NOESY experiment of Fig. 1a should quench the effects of all four hypothetical indirect pathways between H1′ADE and H2ADE, because the chemical shifts of Hα(Gly27), Hα(Asp52), and the methyl protons of Val53 and Ala96 are not likely to lie within the inverted frequency bands. Even if one of the invisible protons accidentally had a shift lying within an inverted frequency band, the doubly selective pulse of 12 ms duration would fail to invert this enzyme proton effectively because of its rapid transverse relaxation. If we assume for simplicity that such a proton would be saturated rather than inverted, simulations indicate that its contribution to spin diffusion would be roughly reduced to one-half (data not shown). Therefore, the cross-relaxation rates of the proton pairs H1′ADE–H2ADE and H1′ADE–H8ADE measured by QUIET–ET–NOESY can be considered to be reliable.
Nicotinamide Base–Ribose Interactions.
In contrast to the adenosine proton pairs, the NOE results for the nicotinamide proton pairs cannot be easily rationalized with reference to the crystallographic structure. It is difficult to account for both the importance of the indirect contributions evident by comparing conventional ET–NOESY and QUIET–ET–NOESY results, and the relative magnitudes of the QUIET–ET–NOESY cross-peaks. One does not expect any significant effect of quenching on the cross-peak intensity H2′NIC–H6NIC considering the interproton distances in the x-ray structure. The NOE intensity arising from this short-distance interaction (2.1 Å) would not be expected to be boosted by spin diffusion because the likelihood of finding intermediate protons at shorter distances is small. Yet, the QUIET–ET–NOESY build-up curve for this spin pair is attenuated to a degree similar to that observed for other interactions, of much larger separation, between a ribose proton and a nicotinamide base proton such as H2′NIC–H2NIC (4.6 Å, Fig. 4c). With regard to NOE magnitudes, neither H2NIC → H1′NIC nor H6NIC → H2′NIC yield intensities that are large enough (compared with those of the adenosine interactions, Fig. 4a) to be consistent with the short distances observed in the crystal. This point is further discussed below. Moreover, the NOE build-up for H6NIC → H2′NIC is slower than that for H2NIC → H2′NIC, in contradiction to the relative intensities expected for distances of 2.1 Å and 4.6 Å, respectively. A satisfactory interpretation of these data requires a more elaborate model than a single structure.
It would not be prudent to attempt to extract absolute internuclear distances from the cross-relaxation rates derived from these experiments. In such a large system with an overall correlation time of about 60 ns, internal motions must affect various internuclear vectors differently, so that it is not sufficient to describe the fluctuations of the dipole-dipole interactions by a single correlation time. However, it appears reasonable to estimate relative distances using Eq. 3, because all pairs considered consist of one ribose proton and one aromatic proton on the neighboring ring. The relative distances determined in this work are given in Table 1, together with relative distances derived from x-ray diffraction. A notable feature of Table 1 is that most of the ratios listed for nicotinamide are in the vicinity of one. Thus both H2NIC and H6NIC would appear to be nearly equidistant from H1′NIC and from H2′NIC. Examination of the structure of NAD+ in Fig. 3 shows that such constraints cannot be satisfied with a single conformation. A conformation that allows H2NIC to be equidistant from H1′NIC and H2′NIC cannot simultaneously account for H6NIC being equidistant from the same two ribose protons. Moreover, any single low-energy rotamer would place either H2NIC or H6NIC at a short distance (say 2.5 Å) to one of the ribose protons, which should give rise to a significantly greater NOE intensity than is measured for the adenosine pair H1′ADE–H8ADE (distance about 3.9 Å.) If we consider the ratio (3.9 Å/2.5 Å)6, one would expect the initial slope of one of the cross-peaks of the nicotinamide moiety to be approximately 14-fold steeper than for the H1′ADE–H8ADE cross-peak. In the actual QUIET–ET–NOESY experiment, only a 4-fold steeper slope was observed. This discrepancy is too large to be accounted for by spurious effects of diagonal elements ρii of the relaxation matrix, or by residual spin-diffusion effects, e.g., by contributions from indirect spins that accidentally resonate within the doubly selective inversion windows. A more likely interpretation of the data suggests motional averaging, in such a manner that the apparent distances are nearly equivalent. One possibility would be that the NAD+ cofactor can bind LDH with the nicotinamide base in both syn and anti. Other models of conformational averaging also may be consistent with the ratios in Table 1. Studies of other dehydrogenases suggest that the dinucleotide binding site of the Rossmann fold does not rigidly restrain the nicotinamide ring. Crystallographic studies at 1.9 Å resolution of malate dehydrogenase (MDH) show a weak density around the nicotinamide ring in a difference map calculated from a binary MDH-citrate complex and a ternary MDH–NAD–citrate complex (43). Conformational averaging, among other factors, could give rise to such a weak electron density. A study of glutamate dehydrogenase provides another clue: the possibility of mixed binding modes of the nicotinamide ring of NADP+ in the complex with glutamate dehydrogenase was suggested by Banerjee and coworkers (44), although effects of spin diffusion and nonselective irradiation in their one-dimensional ET–NOE experiments were not taken into account. If the results reported here, which are free from spin-diffusion effects, are combined with an evaluation of conformational averaging by a complete relaxation matrix analysis, they should allow one to obtain a more elaborate assessment of the conformational equilibrium of NAD+ binding to LDH than was previously possible.
Table 1.
Comparison of ratios of internuclear distances (r) in NAD+ bound in LDH pocket
| Ratio | X-ray* | QUIET-ET-NOESY | ET-NOESY |
|---|---|---|---|
| Adenosine | |||
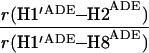 |
1.18 | 1.21 | 1.15 |
| Nicotinamide | |||
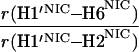 |
1.61 | 1.02 | 1.02 |
 |
2.19 | 0.96 | 0.93 |
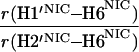 |
1.76 | 0.95 | 1.05 |
Ratios deduced from the energy-minimized x-ray structure.
Conformational Averaging and Hydride Transfer.
The catalysis of hydride transfer by LDH is stereospecific for the A-side hydrogen of nicotinamide by more than a factor of 109 (30). The spatial arrangement of the cofactor and substrate and the preference for A-side transfer are consistent with binding the anti form of NAD+. Binding syn NAD+ with the same spatial arrangement would imply transfer of the B-side hydrogen. Assuming that the conformational averaging involves a combination of syn and anti forms, how can this be consistent with the stereospecificity for the A-side hydrogen? One explanation is that multiple binding modes of nicotinamide are not possible in the ternary complex. LDH is known to bind cofactor and substrate sequentially, and the substrate may dock only if the cofactor is bound in the anti form. However, if multiple binding modes are also possible in the ternary complex, one must conclude that hydride transfer cannot take place in the syn conformation. Although B-side dehydrogenase clearly demonstrates that B-side transfer using syn-NAD+ is chemically feasible in specific cases, only A-side transfer from the anti conformation is productive in the case of LDH, where catalysis requires very precise binding interactions in the active site.
The interpretation of QUIET–ET–NOESY data recorded under conditions where spin diffusion is suppressed is more straightforward than for conventional ET–NOESY data. A simplified analysis using Eq. 3 is thus legitimate and allows one to extract accurate relative internuclear distances. This approach should find applications in many structural studies.
Acknowledgments
We are indebted to Dr. Hervé Desvaux for many stimulating discussions. We acknowledge many suggestions from an exceptionally careful referee. This research was supported by the National High Magnetic Field Laboratory, Tallahassee, FL. C.B.P. and J.W.B. acknowledge support by the National Institutes of Health (Grants GM39478 and GM42668, respectively).
ABBREVIATIONS
- NOE
nuclear Overhauser effect
- ET–NOESY
exchange transferred–NOE spectroscopy
- LDH
lactate dehydrogenase
- QUIET–ET–NOESY
quenching of undesirable indirect external trouble in ET–NOESY
Footnotes
G. C. K. Roberts, 13th European Experimental NMR Conference, May 20–24, 1996, Paris.
References
- 1.Bothner-By A A, Gassend R. Ann NY Acad Sci. 1972;222:668–676. doi: 10.1111/j.1749-6632.1973.tb15293.x. [DOI] [PubMed] [Google Scholar]
- 2.Rosevear P R, Mildvan A S. Methods Enzymol. 1989;177:333–357. doi: 10.1016/0076-6879(89)77019-1. [DOI] [PubMed] [Google Scholar]
- 3.Holbrook J J, Liljas A, Steindel S J, Rossmann M G. In: The Enzymes. Boyer P D, editor. XI. New York: Academic; 1975. pp. 191–292. [Google Scholar]
- 4.White J L, Hackert M L, Buehner M, Adams M J, Ford G C, Lentz P J, Jr, Smiley I E, Steindel S J, Rossmann M G. J Mol Biol. 1976;102:759–779. doi: 10.1016/0022-2836(76)90290-4. [DOI] [PubMed] [Google Scholar]
- 5.Abad-Zapatero C, Griffith J P, Sussman J L, Rossmann M G. J Mol Biol. 1987;198:445–467. doi: 10.1016/0022-2836(87)90293-2. [DOI] [PubMed] [Google Scholar]
- 6.Dobson C M, Olejniczak E T, Poulsen F M, Ratcliffe R G. J Magn Reson. 1982;48:97–110. [Google Scholar]
- 7.Olejniczak E T, Gampe R T, Jr, Fesik S W. J Magn Reson. 1986;67:28–41. [Google Scholar]
- 8.Boelens R, Koning T M G, Kaptein R. J Mol Struct. 1988;173:299–311. [Google Scholar]
- 9.Borgias B A, James T L. J Magn Reson. 1988;79:493–512. [Google Scholar]
- 10.Post C B, Meadows R P, Gorenstein D G. J Am Chem Soc. 1990;112:6796–6803. [Google Scholar]
- 11.Zheng J, Post C B. J Magn Reson B. 1993;101:262–270. [Google Scholar]
- 12.Ni F. Progr NMR Spectroc. 1994;26:517–606. [Google Scholar]
- 13.Zwahlen C, Vincent S J F, Di Bari L, Levitt M H, Bodenhausen G. J Am Chem Soc. 1994;116:362–368. [Google Scholar]
- 14.Levitt M H, Di Bari L. Phys Rev Lett. 1992;69:3124–3127. doi: 10.1103/PhysRevLett.69.3124. [DOI] [PubMed] [Google Scholar]
- 15.Levitt M H, Di Bari L. Bull Magn Reson. 1994;16:94–114. [Google Scholar]
- 16.Vincent S J F, Zwahlen C, Bolton P H, Logan T M, Bodenhausen G. J Am Chem Soc. 1996;118:3531–3532. [Google Scholar]
- 17.Vincent S J F, Zwahlen C, Bodenhausen G. J Biomol NMR. 1996;7:169–172. doi: 10.1007/BF00203828. [DOI] [PubMed] [Google Scholar]
- 18.Massefski W, Jr, Redfield A G. J Magn Reson. 1988;78:150–155. [Google Scholar]
- 19.Fejzo J, Krezel A M, Westler W M, Macura S, Markley J L. J Magn Reson. 1991;92:651–657. [Google Scholar]
- 20.Burghardt I, Konrat R, Boulat B, Vincent S J F, Bodenhausen G. J Chem Phys. 1993;98:1721–1736. [Google Scholar]
- 21.Boulat B, Burghardt I, Bodenhausen G. J Am Chem Soc. 1992;114:10679. [Google Scholar]
- 22.Hoogstraten C G, Westler W M, Macura S, Markley J L. J Magn Reson B. 1993;102:232–235. doi: 10.1006/jmrb.1995.1149. [DOI] [PubMed] [Google Scholar]
- 23.Zolnai Z, Juranic N, Markley J L, Macura S. Chem Phys. 1995;200:161–179. [Google Scholar]
- 24.Zheng J, Post C B. J Phys Chem. 1996;100:2675–2680. [Google Scholar]
- 25.Solomon I. Phys Rev. 1955;99:559–565. [Google Scholar]
- 26.Ernst R R, Bodenhausen G, Wokaun A. Principles of Nuclear Magnetic Resonance in One- and Two-Dimensions. Oxford: Clarendon; 1987. [Google Scholar]
- 27.Neuhaus D, Williamson M. The Nuclear Overhauser Effect in Structural and Conformational Analysis. New York: VCH; 1989. [Google Scholar]
- 28.Kalk A, Berendsen H J C. J Magn Reson. 1976;24:343–366. [Google Scholar]
- 29.Lane A N. J Magn Reson. 1988;78:425–439. [Google Scholar]
- 30.LaReau R D, Anderson V E. Biochem. 1992;31:4174–4180. doi: 10.1021/bi00132a004. [DOI] [PubMed] [Google Scholar]
- 31.Burgner J W, II, Ray W J., Jr Biochem. 1974;13:4229–4237. doi: 10.1021/bi00717a025. [DOI] [PubMed] [Google Scholar]
- 32.Burgner J W, II, Ray W J., Jr Biochem. 1978;17:1654–1661. doi: 10.1021/bi00602a012. [DOI] [PubMed] [Google Scholar]
- 33.Meier B H, Ernst R R. J Am Chem Soc. 1979;101:6441–6442. [Google Scholar]
- 34.Anil Kumar, Ernst R R, Wüthrich K. Biochem Biophys Res Commun. 1980;95:1–6. doi: 10.1016/0006-291x(80)90695-6. [DOI] [PubMed] [Google Scholar]
- 35.matlab (Copyright 1984–1994) (The Mathworks Company, Inc.), Version 4.2a.
- 36.Schwager M, Bodenhausen G. J Magn Reson Ser B. 1996;111:40–49. doi: 10.1006/jmrb.1996.0058. [DOI] [PubMed] [Google Scholar]
- 37.Olejniczak E T, Poulsen F M, Dobson C M. J Am Chem Soc. 1981;103:6574–6580. [Google Scholar]
- 38.Brooks B R, Brucoleri R E, Olafson B D, Slater D J, Swaminathan S, Karplus M. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 39.Young L, Post C B. J Am Chem Soc. 1993;115:1964–1970. [Google Scholar]
- 40.Emsley L, Burghardt I, Bodenhausen G. J Magn Reson. 1990;90:214–220. [Google Scholar]
- 41.Emsley L, Burghardt I, Bodenhausen G. J Magn Reson. 1991;94:448. [Google Scholar]
- 42.Emsley L, Bodenhausen G. J Magn Reson. 1992;97:135–148. [Google Scholar]
- 43.Hall M D, Banaszak L J. J Mol Biol. 1993;232:213–233. doi: 10.1006/jmbi.1993.1377. [DOI] [PubMed] [Google Scholar]
- 44.Banerjee S, Levy H R, Levy G C, Limuti C, Goldstein B M, Bell J E. Biochemistry. 1987;26:8443–8450. doi: 10.1021/bi00399a062. [DOI] [PubMed] [Google Scholar]