Functional and idling rotatory motion within F₁-ATPase

Abstract

ATP synthase mediates proton flow through its membrane portion, F₀, which drives the synthesis of ATP in its headpiece, F₁. The F₁-portion contains a hexagonal array of three subunits α and three β encircling a central subunit γ, that in turn interacts with a smaller ɛ and with F₀. Recently we reported that the application of polarized absorption recovery after photobleaching showed the ATP-driven rotation of γ over at least two, if not three, β. Here we extend probes of such rotation aided by a new theory for assessing continuous versus stepped, Brownian versus unidirectional molecular motion. The observed relaxation of the absorption anisotropy is fully compatible with a unidirectional and stepping rotation of γ over three equidistantly spaced angular positions in the hexagon formed by the alternating subunits α and β. The results strongly support a rotational catalysis with equal participation of all three catalytic sites. In addition we report a limited rotation of γ without added nucleotides, perhaps idling and of Brownian nature, that covers only a narrow angular domain.

ATP synthase supplies the cell with ATP at the expense of the proton- or sodiummotive force across the respective coupling membrane in bacteria, chloroplasts, and mitochondria (1–6). Its structure is bipartite with an integral membrane portion, F₀, and a peripheral portion, F₁. F₀F₁, in the simplest case, consists of eight different subunits and a total of more than 20. The enzyme is present in most prokaryotic and eukaryotic organisms, which diverged in evolution probably more than 3 billion years ago. Astoundingly, the recombination of subunits from different sources has yielded functional chimeric constructs (7–12). Solubilized F₁ is composed of five different subunits, (αβ)₃γδɛ, and is active as an ATPase (2, 3). The crystal structure of mitochondrial F₁ (13) revealed a hexagonal, alternating arrangement of the large subunits α and β (about 55 kDa each) with two coiled α-helices of subunit γ (30 kDa) in its center. Three potentially catalytic nucleotide binding sites are located on the (αβ)₃-hexagon of F₁ (14). This structural feature supports a rotatory tri-site mechanism of catalysis as proposed on biochemical grounds (15–17). A two-site mechanism, however, is still under debate (18).

The selectivity filter for proton transport is located in the F₀-portion (19) (in certain organisms likewise the filter for Na⁺; ref. 20). With the ion selectivity exchangeable with the F_O-portion in chimeric constructs (10) and with the active sites located in the F₁-portion, a mechanical coupling between proton flux and ATP-synthesis is probable. Subunit γ is the prime candidate for a rotational transmission between F₀ and F₁. Some rotational freedom of γ relative to other subunits of F₁ has been demonstrated in the form of still pictures as obtained by cryo-electron microscopy (21). The crystal structure of mitochondrial F₁ is highly suggestive of and has been interpreted in terms of a rotatory mechanism with γ acting as a crankshaft (13). The activity-linked mobility of γ between at least two subunits β has been demonstrated via reversible crosslinking (22, 23).

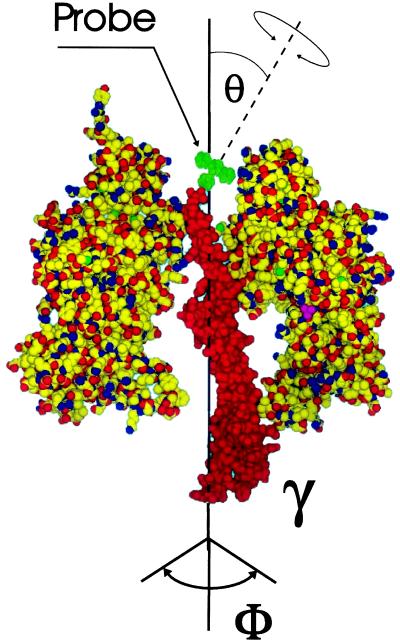
Rotational motion of γ during the hydrolysis of ATP has been reported by using polarized optical spectroscopy in photoselection-technique (24). We observed this rotation by applying polarized absorption recovery after polarized photobleaching to immobilized and γ-labeled chloroplast CF₁. The immobilization of the enzyme body was necessary to prevent its rapid Brownian rotation in solution. Fig. 1 illustrates the position of the probe eosin, which is linked via a maleimide function to a cysteine, the penultimate residue of the central γ-subunit in spinach CF₁. The γ-labeled and immobilized enzyme still hydrolyzes ATP. The bleaching of eosin by the laser flash produces absorption transients that are sufficiently long-lived (>1 s) to reveal the decay of the polarization anisotropy in about 100 ms as caused by the rotation of γ relative to the larger subunits during enzyme turnover (in about 100 ms) (24). This method is applicable to study the rotational molecular motion at a biochemically relevant time-scale not only in F₀F₁ but also in other enzymes and nanostructures. In this article we address the following specific questions:

Figure 1.

Model of the partial structure of chloroplast CF₁ from spinach shaped after the structure of mitochondrial MF₁ (13): the γ-subunit and two subunits of the (αβ)₃-hexagon are shown. The dye eosin (green) was bound by its maleimide function to the penultimate residue, Cys-322, of γ (25, 26). Rotational mobilities of γ and eosin are indicated by arrows. θ denotes the effective inclination angle of the dye’s bond axis relative to the long axis of γ.

1. What was the proportion of inactive molecules among the immobilized set?

2. Was the observed rotational relaxation of the covalently bound dye attributable to the rotation of subunit γ, or to a modulation of the rotational freedom of the dye around its linker-bond without any rotational motion of γ?

3. How large was the angular domain of freedom of γ? In other words, was CF₁ operating by a three-site or a two-site mechanism?

4. Was the rotational motion as caused by ATP-hydrolysis continuous or stepped, Brownian or unidirectional?

MATERIALS AND METHODS

Preparation of CF₁ and CF₁(-δɛ).

CF₁ and CF₁(-δɛ) were prepared by anion-exchange chromatography of EDTA extracts from spinach chloroplasts (27). The specific hydrolysis activity of the enzyme was 25–30 units/mg (measured in the presence of 50 mM Tris⋅HCl, 5 mM ATP, 2 mM MgCl₂, and 30 mM n-octyl β-d-glucopyranoside (Sigma), at 37°C.

Labeling of CF₁ with Eosin-Derivates.

CF₁ and CF₁(-δɛ) (5 μM) were labeled by 10-min reaction at room temperature in the dark at pH 7.0 (50 mM Mops/NaOH) with either 50 μM eosin-5-maleimide (e5m) or 50 μM eosin-5-isothiocyanate (Molecular Probes). The reaction was terminated by the addition of 1 mM N-acetyl-l-cysteine (with e5m) or 100 mM glycine (with eosin-5-isothiocyanate). Labeling with e5m decreased the specific Mg-ATPase activity to 20 units/mg. e-5m-labeled subunit γ (24–26), eosin-5-isothiocyanate labeled both the α and β subunits (28). Under the chosen conditions, e5m is expected to react exclusively with the so-called dark site in spinach chloroplast γ, i.e. the penultimate residue of subunit γ (Cys-322) (25, 26). The stoichiometric ratio of bound dye (extinction coefficient at 530 nm, 10⁵ M⁻¹·cm⁻¹) over enzyme was >0.5 (mol/mol).

Spectroscopic Properties of Eosin.

Eosin has a high quantum yield for singlet (S₁)-triplet (T₁) intersystem crossing (about 70%, compare Fig. 2B). The ground state (S₀) depletion is monitored by absorption and the population of the triplet state (T₁) by phosphorescence. The triplet state, because of its short lifetime, is only useful for photoselection experiments aiming at rotational correlation times shorter than 1 ms. To measure at longer time scales we resorted to the irreversible photodecomposition of eosin. Due to its low quantum yield (0.2%; ref. 24) the signal-to-noise ratio was poor. This problem was overcome by extensive averaging (more than 3,000 flashes) with sample aliquots that were exposed to only 100 flashes each.

Figure 2.

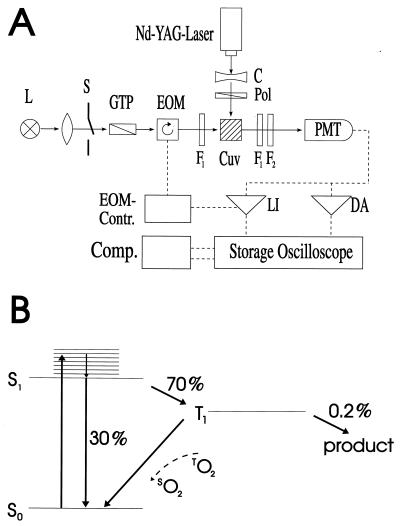
(A) Experimental setup for recordings of the absorption anisotropy in photoselection. L, lamp; S, shutter; GTP, Glan-Thompson polarizer; EOM, electro-optic modulator; Cuv, cuvette; F₁, interference filter; F₂, holographic notch-filter; PMT, photomultiplier tube; C, cylindrical lens; Pol, polarizer foil; LI, lock-in-amplifier; DA, DC-amplifier. (B) Term diagram of eosin. O, oxygen; S, singlet level; T, triplet level. For details see text.

Immobilization of CF₁.

Labeled CF₁ (CF₁ labeled in γ with e5m or eosin-5-isothiocyanate-CF₁) was immobilized on Sephadex DEAE-A50 (29). Unbound CF₁ was removed by extensive washing. Upon immobilization the specific activity of eosin-labeled CF₁ was decreased about 10-fold to 2 ± 1 units/mg (ATP-turnover number 13 ± 7 s⁻¹).

Reconstitution of CF₁-Depleted Thylakoid Membranes with e5m-Labeled CF₁.

F₁-depleted thylakoid vesicles were prepared by NaBr treatment (30). Reconstitution of photophosphorylation to these vesicles was achieved by addition of CF₁(−δɛ)+δ+ɛ in the presence of 10 mM MgCl₂ (31). This treatment raised the photophosphorylation rate from 0 to ≈150 μmol ATP synthesized per mg of chlorophyll per hr.

Experimental Setup for Photoselection Experiments.

Rotational motion in the time domain of 10–1,000 ms was measured in absorption. The experimental setup is shown in Fig. 2A (see also ref. 32). The exciting laser flash and the continuous measuring beam impinged perpendicularly on the sample. Light of a tungsten iodide lamp (Osram RJ6625) was passed through a lens, a Glan-Thompson prism as polarizer, and through an electro-optical device (photoelectric modulator from Hinds, Hillsboro, OR). The latter was rotating the linear polarization of the measuring light at a frequency of 100 kHz. The sample was contained in a water-jacketed, thermostated quartz cuvette (5 mm path length). A photomultiplier tube (EMI 9558B, 6 dynodes) was used to detect the transmitted light. Its photocathode was protected from the exciting flash by a notch filter (Laser Components). The sample was excited by repetitive flashes of a frequency-doubled neodymium-yttrium/aluminum-garnet laser (Quantel Brilliant, λ = 532 nm, pulse length: 5 ns). The laser beam was vertically polarized. Due to its polarization and its nonsaturating energy density the laser flash photoselected an anisotropic ensemble of dye molecules from the originally isotropic sample. The E-vector of the measuring beam was rotating, as mentioned. This served to record simultaneously absorption transients at parallel and perpendicular polarization between the laser flash and the measuring light beam. The photomultiplier output was split and connected in parallel to a regular DC-amplifier (Tektronix A-57) and to a narrow-band lock-in amplifier (Dynatrac 939). The output signals of both amplifiers were stored separately on a two-channel digital oscilloscope (Nicolet Pro10) and further processed on a computer. The lock-in amplifier (input filter setting at 100 kHz, upper bandwidth of the output filter 500 Hz) was tuned to the modulation frequency of the electro-optical modulator. It extracted the difference between absorption transients (ΔΔA) resulting from a parallel (ΔA_∥) and a perpendicular polarization (ΔA_⊥) between the measuring beam and the exciting laser flash. The upper electrical bandwidth of the DC-amplifier was set low (500 Hz) to smooth out the modulated polarization of the measuring light. Its output was thus related to the average absorption transient from both polarizations [ΔA_M = (ΔA_∥ + ΔA_⊥)/2]. From ΔA_M and ΔΔA, the anisotropy parameter was calculated. The polarization anisotropy parameter, r, is defined as follows (33):

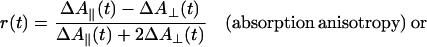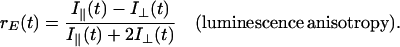As an experimental test for the precision of the experimental setup we determined the initial value of r for totally immobilized eosin (in acrylic glass). At the given wavelength pair, 532 nm for excitation and 522 nm for absorption, the former was r = 0.37 (the theoretical maximum for a nondegenerate transition is r = 0.4). We also determined r for freely and isotropically rotating, eosin-labeled CF₁; it was zero, as expected.

Rotational motion in 1–1,000 μs was monitored either in the absorption mode (as ground state depletion) or by phosphorescence. The electro-optical modulator and the lock-in amplifier were removed, and only the DC-amplifier was kept. Its upper bandwidth, however, was raised to 1 MHz. ΔA_∥ and ΔA_⊥ were now measured separately. The Glan-Thompson polarizer in the detection beam was set in two positions to orient the polarization of the measuring beam at 0° or at 90° between successive series of laser flashes. Fluctuations of the laser energy in each set of recordings were recorded and corrected for. For measurements of phosphorescence emission at even higher time-resolution we used another photomultiplier (EMI 9817B, 12 dynodes). Its output was connected directly to the storage oscilloscope (Tektronix DS-601, bandwidth = 20 MHz). A polarizer foil and an optical bandpass filter (Schott RG645) were placed directly upon the entrance window of the photomultiplier. P_∥ and P_⊥ were recorded separately by rotating the polarizer sheet in front of the photomultiplier by 90°. Whereas the lock-in amplifier was essential for the recordings of the polarization anisotropy at longer time scale (because of the small quantum yield of the irreversible bleaching of eosin) the more shortlived signals (70% triplet yield) could be caught without this complication.

RESULTS AND DISCUSSION

The Rotational Motion of Subunit γ as a Function of Nucleotides.

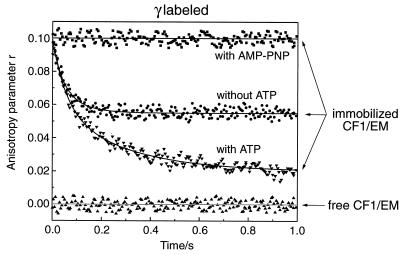
The upper three traces in Fig. 3 represent transients of the absorption anisotropy, r(t). They were obtained with immobilized CF₁ that was labeled with e5m at the penultimate residue of subunit γ. The apparent initial value of r was 0.1 in all three cases. An initial value of 0.37 was observed if eosin was totally immobilized in acrylic glass. The reduction to 0.1 was attributable to the rapid rotation of the dye around its linker bond (see further down). Starting from the apparent initial value of 0.1 the behavior differed depending on the nucleotide present. There was no detectable relaxation over several seconds in the presence of the nonhydrolyzable ATPanalogue adenosine 5′-[β, γ-imido]triphosphate (AMP-PNP) (top trace), there was a limited relaxation in the absence of added adenine nucleotide (middle), and there was a remarkable relaxation down to a steady level of 0.018 in the presence of ATP (bottom trace). The time constant of the latter (about 100 ms) was similar to the turnover-time of the immobilized enzyme. The top and bottom traces have been presented previously and interpreted to show the activity-linked rotational motion of γ over a range of more than 200° (24). This interpretation and the behavior without added nucleotide was scrutinized.

Figure 3.

Transients of the absorption anisotropy after a laser flash at t = 0 in a polarized absorption recovery after polarized photobleaching experiment. The sample, 0.5 mg of γ-labeled CF₁ was immobilized on Sephadex DEAE-A50 (suspended in Tris⋅HCl at pH 7.8), was contained in a quartz cuvette (5×5×5 mm³). β-d(+)-glucose and glucose oxidase/catalase (10/10 μg, Sigma) were added for anaerobicity. The sample was excited by repetitive laser flashes at nonsaturating energy (density 0.4 mJ/mm²). A new sample was introduced after 20% irreversible bleaching of eosin. Each data set represents the average of 3,000 recordings. (Top) AMP-PNP added. (Middle) Without added nucleotide. (Bottom) With ATP added under conditions of ATP-hydrolysis (see Materials and Methods). (Baseline) Free CF₁ in solution.

It needs emphasis that the absorption anisotropy observed in the time window from 1 ms to 1 s resulted entirely from molecules that were both labeled and immobilized. Only labeled molecules produced absorption transients at 522 nm, and only immobilized molecules produced a stationary value of r in the presence of AMP-PNP. The subset of labeled but dissolved molecules as well as free dye lost its anisotropy within less than 1 μs, and produced the baseline shown Fig. 3.

Whereas labeling hardly affected the hydrolysis activity, the immobilization reduced the activity to 10% (2 units/mg) of the one of solubilized CF₁. One had to dichotomize between two extremes, either a subset of 10% of the immobilized enzyme molecules was active, or all were active but at 10-fold lower rate due to the immobilization. The relaxation of the bottom trace in Fig. 3 (+ATP) to a figure of 18% of the initial value of r, proved that at least 82% of all immobilized and labeled molecules were active. Eighteen percent was the upper limit of inactive molecules without relaxation of the anisotropy (see Fig. 3 top trace, +AMP-PNP). That the immobilized CF₁ after resolubilization from DEAE regained its full activity was compatible with the notion of a reduced turnover rate by immobilization.

A straightforward interpretation of the foregoing data was as follows: (i) ATP-hydrolysis caused the rotation of subunit γ over a wide angular domain; (ii) this rotation was blocked by the presence of AMP-PNP; (iii) without added nucleotides, i.e. with one firmly bound ADP on CF₁ (34), γ carried out a more limited rotation. A radically different view was as follows: γ did not rotate relative to the immobilized body of the enzyme. Instead, it carried out a lateral movement during ATP-hydrolysis, thereby modulating the rotational freedom of the dye around its linker-bond. This possibility was scrutinized in the following.

The Rotation of the Probe Around Its Bond to γ as Function of the Enzyme Activity.

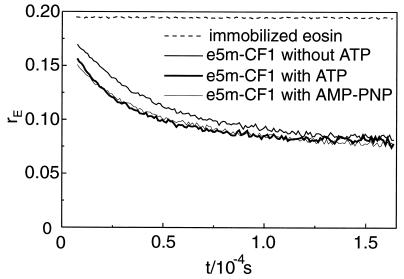
The rotational mobility of bound eosin was assayed by phosphorescence anisotropy again with immobilized CF₁ and eosin-labeled γ. Fig. 4 shows the relaxation of the luminescence anisotropy r_E after firing a laser flash at t = 0. The nonrelaxing upper trace shows the luminescence anisotropy that we observed with fully immobilized eosin in acrylic glass. Its initial value, 0.19, was smaller than the one in absorption, 0.37, because of wide-band observation (superposition of several transition moments). With labeled CF₁ the luminescence anisotropy started from a smaller value of about 0.15. We attributed the drop by 0.04 unit to the very rapid librational motion between narrow boundaries of the bound dye around its linker-bond. The much slower relaxation thereafter (half-decay time 30 μs) represented a rotational diffusion of the bound dye that was governed by the microviscosity of its protein cage. It was noteworthy that neither the rate of relaxation nor the (pseudo-) steady level (0.075) were affected by the activity (ATP present) or inactivity (AMP-PNP present) of the enzyme. The protein environment of the chromophore at the top indentation of CF₁ was therefore not altered by the transition between activity and inactivity. The data presented in Fig. 4 clearly corroborated the notion that the much slower and activity-linked relaxation of r in about 100 ms (see Fig. 3) was attributable to the rotation of γ itself, as previously claimed γ (24), but not to the rotation of the probe relative to γ.

Figure 4.

Transients of the phosphorescence anisotropy of eosin, r_P(t), after a laser flash at t = 0. Samples were illuminated repetitively by 1,000 laser flashes (density 10 μJ/cm⁻²). Data points are the average of six samples (excitation at λ = 532 nm, detection at λ > 645 nm). Upper trace, totally immobilized eosin in polyacrylamide. Three superimposed lower traces, Immmobilized and γ-labeled CF₁ with ATP, with AMP-PNP and without added nucleotide. Other conditions are as in Fig. 3 and see Materials and Methods.

The Angle θ Between the Probe’s Bond and the Long Axis of γ.

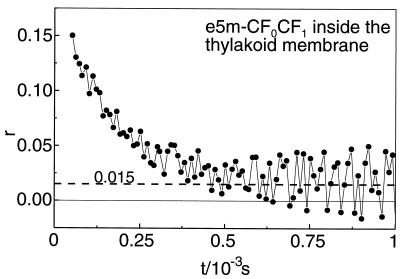
In the presence of ATP the activity-linked relaxation of the absorption anisotropy in Fig. 3 ended at 18% of the apparent initial value of 0.1. This level probably contained a contribution by inactive molecules that were expected to produce a steady figure of r (see the trace with AMP-PNP in Fig. 3). Another contribution to the steady value of r was attributable to both the limited rotational freedom of γ and to the angle between the bond of eosin and the long axis of γ (denoted θ in Fig. 1). It was immediately evident that the rotation of γ had caused no detectable relaxation of r if this angle was zero. This prompted us to determine the bond-angle θ. We chose conditions where γ was forced into the continuous, uniaxial but otherwise unrestricted (Φ = 360°) Brownian rotation of the holoenzyme, CF₀CF₁, around its long axis. Labeled CF₁ was rebound to CF₀ in CF₁-depleted NaBr-vesicles derived from spinach thylakoids. Fig. 5 shows the relaxation of the absorption anisotropy. At 100 μs after firing of the laser flash the polarization anisotropy was 0.1. At this time the relaxation of r due to the intrinsic mobility of the dye (correlation time 30 μs, see Fig. 4) was almost completed. Thereafter the relaxation of r continued down to a value of about 0.015. This decay was attributable to Brownian motion of the protein in the membrane. Its relaxation time (200 μs) was of the same order of magnitude as previously reported (35, 44). We assumed that the rotational relaxation of the dye itself was almost completed after 100 μs (see Fig. 3), and we took a value of r = 0.1 as the starting one to describe the further relaxation of r as a consequence of the Brownian rotation of the holoprotein. From the extent of the relaxation (from 0.1 to about 0.015) the effective inclination angle of the bond of eosin to the long axis of γ, θ, was calculated according to equation 30 in ref. 36:

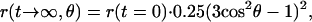We obtained θ = 40° or θ = 74°. These values were used together with the observed relaxation limit of r to calculate the range of rotational freedom of γ in the presence and absence of ATP (see below).

Figure 5.

Transients of the absorption anisotropy, r(t), in a photoselection-experiment with membrane-bound, γ-labeled CF₁. 50nM labeled CF₁ rebound to exposed CF₀ in NaBr vesicles was contained in a quartz cuvette (1×1×2 cm³). Anaerobic conditions were set up as in Fig. 3. To eliminate the contribution of electrochromic absorption transients, 100 μM 3-(3,4-dichlorophenyl)-1,1-dimethylurea and 1 μM gramicidin were added. By excitation at 534 nm and observation at 522 nm the ground state depletion by triplet state population was monitored. The increase of the noise level at longer times was caused by the decay of the triplet state into the ground state.

The Rotation of γ, Unidirectional (Drift) or Brownian–Continuous or Stepped?

Chemical reactions have a stochastic (random walk) aspect. Their equilibria are dynamical, not statical. The chemical (or entropic) term in the electrochemical potential difference, ΔRT⋅ln c, expresses this property. Under nonequilibrium conditions, e.g. with a large overshoot of reagent, as in our experiments on the hydrolysis of ATP, the reaction is forward directed, and the back reaction is negligible. Thus, it is conceivable that γ is driven unidirectionally by the hydrolysis of ATP, say clockwise as viewed from the top of CF₁.

The hexagon of (αβ)₃ alone is intrinsically stable, at least in the thermophilic bacterium PS3. The cooperativity of the nucleotide binding sites and a high rate of ATP hydrolysis are induced only upon the presence of subunit γ (37). In the light of the pivotal role of γ, both for hydrolysis and for synthesis of ATP, a random walk of γ as induced by ATP hydrolysis appears as improbable. That γ was released to idle around when needed in enzyme function was an inattractive view. Without added nucleotides, on the other hand, the holoenzyme, CF₀CF₁, mediates proton slip which we interpreted by the idling of coupling elements (38). This idling motion is blocked in the presence of only 200 nM ADP by a clutch-function, which is located in the F₁-portion of the enzyme and involves subunit γ (39). The above-mentioned arguments favored a directed rotational drift under ATP hydrolysis and, perhaps, a Brownian rotation of γ in the absence of nucleotides.

Published theories on photoselection experiments predict the (damped) oscillation of the anisotropy parameter r for rotational drift (40) as opposed to its monotonous relaxation for Brownian rotation (e.g., ref. 41). These theories are based on motion in an angular continuum. Considering the hexagonal, and functionally trigonal structure of F₁ we questioned this assumption, developed a theory of molecular stepper motors and arrived at predictions for the transient behavior of r (42). The salient result was that random walk and unidirectional drift are identical in a two-stepped rotor, and practically indistinguishable in a three-stepped rotor. In the latter, r decays practically monotonously, both under random walk and drift. In a six-stepped device, drift causes a strongly damped, but discernably oscillatory behavior. In a 50-stepped device many periods appear, until at very many steps the damping becomes negligible, as in the flagellar motor.

According to the foregoing, our data suggest that ATP hydrolysis drives a unidirectional and three-stepped drift of γ within the (αβ)₃-hexagon. In the absence of added nucleotides, γ may randomly rotate within narrower boundaries.

The Angular Domain of Freedom of Subunit γ Under ATP Hydrolysis and Idling Motion.

The relative level at infinite time of the relaxation of the anisotropy parameter, r, is indicative of the rotational freedom of the inspected chromophore. With eosin bound to subunit γ this level differed depending on the nucleotide load of the enzyme (see Fig. 3). It was 100% of the initial value in the presence of a nonhydrolyzable ATP analogue, 55% without added nucleotide, and 18% in the presence of ATP and under conditions of hydrolysis.

From these figures the angular freedom of γ was calculated using the above determined inclination θ of the dye’s bond to the long axis of γ. The calculated value was independent on whether the rotational motion was random or directed because the equilibrium-distribution of γ over the accessible angular space was identical in both cases. The distribution differed, however, depending on the nature of this space. Was it continuous or discrete (stepping motor)? For a continuous rotor we relied on the theory by Hoshikawa and Asai (40), for a discrete rotor on our own one (42).

Rotational Freedom of γ in Terms of a Continuous Rotor.

The relative steady level of r is related to the available angular space for uniaxial rotation, Φ, as follows (see equation 50 in ref. 41):

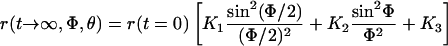with

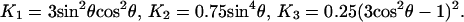With the given bond angles of eosin, θ = 40 or 74°, we calculated an angular range of Φ = 280° (for θ = 40° and 74°) under hydrolyzing conditions and of Φ = 135° (for θ = 40°) or 90° (for θ = 74°) in the absence of added nucleotides. The former was significantly larger than accounted for by a bi-site mechanism of catalysis and therefore attributed to tri-site mobility. The second value was compatible with bi-site mobility. It was noteworthy that these calculated angles, in particular the one for ATP hydrolysis (280°) represented the conservative estimate of a lower limit. If one portion of the steady level of r was caused by inactive molecules the angular domain would be wider.

Rotational Freedom of γ in Terms of a Stepped Rotor.

The assumption of a continuous rotatory motion of γ inside CF₁ is unrealistic. F-ATPase carries approximately C₆-symmetry structurally and C₃-symmetry functionally (13, 43). It was more appealing to consider a stepped motion of γ. In a theory of molecular stepper motors (42) we assumed that the probability distribution of γ was granular with n maxima equidistantly distributed over a circle.

The observed relative steady level of the anisotropy under hydrolyzing conditions, 18%, was incompatible with the calculated minimum of 25% for a two-stepped device (see equation 23 and figure 2 in ref. 42) at 120° angular separation between steps. It was, however, compatible with three or more steps. When three or more steps are equidistantly distributed over 360° the steady level equals for symmetry reasons the one of a continuous rotor (42). The observed steady level in the absence of added nucleotides, 55%, was compatible with a two-stepped device with angular domains of Φ₂ = 85° (for θ = 40°) and Φ₂ = 65° (for θ = 74°). It was incompatible, on the other hand, with three or more steps.

In conclusion, the steady level of the anisotropy in the absence of added nucleotides was compatible with a limited mobility of γ over 135° (continuous model) or between two discrete positions that were less than 85° apart (stepped model). The steady level of the anisotropy in the presence of added ATP was compatible with almost full rotational freedom (>280°, continuous model) or with at least three steps (at 120° intervals).

Independent of the mode of rotation, continuous or stepped, the obvious conclusion is as follows: ATP hydrolysis causes γ to move on a full circle. In the absence of nucleotides, on the other hand, it carries out a more limited motion, perhaps between two neighboring subunits β.

ABBREVIATIONS

e5m

eosin-5-maleimide

AMP-PNP

adenosine 5′-[β, γ-imido]triphosphate

Note Added in Proof

H. Noji et al. (45) most recently observed full and unidirectional rotation of subunit γ by another technique, namely single-molecule fluorescence microscopy.