Sensors for impossible stimuli may solve the stereo correspondence problem

Abstract

A fundamental challenge of binocular vision is that objects project to different positions on the two retinas (binocular disparity). Neurons in visual cortex show two distinct types of tuning to disparity: position and phase disparity, due to differences in receptive field location and profile respectively. Here, we point out that phase disparity does not occur in natural images. Why, then, should the brain encode it? We propose that phase disparity detectors help work out which feature in the left eye corresponds to a given feature in the right. This correspondence problem is bedeviled by false matches: regions of the image which look similar but do not correspond to the same object. We show that phase-disparity neurons tend to be more strongly activated by false matches. Thus, they may act as “lie detectors”, enabling the true correspondence to be deduced by a process of elimination.

Over the past 35 years, neurophysiologists have mapped the response properties of binocular neurons in primary visual cortex and elsewhere in considerable detail. A mathematical model, the stereo energy model¹, has been developed, which successfully describes many of their properties. Within this model, binocular neurons can encode disparity in two basic ways: phase disparity (Fig. 1a), in which receptive fields differ in the arrangement of their ON and OFF regions, but not in retinal position, and position disparity (Fig. 1b), in which left and right-eye receptive fields differ in their position on the retina but not in their profile². Several recent studies in V1^3–6 have concluded that most disparity-selective cells are hybrid⁷, showing both position and phase disparity. These neurophysiological data present a challenge to computational models of stereopsis. Why does the brain devote computational resources to encoding disparity twice over, once through position and once through phase?

Fig. 1.

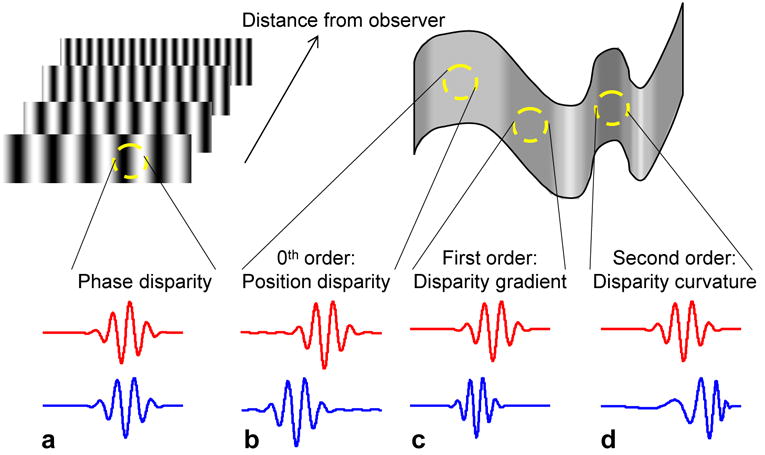
Different types of disparity. Top-left: Disparity stimulus which optimally stimulates a neuron with phase disparity. This is a set of luminance gratings (shown as opaque but actually transparent), at varying distances which depend on their spatial frequency. a: Example RFs of a phase-disparity neuron: odd-symmetric RF in left eye and even-symmetric in right. Top-right: varying-disparity surface, showing different types of physically-possible disparity, and the relationship between the two images of a little patch of narrow-band contrast on the surface (red = left eye, blue = right eye). These can also be thought of as the two receptive fields of a binocular neuron optimally tuned to the disparity of the surface at each position. b: 0^th-order, regions of uniform disparity; optimal detectors have pure position disparity. Detectors of this type are found in V1. c: 1^st-order, regions where disparity is varying linearly; optimal detectors have both a position shift and a spatial frequency difference between the eyes (one RF compressed relative to the other). d: 2^nd-order: disparity curvature. RFs are related by a position offset and compression which varies across the RF. The other major situation which occurs in natural viewing is disparity discontinuities at object boundaries. This is not shown here because it cannot be detected by a single pair of RFs.

Phase disparity presents a particular puzzle, since it does not correspond to anything experienced in natural viewing. For a surface such as a wall in front of the observer, where disparity is locally uniform, the two eyes’ images of a given patch on the surface are related by a simple position shift on the retina (Fig. 1b). For an inclined surface, with a linear disparity gradient, the two image patches are also compressed and/or rotated with respect to one another: i.e., they differ in spatial frequency and/or orientation (Fig. 1c). Higher-order changes in disparity, such as produced by curved surfaces, produce images whose spatial frequency and orientation differences vary across the retina (Fig. 1d ⁸). Disparity discontinuities, which occur at object boundaries, produce different disparities in different regions of the retina⁹. However, phase disparity neurons do not appear to be constructed to detect any of these possible situations. They respond optimally to stimuli in which the left and right eye’s image are related by a constant shift in Fourier phase, i.e. each Fourier component is displaced by an amount proportional to its spatial period. Physically, such a stimulus would correspond to a set of transparent luminance gratings whose distance from the observer is a function of their spatial frequency (Fig. 1a) – a situation which never occurs naturally, and which we therefore characterize as “impossible”, even though it can be simulated in the laboratory.

Recent physiological experiments support this conclusion. When presented with various possible disparity patterns, V1 neurons prefer stimuli with uniform disparity¹⁰, in contrast to higher visual areas, where neurons are found which respond optimally to depth discontinuities (V2^9,11), disparity gradients (V4¹², MT¹³, IT¹⁴, IP¹⁵), and disparity curvature (IT¹⁴). Psychophysical data supports the interpretation that disparity is initially encoded as a set of piecewise frontoparallel patches, which are then combined in higher brain areas to generate tuning for more complicated surfaces^10,16,17. However, when V1 neurons are probed with impossible stimuli designed to be optimal for phase disparity detectors, many of them respond to this better than to any naturally-occurring pattern of disparity¹⁸. Together, these results suggest that apparent tuning to phase disparity is not an artefact of a preference for a physically possible but non-uniform disparity: rather, the phase disparity detectors found in V1 genuinely are tuned to impossible stimuli.

This raises the conundrum of why the brain has apparently built detectors for stimuli which are never encountered. We present one possible answer, by demonstrating that phase disparity detectors could potentially make a unique contribution to solving the stereo correspondence problem. Here, the major challenge is identifying the correct stereo correspondence amid a multitude of false matches. Matching regions of a real image contain no phase disparity. They will therefore preferentially activate pure position-disparity sensors. However, false matches are under no constraints; they will not have either pure position disparity or pure phase disparity, and may be best approximated by a mixture of both. Thus, it is quite possible for them to preferentially activate hybrid neurons with a mixture of position and phase disparity. Consequently, the preferential activation of these neurons is a signature of a false match. Neurons with phase disparity – precisely because they are tuned to impossible stimuli – enable false matches to be detected and rejected.

We prove mathematically that, for uniform-disparity stimuli, this method is guaranteed to find the correct disparity, even within a single spatial-frequency and orientation channel, and even when the disparity is larger than the period of the channel. This is a surprising success, given that previous neuronal correspondence algorithms have had to compare information across channels in order to overcome the false-match problem in this situation, even in uniform-disparity stereograms^7,19–22. Of course, real images contain multiple disparities, so the proof no longer holds. In such images, our method may give conflicting results in different spatial frequency and orientation channels. However, we find that a simple robust average of the results from different channels produces good disparity maps, with no need for any interaction between channels. Thus, this method is also useful in complex natural images where its success is not mathematically certain. We suggest that the brain may similarly use phase disparity neurons to eliminate false matches in its initial piecewise frontoparallel encoding of depth structure. This provides for the first time, a clear computational rationale for the existence of both phase disparity and position disparity coding in early visual cortex.

RESULTS

Neither position nor phase detectors are sufficient to recover disparity

Consider a person standing in front of a wall, with the stucco texture shown in Fig. 2b. This visual scene – a single frontoparallel surface – has no depth structure at all (the stucco texture is flat). Yet even in this simplest of cases, it is by no means straightforward to identify the wall’s disparity from a population of neurons which have solely position disparity. These are cells like those in Fig. 1b, whose receptive fields in the two eyes have identical profiles (zero phase disparity) and differ only in their position on the retina (position disparity). Fig. 2a plots the response of a simulated population of such neurons. Each neuron’s firing rate is calculated according to the stereo energy model¹ (Methods, Equation 1), and plotted as a function of its position disparity. Using the modern version^6,23–25 of the terminology introduced by ref 26, we shall refer to these pure position-disparity cells as tuned-excitatory cells. In this modern usage, these terms describe only the shape of the disparity tuning curve, not the preferred disparity. Thus for us, a tuned-excitatory cell is defined by having a symmetrical tuning curve with a central peak, irrespective of whether this preferred disparity is crossed, uncrossed or zero.

Fig. 2.

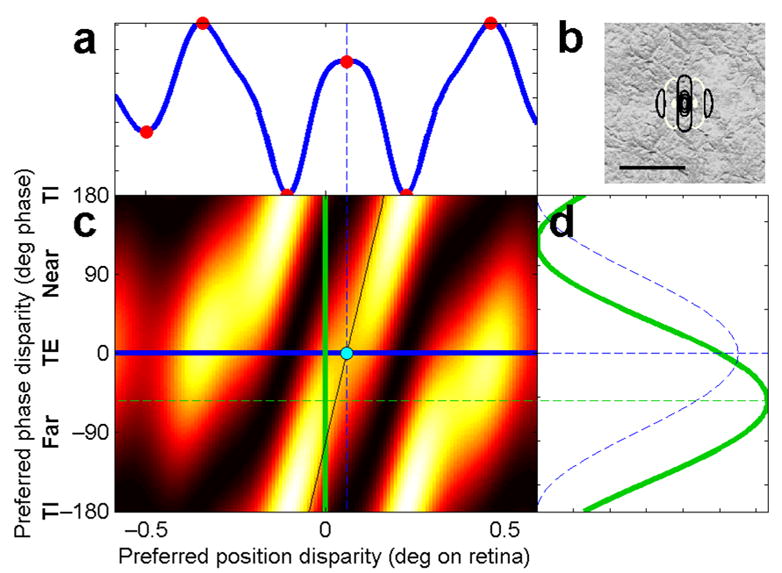
Response of a neuronal population (c) to a broadband image (b) with uniform disparity of 0.06° (cyan dot in c). All neurons are tuned to vertical orientations and a spatial frequency f = 4.8 cycles per deg, bandwidth ~ 1.5octaves. Example RF profile shown in b (black contour lines = ON regions, white = OFF; scale bar is 0.5°). RFs differ in their phase and in their position on the retina, but all cells in this population have the same cyclopean location, i.e. the same mean position of their binocular receptive fields, Supp Fig 3b. Each pixel in c represents one neuron; pixel’s horizontal and vertical location indicates neuron’s preferred position and phase disparity respectively; pixel color indicates neuron’s firing rate in response to this image. This is calculated according to the stereo energy model¹, Equation 1. Neurons with zero phase disparity (blue line) are called tuned-excitatory (TE); neurons with ± 180° of phase disparity are tuned-inhibitory (TI); neurons with +90° are “near” and with −90° are “far”. a, d show cross-sections through this response surface, i.e. activity of two neuronal subpopulations, a with pure position disparity (blue curve), d with pure phase disparity (green curve). Red dots in a mark local extrema of the response. Dashed blue curve in d shows response of subpopulation where all neurons are tuned to position disparity of the stimulus but have varying phase disparity. Sloping black line in c shows the linear relationship between position and phase disparity for sine functions: Δx = Δφ/(2πf). For sufficiently narrow-band neurons, the yellow diagonal stripes of high neuronal response would all be parallel to the black line, and the stimulus disparity, modulo one period, could be read off from the maximally-responding pure phase disparity neuron. However, reading along this line on the present plot, we see that the stimulus disparity of 0.06° corresponds to a phase disparity of −101° (0.28 cycles), yet the maximally-responding pure phase disparity neuron is tuned to just −54° (0.15 cycles, green dashed line).

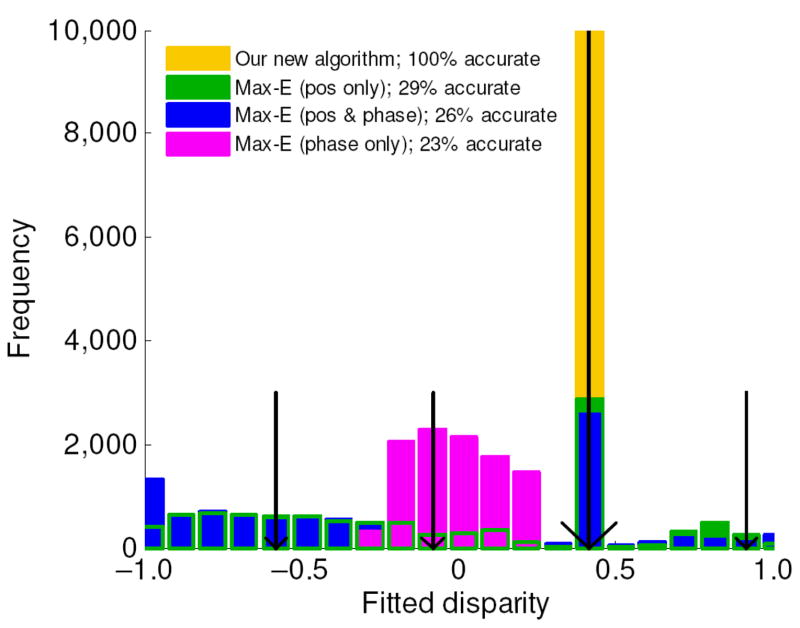
How can we deduce the stimulus disparity from the response of this population? Perhaps the simplest approach is to find the preferred disparity of the maximally-responding tuned-excitatory cell, and take this as an estimate of the stimulus disparity^7,27. However, this maximum-energy algorithm is not guaranteed to give the right answer. The problem is that the stereo energy computed by these model cells depends not just on the correlation between the left and right images, but also on the contrast within each receptive field. Thus, mismatched image patches which have high contrast can easily have more stereo energy than corresponding patches which happen to have low contrast. In experiments, the response of the population is often averaged over many images with the same disparity structure and with purely random contrast structure, as in random-dot patterns²⁸. This means that the effect of contrast will average out, and the cell with the maximum average response will indeed be that tuned to the stimulus disparity. However, in real life the brain does not have this luxury. It has to make a judgment about single stereo images – and here, a maximum-energy algorithm is likely to fail^7,27. For example, in Fig. 2a the false matches at −0.35° and +0.46° both elicit larger responses than the true match at 0.06°. Indeed, we point out here for the first time that the stimulus disparity may not be at even a local maximum. As we show in the Supplementary Information, if the contrast at the cyclopean location happens to be particularly low, then the stimulus disparity can actually fall at a local minimum of the population response (Supp Fig 2). This occurs if the decrease in binocular correlation produced by moving the receptive fields onto non-corresponding regions of the image is outweighed by a fortuitous increase in contrast energy. Thus, all we can deduce from Fig. 2a is that the stimulus disparity must be one of the values marked in red, where the response of tuned-excitatory cells has a local turning point. This still leaves us with 6 possible matches even within this restricted range (3 cycles of the cell’s spatial period). In Fig. 3, we show what happens if we ignore these problems and simply pick the tuned-excitatory cell with the largest response (green histogram). Tested on 10,000 noise images each with a uniform disparity of 0.42°, this maximum-energy algorithm finds the correct answer only 29% of the time.

Fig. 3.

Comparison of our algorithm with four possible implementations of a maximum-energy algorithm, tested on a uniform-disparity noise stimulus. The histogram summarizes results for 10,000 noise images with a disparity of 0.42deg, marked by the large arrow. All results are for the same channel: spatial frequency f = 2cpd, orientation = vertical, bandwidth = 1.5 octaves. The shorter arrows mark disparities which are integer multiples of the spatial period away from the correct disparity. Orange: our algorithm, using both position and phase disparity detectors, always returns the correct disparity. Blue: evaluating the response of the full population, including cells with both position and phase disparity, and taking the stimulus disparity to be the preferred disparity of the maximally-responding cell (i.e. Δxpref − Δφpref/(2πf) ), gives the correct answer only 26% of the time. Green: ditto, except considering only pure position-disparity detectors (tuned-excitatory cells, Δφpref = 0); performance is similar. Purple: ditto, except considering only pure phase-disparity detectors (Δxpref = 0). This can only return answers within half a cycle of zero, i.e. ± 0.25°. “Percentage accurate” means the proportion of results which lie within the bin centered on the true disparity of 0.42°, except for the phase-disparity case (purple), where bins differing from this by integer multiples of the period 0.5° (marked with small arrows) were also considered correct.

Physiologically-inspired stereo correspondence algorithms have more commonly used pure phase disparity detectors^{21,27,29–31}. These algorithms consider a population of model neurons whose receptive field envelopes are centered on the same position in both retinas, but which differ in the pattern of their ON and OFF regions (Fig. 1a). The green curve in Fig. 2d shows the response of a simulated population of pure phase disparity detectors as a function of their preferred phase disparity. It is a sinusoid. As we show in the Supplementary Information, Theorem D, this is a general property of a population of phase disparity detectors tuned to a given position disparity (here zero). For sufficiently narrow-band cells, the stimulus disparity – modulo the preferred spatial period of the cell – can be read off from the peak of this sinusoid. If the sinusoid peaks for cells tuned to a phase disparity of Δφ_pref, then the stimulus disparity is λΔφ_pref/2π±nλ, where λ is the period of the spatial frequency channel under consideration, and n is any integer. Thus, a narrow-band population can correctly identify stimulus disparities up to a half-cycle limit²⁷. Combining information from different spatial frequency channels, in a coarse-to-fine scheme^22,32, could expand this range, at least in uniform-disparity stimuli where the disparity sampled by the large, low-frequency detectors is the same as that experienced by the smaller, high-frequency detectors. However, psychophysical evidence has yielded limited support for the idea of a coarse-to-fine hierarchy^33,34. Pure phase-disparity detectors cannot explain how humans are able to perceive disparity in narrow-band stimuli well above the half-cycle limit^35,36.

Furthermore, pure phase-disparity detectors perform reliably only if they are sufficiently narrow-band. Previous theoretical work has concentrated on this mathematically tractable case. It has not previously been pointed out that, for realistic V1 bandwidths, pure phase-disparity detectors fail even for uniform-disparity stimuli within the half-cycle limit. This is exemplified in Fig. 2. The model neurons in our simulations have a spatial frequency bandwidth of 1.5 octaves, which was the mean value for a sample of 180 V1 neurons in our previous physiological experiments^23,37, in agreement with previous estimates³⁸. The stimulus has a uniform disparity of 0.06°, which is 0.28 of a cycle (101° phase). Yet the most active phase disparity detector is tuned to only 0.15 cycles (54° phase, green curve in Fig. 2d). Thus, the pure phase-disparity population would give the wrong answer in this case. The purple histogram of Fig. 3 shows that this failure is common. Here, the maximum-energy algorithm was tested on pure phase-disparity cells in a uniform-disparity stimulus whose disparity (0.42°) lies outside the half-cycle limit (± 0.25°). Obviously, phase-disparity detectors cannot signal the true disparity in this case. However, they also fail to correctly detect the correct disparity even modulo their spatial period. In this case, the stimulus disparity minus one spatial period is −0.08°, marked with a short black arrow. The maximum-energy algorithm finds this value on less than one-quarter of images. Thus, with a realistic spatial frequency bandwidth, being even 1 cycle away from the stimulus disparity has a catastrophic effect on the accuracy of pure phase-disparity detectors.

Position and phase detectors together can recover disparity

We have seen, then, that neither pure phase disparity (Fig. 1a) nor pure position disparity detectors (Fig. 1b) can reliably signal the correct disparity, even in the simplest possible case where the stimulus contains only one disparity. However, the brain also contains hybrid position/phase disparity sensors. Fig. 2c shows the responses of hybrid energy-model neurons with all possible combinations of position and phase disparity (up to 0.6° position disparity). Simply extending the maximum-energy algorithm to this full population results in little improvement, as the blue histogram in Fig. 3 shows. But as we shall now discuss, there is a guaranteed means of identifying the correct match in uniform-disparity stimuli from the response of this population.

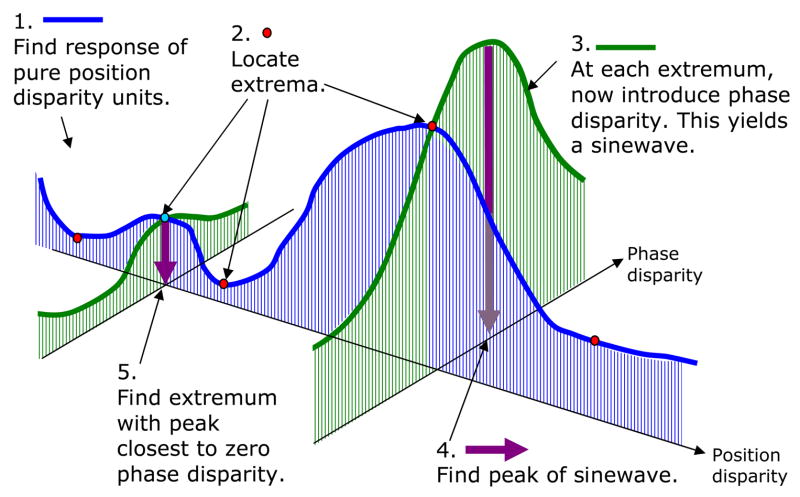
The mathematical proofs underlying this method are given in the Supplementary Information. However, the key insight is very simple. It is that, as we saw in Fig. 1, real stimuli do not contain phase disparity. This means that, if a detector is already tuned to the correct position disparity, then its response can only be reduced by any tuning to non-zero phase disparity (dashed blue curve in Fig. 2d). Thus, for the subpopulation of hybrid sensors whose position disparity matches the stimulus, the maximum response will be in the sensor with zero phase disparity. However, for a subpopulation whose position disparity corresponds to a false match, the response is far more likely to be maximum at a non-zero phase disparity (e.g. green curve in Fig. 2d). Expressed formally, this means that the true match is distinguished by (A) being at zero phase disparity, (B) being at a local extremum (maximum or minimum) with respect to position disparity, and (C) being at a local maximum with respect to phase disparity. Condition (A) says that the true match is located somewhere along the blue slice in Fig. 2ac or Fig. 4. (B) says that the true match is at one of the extrema marked with dots along this slice. Finally (C) tells us that the true match is the cyan dot, since this is the only one located at a local maximum wrt phase disparity. False matches which satisfy (A) and (B) may occur, but are very unlikely to satisfy (C) as well. In other words, phase disparity sensors – precisely because they are tuned to impossible patterns of disparity – can identify false matches. In the Supplementary Information, we prove that these three conditions are guaranteed to hold in any stereo image where the disparity is uniform across the visual field. This enables the correct disparity to be uniquely identified, even within a single spatial-frequency channel where the stimulus disparity is many cycles of the channel frequency.

Fig. 4.

Sketch of the algorithm used to estimate stimulus disparity within a single channel. The blue and green curves represent horizontal and vertical cross-sections through the population response in Fig. 2. Thus, the blue curve represents the response of a population of tuned-excitatory cells (with pure position disparity, no phase disparity), while the green curves represent the response of a population of hybrid cells, with varying phase disparity but all with the same position disparity. Note that “position disparity” and “phase disparity” in this figure refer to the tuning preferences of the cells, not properties of the stimulus.

Anti-correlated images

Anti-correlated images are those where the contrast in one eye’s image is inverted. Dense anti-correlated stimuli provide a multitude of false matches, but no overall depth percept; they have an unsettling, shimmering appearance^39–42. Most existing stereo algorithms pick one false match from each channel. The fact that no depth is perceived in these stimuli is then explained as due to cross-channel conflict, because a different false match is returned from each channel¹⁹. Our observation about the use of phase disparity suggests an additional possibility. Anti-correlation corresponds to a phase disparity of 180°. Thus, out of the subpopulation of detectors tuned to the stimulus position disparity, the ones responding most will be tuned to a phase disparity of 180° (Supp Fig 4). An algorithm which is looking for a subpopulation where the peak falls at 0° will therefore ignore this subpopulation. Indeed, there will in general be no point on the zero-phase-disparity line which is both a local extremum with respect to position disparity, and a local maximum with respect to phase disparity. Thus, even within a single channel, an anti-correlated stimulus visibly fails to conform to the expected pattern of population activity for a uniform-disparity stimulus. Note that this is only true when the whole population of hybrid position and phase disparity sensors is considered – if we consider only a subpopulation of pure position or pure phase disparity detectors, there is nothing in any one channel to indicate that the stimulus is unusual. We suggest that this violation of the expected pattern across the full population, as well as cross-channel conflict, may contribute to the lack of a depth percept and the distinctive appearance of this stimulus.

Performance on more complex depth structures

We implemented the above ideas in a computer algorithm (Fig. 4). This algorithm is guaranteed to return the correct disparity in a uniform-disparity stimulus (Fig. 3, orange histogram). However, real visual scenes seldom have the convenient property of containing only a single disparity! How does our algorithm fare when this requirement is not met? As an example, we tested the algorithm on slanted surfaces (Supp Fig 6). The disparity at the centre of the receptive field was 0°, but 1° to the left or right it was ± 0.02° (Supp Fig 6a) or ± 0.16° (Supp Fig 6b). This latter case is a very extreme disparity gradient. When viewed up close at 30cm, it corresponds to a surface slanted at nearly 40° to the frontoparallel, and at larger viewing distances the slant becomes even more extreme. Nevertheless, even here, the algorithm performs well. On any single image, a single channel stands about a 50% chance of returning the correct disparity, and a 50% chance of returning essentially a random value. Importantly, the errors made by different channels are virtually uncorrelated. Any given channel may be misled by a particular feature of the image, and pick the wrong disparity. But other channels do not see that feature, and are not misled. This means that by combining the outputs from a few different channels, the true disparity can be reliably recovered. For example, performing a robust average over just 6 channels increases the accuracy from 54% to 85%. With less extreme slants, even a single channel is reliable. For example, the surfaces in the first example (Supp Fig 6a) would be slanted 18° away from frontoparallel when viewed at a distance of 1m. Here the algorithm performs with 90% accuracy even within a single channel, and with 100% accuracy when the outputs from 6 channels are robustly averaged.

Fig. 5 shows how our algorithm performs on a test stereogram widely used in the computer vision literature. Good (though noisy) disparity maps are produced from the output of a single spatial-frequency and orientation channel (Fig. 5d–i; all channels are shown in Supp Fig 5). When the outputs of several spatial-frequency and orientation channels are averaged, even better results are obtained. Fig. 5c shows the disparity map produced by robustly averaging the outputs of 36 channels (6 orientation and 6 spatial frequency). Not only the broad outline of the Pentagon itself is reproduced, but also the details of its roof and even the trees in the courtyard.

Fig. 5.

Applying our principle to a classic test stereogram (the Pentagon, ab). d–i: Disparity maps obtained from single channels, with spatial frequencies indicated in the title. Since orientation tuning made little difference to the disparity maps obtained, we show results for only one preferred orientation, 30°. Supp Fig 5 shows results for all 6 orientations. Contours show example RFs for each channel. Colorscale for all panels is as given in c. Gray regions indicate where no candidate matches were encountered within the range examined. c: Robust average of disparity maps obtained by all 36 channels (6 SFs, 6 orientations).

What is striking is that this method allows good disparity maps to be obtained in this complex image, even from a single channel. Of course, the very lowest frequency channel (0.5 cycles per deg, Fig. 5d) is unable to report accurate values, because its large receptive fields span regions of different disparity. Errors introduced by this channel are kept to a minimum because our algorithm is capable of reporting failure – when no extrema were encountered within the disparity range examined, no disparity estimate was produced (gray pixels), and the channel then did not contribute to the overall disparity estimate (Fig. 5c) for this cyclopean position. However, when the channel does return an estimate, it is usually at least roughly correct, so the vague outline of the pentagon emerges even here. For the highest frequency channels, the problem is the exact opposite. Here, the receptive fields are small enough that they usually sample a disparity which remains at least roughly uniform. However, they are exposed to more false matches. One way of overcoming this well-known problem is to use the outputs of lower-frequency channels, in a coarse-to-fine hierarchy^22,32. In contrast, the results of Fig. 5 show that by combining position and phase disparity sensors as we propose, quite reliable disparity maps can be extracted from a single channel, even where the disparity exceeds the half-cycle limit.

We also tested our algorithm on three test images from the Middlebury stereo repository⁴³ (http://cat.middlebury.edu/stereo). Since this database records the correct disparity for each image pair, this enables a quantitative evaluation of our algorithm. Each panel in Fig. 6 shows the left and right images (top), along with the correct disparity map and the map produced by our algorithm (robust average over 6 SF × 6 orientation channels). The stimulus disparity range was similar in each case, about 10 pixels. The algorithm searched over a much wider range, 30 pixels, greatly increasing the chance of false matches. Yet in every case, the algorithm succeeds in recovering good disparity maps. Below the fitted disparity map, we show three quantitative measures of fit quality. R and B are the two measures employed by Scharstein & Szeliski⁴³. R is the RMS error, in pixels, while B is the percentage of pixels where the disparity error is > 1 pixel. M is the median absolute error, in pixels. In every case, this is less than half a pixel. Our algorithm considerably underperforms the best machine-vision stereo algorithms, for which B is typically an order of magnitude less. From Fig. 6, it is clear that the high percentage of “bad” pixels arises predominantly not from high-frequency noise scattered over the disparity map, but from a blurring of the depth discontinuities. Edges which are straight and abrupt in the stimulus are reconstructed as wavy and gradual, while disparity over broad regions is generally correct. This is compatible with a striking feature of human stereopsis: poor spatial resolution for stereoscopic structure^10,16. Thus, although other machine algorithms produce more veridical depth maps, they probably outperform human stereopsis also.

Fig. 6.

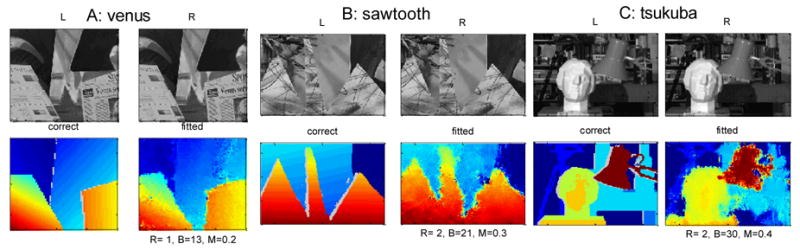
3 test stereo-pairs from the Middlebury repository. In each panel, the top row shows left and right images over the region where disparity was evaluated (for speed, we did not evaluate disparity at every pixel in the image, although the full-size images were used as input to the algorithm). The bottom left pseudocolor plot shows the “ground truth” disparity given in the repository, with occluded regions grayed out. The bottom right pseudocolor plot shows, on the same colorscale, the disparity fitted by our algorithm. Below, this plot are three quantitative measures of fit quality: R = RMS error in pixels, B = percentage of the image where the error exceeds 1 pixel, M = median absolute error, in pixels. All three measures are evaluated over the entire fitted region, including occlusions.

DISCUSSION

Stereopsis is a perceptual module whose neuronal mechanisms are understood in considerable detail. The process begins in primary visual cortex, which contains sensors tuned for both position and phase disparity, and for combinations of both. It is currently unclear why the brain should encode disparity twice over in this way. Phase disparity is particularly puzzling, since it can encode disparities up to only half a cycle, with optimal detection at a quarter-cycle³⁵, whereas position disparity – and human perception – is subject to no such limit^35,36. Furthermore, we point out here that phase disparity detectors are tuned to patterns of luminance which are not found in real stimuli. Of course, such luminance patterns may occasionally occur, for example in regions of the image which are uncorrelated due to occlusions. The point is that, unlike position disparity detectors, they do not reliably signal a particular physical disparity.

Why build detectors for phase disparity?

Why then does the brain contain both sorts of detector? One early suggestion⁴⁴ was that phase disparity might compensate for unwanted position disparities introduced by the finite precision of retinotopy. However, subsequent studies have failed to show the inverse correlation between position and phase disparity tuning which this would imply^4,6.

Only one previous study²² has proposed a theoretical reason why the brain might need both types of detector. The authors suggested, based on the simulated response to many different bar and random-dot patterns, that populations of pure phase disparity detectors are more reliable than their pure position disparity counterparts. They found that for any given image, the maximally-responding phase disparity unit was usually that tuned to the stimulus disparity (Δφ_pref = 2πf Δx_stim), while the position disparity units showed much wider scatter in the location of the peak. Thus, they suggested that position disparity was used to overcome the half-cycle limitation, shifting disparity into the right range, while phase disparity was used to make a precise judgment. However, their observation that phase detectors give more reliable signals depends critically on the particular set of detectors they happened to consider: a group of neurons which all had the same left-eye receptive field (see Supplementary Information, Supp Fig 3a). Thus, in their population, cyclopean location co-varied with position disparity, introducing additional noise into the disparity signal. When cyclopean location and position disparity are varied independently, as here (Supp Fig 3b), position-disparity detectors are actually more reliable than phase-disparity detectors over the same range; compare green and yellow histograms in Fig. 3. Thus, nothing in the existing literature explains why the brain should deliberately construct detectors with phase disparity.

One possibility is that such detectors are not, in fact, constructed deliberately. It may simply be too hard to build neurons tuned strictly to real-world disparities, and so phase disparities represent a form of noise which the visual system copes with. Phase disparity detectors do respond to the disparity in real images, even though they are not ideally suited to these, which is why stereo correspondence algorithms can be constructed out of phase disparity detectors^{27,30,31,45,46}. Perhaps, therefore, there is not enough pressure to iron out accidental phase disparities which arise during development.

Here, we point out a more interesting possibility. Precisely because phase disparity does not occur in real-world images, neurons which have both position- and phase- disparity signal false matches, and so help solve the correspondence problem. If stimulus disparity is uniform across the receptive field, then the neuron optimally tuned to the stimulus will be a pure position disparity neuron (equivalently, a tuned-excitatory or tuned-excitatory cell^2,23,26), with position disparity equal to that of the stimulus and with zero phase disparity. Introducing phase disparity into this cell’s receptive fields would make it less well tuned to the image, and reduce its response. Thus, the tuned-excitatory cell will respond more strongly than its neighbors with the same position disparity but non-zero phase-disparity. This is the signature of the true match. False matches may elicit a strong response in particular tuned-excitatory cells, but the response will be even stronger when an appropriate phase disparity is added in. Thus, these hybrid position/phase disparity sensors act as lie detectors. Their activity unmasks false matches.

Implementation in the brain

The algorithm used for our simulations (Fig. 4 and Supplementary Information) is not physiologically realistic; it was designed for speed in a serial processor, not as a model of a massively parallel system like the brain. Nonetheless, the principle underlying our simulations could be implemented in visual cortex by a cooperative network in which “lie detectors” with hybrid position/phase disparity suppress activity in the corresponding tuned-excitatory cells. A winner-take-all competition between neurons with different phase disparity ensures that the only surviving activity in tuned-excitatory cells is where zero phase disparity produced the best response. This would silence almost all tuned-excitatory cells except those located at the true match. Irrespective of the precise neuronal circuitry, our model predicts that activity in tuned-inhibitory/near/far cells should tend to reduce either the actual activity in the corresponding tuned-excitatory cells, or the downstream effect of that activity. One way in which this might be tested experimentally is to measure the dynamics of responses to stimuli that produce local peaks in a population of tuned-excitatory cells, but which are vetoed by phase disparity detectors (as happens, according to our model, in anticorrelated stereograms). The effect of this veto should appear later in the response, so our model predicts that dynamic measures of responses to anticorrelated stereograms would show a characteristic evolution over time.

Conclusion

We have pointed out a novel way of identifying the stimulus disparity from a population of hybrid position and phase disparity neurons modeled on primary visual cortex. Where the stimulus disparity is uniform, this method gives the correct answer with 100% reliability, even within a single spatial-frequency/orientation channel, and even if the stimulus disparity is many cycles of the channel’s spatial period. This success is striking given that most existing algorithms have to compare information from several channels in order to overcome aliasing, even for a uniform-disparity stimulus. For realistic stimuli with varying disparity, the method is not guaranteed, but simulations suggest that it is still remarkably successful. This is the first theory to explain the existence of large numbers of visual cortical neurons which respond best to stimuli which never occur in natural viewing¹⁸. Our proposal also provides a new insight into why the modulation of V1 neurons for anti-correlated stimuli does not result in a depth percept. The theory was inspired by the observed properties of visual cortex, and can be implemented in a physiologically plausible manner. The idea of “lie detectors” specifically tuned to false matches may also turn out to be useful in machine stereo algorithms.

METHODS

The model neurons in this paper are constructed according to the stereo energy model of Ohzawa, DeAngelis and Freeman¹. We begin with binocular simple cells. These are characterised by a receptive field in each eye: ρ_L(x,y), ρ_R(x,y). The output from each eye is given by the convolution of the retinal image with this receptive field:

$$L={\int }_{-\infty }^{+\infty }\mathit{dxdy}{I}_L(x,y){\rho }_L(x,y)$$

and similarly for the right eye. The retinal images I_L(x,y), I_R(x,y) are expressed relative to the mean luminance, so that positive values of I represent bright features and negative values represent dark. The output of an energy-model binocular simple cell is

$$E={(L+R)}^2.$$ Equation 1

(Strictly, a physiological simple cell would be E = ⌊L + R⌋²; the unrectified expression, Equation 1, would represent the sum of two physiological simple cells¹).

All simulations used Gabor receptive fields with an isotropic Gaussian envelope. The basic “cyclopean” receptive field profile is:

$$\rho (x,y;\phi )=cos(2\pi f{x}^{\prime }-\phi )exp\left(-\frac{{x^{\prime }}^2+{y^{\prime }}^2}{2{\sigma }^2}\right),\hspace{0.17em}\text{where\hspace{0.17em}}{x}^{\prime }=xcos\theta +ysin\theta ;y^{\prime }=ycos\theta -xsin\theta ,$$ Equation 2

where f is the cell’s preferred spatial frequency, θ its preferred orientation and φ its phase. The standard deviation σ is

$$\sigma =\frac{\sqrt{ln\hspace{0.17em}2}}{2\pi f}\frac{2^{1.5}+1}{2^{1.5}-1},$$

resulting in a full-width, half-maximum bandwidth of around 1.5 octaves¹⁹.

The left- and right-eye receptive fields are shifted in position and phase depending on the tuning of the neuron. For a neuron tuned to position disparity Δx_pref and phase disparity Δφ_pref, the left- and right-eye receptive fields are

$${\rho }_L(x,y)=\rho (x+\mathrm{\Delta }{x}_{\mathit{pref}}/2,y;\phi +\mathrm{\Delta }{\phi }_{\mathit{pref}}/2);\hspace{0.17em}{\rho }_R(x,y)=\rho (x-\mathrm{\Delta }{x}_{\mathit{pref}}/2,y;\phi -\mathrm{\Delta }{\phi }_{\mathit{pref}}/2).$$

Tuned-excitatory cells have Δφ_pref = 0 by definition; tuned-inhibitory cells have Δφ_pref = π.

Fig. 2, Supp Fig 2 and Supp Fig 4 show the responses of simple cells (Equation 1), tuned to a particular phase φ. To avoid dependence on any one phase, the results in Fig. 5, Fig. 6, Supp Fig 5 and Supp Fig 6 were obtained using the response of phase-independent complex cells, given by the sum of two simple cells in quadrature¹. As shown in the Supplementary Information, the mathematical results underlying our algorithm hold for both simple and complex cells.

We adopted a simple robust-averaging heuristic for combining the disparity maps produced by different spatial-frequency and orientation channels, Supp Fig 5, into a single best-estimate disparity map, Fig. 5c. At each cyclopean position (x_pref,y_pref), we calculate the average disparity from all channels which returned an estimate of that position <Δx_est(x_pref,y_pref;f,θ)>_f,θ. Then we removed the channel whose estimate was furthest from the mean, and calculated the mean of the remaining channels. We repeated this procedure until only half the channels remained.