Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2007 Nov 12.
Published in final edited form as: J Neurosci Methods. 2006 Nov 2;160(2):359–367. doi: 10.1016/j.jneumeth.2006.09.020

Spike detection in human muscle sympathetic nerve activity using the kurtosis of stationary wavelet transform coefficients

Robert J Brychta a,b, Richard Shiavi b, David Robertson a, André Diedrich a,b,*
PMCID: PMC2075105  NIHMSID: NIHMS19895  PMID: 17083982

Abstract

The accurate assessment of autonomic sympathetic function is important in the diagnosis and study of various autonomic and cardiovascular disorders. Sympathetic function in humans can be assessed by recording the muscle sympathetic nerve activity, which is characterized by synchronous neuronal discharges separated by periods of neural silence dominated by colored Gaussian noise. The raw nerve activity is generally rectified, integrated, and quantified using the integrated burst rate or area. We propose an alternative quantification involving spike detection using a two-stage stationary wavelet transform (SWT) de-noising method. The SWT coefficients are first separated into noise-related and burst-related coefficients on the basis of their local kurtosis. The noise-related coefficients are then used to establish a threshold to identify spikes within the bursts. This method demonstrated better detection performance than an unsupervised amplitude discriminator and similar wavelet-based methods when confronted with simulated data of varying burst rate and signal to noise ratio. Additional validation on data acquired during a graded head-up tilt protocol revealed a strong correlation between the mean spike rate and the mean integrate burst rate (r = 0.85) and burst area rate (r = 0.91). In conclusion, the kurtosis-based wavelet de-noising technique is a potentially useful method of studying sympathetic nerve activity in humans.

Keywords: Wavelet transform, Spike detection, Muscle sympathetic nerve activity, Higher order statistics, Humans

1. Introduction

Accurate assessment of autonomic function is important in the study and diagnosis of disorders such as essential hypertension (Wallin and Sundlof, 1979; Mark, 1996; Gudbjornsdottir et al., 1996), orthostatic intolerance (Furlan et al., 1998), and congestive heart failure (van de Borne et al., 1997). Autonomic sympathetic function can be assessed in humans by direct recordings of the muscle sympathetic nerve activity (MSNA) (Hagbarth and Vallbo, 1968).

The general appearance of the human MSNA has been described as heartbeat-synchronous discharges from a group of sympathetic neurons, separated by periods of neural silence (Wallin and Fagius, 1988) (e.g., see Fig. 2; Section 2.3). These bursts of activity are coupled to changes in the blood pressure and cardiac output through the baroreceptor reflex (Pagani et al., 1997; Furlan et al., 2000; Charkoudian et al., 2005). The most widely used MSNA processing method involves using an R–C circuit to rectifying and integrate the neurogram to achieve its envelope (Delius et al., 1972; Wallin and Sundlof, 1979), a signal known as the integrated-MSNA (Diedrich et al., 2003). At that point, bursts are identified and sympathetic activity can be quantified in terms of burst frequency (bursts/min), burst incidence (bursts/100 heart beats) or burst area rate (arbitrary units2/min) (Sundlof and Wallin, 1977; Sugiyama et al., 1996).

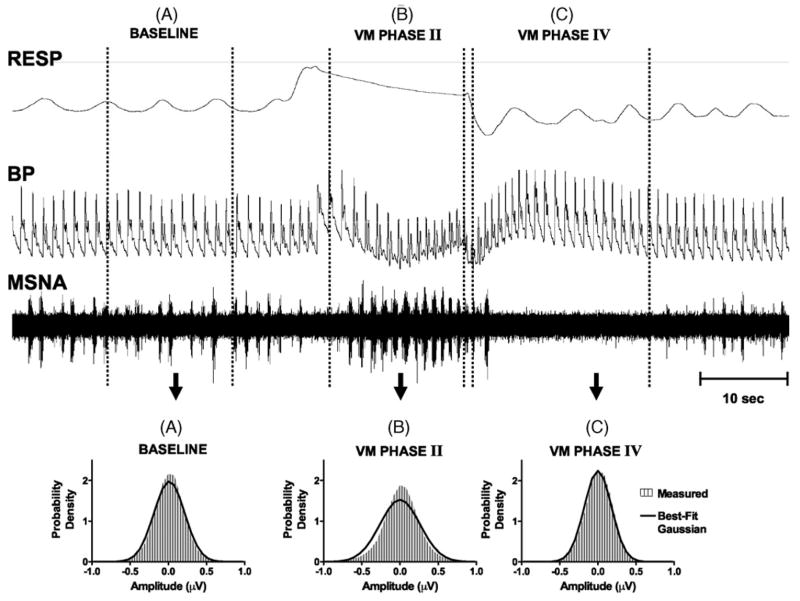
Fig. 2.

Fig. 2

Open in a new tab

Tracings of the respiration (RESP), blood pressure (BP), and raw muscle sympathetic nerve activity (MSNA) during Valsalva Maneuver. During baseline (period A), MSNA burst activity is at a basal rate, and the recorded amplitudes are close to Gaussian (lower left panel). During Phase II of the Valsalva Maneuver (B), BP drops rapidly causing a significant rise in the and MSNA burst rate. The MSNA amplitudes are no longer fit by a Gaussian (lower middle panel). In Phase IV of the Valsalva Maneuver (C), BP overshoots it baseline values and MSNA ceases. This is assumed to be neural noise and is well fit by a Gaussian distribution (lower right panel).

Quantification of the MSNA using bursts in the integrated neurogram has its limitations. For instance, none of the burst parameters are capable of conveying whether a large burst is generated by a few large amplitude sympathetic spikes (or artifacts) or many small amplitude spikes firing in rapid succession. Also, the amount of pass band noise integrated into each burst is dependent on the signal-to-noise ratio (SNR) of each recording, making it difficult to compare the arbitrary unit burst amplitudes and areas across subjects.

An alternative solution to the integrated MSNA quantification problem is to implement a spike detection algorithm in the raw neurogram which allows for the possibility of subsequent, automated sorting of spikes into classes derived from individual single unit neurons (Diedrich et al., 2003). Single-unit recordings have identified important differences in diseases such as congestive heart failure and hypertension which were not demonstrated in the multiunit burst rate (Macefield et al., 1999; Macefield and Wallin, 1999; Mary and Stoker, 2003). Since these single unit recordings are extremely difficult to achieve and sustain manually (Wallin, 2004), automated spike detection and classification methods will be useful in this area.

Automated wavelet-based methods have been successful in detecting and classifying neural spikes in typical colored Gaussian noise (Letelier and Weber, 2000; Nakatani et al., 2001; Oweiss and Anderson, 2002; Nenadic and Burdick, 2005). In particular, a wavelet-based spike detection method has been shown to outperform common, automated amplitude discriminators in the detection of human sympathetic spikes under varying signal to noise ratios (Diedrich et al., 2003). However, the parameters of this algorithm were optimized from recordings during a supine resting state, and its detection performance was not examined at higher or lower spike rates (Diedrich et al., 2003).

One major problem common to most spike detection techniques is the accurate estimation of noise level in the raw neurogram independent of the existing spike rate (Brychta et al., 2006). For example, in the raw MSNA neurogram, the shape of the amplitude distribution is nearly Gaussian during periods of neural silence (e.g., see Fig. 2; Section 2.3), but during a burst of neural activity, the presence of neural spikes changes the amplitude distribution significantly and most common noise estimators overestimate the noise level, leading to incorrect spike rate estimation.

To address this problem, we propose a novel two-stage wavelet-based spike detection approach that takes advantage of the bursting nature of the sympathetic nerve activity. This method uses the local kurtosis to classify wavelet coefficients as belonging to Gaussian pure-noise segments or non-Gaussian signal-plus-noise (burst) segments. The noise-related coefficients will then be used to establish a threshold which can subsequently be applied to the burst-related coefficients. The parameters of the two-stage wavelet method will be optimized using simulated MSNA burst data and validated against common integrate burst measures using recordings made during a head-up tilt protocol.

We plan to investigate the performance of the two-stage kurtosis spike detection method, several common wavelet-based spike detection schemes, and a more traditional amplitude discriminator using simulated sympathetic nerve signals with varying burst rate and SNR. We hypothesize that the two-stage kurtosis spike detection method will have a more robust performance than other commonly used spike detection schemes in terms of sensitivity and specificity across spike rate and noise levels.

2. Methods

2.1. Instrumentation and recording conditions

MSNA was recorded from the peroneal nerve (Vallbo et al., 1979). A unipolar tungsten electrode with an uninsulated tip, diameter 1–5 μm and shaft diameter 200 μm (Frederick Haer and Co., Bowdoinham, MA, USA), was inserted into the muscle nerve fascicles of the peroneal nerve at the fibular head for multi-unit recordings. Raw nerve activity was amplified with a total gain of 100,000, band pass filtered from 0.7 to 2 kHz (662C-3 Nerve Traffic Analysis System, University of Iowa, Iowa City, USA), and recorded. The filtered nerve signal was also placed through an R–C integrating circuit with a 0.1 s time constant and the output (integrated MSNA) was simultaneously recorded. Satisfactory recordings of muscle sympathetic nerve activity were defined by: (1) heart pulse synchronicity; (2) facilitation during Valsalva straining and suppression during the hypertensive overshoot after release; (3) increases in response to breath-holding; and (4) no change during tactile or auditory stimulation (Delius et al., 1972).

The continuous blood pressure (BP) waveform was measured by photoplethysmographic-based volume clamp method (Penaz, 1973) with a finger cuff on the middle finger of the non-dominant hand (Finapres, Ohmeda, Englewood, CO, USA). Respiration was measured using a pneumobelt (Pneumotrace II; UFI, Morro Bay, CA). All data were acquired at 5000 Hz, 14 bit resolution using the Windaq data acquisition system (DI-720, DATAQ Instruments, Akron, OH) and analyzed offline with custom software written in the PV Wave (Visual Numerics Inc., Houston, TX) and MATLAB (Mathworks; Natick, MA) environments.

2.2. Signal processing

2.2.1. Wavelet decomposition

The initial sympathetic spike detection technique proposed by Diedrich et al. (2003) used the discrete wavelet transform (DWT) to decompose the nerve signal into several frequency sub-bands of wavelet coefficients. However, the DWT lacks translation invariance, meaning that a completely different set of wavelet coefficients arises from DWT decomposition when the signal is shifted, or translated, in time (Liang and Parks, 1996). The absence of translation invariance can be detrimental in the de-noising (Silverman, 1999) and detection (Kim and Kim, 2003; Brychta et al., 2006) of transient neural spikes. Alternatively, the stationary wavelet transform (SWT) is translation invariant, and has been shown to improve sympathetic spike detection in mice (Brychta et al., 2006).

The SWT decomposition process (Mallat, 1991) is described by Eqs. (1) and (2). A signal, f, is projected onto a dyadically-spaced set of scales (spaced using a base of 2, i.e., scale = 2j), or levels (level j = log2(scale 2j)), using a set of level dependent quadrature mirror decomposition filters, hj and gj, that have respective band-pass and low-pass properties specific to each wavelet basis (Mallat, 1989). The broad scale, or approximation, coefficients, aj, are convolved separately with gj and hj. This process splits the aj frequency information roughly in half, partitioning it into a set of fine scale, or detail coefficients, dj+1, and a coarser set of approximation coefficients, aj+1. During the next level of processing, a zero is placed in between each consecutive value found in the gj and hj filters (i.e., up-sampling by two) to achieve the gj+1 and hj+1 filters. This procedure can be iteratively continued until the desired level of decomposition, j = J, is obtained. Note that the algorithm is initiated by setting a0 = f.

aj+1(k)=∑nhj(n−k)aj(k) (1)
dj+1(k)=∑ngj(n−k)aj(k) (2)

The aj coefficients can be reconstructed from aj+1 and dj+1 by convolving each with the respective reconstruction filter, hj(−n) or gj(−n), and summing (Eq. (3)). Note that each reconstruction filter is also level dependent and includes 2j − 1 zeros between each filter coefficients. This process can be iteratively continued until the original signal, f, is recovered.

aj(k)∑nhj(k−n)aj+1(n)+∑ngj(k−n)dj+1(n) (3)

2.2.2. Wavelet thresholding

Most wavelet-based spike detection algorithms include some modified form of a process known as wavelet de-noising (Donoho, 1995). In this process, a nerve signal with additive noise, f, is decomposed using the wavelet transform and a threshold is applied to each of the detail coefficient levels. All coefficients with an absolute value greater than the threshold are thought to be part of an action potential and those below the threshold are presumably derived from noise. The noise coefficients can be set to zero and a noise-free signal can then be reconstructed and used for AP detection (Diedrich et al., 2003).

Several standard thresholds have been derived for wavelet de-noising (Donoho, 1995; Johnstone and Silverman, 1997). In the case of correlated or colored noise, the standard deviation of the noise changes with each level and consequently requires a robust, level-dependent estimate, σj (Eq. (4)),

σj=median(∣dj−d¯j∣)0.6745 (4)

which is later used in the calculation of the standard colored noise threshold, TjS (Eq. (5)) (Johnstone and Silverman, 1997).

TjS=σj2loge(N) (5)

A modified form of Eq. (5) has been shown to yield better detection performance in human sympathetic nerve activity (Diedrich et al., 2003). We will refer to this as the modified colored noise threshold, TjM. It is displayed in Eq. (6)

TjM=0.8σj2loge(N) (6)

The performance of both the standard and modified colored noise thresholds will be assessed using simulation.

2.2.3. Wavelet basis and level selection

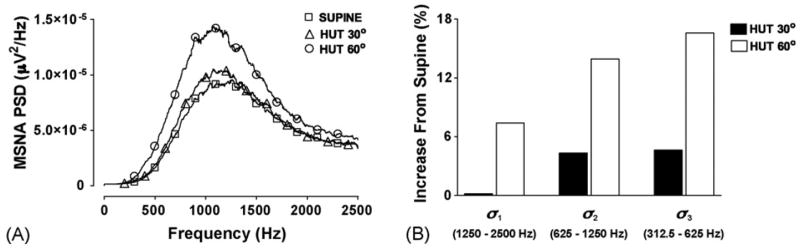
It has been observed that not all wavelet levels are necessary for spike detection and additional levels could actually hinder the performance of wavelet-based detectors (Kim and Kim, 2003). In the human MSNA, we have found that sympathetic activation during physiological interventions, such as a head-up tilt (HUT) protocol, causes increases in the MSNA power spectral density (PSD) between approximately 400 and 2500 Hz (Fig. 1A). This frequency range approximately corresponds to wavelet levels 1–3 for a signal sampled at 5 kHz. However, the wavelet coefficient standard deviation of levels 2 and 3 (σ2 and σ3) appear to have the most pronounced increases during HUT while σ1 does not appear to respond to mild sympathetic activation, for instance 30° HUT (Fig. 1B). We have therefore chosen only to use wavelet levels 2 and 3 while designing and testing the spike detection protocol. Symlet 7 was chosen as the wavelet basis because its morphology is similar to a sympathetic spike (Fig. 4D) (Diedrich et al., 2003).

Fig. 1.

Fig. 1

Open in a new tab

Power spectral density (PSD) (A) and percent increase in wavelet level standard deviations (σj) (B) of human muscle sympathetic nerve activity (MSNA) during different stages of a graded head-up tilt (HUT) protocol. Increasing the angle of tilt further activates the sympathetic nervous system, and increases the power in the frequency range between 400 and 2500 Hz. Wavelet levels 2 and 3 appear to have the most dynamic response to the sympathetic activation. The approximate frequency range of each wavelet level is also displayed.

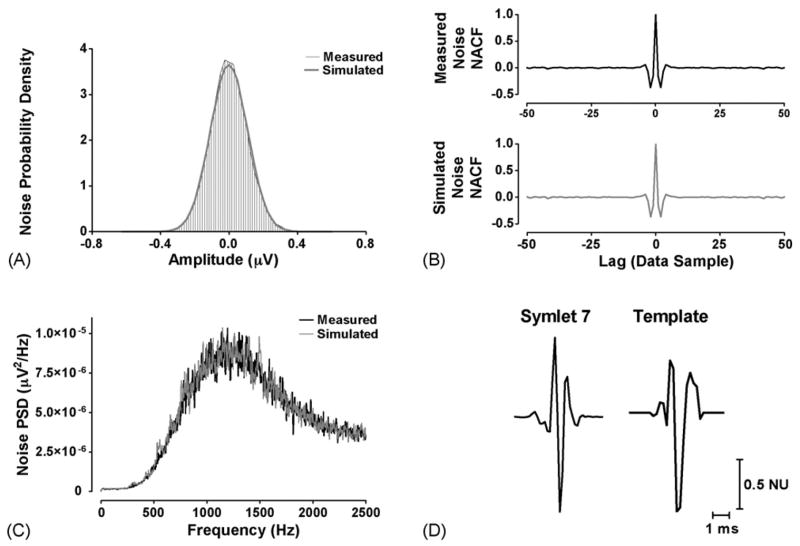
Fig. 4.

Fig. 4

Open in a new tab

Simulation elements. (A) Histograms of the neural noise recorded during Phase IV of the Valsalva Maneuver (measured, black) and random simulated noise after application of an AR filter (simulated, gray). Both demonstrate a normal probability density. (B) The normalized autocorrelation function (NACF) of the measured (top, black) and simulated noise (bottom, gray). (C) The power spectral density (PSD) of the measured (black) and simulated (gray) noise. (D) The Symlet 7 wavelet (left) and two representative template action potentials (right) displayed in normalized units (NU).

2.3. Two-stage kurtosis spike detection

Most standard wavelet threshold algorithms consider all of the coefficients while estimating the noise-threshold, i.e., those associated with both the signal and the noise (Donoho, 1995). However, the variance of the noise affecting the MSNA varies with signal quality and is difficult to estimate using the signal itself or its wavelet coefficients when spike rates vary (Brychta et al., 2006). As an alternative to the traditional wavelet techniques, we propose a method that would initially separate the wavelet coefficients purely derived from the noise from those which contain signal-plus-noise prior to thresholding (Nenadic and Burdick, 2005). In the MSNA signal, this requires identification of the wavelet coefficients related to the neural bursts (signal-plus-noise) and those related to the areas between bursts (noise only).

The Valsalva Maneuver (VM) provides a compact example of the changes that occur in the MSNA signal properties during dynamic fluctuations of mean blood pressure (Fig. 2). The characteristics of the noise can be identified during Phase IV of the VM, when mean blood pressure “overshoots” basal levels and MSNA is suppressed via baroreceptor feedback (Fig. 2C) (Mosqueda-Garcia, 1995). In general, the amplitude distribution of the noise-related regions of the MSNA are Gaussian, a property which is preserved during wavelet transformation (Silverman, 1999). During periods of moderate (Fig. 2A, baseline) and high (Fig. 2B, VM Phase II) burst rates, the tails of the distribution become progressively heavier and the central portion becomes more peaked, meaning a Gaussian fit is no longer accurate.

Local deviations from Gaussinity have been shown to be detectable using higher order statistics (moments and cumulants higher than order two) (Nikias and Petropulu, 1993; Gerek and Ece, 2006). In particular, the kurtosis of wavelet coefficients has been employed to detect non-Gaussian perturbation in cosmologic data (Vielva et al., 2004; Jin et al., 2005). Kurtosis is a measure of the relative peakedness of a distribution and is defined as its fourth central moment normalized by the square of its variance. A distribution will have a high kurtosis if there is a concentration of values near its mean (peaked distribution) or in its tails (heavy tailed distribution) (Moors, 1988). The kurtosis may be useful in detecting wavelet coefficients related to neural bursts. However, to our knowledge, this technique has not been applied to neural signals.

In the next section, we describe a method to separate pure noise wavelet coefficients from those associated with MSNA bursts using the local kurtosis of the wavelet coefficients. The noise-related coefficients are then used to estimate a noise threshold which is in-turn applied to the burst related coefficients for the detection of action potentials. We have termed this algorithm the two-stage kurtosis de-noising method.

2.3.1. Local kurtosis estimate

The local (or sliding) kurtosis computed over Nk detail coefficients of level j, expressed as Kj, was estimated using the following equation:

Kj(k)=(1/NK)∑n=0NK−1(dj(n−k)−mj(k))4((1/NK)∑n=0NK−1(dj(n−k)−mj(k))2)2 (7)

where mj is an estimate of the local mean of Nk level j coefficients, calculated using:

mj(k)=1NK∑n=0NK−1dj(n−k) (8)

The kurtosis of a Gaussian sequence is always 3, regardless of the mean or variance of the distribution. We expect the kurtosis of the burst related coefficients to be greater than 3 due to the presence of action potentials with large positive and negative values, resulting in locally heavy tails.

Once the kurtosis sequence was computed, wavelet de-noising took place in two stages. In stage 1, a kurtosis threshold, TK, was established. All kurtosis values below TK were classified as coming from noise while kurtosis values above TK were assumed to be burst-related. During stage 2, the noise coefficients were used to estimate the noise standard deviation, σj, as shown in Eq. (4). All detail coefficients located within an identified burst segment and whose absolute value was greater than 3.5σj were retained, while all other coefficients were set to zero. The de-noised signal was then reconstructed and action potentials were detected using a simple peak detection scheme that locates maxima above 99% of the signal energy, as described previously (Diedrich et al., 2003). An example of the two-stage kurtosis de-noising scheme applied to a representative MSNA recording is displayed in Fig. 3. The optimal values for NK and TK were determined through simulation, as described below in Section 2.3.1.

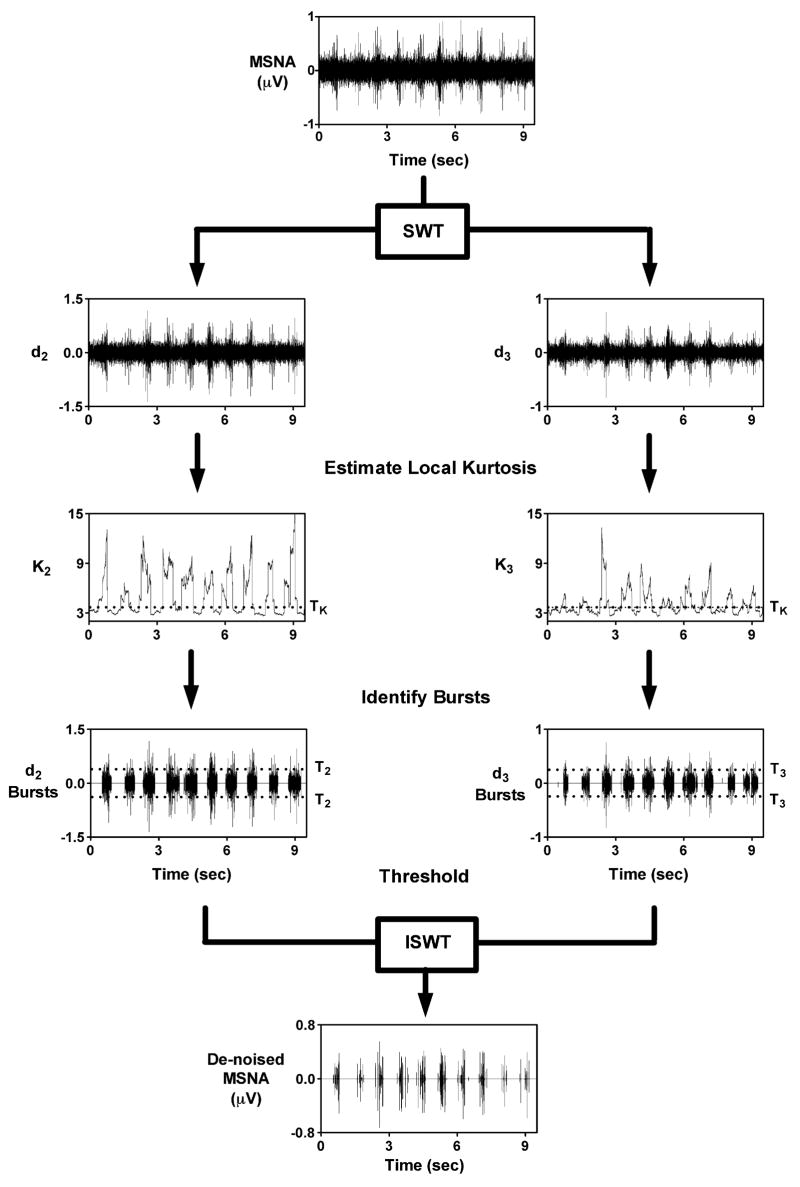
Fig. 3.

Fig. 3

Open in a new tab

Two-stage kurtosis de-noising example. The MSNA is decomposed using the SWT. A moving kurtosis estimate is made of the detail coefficients (d2 and d3). The coefficients are grouped into noise-related (K2 and K3 < TK) and burst-related (K2 and K3 > TK). The noise-related coefficients are used to estimate noise level (σ2 and σ3) and burst-related coefficients undergo thresholding. The de-noised signal is reconstructed with the ISWT.

2.4. Simulated data

Simulated signals were constructed with templates extracted from recordings with sufficiently high signal to noise ratio in eight healthy subjects during periods of sympathetic activation (head-up tilt) (Fig. 4D). Noise was extracted from each recording during Phase IV of the Valsalva maneuver, as shown in Fig. 2. Since the length of the noise was generally too short for an appropriate simulation (<15 s), a 50 order autoregressive (AR) model was created using the Burg method (Shiavi, 1999) and subsequently applied to a sequence of Gaussian random numbers 60 s in length. Prior to AR filtering the Gaussian random numbers have a white noise power spectral density (PSD) and normalized autocorrelation function (NACF). But after filtering, the NACF and PSD of the simulated noise were shown to closely approximate those of the recorded noise (Fig. 4B and C). The overall shape of the Gaussian sequence probability density distribution is not affected by the AR filter (Fig. 4A).

The templates were then randomly inserted into neural noise in burst fashion. The burst position, burst duration, and spike placement within each burst were all randomly assigned according to a Poisson distribution. The average burst duration and spike rate within each burst were fixed at 0.8 s and 60 spikes/s, respectively. Each simulation was assigned either a low (5 burst/min), moderate (25 bursts/min), or high (50 bursts/min) mean burst rate. The signal to noise ratio (SNR) of the simulations was altered from 6 (high signal quality) to 1 (poor signal quality). The SNR was defined as the ratio between the absolute peak amplitude of the action potential and the standard deviation of the noise, as defined elsewhere (Diedrich et al., 2003; Nenadic and Burdick, 2005).

2.4.1. Two-stage kurtosis de-noising method optimization

The parameters of the kurtosis-based wavelet de-noising were optimized using the simulated data described above. The value for the kurtosis threshold, TK, was varied from 2.8 to 5 and the number of samples in each kurtosis calculation, NK, was varied from 250 to 4000 samples. The optimum TK and NK values for each burst rate and each SNR were defined as those which resulted in the maximum difference between the average percentage of correctly identified burst area and the percentage of the remaining area falsely identified as burst related. The optimum TK and NK values were averaged across all subjects, burst rates, and SNRs. The average TK and NK optimums were then used in the tests of spike detection performance and the validation discussed below.

2.4.2. Evaluation of detection performance

The simulated signals were also used to test the performance of several wavelet-based algorithms and an unsupervised amplitude discriminator. The amplitude discriminator detected all peaks with an absolute value greater than 3.5 times the standard deviation of the signal, as discussed elsewhere (Pouzat et al., 2002). The three wavelet algorithms each used different de-noising methods which included the standard wavelet threshold (SWTS, Eq. (5)), the modified threshold (SWTM, Eq. (6)), and the two-stage kurtosis method (SWTK). Both the amplitude discriminator and wavelet detection methods used a 3 ms time-window, which was observed to be the maximum duration of a human sympathetic spike. The detection performance evaluation was repeated 12 separate times for each of the 8 subjects. Each trial contained a different randomly distributed burst pattern noise sequence, yielding 96 trials for each SNR and mean burst rate. The performance of each method was quantified using the percent of correctly detected action potentials (PCD, Eq. (9)) and the percent of false alarms (PFA, Eq. (10)).

PCD=NCDNAP×100 (9)
PFA=NFANCD×100 (10)

NCD is the number of correctly detected APs, NAP the number of APs inserted into the simulation, and NFA is the number of false alarms.

2.5. Validation using graded head-up tilt protocol

Seven healthy subjects (six males and one female, age 23–47) were recruited from the Vanderbilt University General Clinical Research Center volunteer database. All subjects underwent extensive physical examination and abstained from all drugs for at least 72 h prior to the study. The subjects were secured to a tilt table with straps and instructed to remain relaxed and quiet throughout all studies. After 15 min of supine rest the subjects were tilted by 15° increments every 5 min until an angle of 60° was reached. The parameters of the integrated MSNA bursts and the MSNA spike rates were later computed offline and compared using linear regression. The Pearson correlation coefficient (r) was used to quantify the goodness of fit. All studies were conducted at Vanderbilt University General Clinical Research Center and all procedures were approved by the local institutional review board.

3. Results

3.1. Two-stage kurtosis de-noising method optimization

The results of the search for the optimal number of samples in each kurtosis calculation, NK, and the optimal kurtosis threshold, TK, were found to be NK = 961 samples and TK = 3.7. These values were used in the evaluation of the detection performance and the validation during baroreflex testing.

3.2. Evaluation of detection performance

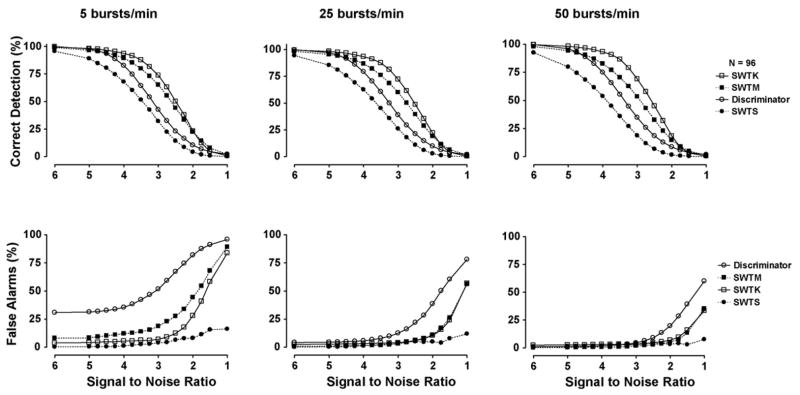
The detection performance of each of the four methods is displayed in Fig. 5. While the standard wavelet threshold (SWTS) has the lowest percentage of false alarms (PFA) during all simulations, its percent of correctly detected action potentials (PCD) is also lowest. The modification to the standard threshold (SWTM), suggested by Diedrich et al., results in a higher PCD and the PFA remains low (<10%) for SNR > 2 during moderate (25 bursts/min) and high (50 bursts/min) burst rates. However, during low burst rates (5 bursts/min), the PFA is greater than 15% at a SNR of 3.25 and steadily increases as SNR drops. The two-stage kurtosis de-noising (SWTK) demonstrates the highest PCD for SNR > 2 during all burst rates and its PFA is similar to that of the modified wavelet threshold at burst rates of 25 and 50 bursts/min and lower during the 5 burst/min simulations. The amplitude discriminator has a PFA that is similar to or greater than all other detection methods during all simulations and its PCD is lower than that of the modified and kurtosis-based wavelet thresholding methods.

Fig. 5.

Fig. 5

Open in a new tab

Mean results for simulations with varied noise levels and mean burst rates. The simulations tested the performance of an unsupervised amplitude discriminator (discriminator), SWT decomposition with standard (SWTS) and modified (SWTM) colored noise thresholds, SWT decomposition with two-stage kurtosis threshold (SWTK). Each point on each curve represents the mean result of 96 simulations.

3.3. Validation using graded head-up tilt protocol

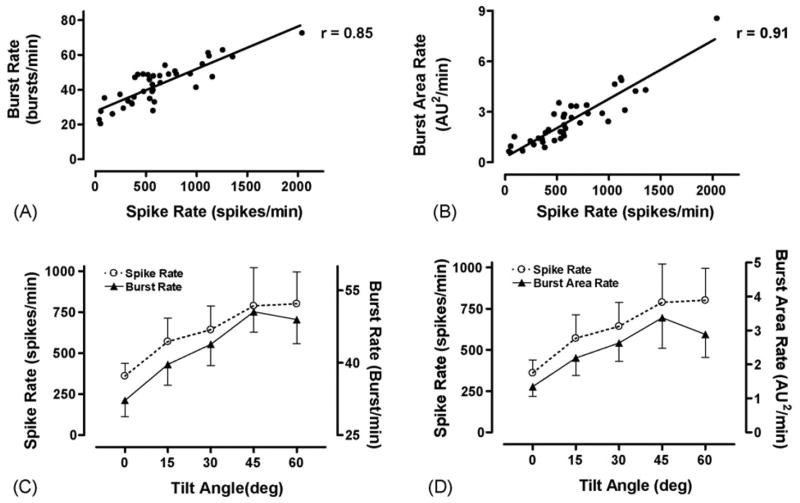
Fig. 6 demonstrates that a good correlation exists between the spike rates detected using the two-phase kurtosis method and the commonly used integrated burst rate (Fig. 6A, r = 0.85) and burst area rate (Fig. 6B, r = 0.91) parameters. The spike rate, burst rate (Fig. 6C), and burst area rate (Fig. 6D) also demonstrate similar increasing trends as the head-up tilt angle is increased and the sympathetic nervous system is activated.

Fig. 6.

Fig. 6

Open in a new tab

Comparison of spike detection and burst parameters during a head-up tilt (HUT) protocol. The mean spike rate shows a good correlation to the mean burst rate (A) and burst area rate (B). The mean spike rate demonstrates the same general increasing pattern as the mean burst rate (C) and mean burst area rate (D) as tilt angle is increased.

4. Discussion

We have demonstrated a novel spike detection scheme for human muscle sympathetic nerve activity that uses the local kurtosis of the stationary wavelet transform coefficients to identify pure noise coefficients, which are used to estimate a noise threshold, and signal-plus-noise (burst-related) coefficients, which undergo thresholding. This method was shown to outperform a similar modified-wavelet technique specifically designed for the MSNA, which was not previously evaluated at varying burst rates (Diedrich et al., 2003). It was also shown to have better overall detection performance than an unsupervised amplitude discriminator and a higher percent of correctly detected action potentials than standard wavelet thresholding. The mean spike rates detected using the two-stage kurtosis de-noising method during a graded head-up tilt protocol were also shown to be highly correlated to commonly used integrated burst rate (r = 0.85) and burst area rate (r = 0.91) parameters. These correlations were improved from than those previously reported with the modified wavelet threshold (r = 0.79 and r = 0.52, respectively) (Diedrich et al., 2003). The spike rates, burst rates, and burst area rates also displayed similar increasing responses to increased tilt angle.

4.1. Limitations

In this study, we have focused our optimization and evaluations on recordings of the human muscle sympathetic nerve activity. This detection technique may be applicable to other neural or bioelectric signals with bursting characteristics, but this has not yet been investigated. In the case of the MSNA, the kurtosis-based wavelet de-noising method was found to possess reasonably accurate detection performance for signal-to-noise ratios greater than three independent of the burst rate, with over 70% of the action potentials correctly identified and less than 10% false alarms. However, detections made using this method, or any other method tested here, on signals with SNR < 3 may not be reliable. Also, the kurtosis-based wavelet de-nosing method may not detect levels of tonic activity that occurs between bursts. But, the initial separation of noise segments using kurtosis may be useful in a hypothesis testing framework, such as the general hypothesis based wavelet spike detection method suggested by Nenadic and Burdick. (Nenadic and Burdick, 2005).

4.2. Conclusions

Sympathetic spike detection holds several potential advantages over traditional MSNA burst detection. For instance, sympathetic spikes detection allows for the possibility of subsequent, automated single unit analysis which has previously revealed important differences in human pathologies such as congestive heart failure and hypertension (Macefield et al., 1999; Macefield and Wallin, 1999; Mary and Stoker, 2003). Automated detection and classification of sympathetic spikes also allows for the study of interaction between various single units. Additionally, temporal and spectral analysis using spike-based quantification, as opposed to the standard burst methods, yields parameters that are more easily compared between subjects (Brychta et al., 2002). In conclusion, the kurtosis-based wavelet de-noising technique is a potentially useful method of studying sympathetic nerve activity in humans.

Acknowledgments

This work was supported in part by National Institutes of Health Grants RR00095, and 1PO1 HL56693. We thank Sachin Y. Paranjape, Indu Taneja, and Bonnie Black for the support of this study.

References

  1. Brychta RJ, Charoensuk W, Bernardi L, Furlan R, Shiavi R, Diedrich A. Spectral analysis of multiunit action potential trains of muscle sympathetic nerve activity in humans. Comput Cardiol. 2002;29:457–60. [Google Scholar]
  2. Brychta RJ, Tuntrakool S, Appalsamy M, Keller NR, Finney C, Robertson D, et al. Spike detection in mouse renal sympathetic nerve activity using the stationary wavelet transform with automated noise level estimation. IEEE Trans Biomed Eng. 2006 Dec54 [Google Scholar]
  3. Charkoudian N, Joyner MJ, Johnson CP, Eisenach JH, Dietz NM, Wallin BG. Balance between cardiac output and sympathetic nerve activity in resting humans: role in arterial pressure regulation. J Physiol. 2005;568:315–21. doi: 10.1113/jphysiol.2005.090076. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Delius W, Hagbarth KE, Hongell A, Wallin BG. General characteristics of sympathetic activity in human muscle nerves. Acta Physiol Scand. 1972;84:65–81. doi: 10.1111/j.1748-1716.1972.tb05158.x. [DOI] [PubMed] [Google Scholar]
  5. Diedrich A, Charoensuk W, Brychta RJ, Ertl AC, Shiavi R. Analysis of raw microneurographic recordings based on wavelet de-noising technique and classification algorithm: wavelet analysis in microneurography. IEEE Trans Biomed Eng. 2003;50:41–50. doi: 10.1109/TBME.2002.807323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Donoho DL. De-noising by soft-thresholding. IEEE Trans Inform Theory. 1995;41:613–24. [Google Scholar]
  7. Furlan R, Jacob G, Snell M, Robertson D, Porta A, Harris P, et al. Chronic orthostatic intolerance: a disorder with discordant cardiac and vascular sympathetic control. Circulation. 1998;98:2154–9. doi: 10.1161/01.cir.98.20.2154. [DOI] [PubMed] [Google Scholar]
  8. Furlan R, Porta A, Costa F, Tank J, Baker L, Schiavi R, et al. Oscillatory patterns in sympathetic neural discharge and cardiovascular variables during orthostatic stimulus. Circulation. 2000;101:886–92. doi: 10.1161/01.cir.101.8.886. [DOI] [PubMed] [Google Scholar]
  9. Gerek ON, Ece DG. Power-quality event analysis using higher order cumulants and quadratic classifiers. IEEE Trans Power Deliv. 2006;21:883–9. [Google Scholar]
  10. Gudbjornsdottir S, Lonnroth P, Sverrisdottir YB, Wallin BG, Elam M. Sympathetic nerve activity and insulin in obese normotensive and hypertensive men. Hypertension. 1996;27:276–80. doi: 10.1161/01.hyp.27.2.276. [DOI] [PubMed] [Google Scholar]
  11. Hagbarth KE, Vallbo AB. Pulse and respiratory grouping of sympathetic impulses in human muscle-nerves. Acta Physiol Scand. 1968;74:96–108. doi: 10.1111/j.1748-1716.1968.tb04218.x. [DOI] [PubMed] [Google Scholar]
  12. Jin J, Starck JL, Donoho DL, Aghanim N, Forni O. Cosmological non-Gaussian signature detection: comparing performance of statistical tests. EURASIP J Appl Signal Process. 2005;15:2470–85. [Google Scholar]
  13. Johnstone I, Silverman B. Wavelet threshold estimators for data with correlated noise. J R Stat Soc. 1997;59:319–51. [Google Scholar]
  14. Kim KH, Kim SJ. A wavelet-based method for action potential detection from extracellular neural signal recording with low signal-to-noise ratio. IEEE Trans Biomed Eng. 2003;50:999–1011. doi: 10.1109/TBME.2003.814523. [DOI] [PubMed] [Google Scholar]
  15. Letelier JC, Weber PP. Spike sorting based on discrete wavelet transform coefficients. J Neurosci Methods. 2000;101:93–106. doi: 10.1016/s0165-0270(00)00250-8. [DOI] [PubMed] [Google Scholar]
  16. Liang J, Parks TW. A translation-invariant wavelet representation algorithm with applications. IEEE T Signal Process. 1996;44:225–32. [Google Scholar]
  17. Macefield VG, Rundqvist B, Sverrisdottir YB, Wallin BG, Elam M. Firing properties of single muscle vasoconstrictor neurons in the sympathoexcitation associated with congestive heart failure. Circulation. 1999;100:1708–13. doi: 10.1161/01.cir.100.16.1708. [DOI] [PubMed] [Google Scholar]
  18. Macefield VG, Wallin BG. Firing properties of single vasoconstrictor neurones in human subjects with high levels of muscle sympathetic activity. J Physiol (Lond) 1999;516(Pt 1):293–301. doi: 10.1111/j.1469-7793.1999.293aa.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mallat S. Zero-crossings of a wavelet transform. IEEE Trans Inform Theory. 1991;37:1019–33. [Google Scholar]
  20. Mallat SG. A theory for multiresolution signal decomposition—the wavelet representation. IEEE T Pattern Anal. 1989;11:674–93. [Google Scholar]
  21. Mark AL. The sympathetic nervous system in hypertension: a potential long-term regulator of arterial pressure. J Hypertens Suppl. 1996;14:S159–65. [PubMed] [Google Scholar]
  22. Mary DA, Stoker JB. The activity of single vasoconstrictor nerve units in hypertension. Acta Physiol Scand. 2003;177:367–76. doi: 10.1046/j.1365-201X.2003.01082.x. [DOI] [PubMed] [Google Scholar]
  23. Moors JJA. A quantile alternative for kurtosis. Statistician. 1988;37:25–32. [Google Scholar]
  24. Mosqueda-Garcia R. Evaluation of autonomic failure. In: Burnstock G, editor. The autonomic nervous system. Luxembourg: Harwood Academic Press; 1995. pp. 25–59. [Google Scholar]
  25. Nakatani H, Watanabe T, Hoshimiya N. Detection of nerve action potentials under low signal-to-noise ratio condition. IEEE Trans Biomed Eng. 2001;48:845–9. doi: 10.1109/10.936360. [DOI] [PubMed] [Google Scholar]
  26. Nenadic Z, Burdick JW. Spike detection using the continuous wavelet transform. IEEE Trans Biomed Eng. 2005;52:74–87. doi: 10.1109/TBME.2004.839800. [DOI] [PubMed] [Google Scholar]
  27. Nikias CL, Petropulu AP. Higher-order spectra analysis: a nonlinear signal processing framework. Englewood Cliffs, NJ: Prentice Hall; 1993. [Google Scholar]
  28. Oweiss KG, Anderson DJ. Spike sorting: a novel shift and amplitude invariant technique. Neurocomput Neurocomput. 2002;44–46:1133–9. [Google Scholar]
  29. Pagani M, Montano N, Porta A, Malliani A, Abboud FM, Birkett C, et al. Relationship between spectral components of cardiovascular variabilities and direct measures of muscle sympathetic nerve activity in humans. Circulation. 1997;95:1441–8. doi: 10.1161/01.cir.95.6.1441. [DOI] [PubMed] [Google Scholar]
  30. Penaz J. Photoelectric measurement of blood pressure, volume and flow in the finger. Digest of the 10th international conference on medical and biological engineering; p. 1973.p. 104. [Google Scholar]
  31. Pouzat C, Mazor O, Laurent G. Using noise signature to optimize spike-sorting and to assess neuronal classification quality. J Neurosci Meth. 2002;122:43–57. doi: 10.1016/s0165-0270(02)00276-5. [DOI] [PubMed] [Google Scholar]
  32. Shiavi RG. Introduction to applied statistical signal analysis. 2. San Diego: Academic Press; 1999. [Google Scholar]
  33. Silverman B. Wavelets in statistics: beyond the standard assumptions. Philos T R Soc A. 1999;357:2459–73. [Google Scholar]
  34. Sugiyama Y, Matsukawa T, Suzuki H, Iwase S, Shamsuzzaman AS, Mano T. A new method of quantifying human muscle sympathetic nerve activity for frequency domain analysis. Electroencephalogr Clin Neurophysiol. 1996;101:121–8. doi: 10.1016/0924-980x(95)00219-b. [DOI] [PubMed] [Google Scholar]
  35. Sundlof G, Wallin BG. The variability of muscle nerve sympathetic activity in resting recumbent man. J Physiol (Lond) 1977;272:383–97. doi: 10.1113/jphysiol.1977.sp012050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Vallbo AB, Hagbarth KE, Torebjork HE, Wallin BG. Somatosensory, proprioceptive, and sympathetic activity in human peripheral nerves. Physiol Rev. 1979;59:919–57. doi: 10.1152/physrev.1979.59.4.919. [DOI] [PubMed] [Google Scholar]
  37. van de Borne P, Montano N, Pagani M, Oren R, Somers VK. Absence of low-frequency variability of sympathetic nerve activity in severe heart failure. Circulation. 1997;95:1449–54. doi: 10.1161/01.cir.95.6.1449. [DOI] [PubMed] [Google Scholar]
  38. Vielva P, Martinez-Gonzalez E, Barreiro RB, Sanz JL, Cayon L. Detection of non-Gaussinity in the Wilkinson Microwave Anisotopy Probe first-year data using spherical wavelets. Astrophys J. 2004;609:22–34. [Google Scholar]
  39. Wallin BG. Sympathetic microneurography. In: Robertson D, editor. Primer on the autonomic nervous system. Oxford, UK: Elsevier; 2004. pp. 224–7. [Google Scholar]
  40. Wallin BG, Fagius J. Peripheral sympathetic neural activity in conscious humans. Annu Rev Physiol. 1988;50:565–76. doi: 10.1146/annurev.ph.50.030188.003025. [DOI] [PubMed] [Google Scholar]
  41. Wallin BG, Sundlof G. A quantitative study of muscle nerve sympathetic activity in resting normotensive and hypertensive subjects. Hypertension. 1979;1:67–77. doi: 10.1161/01.hyp.1.2.67. [DOI] [PubMed] [Google Scholar]

RESOURCES