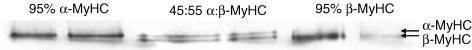Sarcomere length dependence of rat skinned cardiac myocyte mechanical properties: dependence on myosin heavy chain

Abstract

The effects of sarcomere length (SL) on sarcomeric loaded shortening velocity, power output and rates of force development were examined in rat skinned cardiac myocytes that contained either α-myosin heavy chain (α-MyHC) or β-MyHC at 12 ± 1°C. When SL was decreased from 2.3 μm to 2.0 μm submaximal isometric force decreased ∼40% in both α-MyHC and β-MyHC myocytes while peak absolute power output decreased 55% in α-MyHC myocytes and 70% in β-MyHC myocytes. After normalization for the fall in force, peak power output decreased about twice as much in β-MyHC as in α-MyHC myocytes (41%versus 20%). To determine whether the fall in normalized power was due to the lower force levels, [Ca²⁺] was increased at short SL to match force at long SL. Surprisingly, this led to a 32% greater peak normalized power output at short SL compared to long SL in α-MyHC myocytes, whereas in β-MyHC myocytes peak normalized power output remained depressed at short SL. The role that interfilament spacing plays in determining SL dependence of power was tested by myocyte compression at short SL. Addition of 2% dextran at short SL decreased myocyte width and increased force to levels obtained at long SL, and increased peak normalized power output to values greater than at long SL in both α-MyHC and β-MyHC myocytes. The rate constant of force development (k_tr) was also measured and was not different between long and short SL at the same [Ca²⁺] in α-MyHC myocytes but was greater at short SL in β-MyHC myocytes. At short SL with matched force by either dextran or [Ca²⁺], k_tr was greater than at long SL in both α-MyHC and β-MyHC myocytes. Overall, these results are consistent with the idea that an intrinsic length component increases loaded crossbridge cycling rates at short SL and β-MyHC myocytes exhibit a greater sarcomere length dependence of power output.

Increased end-diastolic volume has been shown to increase stroke volume in isolated heart preparations (Patterson et al. 1914) and in intact animals (Braunwald et al. 1960), a relationship commonly referred to as the Frank–Starling relationship. The underlying cellular mechanism of this relationship is thought to involve, at least in part, an increase in the tension generating capacity of individual myocytes with increased sarcomere length (SL) in accordance with the length–tension relationship of striated muscle (Sonnenblick, 1962; Gordon et al. 1966; Fabiato & Fabiato, 1978). This is especially steep in cardiac muscle at submaximal Ca²⁺ activations (Kentish et al. 1986), which myocytes are thought to encounter in vivo. During ejection, however, the ventricles are contracting against an afterload and are therefore undergoing loaded shortening (i.e. performing work). Despite the physiological and pathophysiological importance of the Frank–Starling relationship, few experiments have attempted to determine the effects of SL on loaded shortening in cardiac myocytes. We tested the hypothesis that cardiac myocyte power output is tightly regulated by initial SL, which was examined by measuring load dependence of shortening velocity and power output at two initial sarcomere lengths (2.3 μm and 2.0 μm).

Numerous studies suggest a primary cause of length dependence of myocardial function arises from a change in myofilament Ca²⁺ sensitivity of force (Hibberd & Jewell, 1982; Allen & Kentish, 1985), brought about, in part, by a change in interfilament lattice spacing (for review see Fuchs & Martyn, 2005). As a myocyte is shortened, the lateral spacing between the thick and thin filaments is increased (Rome, 1967; Irving et al. 2000; Pearson et al. 2004; Yagi et al. 2004), which likely decreases the probability of myosin binding to actin and yields fewer force-generating crossbridges that activate the thin filament. This study additionally tested the hypothesis that SL dependence of power output results from changes in thin filament activation levels and/or lattice spacing. We measured loaded shortening velocity and power output at short SL at the same force (by addition of activating Ca²⁺) or the same force and myocyte width (by addition of 2% dextran) to those at long SL.

Myosin heavy chain (MyHC) isoform content also has been shown to be a key regulator of loaded shortening and power output (Herron et al. 2001; Korte et al. 2005). No studies, however, have addressed how MyHC affects SL dependence of power output in spite of the observation that several disease states in rodents and humans have been shown to up-regulate β-MyHC and down-regulate α-MyHC (Dillman, 1980; Miyata et al. 2000). Increased β-MyHC has negative consequences for power (Herron & McDonald, 2002; Korte et al. 2005) but seems to increase the economy of contraction (Rundell et al. 2005). Additionally, it has been shown that heart rate is inversely related to β-MyHC content (Hamilton & Ianuzzo, 1991). Since a slower heart rate allows more filling time it may be that ventricles containing β-MyHC rely more on SL changes to modulate stroke volume than do ventricles with α-MyHC. This is consistent with the finding that rat left ventricles which contained > 70%β-MyHC exhibited steeper ventricular function curves than left ventricles which contained predominantly α-MyHC (Fitzsimons et al. 1999). Therefore, we also tested the hypothesis that β-MyHC myocytes have increased SL dependence of power output compared to α-MyHC myocytes.

Last, we examined whether there are inherent differences between α-MyHC and β-MyHC myocytes in the sarcomere length dependence of the rates of force development. These experiments were designed as a means to further investigate potential myofibrillar mechanisms that may underlie the Frank–Starling relationship and the variations in this relationship between α-MyHC and β-MyHC hearts.

Methods

Experimental animals

Male Sprague–Dawley rats (6 weeks old) were obtained from Harlan (Madison, WI, USA), housed in groups of two or three and provided access to food and water ad libitum. Rats were made hypothyroid by adding 6-propylthiouracil (PTU, 0.8 mg ml^–1) to the drinking water. PTU treatment shifted cardiac MyHC isoform content from ∼100%α-MyHC to ∼100%β-MyHC over a 3 week period. Thyroidectomy, PTU (intraperitoneally or orally) administration, or the combination of thyroidectomy and PTU have been shown to alter MyHC isoform expression with no detected alteration in the expression of other key myofilament proteins (Fitzsimons et al. 1998; Metzger et al. 1999; Herron et al. 2001), although not all sarcomeric proteins have been directly examined. All procedures involving animal use were performed according to the Animal Care and Use Committee of the University of Missouri.

Solutions

The compositions of relaxing and activating solutions were as follows (in mmol l^–1, obtained from Sigma at highest possible purity): free Mg²⁺ 1, EGTA 7, MgATP 4, imidazole 20, and creatine phosphate 14.5 (pH 7.0); specific [Ca²⁺] between 10^–4.5 (maximal Ca²⁺ activating solution) and 10^–9 (relaxing solution); and sufficient KCl to adjust ionic strength to 180 mmol l^–1. Relaxing solution also contained 2 mm Pefabloc (Roche) and 0.25 mm leupeptin (Sigma) to inhibit proteases and preserve the integrity of the myocytes.

Myocardial preparations

Skinned cardiac myocytes were obtained by mechanical disruption of hearts from Sprague–Dawley rats as previously described (McDonald, 2000a). Briefly, rats were anaesthetized by inhalation of isoflurane (20% v/v in olive oil), and their hearts were excised and rapidly placed in ice cold relaxing solution. The left ventricle was separated from the right ventricle and dissected from the atria, cut into 2–3 mm pieces and further disrupted for 5 s in a Waring blender. The resulting suspension of cells was centrifuged for 105 s at 165 g, after which the supernatant fluid was discarded. The myocytes were skinned by suspending the cell pellet for 5 min in 0.3% ultrapure Triton X-100 (Pierce, Biotechnologies Inc. Rockford, IL, USA) in cold relaxing solution. The skinned cells were washed twice with cold relaxing solution, suspended in 10 ml of relaxing solution and kept on ice. One myocyte per heart was used.

Experimental apparatus

The experimental apparatus for physiological measurements of myocyte preparations was similar to one previously described in detail (Moss, 1979) and modified specifically for cardiac myocyte preparations (McDonald, 2000a). Briefly, a myocyte was attached between a force transducer and high speed motor by gently placing the ends of the myocyte into stainless steel troughs (25 gauge). The ends of the myocyte were secured by overlaying a 0.5 mm long piece of 3–0 monofilament nylon suture (Ethicon, Inc., Somerville, NJ, USA) onto each end of the myocyte, and then tying the suture into the troughs with two loops of 10–0 monofilament suture (Ethicon, Inc.). The attachment procedure was performed under a stereomicroscope (∼100× magnification) using very fine tipped forceps.

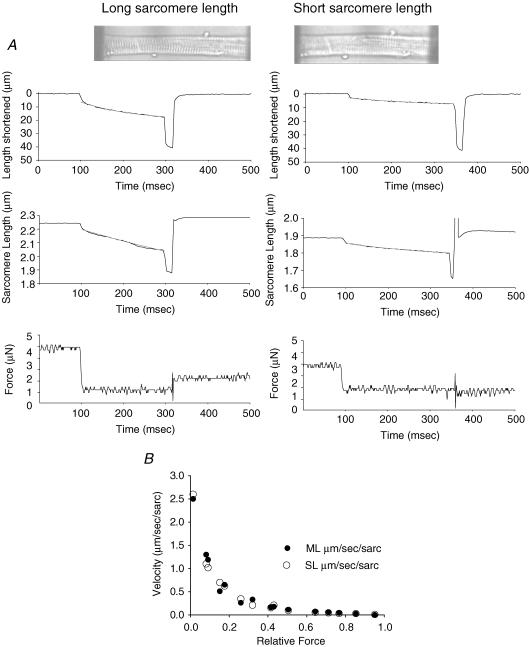
Prior to mechanical measurements the experimental apparatus was mounted on the stage of an inverted microscope (model IX-70, Olympus Instrument Co., Japan), which rested on a pneumatic antivibration table with a cut-off frequency of ∼1 Hz. Force measurements were made using a capacitance-gauge transducer (Model 403, sensitivity of 20 mV mg^–1 plus a × 10 amplifier and resonant frequency of 600 Hz; Aurora Scientific, Inc., Aurora, ON, Canada). Length changes during mechanical measurements were introduced at one end of the preparation using a DC torque motor (model 308, Aurora Scientific, Inc.) driven by voltage commands from a personal computer via a 12-bit D/A converter (AT-MIO-16E-1, National Instruments Corp., Austin, TX, USA). Force and length signals were digitized at 1 kHz using a 12 bit A/D converter and each was displayed and stored on a personal computer using custom software based on LabView for Windows (National Instruments Corp.). Sarcomere length was monitored and recorded using IonOptix SarcLen system (IonOptix, Milton, MA, USA), which used a fast fourier transform algorithm of the video image of the myocyte (Fig. 1). Figure 1A illustrates muscle length (top) and sarcomere length (middle) traces during a load clamp (bottom) at both long and short SL. Figure 1B illustrates that muscle length and sarcomere length traces are closely matched over the entire range of relative loads and, in fact, power load curves in this study are comparable to our previous studies that reported velocities in muscle lengths per second. Video microscopy was completed using a 40× objective (Olympus UWD 40) and 25× intermediate lenses.

Figure 1. Muscle length, sarcomere length and force traces of a submaximally Ca²⁺ activated cardiac myocyte.

A, examples of myocyte shortening (top) and sarcomere shortening (middle) at clamped force (bottom) at long and short sarcomere length during submaximal Ca²⁺ activations. Photomicrographs of Ca²⁺ activated myocyte at long and short sarcomere length are inset. B, force–velocity points generated from muscle length (ML) traces (•) and sarcomere length (SL) traces (○) demonstrate that muscle length and sarcomere length traces are closely matched.

Force–velocity and power–load measurements

The protocol to obtain force–velocity and power–load measurements has been described in detail (McDonald, 2000) and all measurements were done at 12 ± 1°C. An attached myocyte was first transferred into maximal Ca²⁺ activating solution (pCa 4.5) and allowed to obtain maximal steady-state isometric force. It was then transferred to a submaximal Ca²⁺ activating solution and a series of subisometric force clamps were applied to determine isotonic shortening velocities. The isotonic force was maintained using a servo system for 150–250 ms while muscle length and sarcomere length changes during this time were monitored. Figure 1A illustrates a force clamp and corresponding muscle length and sarcomere length changes. Following the force clamp, the myocyte was slackened to near zero force to estimate the relative load sustained during the isotonic shortening, after which the myocyte was re-extended to its starting length. Due to the short lengths of the myocytes the rapid slackening following isotonic shortening did not always result in an accurate baseline force value and consequently resulted in an underestimation of peak force and, thus, of the relative force during loaded contractions. In these cases, more accurate estimates of the relative forces during isotonic shortening were obtained by interpolating between the peak forces in isometric contractions that were performed before and after every series of loaded contractions. The myocytes were kept in submaximal Ca²⁺ activating solution 2–4 min during which 10–20 force clamps were performed without significant loss of force. If force fell below 80% of initial force, data from that myocyte were discarded. Force–velocity measurements were obtained in this manner for all experimental conditions. The pCa solution that yielded approximately half-maximal force at long SL was 5.61 ± 0.16 for α-MyHC myocytes and 5.55 ± 0.10 for β-MyHC myocytes. To match force at short SL, the [Ca²⁺] had to be increased so the pCa solutions used were 5.51 ± 0.16 for α-MyHC myocytes and 5.45 ± 0.10 for β-MyHC myocytes.

Measurement of rate constant of force development

Measurement of tension development kinetics was accomplished by using a modification of Brenner & Eisenberg (1986) as previously described (McDonald et al. 1997) and adjusted for cardiac myocytes. Briefly, a myocyte in activating solution was allowed to develop tension to plateau after which it was rapidly slacked by 15–20% of original myocyte length (L₀) and held for 20 ms and then was rapidly restretched to a value slightly greater than L₀ for 2 ms before it was returned to L₀. This slack-restretch manoeuvre is thought to cause dissociation of crossbridges, and thus tension redevelopment arises from reattachment of crossbridges to the thin filament and subsequent transition to force generating states.

SDS-PAGE and silver staining

Following power output measurements the relative expression of MyHC was determined for each myocyte. The myocyte was removed from the experimental apparatus and stored in 10 μl of SDS sample buffer at –80°C for subsequent SDS-PAGE analysis. The gel electrophoresis procedure was similar to one previously described (Herron et al. 2001; Herron & McDonald, 2002). The gels were prepared with 3.5% acrylamide in the stacking gel and 12% acrylamide in the resolving gel. Myocyte proteins were separated at constant current (12 mA) for 8.5 h. The separated proteins were fixed in an acid-alcohol solution followed by glutaraldehyde. MyHC isoforms were visualized by ultrasensitive silver staining and then gels were dried and stored between Mylar sheets (Fig. 2). The relative expression of each MyHC isoform was determined by using QuantiScan (Biosoft) software and an Epson scanner to measure the relative intensities and areas of each MyHC band. MyHC content expressed as relative β-MyHC content is summarized in Table 1.

Figure 2. MyHC separation using SDS-PAGE.

Silver stained gel image of single cardiac myocytes using SDS-PAGE to specifically separate α-myosin heavy chain (MyHC) and β-MyHC.

Table 1.

Properties of cardiac myocyte preparations

	%β-MyHC		SL (μm)	Length (μm)	Width (μm)	Maximum Force (μN)	P/P4.5
α-MyHC myocytes (n = 12)	0.8 ± 2.8	Long SL	2.31 ± 0.04	132 ± 20	18 ± 2.5	5.9 ± 1.8	0.53 ± 0.11
		Short SL	2.00 ± 0.04*	106 ± 25*	20 ± 2.8*	3.6 ± 1.7*	0.32 ± 0.10*
β-MyHC myocytes (n = 11)	93.6 ± 8.1	Long SL	2.31 ± 0.06	138 ± 22	20 ± 3.2	5.9 ± 1.6	0.54 ± 0.13
		Short SL	2.01 ± 0.04*	114 ± 17*	22 ± 3.6*	3.5 ± 1.3*	0.32 ± 0.09*

Values are means ±s.d. SL, sarcomere length at submaximal Ca²⁺ activation; P/P_4.5, fraction of maximal isometric force (P_4.5).

^*Significant difference from long SL, P < 0.05;

†Significant difference from corresponding α-MyHC value, P < 0.05.

Data analyses

Myocyte length traces, force–velocity curves, and power–load curves were analysed as previously described (McDonald, 2000). Myocyte length and sarcomere length traces during loaded shortening were fit to a single decaying exponential equation:

(1)

where L is cell length at time t, A and C are constants with dimensions of length, and k is the rate constant of shortening (k_shortening). Velocity of shortening at any given time, t, was determined as the slope of the tangent to the fitted curve at that time point. In this study velocities of shortening were calculated by extrapolation of the fitted curve to the onset of the force clamp (i.e. t = 0).

Hyperbolic force–velocity curves were fitted to the relative force–velocity data using the Hill equation (Hill, 1938)

(2)

where P is force during shortening at velocity V; P_o is the peak isometric force; and a and b are constants with dimensions of force and velocity, respectively. Power–load curves were obtained by multiplying force x velocity at each load on the force–velocity curve. The optimum force for mechanical power output (F_opt) was calculated using the equation (Woledge et al. 1985)

(3)

Curve fitting was performed using a customized program written in Qbasic, as well as commercial software (Sigmaplot). Tension redevelopment following slack-restretch manoeuvre was fit by a single exponential equation

where F is tension at time t, F_max is maximal tension, and k_tr is the rate constant of force development.

To determine if SL significantly affected loaded shortening velocity, power, or k_tr, paired t tests were used. Student's t test was used to test for differences in velocity, power, or k_tr between α-MyHC and β-MyHC myocytes. One-way ANOVA was used to determine differences between long SL, short SL + matched force, and short SL + matched width groups, and a Student–Neuman–Keuls was performed as a post hoc test to assess differences between group means. In all cases, P < 0.05 was accepted as a significant difference. Data are presented as means ±s.d.n = the number of myocyte preparations.

Results

Sarcomere length dependence of absolute and normalized power output in α-MyHC myocytes

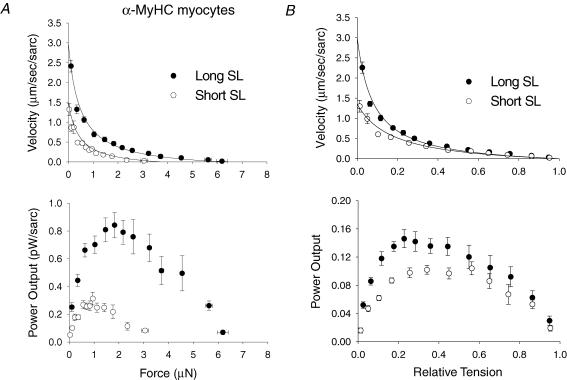
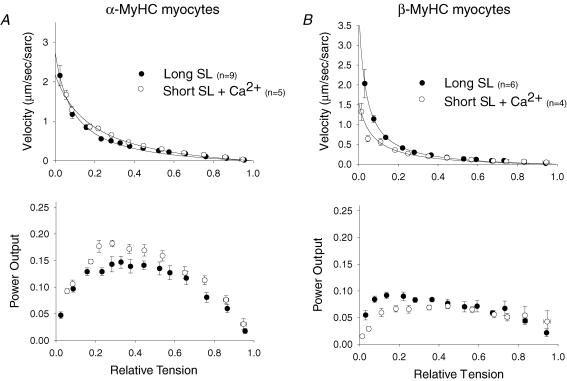
The sarcomere length dependence of loaded shortening was examined by characterizing force–velocity and power-load curves during submaximal Ca²⁺ activation at long SL (∼2.3 μm) and short SL (∼2.0 μm) in α-MyHC myocytes (n = 12). Figure 3A illustrates the sarcomere length dependence of loaded shortening and absolute power output from skinned cardiac myocytes containing α-MyHC. At short SL as compared to long SL, isometric force was decreased 40% while peak absolute power fell 55%, indicating power fell by mechanisms other than just decreased isometric force. This can be more clearly seen in force–velocity and power–load curves after normalization to isometric force (Fig. 3B) The normalized force–velocity curve shows that loaded shortening velocity was decreased at short SL versus long SL for given relative loads less than ∼40% of isometric force, which resulted in a 20% decrease in peak normalized power output. Interestingly, shortening velocity did not appear to be slower at short SL at loads greater than 40% of isometric force. The mechanical properties of α-MyHC myocytes are presented in Table 2.

Figure 3. Sarcomere length dependence of isotonic shortening velocity and power output in α-MyHC cardiac myocytes.

A, absolute force–velocity (top) and power output (bottom) curves from myocytes that contained α-MyHC at long SL (•) and short SL (○). B, normalized force–velocity (top) and power output (bottom) curves from α-MyHC myocytes at long SL (•) and short SL (○) as labelled. At short SL, isometric force was decreased, which caused a fall in absolute power output. However, the decrease in absolute power output was greater than the decrease in force, which indicates slower shortening velocities for a given relative load as seen in the normalized force–velocity and power–load curves. Data points are means ±s.d.

Table 2.

α-MyHC myocyte mechanical properties (n = 12)

SL (μm)	ktr	Fopt	Vopt (μm sarc−1 s−1)	a/P0	Peak absolute power output (μW mg−1)	Peak normalized power output (P/P0μm sarc−1 s−1)
2.31 ± 0.04	2.38 ± 0.56	0.21 ± 0.05	0.66 ± 0.15	0.10 ± 0.06	1.49 ± 0.67	0.14 ± 0.03
2.00 ± 0.04*	2.52 ± 0.69	0.29 ± 0.07*	0.40 ± 0.14*	0.23 ± 0.20*	0.66 ± 0.31*	0.11 ± 0.03*

Values are means ±s.d. SL, sarcomere length at submaximal Ca²⁺ activation; k_tr, rate constant of force development; F_opt, relative force at which power was optimal; V_opt, velocity at F_opt; a/P0, curvature of force–velocity relationship; P/P₀, fraction of isometric force (P₀).

^*Significant difference from long SL, P < 0.05.

Sarcomere length dependence of absolute and normalized power output in β-MyHC myocytes

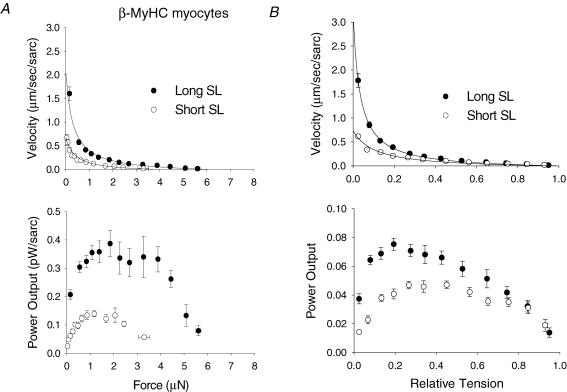
The sarcomere length dependence of loaded shortening and power output was also examined at long and short SL in β-MyHC myocytes (n = 11). Figure 4A illustrates the sarcomere length dependence of absolute loaded shortening and power output in β-MyHC myocytes. As with α-MyHC myocytes, isometric force was decreased at short SL, which led to a decrease in absolute power. However, the fall in absolute power was even more pronounced in β-MyHC myocytes. Isometric force was decreased 41% while peak absolute power fell nearly 70%. After normalization of the curves to isometric force (Fig. 4B), loaded shortening velocity was clearly decreased at short SL versus long SL for a given relative load less than ∼50% of isometric force; this resulted in a 41% decrease in peak normalized power output in β-MyHC myocytes. Thus, β-MyHC myocyte preparations are more sensitive to changes in SL at a given [Ca²⁺] than are α-MyHC myocytes. However, similar to α-MyHC, shortening velocities at short SL did not appear to be slower at loads greater than 50% of isometric force. The mechanical properties of β-MyHC myocytes are presented in Table 3.

Figure 4. Sarcomere length dependence of isotonic shortening velocity and power output in β-MyHC cardiac myocytes.

A, absolute force–velocity (top) and power output (bottom) curves from myocytes contained β-MyHC at long SL (•) and short SL (○). B, normalized force–velocity (top) and power output (bottom) curves from β-MyHC myocytes at long SL (•) and short SL (○). As in α-MyHC myocytes, isometric force and absolute power output were decreased at short SL, but the decrease in shortening velocity and power was even more pronounced in β-MyHC myocytes as indicated by the greater fall in peak normalized power output. Data points are means ±s.d.

Table 3.

β-MyHC myocyte mechanical properties (n = 11)

SL (μm)	ktr	Fopt	Vopt (μm sarc−1 s−1)	a/P0	Peak absolute power output (μW mg−1)	Peak normalized power output (P/P0μm sarc−1 s−1)
2.31 ± 0.06	1.18 ± 0.35	0.16 ± 0.04	0.43 ± 0.08	0.05 ± 0.03	0.63 ± 0.16	0.075 ± 0.018
2.01 ± 0.04*	1.79 ± 0.40*	0.27 ± 0.08*	0.17 ± 0.05*	0.18 ± 0.15*	0.20 ± 0.04*	0.044 ± 0.009*

Values are means ±s.d. SL, sarcomere length at submaximal Ca²⁺ activation; k_tr, rate constant of force development; F_opt, relative force at which power was optimal; V_opt, velocity at F_opt; a/P₀, curvature of force–velocity relationship; P/P₀, fraction of isometric force (P₀).

^*Significant difference from long SL, P < 0.05.

Effects of Ca²⁺ activation on normalized loaded shortening and power output

It was previously shown that shorter SL decreased Ca²⁺ sensitivity of force (Hibberd & Jewell, 1982; Kentish et al. 1986) and that loaded shortening velocity was tightly regulated by force and thin filament activation levels (Iwamoto, 1998; McDonald, 2000a; McDonald & Moss, 2000). Thus, a possible mechanism underlying the decreased loaded shortening velocity and power output at short SL could be the associated decrease in force and, thus, thin filament activation levels. To probe this mechanism, force and, presumably, thin filament activation levels were matched at short SL to those at long SL by simply increasing the Ca²⁺ concentration. Figure 5A illustrates that matched force at long SL and short SL actually led to faster loaded shortening velocities and 32% greater peak normalized power output at short SL (0.18 ± 0.02P/P₀μm sarc^–1 s^–1) than observed at long SL (0.14 ± 0.03P/P₀μm sarc^–1 s^–1) in α-MyHC myocytes. This implies a myofibrillar mechanism that ultimately speeds loaded crossbridge cycling at shorter SL in α-MyHC myocytes. In β-MyHC myocytes matched force at short SL slightly sped loaded shortening and increased power output as would be expected with the increase in force but, in contrast to α-MyHC myocytes, peak normalized power output remained decreased by 28% at short SL (0.07 ± 0.02P/P₀μm sarc^–1 s^–1) compared to long SL (0.09 ± 0.02P/P₀μm sarc^–1 s^–1) (Fig. 5B).

Figure 5. Sarcomere length dependence of isotonic shortening velocity and power output in α-MyHC and β-MyHC cardiac myocytes with matched Ca²⁺ activation levels.

A, normalized force–velocity (top) and power output (bottom) curves from α-MyHC myocytes at long SL (•) and short SL with increased Ca²⁺ to match force (○). Loaded shortening velocity and peak normalized power output are elevated at short SL to levels greater than at long SL when activation levels are matched by increased [Ca²⁺] in α-MyHC myocytes. B, normalized force–velocity (top) and power output (bottom) curves from myocytes that contained β-MyHC at long SL (•) and short SL with increased Ca²⁺ to match force (○). In β-MyHC myocytes, matched activation through increased [Ca²⁺] only sped loaded shortening to levels equivalent to that seen at long SL, and only at loads less than ∼30% of isometric force. Data points are means ±s.d.

Effects of osmotic compression on normalized loaded shortening and power output

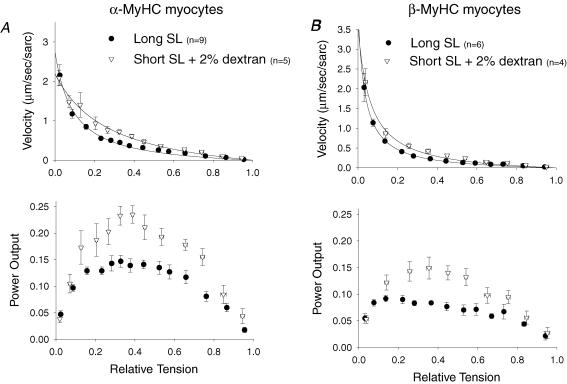
The effects of changes in lattice spacing that occur with changes in sarcomere length were examined by adding the osmotic polymer dextran to Ca²⁺ activating solution at short SL. Dextran osmotically decreased myocyte width by decreasing cell volume. In this study, 2% dextran at short SL was sufficient to decrease the width of the myocyte and to increase force to match both the width and force seen at long SL in α-MyHC and β-MyHC myocytes. In α-MyHC myocytes at short SL, 2% dextran increased loaded shortening velocity at nearly all relative loads and increased peak normalized power output 59% (0.22 ± 0.05P/P₀μm sarc^–1 s^–1) compared to long SL (Fig. 6A). This further implicates a myofibrillar mechanism that leads to faster loaded crossbridge cycling at short SL in α-MyHC myocytes. Interestingly, addition of 2% dextran to β-MyHC myocytes increased loaded shortening velocity at nearly all relative loads, and peak normalized power output was increased 52% (0.14 ± 0.06P/P₀μm sarc^–1 s^–1) above that at long SL (Fig. 6B); this was more than double that seen at short SL with matched force. Therefore, β-MyHC myocytes also appears to have a myofibrillar-based process that leads to faster loaded crossbridge cycling at shorter SL but, in contrast to α-MyHC myocytes where power increased at short SL with both matched force (via increased [Ca²⁺]) and matched width (via dextran), power output in β-MyHC myocytes only increased with matched width. Thus, β-MyHC myocytes appears to be more responsive to changes in interfilament spacing and, as a result, the increase in lattice spacing associated with short SL was likely, in part, responsible for the lower loaded shortening velocity and power even at matched Ca²⁺ activation levels. This also is consistent with the observed greater SL dependence of loaded shortening in β-MyHC myocytes.

Figure 6. Sarcomere length dependence of isotonic shortening velocity and power output in α-MyHC and β-MyHC cardiac myocytes with matched activation levels and width.

A, normalized force-velocity (top) and power output (bottom) curves from α-MyHC myocytes at long SL (•) and short SL + Dextran (▵). Loaded shortening velocity and peak normalized power output are elevated at short SL to levels greater than at long SL when activation levels are matched by osmotic compression in α-MyHC myocytes. B, normalized force-velocity (top) and power output (bottom) curves from myocytes that contained β-MyHC at long SL (•) and short SL + Dextran (▵). In β-MyHC myocytes, matched activation by osmotic compression sped loaded shortening and increased normalized power output to levels greater than at long SL. Data points are means ±s.d.

Effects of sarcomere length, osmotic compression, and Ca²⁺ activation on force development

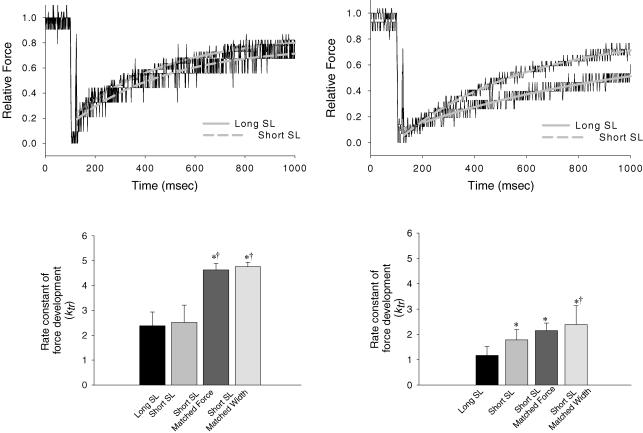
In α-MyHC myocytes, there was no difference in the rate constants of force development (k_tr) between long (k_tr= 2.38 ± 0.56 s^–1) and short SL (k_tr= 2.52 ± 0.69 s^–1) (Fig. 7A). At short SL, however, increasing [Ca²⁺] to match force activation levels at long SL (k_tr= 4.63 ± 0.26 s^–1) or adding 2% dextran to match myocyte width (k_tr= 4.76 ± 0.18 s^–1) led to significantly greater rates of force redevelopment compared to long SL or short SL alone (Fig. 7C). This strengthens the implication that loaded crossbridge cycling is faster at short SL in α-MyHC myocytes. Interestingly, β-MyHC myocytes exhibited faster rates of force development at short SL (k_tr= 1.79 ± 0.40 s^–1), short SL with matched force (k_tr= 2.15 ± 0.30 s^–1), and short SL with matched width (k_tr= 2.39 ± 0.74 s^–1), compared to long SL (k_tr= 1.18 ± 0.35 s^–1) (Fig. 7B and D). Moreover, force development rates were not statistically faster at short SL with matched force versus short SL alone, but were faster at short SL with matched width in β-MyHC myocytes. Again, this implies increased crossbridge cycling at short SL but β-MyHC myocytes appear to be more affected by lattice spacing (vis-à-vis the change in myocyte width) than force levels per se, whereas α-MyHC myocytes appear to be more equally responsive to both width and force.

Figure 7. Sarcomere length dependence of rate constant of force development in α-MyHC and β-MyHC cardiac myocytes.

A, normalized force traces fitted with a rising exponential to calculate the rate constant of force development from an α-MyHC myocyte at long SL (upper continuous line) and short SL (lower dashed line). B, normalized force traces fitted with a rising exponential from a β-MyHC myocyte at long SL (lower continuous line) and short SL (upper dashed line). C, rate constants of force development for α-MyHC myocytes at long SL, short SL, short SL with matched force, and short SL with matched width. D, rate constants of force development for β-MyHC myocytes at long SL, short SL, short SL with matched force, and short SL with matched width. *Significantly different from long SL (P < 0.05). †Significantly different from short SL (P < 0.05). Data are means ±s.d.

Discussion

The cellular basis for the Frank–Starling relationship arises from beat-to-beat changes in diastolic myocyte length, and thus changes in myocyte sarcomere length. Increasing sarcomere length within the working range of the myocardium (∼1.9 μm to 2.3 μm) (Pollack & Huntsman, 1974; Grimm et al. 1980; Guccione et al. 1997) increases force generating capacity due, in part, to more optimal overlap of the thick and thin filaments (Gordon et al. 1966) and enhanced myofibrillar sensitivity to Ca²⁺ (Allen & Kurihara, 1982; Kentish et al. 1986; Hofmann & Fuchs, 1987; McDonald et al. 1995). A study by Sonnenblick (1962) found that increasing initial muscle length increased force without an apparent change in the maximal velocity of shortening (V_max), as extrapolated from force–velocity curves. However, others studying lightly loaded ferret papillary muscle showed that shortening velocity of a well-defined central muscle segment declined with decreased initial muscle segment lengths (Martyn et al. 1983). Also, another study showed that near maximum velocities of sarcomere shortening increased in proportion to SL between 1.9 μm and 2.3 μm during submaximal Ca²⁺ activations of rat intact cardiac trabeculae (De Tombe & ter Keurs, 1992). These studies imply a SL-dependent effect of cardiac muscle shortening. We sought to directly address whether SL modulates myocyte shortening by measuring sarcomere shortening velocity during load clamps in skinned cardiac myocyte preparations, which allow control of Ca²⁺ activation levels and that lack extracellular viscoelastic elements that may affect shortening. We also felt it important to determine if there are differences in SL responsiveness between α-MyHC and β-MyHC since there are changes in MyHC content in response to a number of physiological and pathophysiological conditions, including up-regulation of β-MyHC in rodents in response to diabetes (Dillman, 1980; Garber & Neely, 1983) and pressure overload (Litten et al. 1982; Lompre et al. 1984; Mann et al. 1991) and in failing human myocardium (Miyata et al. 2000). The latter carries clinical relevance, as there are a number of studies that have demonstrated the Frank–Starling mechanism is compromised in animal models of heart failure (Ross et al. 1971; Komamura et al. 1993) and in human failing myocardium (Schwinger et al. 1994; Holubarsch et al. 1996).

Sarcomere length dependence of loaded shortening and power output

This study found a sarcomere length dependence of absolute loaded shortening velocity and power output in both α-MyHC and β-MyHC skinned cardiac myocytes, but the effect of sarcomere length was more pronounced in β-MyHC myocytes. Much of the sarcomere length dependence arose from changes in isometric force but force–velocity relationships, even after normalization for the changes in force, still showed SL dependence of loaded shortening velocity and power output, especially at loads around 10–30% of isometric force where the heart is thought to work in vivo. A plausible reason for slower shortening velocity at short SL is greater cooperative inactivation of the thin filament during myocyte shortening (Iwamoto, 1998; McDonald, 2000). For instance, at shorter sarcomere length there is decreased Ca²⁺ sensitivity of force arising at least in part from fewer crossbridges (Swartz & Moss, 1992; Fitzsimmons & Moss, 1998; McDonald & Moss, 2000; Fitzsimons et al. 2001). The reduction in shortening velocity could then arise from more cooperative inactivation of the thin filament at the onset of and throughout the force clamp, leaving fewer crossbridges to bear a fixed relative load at short SL. This is supported by our previous work (McDonald, 2000) that showed decreased [Ca²⁺] (which yielded force changes similar to those seen in the present study between long SL and short SL) resulted in significantly slower loaded shortening velocity and a quantitatively similar decrease in peak normalized power output as seen in the present study. However, changes in Ca²⁺ activation alone resulted in lower power output at nearly all relative loads, whereas decreased SL seemed to only alter loaded shortening and power at loads less than ∼40% of isometric force. This implies that a sarcomere length component alters loaded shortening velocity in a manner that differs from Ca²⁺-induced activation of the thin filament alone.

Sarcomere length dependence of loaded shortening and power output at matched levels of thin filament activation. We determined if decreased power between long and short SL was due to decreased thin filament activation by normalizing thin filament activation levels with increased [Ca²⁺] at short SL to match force seen at long SL. Interestingly, α-MyHC myocytes exhibited significantly faster loaded shortening velocities and increased power output at short SL with matched force when compared to long SL, implying that short SL directly speeds crossbridge cycling kinetics and/or, at short SL, there is a crossbridge population that is better able to maintain thin filament activation during shortening, which allows more crossbridges to work against the load so each crossbridge cycles faster. The increased loaded shortening and power were observed at matched force despite increased myocyte width and lattice spacing that occurs with shorter SL. This result may arise because α-MyHC crossbridges either become more flexible in the azimuthal direction or extend away from the thick filament in the radial direction at short SL, resulting in faster individual crossbridge turnover kinetics and/or crossbridges that more readily interact with the thin filament to sustain its activation during shortening. In contrast, peak normalized power output in β-MyHC myocytes remained depressed at short SL compared to long SL even with matched force levels. This may be because β-MyHC crossbridges do not undergo as much of a change in azimuthal flexibility or radial extension from the thick filament with changes in SL, at least as compared to α-MyHC, and this may explain, in part, why β-MyHC myocytes exhibit a greater SL dependent decrease in loaded shortening velocity and power than α-MyHC myocytes.

Another potential mechanism for decreased loaded shortening velocity at short SL is the resultant increase in lattice spacing, which would lead to less than optimal crossbridge interactions and, thus, greater cooperative inactivation at the onset and throughout shortening. Reduced myocyte width and, thus, lattice spacing in our myocytes caused a striking increase in loaded shortening velocity and power output in both α-MyHC and β-MyHC. This certainly implies that lattice spacing plays a major role in the reduced loaded shortening velocity and power output going from long SL to short SL. In addition, since loaded shortening was so much faster at short SL when interfilament lattice spacing was normalized this further implicates a SL dependent change in crossbridge interaction kinetics, which may be due to greater crossbridge flexibility at short SL. Evidence for such a conformational change in cardiac muscle is lacking, but changes in radial and azimuthal flexibility have been seen as a consequence of lattice spacing and temperature in activated skeletal muscles (Cecchi et al. 1990; Linari et al. 2005).

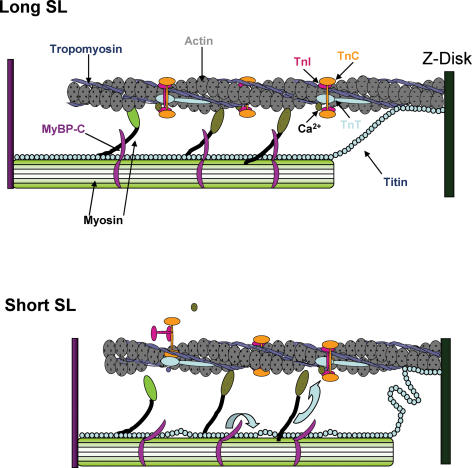
Interestingly, it has been shown that phosphorylation of myosin binding protein-C by PKA results in extension of crossbridges from the thick filament backbone (Weisberg & Winegrad, 1996). MyBP-C is thought to form a collar around the thick filament, with extensions that bind the myosin head in an inhibitory manner (Moolman-Smook et al. 2002). Phosphorylation of MyBP-C has been shown to relieve this inhibition and increase force (Kunst et al. 2000), and myocytes from MyBP-C null mice have been shown to have increased rates of force development, loaded shortening velocity, and power output generating capacity (Korte et al. 2003; Stelzer et al. 2006). The thick filament anchoring protein titin is responsible for nearly all of the passive force encountered at physiological sarcomere lengths (Granzier & Irving, 1995; Freiburg & Gautel, 1996), and is known to bind to MyBP-C (Freiburg & Gautel, 1996). It may be that as the sarcomere length is increased and titin becomes taut, it exerts a force on MyBP-C that in turn affects myosin head radial or azimuthal mobility. Conversely, as SL is shortened titin may slacken and exert less force on MyBP-C that in turn reduces MyBP-C constraint on myosin head mobility. Force and power decrease at short SL because interfilament distance is increased and there are fewer myosin crossbridges to cooperatively activate the thin filament thereby increasing the likelihood of greater thin filament inactivation at the onset of shortening, which would slow loaded shortening. However, in α-MyHC myocytes, the decrease in normalized power output was not as large as might be expected with a decrease in SL and, in fact, there was virtually no effect on loaded shortening velocity at loads greater than 40% isometric force perhaps due to more myosin head extension/mobility and, thus, less cross-bridge induced inactivation of the thin filament. We previously observed a similar phenomenon in MyBP-C null myocytes in which loaded shortening velocities were greatly elevated at high loads (Korte et al. 2003). Additionally, when thin filament Ca²⁺ activation was increased or the interfilament distance decreased at short SL there was faster loaded crossbridge cycling, again perhaps due to more flexible crossbridges, which either inherently turnover faster or more readily sustain thin filament activation levels. These ideas is schematically illustrated in Fig. 8, where a decrease in SL causes titin to slack, which induces a conformational change in MyBP-C that results in release of myosin constraint (similar to MyBP-C phosphorylation) and radial extension of myosin heads from the thick filament backbone (in α-MyHC). Interestingly, Weisberg & Winegrad (1996) did not see a change in β-MyHC crossbridge extension with PKA-phosphorylation of MyBP-C, indicating that MyBP-C may have less of an effect on radial extensibility with β-MyHC thick filaments, which is mechanistically consistent with our finding of a larger decrease in normalized power output from long SL to short SL in β-MyHC myocytes than α-MyHC myocytes.

Figure 8. Myofibrillar model for increased cross-bridge kinetics at short sarcomere length.

A, representation of sarcomeric proteins at long sarcomere length. Titin is extended and provides passive tension that may help maintain extension of MyBP-C from the thick filament to provide constraint on the myosin crossbridge. B, at short sarcomere length, titin is slack and this decrease in passive tension may alleviate MyBP-C constraint of the crossbridge, which (perhaps to a greater extent in α-MyHC thick filaments) may lead to more flexible crossbridges, which may have faster turnover kinetics and/or more readily activate the thin filament.

Sarcomere length and myosin heavy chain dependence on the rate constant of force development

MyHC has been shown to be a key determinant of the rate of tension development (k_tr), whereby α-MyHC exhibited ∼3 times greater k_tr than β-MyHC in rat skinned ventricular muscle preparations (Rundell et al. 2005). Our current findings are in agreement with that study in that α-MyHC myocytes exhibited k_tr rates that were about twice as fast as β-MyHC myocytes. The SL dependence of k_tr was previously addressed by others (Adhikari et al. 2004; Stelzer & Moss, 2006), who discovered that rates of force development at 2.3 μm and 2.0 μm were comparable at maximal Ca²⁺ activation and faster at force-matched submaximal Ca²⁺ activation in rat skinned cardiac trabeculae. We also saw no difference in k_tr at long and short SL in α-MyHC myocytes, but it was higher at short SL at the same Ca²⁺ activation level and when myocyte width was matched. Interestingly, a novel finding of this study is that β-MyHC myocytes exhibited higher k_tr at short SL than long SL despite lower force levels. Interestingly, the rate of force development at short SL with matched force was not significantly different from short SL. However, the rate of force development at short SL with matched width was significantly faster than at short SL, again illustrating the susceptibility of β-MyHC to width. Overall, our estimates of the rate constant of force development are in agreement with the idea that loaded crossbridge interaction kinetics are faster at short SL in both α-MyHC and β-MyHC myocytes.

Physiological significance

The Frank–Starling mechanism is a physiological phenomenon that tunes myocardial function on a beat-to-beat basis by altering stroke volume, a primary index of the heart's ability to function as a pump (Starr et al. 1933). Ventricular function curves plotted as end-diastolic volume versus stroke volume have been considered a unifying basis for changes in ventricular function (Sarnoff, 1955), and depression of this relationship is associated with heart failure (Braunwald et al. 1967; Najad et al. 1971; Schwinger et al. 1994; Holubarsch et al. 1996; ter Keurs, 1996). Interestingly, failing human myocardium has increased β-MyHC content (Miyata et al. 2000). It may be possible that β-MyHC is expressed early in the compensatory phase of heart failure as it is more energetically favourable (Loiselle et al. 1982; Holubarsch et al. 1985; Harris et al. 1994; Rundell et al. 2005) and is associated with a slower heart rate (Hamilton & Ianuzzo, 1991). Teleologically, a slower heart rate allows for more filling time and, thus, a potentially greater end-diastolic volume. Based on our results a heart containing β-MyHC may be more responsive to a change in end-diastolic volume, meaning greater reliance on the Frank–Starling relationship as a way to tune ventricular power output (and stroke volume). This is consistent with observations that rat left ventricles that contained > 70%β-MyHC exhibited steeper ventricular function curves than left ventricles that contained predominantly α-MyHC (Fitzsimons et al. 1999). Additionally, we have seen that working rat heart preparations that contained primarily α-MyHC had a ∼55% increase in left ventricular power output when left atrial filling pressure was increased from 7.5 to 15 cmH₂O, whereas hearts containing primarily β-MyHC exhibited an ∼120% increase in left ventricular power (Korte et al. 2007). It is important to note, however, that the change in MyHC content in failing human myocardium is thought to be relatively small (from ∼90% to 100%β-MyHC) (Miyata et al. 2000) and we were unable to resolve a difference in sarcomere length dependence of power output between myocytes with this small difference in MyHC isoform content (data not shown). Overall, the main finding of this study is that the rate of loaded sarcomere shortening changed as a complex function of sarcomere length and lattice spacing in cardiac myocytes. Additionally, β-MyHC myocytes were more responsive to changes in sarcomere length and lattice spacing, which may underlie a steeper Frank–Starling relationship in left ventricles that contain β-MyHC.