Improved Diffusion Measurement in Heterogeneous Systems Using the Magic Asymmetric Gradient Stimulated Echo (MAGSTE) Technique

Abstract

A magic asymmetric gradient stimulated echo (MAGSTE) sequence was recently proposed to improve molecular diffusion measurements in the presence of spatially varying background gradients. Its effectiveness has been demonstrated previously with simulated background gradients and in phantoms that contain bulk susceptibility differences. In this study, we investigated the MAGSTE technique in microscopically heterogeneous systems, and compared it with the conventional bipolar pulsed gradient stimulated echo (bPGSTE) sequence. We demonstrated that the MASGTE measurements, compared to the bPGSTE method, varied significantly less when the diffusion encoding/decoding interval (δ) was changed. In addition, the MAGSTE technique provided good characterization of the surface area-to-volume ratio for heterogeneous systems investigated in this study. In sum, this study showed that the MAGSTE technique provided diffusion measurements superior to those of the bPGSTE sequence, especially in the presence of severe heterogeneous background gradients.

1. INTRODUCTION

Since the pioneering work of Stejeskal and Tanner, the nuclear magnetic resonance (NMR) technique for measuring molecular diffusion coefficient has been widely used to characterize microscopic displacement processes [1; 2]. Under ideal conditions (i.e., delta gradient pulse approximation), the spatial position of spins is instantaneously encoded and spin displacement such as that caused by diffusion leads to incomplete refocusing of the magnetization, and therefore attenuation of the detected signal. However, during the NMR diffusion experiments, the gradient pulse duration needed to generate sufficient spatial encoding with finite gradient strength may be as long as tens of milliseconds. Furthermore, shaped gradients are often chosen to minimize eddy currents, which may result in further increases in the gradient pulse duration. Fortunately, if the applied gradient is the only gradient that the spins experience, the effects of the shaped and finite gradients upon diffusion measurements can be quantified and fully compensated [3].

Some interesting applications of NMR diffusion techniques involve investigating complex systems with inherent field inhomogeneities. Such background gradients vary with the susceptibility mismatch and local structure of the system, and also depend upon the magnetic field strength at which the experiment is being conducted [4–7]. For instance, in heterogeneous systems studied at high magnetic field strengths, background gradients can be comparable to or possibly stronger than laboratory gradients; if not properly accounted for, these background gradients may introduce severe errors when diffusion NMR techniques are used to characterize local structure. In fact, it has been shown that for phantoms containing ferrite particles (a case of microscopic magnetic heterogeneity), the diffusion coefficients vary with both evolution time and the concentration of magnetic impurities [8]. Several NMR diffusion techniques have been developed to suppress such artifacts [9; 10]. Because the longitudinal relaxation time for heterogeneous systems is usually much longer than the transverse relaxation constant, the bipolar pulsed gradient stimulated echo (bPGSTE) sequence, which is susceptible to minimal transverse relaxation attenuation, has found widespread application for characterization of complex systems such as porous media [11–13]. Moreover, its stimulated echo nature allows this technique to probe displacements over very long evolution intervals, comparable to the longitudinal relaxation time; it is therefore applicable in q-space imaging of heterogeneous systems [14–16].

It is known, however, that the bPGSTE sequence suppresses only static background gradients. The bPGSTE sequence compensates for the background gradient artifacts that occur during the encoding interval with those that arise during the decoding interval. As such, if the background gradients vary between the encoding and decoding intervals, the bPGSTE sequence will not be able to fully correct the background gradient artifacts. On the other hand, the spatial distribution of background gradients is very complex, depending upon both the magnetic properties and local structure of the system, and can vary over the length scale of typical spin displacement [6]. Consequently, spins may experience uncorrelated background gradients during the encoding and decoding intervals; when this happens, the bPGSTE method cannot fully suppress the background gradients, and therefore is susceptible to non-negligible measurement errors [17; 18].

Recently, Sun et. al. proposed a magic asymmetric gradient stimulated echo (MAGSTE) sequence and showed that the coupling between the applied and background gradients can be suppressed independently during the encoding and decoding intervals [19; 20]. Galvosas et al. showed that in systems with bulk susceptibility differences, the MAGSTE technique provides accurate diffusion measurements [21]. Because the MAGSTE sequence requires that the background gradients remain constant only during the coding interval (i.e., 2τ), independent of the evolution time (TS), the MAGSTE sequence can suppress heterogeneous background gradients that vary during the evolution time but remain constant throughout the encoding/decoding interval, and therefore, provides better quantification of diffusion than the bPGSTE technique. In this study, we compared the MAGSTE and bPGSTE diffusion measurements in simple yet representative heterogeneous systems, consisting of packed microspherical glass beads, across a wide range of evolution intervals. We also modeled the background gradients using representative magnitude distribution and temporal correlation functions, and investigated the effects of heterogeneous background gradients upon diffusion measurements. Moreover, we demonstrated that MAGSTE measurements can better quantify the surface area-to-volume (S/V) ratio and are less susceptible to variations in the gradient coding interval. In sum, we showed that the MAGSTE technique provides improved diffusion measurement in systems with severe heterogeneity, and therefore should be applied to quantify spin displacement processes in complex systems.

2. THEORY

For diffusion measurement in a homogeneous system of infinite size, the normalized signal can be shown to be equal to:

$$\frac{\text{E}(\text{g})}{\text{E}(0)}={\text{e}}^{-\text{bD}}$$ (1)

where E(g) and E(0) are echo intensities with applied gradients of g and 0, respectively, D is the diffusion constant, and b is the diffusion b-factor. For a typical spin echo diffusion sequence, b = γ²g² δ² (Δ − δ/3), where γ is the gyromagnetic ratio, δ is the gradient pulse duration and Δ is the delay between the rising edges of encoding and decoding gradients [1].

In complex systems such as porous media and biological tissue, heterogeneous magnetic susceptibility and structure cause concomitant background gradients (g_b) in addition to the applied gradients (g). Therefore, the diffusion b-factor contains not only the terms of the applied gradient (g), but also those that arise from the heterogeneous background gradients (g_b). For instance, the diffusion b-factor for a representative stimulated echo sequence can be shown as:

$$\text{b}={\gamma }^2\left\{\text{A\hspace{0.17em}}{\text{g}}^2+\text{B}\left\{{\left[{\text{g}}_{\text{b}}(2\tau )\right]}^2+{\left[{\text{g}}_{\text{b}}(\text{TS}+2\tau )\right]}^2\right\}\hspace{0.17em}+\text{C\hspace{0.17em}g}\left[{\text{g}}_{\text{b}}(2\tau )-{\text{g}}_{\text{b}}(\text{TS}+4\tau )\right]\right\}$$ (2)

where g_b (2τ) and g_b (TS + 2τ) are background gradients during the encoding and decoding interval, respectively, and A, B and C are coefficients for the applied gradient, background gradient and their coupling term, respectively.

The normalized echo attenuation is equal to:

$$\langle \frac{\text{E}(\text{g})}{\text{E}(0)}\rangle ={\text{e}}^{-\text{D\hspace{0.17em}A}{\gamma }^2{\text{g}}^2}\int \text{p}({\text{g}}_{\text{b}})\langle {\text{e}}^{-\text{D\hspace{0.17em}C}{\gamma }^2\hspace{0.17em}\text{g}\left[{\text{g}}_{\text{b}}(\text{t})-{\text{g}}_{\text{b}}(0)\right]}\rangle {\text{dg}}_{\text{b}}$$ (3)

where p(g_b) is the probability distribution function (PDF) of the background gradients and the bracket represents the ensemble average over spin density. Terms containing background gradients only (i.e., terms with coefficient B) are equivalent for E(g) and E(0), and thus are normalized in Eq (3). Since the background gradients can be assumed to be symmetric about zero, the normalized echo intensity is equal to:

$$\langle \frac{\text{E}({\text{g}}_{\text{a}})}{\text{E}(0)}\rangle \approx {\text{e}}^{-\text{D\hspace{0.17em}A}{\gamma }^2{\text{g}}^2}\int \text{p}({\text{g}}_{\text{b}})\left\{\begin{array}{l}1+\text{D\hspace{0.17em}}\left(\text{C}{\gamma }^2\text{g}\right)\langle {\text{g}}_{\text{b}}(\text{t})-{\text{g}}_{\text{b}}(0)\rangle +\\ \frac{{\text{D}}^2{\left(\text{C}{\gamma }^2\text{g}\right)}^2\langle {[{\text{g}}_{\text{b}}(\text{t})-{\text{g}}_{\text{b}}(0)]}^2\rangle }{2!}+\text{O}\left({\left[{\text{g}}_{\text{b}}(\text{t})-{\text{g}}_{\text{b}}(0)\right]}^4\right)\end{array}\right\}{\text{dg}}_{\text{b}}$$ (4)

where odd orders of background gradients are zero as a result of the assumed symmetric distribution of the background gradients, and terms with orders higher than quadratic can be neglected. Furthermore, we assume that the spatial variation of background gradients in random structures can be modeled by a correlation function $\text{F}(\text{t})=\langle {\text{g}}_{\text{b}}(\text{t})\hspace{0.17em}{\text{g}}_{\text{b}}(0)\rangle /\langle {{\text{g}}_{\text{b}}}^2\rangle$, and the normalized echo intensity is equal to:

$$\langle \frac{\text{E}(\text{g})}{\text{E}(0)}\rangle \approx {\text{e}}^{\text{D\hspace{0.17em}A}{\gamma }^2{\text{g}}^2}\int \text{p}({\text{g}}_{\text{b}})\left\{1+\frac{{\text{D}}^2{\left(\text{C}{\gamma }^2\text{g}\right)}^2\langle {{\text{g}}_{\text{b}}}^2\rangle {\left[1-\text{F}(\text{t})\right]}^2}{2}\right\}{\text{dg}}_{\text{b}}$$ (5)

In order to illustrate the effects of background gradients upon the diffusion measurements, we assume that the temporal correlation and PDF of the background gradients can be modeled by ${\text{e}}^{-\frac{\text{t}}{\zeta }}$ and $\frac{1}{\sqrt{2\pi }\sigma }{\text{e}}^{-\frac{{{\text{g}}_{\text{b}}}^2}{2{\sigma }^2}}$, respectively, where ζ is the characteristic correlation time and σ is the variance of the background gradients. Because ζ depends on the spin displacement rate, characteristic pore size, as well as the local structure, its exact analytical form may not be known. The normalized echo intensity is:

$$\langle \frac{\text{E}(\text{g})}{\text{E}(0)}\rangle \approx {\text{e}}^{-\text{D\hspace{0.17em}A}{\gamma }^2{\text{g}}^2}+{\text{e}}^{-\text{D\hspace{0.17em}A}{\gamma }^2{\text{g}}^2}\left[\frac{{\text{D}}^2{\left(\text{C}{\gamma }^2\text{g}\sigma \right)}^2{\left(1-{\text{e}}^{-\text{t}/\zeta }\right)}^2}{2}\right]$$ (6)

where the first term is the diffusion attenuation due to the applied gradients only, and the correction term in parenthesis represents the compensation factor arising from the coupling of the applied and background gradients. When the diffusion coefficient is derived by fitting the echo attenuation with a mono-exponential function (i.e., Eq.(1)), the obtained apparent diffusion coefficient (ADC) can be shown as:

$$\text{ADC}\approx \text{D}\left[1-\frac{{\text{C}}^2{\gamma }^2{\sigma }^2{\left(1-{\text{e}}^{-\text{t}/\zeta }\right)}^2\text{D}}{\text{A}\left(2+{\text{C}}^2{\text{D}}^2{\gamma }^4{\sigma }^2{\text{g}}^2{\left(1-{\text{e}}^{-\text{t}/\zeta }\right)}^2\right)}\right]$$ (7)

At short evolution times (i.e., t ≪ ζ), the temporal correlation correction term is negligible (i.e., 1 − e^−t/ζ ≈ 0), such that ADC ≈ D. This is essentially the case for delta gradient pulse approximation. On the other hand, when diffusion time is much greater than correlation time, coefficient A is shown to dominate term C, and again ADC ≈ D. For intermediate evolution intervals, however, the derived ADC depends upon the properties of the background gradients (i.e., magnitude distribution and temporal correlation) as well as the diffusion coefficient and applied gradients, and therefore can be very complex.

In the case of porous media, true diffusion rate varies with the diffusion interval and also depends upon pore size, connectivity, surface relaxation and the exact form of packing; therefore, we substitute the true diffusion rate D with the experimentally measurable diffusion coefficient from the MAGSTE technique (D_MAGSTE), with a scaling factor of η defined as D=η·D_MAGSTE. Thus, Eq. (7) can be shown to be equal to:

$$\frac{\text{ADC}}{{\text{D}}_{\text{MAGSTE}}}\approx \eta \left[1-\frac{{\text{C}}^2{\gamma }^2{\sigma }^2{\left(1-{\text{e}}^{-\text{t}/\zeta }\right)}^2\eta {\text{D}}_{\text{MAGSTE}}}{\text{A}\left(2+{\text{C}}^2{\eta }^{\text{2}}{{\text{D}}_{\text{MAGSTE}}}^2{\gamma }^4{\sigma }^2{\text{g}}^2{\left(1-{\text{e}}^{-\text{t}/\zeta }\right)}^2\right)}\right]$$ (8)

If the MAGSTE technique can completely correct for background gradient artifacts, D_MAGSTE will be equal to the true diffusion rate D, such that η=1.

3. MATERIALS AND METHODS

Microspherical soda-lime glass beads with mean sizes of 90 μm (70–110 μm) and 150μm (100–200 μm) (GlenMills Inc., Clifton, NJ) were immersed into 1% hydrochloric acid solution (Sigma Aldrich, St Louis, MO) for 15 minutes to remove surface impurities. The beads were then washed with deionized water, vortexed, and vacuumed to remove trapped air bubbles. Afterwards, the glass beads were transferred into two 5 mm NMR tubes (Sigma Aldrich, St Louis, MO) filled with 0.25 mM copper sulfate pentahydrate solution (C_uSO₄·5H₂O). Another 5 mm NMR tube containing 0.25 mM C_uSO₄·5H₂O solution was used as a reference phantom.

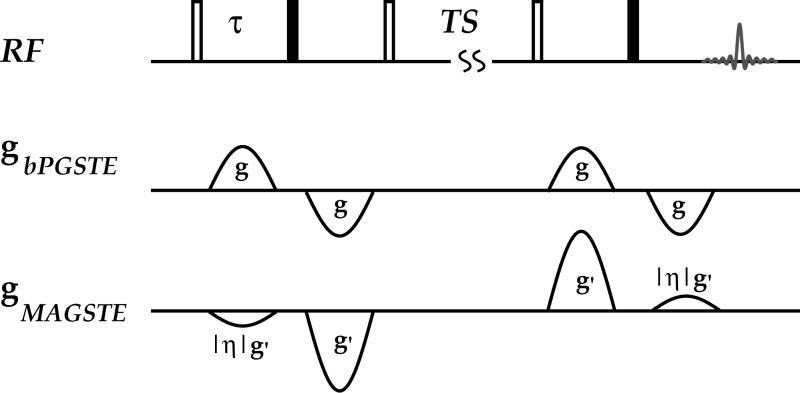
All measurements were conducted on a 500 MHz Avance NMR spectrometer (Bruker Biopsin, Billerica, MA) at 25 °C. The molecular diffusion was measured using both bPGSTE and MAGSTE sequences with half sine-shaped gradients as shown in Fig. 1 (TR=6,000 ms, Dummy Scan=8, Number of Average=16). The pre and post gradient delays were set to be equal, (i.e., δ ₁ = δ ₂) and the gradient pulse duration was twice the pre/post gradient delay (i.e., δ =2 δ_1,2). Two encoding intervals were used (τ=6 and 4 ms) for both sequences to explore the effect of reduced encoding time on diffusion calibration. Each measurement involved 16 gradient strengths that varied linearly from zero to the maximal applied gradients, 14.8 and 34.9 G/cm for the bPGSTE and MAGSTE sequence, respectively [22]. The x and y gradients were applied concurrently to reduce the load on any individual gradient coil and amplifier. Seven storage times (TS) were used: 8, 16, 32, 64, 128, 256 and 512 ms. The stimulated echo was selected by applying a weak constant gradient along the z-axis. In addition, an eight-step phase cycling of the RF pulses and receiver was used to suppress other concomitant coherence pathways [19].

Fig 1.

Illustration of the conventional 13-interval bPGSTE sequence and the proposed MAGSTE sequence with half sine shaped applied gradients, in which τ and TS are the encoding interval and storage time, respectively. The unfilled and filled block represents π/2 and π pulse, respectively. Unlike the bPGSTE sequence whose two bipolar gradients are of the same magnitude (g), the two gradients for MAGSTE sequence are of strength ηg′ and g′, respectively, with ${\text{g}}^{\prime }=\frac{2}{1+\eta }\text{g}$ and η being the magic asymmetric gradient ratio. A weak constant gradient along z-axis was applied throughout the stimulated echo time for both sequences in order to suppress undesired coherence pathway as well as radiation damping artifacts.

All data were processed using routines written in Matlab (Mathworks, Natick, MA). The apparent diffusion coefficient (ADC) was derived using a mono-exponential fitting of echo intensities of low b values (b<1,000 s/mm²). Because the exponential decay behavior of diffusion measurement is fulfilled only if the displacement encoding is greater than the inverse of the sample length (i.e. γ.g.τ < 1/L). The initial diffusion data (i.e., g=0) were discarded from the fitting to avoid discontinuity of diffusion attenuation [23].

4. RESULTS

The full width at half maximum (FWHM) for the Fourier transform of the free induction decay (FID) signals for the 90, 150 μm glass beads phantoms were 1,130 and 615 Hz, respectively; the reference phantom had a linewidth of only 60 Hz. This variation indicated that, compared to the control phantom, the glass bead systems were characterized by severe magnetic heterogeneities. The magnitudes of the background gradients were estimated to be 29.5 and 9.6 G/cm for the 90 and 150 μm glass bead phantoms, respectively [18].

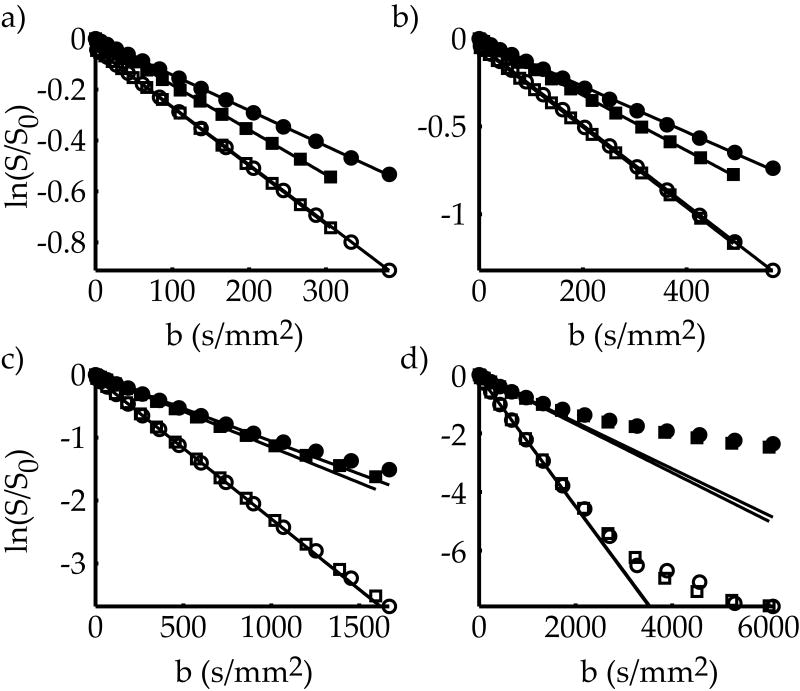
For the reference phantom, the log of the normalized echo intensity for each sequence was attenuated linearly against b values, as shown in Fig. 2 a–c. The mono-exponential fitting of bPGSTE and MAGSTE measurements overlapped, indicating that the measurements were equal (open circles and open squares, respectively). For diffusion intervals of 256 ms or more, the echo intensity at high b values reached the sensitivity limit and the normalized signal began to deviate from the mono-exponential fitting (Fig. 2 d). The obtained diffusion rates were 2.24 ± 0.02 and 2.25 ± 0.03 μm² / ms (mean ± S.D.) for bPGSTE and MAGSTE sequences, respectively. Given that the reference phantom was reasonably homogeneous, identical results were expected. For the glass bead phantoms, however, the bPGSTE measurements (solid circles) showed less attenuation than the MAGSTE sequence (solid squares), especially at short diffusion times, indicating that the diffusion coefficient measured with the bPGSTE sequence is less than that attained using the MAGSTE method. Their difference was reduced at longer evolution intervals, and the measurements almost converged for diffusion times of 128 ms or more. Furthermore, for long diffusion times, the signal at high b values clearly deviated from the mono-exponential fitting. This deviation may be attributed to the fact that the diffusion process within porous media at long diffusion time is not strictly Gaussian, which can be caused by diffusion restriction and surface relaxation. Such non-Guassian behavior becomes more prominent at large b-values, as shown in Fig. 2d.

Fig 2.

Representative plots of diffusion attenuation from the reference phantom (open squares and circles) and glass beads phantom with the mean size of 90 μm (filled squares and circles) at evolution times of 8, 16, 64 and 256 ms (a–d). The bPGSTE and MAGSTE measurements were shown in circles and squares, respectively, with the least square fitting of low b values (<1,000 s/mm²) shown in solid lines.

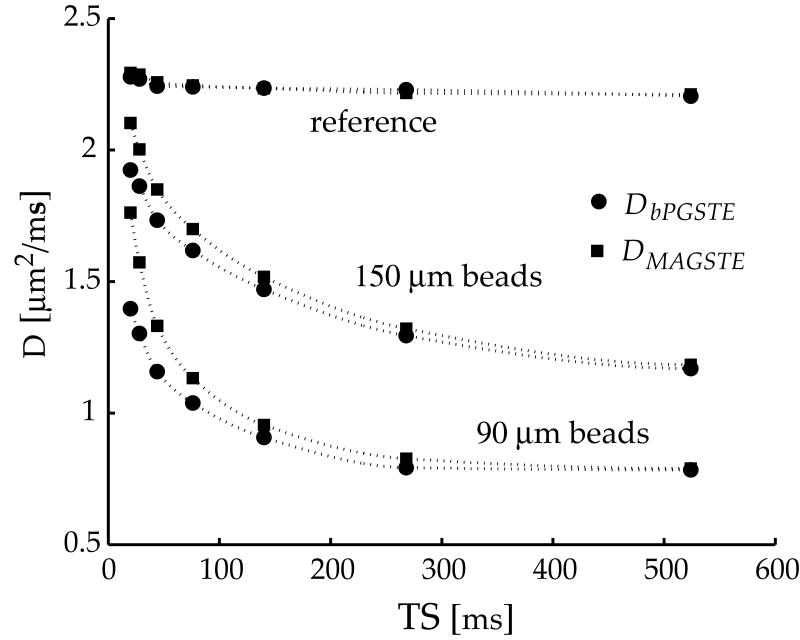
The measured diffusion coefficients are shown in Fig 3. Measurements from both sequences overlapped across all diffusion intervals for the reference phantom. Diffusion rates for the glass bead phantoms, however, were significantly less than those of the reference phantom, especially at long diffusion time. The reduced diffusion rate of the glass bead phantom can be attributed to restricted diffusion when spin displacement is comparable to the representative length scale of the diffusion barriers, causing the ADC at longer diffusion times to plateau. For the 90 μm bead phantom, diffusion coefficient plateaued near 0.8μm²/ms. In contrast, diffusion measurement continued to decrease until the last observation time point (i.e., 512 ms) for the 150 μm bead phantom, attesting to its larger pore size. In addition, when the bPGSTE and MAGSTE measurements at equal diffusion times were compared, the bPGSTE measurements were consistently lower than the MAGSTE results. For instance, the bPGSTE diffusion coefficients for the shortest storage time point (i.e., TS= 8ms) were 1.4 and 1.92 μm²/ms, whereas the MAGSTE measurements were 1.76 and 2.1 μm²/ms for 90 and 150 μm glass bead phantoms, respectively (Table 1). Additional experiments were conducted with a reduced coding interval (i.e., the coding interval was reduced from τ = 6 ms to τ = 4 ms). As expected, the reference phantom measurements did not change. On the other hand, an increase in the apparent diffusion coefficients (ADC) at the shorter coding interval was observed in both glass bead systems. The bPGSTE measurements increased by 15% and 6%, while the MAGSTE measurements changed by 7% and 3%, respectively, for the 90 and 150 μm bead phantoms, providing evidence that although the heterogeneous background gradients may affect both bPGSTE and the MAGSTE measurements, the MAGSTE method is clearly less susceptible to such artifacts. In addition, the surface-to-volume ratio (S/V) was derived by fitting the normalized diffusion rate with diffusion length of short duration (i.e., $\sqrt{{\text{D}}_0\text{t}}<15\mu \text{m}$) using [24; 25],

Fig 3.

The measured diffusion rates as a function of the evolution time. The MAGSTE and bPGSTE measurements were shown in filled squares and circles, respectively. For the reference phantom, the measurements from both sequences were identical. However, for the glass beads phantoms, bPGSTE measurements were significantly lower than those measured using MAGSTE technique, especially at short evolution intervals. On the other hand, the bPGSTE and MAGSTE measurements became equal at long evolution time as a result of restricted diffusion and dominating diffusion attenuation during the evolution intervals.

Table 1.

Diffusion coefficients calibrated using the bPGSTE and MAGSTE methods from the reference and glass beads phantoms. For the reference phantom, measurements from both sequences were equal and showed very little change when the encoding time was varied. On the other hand, for glass beads phantoms, the MAGSTE diffusion measurements were significantly higher than those measured using bPGSTE method. When the coding interval (τ) was reduced from 6 to 4 ms, bPGSTE measurements for the shortest storage time (i.e. TS= 8ms) increased by 15% and 6% for 90 and 150μm beads phantoms, respectively, while the MAGSTE measurements showed only a moderate change of 7% and 3%, respectively.

Phantom	DbPGSTE (μm2/ms)		Change (%)	DMAGSTE (μm2/ms)		Change (%)
	τ =6 ms	τ=4 ms		τ=6 ms	τ=4 ms
90 μm beads	1.40	1.65	15%	1.76	1.90	7%
150 μm beads	1.92	2.05	6 %	2.1	2.17	3%
Reference	2.24 ± 0.02			2.25 ± 0.03

$$\frac{\text{D}(\text{t})}{{\text{D}}_0}=1-\frac{4}{9\sqrt{\pi }}\frac{\text{S}}{{\text{V}}_{\text{p}}}\sqrt{{\text{D}}_0\text{t}}+\text{O}({\text{D}}_0\text{t})$$ (9)

The S/V characterized using the MAGSTE measurements were 0.16 and 0.10 μm⁻¹ for the 90 and 150 μm beads, respectively. On the other hand, the S/V derived using bPGSTE measurements were 0.09 and 0.08 μm⁻¹. For monospherical glass beads, the theoretical estimation of S/V has been shown as $\frac{\text{S}}{\text{V}}=\frac{6(1-\phi )}{\phi \text{b}}$, where φ is the porosity and b is the diameter of the beads [26]. Therefore, with a porosity of 0.26, the theoretical prediction of S/V for the 90 and 150μm beads phantoms is 0.19 and 0.11 μm⁻¹, respectively. That the S/V characterized using the MAGSTE sequence is roughly the same as theoretical predictions and the ratio of S/V for the two glass beads phantoms (i.e., 0.16/0.1=1.6) is about inversely proportional to the mean bead diameter suggests that the MAGSTE diffusion technique is a reasonably accurate means of characterizing structure. In contrast, the S/V measured with conventional bPGSTE were significantly less than the theoretical values and, in fact, the experimental measurements for the 90 and 150 μm bead phantoms were nearly equal (0.09 versus 0.08), suggesting that the bPGSTE technique is susceptible to background gradient artifacts.

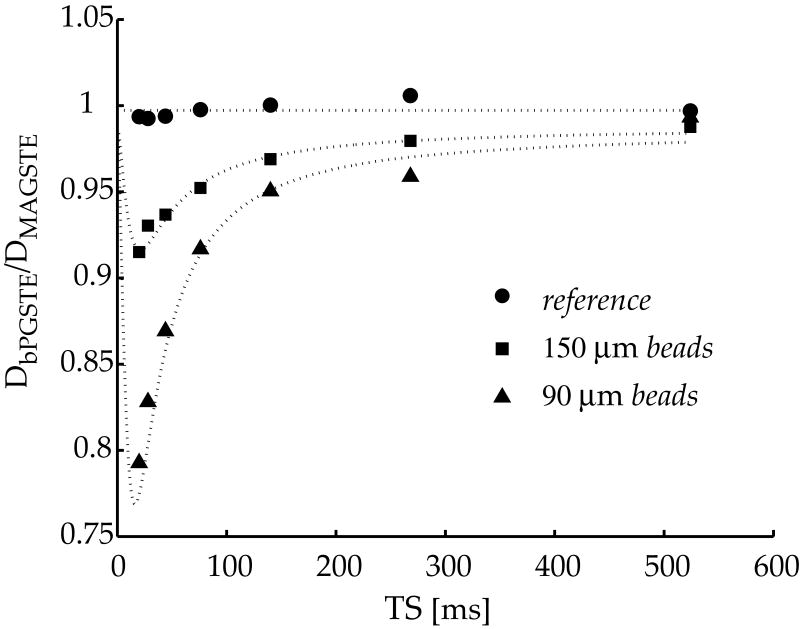
Shown in Fig. 4 are the bPGSTE diffusion coefficients normalized by MAGSTE measurements (i.e., D_bPGSTE/D_MAGSTE) as functions of diffusion intervals. At storage time of 8 ms, the normalized diffusion rates were 79.3% and 91.5%, respectively, for 90 and 150 μm glass bead phantoms. They were significantly less than 1 due to the incomplete suppression of the heterogeneous background gradients, especially for the bPGSTE technique. In order to explore the effects of background gradients on the bPGSTE measurements, the normalized diffusion rate was fitted against the evolution time, as given in Eq. (8), and shown by dotted lines. The variances of the background gradients were 11.6, 6.3 and 0 Gauss/cm with η=1, and the correlation times were 12 ms, 14 ms and 2.1 s for the 90 and 150 μm glass beads and reference phantoms, respectively.

Fig 4.

Fitting of the normalized diffusion rates, (i.e., D_bPGSTE/D_MAGSTE) using Eq. (8). The variances of the background gradients were obtained as 11.6, 6.3 and 0 G/cm, with their correlation times being 12 ms, 14 ms and 2.1 s for the 90, 150μm glass beads and reference phantoms, respectively.

5. DISCUSSION

In this study, we showed that when the coding interval is reduced, the diffusion values measured with the bPGSTE sequence increased significantly; meanwhile only a moderate change in the calibrated diffusion rate was observed when using the MAGSTE technique. Although both diffusion coefficients increased with a reduced encoding interval, the MAGSTE measurement was clearly less affected, showing that the MAGSTE technique can better suppress the heterogeneous background gradients of intermediate range, and is therefore superior to the bPGSTE method. The moderate increase in the MAGSTE measurement may be caused by variation in the background gradients within the gradient encoding/decoding interval; neither the bPGSTE nor the MAGSTE sequence can fully suppress such fast varying background gradients, which may be very pertinent in systems with microscopic heterogeneities, where spin displacement during the encoding/decoding intervals can be comparable to the length scale of the local structure. The MAGSTE technique can suppress long-range background gradients equally as well as the bPGSTE method, and its effectiveness in suppressing background gradients of intermediate range makes it superior to the bPGSTE technique and suitable for measuring diffusion processes within heterogeneous systems.

That the surface area-to-volume ratio characterized with the MAGSTE technique agreed reasonably well with theoretical derivation suggests that MAGSTE can effectively suppress background gradient artifacts and provide accurate diffusion measurements even in systems with severe heterogeneity. On the other hand, characterization using the bPGSTE technique showed nearly equal S/V with significant deviation from the theoretical predictions, which suggests that we must be very careful when interpreting structures derived with the conventional sequence, especially when variation of background gradients during the evolution intervals is not negligible. In addition, that the normalized bPGSTE measurements deviated significantly from 1 for t=0 indicates that artifacts arising from background gradients invalidate Pade approximation for describing the bPGSTE diffusion measurement. Therefore, only S/V fitting using short diffusion length was investigated [12; 27].

The normalized diffusion rate is expected to be one at infinitesimal diffusion times, as it falls into the delta gradient pulse approximation. However, in this study, the greatest difference was observed at the shortest storage time of 8 ms. Such a discrepancy may be attributable to the fact that proper suppression of the background gradient by the bPGSTE measurement requires a static gradient throughout the echo time. In our study, the shortest evolution time was 20 ms (i.e., Δ + 2τ, with Δ = 8ms and τ=6ms); which may not be completely negligible when compared with the derived characteristic correlation time of 12–14 ms. If the diffusion time can be further reduced, it is expected that the bPGSTE and MAGSTE measurements will be equal at very short evolution intervals. However, sufficient labeling of the spatial position of spins requires extraordinarily strong applied gradients that are beyond the limits of our hardware. Conversely, it suggested that use of the MAGSTE method is advantageous for quantification of diffusion coefficients when the delta gradient pulse approximation cannot be completely fulfilled.

It is interesting to note that the background gradients estimated with the spectral linewidth were larger than those obtained by fitting the bPGSTE and MAGSTE diffusion measurements. This may be attributed to the fact that there is a distribution of background gradients for the glass beads used in our study, which had a wide range of sizes and a sphericity about 80%. It is also likely that those spins that experience very strong background gradients have shorter dephasing times; they therefore lose coherence prior to the refocusing pulse (i.e., π pulse) and do not contribute to the signal. Thus, the background gradient estimated with diffusion results may mainly reflect spins with long relaxation time, making the deduced background gradients less than those obtained from spectral linewidth measurements. However, we hypothesize that glass beads with moderate magnetic heterogeneity and size distribution may better model porous media than high-grade monospheres, and therefore, can provide useful insights for diffusion NMR measurements of porous media.

In this study, we explored an exponential correlation function with the assumption that background gradients remain static throughout encoding and decoding intervals, independently, and change only during the evolution interval. However, the encoding/decoding time used in our study (2τ=8 and 12ms) is equal to or longer than the shortest storage time (Δ =8ms) we explored, thus our assumption may be too simplistic. Indeed, the derived correlation time is about 12 ms, indicating that the encoding/decoding time may involve non-negligible change in the background gradient. However, it is likely that there will be a distribution of correlation times. The MAGSTE technique can effectively suppress background gradients of moderate and long correlation times, and therefore, the background gradients derived through diffusion measurements could be considered the lower limit. For instance, the correlation coefficients for the background gradients of 90 μm glass beads are 51% and 37% for gradient encoding intervals of 8 and 12 ms, respectively. For 150 μm glass beads, the correlation coefficient will be even greater given its longer correlation time. The coding interval can be further reduced to minimize the fluctuation of background gradient, which will improve the suitability of the proposed model for background gradients. In this study, we explored only simple exponential correlation and Gaussian distribution functions for modeling the background gradients. Other models such as those with stretched exponents may better represent the behaviors of heterogeneous background gradients.

6. CONCLUSION

In this study, we showed that the MAGSTE technique provides significantly improved diffusion measurements when compared to the conventional bPGSTE technique in phantoms with microscopic heterogeneities. In addition, the surface area-to-volume ratio derived with the MAGSTE technique matched well with those from theoretical predictions, suggesting that MAGSTE can effectively suppress measurement errors induced by heterogeneous background gradients. Moreover, we also developed a simple model to qualitatively describe the effects of heterogeneous background gradients on the pulsed gradient stimulated echo diffusion measurements.