Response variability of marmoset parvocellular neurons

Abstract

This study concerns the properties of neurons carrying signals for colour vision in primates. We investigated the variability of responses of individual parvocellular lateral geniculate neurons of dichromatic and trichromatic marmosets to drifting sinusoidal luminance and chromatic gratings. Response variability was quantified by the cycle-to-cycle variation in Fourier components of the response. Averaged across the population, the variability at low contrasts was greater than predicted by a Poisson process, and at high contrasts the responses were approximately 40% more variable than responses at low contrasts. The contrast-dependent increase in variability was nevertheless below that expected from the increase in firing rate. Variability falls below the Poisson prediction at high contrast, and intrinsic variability of the spike train decreases as contrast increases. Thus, while deeply modulated responses in parvocellular cells have a larger absolute variability than weakly modulated ones, they have a more favourable signal: noise ratio than predicted by a Poisson process. Similar results were obtained from a small sample of magnocellular and koniocellular (‘blue-on’) neurons. For parvocellular neurons with pronounced colour opponency, chromatic responses were, on average, less variable (10–15%, p < 0.01) than luminance responses of equal magnitude. Conversely, non-opponent parvocellular neurons showed the opposite tendency. This is consistent with a supra-additive noise source prior to combination of cone signals. In summary, though variability of parvocellular neurons is largely independent of the way in which they combine cone signals, the noise characteristics of retinal circuitry may augment specialization of parvocellular neurons to signal luminance or chromatic contrast.

Trichromatic colour vision is a distinctive feature (amongst mammals) of primate vision. The great majority of diurnal primate species studied so far express more than one spectral class of cone in the medium-to-long wavelength range of the visible spectrum (Jacobs, 1998; Tan & Li, 1999). Primate red–green colour vision appears inextricably linked to the presence of a cone-dominated fovea and a distinct post-receptoral midget-parvocellular pathway. Knowledge of how luminance and chromatic signals are transmitted by the main afferent (parvocellular, magnocellular and koniocellular) pathways is fundamental for an understanding of primate vision, and perhaps for understanding parallel sensory pathways in general.

Parvocellular (PC) neurons in trichromatic primates typically derive functional input from medium- (M) and long-wavelength-sensitive (L) cone photoreceptors. These receptors make differential contributions to the excitatory (‘centre’) and inhibitory (‘surround’) components of the receptive field. This leads most parvocellular neurones to display red–green opponent response properties (Wiesel & Hubel, 1966; Dreher et al. 1976; Derrington et al. 1984; Smith et al. 1992). Since the parvocellular neurones show the smallest receptive fields at any visual field position, this cell class is also considered to contribute to high-acuity spatial vision at high image contrast (Derrington & Lennie, 1984; Blessing et al. 2004). However, the question as to whether parvocellular receptive fields are specialized to signal chromatic or luminance variation has not been resolved (Shapley & Perry, 1986; Rodieck, 1998; Reid & Shapley, 2002). Understanding the functional specialization of parvocellular neurons is the main goal of the present study.

Understanding the functional specialization of parvocellular neurons requires a characterization of not only sensitivity, but also response variability. Noise in the phototransduction process sets a lower limit to response variability. However, it is possible that there are differences in the details of spike generation associated with varying degrees of chromatic opponency, much as there are differences between parvocellular and magnocellular neurons (Kremers et al. 2001). Moreover, the intraretinal circuitry that underlies the combination of M and L cone signals may result in differences in response variability across parvocellular neurons with varying degrees of opponency, even at constant response magnitude.

Previous studies of the functional specialization of parvocellular neurons for chromatic signals have indicated that noise is independent of signal size (Croner et al. 1993; Kremers et al. 2001; Sun et al. 2004), or at least, assumed that noise is independent of the chromatic composition of the input (Kara et al. 2000; Reid & Shapley, 2002; Blessing et al. 2004; Uzzell & Chichilnisky, 2004). However, these assumptions have not been tested specifically. We therefore undertook a detailed analysis of response variability and its relation to red–green opponency in parvocellular neurons of the marmoset lateral geniculate nucleus.

In the marmoset, a single genetic locus (on the X chromosome) encodes for medium- to long-wavelength photopigments (Hunt et al. 1993; Yeh et al. 1995; Blessing et al. 2004). There are three alleles at this locus which encode for pigments with absorption maxima close to 543, 556 and 563 nm. Consequently, all males are dichromats. There are six female phenotypes: three dichromatic phenotypes (homozygous for the M/L allele) and three phenotypes with trichromatic potential (heterozygous for the M/L allele). In the present study, we determined the photopigment complement of trichromatic animals prior to physiological measurements (Blessing et al. 2004), thus allowing construction of stimuli which generate defined levels of contrast in the M/L cones expressed by each animal. Moreover, these well-characterized genetics allowed us to compare the signal and noise characteristics not only between dichromatic animals and animals with the potential for trichromacy, but also between animals with a narrow (7 nm), medium (13 nm) and wide (20 nm) separation between their M/L photopigments.

Some of the current findings have been reported in abstract form (Victor et al. 2005). Response amplitude for some stimuli for a subset of the neurons was previously described (Blessing et al. 2004; Buzás et al. 2006; Forte et al. 2006).

Methods

We analysed extracellular recordings of neurons in the lateral geniculate nucleus of the marmoset Callithrix jacchus. The vast majority were PC neurones; for purposes of comparison a small number of magnocellular (MC) and koniocellular (KC) ‘blue-on’ neurons (KC-bon) was also recorded. Procedures are approved by the Animal Ethics Committee of the Victorian College of Optometry, and conform to the American Society for Neuroscience and Australian National Health and Medical Research Council policies on the use of animals in neuroscience research. Animals were anaesthetized with inhaled isoflurane (Forthane, Abbott, Sydney, Australia, 1.5–2%) and intramuscular ketamine (Ketalar, Parke-Davis, Sydney, 30 mg kg⁻¹) for surgery. A femoral vein and the trachea were cannulated. Animals were artificially respired with a 70%: 30% mixture of NO₂: Carbogen (5% CO₂ in O₂). A venous infusion of 40 μg kg⁻¹ alcuronium chloride (Alloferin, Roche, Sydney) in dextrose Ringer solution (Baxter, Sydney) was infused at a rate of 1 ml h⁻¹ to maintain muscular relaxation. Anaesthesia was maintained during recording with a venous infusion of sufentanil citrate (Sufenta-Forte; 4–8 μg kg⁻¹ h⁻¹). Electroencephalogram (EEG) and electrocardiogram signals were monitored to ensure adequate depth of anaesthesia.

The EEG signal was subjected to Fourier analysis. Dominance of low frequencies (1–5 Hz) in the EEG recording, and absence of EEG changes under noxious stimulus (tail pinch) were taken as the chief sign of an adequate level of anaesthesia. Heart rate was likewise unaffected by this noxious stimulus. We found that low dose rates in the range cited above were always very effective during the first 24 h of recording; thereafter if drifts towards higher frequencies in the EEG record became evident, they were counteracted by increasing the rate of venous infusion.

The typical duration of a recording session was 48–72 h. Additional details of the animal preparation, methods of visual stimulation, and cell classification are described elsewhere (Blessing et al. 2004). At the termination of the recording session the animal was killed with an overdose of pentobarbitone sodium (80–150 mg kg⁻¹, i.v.).

Data consisted of response to drifting sinusoidal gratings generated using a VSG Series Three video signal generator (Cambridge Research Systems, Cambridge, UK) and presented on a television monitor (Reference Calibrator Plus, Barco, Kortrijk, Belgium) at a frame rate of 80 Hz and a mean luminance close to 25 cd m⁻². Stimuli were viewed through the natural pupil. Pupil diameter varied between ∼2–4 mm, yielding retinal illuminance between 78 and 315 Td. The reader should note that the relatively small size of the marmoset eye (Troilo et al. 1993) means that retinal flux will be about 4-fold higher than for human at a given stimulus intensity. For PC neurons, responses to red–green chromatic modulation (‘RG’) and luminance modulation (‘LUM’) were recorded at 10 contrast levels, 0, 0.0156, 0.0312, 0.0625, 0.0937, 0.125, 0.25, 0.375, 0.5 and 1, where a contrast of 1 represents the maximum deliverable contrast for the chromatic stimulus, and the maximum deliverable Michelson contrast for the luminance stimulus. For trichromats, the relative intensity of the red and green guns of the monitor was set to provide approximately equal-and-opposite contrast to the M and L cones predicted by prior genetic analysis (using PCR–restriction fragment length polymorphism) of the cone opsin-encoding genes (for details see Blessing et al. 2004). The cone contrasts delivered by these stimuli are shown in Table 1. For dichromats the relative intensity of the red and green guns was set at the ‘silent substitution’ point for the single class of M/L cone present. This strategy was chosen to give the best functional equivalent of an isoluminant red–green stimulus across the six phenotypes tested. For simplicity we assume that M and L cones are present in equal proportions in the retina of trichromatic female animals. Behavioural data (Tovée et al. 1992) and limited anatomical data from the marmoset fovea (Bowmaker et al. 2003) are consistent with this assumption.

Table 1.

Cone contrasts for red–green (RG) and luminance (LUM) stimulus conditions

	Δ7	Δ7	Δ13	Δ13	Δ20	Δ20
	M (556)	L (563)	M (543)	L (556)	M (543)	L (563)
RG	0.035	–0.072	0.1245	–0.1257	0. 1756	–0.1813
LUM	1.000	1.000	1.000	1.000	1.000	1.000

Michelson cone contrasts given by red–green (RG) or luminance (LUM) modulation are shown for the M and L cone types in the Δ7, Δ13 or Δ20 phenotypes. Numbers in parentheses show the λ_max of the M or L cone pigment. Positive values for RG indicate that modulation from red (phase 0 deg) to green (phase 180 deg) increases cone excitation; negative values indicates the converse.

Data from MC and KC blue-on cells comprised responses to the LUM stimulus, responses to an achromatic contrast series presented at the same contrast levels as the LUM stimulus and, for KC blue-on cells, responses to short wavelength-sensitive (S) cone-isolating gratings (SWS). The SWS grating delivered ∼0.66 Michelson contrast to the S cone and less than 0.04 Michelson contrast to the M/L class cones. See Blessing et al. (2004) and Forte et al. (2006) for additional details related to colour calibration, and genetic determination of cone complements.

The PC cells were classified as ‘opponent’ if the response amplitude to chromatic modulation at maximal contrast was greater than 10 impulses s⁻¹, and was also greater than the response amplitude when the M and L cones were modulated in-phase at the equivalent cone contrast (for example, ∼25% luminance contrast (0.1245 + 0.1257) for the Δ13 phenotype). However, the reader should note that the PC cells displayed a continuum of opponent properties, so this classification is made for the purpose of analysis, rather than implying the existence of discrete opponent and non-opponent cell classes.

Stimulation protocol

For each neuron, the spatial frequency and orientation yielding maximum (‘optimum’) response to a drifting luminance modulated grating were first determined. Data were collected under four conditions: luminance modulation at low (< 0.02 cycles deg⁻¹) spatial frequency (‘LUM’), low spatial frequency red–green chromatic modulation (‘RG’), optimum spatial frequency and orientation luminance modulation (‘LUM-high’), and optimum spatial frequency and orientation red–green chromatic modulation (‘RG-high’). Stimuli were normally vignetted with a 4 deg circular aperture. A set of responses to the 10 contrasts under one of these conditions will be designated a ‘dataset’ (Table 2). The temporal frequency of the stimulus was the same for all measurements on any given neuron. For nearly all (143/156) PC neurons studied, the temporal frequency was between 3.5 and 4.5 Hz (one neuron was studied at 5 Hz, six at 6 Hz, two at 7 Hz, and four at 8 Hz). Temporal frequency range for MC and KC cells was similar (26 datasets at 4 Hz, 2 at 5 Hz, 1 at 5.5 Hz, 10 at 6 Hz, and 3 at 8 Hz). Spatial frequency tuning, orientation tuning, and contrast sensitivity in subcortical neurons show little dependence on temporal frequency in this range (Frishman et al. 1987; Kremers et al. 2001; Forte et al. 2006).

Table 2.

Summary of parvocellular data sets analysed

				Number of datasets
Phenotype	Number of animals	Opponency	Number of cells	LUM	RG	LUM-high	RG-high	Total
d543	4	Non-opp	26	25	14	6	2	47
d556	2	Non-opp	15	13	14	8	8	43
d563	1	Non-opp	8	5	4	5	5	19
d543 + d556 + d563	7	Non-opp	49	43	32	19	15	109
Δ7	1	Non-opp	19	9	9	14	17	49
Δ13	3	Non-opp	34	29	30	25	22	106
		Opponent	18	16	16	13	14	59
Δ13	3	All	52	45	46	38	36	165
Δ20	2	Non-opp	6	4	5	1	4	14
		Opponent	30	27	26	21	20	94
Δ20	2	All	36	31	31	22	24	108
All	13	All	156	128	118	93	92	431

Dichromatic phenotypes are designated d543, d556, or d563 depending on the maximal absorption of the L/M photopigment (543, 556 or 563 nm); trichromatic phenotypes are designated Δ7, Δ13 and Δ20 indicating narrow (7 nm), medium (13 nm) and wide (20 nm) separation between their medium to long-wavelength photopigments. Embolded lines are subtotals.

For PC cells each stimulus was presented in N_trial = 3 blocks of ascending contrasts (approximately 3.5 s each, containing N_cycle = 13 complete periods of a 4 Hz stimulus at one contrast). This typically provided a total of N_trial × N_cycle = 39 recorded periods of responses to each stimulus. Stimulation trials were interleaved with blank intervals (during which the display was held at mean luminance). In some (126/431) datasets, data were collected during these blanks (N_trial = 30), typically providing N_trial × N_cycle = 390 periods of data. In others, data were collected during blank periods only at the end of each contrast series, providing N_trial × N_cycle = 39 periods of data. In the latter experiments the blank intervals between stimulation trials were of shorter duration (approximately 0.5 s each). These two experimental protocols yielded similar results, and the data are therefore pooled. Data collection normally began at least 125 ms following stimulus onset. We analysed each data set for evidence of non-stationarity (Appendix 1), but did not see any sign of contrast adaptation effects at the beginning of the collection period. The stimulus and non-stationarity analysis for MC and KC-bon cells were the same as for PC cells with two exceptions. First, about half of the datasets (19/42) comprised two contrast blocks where each contrast condition was presented for 3–5 s. Second, responses were only recorded at or near optimal spatial frequency for the majority of these cells (34/36, 95%).

Data analysis

Measures of response and response variability

Our primary response measures were the Fourier components of the response from each stimulus cycle. We denote the kth Fourier component of the response during cycle n_cycle of trial n_trial by z_k(n_trial, n_cycle). Thus,

(1)

where the summation is over all spike times that occurred on trial n_trial during stimulus cycle n_cycle, and P is the period (i.e. the duration of each stimulus cycle). Thus, the summation in eqn (1) includes spikes that occur at times t between (n_cycle − 1)P and n_cycleP. We chose normalizing constants b₀ = 1 so that the 0th Fourier coefficient corresponds to the mean firing rate, and b_k = 2 for k ≠ 0 so that the magnitude of the higher Fourier coefficients z_k(n_trial, n_cycle) correspond to the amplitude of the rate modulation at the frequency f_k = k/P. This analysis was carried out for k = 0 (the mean firing rate), k = 1 (the fundamental response, at or close to 4 Hz), k = 2, and k = 20 (close to the frame rate of the display, 80 Hz).

The mean Fourier response component at the harmonic k, z_k, is determined by the (vector) grand average of z_k(n_trial, n_cycle) across all cycles and trials:

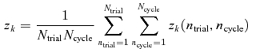(2)

The variability V_k of the kth Fourier component was quantified by the variance of Z_k(N_trialN_cycle) across all trials and cycles, as estimated by:

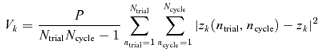(3)

Note that we have included a factor of P, the stimulus period, so that variances have units of (impulses² s⁻¹). With this convention, the expected variance of the DC component V₀ of a Poisson process is equal to the mean firing rate, z₀.

We examined each dataset (see Appendix I for details) for evidence of a systematic change in responses across trials of the same contrast, or evidence of adaptation within trials. Of the 523 PC datasets screened, 92 were excluded on the basis of a change in response amplitude across trials, yielding the 431 datasets described above. A slightly larger proportion of datasets was excluded for MC cells (25 screened, 6 excluded) and KC-bon cells (42 screened, 19 excluded).

For each stimulus set, we compared variance at the highest contrast with variance at the lowest contrast, using an F-statistic with b_kN_cycle(N_trial − 1) degrees of freedom in both the numerator and the denominator. We also used a standard non-parametric method, the jackknife (Efron, 1982), to estimate confidence limits on the variance. The jackknife estimates confidence limits (and bias) by comparing the analysis of the full dataset with an analysis of a dataset in which one sample has been deleted. As expected from a non-parametric method, confidence limits obtained by the jackknife varied more from contrast to contrast within each dataset, but otherwise agreed with those obtained from the F-statistic. We also assessed the shape of the distribution of response estimates around their mean, by calculating a normalized ratio of the major and minor axes of the best-fitting Gaussian:

(4)

where d_max and d_min are, respectively, the maximum and minimum ellipse diameter. Estimates of I_ellipse were debiased, and confidence limits were obtained, via a jackknife based on individual periods. No substantial deviation from circularity was found (I_ellipse typically < 0.1; see for example Fig. 1C). This circularity simplifies the subsequent analysis. If the responses were distributed asymmetrically, one could not characterize its spread by a single parameter (i.e. the size of a best-fitting circular Gaussian); one would instead have to use at least three parameters – e.g. major axis, minor axis and tilt.

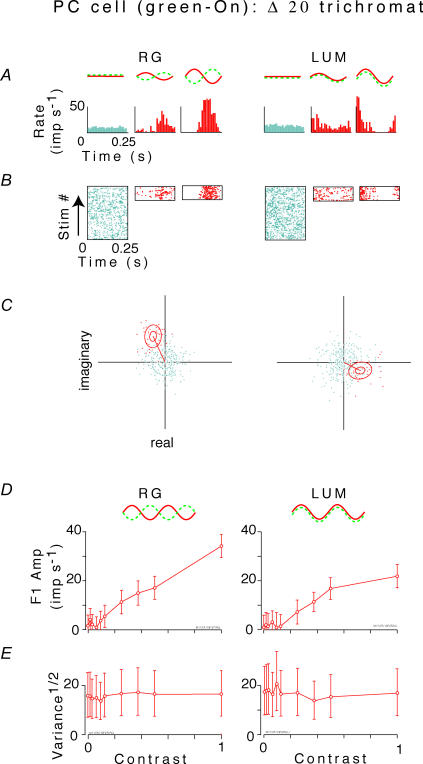
Figure 1. Analysis of the fundamental (first harmonic) response of an opponent parvocellular neuron in a?20 animal to red–green chromatic (RG) and luminance (LUM) flicker.

A and B, post-stimulus histograms and rasters of responses to gratings at contrast of 0, 0.25 and 1.0. C, fundamental Fourier component z₁(n_trial, n_cycle) of responses to each stimulus cycle, for zero contrast (blue or grey) and a contrast of 1.0 (red or black). Each point's position in the complex plane represents a value of z₁(n_trial, n_cycle) (eqn (1)). The outer ellipse is the 1/e level curve of the Gaussian with mean and variance that match those of the data. The inner ellipse is a 95% confidence region on the average response, determined by the Hotelling T² test (Anderson, 1958). D, amplitude of mean first harmonic response |z₁(C) | (eqn (2)) as a function of contrast C. Error bars represent 95% confidence limits, as calculated by T²_circ (Victor & Mast, 1991). E, variability of the first harmonic response, plotted as 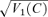, at each contrast C. Error bars represent 95% confidence limits, as calculated by an F statistic (see Appendix I).

The validity of these statistical tests requires that response estimates from separate cycles can be regarded as independent. Responses to adjacent cycles may not be completely independent (e.g. since a spike at the end of one cycle has a refractory period that extends into the next cycle). Therefore, we also repeated the analysis by calculating Fourier components and their variances from sets of four adjacent cycles, and obtained substantially similar results. This correspondence (Victor & Mast, 1991), and the consistency of confidence limits based on parametric (F-statistics) and the jackknife, supports the use of the parametric statistics below.

Empirical variance–mean relationship

For each harmonic k and each spatio-chromatic stimulation condition (LUM, RG, LUM-high RG-high), we sought an empirical relationship between the mean Fourier amplitude |z_k(C)| and its variability V_k(C), as contrast C varied. The goal of the analysis was to provide a way to interpolate the variance–mean relationship and thereby ‘read off ’ the variance that corresponds to an arbitrary response size, for each cell. Pilot analysis indicated that this relationship was not always described by simple functional relationships (e.g. V_k(C) proportional to |z_k(C)| or V_k(C) independent of |z_k(C)|). Therefore, we chose to use a variety of functional forms, each of which was an instance of

(5)

As described in Appendix I, we used a hierarchical procedure in which we first sought fits in which one or more of the terms of eqn (5) were omitted, or with γ = 1, and the general form of eqn (5) was only used if simpler functional forms failed. This approach avoids overfitting to a four-parameter form if a simple one suffices, and also avoids biasing an interpolation by underfitting, i.e. forcing the data into a form that it does not fit.

Empirical contrast–response function

For each harmonic k and each spatio-chromatic stimulation condition, we determined an empirical relationship between the mean Fourier amplitude |z_k(C)| and the nominal stimulus contrast C. As with the variance–mean relationship, our goal was not a mechanistic model, but merely to provide a robust estimate of the contrast C needed to evoke a particular response amplitude |z_k(C)|, from the measured set of responses (10 contrasts). We used a generalized Naka-Rushton (Naka & Rushton, 1966) relationship

(6)

with one or more of the parameters a, b, γ and η held fixed to avoid overfitting.

Results

Responses of 156 PC neurons in 13 marmosets were studied, yielding 523 datasets (not all neurons were studied under all four conditions). After elimination of datasets that had statistical evidence of non-stationarity, 431 datasets were available for quantitative analysis (see Table 2). The population included dichromats with all three of the long-wavelength alleles (hereinafter, these dichromatic (d) phenotypes are designated d543, d556 and d563), and trichromats with all three pairs of the long-wavelength alleles (designated according to the spectral separation (Δ) between the medium and long-wavelength pigments: Δ7, Δ13 or Δ20). Note that under the criteria we used, none of the 19 cells recorded in the Δ7 animal were classified as cone-opponent.

Responses of 19 magnocellular neurons and 17 koniocellular (blue-on) neurons in 14 marmosets were studied. Eleven of these animals were also in the group described above. The goal of this analysis was to establish whether the response amplitude and variance relationships show substantial differences among afferent cell classes, rather than to study details related to the chromatic properties of the stimulus. Results for MC and KC-bon cells were therefore pooled across stimulus conditions, and across colour vision phenotypes.

Variance as a function of contrast

Figure 1 illustrates analysis of the fundamental response component of an opponent parvocellular neuron, elicited by sinusoidal red–green (RG) and luminance (LUM) flicker. Conventional post-stimulus histograms and rasters are shown in panels A and B for contrasts of 0, 0.25 and 1.0. Panel C shows the cycle-by-cycle measurements of the fundamental Fourier components (e.g. as in Croner et al. 1993; Kremers et al. 2001) for the highest contrast stimulus, and in the absence of stimulation. This cloud of the cycle-by-cycle Fourier components (Fig. 1C) is a graphical indication of the variability of the fundamental Fourier component. Note that each cloud is very nearly circular. Since there were 39 cycles of C = 1.0 but 390 cycles of C = 0, there appear to be more outliers in the latter case. However, when response variability is quantified (eqn (3)), there is no difference in variability of the fundamental response between high-contrast stimulation and low-contrast stimulation (radii of the circles in panel C). Responses grew approximately linearly with chromatic contrast (panel D, left). Responses to luminance contrast (panel D, right) were somewhat smaller, and showed mild evidence of saturation. There are small differences in response amplitude for the zero contrast LUM and zero contrast RG conditions, although these stimuli are identical. This can be attributed to the fact that the RG and LUM data collection were done in separate blocks, and the difference is within the limits set by our statistical tests for response stationarity and independence (Appendix 1). There was no significant change in variability as a function of contrast (Fig. 1E) for this cell.

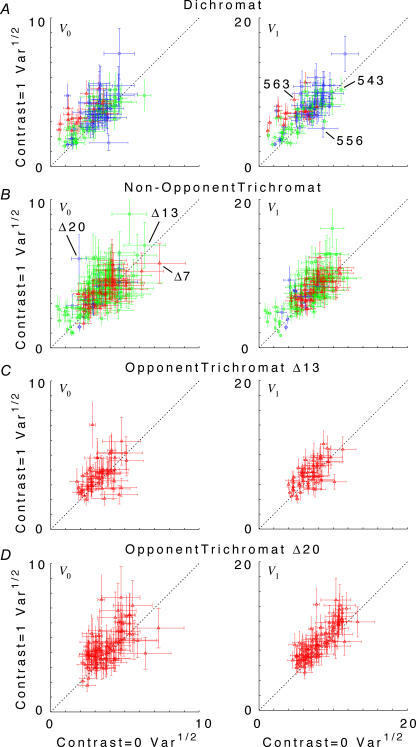
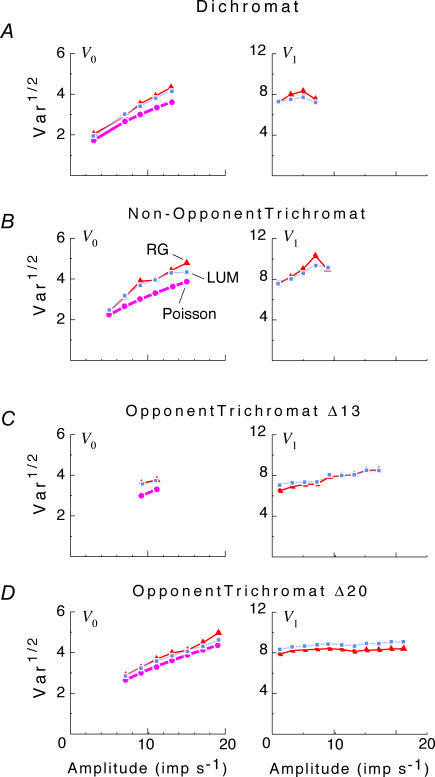
Individual cells showed a substantial range of behaviour (Fig. 2). As is evident from the confidence limits on the variance estimates, much of this diversity across the population reflects true cell-to-cell differences, rather than measurement error. The ratios of variance at high versus low contrast for individual neurons were distributed approximately in a Gaussian fashion, with a standard deviation of a factor of 1.73 (f₀) and 1.58 (f₁). However, these distributions were not centred around 1, the expectation for purely additive noise. Rather, there was a modest tendency in the direction of increased variance under high-contrast conditions. This is evident in Fig. 2, where each ‘cloud’ of data points appears slightly displaced above the 1: 1 line. The average change in variance between high contrast and low contrast conditions was a factor of 1.40 (geometric mean; 95% confidence limits, 1.32–1.49) for f₀, and a factor of 1.38 (1.30–1.46) for f₁. There was no significant difference between cell subgroups (dichromats, non-opponent cells in trichromats, and opponent cells in trichromats), or between stimulation conditions (luminance versus chromatic, low spatial frequency versus high spatial frequency).

Figure 2. Scattergrams of variance at C = 1.0 versus variance at C = 0 for the DC response (f₀), left column, and the fundamental Fourier component (f₁), right column.

Top row, all dichromat neurons. Second row, non-opponent neurons from all trichromats. Third row, opponent neurons from Δ13 trichromats. Fourth row, opponent neurons from Δ20 trichromats. Variances plotted are V₀ and V₁, as defined by eqn (3). Error bars represent 95% confidence limits on the variance estimates for each neuron, as calculated by F statistics (see Appendix 1). While there is considerable scatter across the population, the average tendency is that of greater variance at the high contrast. Note that C = 1 for a chromatic stimulus has a much lower cone contrast than a C = 1 luminance stimulus, depending on phenotype (Table 1).

We also examined the response variability at higher harmonics. Behaviour at f₂ was similar to that at f₀ and f₁: the variance at high contrast was greater than at low contrast. On average, the variance increased by a factor of 1.54 (1.46–1.63) across cells, and a standard deviation of a factor of 1.55 for distribution of ratios in individual cells. Behaviour at f₂₀ was different. As this frequency (80 Hz) was equal to the CRT monitor frame frequency in nearly all datasets, there was substantial luminance flicker at this frequency even when no stimulus was present. Consistently, in cells recorded at high visual field eccentricities we often observed overt phase-locking to the monitor frame rate at high LUM contrasts (Derrington & Fuchs, 1979; Derrington & Lennie, 1984; Williams et al. 2004). This might be expected to reduce the variance for the 80 Hz Fourier component. However, at this frequency there was a somewhat greater increase in variance between high and low contrast conditions: a factor of 1.83 (1.63–2.06) across all cell subgroups and conditions. This increase was especially large in dichromats (3.52, confidence limits 2.09–5.91) and non-opponent cells in trichromats (4.95, confidence limits 1.79–13.68) during stimulation with optimal spatial frequency luminance gratings. These increases in variance are difficult to analyse; they probably represent an interaction between driving by the low-frequency applied contrast signal and the high-frequency contrast signal of the raster display. We do not consider them further.

Before presenting the details of response variability in PC cells, we briefly describe some predictions of simple statistical models for spike trains. Consider the responses of a neuron to repeated presentations of a stimulus. The response to each presentation of the stimulus is a spike train, i.e. a sequence of events in time. Identical stimuli do not necessarily produce identical spike trains: each spike train shows some apparently random variation. Nevertheless, given a sufficiently large number of trials, the average number of spikes per unit time, a deterministic rate function r(t), can be estimated (although the reader should note that precise estimation of r(t) is not as straightforward as it might seem: Kass et al. 2005). The deterministic rate function r(t) characterizes the ‘average’ response, but does not characterize response variability. In the present study, we characterize response variability by comparing Fourier components estimated from each stimulus presentation. Since the Fourier sequence is a linear transformation of the data, the mean value of Fourier estimates from individual trials is the same as the value that would have been estimated from all of the spikes accumulated across trials. Accordingly, the mean value also converges on the Fourier components of r(t). Consequently, the variability of estimates of Fourier components on individual trials about their mean can describe response variability – and bypasses the need to estimate r(t) directly.

To interpret measures of variability in spike trains, we use simple models of the processes which give rise to spike trains, as reference points or ‘benchmarks’. In a Poisson process, the occurrence of a spike at any given time is independent of the occurrence of a spike at any other time. The term ‘Poisson’ usually implies a homogeneous Poisson process, i.e. one for which the underlying rate function r(t) is constant. However, responses to periodic modulation typically show periodic variation in response rate. Thus, a better model in this case is a modulated Poisson process: one in which the underlying rate function r(t) is time-varying, but the occurrences of spikes at different times are statistically independent events.

The statistical properties of a Poisson process (homogeneous or modulated) are entirely determined by the underlying rate function r(t). For a homogeneous Poisson process, the spike count variance (V₀) is equal to the mean spike rate (that is, the zero-order Fourier component z₀). For a modulated Poisson process, the equivalence of spike count variance and mean (V₀ = z₀) also holds, a well-known fact that is a consequence of the time-rescaling theorem (Brown et al. 2002). Furthermore, we show in Appendix II that a Poisson model also yields a simple relationship between variance and mean for non-zero Fourier coefficients: V_k = 4z₀ (for k > 0). This new result enables a principled interpretation of the variance of Fourier components.

The variance: mean ratio, known as the Fano factor (Teich, 1989), can be used to determine whether a spike train is more variable than Poisson (variance: mean > 1), or less variable. For a linear neuron with a modulated Poisson output, in which the mean firing rate z₀ does not change in the presence of sinusoidal stimulation, one anticipates that the Fourier component variance will also not change as a function of contrast, as has been observed (Croner et al. 1993; Kremers et al. 2001; Sun et al. 2004). However, for a Poisson neuron with a firing threshold, the mean firing rate z₀ will be contrast-dependent – and thus, one anticipates an increase in response variance as contrast increases, according to V₀(C) = z₀(C) for the DC response, or V_k(C) = 4z₀(C) for the kth Fourier component (Appendix II). The reader should note that this analysis depends on the relationship between the individual spike trains and r(t), but not the relationship of r(t) to the stimulus – so it is equally applicable to linear and non-linear models for the deterministic rate function r(t).

A Poisson process is the most random (i.e. highest entropy) statistical model consistent with a given underlying rate function r(t) (Rieke et al. 1997), and thus serves as a useful null hypothesis and basis for comparison with experimental data. Real neurons typically have a refractory period of 1–2 ms, which means that spike events become more regular or ‘clock-like’ when firing rates are high. In this situation the variance is lower than anticipated from a Poisson process (Fano factor < 1). Subcortical visual neurons have been successfully modelled using ‘integrate-and-fire’ dynamics (Knight, 1972; Reich et al. 1998; Smith et al. 2000) – i.e. a spike can only occur when a sufficient input signal has accumulated over time. Integrate-and-fire dynamics also yield firing patterns that are more clock-like than Poisson processes, and will also have a reduced variance compared with Poisson predictions.

A refractory period and integrate-and-fire dynamics produce correlations that are largely negative (i.e. a spike event reduces the probability of a subsequent spike event). The opposite situation (positive correlations among spike events) can also arise as a result of clustered or ‘bursting’ spike activity (Smith et al. 2000; Reinagel & Reid, 2002; Krahe & Gabbiani, 2004). Such bursts can produce spike trains with greater variability than Poisson processes – even though these spike trains are less random than a Poisson process with the same rate function r(t). The net result of these opposing influences on response variability is unknown, and this is the main question we address in the following.

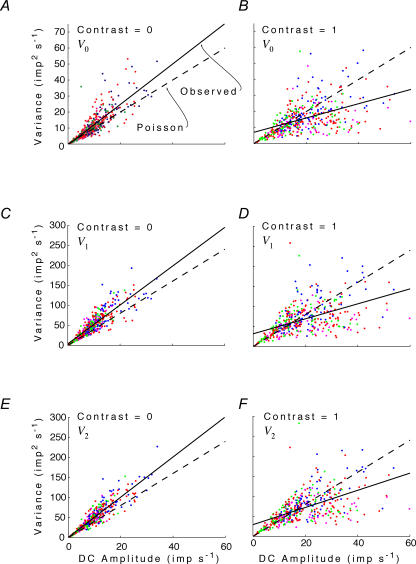
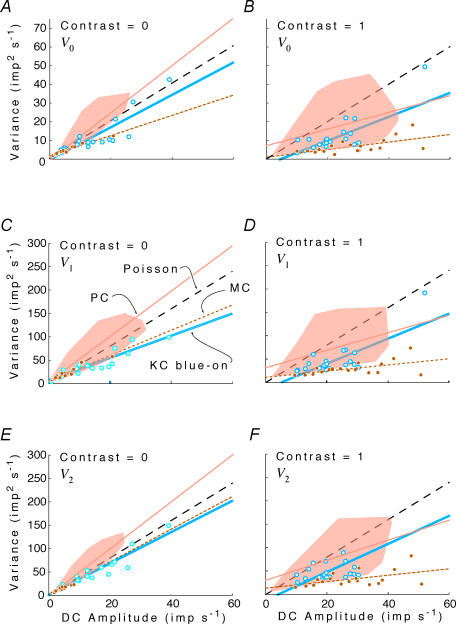
Figure 3 compares observed behaviour of PC cells to the Poisson prediction. As noted above, the Poisson prediction has a slope of 1 for V₀ and a slope of 4 for V₁ and V₂. On the left, response variance for V₀, V₁ and V₂ is plotted as a function of mean firing rate z₀ when stimulus contrast is 0. The measured variances tend to lie above the Poisson prediction. The overall variance: mean ratio (V_k/z₀, calculated as the slope of a regression line constrained to pass through the origin) is 1.23 (1.18–1.27) for V₀, 5.14 (5.01–5.27) for V₁, and 5.05 (4.93–5.16) for V₂. These all exceed the Poisson prediction by a Fano factor of about 1.25. On the right, variability is assessed at maximum contrast (C = 1). Here, variances are less than the Poisson prediction: the variance: mean ratios are 0.73 (0.69–0.78) for V₀, 3.16 (3.00–3.32) for V₁ and 3.33 (3.17–3.48) for V₂. In summary, at zero contrast, variability is greater than Poisson expectations (a Fano factor of about 1.25), while at high contrasts, variability is less than expected from a Poisson process with the same number of spikes (a Fano factor of about 0.75). The transition between these behaviours occurs near an intermediate contrast of C = 0.25 (not shown), where the regressions through the origin have slopes that are indistinguishable from the Poisson prediction. Analogous decreases in variability (albeit at much lower spiking rates) were previously demonstrated for non-midget ganglion cells recorded in vitro (Berry et al. 1997; Uzzell & Chichilnisky, 2004).

Figure 3. Response variance V_0,V₁ and V₂ for the DC response and the first two harmonics as a function of the mean firing rate z₀.

Left column, Contrast = 0; right column, Contrast = 1. Data from all neurons, under all spatial and chromatic conditions. Dashed line, Poisson prediction (see text and Appendix II). Continuous line, linear (observed) regression.

As contrast increases, the mean firing rate of neurons whose spontaneous firing rate is low will increase – because increases in firing during the peak of the response cannot be balanced by decreases in firing below zero. Consequently, the range of mean firing rates seen at high contrast (right column of Fig. 3) is greater than the range seen at low contrasts (left column of Fig. 3). Interestingly, the neurons whose mean firing rates are highest have a response variability that is disproportionately small. This can be seen by the positive intercept and more shallow slope of the unconstrained regression line, compared with the Poisson prediction.

In summary, responses to low contrast tend to be more variable than predicted by a Poisson process. Responses to high contrast (especially those that generate more spikes because of rectification effects) tend to be less variable than predicted by a Poisson process.

Variance as a function of response size

The foregoing analysis revealed how changing the inputs to a parvocellular neuron (i.e. stimulus contrast) can influence response variance. We now focus on how response variance depends on response size, rather than stimulus contrast. The goal of this analysis was to reveal how intrinsic properties of parvocellular neurons can influence response variance. Since the response amplitudes covered different ranges for different stimulus conditions, we proceeded as follows. For each neuron and each harmonic k, we determined the range of response amplitudes |z_k | elicited by the full range of luminance and chromatic contrast stimuli used. If these ranges overlapped, we chose the response size that was at the midpoint of this overlap. We then used eqn (5) and its variants, as described in Methods, to estimate the variance for chromatic and luminance stimulation at that response size. Thus, the neuron's response variances were compared for luminance and chromatic stimuli that elicited the same response amplitude. This procedure also guaranteed that the chosen response amplitude for both stimuli was in the middle of the response range for that neuron. If the luminance and chromatic response ranges did not overlap, no further analysis was performed on this neuron for this harmonic. As described in Methods, this variance was determined by reading out the empirical relationship between variance V_k and response amplitude |z_k| at this overlap amplitude, eqn (5). The result is shown in Fig. 4.

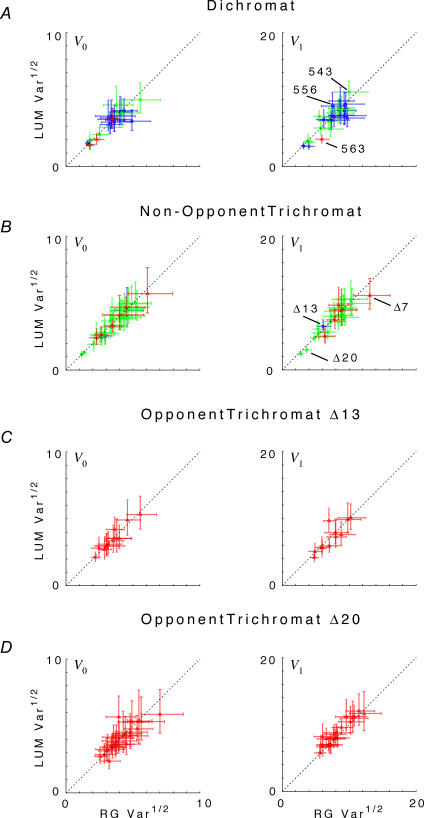
Figure 4. Comparison of response variance V_k at constant response size under RG (abscissa) and LUM (ordinate) conditions for the DC response (f₀), left column, and the fundamental Fourier component (f₁), right column.

The response size chosen for comparison is the midpoint of the range of overlap of the RG and LUM response amplitudes. Top row, all dichromat neurons. Second row, non-opponent neurons from all trichromats. Third row, opponent neurons from Δ13 trichromats. Fourth row: opponent neurons from Δ20 trichromats. For f₁ responses in Δ20 trichromats, there is a larger variance under LUM than RG conditions. There is a trend in the opposite direction for the other cell types. Variances plotted are V₀ and V₁, as defined by eqn (3) and interpolated by eqn (5), at constant response size. Error bars represent 95% confidence limits on the variance estimates for each neuron, and include the uncertainty of the variance estimates and the model error of the empirical variance versus mean relationship, eqn (5).

For nearly all cell types (parvocellular neurons in dichromats, non-opponent neurons in all trichromats, and opponent neurons in Δ13 trichromats), there was little difference between response variance under RG and LUM conditions. However, for most opponent neurons in Δ20 trichromats (Fig. 4, bottom row, right panel), the variance in the f₁ response to RG stimulation was smaller than the response to LUM stimulation. Across this population, the variance ratio (i.e. the variance for RG divided by the variance for LUM) was 0.89 (p < 0.01, two-tailed, paired t test). The f₂ response (data not shown) showed the same phenomenon (variance ratio of 0.90, p < 0.05). In contrast (Fig. 4, bottom left), there was no difference in the variance ratio for the DC (f₀) response (variance ratio 1.02, p > 0.5). For high spatial frequency stimuli (LUM-high versus RG-high, data not shown), trends were in the same direction, but were statistically insignificant (ratio of 1.06 at f₀, 0.94 at f₁, 0.98 at f₂, all p > 0.15). For opponent neurons in Δ13 trichromats, there was no indication of a lower variance under chromatic conditions; indeed, the trend was in the opposite direction: variance ratios were in the range 1.01–1.13 (p > 0.02), but there were fewer than six neurons available for pair-wise comparisons. Dichromats and non-opponent neurons in trichromats also showed a weak trend in the direction of greater variance under chromatic than luminance conditions: pooled ratios 1.05 at f₀ (p > 0.05), 1.09 (p < 0.05) at f₁, and 0.95 (p > 0.05) at f₂.

Figure 5 compares variances under RG and LUM conditions across the entire range of response sizes. Here, at intervals of 2 impulses s⁻¹, we determined the variance (from the empirical variance versus mean curves of eqn (5)) for each neuron, and averaged across the population. For each criterion response, neurons were only included if they attained that response under both luminance and contrast conditions (but typically, for unequal contrasts). In this way, the curves represent paired comparisons. Average variances are only plotted for contrasts at which at least six neurons contributed. As seen in Fig. 5, in Δ20 animals the opponent neurons showed a larger variance for LUM than RG across the entire response range for f₁ (p < 0.025 for all but the largest response amplitude). At the largest amplitude, an even larger difference is present, but did not reach significance because fewer cells were available to make the comparison. No such difference was seen for f₀, or for the opponent neurons in Δ13 animals. In the dichromats and the non-opponent neurons in trichromats, there was a weak trend in the opposite direction (i.e. larger variance for RG than LUM) at the larger response sizes; this trend was not statistically significant.

Figure 5. Comparison of response variance V_k at as a function of response size ∣z_k∣ for RG and LUM conditions for the DC response (f₀), left column, and the fundamental Fourier component (f₁), right column.

Top row, all dichromat neurons. Second row, non-opponent neurons from all trichromats. Third row, opponent neurons from Δ13 trichromats. Fourth row, opponent neurons from Δ20 trichromats. Variances plotted are V₀ and V₁, as defined by eqn (3) and interpolated by eqn (5). For f₁ responses in Δ20 trichromats, there is a larger variance under LUM than RG conditions at all response sizes. For f₀, the Poisson prediction V₀ =z₀ is also shown. All variances are somewhat greater than the Poisson prediction.

The left column of Fig. 5 provides a second opportunity to test the Poisson prediction that the spike count variability is equal to the mean spike count. It summarizes the variability of the firing rate (f₀) as a function of the size of the mean response (V₀). This analysis is distinct from that of Fig. 3 in three ways. Firstly, it is based on a smoothed variance: mean curve, interpolated by eqn (5), rather than single data points. Secondly, it considers only low and moderate response modulation depths (which can be achieved either with luminance or chromatic stimuli). Finally, the results are subdivided by cell subgroup. For all subgroups of cells, the observed variance was greater than the Poisson prediction, across all responses sizes (p < 0.01 at most points). This result is consistent with the analysis of the data shown in Fig. 3, despite the differences in approach. Both analyses show an increase in variance with response contrast, and supra-Poisson variance in parvocellular cells at low contrast.

Dependence on cone contrast

Due to the nature of their inputs, non-opponent neurons are expected to attain a criterion response size at lower cone contrasts when cone signals reinforce (LUM) than when cone signals are in antiphase (RG). Conversely, opponent neurons are expected to attain a criterion response size at lower cone contrasts when cone signals are in antiphase (RG), than in the LUM condition. Thus, one possibility is that the pattern of variance observed in Figs 4 and 5 is related to the differences in cone contrasts required to attain equal responses under RG and LUM conditions.

To test this, we determined the cone contrasts which produced the same response amplitude under RG and LUM conditions. We proceeded as follows. First, we fitted the observed contrast–response function to a generalized Naka-Rushton (Naka & Rushton, 1966) relationship (eqn (6)). Then, at the criterion response size |z₁ |, we inverted this relationship (eqn (16)) to obtain the corresponding stimulus contrast C. The stimulus contrast C was converted to cone contrasts 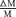and 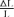(Table 1). The two cone contrasts were then summarized by

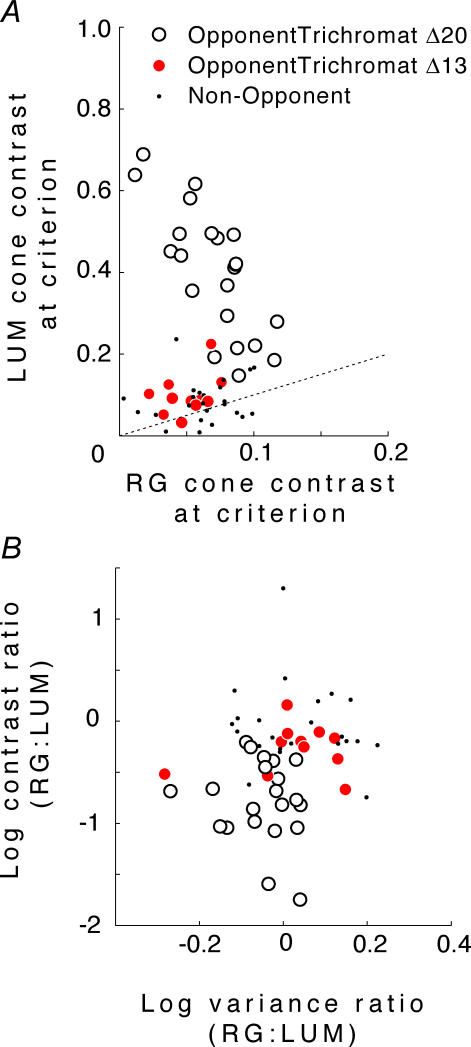
The results are shown in Fig. 6. As expected from the definition of opponency, for most opponent neurons c_avg(LUM) >c_avg(RG) (Fig. 6A). Moreover, the opponent neurons in the Δ20 animals are the only neurons for which c_avg(LUM) is more than twice as large as c_avg(RG).

Figure 6. Dependence of response variance on core contrast.

A, cone contrasts 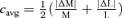at the same criterion response amplitude as shown in Fig. 4 for RG and LUM conditions. The straight line corresponds to c_avg(RG) =c_avg(LUM). B, relationship of variance ratio 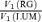to cone contrast ratio 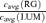. Opponent neurons in Δ20 animals have a lower value of 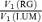than opponent neurons in Δ13 animals, even at the same cone contrast ratio. Note that Contrast = 1 for a chromatic stimulus has a much lower cone contrast than a Contrast = 1 luminance stimulus, depending on phenotype (Table 1).

Figure 6B compares the variance ratio 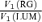to the cone contrast ratio, 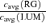. It demonstrates a tendency towards higher variance under conditions of higher cone contrast. However, even at a constant cone contrast ratio, the Δ20 opponent neurons show a lower variance ratio 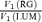than the Δ13 opponent neurons. These data suggest that for opponent neurons the lower response variability for RG modulation is a result of the opponent interaction between cone inputs rather than a higher signal: noise ratio in the cone inputs prior to their combination.

Responses of magnocellular and koniocellular blue-on cells

To understand whether the principles we have established are likely to apply to other cell groups in the subcortical visual system, we analysed responses of 19 magnocellular cells and 17 blue-on cells. As fewer cells were available, we restricted our analysis to the basic relationship of response amplitude and response variance, without regard to chromatic conditions of stimulation, or the colour vision phenotype of the animals. Histological reconstruction of the recording location of 10 of the blue-on cells showed the great majority (8/10, 80%) were located in koniocellular layer K3 between the parvocellular and magnocellular layers (Ding & Casagrande, 1997; White et al. 2001). For simplicity in the following we therefore refer to this population as koniocellular blue-on cells.

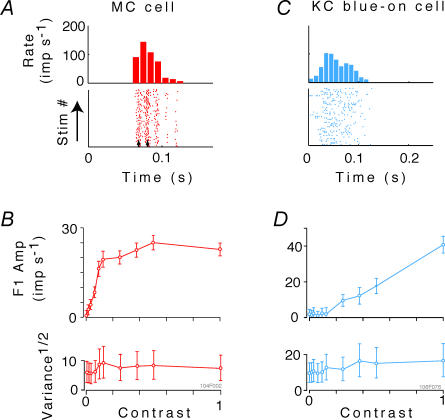
Figure 7A and B shows the response of an example magnocellular neuron to drifting LUM gratings of increasing contrast. Figure 7C and D shows similar data from a blue-on koniocellular cell in response to drifting SWS gratings. For the magnocellular cell, typical high contrast gain and saturation at low contrast is present, along with evident synchronization to the monitor refresh (small vertical arrows, Fig. 7A). Synchronization to the monitor refresh at high contrast was present in 17/19 of the magnocellular cells, but was much less prevalent in parvocellular and koniocellular cells. Both the MC and the koniocellular blue-on cells show a weak trend towards an increase in response variance as contrast increases.

Figure 7. Analysis of the fundamental (first harmonic) responses of a magnocellular (MC) cell to luminance modulation, and of a koniocellular (KC) blue-on cell to short-wavelength-sensitive (SWS) cone-isolating modulation.

A and C, post-stimulus histograms and raster plots of responses to gratings at contrast of 1.0. The upper panels in B and D show amplitude of mean first harmonic response |z₁(C) | (eqn (2)) as a function of contrast C. Error bars represent 95% confidence limits, as calculated by T²_circ (Victor & Mast, 1991). The lower panels show variability of the first harmonic response, plotted as 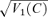, at each contrast C. Error bars represent 95% confidence limits, as calculated by an F statistic (see Appendix 1).

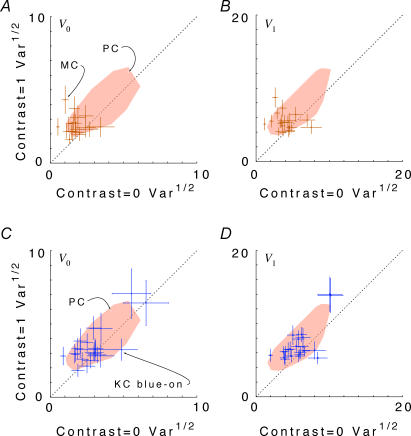
Figure 8, analogous to Fig. 2, compares response variance at C = 1 to response variance at C = 0 across the population of koniocellular blue-on cells (Fig. 8A and B) and magnocellular cells (Fig. 8C and D). As in the parvocellular population, responses of magnocellular and koniocellular blue-on cells to high contrasts tend to be more variable than responses at low contrast. The response variability for koniocellular blue-on and magnocellular neurons overlaps with an envelope of the corresponding data of parvocellular cells (shaded regions, Fig. 8), both in overall size and in dependence on contrast. For the population of 22 koniocellular blue-on cells, the variance ratio had a geometric mean (and 95% confidence limits) of 1.58 (1.13–2.19) at f₀ and 1.58 (1.19–2.09) at f₁. For the population of 19 magnocellular cells, the variance ratio had a geometric mean (and 95% confidence limits) of 2.37 (1.47–3.84) at f₀ and 2.09 (1.25–3.50) at f₁. (Confidence limits are large because of the relatively small number of cells, and the variability within the sampled population.)

Figure 8. Scattergrams of variance at C = 1.0 versus variance at C = 0 for the DC response (F₀), left column, and the fundamental Fourier component (F₁), right column.

Responses of magnocellular (MC) cells are shown in A and B. Responses of koniocellular (KC) blue-on cells are shown in C and D. Variances plotted are V₀ and V₁, as defined by eqn (3). Error bars represent 95% confidence limits on the variance estimates for each neuron, as calculated by F statistics (see Appendix 1). Values are pooled across chromatic stimulation conditions for MC and KC blue-on cells. The shaded area in each graph shows an envelope of PC cell responses from Fig. 4A. Outliers from the PC distribution were removed by iterative (3x) enclosure with a convex hull and removal of points at the hull vertices. Note that the majority of points for both MC and KC blue-on cells show greater variance at C = 1 than at C = 0, and thus lie within the PC cell envelope.

Figure 9, analogous to Fig. 3, shows how response variability V_k of f₀, f₁ and f₂ depend on mean firing rate z₀, and compares this with the Poisson predictions of V_k = z_k (for k = 0), and V_k = 4z₀ (for k > 0). The behaviour of the magnocellular and koniocellular blue-on cells is broadly compatible with that of parvocellular cells, but there are differences in the details. In contrast to the parvocellular data, the variance versus mean firing rate relationship for C = 0 is sub-Poisson (slope less than Poisson prediction at p < 0.05) for f₀ in magnocellular cells. The same is true for f₁ and f₂ in both magnocellular and koniocellular blue-on cells (left panels). At C = 1 (right panels), variance is further reduced below Poisson expectations for f₀, f₁ and f₂. This reduction is most obvious for magnocellular cells (approximately 25% of the Poisson prediction) but is also apparent for koniocellular blue-on cells (approximately 70% of the Poisson expectation). Some of the reduction in variance seen in magnocellular cells may be related to synchronization to the monitor refresh.

Figure 9. Response variance V₀, V₁ and V₂ for the DC response (F₀) and the first two harmonics (F₁, F₂) as a function of the DC amplitude (mean firing rate) z₀ in magnocellular (MC) and koniocellular (KC) blue-on cells.

Left column, Contrast = 0; right column: Contrast = 1. The shaded area in each graph shows an envelope of PC cell responses from Fig. 5 for each contrast and harmonic. Outliers from the PC distribution were removed by iterative (3x) enclosure with a convex hull and removal of points at the hull vertices. Open symbols and thick continous lines show KC blue-on cells and linear regression line. Filled symbols and dotted lines show MC cells and linear regression. Thin continous lines show PC cell linear regressions from Fig. 5. Data from all neurons, under all spatial and chromatic conditions. Dashed line, Poisson prediction (see text and Appendix II). Note that for all populations the variance at high contrast falls below the Poisson prediction.

In summary, magnocellular and koniocellular blue-on cells show on average lower variability than parvocellular cells, and many show sub-Poisson variability at all stimulus contrasts. However, the way that variance changes with firing rate across contrasts is common to all cell classes: all cells show a reduction in Fano factor as contrast increases. Thus, responses become slightly more variable with increasing contrast, yet they drop below the Poisson prediction.

Discussion

Our approach made use of a parametric measure of variability, namely, the variance of Fourier components of the spike train elicited during sinusoidal stimulation. We recognize that non-parametric (e.g. information-theoretical) methods, which use a more varied stimulus set and avoid making an assumption about the particular form of the response, might reveal other aspects of spike train dynamics overlooked by this approach (Berry et al. 1997; Strong et al. 1998; Reinagel et al. 1999; Reinagel & Reid, 2000, 2002; Uzzell & Chichilnisky, 2004). However, the disadvantage of these non-parametric measures is that they require substantially more data (per cell) to generate precise estimates of variability, and the properties of large populations of neurons have not yet been reported using these methods.

The driven responses of parvocellular neurons to sinusoidal stimuli are, to a good approximation, rectified sinusoids (Croner et al. 1993; Yeh et al. 1995; Kremers et al. 1997, 2001; Blessing et al. 2004; Sun et al. 2004). However, to consider only the variability of the first harmonic might overlook important detail, since noise sources such as bursts, threshold fluctuations and integrate-and-fire dynamics (Knight, 1972; Reinagel et al. 1999; Smith et al. 2000) might differentially affect the various harmonics.

With these considerations in mind, we adopted an intermediate strategy: we used Fourier analysis, but we examined the variability not just of the fundamental component. This parameterization allowed for a much more precise analysis than an information-theoretical approach, without making overly simplistic assumptions about the underlying dynamics. In particular, our analysis allowed us to draw two new basic conclusions: overall variability increases with contrast, but not as rapidly as expected for a Poisson process, and variability of parvocellular cells depends not only on response size but also on chromatic composition of the stimulus.

Response variability increases with contrast

Our first main finding is that response variability in parvocellular neurons is only approximately independent of contrast: variability is on average, approximately 40% larger at high contrast than at low contrast. Similar trends were seen in the magnocellular and koniocellular blue-on populations: in both populations, variability at F₀ and F₁ increased with contrast, and the ratio of variances of responses at high and low contrast was consistent, on average, with the 40% change seen in parvocellular neurons. Previous authors (Croner et al. 1993; Kremers et al. 2001; Sun et al. 2004) did not find any such contrast dependence. Several factors could contribute to these discrepancies. Croner et al. (1993) and Sun et al. (2004) studied the macaque whereas Kremers et al. (2001) studied marmosets; species difference is therefore an unlikely possibility. Croner et al. (1993) examined retinal ganglion cells, and additional variability is present in the lateral geniculate (Kara et al. 2000). Moreover, there is a diversity of behaviour within parvocellular cells (Fig. 2), and for many cells, the increase in variance is minimal or non-existent. However, the most parsimonious explanation is apparent from our data and analysis: it is difficult to measure variances reliably. This may seem surprising, but it is a simple consequence of the fact that variance depends on the shape of the distribution of response amplitudes, not on its mean value. For example, for the DC response, approximately 140 sweeps for each condition are necessary to distinguish a variance ratio of 1.4 from a variance ratio of 1.0 for p < 0.05, two-tailed; t test for modulated responses, approximately 70 sweeps are necessary (F_0.025 [138, 138] = 1.398). This requirement was generally not fulfilled in the studies cited above. Kara et al. (2000) did use a large enough number of sweeps to be able to detect a 40% change reliably, but these authors did not study systematically the effect of contrast on response variability, nor did they quantify variability in the response phase.

If a large number of trials is necessary to detect small changes in variance, are these changes therefore too small to be of relevance for the behaving organism? The answer to this question lies in the fact that we analysed individual cells, whereas the organism would have access to the activity of an entire neuron population for each trial. For example, one can estimate that a stimulus which subtends 1 deg² in the marmoset fovea will cover the receptive field of about 10 000 parvocellular neurons (Wilder et al. 1996). As noted above, many trials are necessary to detect a relatively small change in variance in a single cell. Had we been able to analyse such a large population of neurons simultaneously, the change in variance would have been evident from only one or a few trials.

From the point of view of a behaving organism, and a typical visual task for which the activity of a population of neurons is relevant, a change in variance by a factor K is anticipated to change, by a factor of √K, the number of cells (or the observation interval) required to achieve a criterion signal-to-noise ratio. For the variance ratios we observed (1.4 for f₀, 1.38 for f₁ and 1.55 for f₂), this amounts to about 20% increase in cell number (or observation time). Such changes may well be relevant for the primate visual system, where spatial resolution and temporal resolution are critically important. Current understanding of how population activity in the visual system is used to perform spatially extensive tasks is poor. Thus it is difficult to use our results to make specific psychophysical predictions. Nevertheless, our results do show how the performance of a real visual system compares with that of a hypothetical system constituted of ‘Poisson neurons’. We show that real patterns of firing in principle would allow for a reduction in the number of neurons, without loss of performance. The optic nerve and lateral genuiculate nucleus (LGN) are considered a ‘bottleneck’ for visual signal transmission (Barlow, 1981). Such increases in efficiency could thus, in principle, yield an adaptive advantage for the behaving organism.

For a neuron that fires in a Poisson fashion, the ratio of the variability of the spike count to the mean spike count (the Fano factor, Teich, 1989) is expected to be equal to 1. A corresponding result holds for the ratio of the variability of a modulated response to the spike count (Appendix II). In an otherwise linear neuron with a low maintained discharge, sufficiently strong response modulation must increase the mean firing rate, since high firing rates at the peak of the response cannot be balanced by a corresponding decrease in firing at the troughs of the response. In such neurons, an increase in response variability is expected for deeply modulated responses. Thus, one possibility for the difference between our findings and those of others is that our sample of neurons had a lower background discharge, and thus, greater proportional changes in the number of spikes as contrast increased.

However, Fig. 3 shows that firing rate elevation does not fully account for how response variability changes with contrast. Indeed, for parvocellular cells, although variance of the modulated response increases as mean firing rate increases, nevertheless the proportionality of variance to firing rate is ∼25% higher than the Poisson expectation when contrasts and firing rates are low, and ∼25% lower than the Poisson expectation when contrasts and firing rates are high. That is, a neuron with Poisson variance statistics would have shown an even greater increase in variability with contrast than we observed with parvocellular cells. The same broad trend to sub-Poission variance at high contrast was seen with magnocellular and koniocellular blue-on cells. These populations showed overall slightly lower variance than the parvocellular populations, in that nearly all magnocellular and koniocellular neurons had a variance versus f₀ relationship that was below the regression line for parvocellular neurons (Fig. 9). Consistently, steady discharges of parvocellular cells show higher variability than steady discharges of magnocellular and koniocellular blue-on cells (Troy & Lee, 1994).

For modest contrasts and response amplitudes, parvocellular neurons' DC (f₀) component is more variable than the Poisson prediction (Figs 3 and 5), with V₀/z₀ in the range 1.2–1.4. This supra-Poisson variability may be due to bursting (Sheth et al. 1996; Berry et al. 1997), but we did not analyse these aspects of timing here. Excess variability related to state changes (such as changes between burst and tonic mode firing; Ramcharan et al. 2000; Krahe & Gabbiani, 2004) is not likely to contribute, since we had explicitly excluded datasets with statistical evidence of response variability over long timescales of seconds to minutes.

The reduction in response variability at high modulation depths implies more than merely a loss of bursting. This is because a loss of bursting can decrease variability to that expected from Poisson behaviour (Fano factor 1), but cannot account for variability that is lower than Poisson (Fano factor < 1). Qualitatively, the sub-Poisson variability suggests that integrate-and-fire dynamics (Knight, 1972; Smith et al. 2000) begin to dominate in this range. Additionally, synaptic convergence may allow stimulus-driven activity, rather than spontaneous activity, to be selectively encoded in the retinal ganglion cell spike train (Demb et al. 2004). In other words, activity driven by a stimulus is more likely to be correlated in time than is activity resulting from spontaneous (quasi-random) activity in presynaptic neurones. Other authors accounted for the decrease in variability with increasing firing rate in retina (Kara et al. 2000; Uzzell & Chichilnisky, 2004) and LGN (Kara et al. 2000) on the basis of increasing influence of the absolute and relative refractory period (Berry et al. 1997; Berry & Meister, 1998). As firing rate increases, the Poisson approximation becomes progressively poorer, since it predicts that a progressively larger fraction of spikes will occur during the absolute or relative refractory period. This phenomenon could account for the sub-Poisson growth in variability that we observe with increasing contrast. However, absolute and relative refractory periods do not account for the manner in which spike train variability depends on position in the stimulus cycle (Reich et al. 1998), either in the retina or the LGN; integrate-and-fire (or integrate-and-fire-or-burst) dynamics appear to be required (Reich et al. 1998; Smith et al. 2000; Pillow et al. 2005). Integrate-and-fire or similar dynamics would also be expected to make response timing more reliable when the input varies more rapidly, or more deeply, in time (Mainen & Sejnowski, 1995; Buracas et al. 1998; Mechler et al. 1998; Reich et al. 1998; Kara et al. 2000).

Response variability and chromatic composition: possible mechanisms

Our second main finding was at constant response size, Δ20 chromatically opponent neurons had smaller variability for chromatic stimulation than for luminance stimulation. Since this comparison was made at constant response size, it is difficult to attribute it to threshold or spike generation dynamics in the parvocellular neuron, since cone-specific signals have already combined. The Δ13 cells did not show this difference, and non-opponent parvocellular neurons showed a trend in the opposite direction. Thus, it is also difficult to attribute this finding to an overall difference in sensitivity between classes of parvocellular neurons (e.g. Kilavik et al. 2003), or to the possibility that the retina is somehow generally noisier under chromatic stimulation conditions than under luminance conditions.

To achieve a criterion response size, larger cone contrasts will be required for stimuli whose chromatic composition is suboptimal. For example, a strongly chromatically opponent neuron will require a greater contrast to achieve a criterion response size for luminance stimuli, than for opponent stimuli (Fig. 6A). Moreover, Δ20 opponent neurons typically required a smaller RG: LUM cone contrast ratio for a criterion response than Δ13 opponent neurons, and non-opponent neurons required larger RG: LUM cone contrast ratios to achieve a criterion response to chromatic stimuli than to luminance stimuli.

Thus, the above findings are consistent with the notion that under conditions of constant response size, variability is larger when cone contrasts are higher. Consequently, supra-additive noise prior to cone signal combination could account for the basic pattern of our results. Cone noise arises both from spontaneous isomerizations (Rieke & Baylor, 2000) and post-transduction processes (Rieke & Baylor, 2000; Holcman & Korenbrot, 2005). While there is evidence that cone noise indeed increases as luminance increases, this increase is extremely gentle (Fig. 1 of Rieke & Baylor, 2000 shows at 4 Hz there is less than a factor of 2 between darkness and response saturation), and not likely to contribute significantly for cone contrasts of 0.1–0.5, the range in which variance comparisons were made in the present study.

Supra-additive noise sources in processes that are post-receptoral but prior to cone signal combination (i.e. the bipolar cell and its synaptic connections) are therefore a likely main contributor to our findings, given evidence for substantial amplification at this stage (Burkhardt & Fahey, 1998; Burkhardt et al. 2004). However, a direct assessment of this hypothesis would require recordings from bipolar cells with minimal recording noise, and this is a difficult technical challenge. Figure 6B suggests that even at equivalent cone contrast ratios, neurons in Δ20 trichromats have lower noise under chromatic conditions. This could be a sign of additional specialization for processing of chromatic signals in the cone-opponent pathway.

Functional relevance

Retinal noise is often limiting for detection tasks, both of luminance (Hecht et al. 1942; Donner, 1992) and of contrast (Hornstein et al. 1999). It is well-recognized that, given the statistics of natural scenes, a segregation of information into chromatic and luminance channels leads to a more efficient transmission strategy than one based on the ‘raw’ cone signals (Buchsbaum & Gottschalk, 1983; Ruderman et al. 1998). The present results suggest that this retinal recombination of signals has a benefit, distinct from the coding efficiencies gained by de-correlation (Atick & Redlich, 1990). We show that deeply modulated responses have a larger absolute variability than weakly modulated ones, but a more favourable signal: noise ratio. Furthermore, the improvement in signal: noise ratio is greater than expected from naïve (i.e. Poisson) spiking models. Thus, the recombination of signals to generate a sparse code (Olshausen & Field, 2004) in which some neurons are deeply modulated and most are quiescent may enhance signal: noise ratio, as well as energy efficiency.

It is difficult to make a fully satisfying assessment of the net benefit conferred by the lower variance of chromatic compared with luminance signals in opponent PC cells. This would require a detailed understanding of the spatial, temporal and chromatic characteristics of the retinal image under natural viewing conditions, and knowledge of the ultimate benefits to the organism of correct (or incorrect) decisions driven by luminance or chromatic information. Nevertheless, the overall size of the variance effects can be estimated. Figures 2 and 3 show that the variance when responses are large is 1.5- to 2-fold less than would be predicted from variance when responses are small. This amounts to a 25–40% improvement in equivalent spatial or temporal resolution. There is an additional reduction in variance of approximately 10% associated with chromatic stimulation of opponent PC cells (Fig. 4), which adds an additional 5% benefit. Although neither of these effects has large magnitude, their combined effect will work to improve the sensitivity of chromatic signals in the parvocellular pathway.

Screening responses for trial-to-trial variation and adaptation

Data were collected in trials lasting 3.5 s, with typically three trials of each contrast, separated by several minutes. We screened datasets for variation during the course of a trial, or, as trials progressed during the experiment, to exclude datasets with manifest variability due to faulty triggering or adaptation to light or contrast. Adaptation to light or contrast is considered ‘spurious’ in the sense that such adaptation would not result in variability in responses to separate ‘glances’ at the stimulus, sufficiently separated in time (Shapley & Victor, 1978; Ohzawa et al. 1982; Ohzawa et al. 1985). We used an ANOVA-like approach (modified to recognize the complex-valued nature of the Fourier components) to carry out this screening.

To identify trial-to-trial variation, we calculated the mean Fourier components within each trial by pooling across cycles, That is, we calculated z_k(n_trial, •) (here and below, the • indicates pooling over the argument that it replaces) from the cycle-by-cycle Fourier components z_k(n_trial, n_cycle) (eqn (1)) by

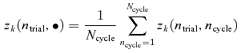(A1)

where z_k(n_trial, n_cycle) is the Fourier component estimated from a single cycle. The variance of responses averaged within each trial, V^trial_k, is

(A2)

If there were no systematic changes from trial to trial, then V^trial_k = V_k/N_cycle, since N_cycle individual Fourier estimates (eqn (A1)) are averaged for each within-trial estimate. If systematic changes from trial to trial were present, there would be excess variance described by V^trial_k (eqn (A2)). In this case, the ratio of the trial-to-trial variance to the variance not explained by trial-to-trial variation would be large. To test, this, we compared the variance ratio

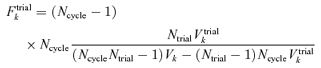(A3)

with the F distribution expected for b_k(N_trial − 1) degrees of freedom in the numerator, and b_kN_trial(N_cycle − 1) degrees of freedom in the denominator (80 tests: Fourier components 0, 1, 2 and 20 at each of 10 contrasts).

To detect systematic excess variation within trials, we calculated the mean Fourier components of corresponding cycles (across trials)

(A4)

and their variance V^cycle_k:

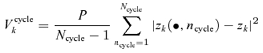(A5)

If there were no systematic changes across cycles, then V^cycle_k = V_k/N_trial, since N_trial individual Fourier estimates (eqn (A4)) are averaged for each within-trial estimate. If systematic variation from cycle to cycle within trials (e.g. adaptation) were present, there would be excess variance described by V^cycle_k (eqn (A2)). For example, if adaptation were present, the response to the first cycle of each trial might always be larger than the response to the last cycle of each trial. In this case, the ratio of the cycle-to-cycle variance to variance not explained by cycle-to-cycle variation would be large. To test, this, we calculated the F ratio

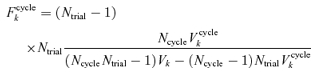(A6)

which has b_k(N_cycle − 1) degrees of freedom in the numerator, and b_kN_cycle(N_trial − 1) degrees of freedom in the denominator.

We discarded datasets for which, at any harmonic k, three or more contrasts out of the set of 10 contrasts resulted in values of F^cycle_k or F^trial_k above the p = 0.05 level of the corresponding F distribution. These datasets corresponded to those in which inspection of the rasters revealed an apparent change in mean firing rate during the course of the experiment. Strictly speaking, these statistical tests assume that mean firing rates are Gaussian distributed (k = 0) and that complex-valued Fourier coefficients are distributed in a circularly symmetric Gaussian fashion about their mean (k > 0). This cannot be rigorously correct (since Fourier components are constrained by the fact that there can only be an integer number of spikes per cycle), but our purpose was simply to screen the data for evidence of non-stationarity.

Fitting an empirical variance–mean relationship: details

The following hierarchical strategy was used to fit eqn (5). All datasets were fitted to eqn (5) with the following sets of constraints: (i) a = c = 0, γ = 1, b = 1 (i.e. variance equals mean, in units of spike count – this is Poisson behaviour for the 0th harmonic); (ii) b = c = 0, γ = 1, a free to vary (i.e. variance independent of mean, as reported by Croner et al. (1993)); and (iii) a = c = 0, γ = 1, b free to vary (i.e. variance proportional to mean). If none of these 0-parameter or 1-parameter fits were consistent with the data at p < 0.2 via χ² (see below), then the following 2-parameter fits were considered: (iv) a = c = 0, b and γ free to vary (but γ restricted to [–10,10]), and (v) c = 0, γ = 1, a and b free to vary. If neither of these 2-parameter fits were consistent with the data at p < 0.2, then the following 3-parameter fits were considered: (vi) c = 0, a, b and γ free to vary (but γ restricted to [–10,10]), and (vii) γ = 1, a, b and c free to vary. We used the ‘liberal’ cut-off of p < 0.2 at each stage to avoid overfitting but simultaneously ensure that we did not overlook a better fit with a slightly more complex model. Following these sequential fits, the model with the highest p value was chosen. This corresponds to choosing the model with the lowest reduced χ².

Fits to forms derived from eqn (5) were carried out as follows. Since both the Fourier amplitude at the contrast C, |z_k(C)|, and its variance, V_k(C), were quantities estimated from the data rather than independent variables, we did not fit eqn (5) by a regression. Instead, we minimized

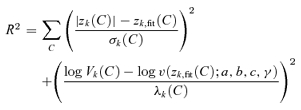(A7)

where σ_k(C) is the standard error of measurement of |z_k(C)| and λ_k(C) is the standard error of measurement of log V_k(C). That is, the minimization procedure sought to fit the observed (mean Fourier amplitude, variance) pairs (|z_k(C)|, V_k(C)) with pairs (|z_k,fit(C)|, V(z_k,fit(C);a, b, c, γ)) consistent with eqn (5), but had freedom to adjust the measured mean Fourier amplitude to a fitted value. Deviations of the fitted value z_k,fit(C) for the Fourier amplitude away from the measured value |z_k(C)|, and deviations of the fitted value of the variance V(z_k,fit(C);a, b, c, γ) from its measured value V_k(C), were both weighted by amounts inversely proportional to the uncertainty of the measured values. The 95% confidence intervals for mean Fourier amplitudes were estimated as follows: for the mean firing rate z₀(C), we used t tests based on the measurement from each cycle (N_trialN_cycle − 1 degrees of freedom). For Fourier amplitudes at non-zero frequencies |z_k(C)|, we used the T²_circ statistic (Victor & Mast, 1991). For variances, fitting was performed following logarithmic transformation. 95% confidence intervals were estimated from an F distribution with b_k(N_trialN_cycle − 1) degrees of freedom in the numerator, and infinite degrees of freedom in the denominator (since this describes the expected distribution of spectral estimates for Gaussian data). The quantities σ_k(C) and λ_k(C) were determined by matching a Gaussian distribution to the estimated confidence intervals for |z_k(C)| and log V_k(C), respectively. The main assumptions in the above analysis are that data from each response cycle are independent, that measurement errors and modelling errors are independent, and that there are a sufficient number of response cycles so that Gaussian asymptotics apply. With these assumptions, random variation of |z_k(C)| and log V_k(C) around values modelled by eqn (5) implies that the mean total transformed squared error R² (eqn (13)) is distributed approximately like χ², with the number of degrees of freedom equal to the number of contrasts N_C minus the number of fitted parameters (0, 1, 2 or 3) in eqn (5). This is because there are 2N_C summands in eqn (13), but the number of fitted parameters includes each z_k,fit(C) (N_C parameters), as well as those of the fitted functional form (eqn (5)).

We also tested the hypothesis that neither the mean Fourier amplitude nor their variances depended on stimulus contrast, by minimizing

(A8)

as a function of contrast-independent values z_k,fit and v_k,fit. Under the null hypothesis of random variation of |z_k(C)| and log V_k(C) about their respective contrast-independent values, R² is distributed approximately like χ², with 2N_C − 2 degrees of freedom.

Based on the fit that had the highest p value (from the χ² distribution for R², for the appropriate number of degrees of freedom), one of the models described by eqn (5), or the contrast-independent value v_k,fit, was chosen as a description for the relationship that could be used to ‘read off’ the variance v(|z|) of Fourier coefficient whose mean is |z|. The squared error associated with ‘reading off’ the value of the variance for a particular Fourier amplitude |z| was taken as the sum of two components: the squared error in estimating the variances themselves (calculated from b_kN_C(N_trialN_cycle − 1) samples, estimated as above), and the squared modelling error per data point, R²/N_C.

As confirmation of the validity of the above assumptions and curve-fitting procedures, the distribution of p values for values of χ² obtained from these fits was approximately uniform in [0,1]. The distribution is shown in Fig. 10. The mean of the distribution is 0.51, very close to the ideal mean of 0.5 anticipated from a uniform distribution. There was a slight (∼10%) excess of low p values for fits to the first harmonic, suggesting that there was a small systematic portion of the variance versus mean relationship that was not captured by any of the functional forms considered. There was a similar excess of high p values (near 1.0), suggesting that a small number of datasets were overfitted. In contrast, the p value distribution grossly deviated from uniformity if we used a linear, rather than logarithmic, transformation of the variance V_k(C), or if we used a logarithmic, rather than linear, transformation of the amplitude |z_k(C)| (not shown).

Figure 10.

Distribution of probability (p) values from the empirical variance–mean relationship fits described in Appendix I.

Fitting an empirical contrast-response function: details

Datasets were fitted to eqn (6) by minimizing

(A9)

where, as in eqn (A7), σ_k(C) is the standard error of measurement of |z_k(C)|, obtained via T²_circ (Victor & Mast, 1991). The following sets of constraints were used to avoid overfitting: (i) a = η = 0, γ = 1 (linear relationship); (ii) η = 1, γ = 1 (linear relationship with offset); (iii) a = η = 0 (power–law relationship); (iv) η = 0 (power–law relationship with offset); (v) a = 0, γ = 1 (Naka-Rushton law, with semisaturation 1/η); (vi) γ = 1 (Naka-Rushton law with offset), and a = 0 (Naka-Rushton law with arbitrary power). If none of these 1-, 2- or 3-parameter fits were consistent with the data at p = 0.2, then the full 4-parameter form (eqn (6)) was fitted to the data. The fit with the lowest reduced χ² was retained. From this fit, an estimated contrast that produced a criterion response r_criterion could be estimated by inverting (eqn (6)):

(A10)

Had we only considered linear fits, some datasets, especially for the fits to the variance V₀, would have been overfitted (excess of datasets with p values near 1), while the population as a whole would have been underfitted (average p value of 0.22). With the above procedure, overfitting of the V₀ was reduced by including V_k = constant and underfitting was reduced by allowing for additional functional forms. The end result, as shown in Fig. 10, was a reasonably flat distribution of p values for the goodness of fit, with a mean p value of 0.51. The discontinuity at p = 0.2 is a result of the cut-point of our stepwise procedure.

Appendix I

Data analysis details

All calculations were carried out in Matlab 7.0. The minimizations of eqns (A7) and (A9) are generically non-linear, and were carried out by via a Nelder-Mead simplex algorithm (Press et al. 1988), as implemented in Matlab's fminsearch.

Appendix II

Variability of Fourier components of a periodically modulated Poisson process

Here we show that for an inhomogeneous Poisson process whose expected event rate varies periodically with period P, the variances of all Fourier components are proportional to the cycle-averaged mean firing rate.

Following eqn (1), we can write an estimate of a Fourier component at the kth harmonic from a single period beginning at time T as

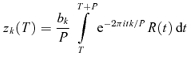(A11)

Here, b_k is a normalization factor (b₀= 1, b_k = 2 for k ≠ 0), and R(t), the spike train, is a sum of delta-functions, one at the time of each spike:

(A12)

We want to calculate the variance of z_k(T), which is related to our measure of variability V_k (eqn (3)) by

(A13)

〈〉 denotes the expected value over all cycles, or over all starting times T.

Since

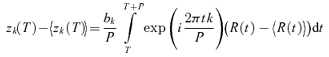(A14)

it follows that

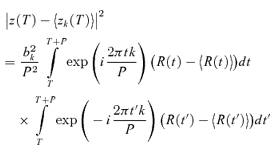(A15)

and therefore that

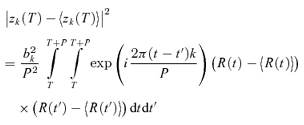(A16)

For a Poisson process, the variance is equal to the mean event rate, and events at distinct times are independent. That is,

(A17)

Taking an ensemble average of eqn (A16) and substituting eqn (A17) yields

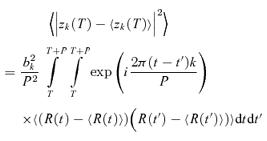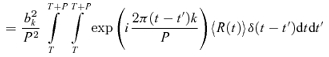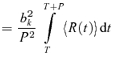(A18)

Since the expected value of the cycle-averaged firing rate is

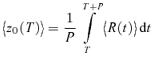(A19)

eqns (A13) and (A18) yield

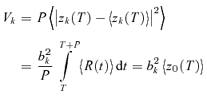(A20)