The kinetics of inhibition of rat recombinant heteromeric α1β glycine receptors by the low-affinity antagonist SR-95531

Abstract

The GABA_A antagonist SR-95531 (gabazine) is known to block glycine receptors, albeit with low affinity. We have studied the effect of SR-95531 on rat recombinant α1β glycine receptors expressed in human embryonic kidney (HEK293) cells by recording macroscopic currents elicited by rapid glycine application to outside-out patches. SR-95531 has a fast unbinding rate (k_offSR, about 3000 s⁻¹) and this means that the time course of its unbinding is comparable to the expected time course of the transmitter in the cleft. We also found that equilibrium applications of SR-95531 reduced the response to brief glycine applications by an amount inversely proportional to the duration of glycine application. The fast unbinding rate of SR-95531 from the glycine receptor will make it useful for establishing the time course of glycine concentration at glycinergic synapses.

Antagonists for ligand-gated ion channels are often employed as tools to isolate synaptic activity due to different neurotransmitters and therefore need to have high selectivity and high affinity for the target receptor. However, in some circumstances a low-affinity antagonist is needed: indeed, it was by using low-affinity competitive antagonists at NMDA or AMPA receptors that Clements et al. (1992) and Tong & Jahr (1994) obtained very robust estimates of the glutamate synaptic concentration and time course. The method relies on an accurate kinetic description of the agonist-induced activation of postsynaptic channels and on the availability of an antagonist with a time course of unbinding that is similar to that of neurotransmitter in the cleft (approximately 1 ms). In these conditions, the amount of inhibition induced by the antagonist is inversely proportional to the permanence and concentration of the agonist in the cleft.

Among the relatively few antagonists for glycine receptors, the best known, strychnine, is unsuitable for this role because, although highly selective and competitive (see the Schild analysis in Kumamoto & Murata, 1996; Lewis et al. 1998), it has a high affinity (in the nanomolar range; Saul et al. 1994). A more suitable candidate is SR-95531 (gabazine), a potent GABA_A antagonist that behaves as a low-affinity competitive antagonist of native glycine receptors (Wang & Slaughter, 2005). Whether this antagonist could be useful depends on the actual value of its unbinding rate. Whereas the equilibrium dissociation constant (K_B) of a competitive antagonist can be measured by macroscopic methods (i.e. Schild analysis; Arunlakshana & Schild, 1959), the individual microscopic rate constants can be estimated only using fast concentration jumps and only by postulating a kinetic scheme of activation that describes the properties of the receptors. This is the aim of the present work. By applying kinetic modelling we have obtained an estimate of the microscopic rates for binding of SR-95531 at glycine receptors. These rates have values compatible with our independent macroscopic K_B estimate for the antagonist and reveal a fast unbinding, occurring at a rate of about 3000 s⁻¹, enough to be comparable with the expected time course of synaptically released glycine.

Methods

Human embryonic kidney cells (HEK 293) were maintained in an incubator with 95% air−5% CO₂ in Dulbecco's modified Eagle's medium, plated on glass coverslips and transfected after 10 h by a calcium phosphate–DNA co-precipitation method with cDNAs coding for the enhanced green fluorescence protein (EGFP) and for the rat α1 and β glycine receptor subunits in a 1: 40 ratio (Groot-Kormelink et al. 2002). Such a high ratio was chosen to minimize the expression of homomeric α1 channels (Burzomato et al. 2003). Each dish was transfected with 3 μg DNA and patch-clamp recordings were made 14–48 h after transfection.

Recordings were performed in the whole-cell or outside-out patch-clamp configuration; in both cases the extracellular solution contained (mm): NaCl 102.7, sodium gluconate 20, KCl 2, CaCl₂ 2, MgCl₂ 1.2, Hepes 10, glucose 14, sucrose 15 and tetraethylammonium chloride 20; pH adjusted to 7.4 with NaOH, and the intracellular solution contained (mm): KCl 107.1, CaCl₂ 1, MgCl₂ 1, Hepes 10, EGTA 11, tetraethylammonium chloride 20, MgATP 2; pH adjusted to 7.2 with KOH.

For both configurations, the cell or the patch was held at −60 mV, without correction for junction potential. Borosilicate glass capillaries (GC150TF, Clark Electromedical, Warner, UK) were pulled to a resistance of 1–2 MΩ (whole cell) or 7–10 MΩ (outside-out patch).

In whole-cell experiments, fast drug application was achieved by a modified U-tube system that allowed 1–2 ms solution exchange, measured using the open tip potential change following application of a 30% diluted extracellular solution (Burzomato et al. 2003). Series resistance (3–8 MΩ) was routinely compensated (80–95%). Fast concentration jumps were performed using a theta tube (14-072-01, Hilgenberg, Malsfeld, Germany) with the tip cut to a final diameter of approximately 150 μm and driven by a piezo-stepper (Burleigh Instruments, NY, USA). Glycine (Fluka) and SR-95531 (gabazine, Sigma) were washed in or out through the double-barrelled perfusion system. The exchange time was measured by application of a diluted solution both before each experiment (to optimize the position of the electrode) and after rupture of the patch. Typical exchange times were approximately 80–100 μs (10–90% rise time) and only those patches in which the exchange time was faster than 150 μs were included in the analysis.

Current responses were recorded with an Axopatch 200B amplifier, filtered at 5 kHz and digitized using a Digidata 1322A data acquisition system (sampling rate, 25–50 kHz) and Clampex software (all Axon Instruments Inc.).

For the Schild analysis experiments, partial glycine concentration–response curves in control condition and in the presence of 100, 300 or 500 μm SR-95531 were fitted simultaneously with power functions with the constraint of equal slopes (CVFIT program, available from http://www.ucl.ac.uk/Pharmacology/dcpr95.html). For each concentration of antagonist, this produced an estimate of the dose ratio (r; i.e. by how much a glycine concentration must be increased in the presence of antagonist in order to obtain the same response as in control).

The mean values of r for each concentration of SR-95531 were plotted on a log–log scale and fitted by the Schild equation:

where [B] is the concentration of SR-95531 and K_B is the dissociation equilibrium constant.

The Schild plot of log(r−1) versus log[B] was initially fitted with a power function of the form:

where a is a constant and n is the slope of the Schild plot which is predicted to be one for a purely competitive antagonist. As the slope was sufficiently close to one, the data were re-fitted using the Schild equation (i.e. slope constrained to one) to estimate K_B.

For the analysis of outside-out patch experiments, 10–50 individual responses to glycine were averaged. In most experiments, rundown was apparent only in the first 2–3 min of recording, by which time the response amplitude reached a plateau. Once steady state was reached, only those experiments in which the difference between the average of the first and last three responses in a series was less than 5% were included in the analysis. Glycine pulses were repeated every 10 (short applications) or 15 s (long applications), allowing full recovery from desensitization between each pulse (Gentet & Clements, 2002). All rise times (i.e. for agonist responses and tip potentials) were measured from 10% to 90% of the peak amplitude. The time course of desensitization during prolonged pulses of agonist and that of deactivation following short pulses were fitted with a mixture of exponentials (usually two). Rate constants were determined using ChanneLab software (Synaptosoft Inc.), which optimizes rate constant values by a simplex algorithm. The quality of the fit was assessed by calculating the sum of squared differences between the data points and the fit (divided by the sum of squared data points and normalized by the number of points; see Clements & Westbrook, 1994). We used the open tip potential measured at the end of each experiment (scaled appropriately) as an input for the concentration profile. The fitting procedure and the constraints used are described in the Results. Data are expressed as means ± s.d. of the mean. The coefficient of variation of the mean (CVM) for rate constants was calculated across experiments.

Results

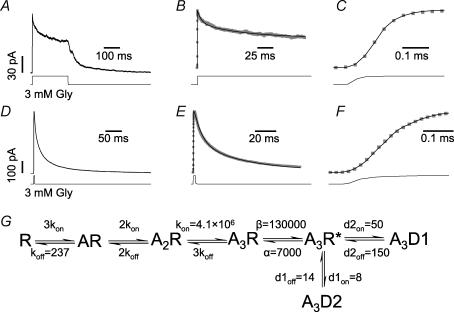
The traces in Fig. 1 show the first two protocols in our experiments: a saturating concentration of the agonist glycine (Gly, 3 mm) was applied in control conditions either for 200 ms, to determine the kinetics of desensitization (Fig. 1A–C), or for 3 ms, to determine the rate constants for deactivation (i.e. the decay of the current once glycine is removed, Fig. 1D–F). This was done because, in order to measure the microscopic binding rates of the glycine receptor antagonist SR-95531, it was first necessary to define a kinetic scheme that could describe glycine responses in control conditions (and to determine its rates).

Figure 1. Kinetic scheme for the activation of heteromeric glycine receptors by saturating concentrations of glycine.

A, shows the averaged current response of an outside-out patch to a 200 ms application of 3 mm glycine. The time course of glycine concentration (taken from the open tip potential recorded at the end of the experiment) is shown at the bottom of the trace in this and the following figures. B, continuous black line shows the fit to the data () obtained after optimizing the rate constants in the model shown in G. C, shows the response onset on an expanded timescale; note the good agreement of the fitted curve (black line) to the experimental inward current. D, shows the averaged current response to a short (3 ms) application of 3 mm glycine. The deactivation phase was empirically fitted with two exponentials (see Results). The data were fitted to the model in G with association and dissociation rate constants (k_on and k_off, respectively) as free parameters and the desensitization and resensitization rates fixed to the average values obtained from the fits of 200 ms steps. F, shows the rising phase of the trace and the fit of E on an expanded timescale (note the different sampling rate of 20 μs, instead of 40 μs as in C). G, the scheme was used to fit the data and shows the average of the rate constants fitted to the data from five patches (for the 200 ms steps) and six patches (for the 3 ms steps; units are s⁻¹ or s⁻¹ μm⁻¹ as appropriate).

Figure 1A shows a response (average of 15 applications) to a 200 ms pulse of Gly. The average 10–90% rise time of the response was 140 ± 20 μs (n = 5). In this and all other experiments, the desensitization phase was best fitted by two exponential components with time constants τ₁ = 12 ± 2 (amplitude 41 ± 11%) and τ₂ = 104 ± 22 ms (59 ± 11%, n = 5). This observation implies that at least two desensitized states (with different lifetimes) are required in order to fit the data adequately. Because our main aim was to determine the binding rates for the antagonist, we decided to use the simplest possible model that could describe the response to glycine pulses. This mechanism (shown in Fig. 1G) contains two independent desensitized states connected to a single fully bound open state and three binding sites for glycine, as in our recent analysis of single-channel data at a range of glycine concentrations (Burzomato et al. 2004). Although there is no knowledge of how desensitized states are connected, our purpose here was to correct for desensitization rather than to study it. Glycine heteromeric channels have three open states (Burzomato et al. 2004), but we have included only one open state (reached from the fully liganded shut state), because the present experiments were performed at saturating concentrations of glycine, and any contribution by lower liganded states of the receptor would be negligible. The gating rates were fixed to our previously obtained values (7000 and 130 000 s⁻¹ for α and β, respectively; Burzomato et al. 2004). This is an approximation, because these values were obtained from cell-attached recordings and with a more detailed mechanism than the one used here. However, gating rates in the outside-out patch configuration are not slower (M. Beato, unpublished data). Heteromeric glycine receptor gating is therefore very fast and would contribute relaxation time constants of the order of 10–100 μs, which could not be resolved in concentration jump experiments.

Current responses to 200 ms jumps were fitted in two stages. First, the whole average trace was fitted, from the onset of the application up to the time when desensitization reached a steady level (180 ms later). This fit allowed the estimation of the rates for entry and exit into the desensitized states together with the association rate constant (k_on) for glycine. Gating constants α and β were fixed to the above values and the dissociation rate constant (k_off) fixed to 300 s⁻¹, as in our single-channel experiments (Burzomato et al. 2004). The rate constants for binding were constrained to be the same for each binding step, except for the statistical factors accounting for the number of available sites. The entry and exit rates were 50 s⁻¹ ± 36% (CVM) and 150 s⁻¹ ± 13% for the fast desensitized state (A₃D1 in Fig. 1G) and 8 s⁻¹ ± 32% and 14 s⁻¹ ± 17% (n = 5) for the slow desensitized state (A₃D2). Once a satisfactory fit of the time course of desensitization was obtained for each patch (Fig. 1B), we used these estimates to fix the desensitization rates (within the scheme of Fig. 1G) and re-fitted only the rising phase of the response (up to the peak), with k_on as the only free variable. As shown in Fig. 1C, this produced a good fit of the rising phase and the average estimate of k_on was 5.4 × 10⁶ s⁻¹ μm⁻¹ ± 22%, n = 5. It is important to note that the rise time of the response to glycine (140 ± 20 μs) is comparable with that of the solution exchange (110 ± 10 μs on average); as a consequence, our estimate of k_on must be interpreted as a lower limit of its actual value.

As there is some controversy about the number of α subunits (the main binding subunit) in heteromeric glycine receptors (Langosch et al. 1988; Kuhse et al. 1993; Burzomato et al. 2003; Grudzinska et al. 2005), we have also tried the same fitting procedure with a model that included only two binding sites. The quality of the fits was only marginally worse than with three binding sites and the difference was not statistically significant (paired t test on the normalized sum of squares, see Methods, P = 0.2). Nevertheless, the use of a model with three binding steps, such as the one in Fig. 1G, is justified by the results of our own analysis of single-channel experiments (Burzomato et al. 2004) and by the observation by Grudzinska et al. (2005) that αβ heteromeric glycine receptors are likely to contain more than two binding sites for Gly, even if the pentamer contains only two copies of the α subunit.

In order to determine k_off for glycine, we switched to a protocol of short (3 ms) glycine applications (as shown in Fig. 1D, which is the average of 21 responses). The average rise time of the response was 180 ± 20 μs (n = 6) and that of the solution exchange was 130 ± 20 μs, both somewhat slower, but not significantly different from the rise time of the responses to 200 ms steps (140 ± 20 μs). The deactivation phase was best fitted with two exponential components, with time constants and amplitude τ₁ = 9 ± 1 ms (51 ± 5%) and τ₂ = 61 ± 11 ms (49 ± 5%; n = 6). In all fits, desensitization rates were fixed to the overall average values obtained from the 200 ms step responses. Fits were performed in two stages: first the whole trace (up to 160 ms after the peak) was fitted with k_on and k_off as free parameters (Fig. 1E) in order to estimate k_off (237 s⁻¹ ± 6%, n = 6); second, k_off was fixed to the value obtained in each patch and only the rising phase of the response was fitted with k_on as the free parameter (Fig. 1F). The estimate of k_on from the short pulses was 2.6 × 10⁶ s⁻¹ μm⁻¹ ± 21%; this is slower than the estimate obtained from the 200 ms step experiments, but the difference was not significant (unpaired t test, P = 0.16) and could be due to the relatively slower exchange time achieved with short pulses (130 versus 110 μs). Therefore the two sets of estimates were averaged, giving a mean k_on of 4.1 × 10⁶ s⁻¹ μm⁻¹ ± 20% (n = 11). The final average values for the rates are shown in the scheme of Fig. 1G.

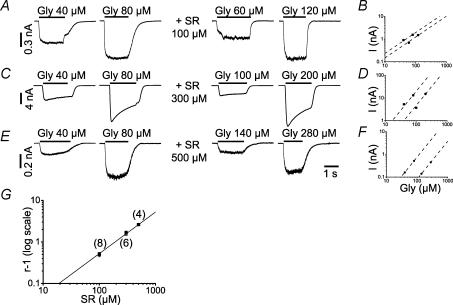
In order to decide the SR-95531 concentration for subsequent experiments, it was necessary to estimate its affinity for glycine receptors. Antagonist potency is commonly reported in the literature as IC₅₀, even though this value depends on the agonist concentration and cannot be easily related to antagonist occupancy of the receptor or to any of the microscopic or macroscopic binding rates. Because of that, we had to obtain an experimental estimate of the binding equilibrium constant (K_B) of SR-95531. This was done by Schild analysis, by recording partial glycine concentration–response curves in the whole-cell configuration in control solution and in the continuous presence of 100, 300 or 500 μm SR-95531. The traces on the left of Fig. 2A, C and E show the response to 40 and 80 μm glycine in control solution. For each dose of antagonist, glycine concentrations were chosen in order to elicit currents similar in amplitude to those recorded in control solution (right traces in Fig. 2A, C and E). The partial dose–response curves for glycine with and without SR-95531 were simultaneously fitted with a power function and constrained to be parallel, as shown in the log–log plots of Fig. 2B, D and F for each concentration of antagonist. The average values of r−1 were plotted on a log–log scale versus the concentration of antagonist (Fig. 2G, where the number of cells is indicated above each point) and fitted with a power function (see Methods). The value of the slope was 1.02 ± 0.08, confirming the competitive nature of the antagonist. Data were re-fitted with the slope constrained to 1 and this gave a value of K_B of 191 ± 8 μm. In a minority of cells (n = 4), we obtained two dose ratios (i.e. for 100 and 500 μm SR-95531). These experiments gave four independent Schild plots, with a slope of 1.01 ± 0.04 and a K_B of 190 ± 10 μm (data not shown), these values were not different from those obtained from pooled data.

Figure 2. Schild analysis of the effect of co-application of SR-95531 (100, 300 and 500 μm) on whole-cell responses to glycine.

A, C and E, show inward currents in response to approximately equipotent glycine concentrations with and without three different concentrations of antagonist. B, D and F, show the shifts in the glycine dose–response curves produced by these three antagonist concentrations and are the fits of two power functions (with the constraint of equal slopes) to the peak currents measured in each experiment. For each antagonist concentration the dose ratio (r) was calculated as the distance between the two parallel lines. G, the Schild plot uses the average dose ratio values from all recordings (plotted on a log–log scale versus the antagonist concentrations). The fit to the Schild equation (slope constrained to one) gave a value of equilibrium dissociation constant (K_B) of 191 ± 8 μm (the number of cells at each concentration is indicated above each point).

The Schild plot is a null method and because of that, it gives a correct estimate of K_B for a very wide class of models (Colquhoun, 1973).

The K_B value we estimated is clearly high, but low affinity is not necessarily due only to fast unbinding. In order to check that in this case it is, we preincubated our patches with 1 mm SR-95531; according to our K_B estimate of 191 μm, that should give a 99.6% occupancy of antagonist bound states. This occupancy is calculated from the equation:

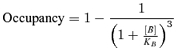where [B] is the antagonist concentration. The equation assumes there are three identical and independent antagonist binding sites.

We then performed fast applications of 3 mm glycine (3 or 200 ms pulses) at the same time as the antagonist was washed out (Fig. 3). If antagonist unbinding is fast, the glycine response should have a slower rise time, but reach a peak similar to that observed in control.

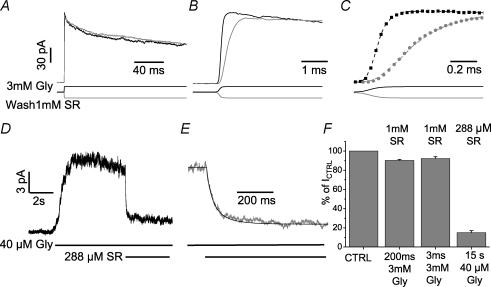
Figure 3. The offset and onset of SR-95531 antagonism.

A, shows the responses to 200 ms applications of 3 mm glycine with (grey trace) and without (black trace) pre-equilibration with SR-95531. The onset of desensitization is very similar in the two experimental conditions. B, the rise time of the current response is approximately 3-fold slower after pre-equilibration with SR-95531 (compare grey and black traces in). This is due to the progressive increase of available receptors as the antagonist washes out. C, shows the simultaneous fit of the rise time of the responses (with and without antagonist) to the model of Fig. 4D with only the unbinding rate of SR-95531 (k_offSR) as a free variable and the association rate constant k_onSR constrained to give a value of equilibrium dissociation constant (K_B) of 200 μm. D, shows the response to 40 μm glycine (average of 50 individual traces). Once a steady level of current in response to glycine was reached, 288 μm SR-95531 was co-applied with glycine (see bars below the traces). Note that because of the technical limitations of the theta tube application (i.e. the number of barrels available), the onset of glycine application was obtained by manually switching on glycine perfusion, whereas the transition to glycine + antagonist is a true concentration jump. The current decreased to 15% of its control value and the onset of the antagonist effect was fitted to the model of Fig. 4D with k_onSR as the only free variable. E, the fit (black line) is shown on an expanded timescale superimposed on the data (grey trace). F, histogram shows the percentage reduction in the peak current elicited by 200 ms or 3 ms steps to 3 mm glycine after pre-equilibration with 1 mm SR-95531 and the reduction induced by 288 μm SR-95531 co-applied with 40 μm glycine.

Figure 3A shows responses to a 200 ms glycine pulse in control (black) and after preincubation with SR-95531 (grey): clearly the shape of the response is barely changed in that the desensitized phase is described by two exponentials with time constant and amplitude of τ₁ = 16 ± 2 ms (66 ± 16%) and τ₂ = 129 ± 36 ms (34 ± 16%; n = 5, not significantly different from the control values). For short (3 ms) glycine pulses, the deactivation time course of responses did not change either, and was fitted with two exponential components of time constant and amplitude τ₁ = 8 ± 1 ms (53 ± 6%) and τ₂ = 47 ± 9 (47 ± 9%; n = 6, data not shown). On the other hand, the response rise time (shown on an expanded timescale in Fig. 3B) increased from 140 ± 20 μs in control to 640 ± 110 μs following preincubation with the antagonist (n = 11, data pooled from 3 and 200 ms applications). The peak amplitude of glycine responses in the presence of SR-95531 was, however, only slightly reduced to 90 ± 1% (n = 6, 200 ms steps) or 92 ± 2% (3 ms steps, see histogram of Fig. 3F). This indicates that receptors that were bound to the antagonist become rapidly available during SR-95531 washout on a timescale of milliseconds. We fitted the rise time of the response after antagonist preincubation using a classical competitive mechanism (Fig. 4D), which postulates that there are three equal and independent binding sites for SR-95331 and that any state bound to the antagonist cannot open.

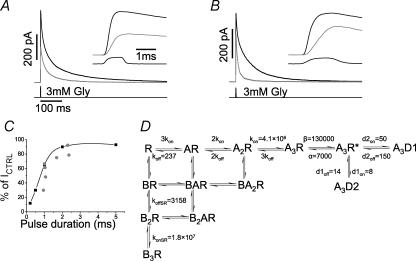
Figure 4. Inhibition of responses to short glycine pulses by equilibrium application of SR-95531.

A and B, show two examples of responses to 3 mm glycine before (black trace) and during (grey trace) steady-state application of 288 μm antagonist. There is a consistent increase in the rise time of the response (see insets), but the percentage inhibition of the peak is different in the two cases. This is correlated with the actual length of the glycine concentration pulse, which is shorter in A (∼1 ms) than in B (∼1.6 ms). C, this is shown for seven experiments in which the actual length of the pulse was plotted against the percentage reduction of peak current in the presence of SR-95531 (). The prediction of the response to square pulses of glycine of variable duration are shown in the same graph (▪; joined by cubic splines for clarity). D, gives a summary of the values of the rate constants fitted from the different experimental protocols.

The protocol in Fig. 3A can give information only on the unbinding rate of SR-95531 (k_offSR), so initially we fitted the rise time of the response fixing all the binding, gating and desensitization rates to the optimized values of Fig. 1G. The fit is not sensitive to variations in the association rate constant of the antagonist, k_onSR and we constrained it to give a value of K_B of 200 μm (within the range of our estimate from the whole cell experiments in fig. 2). The data together with the fit are shown on an expanded timescale in Fig. 3C and gave an average value for k_offSR of 3158 s⁻¹ ± 10% (n = 11). Hence the mean lifetime of an occupancy by the antagonist is of the order of 300 μs.

Our estimate of k_offSR relies on the observation that SR-95531 acts as a purely competitive antagonist, as shown by Wang & Slaughter (2005) and confirmed by our Schild analysis (Fig. 2), and on the assumptions of the kinetic model used to describe glycine currents in control. In order to test how robust this estimate is to the initial assumptions that we used to describe our control data, we re-fitted the rise time of the responses to 200 ms glycine pulses fixing the gating rate constants to much lower values than the ones we determined from our single-channel analysis (Burzomato et al. 2004). We now constrained β and α to 5000 and 500 s⁻¹, respectively (i.e. 25- and 12-fold lower than the rates we used before). These values are in the range of those chosen by Gentet & Clements (2002) to fit their data. Re-fitting the values of the binding rates for glycine and for SR-95531 with this constraint on the gating rates, gave a k_on estimate 4-fold higher (22.4 × 10⁶ s⁻¹ μm⁻¹ ± 21%) that accounted for the fast observed rise time of glycine-induced currents. The value obtained for k_offSR from the preincubation experiments was 2950 s⁻¹ ± 13% (n = 5; not significantly different from that obtained earlier, paired t test, P = 0.35).

The effect of an antagonist will follow the Schild equation only if there is true competition between agonist and antagonist at each binding site (Colquhoun, 1973). Thus the results of our Schild analysis imply that glycine and SR-95531 share the same binding sites. Note, however, that the effect of SR-95531 on macroscopic GABA_A responses has also been successfully described by a model with two binding sites for agonist and one for the antagonist (Jones et al. 1998, 2001). Therefore we attempted to fit the data of Fig. 3A to models that had one or two binding sites for the antagonist (but retained three binding sites for glycine). Fits with a single binding site for SR-95531 were not in good agreement with the data: the estimated k_offSR was 1950 s⁻¹ ± 17% (n = 5), but the normalized square difference between the data and the fit was significantly worse than that for the fits with three binding sites (paired t test, P > 0.05). However, allowing for two antagonist binding sites gave a good description of the data with an average k_offSR of 3973 s⁻¹ ± 36% (n = 5) and the normalized square difference was not significantly different from that obtained for models with three binding sites (P = 0.16). This confirms that fitting macroscopic currents to kinetic schemes does not allow an unequivocal distinction between two or three binding sites for both the agonist and the antagonist. However, the observation that the slope of the Schild plot is very close to one rules out any model in which the agonist and antagonist do not compete for the same number of sites.

An independent estimate of k_onSR was obtained by applying antagonist during a long application of glycine. A low concentration of glycine (40 μm) was chosen in order to minimize the occupancy of desensitized states. When the response reached a steady state, a solution containing 288 μm SR-95531 and 40 μm glycine was applied through the theta tube (Fig. 3D). The onset of the antagonist action was fitted, fixing all the rate constants (including k_offSR) to the previously optimized values and leaving only k_onSR as a free parameter. The current declined to 15 ± 2% of control values (Fig. 3F) and the fitted curve was in good agreement with the data (see the expanded trace in Fig. 3E). The average estimate for k_onSR was 1.8 × 10⁷ s⁻¹ μm⁻¹ ± 13% (n = 5). Together with our estimate of k_offSR (see above), this gives a value for K_B of 175 μm, which is similar to that obtained from the Schild analysis (191 μm).

We then tested the effect of steady-state application of SR-95531 on the response to very short pulses of saturating glycine (i.e. the protocol that best approximates the behaviour of channels at a synapse). The rise time of the response to glycine in the continuous presence of 288 μm SR-95531 (a concentration at which, given a K_B of 175 μm, only 5% of the channels should be available) was consistently slowed from 190 ± 4 to 620 ± 20 μs (n = 7). It was somewhat surprising to find that the reduction in peak amplitude was quite variable and ranged from 30% to 90% of control (average value, 65 ± 8%) as shown by the examples in Fig. 4A (50% inhibition) and Fig. 4B (30% inhibition) where responses in control (black) are superimposed on those in the presence of SR-95531 (grey). However, measuring the open tip potential at the end of each experiment showed that the actual concentration profiles produced delivering a 1 ms voltage step to the piezo-translator did vary considerably from patch to patch. For the examples in Fig. 4A and B, the true half-width of the glycine application was 0.98 (inset of Fig. 4A) and 1.68 ms (inset of Fig. 4B). We therefore calculated how the peak response to pulses of glycine is expected to vary in the presence of antagonist as a function of pulse length. The values expected from the rates of the model in Fig. 4D at selected pulse durations are plotted as percentage of control as black squares in Fig. 4C. The grey dots are the observed values (n = 7 experiments). As expected, there is a strong correlation between the actual pulse duration and the amount of inhibition. The calculated points systematically underestimate the antagonist effect, probably because they are calculated for an ideal square pulse, whereas the glycine concentration at the patch is likely to rise more slowly. This could increase the contribution of desensitized states and reduce the observed amplitude.

Discussion

Our data show that the low-affinity competitive antagonist SR-95531 (Wang & Slaughter, 2005) dissociates from heteromeric α1β glycine receptors at a rate of approximately 3000 s⁻¹: this means that, in a fraction of a millisecond (a time comparable to the postulated lifetime of the transmitter at the synapse), the antagonist can unbind from a sizeable proportion of the channels it occupied initially. With this rate of unbinding, the amount of inhibition induced by the antagonist is expected to be inversely proportional both to the concentration of glycine and to the time glycine is present in the cleft. This prediction is confirmed by the observation that the amount of inhibition induced by a subsaturating concentration of the antagonist decreases as the length of the glycine pulse is increased.

Measurement of the association and dissociation rates for competitive antagonists has long been a goal for pharmacologists (Hill, 1909; Jenkinson, 1960; Colquhoun, 1981), but the limits on the speed of solution exchange, and lack of voltage dependence, made this impossible for all but the slowest antagonists, until the recent advent of fast-application techniques (Clements et al. 1992; Wenningmann & Dilger, 2001). Unbinding rates for high-affinity antagonists, such as the NMDA receptor antagonists 3-((r)-2-carboxy-piperazin-4-yl)-propyl-1-phosphonic acid (d-CPP) and and d-(–)-2-aminophosphonopentanoic acid (d-AP5) are relatively slow (up to 20 s⁻¹), and can therefore be measured in experiments on whole cells, where concentration changes are achieved in about 10 ms (Benveniste & Mayer, 1991). The faster unbinding rates of low-affinity antagonists require faster applications, which are possible only on outside-out patches. Examples range from 160 s⁻¹ for d-aminoadipate on NMDA receptors (Clements et al. 1992) to 1700 s⁻¹ for (1,2,5,6-tetrahydropyridine-4-yl)-methylphosphinic acid (TPMPA) on GABA_A receptors (Jones et al. 2001). Clearly the dissociation rate for SR-95531 from glycine receptors is greater than this at 3000 s⁻¹.

In our analysis we have described receptor activation by as simple as possible a model, using three sequential binding steps and one fully liganded open state. This model describes adequately the features of macroscopic glycine responses in their desensitization (Fig. 1B), deactivation (Fig. 1E) and rise time (Fig. 1C and F). The main features of the model (Fig. 4D) for the antagonist are the assumption that occupancy of the receptor by a single molecule of antagonist is sufficient to prevent opening and that binding of antagonist and agonist are mutually exclusive.

The activation model fitted here differs from the mechanisms that we found were best at describing steady-state glycine receptor single-channel activity (flip (Burzomato et al. 2004) and a modified Jones & Westbrook-type mechanism (Jones & Westbrook, 1995). No mechanistic significance should be attached to that – the poor resolution of the macroscopic technique means that it is not realistic to fit to these data mechanisms that include detailed description of partially liganded states. In addition to that, any model that aims to describe responses to the concentration jumps performed here must include desensitized states that are explicitly excluded from single-channel analysis because of the division of the data into clusters. We nevertheless found that our estimates of the binding rates for SR-95531 were unaffected by changes in the details of the mechanism, such as the values to which glycine gating rates were constrained.

The use of the competitive antagonist method on an isolated glycinergic synaptic input will provide a powerful tool to assess the concentration of glycine in the cleft following spike-induced release and could clarify one of the main presynaptic determinants of synaptic strength.