Effects of muscle conditioning on position sense at the human forearm during loading or fatigue of elbow flexors and the role of the sense of effort

Abstract

In a forearm position-matching task in the horizontal plane, when one (reference) arm is conditioned by contraction and length changes, subjects make systematic errors in the placement of their other, indicator arm. Here we describe experiments that demonstrate the importance not just of conditioning the reference arm, but of the indicator arm as well. Total errors from muscle conditioning represented up to a quarter of the angular range available to subjects. The sizes of the observed effects have led us to repeat other, previously reported experiments. In a matching task in the vertical plane, when muscles of both arms were conditioned identically, if the subject supported their arms themselves, or when the arms were loaded by the addition of weights, the loading did not introduce new position errors. To test the effect of exercise, subjects' elbow flexors were exercised eccentrically or concentrically by asking them to lower or raise a set of weights using forearm muscles. The exercise produced 25–30% decreases in maximum voluntary contraction strength of elbow flexors and this led to significant position-matching errors. The directions and magnitudes of the errors were similar after the two forms of exercise and indicated that subjects perceived their exercised muscles to be longer than they actually were. To conclude, the new data from loading the arm are not consistent with the idea that the sense of effort accompanying support of a load, provides positional information in any simple way. Our current working hypothesis is that when muscles are active, position-sense involves operation of a forward internal model. Loading the arm produces predictable changes in motor output and afferent feedback whereas changes after exercise are unpredictable. This difference leads to exercise-dependent errors.

Position sense has often been studied, particularly at the forearm (Goodwin et al. 1972; Capaday & Cooke, 1981; Sittig et al. 1985; Lackner and DiZio, 1992). Our own experiments have similarly focused on the forearm. For a review see Proske (2006). Most experiments concerned with position sense at the forearm measure errors in a position-matching task for movements at the elbow joint, in the vertical plane. The blindfolded subject is asked to match with their indicator forearm the perceived position of the reference arm whose position has been set by the experimenter.

In these experiments, the subject is typically sitting at a table with both forearms strapped to lightweight splints. The splints are hinged at a point coaxial with the elbow joint and potentiometers attached to the hinges provide a continuous signal of elbow angle. Traditionally, a matching trial begins with both arms lying on the table. It means that elbow flexors of both arms are in an extended position before the trial. The experimenter then places the reference arm at the test angle, for example 45 deg to the horizontal, asks the blindfolded subject to support the arm in that position and the subject brings up their indicator arm to make a match. There are two important considerations when the experiment is done in this way, considerations that have not always been taken into account. Firstly, during the match the subject is holding their arms, unsupported, so that there is necessarily some activity in elbow muscles, sufficient to support the weight of the arms against gravity. Secondly, the arms are both brought to their test position from a previously extended position. It means that sensitivity of muscle spindles of elbow flexors of both arms is determined by this position before each match.

It is currently thought that an important source of positional information comes from the discharge of muscle spindles (Goodwin et al. 1972). Supporting evidence is provided by muscle conditioning-dependent errors in position sense (Gregory et al. 1988). These errors are thought to be due to muscle thixotropy. We have been aware that the thixotropic property of skeletal muscle means that its passive mechanical state depends on the recent history of contraction and length changes (Proske et al. 1993). Furthermore, because the intrafusal fibres of spindles are thixotropic themselves, this can lead to errors in position-sense depending on how the muscle was conditioned beforehand (Gregory et al. 1988; Winter et al. 2005). If the forearm position-matching experiment is carried out in the traditional way, without systematic conditioning of arm muscles, and starting with the arms lying extended on the table, matching errors are often seen biased in the direction of extension, relative to the position of the reference arm (Goodwin et al. 1972). A possible reason is that slack develops in the intrafusal fibres of elbow flexors of the indicator arm, as it is moved to make a match. Therefore its spindles are not under the same amount of stretch as in the reference arm. This is expressed by the indicator arm adopting a more extended position relative to the reference arm, in order to stretch its elbow flexors and raise spindle firing rates to levels comparable to those in the reference flexors.

When the reference elbow flexors are systematically conditioned (i.e contracting elbow muscles with the arm held flexed or extended; Ansems et al. 2006), for position-matching in the vertical plane, conditioning-dependent errors are largest when the arm is held by the experimenter (i.e. when arm muscles remain relaxed during the match). Matching accuracy improves and is less dependent on conditioning when subjects support the arms themselves (Paillard & Brouchon, 1974; Winter et al. 2005). The reason for the improvement is that the motor activity required to support the weight of the arm will tend to remove any conditioning-dependent slack in intrafusal fibres, sensitizing spindles and leading to more reproducible matches. However, the muscle force required to support the weight of the arm depends on the torque generated at the test angle and at 45 deg this is likely to be less than 5% of the maximum voluntary contraction (MVC) strength (Winter et al. 2005). Given that there is evidence of persisting conditioning effects up to 25% MVC (Ansems et al. 2006), the differences in errors following conditioning are likely to be only partially removed.

In our previous matching experiments we always took care to systematically condition the reference arm. We did not pay much attention to the indicator arm for two reasons. Firstly, during the match subjects were asked to move their indicator arm themselves to make the match. It was assumed that the voluntary movement up to the test angle acted as a conditioning stimulus in its own right. Secondly, it was tacitly assumed that the position adopted by the indicator arm during the match was largely determined by signals arising from the reference arm, not the indicator arm.

Here we have examined the effects of conditioning the indicator arm in more detail by measuring position sense in the horizontal plane, where the force of gravity has little effect on the maintenance of arm position (Ansems et al. 2006). Restricting conditioning of elbow muscles to the reference arm had the expected effect, producing errors of about 7 deg. This compares with mean errors of 4.3 deg for matching in the vertical plane (Winter et al. 2005). When we conditioned not only the reference arm but the indicator arm too, the sizes of the observed errors caused us to reassess a number of our earlier observations. We have therefore repeated the experiments of loading the arm (Winter et al. 2005), and of exercising arm muscles by means of concentric exercise (Allen & Proske, 2006), eccentric exercise (Walsh et al. 2006) or both (Walsh et al. 2004), making sure that both arms were conditioned identically, and so eliminating any effects of conditioning on the distribution of the errors.

Methods

A total of three experiments were carried out involving the testing of 40 subjects (22 females, 18 males). Position sense in the horizontal plane was tested in eight subjects. The experiment on loading the arm was done with 13 subjects, one of whom was excluded as their matching errors exceeded the minimum required for matching reliability (s.d. < 5 deg).

In the experiment on eccentric exercise, 11 subjects were used. Of these, two were excluded because they did not experience any delayed muscle soreness and had < 15% decrease in force. It turned out that these were individuals who were undergoing regular training. The concentrically exercised group included eight subjects.

All subjects gave their written informed consent before undertaking the experiments which were approved by the Monash University Committee for Human Experimentation, and ethical aspects conformed to the Declaration of Helsinki.

For each subject, a series of control trials was carried out. Subjects were asked to participate further only if they achieved acceptable levels of reliability in the matching performance which was set at a s.d. of matching errors of less than 5 deg.

Experiment 1: conditioning the indicator arm in the horizontal plane

The details of the set-up for this experiment have been provided previously (see Ansems et al. 2006). In brief, blindfolded subjects sat at a table with each forearm and upper arm supported horizontally by a cradle hinged at a point coaxial with the elbow joint. Position of the arms was indicated by a pointer below each hand. The arrangement allowed determination of arm position with a resolution of 0.5 deg. The height of the apparatus was adjusted for each subject so that the upper arm was at approximately 45 deg to the horizontal throughout the experiment. The horizontal movement of the unloaded arm was almost frictionless and required little or no effort to maintain a given elbow angle. Angles were reported as the included angle between forearm and upper arm. When the forearm was extended, so that its position was at right angles to the trunk, this corresponded to 130 deg included elbow angle. Stops were attached to the apparatus to prevent subjects from moving their arms further into extension. They could move their forearm into flexion to an elbow angle of 50 deg, giving a total movement range of 80 deg. The test angle chosen was 85 deg. In this position passive resistance from flexors and extensors was minimal. The precise value of the test angle depended on how accurately the reference arm had been placed by the experimenter. In practice, angles in the range 80–90 deg were achieved.

The experiment tested four different conditions. In the first, the subject began with both elbows extended and they were asked to push them into extension, generating a contraction of about 30% of maximum in their elbow extensors. This was termed extension conditioning for both arms. Second, the experimenter moved the reference arm to the test angle and asked the subject to maintain that position while they moved the other (indicator) arm to match the angle. Position errors were calculated by taking the difference between reference angle and indicator angle. The convention used was that a positive error meant that the matching arm had adopted a more extended position relative to the reference arm. Subjects carried out a series of five trials with both arms extension conditioned and then another five after both arms had been flexion conditioned. Here the arms were brought to 50 deg and elbow flexors were contracted by asking the subject to flex their arms. Once they had relaxed, the reference arm was brought to its test angle by the experimenter and the subject matched it with the indicator arm.

In the third task, the reference arm was extension conditioned and the indicator arm flexion conditioned, while in the fourth the reference arm was flexion conditioned and the indicator arm extension conditioned. The order of the four sets of trials was randomised between subjects. After each set of five trials, subjects were given a few minutes rest with the blindfold removed.

Experiment 2: matching in the vertical plane with and without a load

In this experiment we used a different piece of apparatus, similar to that previously described (Allen & Proske, 2006). Subjects had both forearms strapped to lightweight paddles that moved in the vertical plane. The paddles were hinged at a point coaxial with the elbow joint. The upper arm, again kept at approximately 45 deg to the vertical, rested on horizontal padded supports so that the included elbow angle was 90 deg when the paddles were placed vertically. Potentiometers attached to the paddle hinges provided an analog signal proportional to elbow joint angle. At the beginning of each experimental series, potentiometer output on the two sides was carefully checked by simultaneously displaying the two signals while the two paddles were clamped together by means of a wooden strut. Output on the two sides was compared when the strut was moved through a range of angles.

In these experiments we chose a single test angle in the mid-range of elbow movement at 45 deg from horizontal (135 deg included angle). When the arm was horizontal, forearm angle was 0 deg; when it was vertical, forearm angle was 90 deg. As before, the actual test angle used depended on accuracy of placement by the experimenter and test angles in the range of 40–50 deg (130–140 deg included angle) were typically achieved. Subjects were asked to match the test position of the reference arm by moving their indicator arm.

In this experiment we wanted to avoid the effects on position sense of having the two arms conditioned differently. Therefore both arms were either flexion conditioned or extension conditioned. For flexion conditioning, subjects were asked to contract elbow flexors by flexing their arms at 90 deg. After they had relaxed, the experimenter moved the reference arm to the test angle and the subject moved their indicator arm to make a match. Therefore both arms were moved from an initially flexed position.

For extension conditioning, subjects placed their arms on the table in front of them and they were asked to push the arms downwards onto the table. After they had relaxed, the experimenter moved the reference arm to the test angle and the subject made a match. So this time both arms moved from an initially extended position. Five trials were carried out for each condition, separated by a rest period. Position errors were calculated as before, as the difference between reference and indicator angles, where a positive value was assigned to the error when the indicator lay in the direction of extension relative to the reference.

This experiment was carried out under a total of four different loading conditions of the reference arm. In the first, the reference arm was supported. Subjects were instructed to fully relax their arms after the flexion or extension conditioning. The relaxed reference arm was moved to the test angle where it was placed on a support. The experimenter then moved the subject's indicator arm, asking the subject to remain relaxed during the movement, and to indicate when an accurate match had been achieved.

To ensure that subjects remained relaxed during placement of the arms, they were provided with feedback of electromyographic (EMG) activity recorded from the surface of biceps and triceps. This was done using Ag–AgCl electrodes with an adhesive base and solid gel contact points (3M Health Care, London, Ontario, Canada).

In the second condition, subjects supported their arms themselves (both the reference arm after it had been placed at the test angle and the indicator arm while it was making a match). In the third condition, the reference arm had a load placed on the arm, representing approximately 10% of the MVC of elbow flexors and in the fourth the load was increased to 25% MVC.

For the loading trials, MVC was measured with the paddles locked in position at the test angle of 45 deg. This was used to calculate the 10% and 25% loads which were bolted to the top of the paddle. For the exercise experiment, MVC was measured by locking the paddles in the vertical position (90 deg elbow angle). During all MVC measurements, subjects were asked to maximally contract their elbow flexors while receiving verbal encouragement and visual feedback during the contraction. They were shown on the computer screen the force levels they had achieved during a contraction and were encouraged to exceed them during the next attempt. Three successive measurements of MVC were made and the highest value was used to calculate the loads as a percentage of maximum.

Experiment 3: matching in the vertical plane after exercise

This experiment was carried out on the same apparatus as the previous experiment. The measurements were made before and after exercise of the non-dominant arm. Position matching was done after both arms had been flexion conditioned and subjects supported their arms themselves. The reference arm was moved to the test angle (45 deg) by the experimenter and subjects matched its position by placement of their other arm.

To submit elbow flexors to a period of exercise, subjects were sat at a table, with their elbows supported. The arm to be exercised grasped a handle that was attached by a rope and pulley to weights on the floor on the other side of the table. A second pulley allowed the weights to be raised or lowered by the experimenter, so that the subject moved the weights in one direction only.

Eccentric exercise

For the eccentric exercise, subjects were required to slowly extend their arm (from ∼70–170 deg included elbow angle) while lowering the weights to the floor. The weights were then lifted up again by the experimenter before the subject lowered them a second time. The number of weights was set to correspond to approximately 50% MVC of elbow flexors. Subjects required an average of 211 ± 44 contractions to achieve a large enough drop in MVC (31% ± 3.4%). All but two of the subjects who underwent eccentric exercise reported muscle soreness in their elbow flexors the day after the exercise. The two who did not become sore also had only small decreases in force and their data were not included in the analysis.

Concentric exercise

For the concentric exercise, the same apparatus was used but subjects were required to lift the weights by flexing their arms (from ∼170–70 deg included elbow angle). The number of repetitions that subjects underwent depended on their fitness. Subjects required 378 ± 42 contractions to achieve a 25.4 ± 3.9% fall in MVC. For the concentric exercise, the load was lightened as fatigue progressed. This made it possible to achieve fatigue that persisted for long enough during the position-matching trials. MVC force was measured before exercise, immediately after exercise, and after position-matching trials were complete (∼20 min post exercise) to monitor recovery from fatigue.

Statistics

Position errors were calculated as follows: angle (reference arm) − angle (indicator arm).

For data in both the horizontal and vertical position-matching experiments, potentiometer output was acquired at 40 Hz using a MacLab/4s running Chart software (ADInstruments, Castle Hill, NSW, Australia) on a Macintosh computer. Resolution of elbow angles was ≤ 0.5 deg. Data were analysed using the software Igor Pro v.4 (Wavemetrics, Lake Oswego, OR, USA). Statistical analysis used the package SPSS version 12.01 (Systat Software Inc., Point Richmond, CA, USA).

Analysis used one-way and two-way ANOVAs with repeated measures to test for differences in position errors between the paired conditions of flexion conditioning and extension conditioning for each arm for matches in the horizontal plane, and for exercised versus unexercised, or weighted versus unweighted arms for the matches in the vertical plane. Where significance was found, a least squares difference (LSD) post hoc analysis tested for differences between groups. Significance was recorded at a P value < 0.05. Values are given as means ± s.e.m.)

Results

Experiment 1: conditioning the indicator arm in the horizontal plane

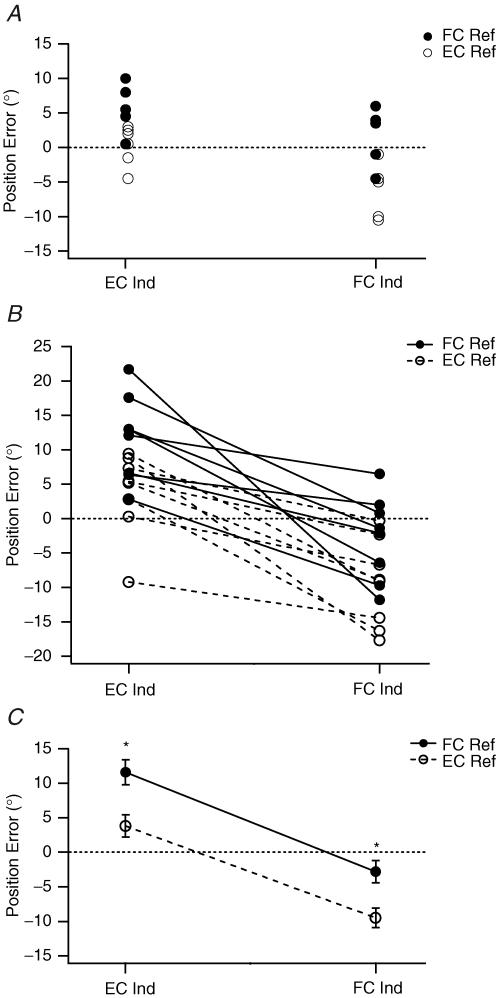
Data for one subject are shown in Fig. 1A. The reference arm was conditioned by a contraction while in either a flexed or extended position and then placed at the test angle by the experimenter. In the first set of measurements its perceived position was indicated by the other (indicator) arm after it had undergone a conditioning contraction while held extended. This was similar to the way we had carried out the experiment in the past. Under these conditions, all matching errors lay in the direction of extension relative to the target angle (85 deg). After flexion conditioning of the reference arm the mean position adopted by the indicator arm in this subject was 6.4 ± 1.5 deg beyond the target; that is, in the direction of extension relative to the target (positive errors). When the reference was extension conditioned, mean errors lay 0.3 ± 1.2 deg beyond the target. So for this subject, under these conditions, the flexion–extension conditioning difference was 6.1 deg. This result was consistent with our previous observations (Ansems et al. 2006).

Figure 1. Position-matching errors in the horizontal plane.

A, individual values for matching errors for a single subject. The subject's reference arm was placed at 85 deg, included angle, and the subject was asked to match its position with the other, indicator arm. Left-hand values, where the indicator had been extension conditioned (EC Ind). Right-hand values, where the indicator had been flexion conditioned (FC Ind). •, reference arm flexion conditioned (FC Ref); ○, reference arm extension conditioned (EC Ref). Errors were calculated as the difference in matching position between reference and indicator arms. Errors were scored as positive when position of the indicator arm was more extended than the reference arm and negative when the indicator arm was more flexed than the reference arm. Dotted line, zero error. B, mean position errors for each of eight subjects for the four conditions: FC Ref, EC Ref, EC Ind and FC Ind. Symbols as in A. To show the trends in the data, a solid line has been drawn between the FC Ref values and a dashed line joining EC Ref values. Dotted line, zero error. C, pooled means (± s.e.m) for the eight subjects. *Significant differences.

The experiment was repeated but this time the indicator arm was always flexion conditioned; that is, it was contracted while held in the flexed position. The subject then moved the indicator arm in the direction of extension to make the match. This time the matching errors lay in the direction of flexion relative to the target (Fig. 1A). For flexion conditioning of the reference arm the mean matching angle was 2.0 ± 1.6 deg, whereas for extension conditioning it was −6.2 ± 1.8 deg. A negative value indicates errors in the direction of flexion relative to the target. So for this subject the flexion–extension difference had increased to 8.2 deg and errors had shifted in the direction of flexion by about 5 deg.

The experiment was repeated with a total of eight subjects. Mean position errors for each subject are shown (Fig. 1B). The group means are given in Fig. 1C. The data showed that when the subject's reference arm had been flexion conditioned and the indicator extension conditioned, mean matching errors lay in the direction of extension by 11.6 ± 1.8 deg. When both arms were extension conditioned, errors still lay in the direction of extension but only by 3.8 ± 1.6 deg. When both arms were flexion conditioned, mean errors lay on the flexion side of the target position by 2.8 ± 1.6 deg. When the reference arm was extension conditioned and the indicator flexion conditioned, errors lay further in the direction of flexion (9.5 ± 1.4 deg). Statistical analysis using a repeated measures ANOVA showed that for the four conditions the errors were significantly different (F3,7=24.06, P < 0.05). An LSD post hoc test showed that errors for all four conditions were significantly different from one another (Fig. 1C).

The above demonstrated that errors from conditioning the indicator arm were just as large as from conditioning the reference arm. This emphasized the importance of conditioning both arms, and also raised the question of whether some of the trends seen in previously reported experiments were not entirely a result of the state of the reference arm but could be attributed, in part, to the indicator arm. It was therefore necessary to repeat some of the experiments, taking care each time to condition both arms identically. Only in that way could conditioning-dependent errors be eliminated from the experiment.

Experiment 2: matching in the vertical plane with and without a load

Here we have reassessed the effect of loading the arm (Winter et al. 2005) after identical conditioning of both arms. A total of 13 subjects undertook the experiment. The exclusion criterion of an unloaded matching consistency with an s.d. of < 5 deg excluded one subject, leaving data from 12 subjects.

Before each trial, subjects' arms were identically conditioned with a contraction in the direction of flexion while both arms were held flexed, or a contraction in the direction of extension while both were held extended. The experimenter then moved the reference arm to the test angle (45 deg) and the subject brought up their other arm to make a match. In the first series both arms were held supported during the match. In the second, both arms were held by the subject themselves. In the third series, the unsupported arm was loaded with a weight representing 10% MVC of elbow flexors and in the fourth the weight was increased to 25% MVC.

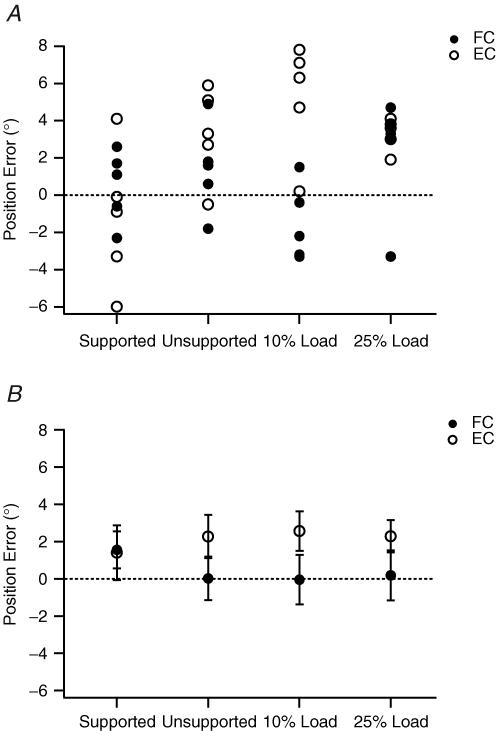
Example errors from one subject matching forearm position in the vertical plane are shown in Fig. 2A. The most obvious trend was that the distributions of errors following the two forms of conditioning were no longer very different. Values lay over the top of one another and covered similar ranges. In addition, there was no obvious change in the distribution of the errors when the arm was loaded.

Figure 2. Position-matching errors in the vertical plane from loading the arm.

A, individual values for one subject after flexion conditioning of both arms (FC, •) and after extension conditioning of both arms (EC, ○). Matching was carried out under four conditions: (1) with the reference arm supported so that arm muscles remained relaxed; (2) the subject supported the reference arm themselves (unsupported); (3) a weight representing 10% maximum voluntary contraction (MVC) force for elbow flexors was added to the reference arm when it had been placed at the test angle; and (4) the weight was increased to 25% MVC force. Dotted line, zero error. Errors in the direction of extension are positive, and in the direction of flexion are negative. B, Pooled data from 12 subjects. Errors shown as means (± s.e.m). Symbols and their display as in A. Dotted line indicates zero error.

The pooled data for the 12 subjects showed similar trends and are illustrated in Fig. 2B. The most important feature was that with the reference arm unsupported, or unsupported and loaded the distribution of position errors did not change. In addition, as the arm was loaded, there was no evidence of subjects becoming more erratic in their matching ability. For the four conditions, supported arm, subject-held arm, 10% MVC load and 25% MVC load, errors after double flexion conditioning were 1.4 ± 1.5, 0.0 ± 1.2, 0.0 ± 1.3 and 0.2 ± 1.3 deg, respectively. After double extension, conditioning errors lay slightly, but not significantly, in the direction of extension at 1.6 ± 1.0, 2.3 ± 1.2, 2.6 ± 1.1 and 2.3 ± 0.9 deg, respectively. Statistical analysis showed that there were no significant differences in the distributions of the errors.

Experiment 3: matching in the vertical plane after exercise

In view of the observations made in Experiment 1, we wanted to reassess the effect of exercise by studying position sense after both arms had been identically conditioned. In this experiment, for the sake of simplicity, trends were studied only after double flexion conditioning and subjects held their arms themselves unsupported.

Eccentric exercise

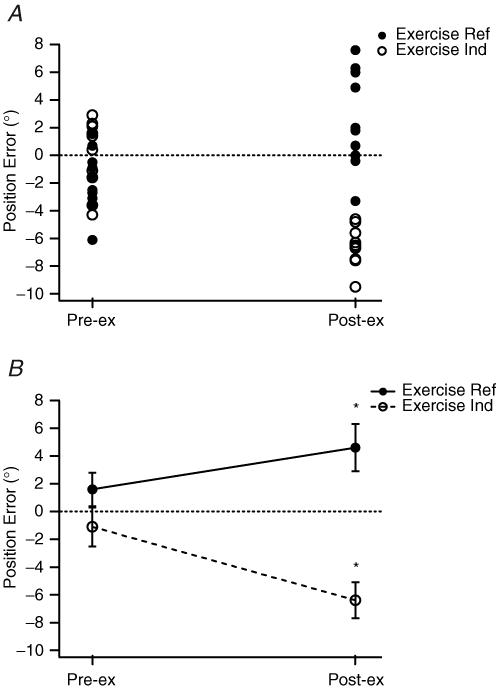
The experiment was carried out with a total of 11 subjects. Of these, two were excluded because their decreases in force after exercise were less than 15% and they reported no delayed muscle soreness. That left data from nine subjects. The exercise led to a post-exercise fall in force in elbow flexors of 31.0 ± 3.4%. Position errors for one subject are shown in Fig. 3A.

Figure 3. Position-matching error in the vertical plane after eccentric exercise.

A, data from a single subject. For all matching trials both arms were flexion conditioned beforehand. The experimenter placed the reference arm at the test angle where the subject held it, unsupported and they moved their unsupported indicator arm to match its position. •, exercised arm as the reference; ○, control arm as the reference. Values on the left, before exercise (Pre-ex); values on the right, after exercise (Post-ex). Dotted line indicates zero error. B, pooled data from nine subjects. Means (± s.e.m) for values before and after exercise. To indicate the trends in the data, values before and after exercise have been joined by lines: solid line when the arm to be exercised acted as the reference, and dashed line, when it acted as the indicator. Dotted line, zero error. *Significant differences, before and after exercise.

Mean control errors with the right arm as the reference were close to zero (0.0 ± 0.8 deg). When the left arm was the reference, mean values were −1.0 ± 0.7 deg. After the exercise, errors lay systematically further in the direction of extension (2.6 ± 1.1 deg) when the exercised arm acted as the reference. When the exercised arm acted as the indicator, errors lay in the direction of flexion (−6.6 ± 0.5 deg).

The pooled data for the nine subjects is shown in Fig. 3B. Control errors were 1.6 ± 1.2 deg when the right arm was the reference compared with −1.1 ± 1.4 deg when the left arm was the reference. After the exercise, with the exercised arm as the reference, errors lay 4.6 ± 1.7 deg in the direction of extension. The opposite trend was apparent when the exercised arm was the indicator; errors lay significantly in the direction of flexion (−6.4 ± 1.3 deg). That is, the subject perceived their exercised arm to be more extended than it really was. Statistical analysis showed that the effect of exercise on the distribution of position errors was significant (P < 0.05).

Eccentric exercise is different from other forms of exercise in that fatigue from the exercise is accompanied by some muscle damage. It raised the possibility that position errors observed after such exercise might be attributable to the damage. It was therefore necessary, by way of a control, to fatigue the muscle without producing any damage and see whether this had any effect on position sense too. To do this we used concentric exercise.

Concentric exercise

It is known that concentric exercise is not typically accompanied by evidence of damage (Newham et al. 1983a,b). The exercise was accompanied by a 25.4 ± 3.9% MVC force decrease in elbow flexors. Because recovery of force after concentric exercise is quite rapid, some recovery took place during the position sense measurements, post exercise. The quoted percentage decreases in force were measured immediately after the exercise. There was a 5–10% recovery during the measurements.

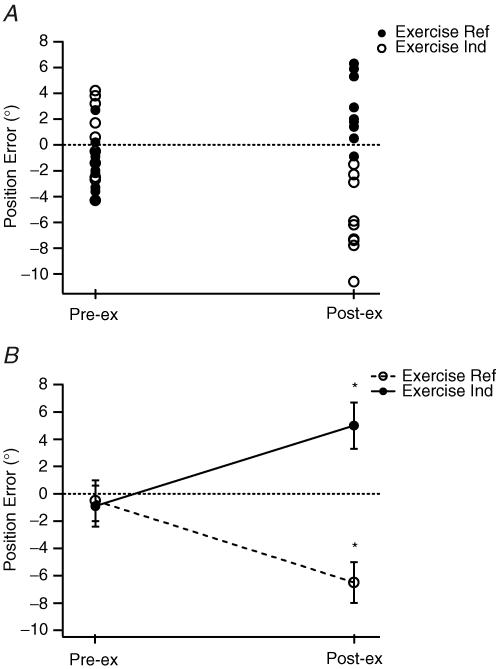
The experiment was carried out with a total of eight subjects. Data from a single subject are shown in Fig. 4A. The trends in the data were essentially comparable to those seen after eccentric exercise. Control errors with the right arm as the reference were 0.2 ± 0.9 deg. Errors with the left arm as the reference were −1.5 ± 0.6 deg. After exercise, with the exercised arm as the reference, mean errors lay further in the direction of extension (2.7 ± 0.8 deg), and with the exercised arm as the indicator, they lay in the direction of flexion (−5.8 ± 0.9 deg).

Figure 4. Position-matching errors in the vertical plane after concentric exercise.

A, data from a single subject. Matching conditions as in Fig. 3. •, exercised arm as the reference; ○, unexercised arm as the reference. Values on the left before exercise (Pre-ex); values on the right after the exercise (Post-ex). B, pooled data from eight subjects. Values shown as means (± s.e.m) before and after exercise. These have been joined by a solid line for values where the arm to be exercised was the reference and a dashed line where it was the indicator. *Significant differences, before and after exercise.

The pooled data for the eight subjects are shown in Fig. 4B. Mean control errors for left and right arms were −0.5 ± 1.5 and −0.9 ± 1.5 deg. After exercise, with the exercised arm as the reference, errors were in the direction of extension (5.0 ± 1.7 deg), and they were in the direction of flexion (−6.5 ± 1.5 deg) when the exercised arm was the indicator. Statistical analysis showed that the exercise had a significant effect on the distribution of the errors (P < 0.05).

Discussion

Experiment 1: conditioning the indicator arm in the horizontal plane

The main objective of this experiment was to demonstrate in a forearm position-matching task that an important consideration was the state of conditioning, not just of the reference arm, but of the indicator arm too. In the event, we were not only able to document effects of conditioning the indicator, but we obtained some insight into the central interpretation of the peripheral position signals.

In our original experiments describing the effects of muscle conditioning on errors in position sense (Gregory et al. 1988), we proposed that contracting elbow flexors while the arm was flexed and contracting extensors while the arm was extended provided a means of maximizing the difference in spindle afferent output from the two muscles. We proposed that this difference led to position-matching errors. This interpretation was backed up by some direct recordings of spindle afferents in the soleus muscle of the anaesthetized cat after conditioning manoeuvres comparable to those used in human experiments.

The underlying idea is that, as stretch receptors, muscle spindles increase their discharge rate in direct proportion to the amount of stretch imposed on the muscle. A higher rate is interpreted by the brain as a longer muscle. What we perceive, of course, is not a longer muscle but a more flexed or extended joint. Muscle thixotropy allows spindle discharge rate to be increased or decreased without changing muscle length. It leads the brain to misinterpret the length of the muscle and therefore, in the absence of vision, the subject makes errors in a position-matching task. For position sense at the elbow there is presumably a central map (Sittig et al. 1985) where, based on experience, a given net rate of spindle firing coming from the antagonist pair (Ribot-Ciscar & Roll, 1998) is interpreted as the relative lengths of the pair and therefore the degree of flexion/extension about the elbow joint. When the signal is coming predominantly from elbow flexors the arm is perceived as extended, and when it is coming from extensors it is perceived as flexed.

Some additional information is provided by the experiment where both arms were conditioned identically. It might have been expected that position errors would reduce to zero when both arms were conditioned identically because, according to our hypothesis, under these conditions the spindle signals coming from them would be the same. In the matching experiments in the vertical plane that was indeed the case (Figs 2–4). However for matching in the horizontal plane, after extension conditioning of both arms (i.e. with the extensor signal dominating), the matching error was 3.8 deg in the direction of extension (Fig. 1C). Perhaps the signal coming from the indicator extensors was a little higher than for the reference arm so that the indicator arm adopted a less flexed position, to induce less stretch on the extensors. A possible reason is that the indicator was moved voluntarily by the subject while the reference arm had remained relaxed following its placement by the experimenter. This would allow extensor spindles in the reference arm to show some adaptation of discharge. Similar considerations apply to the mean matching error of 2.8 deg in the direction of flexion after both arms had been flexion conditioned.

Following identical flexion conditioning of the two arms, if then the indicator was switched to extension conditioning, errors moved from −2.8 to +11.6 deg, a total of 14.4 deg. Similarly after identical extension conditioning of the two arms, when the indicator was switched to flexion conditioning, errors moved from +3.8 to −9.5 deg, a total of 13.3 deg. Yet the flexion–extension conditioning difference for the reference alone was 7.8 deg when the indicator was extension conditioned and 6.7 deg when the indicator was flexion conditioned (Fig. 1C). So conditioning-dependent errors attributable to the reference arm alone, were only half as large as errors when the two arms were conditioned in opposite directions.

When conditioning is of flexors in the reference arm, matching errors lie in the direction of extension. Flexion conditioning of the indicator arm, on the other hand, produces errors in the direction of flexion. This is because in attempting to achieve a match the subject is ‘shortening’ their indicator flexors, as a means of reducing the high discharge rates from flexion conditioning and bring them closer to the reference level. Therefore conditioning of the two arms in the same direction produces errors in opposite directions. Conditioning of the arms in opposite directions has an additive effect on matching errors. All of this leads to the conclusion that position errors in each arm produced by muscle conditioning are similar in size. There is no evidence of prioritization of proprioceptive information coming from the reference arm during a position-matching task. Finally, it is worth reflecting on the fact, that in a relaxed arm, muscle conditioning can lead to a total of 21 deg of error, representing 25% of the range available to subjects.

Experiment 2: matching in the vertical plane with and without a load

In this experiment, when the arms were supported and therefore arm muscles were relaxed, errors following the two forms of conditioning were small and nearly identical (Fig. 2B). When the reference arm was loaded, there were almost no errors after flexion conditioning. Errors following extension conditioning lay a little above those following flexion conditioning; that is, in the direction of extension. The probable reason is that because the load was on the reference flexors, following conditioning, these would be expected to lose some of their slack as a result of load bearing. That would lead to a rise in the reference flexor spindle signal and the arm would be perceived as more extended than it had been when it was unloaded. This is similar to the trends observed by Winter et al. (2005). A more important trend apparent when both arms were conditioned identically was that as the reference arm was loaded the distribution of the errors did not change. For all three loads they remained between 0 and 3 deg (Fig. 2B).

This result was different from that reported by Winter et al. (2005) who observed errors lying progressively further in the direction of extension as the arm was loaded. In those experiments only the reference arm had been conditioned and the distribution of the errors may have been a consequence of leaving the indicator arm unconditioned. So the observations were correct but their interpretation was not. This emphasizes the importance of taking muscle conditioning of both arms into account in experiments on position sense. In any case, in the present experiments no such trend was apparent and our finding is consistent with observations on support of a static load during position matching in the horizontal plane (Ansems et al. 2006).

The new result is important in terms of what it implies about the mechanisms underlying position sense during muscle contraction. All of our previous observations and those of others had suggested that when muscles of the arm were relaxed (arm supported), position sense was attributable to the signals from muscle spindles (Gregory et al. 1988; Walsh et al. 2004; Winter et al. 2005) with a subsidiary contribution from skin (Collins et al. 2005) and joints (Ferrell et al. 1987). It is also known that when muscles are voluntarily contracted, both skeletomotor and fusimotor neurones are recruited (co-activation; Vallbo, 1971,1974). In other words, when the arm was loaded the spindle signal would be expected to increase dramatically as spindles became coactivated through the fusimotor system. Yet the position errors and their variability remained essentially unchanged (Fig. 2B). Such a finding will have to be taken into account when considering the role of muscle spindles in position sense during muscle contractions.

The explanation generally accepted to account for the result shown in Fig. 2B is to propose that when a muscle becomes active, spindle signals, which arise as a result of fusimotor activity, are subtracted out centrally (McCloskey, 1981; McCloskey et al. 1983) by means of an efference copy of the motor command (Von Holst and Mittelstaedt, 1950). This implies that the brain acquires a de facto passive spindle signal after processing of the gross spindle activity coming from the muscle. The reason for such a ‘spindle-centric’ view of kinaesthesia relates to the background information available at the time that McCloskey et al. (1983) proposed their model. In an earlier study (McCloskey & Torda, 1975) they concluded ‘that corollary motor discharges are not in themselves sufficient to cause perceived sensations of movement…’ However our own recent observations on this point have led to a rather different view (Gandevia et al. 2006).

Subjects had all large sensory and motor nerve fibres to muscles of the wrist blocked by a cuff on the upper arm. With the hand anaesthetized and paralysed, subjects were asked to try to flex or extend the wrist. They reported that ‘willing’ the wrist to move led to large and sustained sensations of wrist displacement. In other words, under the conditions of nerve block it is possible to unmask a large position signal of central origin. This signal is probably not normally consciously perceived (Fourneret et al. 2002), but presumably we use it routinely during load bearing and it reaches consciousness during nerve block, under conditions resembling phantom limb sensations (Melzack & Bromage, 1973).

Rather than opting for a simple subtraction process, Matthews (1982) suggested that the corollary discharge from a motor command might be used to compute the expected pattern of spindle firing and that could act as a reference for the actual afferent feedback that occurred as a result of the command. Similar comparison mechanisms have been proposed more recently (Wolpert et al. 1995; Kawato, 1999; Cullen, 2004). The proposal is for the operation of a forward internal model. In a forward model, central feedback of the motor command would lead to estimation of an expected sensory consequence, based on past experience. The expected feedback and actual feedback are compared and cancel each other out if they match. Any mismatch is carefully maintained and used to update the body image.

When we match forearm position with both arms supported, the muscles remain relaxed and there is no motor command. Therefore the forward signal is zero and there is no central prediction of anticipated feedback. As soon as some contraction is required to support the arm, a command signal becomes available and that provides access to forward models. When the arm is made heavier by loading it, the command signal increases and that alters the anticipated sensory feedback. In a stereotypic task such as matching limb position, forward models would be expected to be available for different loads and because the target angle has remained the same, expected and achieved feedback would continue to coincide, allowing for accurate matching. The difference between this approach and the McCloskey model (McCloskey et al. 1983) would be that all feedback would be subtracted out, including spindle signals, irrespective of whether they were fusimotor-evoked or not. What would matter was the difference between the expected and observed feedback, not its origin.

Experiment 3: matching in the vertical plane after exercise

Eccentric exercise

Our previous observations on position sense after eccentric exercise showed similar trends in the errors to those reported here (Walsh et al. 2004, 2006). We found that when the reference arm had been exercised, it was perceived at the test angle to be more extended by 3 deg than it really was (Fig. 3). Similarly when the indicator arm was exercised, errors were 5 deg in the direction of flexion. The fact that the errors reversed in direction, depending on whether the reference or indicator had been exercised, we take as evidence in support of a systematic effect of the exercise. On each occasion, the exercised arm was perceived as being more extended than it really was.

Previously we had proposed that the disturbed relationship between force and effort after fatigue from exercise was responsible for the position errors. This was similar to the interpretation of the effect of weighting the arms (Winter et al. 2005). In other words, we had accommodated both the effects of exercise and of increases in load into the one hypothesis. In view of the new result, presented here, that loading the arm did not produce the expected errors (Experiment 2), we had to reconsider our explanation for the effects of exercise. It had been shown previously that after eccentric exercise, but not concentric exercise, the EMG for a given level of force becomes larger during submaximal voluntary contractions (Weerakkody et al. 2003; Prasartwuth et al. 2005). We therefore considered the possibility that the changed EMG–force relationship after eccentric exercise could account for the observed position errors. If so, similar errors might not be expected after concentric exercise.

Concentric exercise

The data in Fig. 4 clearly show a disturbance of position sense after concentric exercise too. It is interesting that the sizes of the errors were larger (6 deg) than in previous reports (2 deg; Allen & Proske, 2006); perhaps this was a consequence of the way we conditioned the muscles. The presence of significant position errors after concentric exercise meant that any hypothesis that was based on central changes related to the damage process associated with eccentric exercise had to be reconsidered. It seemed unlikely that eccentric and concentric exercise had similar effects on position sense, but for different reasons. For concentric exercise, as for eccentric exercise, when the exercised arm was the reference, its position was matched by the indicator arm adopting a position that overshot the target by 6 deg in the direction of extension. Errors were 5 deg in the direction of flexion when the indicator arm had been conditioned.

For both eccentric and concentric exercise, given that before each matching trial muscles of both arms had been conditioned identically, there is no simple way to explain the errors in terms of conditioning-dependent differences in spindle discharge rates.

Subjects maintained the positions of their arms themselves, so with 30% fatigue, muscle activation had to increase significantly to support the weight of the fatigued arm. That appears to be responsible for the errors. Yet when unfatigued arms were made heavier by adding weights to them no such errors were present (Fig. 2B). So we were confronted by the dilemma of trying to explain position errors that arise from increases in the apparent weight of the arm from fatigue but not from loading it. We propose that an explanation for the effects of exercise may again lie in the operation of a forward model. Perceiving a change in the sensory feedback from loading the arm might be a common experience, and therefore be predictable. A similar prediction would not be possible for the effects of exercise. Based on previous experience from supporting a non-fatigued arm, sensory feedback from the fatigued muscles might be larger than anticipated from the motor command. That, in turn, would lead to a discrepancy between actual and predicted feedback and be interpreted by the brain as a longer muscle. Such an interpretation is consistent with the observed pattern of errors.

To conclude, in a forearm position-matching task, the observations of muscle conditioning effects on both reference and indicator arms made it necessary to reassess previously reported conclusions about the role of an effort signal in position sense. To control for any effects from muscle conditioning, both arms were conditioned identically. In a matching task in the vertical plane, this led to abolition of position errors during weighting of the arm. However, errors following fatigue from exercise persisted. These observations could be included under a single hypothesis by postulating that when limb position sense involved muscle contraction, a comparison took place between the anticipated sensory consequence of the act of limb placement, based on experience and the actual feedback, by way of operation of a forward internal model.

If we accept that in a passive muscle kinaesthetic information comes entirely from peripheral sources, then it is important to understand the integration of peripheral and central influences during a graded voluntary contraction. The small amount of information we have regarding this suggests that during submaximal contractions, any change in the passive spindle signal (e.g. from removal of intrafusal slack) expresses itself as a change in position errors. Once all slack has been removed there are no further errors (Ansems et al. 2006). Our current working hypothesis is that, when available, a passive spindle signal is prioritized by the central nervous system. Once all spindles are fusimotor-activated, the full effects of the forward model come into play. These ideas provide the basis for future experiments.